The Effect of Land Cover/Land Use Changes on the Regional Climate of the USA High Plains
Abstract
:1. Introduction
2. Methodology and Analyses
2.1. Study Area and Input Data
2.2. Spatial Gridding
3. ARMA Pre-Filters
3.1. Optimal Fingerprinting Technique and Hypothesis Testing
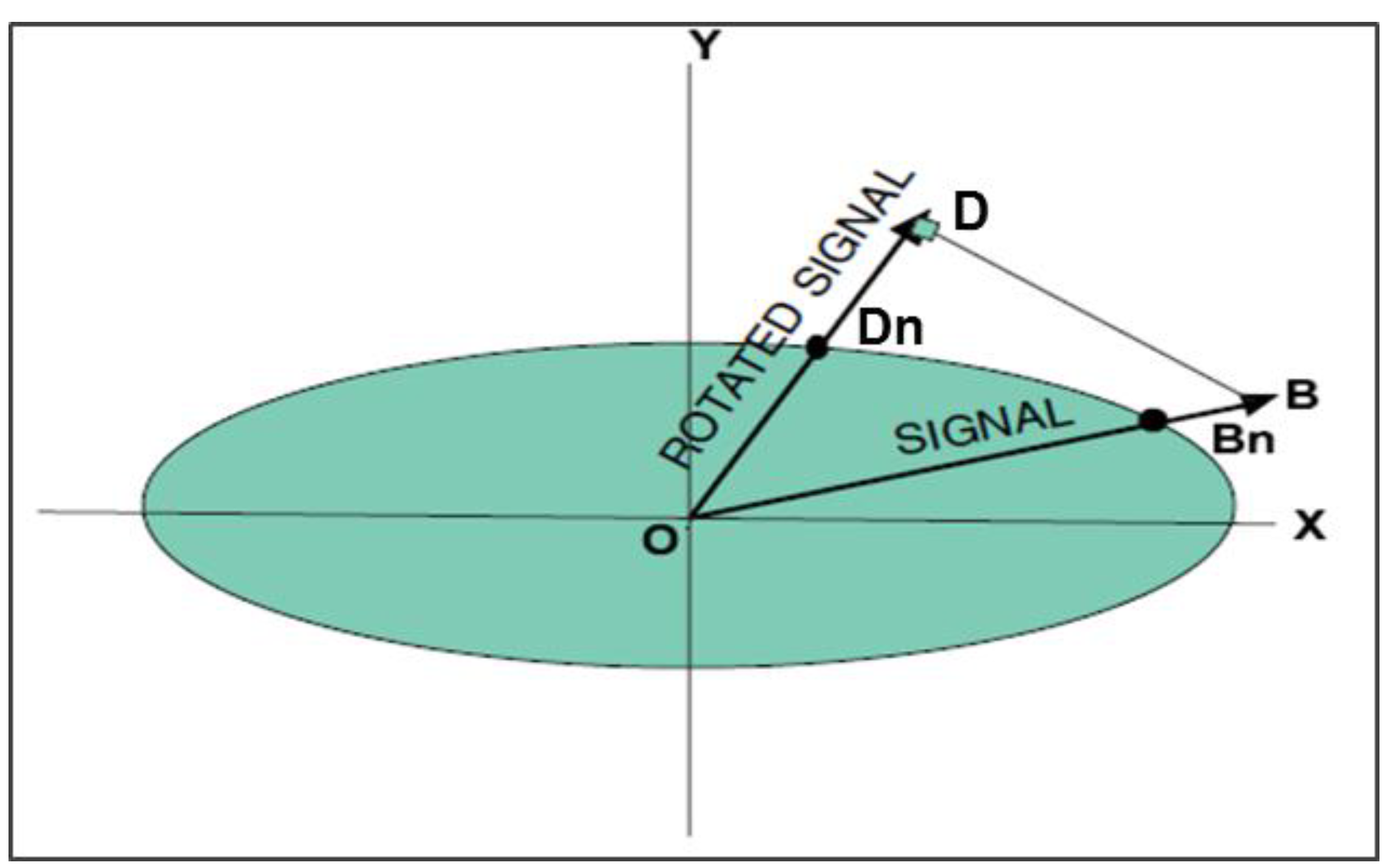
4. Results and Discussion
4.1. Model Fitting on Observed Summer Temperature Data
4.2. Spatial Signatures of Climate Response to LULC Changes Using NDVI Proxy
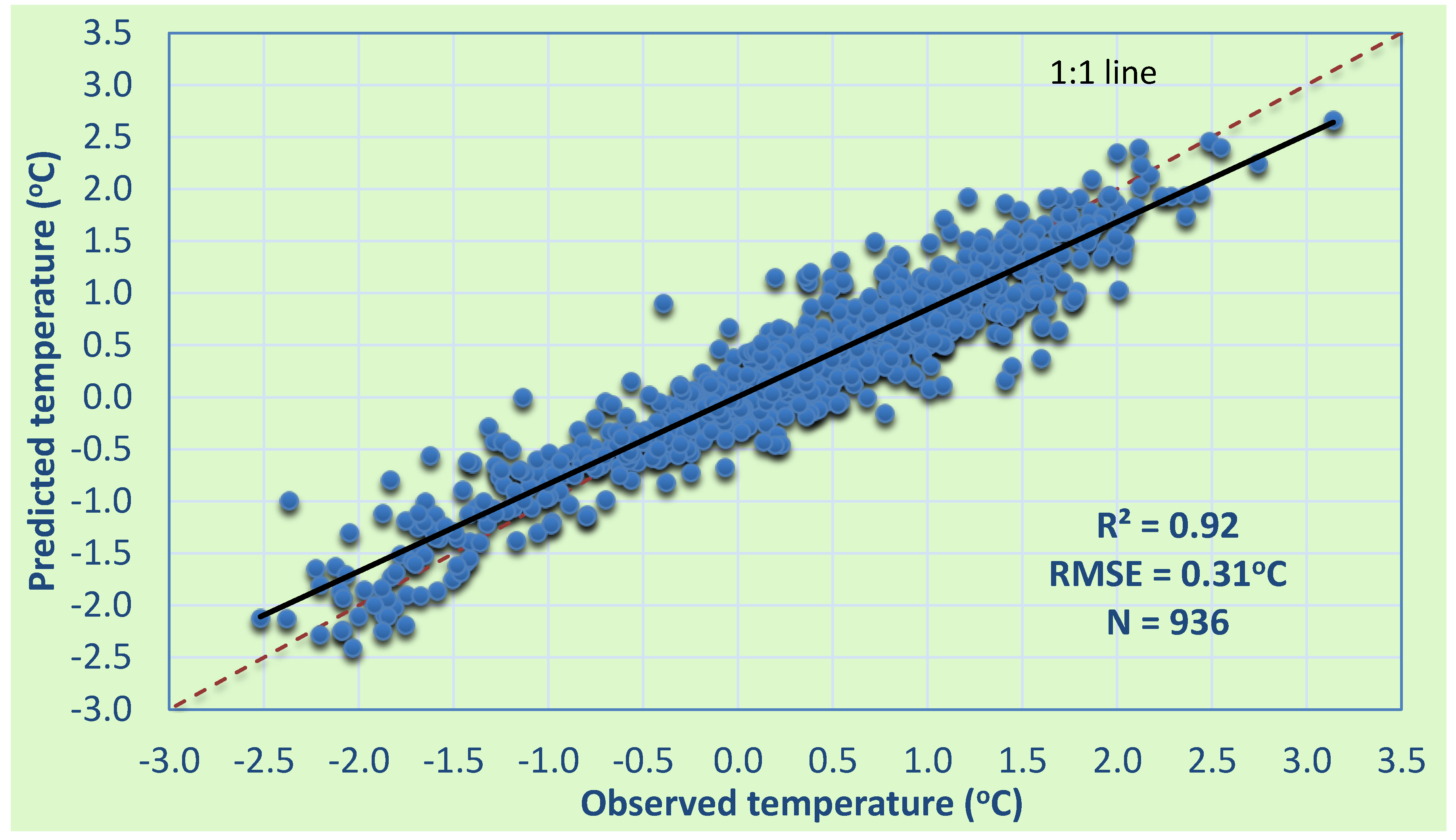
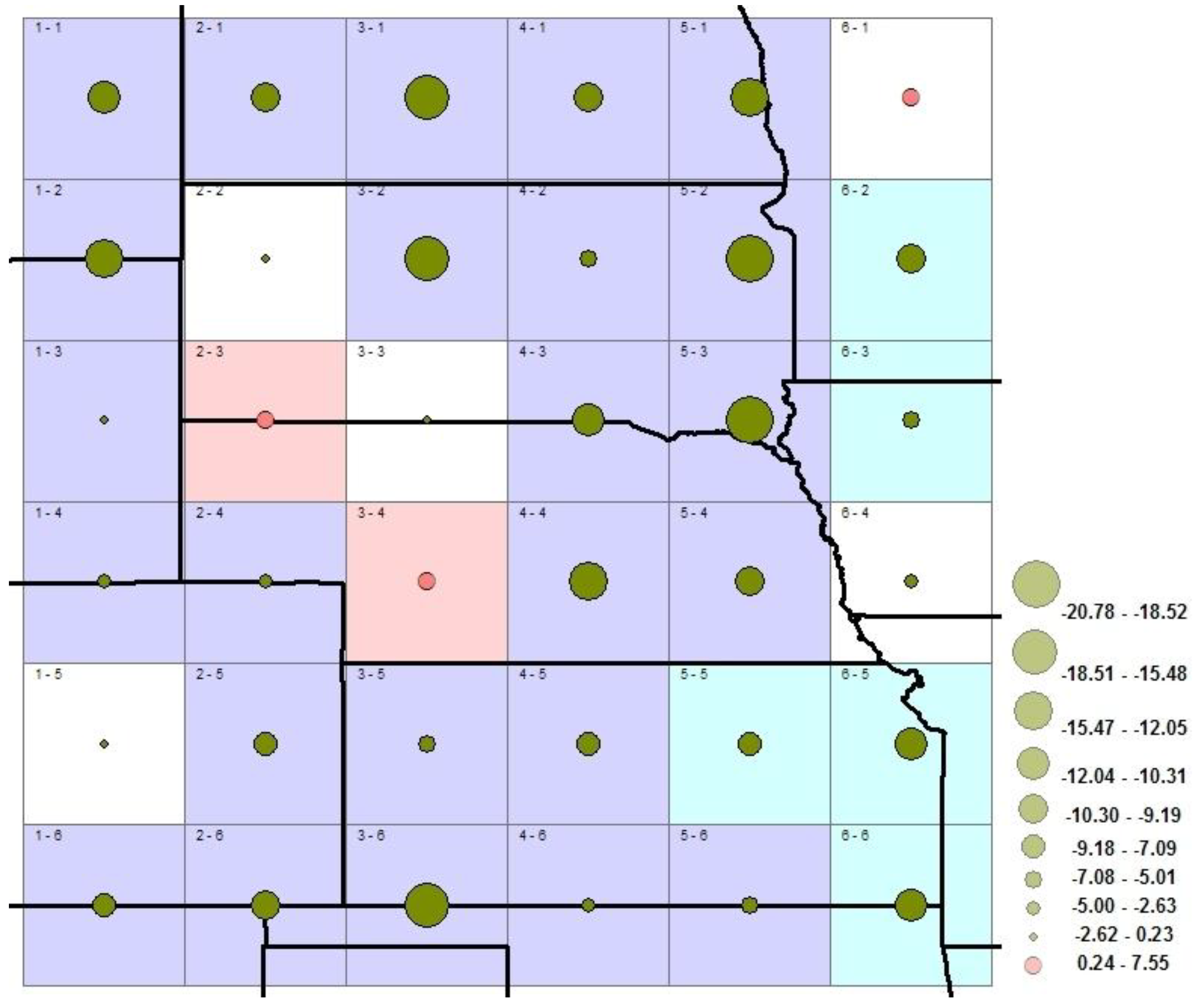
4.3. Spatial Signatures of Climate Response to Greenhouse Gases Using CO2 as Proxy
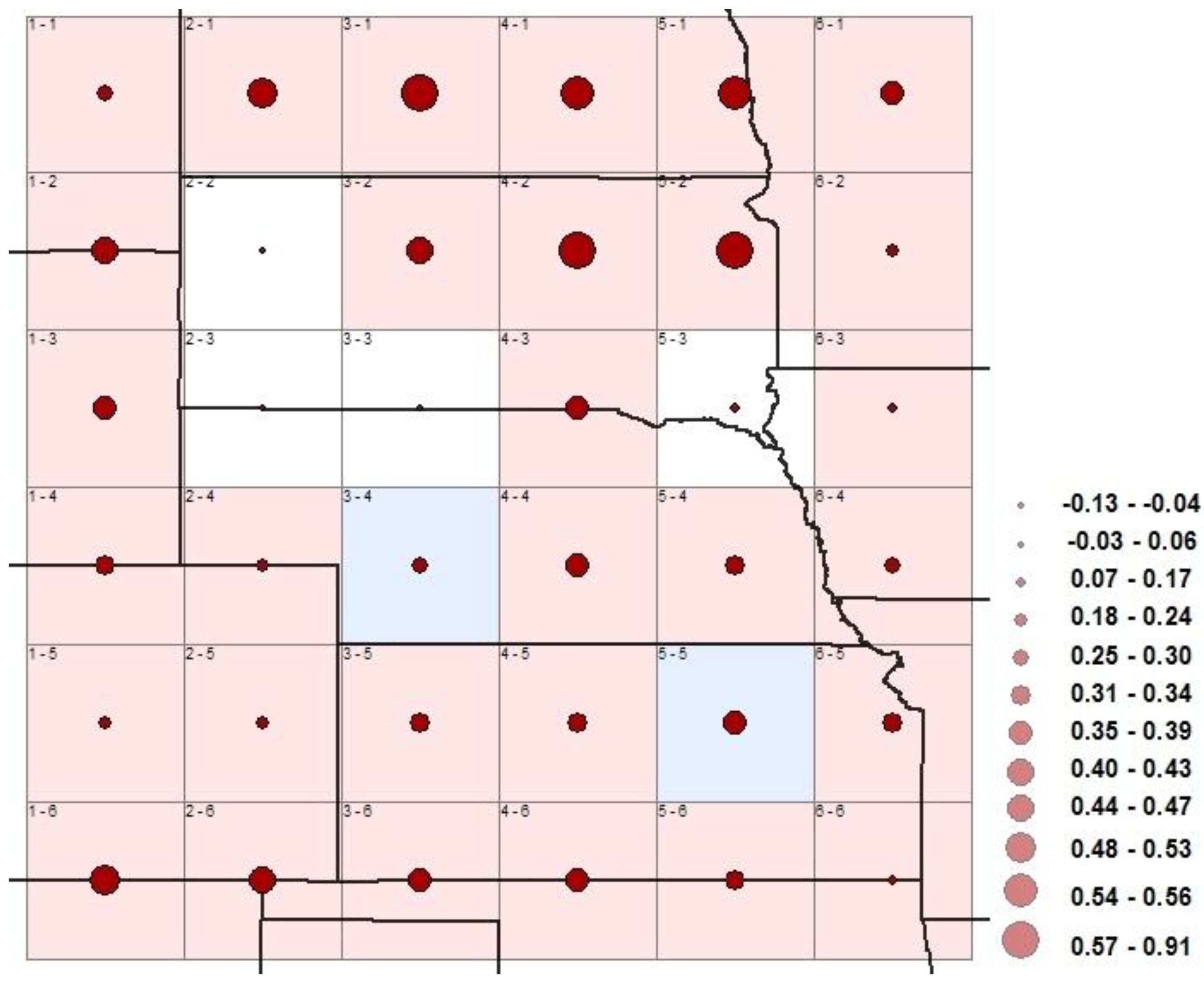
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Mahmood, R.; Pielke, R.A.; Hubbard, G.K.; Niyogi, D.; Bonan, G.; Lawrence, P.; Mcnider, R.; Mcalpine, C.; Etter, A; Gameda, S. Impacts of land use/land cover change on climate and future research priorities. Bull. Amer. Meteorol. Soc. 2010, 91, 37–46. [Google Scholar]
- Chase, T.N.; Pielke, R.A., Sr.; Kittel, T.G.F.; Nemani, R.R.; Running, W.S. Simulated impacts of historical land cover changes on global climate in northern winter. Clim. Dyn. 2000, 16, 93–105. [Google Scholar] [CrossRef]
- Kalnay, E.; Cai, M. Impact of urbanization and land use on climate change. Nature 2003, 423, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Cai, M.; Kalnay, E. Response to the comments by Vose et al. and Trenberth. Nature 2004. [Google Scholar] [CrossRef]
- Trenberth, K.E. Rural land-use change and climate. Nature 2005. [Google Scholar] [CrossRef]
- Vose, R.S.; Karl, T.R.; Easterling, D.R.; Williams, C.N.; Menne, M.J. Impact of land-use change on climate. Nature 2004, 427, 213–214. [Google Scholar] [CrossRef] [PubMed]
- Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Mearns, L.O.; Buja, L.E.; Meehl, G.A.; Washington, W.M. The importance of land-cover change in simulating future climates. Science 2005, 310, 1674–1678. [Google Scholar] [CrossRef] [PubMed]
- Christy, J.R.; Norris, W.B.; Redmond, K.; Gallo, K.P. Methodology and results of calculating central California surface temperature trends: Evidence of human-induced climate change? J. Clim. 2006, 19, 548–563. [Google Scholar]
- Mahmood, R.; Keeling, T.; Hubbard, K.G.; Carlson, C.; Leeper, R. Impacts of irrigation on 20th century temperatures in the Northern Great Plains. Global Planet. Change 2006, 54, 1–18. [Google Scholar] [CrossRef]
- Mahmood, R.; Pielke, R.A., Sr.; Hubbard, K.; Niyogi, D.; Dirmeyer, P.; McAlpine, C.; Carleton, A.; Hale, R.; Gameda, S.; Beltrán-Przekurat, A.; et al. Land cover changes and their biogeophysical effects on climate. Int. J. Climatol. 2014, 34, 929–953. [Google Scholar] [CrossRef]
- Ezber, Y.; Sen, O.L.; Kindap, T.M.; Karaca, M. Climatic effects of urbanization in Istanbul: A statistical and modeling analysis. Int. J. Climatol. 2007, 27, 667–679. [Google Scholar] [CrossRef]
- De Noblet-Ducoudré, N.; Boisier, J.P.; Pitman, A.J.; Bonan, G.B.; Brovkin, V.; Cruz, F.; Delire, C.; Gayler, V.; van den Hurk, B.J.J.M.; Lawrence, P.J.; et al. Determining robust impacts of land-use induced land-cover changes on surface climate over North America and Eurasia: Results from the first of LUCID experiments. J. Clim. 2011, 25, 3261–3281. [Google Scholar] [CrossRef]
- Cotton, W.R.; Pielke, R.A., Sr. Human Impacts on Weather and Climate; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Guillevic, P.C.; Privette, J.L.; Coudert, B.; Palecki, M.A.; Demarty, J.; Ottle, C.; Augustine, J.A. Land Surface Temperature product validation using NOAA’s surface climate observation networks—Scaling methodology for the Visible Infrared Imager Radiometer Suite (VIIRS). Remote Sens. Environ. 2012, 124, 282–298. [Google Scholar] [CrossRef]
- Houghton, J.T.; Ephraums, J.J. Climate Change: The IPCC Scientific Assessment; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Hasselmann, K. On the signal-to-noise problem in atmospheric response studies. In Meteorology of Tropical Oceans; Shawn, D.B., Ed.; Royal Meteorological Society: London, UK, 1979; pp. 251–259. [Google Scholar]
- Barnett, T.P.; Schlesinger, M.E. Detecting changes in global climate induced by greenhouse gases. J. Geophys. Res. 1997, 92, 14772–14780. [Google Scholar] [CrossRef]
- Santer, B.D.; Wigley, T.M.L.; Schlesinger, M.E.; Jones, P.D. Greenhouse-Gas-Induced Climatic Change. In Multi-Variate Methods for a Detection of Greenhouse-Gas-Induced Change: A Critical Appraisal of Simulations and Observations; Elsevier: Amsterdam, The Netherland, 1991; pp. 511–536. [Google Scholar]
- Santer, B.D.; Bruggermann, W.; Cubasch, U.; Hasselmann, K.; Hock, H.; Maier-Reimer, E.; Mikolajewicz, U. Signal-to-noise analysis of time-dependent greenhouse warming experiments. Part 1: Pattern analysis. In Max-Planck-Institut Fur Meteorogie Report 98; Max-Planck Institut for Meteorologie Bundesstrasse: Hamburg, Germany, 1993; pp. 46–62. [Google Scholar]
- Cubasch, U.; Santer, B.D.; Hellach, A.; Hegerl, G.; Hӧck, H.; Maier-Reimer, E.; Mikolajewicz, U.; Stassl, A. Monte Carlo climate change forecasts with a global coupled ocean-atmosphere model. Clim. Dyn. 1994, 10, 1–19. [Google Scholar]
- Hasselmann, K. PIPs and POPs: The reduction of complex dynamical systems using principal interaction and oscillation patterns. J. Geophys. Res. 1988, 93, 11015–11021. [Google Scholar] [CrossRef]
- Von Storch, H.; Bruns, T.; Fischer-Bruns, I.; Hasselmann, K. Principal oscillation pattern analysis of the 30- to 60-day oscillation in a general circulation model equatorial troposphere. J. Geophys. Res. 1988, 93, 11022–11036. [Google Scholar] [CrossRef]
- Rossum, S.; Lavin, S. Where are the Great Plains? A cartographic analysis. Prof. Geogr. 2000, 52, 543–552. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W.; Peterson, T.C.; Lawrimore, J. Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J. Clim. 2008, 21, 2283–2293. [Google Scholar] [CrossRef]
- Jones, P.D. Hemispheric surface air temperature variations: A reanalysis and an update to 1993. J. Clim. 1994, 7, 1794–1802. [Google Scholar] [CrossRef]
- Pinzon, J. Using HHT to successfully uncouple seasonal and interannual components in remotely sensed data. In Proceedings of the SCI 2002 Conference, Orlando, FL, USA, 14–18 July 2002.
- Pinzon, J.; Brown, M.E.; Tucker, C.J. Satellite time series correction of orbital drift artifacts using empirical mode decomposition. In Hilbert-Huang Transform: Introduction and Applications; Huang, N.E., Shen, S.S., Eds.; World Scientific: Hackensack, NJ, USA, 2004; pp. 17–29. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.; Pak, E.W.; Mahoney, R.; Vermote, E.; Nazmi, E.S. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Sexton, M.H.D.; Grubb, H.; Shine, P.K.; Folland, K.C. Design and analysis of climate model experiments for the efficient estimation of anthropogenic signals. J. Clim. 2003, 16, 1320–1336. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Allen, M.R.; Stott, P.A. Estimating signal amplitudes in optimal fingerprinting (I), Theory. Clim. Dyn. 2003, 21, 477–491. [Google Scholar] [CrossRef]
- Levine, A.R.; Berliner, M.L. Statistical principles for climate change studies. J. Clim. 1999, 12, 564–574. [Google Scholar] [CrossRef]
- Allen, M.R.; Tett, S.F.B. Checking for model consistency in optimal fingerprinting. Clim. Dyn. 1999, 15, 419–434. [Google Scholar] [CrossRef]
- Hasselmann, K. Optimal fingerprints for the detection of time dependent climate change. J. Clim. 1993, 6, 1957–1971. [Google Scholar] [CrossRef]
- Hansen, J.; Lacis, A.; Ruedy, R.; Sato, M. Potential climate impact of Mountain Pinatubo eruption. Geophys. Res. Lett. 1992, 19, 215–218. [Google Scholar] [CrossRef]
- Riebsame, W.E.; Changnon, S.A.; Karl, T.R. Drought and Natural Resources Management in the United States: Impacts and Implications of the 1987–1989 Drought; Westview Press: Boulder, CO, USA, 1991. [Google Scholar]
- Judge, G.G.; Griffiths, W.E.; Hill, R.C.; Lutkepohl, H.; Lee, T.C. The Theory and Practice of Econometrics, Second Edition; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Pan, Z.; Arritt, R.W.; Takle, E.S.; Gutowski, W.J., Jr.; Anderson, C.J.; Segal, M.M. Altered hydrologic feedback in a warming climate introduces a “warming hole”. Geophys. Res. Lett. 2004. [Google Scholar] [CrossRef]
- Ganguly, A.R.; Parish, E.S.; Singh, N.; Steinhaeuser, K.; Erickson, D.J.; Branstetter, M.L.; King, A.W.; Middleton, E.J. Regional and decadal analysis of climate change induced extreme hydro-meteorological stresses informs adaptation and mitigation policies. In Proceedings of the 21st Conference on Climate Variability and Change, Phoenix, AZ, USA, 13 January 2009.
- Pielke, R.A., Sr.; Pitman, A.; Niyogi, D.; Mahmood, R.; McAlpine, C.; Hossain, F.; Goldewijk, K.; Nair, U.; Betts, R.; Fall, S.; et al. Land use/land cover changes and climate: Modeling analysis and observational evidence. WIREs Clim. Change 2011. [Google Scholar] [CrossRef]
- Lobell, D.; Bala, G.; Mirin, A.; Phillips, T.; Maxwell, R. Regional differences in the influence of irrigation on climate. J. Clim. 2009, 22, 2248–2255. [Google Scholar] [CrossRef]
- Kueppers, L.M.; Snyder, M.A.; Sloan, L.C. Irrigation cooling effect: Regional climate forcing by land-use change. Geophys. Res. Lett. 2007. [Google Scholar] [CrossRef]
- Bonfils, C.; Lobell, D. Empirical evidence for a recent slowdown in irrigation-induced cooling. Proc. Natl. Acad. Sci. USA 2007, 104, 13582–13587. [Google Scholar] [CrossRef] [PubMed]
- Boucher, O.; Myhre, G.; Myhre, A. Direct human influence of irrigation on atmospheric water vapor and climate. Clim. Dyn. 2004, 22, 597–603. [Google Scholar] [CrossRef]
- Adegoke, J.O.; Pielke, R.A., Sr.; Carleton, A.M. Observational and modeling studies of the impacts of agriculture-related land use change on climate in the central U.S. Agric. For. Meteorol. 2007. [Google Scholar] [CrossRef]
- Houghton, J.T.; Meira Filho, L.G.; Callander, B.A.; Harris, N.; Kattenberg, A.; Maskell, K. Climate Change 1995: The IPCC Second Scientific Assessment; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- High Plains Regional Climate Center (HPRCC). Climate Change on the Prairie: A Basic Guide to Climate Change in the High Plains Region. Available online: http://www.hprcc.unl.edu/publications/files/HighPlainsClimateChangeGuide.pdf (accessed on 7 January 2012).
- Hegerl, G.C.; von Storch, H.; Hasselmann, K.; Santer, B.D.; Cubasch, U.; Jones, P.D. Detecting greenhouse gas-induced climate change with an optimal fingerprint method. J. Clim. 1996, 9, 2281–2306. [Google Scholar] [CrossRef]
- Pitman, A.J.; de Noblet-Ducoudre, N.; Cruz, F.T.; Davin, E.L.; Bonan, G.B.; Brovkin, V.; Claussen, M.; Delire, C.; Ganzeveld, L.; Gayler, V.; et al. Uncertainties in climate responses to past land cover change: First results from the LUCID intercomparison study. Geophys. Res. Lett. 2009. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mutiibwa, D.; Kilic, A.; Irmak, S. The Effect of Land Cover/Land Use Changes on the Regional Climate of the USA High Plains. Climate 2014, 2, 153-167. https://doi.org/10.3390/cli2030153
Mutiibwa D, Kilic A, Irmak S. The Effect of Land Cover/Land Use Changes on the Regional Climate of the USA High Plains. Climate. 2014; 2(3):153-167. https://doi.org/10.3390/cli2030153
Chicago/Turabian StyleMutiibwa, Denis, Ayse Kilic, and Suat Irmak. 2014. "The Effect of Land Cover/Land Use Changes on the Regional Climate of the USA High Plains" Climate 2, no. 3: 153-167. https://doi.org/10.3390/cli2030153



