1. Introduction
Human location, as the most straightforward correlation clue in object tracking and mobile computing, is of great significance in location-based services (LBS) and ambient assisted living [
1,
2]. Currently, most human localization technologies have focused on two categories: active solutions and device-free localization (DFL) [
3]. Traditional active positioning technologies such as the global positioning system (GPS), mobile phones, radio frequency identification (RFID), ultrasonic technologies and so on, are used to provide location information for outdoor navigation or indoor surveillance, and the locations are determined by reference landmarks deployed at known positions. However, these technologies usually need the user to be tagged by attaching tiny wireless transceivers, and the precise localization depends on well-characterized physical measurements such as time-of-flight (ToF), time-difference-of-arrival (TDoA), angle-of-arrival (AoA) and received-signal-strength (RSS) [
4]. In addition, the harsher indoor environment, the lack of line-of-sight (LOS) and occlusion of the human body may lead to large estimation error.
In DFL-based systems, subjects are localized without attaching any wireless tags [
5,
6]. These are noninvasive sensing methods and are appropriate for indoor applications. Well-established studies of DFL employ distributed cameras [
7], depth imaging sensors [
8] and pyroelectric infrared (PIR) sensors [
9] to detect and obtain human position. However, these optical sensing-based methods are limited by smoke, varying illumination, blind field-of-view (FOV), and the occlusion of obstacles. Through-wall imaging-based methods are widespread, and employ monostatic or multi-mobile radar technology, such as ultra-wide band (UWB) [
10,
11], ultra-narrow band (UNB) [
12] and multiple input multiple output (MIMO) radar arrays [
13,
14] to infer the presence distribution of the environment by measuring and analysing the reflected signals. However, how to deal with mixed multipath effects, dependence of the delay and phase information, and large-scale coverage, while taking into account low-cost implementation, remain challenging issues for radar-based methods.
Radio tomographic imaging (RTI) is an emerging approach for inferring environmental information by analysing the characteristics of shadowing loss in radio frequency (RF) signals [
15,
16]. The peer-to-peer networking formed by wireless sensor networks (WSNs) is a widely adopted implementation architecture for RTI. The goal of RTI is to reconstruct the distribution image of targets and obstacles in the coverage area by following the spatial accumulation effect of shadowing loss of the RSS [
17]. In essence, RTI is a part of the non-isomorphic computational imaging technique and has the capability of seeing through walls. The locations are not directly observable and the DFL is recast for finding the coordinates of the brightest pixels in the recovered attenuation image. Compared with the traditional optical sensing methods, RTI does not only have advantages with presence-specific sensing and non-intrusive privacy, but also it can overcome unstable interference such changing illumination, texture and so on. In contrast to the monostatic radar-based DFL methods, the transmission loss of the narrow-band RF signal is lower in the same conditions, and the effective detection distance is larger, which is suitable for the task of large-scale imaging. On the other hand, RTI is less sensitive to the phase of the detected signal than radar-based methods [
18]. What is more, with the implementation of mobile cooperative networking, robot-aided RTI will actively boost the ability to explore and adapt to the unknown environment [
19,
20]. In the past few years, the WSN-based RTI has been applied in a wide number of tasks, ranging from floor plan estimation [
19,
20,
21] and human spatial localization and tracking [
16,
22,
23], through lightweight biometric sensing [
24] and respiratory monitoring [
25], to fall detection [
26,
27] and action recognition [
28].
RTI-based DFL can be divided into two categories: ellipse model-based imaging and RSS fingerprint-based matching [
28]. The ellipse model-based methods make great efforts to build the refined spatial sampling model of each link and use the regularization algorithms to resolve ill-posed image reconstruction [
16,
17,
21,
29,
30,
31]. The RSS fingerprint-based approaches seek to model the fading feature of the subject at each predefined location, and the localization is cast into a pattern-matching problem [
32,
33,
34]. The above methods have been shown to be effective both in outdoor and indoor environments. However, the prior of sparse distribution of the targets in the monitored area has not been fully utilized. The sparse nature of location estimation has been exploited by compressive sensing (CS) theory for indoor active localization [
35,
36]. Although these studies demonstrate that accurate positioning can be recovered from a small number of RSS measurements, the 1-sparse position estimation requires users to carry the RF transceiver and is dependent on knowledge of the prior of exact number of targets.
In this article, we propose a DFL method based on enhanced sparse representation with radio tomography networks. The method is capable of making full potential of the sparse distribution prior of human bodies in the monitored area, and can simultaneously support the preset ellipse model and the RSS fingerprint-based model for localization of multiple targets. This idea is derived from the emerging theory of sparse representation-based classification (SRC), which works based on the CS theory [
37,
38,
39]. The implementation of our method introduces an expanded sensing matrix spanned by the combination of a sampling matrix and a unit error-correcting base. The sampling matrix can be composed of the ellipse model from calibrated networks or the fingerprint-based model formed by training samples at predefined locations. The sparsity of location information is enhanced, being represented in the basis space of the expanded sensing matrix. The problem of multitarget localization is converted into recovering a sparse vector with a few nonzero entries. The
-minimization-based approximations are calculated and compared by using classical linear programming (LP) and orthogonal matching pursuit (OMP), respectively. Entries with larger amplitude in the recovered vector are extracted as the estimated locations. Experiments in an open outdoor scenario, in an indoor LOS scenario, and in an indoor non-line-of-sight (NLOS) scenario are conducted to evaluate the effectiveness of the proposed method. We prove that the new DFL method outperforms the classical RTI methods and is able to localize multiple targets with high accuracy in all the scenarios.
The rest of this article is organized as follows. The problem of RTI-based DFL is introduced in
Section 2. In
Section 3, the enhanced sparse representation-based method is derived. Experimental results for person localization using the proposed method are presented in
Section 4. The summary and conclusions are provided in
Section 5.
2. System Model
The task of RF tomography is to obtain a presence image of the attenuation induced by targets in a coverage area. The desired location or image is not observable directly from the RSS measurements. According to the study of spatial ellipse-based sampling models, the RSS loss marked by a single link
from the transmitting node located at position
to the receiving node
has the following expression denoted in dBm [
16],
where
is the path loss component that depends only on the link distance
,
is the shadowing loss caused by the attenuation of covered objects, and
is the random loss induced by the multipath environment and measurement noise.
From the perspective of obtaining the attenuation image of targets, is the component that is independent of shadowing fading and random loss, and can be removed by measuring RSS changes. is the environment-dependent uncertainty associated with the sampling measurement, which poses a significant obstacle to precise localization. This difficulty is mainly derived from the unpredictable nature of constructive and destructive interference of narrow-band RF signals in multipath sensing area and the measurement noise. is the component directly related to the shadowing fading, which can be regarded as the cumulative projection of the environmental attenuation image on the link .
It can be assumed that the two-dimensional plane of a monitored area
is discretized into
N subregions or pixels that do not overlap each other, that is,
and
. If the attenuation intensity at the centre
is quantized as
, the attenuation image of
can be stacked up to form a vector
. Then, the
can be obtained by calculating the difference between the online RSS measurement and a reference value. Here, the RSS reference is recorded with the absence of person in the coverage area. The mathematical form of the sampling model is denoted by
where
is the attenuation representation in the
nth pixel, and
is the sampling weight of the link
for pixel
. The sampling weight
can be approximated by an ellipse model with foci at the transmitter and receiver locations [
16], as follows:
where
and
are the distances of the pixel
to the two terminal nodes of link
, and
is a tunable width of the ellipse. In actual use, the parameter
is empirically determined to minimize the modeling error and imaging distortion.
For a measurement model consisting of
K densely distributed RF nodes around the measured area, the number of links will be
in the peer-to-peer interconnection. The set of all links can be expressed as
, and the measurements
from all links have the following system representation:
where
is a sampling matrix determined by the calibrated RF nodes, and
is the random loss during the sampling process, usually seen as the white Gaussian noise [
17,
30,
31]. It has been found that the recovery of attenuation image
is an ill-posed inverse problem, and the regularization methods need to be introduced to solve this problem [
21,
31].
The existing imaging-based localization methods using the ellipse model and its improved model have been proven to have good performance in the outdoor environment [
16,
17,
29,
30], but they have two limitations. Firstly, the elliptical sampling model is dependent on the spatial coordinates of the transceiver nodes. Therefore, the rigorous construction of sampling matrix requires precise localization of nodes. The localization of WSN nodes is a challenging problem in the indoor environment. Secondly, the high-precision positioning from the presence indicator of attenuation image is an unsolved problem since the undetermined sampling matrix is used. This difficulty is mainly due to the dense granularity of pixels designed for imaging the presence of objects. The dimension of the collected RSS measurements is smaller than the number of pixels. Several approaches have explored the sparse nature of the presence of objects in the sensing area, and seek a variety of optimization strategies for finding a unique solution [
29,
30,
40]. However, it is obviously reasonable to assume that if a static subject or a dynamic interest target in the environment occupies a single or several pixels, the excessive image resolution may result in confused decisions when extracting multiple targets’ locations.
Another category of localization approaches is based on RSS fingerprint matching [
32,
33,
34]. Researchers collect and extract temporal RSS indicators generated by a single person at each preset indoor location. Then, these indicators are directly used as fingerprints which can be denoted as
, where
are the recorded RSS magnitudes from the set of
M links with one person located at position
. The person localization is transformed into finding the category of a test RSS vector
with minimum matching distortion. In the practical modeling process, the labor force of building a fingerprint database is directly proportional to the number of positions to be located. When large-scale and dense-granularity localization is required, it is impractical to employ the RSS fingerprint-based matching due to the amount of training samples required. In addition, multiperson localization is still a challenging issue for RSS fingerprint matching-based DFL. However, the RSS fingerprint matching-based methods have been confirmed with good performance for single-person localization in the indoor environment [
32,
33,
34].
3. Enhanced Sparse Representation-Based Target Localization
Recent developments in computer vision and pattern recognition have proven that the semantic information of a test sample is able to be extracted by sparse linear representation in terms of an overcomplete dictionary whose bases are the concatenation of training samples and the error compensation base [
37,
38,
39]. In a radio tomography network-based DFL system, if the sink node is capable of acquiring sufficiently representative samples for constructing the sampling matrix, we can create an overcomplete expanded sensing matrix by adding an error-correcting base. The unknown location hidden in a test sample is recovered by using the enhanced sparse representation in terms of the expanded sensing matrix.
Our proposed method for person localization firstly assumes that the monitored area has
N possible locations of a target and is surrounded by an RF sensor network consisting of
K nodes. Multiple subjects with different heights and weights are requested to stand at the predefined points successively for RSS fingerprint acquisition. The standing postures are with different orientations of freedom and the RSS values from all links are collected simultaneously. The RSS fingerprint at the
nth coordinate can be recorded as
and
for each subject; here,
P is the total number of subjects. Then, the average RSS
produced by multiple subjects is used to represent the contribution of attenuation at
to the overall RSS. Therefore, a new sampling matrix
derived from the well-aligned training samples will be generated for all possible locations. For outdoor localization scenarios, the sampling matrix
can directly be derived from the calibrated sensing networks, since the existing research shows that the measurement model of a single RF link is capable of being approximated based on spatial ellipse sampling [
16,
17].
For single- and multiperson localization, it is reasonable to assume that an unknown collected RSS vector
can be represented by the following linear combination ideally:
Here, the
can be regarded as the representative coefficient for the presence of targets at the
nth position. This linear representation can be rewritten as:
Based on the natural assumption that the number of people to be located is far less than the number of positions, the semantic location can be decoded by finding the nonzero entries of the sparse vector from a test sample .
In many practical outdoor and indoor scenarios, the test sample
may contain random loss caused by multipath fading and measurement noise. It is not possible to express the test RSS sample exactly as a sparse superposition of the column atoms of the sampling matrix. Considering noisy cases, the above measurement model should be modified as:
where
is the noise term. Existing studies have applied sparse prior and additional model constraints to seek the optional solution [
21,
31]. Each entry of the error vector
represents the noise of the associated RF link in the measurement. Nevertheless, this error may affect only a small fraction of RF links since the spatial sampling area of each link is limited and the people to be located are sparsely distributed. Therefore, we assume that only a small fraction of the noise term
is nonzero with the bounded energy
, and can be expressed as a sparse superposition of the standard error-correcting basis. The magnitude and the number of nonzero entries in
are unknown due to the unpredictable multipath environment and measurement noise. An identity matrix
can be added uniformly as the augmented error-correcting base for approximating the nonzero noise entries [
38]. The measurement process can be rewritten as:
where
,
is the identity vector with the only unit at
mth entry, and
is the adjoint error coefficient vector. Then, we denote
as the expanded sensing matrix. Obviously, the
is an overcomplete dictionary and the problem (
8) usually does not have a unique solution for the expanded
. However, based on our previous joint sparsity assumption on
and
, we will cast the problem of finding the sparsest solution as a convex optimization task.
The problem of extracting the sparsest solution for the equation
is able to be solved by the following optimization:
where
is the number of nonzero supports in a vector, and
counts the number of nonzero entries in
. In general, solving the
-minimization requires an exhaustive search and the existence of the unique sparsest solution should meet certain conditions. This problem is regarded as NP-hard and has combinatorial complexity [
41]. Recent developments in the theoretical results of CS reveal that the
-minimization can be replaced by the
-minimization if only a small fraction of the entries in
are nonzero [
42,
43]. Then, seeking to represent
as a sparse linear representation with respect to the expanded sensing matrix as a whole, it is cast into solving the following
-based convex relaxation:
where
is defined as
.
The above problem is an
-minimization problem and there are provably effective and efficient methods for solving it with polynomial computational complexity. The convex optimization and greedy pursuit are two representative methods for seeking the sparsest solution [
42]. The convex optimization-based solution can be solved via LP [
44]. Meanwhile, the OMP is a widely used method in the greedy algorithm family due to its simplicity and good performance [
45]. In this article, we first use the standard LP for solving the
-minimization, and then find the sparsest support of recovered signal using the standard OMP.
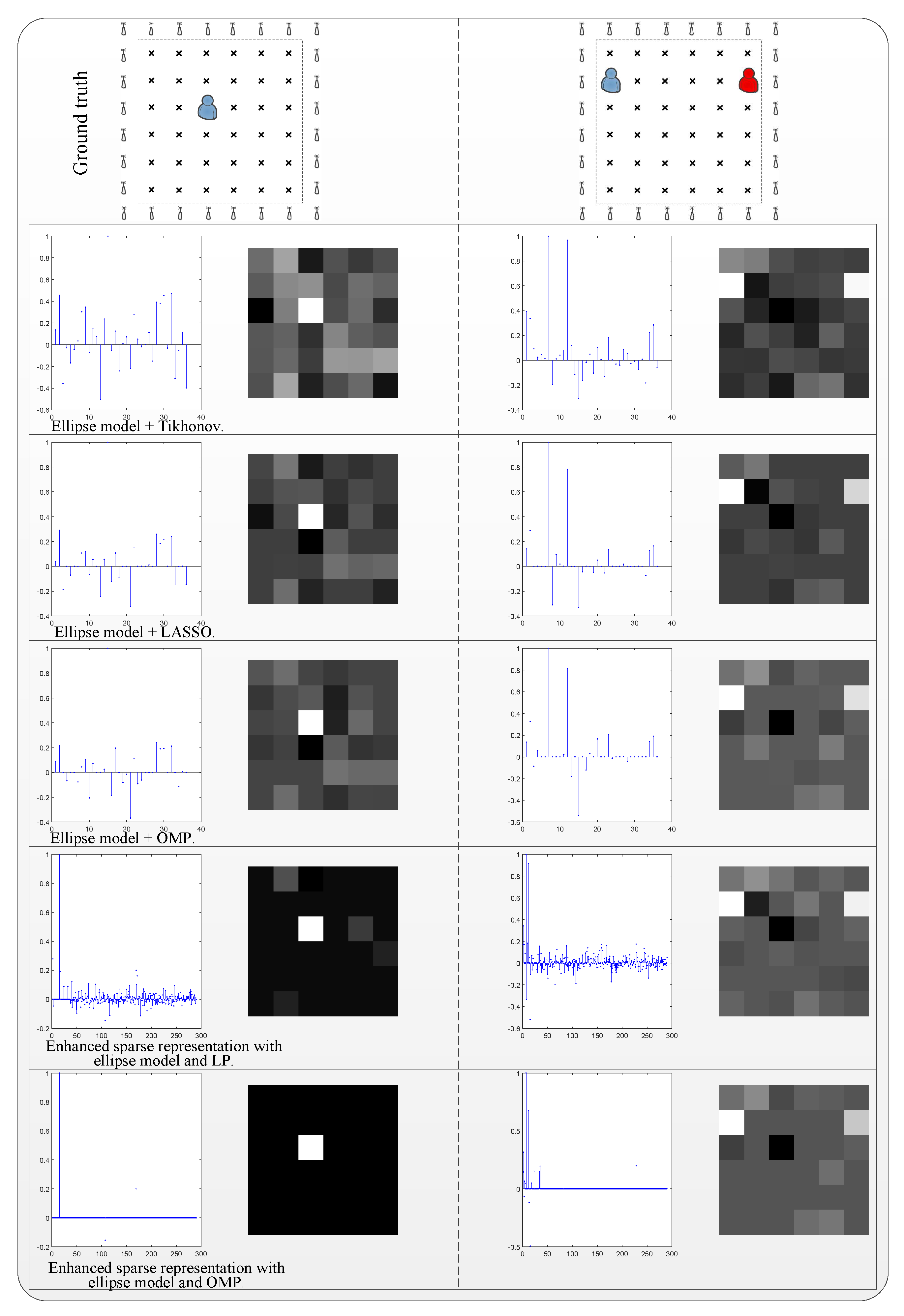
Figure 1 illustrates the overview localization framework in an indoor NLOS environment; there are three subjects in the monitored area and the sparse recovery is based on LP. The ellipse model-based sampling matrix is incapable of fitting the spatial sampling for each link in the rich mutlipath indoor environment. Hence, the proposed method first collects the contribution of attenuation at each coordinate occupied by targets, and constructs the expanded sensing matrix by using RSS fingerprints. Then, the LP is used to represent a test RSS
as a sparse linear combination of the expanded sensing matrix. Finally, the locations of targets are extracted from the estimated location representation
by finding the several largest elements.
4. Experimental Evaluation
In order to verify the effectiveness of our proposed method, the open outdoor environment, the indoor LOS environment, and the indoor NLOS environment were experimentally evaluated. In the outdoor environment, we selected the public data from the Sensing and Processing Across Networks (SPAN) Lab at the University of Utah [
16]. Since the sampling range of links can be approximated by elliptic models in the outdoor environment, we adopted the ellipse model directly to construct the expanded sensing matrix. For the indoor LOS and NLOS experiments, we constructed a database with single, double and triple targets. A total of five volunteers participated in the collection of experimental data: four males and one female. In the construction of the expanded sensing matrix stage, the RSS fingerprints are the average of RSS generated by five volunteers standing at all preset positions. The coordinates of all RF nodes in the indoor environment are also well calibrated, so the expanded sensing matrix can also be generated by the ideal elliptical model. Then, we respectively recorded the test samples with single, double and triple targets with 200 random distributions for experimental assessment.
In the three environmental tests, we compared the enhanced sparse representation-based method outlined here with several classical approaches from the literature: the Tikhonov regularization using ellipse model [
16,
31], the standard sparse imaging solved by least absolute shrinkage and selection operator (LASSO), and the OMP with the ellipse model [
40]. The above methods provide the standard baseline for comparison and we introduce three quantitative indicators to compare the relative methods. The first quantitative indicator is the spatial distance error of DFL, which can be used for accuracy evaluation:
where
is the distance function,
is the representation of true location for the
pth target, and
is the estimated location extracted from
. The second quantitative indicator is the signal-to-noise ratio (SNR) of a true location representation
with respect to a recovered location representation
by writing:
The SNR-based assessment can exhibit the difficulty of extracting location information from the recovered signal. The third quantitative indicator is the average consumed time, and the execution of all methods is based on Intel –6100 CPU and Matlab software.
4.1. Experimental Results in the Outdoor Scenario
With the rapid growth in RF-integrated circuits, a large-scale radio tomography network is available to be deployed for data acquisition. The outdoor experiment is carried out using the public data shared by the University of Utah [
16]. The radio tomography network consists of a star network with 28 nodes, and the monitored area has a square perimeter of lawn of 21 feet × 21 feet. The distance between adjacent nodes is 3 feet. The commercially available TelosB RF node from Crossbow Technology Inc. (San Jose, CA, USA) is selected as the transceiver, and the network is run in the 2.4-GHz frequency band following the Institute of Electrical and Electronics Engineers (IEEE) 802.15.4 protocol. There are 36 valid locating coordinates in this experiment, and the coordinates of all nodes have been calibrated.
Previous studies have shown that the attenuation by the human body is approximately satisfied using the ellipse sampling model in the outdoor environment [
16]. Hence, we can directly use the ellipse model to build the expanded sensing matrix. We respectively test the samples with single and double targets in the database and display the location results by imaging.
Figure 2 shows the typical results for the localizations with single and double targets. For single-target localization, it turns out that each method has good performance, and the location can be easily extracted. The proposed enhanced sparse representation-based methods solved by LP and OMP are able to provide less-noisy interference. For double-target localization, the methods solved by Tikhonov regularization and LASSO introduce more confusing information, and as such, accurate locations are hard to extract. The better localization results are achieved also by the enhanced sparse representation-based methods, and locations can be extracted by finding the two maximum values from the recovered coefficients.
Figure 3 shows the average accuracies of different methods for single and double subjects. For single-person localization, the proposed method exhibits approximately ideal accuracy, and the average localization error does not exceed 0.05 feet. Moreover, for double-target localization, the proposed methods outperform the Tikhonov regularization, Lasso, and OMP with only the ellipse model. The average distance error can be controlled under 0.2 feet.
Table 1 gives the average SNR and execution time with different localization methods. It can be found that the enhanced sparse representation-based methods using the ellipse model and error-correcting base will contribute the largest SNR when the LP is employed for signal recovery, which means that the correct position can be easily extracted from the recovered signal. However, the LP-based recovery consumes much execution time. Meanwhile, the enhanced sparse representation solved by OMP has similar average SNR with little time consumption. In combination with the aforementioned analysis of imaging-based DFL, we conclude that the adoption of the enhanced sparse representation-based method solved by OMP is a better choice for single and multiple targets in outdoor environments.
4.2. Experimental Results in Indoor LOS Scenario
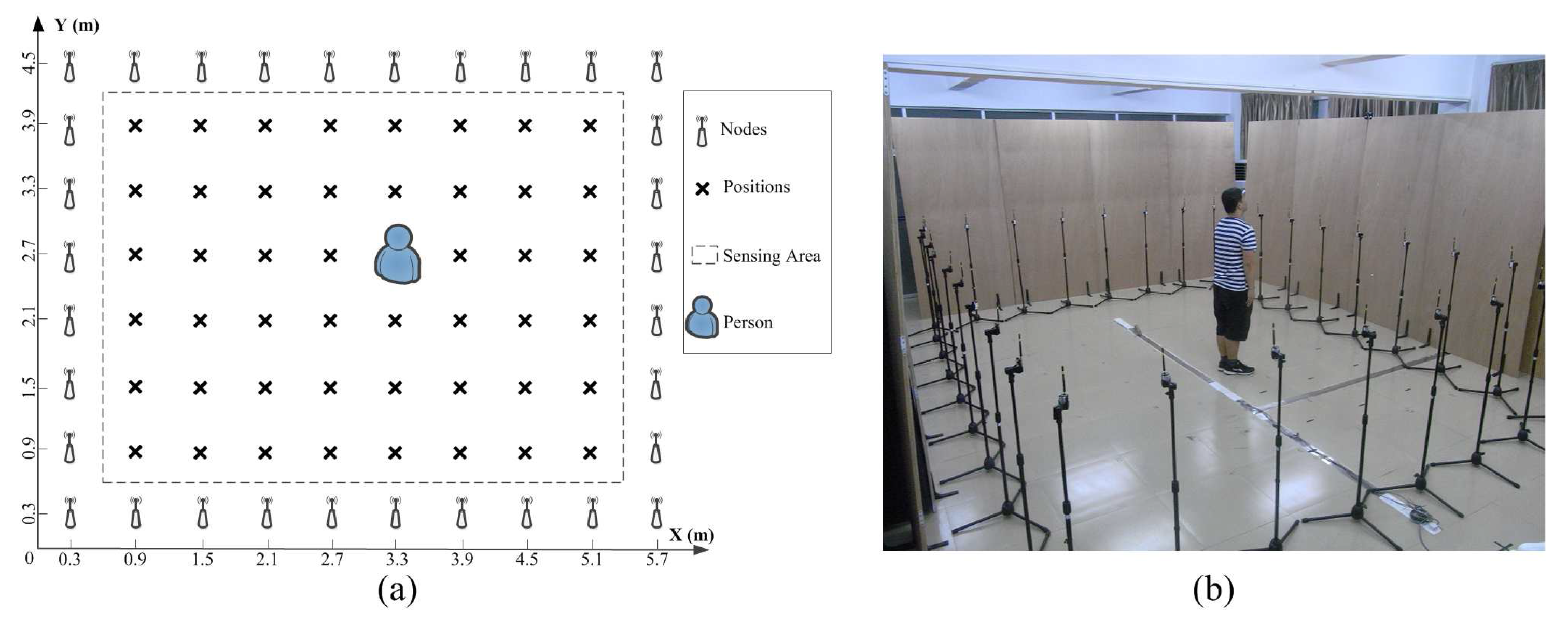
For the multipath-rich indoor environment, as shown in
Figure 4, there are 32 nodes deployed in a square perimeter of 4.8 m × 3.6 m with the LOS scenario. The distance between the neighbouring nodes is 0.6 m. The integrated module XM2110CB from MEMSIC Inc. (Andover, MA, USA) is used as the RF nodes. Through the TinyOs-based software configuration, the RF signal will run in the 2.4-GHz frequency band following protocol IEEE 802.15.4. The scanning rate of this network is 8 Hz, and a sink node is used to collect the RSS of all RF links. According to the experimental setup shown in
Figure 4, there are 48 effective points to be localized.
The imaging comparison of the related single localization is shown in the left column of
Figure 5. The methods without enhanced sparse representation solved by Tikhonov, LASSO and OMP can be used to extract the location effectively but with lots of interference in the coefficients of recovery. The enhanced sparse representation-based methods will provide the accurate location clearly, regardless of the usage of elliptical model or RSS fingerprints.
When the number of targets is increased to two and three, the imaging comparisons are shown in the middle and the right columns of
Figure 5, respectively. The confusing coefficients are increased in the methods of traditional Tikhonov, LASSO and OMP. From the recovered coordinate coefficients, it is difficult to find which one corresponds to the correct location. However, the enhanced sparse representation-based methods show better performance, even in the case of triple targets. Among them, the combined use of RSS fingerprints and error-correcting base solved by LP produces the least noise.
The average accuracy of localization for all cases is shown in
Figure 6. It can be found the there will be large error if the elliptical model is directly used to approximate the sampling link in the indoor multipath-rich environment, and it can not obtain good accuracy when multiple people appear in the surveillance area. However, the enhanced sparse representation-based methods with ellipse model outperform those using the ellipse model only. Furthermore, if the RSS fingerprints–which are derived from the contribution of each coordinate to the whole sampling in the real scene–are used to build the expanded sensing matrix associated with the error-correcting base, both the LP- and OMP-based recovery can provide higher accuracy.
The comparison of average SNR and time consumption is listed in
Table 2. It can be found that the ellipse model-based location estimations obtain a negative SNR, which means that the correct location information is submerged in the noisy recovered signal. Meanwhile, if the enhanced sparse representation-based methods are used regardless of the ellipse model or RSS fingerprint-based model, the SNR is positive and the correct locations are brighter in the recovered image. The combined use of RSS fingerprints and LP algorithm produces the best results but with longer running time. Therefore, the OMP-based recovery can be chosen for real-time localization due to the low computational complexity and high accuracy.
4.3. Experimental Results in Indoor NLOS Scenario
We carried out data collection in an indoor NLOS environment for further assessment, as shown in
Figure 7. A square perimeter area of 4.8 m × 3.6 m is surrounded by 29 nodes, and all RF links work in the NLOS pattern. Wood boards with thickness of 2.2 cm and height of 2.4 m are used to block the LOS. The distance between the neighbouring nodes is also 0.6 m. The nodes used and the network configuration are the same as those of the previous system in the indoor LOS environment.
Figure 8 shows the recovered images using related methods for typical localizations. It is not difficult to find that when the LOS is occluded, the localization methods based on the ellipse sampling model will produce greater distortion. The location of the human body is hard to be extracted even with the prior of the target’s number. The introduction of enhanced sparse representation will boost the robustness for single localization, no matter which ellipse sampling models or RSS fingerprints are used for the construction of the expanded sensing matrix. For multiperson localization in the indoor NLOS environment, only partial locations can be recovered based on the ellipse sampling model. However, the enhanced sparse representation-based methods using RSS fingerprints will give the best performance.
Figure 9 presents the average accuracy of the related methods in NLOS scenarios. According to the results of the statistics, the use of only ellipse model-based DFL produces greater errors for single, double and triple localizations, with average accuracy of more than 0.5 m. If the enhanced sparse representation with an ellipse model is introduced, the improvement in localization accuracy is limited. Moreover, the accuracy will decrease with the increasing number of targets. However, the RSS fingerprint-based expanded sensing matrix and enhanced sparse representation will jointly contribute to the ideal accuracy.
Table 3 gives the average results of SNR and time consumption in the indoor NLOS scenario with different localization methods. It can still be found that the enhanced sparse representation with ellipse model or RSS fingerprints provides higher SNR; the truly localized targets are clearly displayed in the recovered attenuation image. The recovery algorithms by LP and OMP have close performance, but the convex optimization strategy-based LP will consume an average time of 495.50 ms, which is difficult to apply in a real-time system. The OMP algorithm is favoured with better efficiency and accuracy for indoor NLOS scenarios.
5. Discussion and Conclusions
Radio tomography networks established by organizing the densely distributed RF nodes around the measured area are the most common approach for DFL. In general, the number of targets is sparsely distributed with respect to the area resolution. In order to make full potential of the sparse prior and to enhance the sparseness of the location signal, we propose the enhanced sparse representation-based DFL, which constructs a new expanded sensing matrix for modelling the measurement. This expanded sensing matrix is composed of a sampling matrix and an error-correcting base; the recovery of sparse locations is achieved by using the -minimization-based optimal approximations. The sampling matrix can be derived from the well-established ellipse model from calibrated networks or the RSS feature-based model induced by RSS fingerprints with one person at predefined locations. Through the outdoor and indoor experimental assessments, it has been shown that the enhanced sparse representation method with the ellipse model is effective in the open outdoor and indoor LOS scenarios. For the indoor NLOS scenario, the enhanced sparse representation method with RSS fingerprints supports accurate single- and multiperson positioning.
Although the experimental results have verified the efficacy of our proposed approach for accurate multiperson positioning, there are a lot of challenging problems that need to be addressed. One potential improvement is how to reduce the network load and computational complexity. Research on the CS-based sensing efficiency analysis for guaranteeing the positioning accuracy may provide possible ways for building energy-efficient systems. Other research questions are whether and how the gender of the subjects affects the results, since the physiological and behavioral attributes are different between males and females. Some efforts, including device-free soft biometric sensing and abnormal activity detection by sensory fusion of a variety of signal modalities (e.g., PIR sensors), are being made for building behavior- and healthcare-monitoring systems.