1. Introduction
Wireless sensor networks are very useful for performing a variety of tasks. In particular, they are well suited to monitor and sense natural phenomenon and are useful for projects such as earthquake detection, biohazard detection, flood detection, weather forecasting, and fire detection. In addition to these applications, wireless sensor networks can also be deployed for different type of civilian and military applications such as border line surveillance, intrusion detection, nuclear and chemical attack detection, traffic surveillance and patient monitoring [
1,
2].
However, wireless sensor networks could face with the risk of being compromised by the attacker. More specifically, sensor nodes could be easily captured and compromised by the attacker when wireless sensor networks are deployed in hostile environment. (According to the research result of [
3], attacker needs approximately one minute to compromise a sensor node.) The attacker can exploit the compromised nodes to mount various attacks [
4,
5] against sensor networks. For example, he can disrupt various network operations such as clustering, localization, routing, and time synchronization. He can also inject false data into the network in order to undermine the normal data-acquisition process. Moreover, he can launch jamming attacks to interfere with the communications between sensor nodes.
To generate the widespread effects on the network, he can mount
replica node attacks [
6] with the compromised nodes. More specifically, he can obtain the secret keying materials and ID from a compromised node. Using these secret keying materials and ID, he can produce
replica nodes, which are sensor nodes that share the compromised node’s secret keying materials and ID, and then spread these replicas throughout the network and launch various types of attacks by exploiting these replicas. These replica node attacks are very hazardous to the operation of sensor networks because they make it possible for the attacker to gain control over much of the network. Specifically, replicas have the same secret keying materials and IDs as the compromised node and thus they would be treated as the original compromised nodes. This means that they could be allowed to communicate with other nodes and the base station as if they were legitimate nodes. By leveraging this insider position of the replicas, the attacker with a large number of replica nodes could acquire control over much of the network and thus quickly undermine many different types of normal operations in sensor networks.
Several replica node detection schemes [
7,
8,
6,
9,
10,
11] have been proposed for wireless sensor networks. The primary method used by the majority of these schemes is to have nodes report location claims that identify their positions and attempt to detect colliding reports that indicate one node in multiple locations. Since this method leverages the location information for replica detection, it cannot work without the help of secure localization or GPS techniques. If we could detect replicas without the aid of these techniques, we would save the detection costs subject to employing these techniques.
Indeed, we could detect replicas without the use of location information in case of
replica cluster attacks, in which multiple replicas of a single compromised node form a cluster in such a way that they are placed close to each other in the cluster. Specifically, in replica cluster attacks, multiple replicas with the same identity and secret keying materials are placed in the same small regions. All of these replicas want to maximize their malicious impact on the network and thus communicate with as many nodes as possible at the same time. Accordingly, it is highly likely that the number of nodes with which these replicas would communicate at a time would be much more than the one of their benign neighbors. By leveraging this intuition, every node performs the Sequential Probability Ratio Test (SPRT) [
12] on its neighbor node using a null hypothesis that a replica cluster of the neighbor node does not exist and an alternate hypothesis that a replica cluster of the neighbor node exists. In using the SPRT, if the number of communication peers of a neighbor node falls short of or exceeds a pre-configured threshold, it will lead to acceptance of the null or alternate hypotheses, respectively. Once the alternate hypothesis is accepted, the node will disconnect the communication with the neighbor node. (A preliminary version of this work appeared in [
13].)
We analytically show that our proposed scheme fulfills high replica cluster detection capability with a few number of samples. The simulation results also demonstrate that it detects replica clusters with at most 3.28 and 6.78 samples while reaching zero false positive and false negative rates.
The rest of paper is organized as follows. In
Section 2, we describe the related works. In
Section 3, we describe the network assumptions and attacker models that are necessary for our proposed scheme. We also present an overview of the SPRT. In
Section 4, we propose a replica cluster detection scheme in sensor networks. In
Section 5, we analyze the performance and security of our scheme. In
Section 6, we present the simulation results of our proposed scheme. In
Section 7, we conclude the paper.
2. Related Work
In this section, we present the related work for replica detection in sensor networks. Parno
et al. [
6] proposed randomized and line-selected multicast schemes to detect replicas in sensor networks. In the randomized multicast scheme, every node is required to multicast a signed
location claim to randomly chosen witness nodes. A witness node that receives two colliding location claims for a node decides that the node has been replicated and starts a revocation process on the node. The line-selected multicast scheme diminishes communication overhead of the randomized multicast scheme by controlling every claim-forwarding node to get involved in the replica detection and revocation process. Conti
et al. [
8] proposed a new method for choosing witness nodes for replica detection. This method improves the replica detection probability, storage and computation overheads of the line-selected multicast scheme in [
6]. Zhu
et al. [
11] proposed localized multicast schemes based on grid cell topology. In this scheme, a location claim is multicast to a single cell or multiple cells and a cell receiving two conflicting locations claims initiates replica detection and revocation process. It achieves higher detection rates and lower storage overheads than the line-selected multicast scheme of [
6]. Zeng
et al. [
10] proposed a random-walk based replica node detection scheme. This scheme uses random walks as the distribution mechanism of location claims in the network. In this scheme, location claims are highly randomly distributed to witness nodes.
Choi
et al. [
7] proposed a replica detection scheme in which the network is divided into a set of non-overlapping subregions and an exclusive subset is formed in each subregion. If the intersection of subsets is not empty, it signals that replicas are contained in those subsets.
Xing
et al. [
9] proposed a fingerprint-based replica node detection scheme. In this scheme, nodes inform the base station of fingerprints, which identify a set of their neighbors. The base station performs replica detection by using the property that fingerprints of replicas collide with each other.
Ho
et al. [
14] leverages group deployment knowledge to detect static replica nodes with little overhead.
Ho
et al. [
15] adapts the SPRT to tackle a replica node detection problem in mobile sensor networks.
Yu
et al. [
16] proposed a mobile replica detection scheme by leveraging the intuition that the number of mobile nodes contacted by mobile replicas in a time slot is larger than the one contacted by a benign mobile node.
Wang
et al. [
17] detects the replicas nodes by using mobile patrollers in sensor networks.
Bonaci
et al. [
18] proposed an optimization framework for replica node detection in sensor networks.
Although the related work could effectively detect replica nodes that are widely spread over the network, they likely treat the replicas in a cluster as a single node and thus would likely fail to detect replica clusters. To justify this argument, we first assume that multiple replicas form a cluster C such that they are placed in a circle whose center is (x,y) and radius is r. Moreover, we assume that there are multiple neighbor nodes outside the circle cluster C and the longest distance from these neighbor nodes to the circumference of cluster C is l. Let us denote R be a communication radius of a sensor node. As long as 2r + l ≤ R holds, each neighbor node outside the cluster C can directly communicate each replica in the cluster C. Putting it in differently, if all replicas in the cluster C claim the same location (x,y) irrespective of their actual locations, they could cheat the neighbor nodes outside the cluster C as if they were a single node placed in (x,y). Hence, this will result in the failure of replica cluster detection. Our proposed scheme mitigates this limitation of the related work by efficiently adapting the SPRT to the replica cluster detection problem.
3. Preliminaries
In this section, we first present the network assumptions and then describe our attacker models. Finally, we present an overview of the SPRT.
3.1. Network Assumptions
We assume a static sensor network where each sensor node is fixed to its initial deployment position. Although sensor nodes are static, their neighboring nodes could be changed because the network operator could replace the dead nodes with new ones or keep performing additional node deployments for the better sensing operations. Moreover, every sensor node is assumed to be capable of identifying the destinations of all messages originating from its neighbors. This can be achieved by letting node operate in promiscuous mode. More specifically, every node collects only the source and destination node information of each incoming packet while not looking into the main contents of the packet.
3.2. Attacker Models
We assume that an adversary can compromise a subset of sensor nodes and have full control of them. In other words, an adversary can leverage the compromised nodes to perform any malicious activities that damage the network. Moreover, he can create the widespread effects on the network by generating many replicas of the compromised nodes, where a replica node is defined as a node having the same ID and secret keying materials as a compromised node. In terms of replica node deployment, we assume that adversary will attempt to form a cluster consisting of multiple replicas of a single compromised node in a small region, and then launch a variety of types of attacks by leveraging replica cluster. To amplify the impacted regions by replica cluster attacks, he can compromise multiple nodes, create multiple replica clusters in such a way that each replica cluster is constructed from each compromised node, and place multiple replica clusters in the different small regions.
3.3. Sequential Probability Ratio Test (SPRT)
The Sequential Probability Ratio Test (SPRT) [
12] is a statistical decision process that comes to a decision with multiple pieces of evidence. It is also considered to be one-dimensional random walk with lower and upper limits [
19]. Specifically, random walk starts from a point between two limits and moves toward the lower or upper limit in line with the type of each incoming evidence. If the walk comes to (or exceeds) the lower (resp. upper) limit, it terminates and accepts the null (resp. alternate) hypothesis.
The main benefit of using the SPRT is that it requires only few pieces of evidence to make a correct decision at the cost of low false positive rate and false negative rate [
12].
4. Replica Cluster Attack Detection
In replica cluster attacks, multiple replicas with the same ID and secret keying materials are closely deployed to each other in a small region. Since the replicas in a cluster want to affect maliciously as many nodes as possible in the network, they would actively communicate with as many nodes as possible at the same time. Hence, the replicas in a cluster would likely communicate with more peers at a time than the ones of their benign neighbors. By leveraging this intuition, we adapt the SPRT to tackle the replica cluster detection problem. Specifically, every node performs the SPRT on its neighbor node with a null hypothesis that a replica cluster of the neighbor node does not exist and an alternate hypothesis that a replica cluster of the neighbor node exists. In the SPRT, as the number of communication peers of a neighbor node falls short of (resp. exceeds) a pre-configured threshold, the random walk will move toward the lower (resp. upper) limit, leading to the acceptance of the null (resp. alternate) hypothesis. Once the SPRT accepts the alternate hypothesis, the node will stop the communication with the neighbor node. The replica cluster detection procedure is described as follows.
After deployment, every sensor node u discovers its neighboring nodes. Node u monitors all messages originating from every neighbor node v and identifies the destinations of these messages. Assume that the entire time domain of u is divided into a series of time slots. Node u computes Xi (i ≥ 1), which is defined as the number of distinct destinations of all messages from v during the ith time slot.
Let N be a total number of nodes in the network. Let Ri be a Bernoulli random variable that is defined as:
The success probability p of Bernoulli distribution is defined as:
If p is smaller than or equal to a preset threshold p0, it is likely that a replica cluster of v does not exist. On the other hand, if p is greater than or equal to a preset threshold p1 (p0 < p1), it is likely that a replica cluster of v exists. The problem of deciding whether a replica cluster of v exists can be formulated as a hypothesis testing problem with null and alternate hypotheses of p ≤ p0 and p ≥ p1, respectively. In this problem, we define a false positive α (resp. a false negative β) as the likelihood that the alternate (resp. null) hypothesis is erroneously accepted when p ≤ p0 (resp. p ≥ p1). In order to make a correct decision in hypothesis testing problem, the false positive (resp. false negative) does not exceed user-configured false positive (resp. user-configured false negative).
In line with this sampling plan, we present how a node u performs the SPRT to decide about a node v from the n observed samples, which are R1,R2,…,Rn. We first define the null hypothesis H0and the alternate one H1 as follows: H0 is the hypothesis that a replica cluster of a node v does not exist and H1 is the hypothesis that a replica cluster of a node v exists. We then define Ln as the log-probability ratio on n samples, given as:
Assume that Ri is independent and identically distributed. Then Ln can be rewritten as:
Let θn denote the number of times that Ri = 1 in the n samples. Then we have
where
Based on the log-probability ratio Ln, the SPRT for H0 against H1 is given as follows:
•
![Jsan 01 00153 i024]()
: accept
H0 and terminate the test;
•
![Jsan 01 00153 i025]()
: accept
H1 and terminate the test;
•
![Jsan 01 00153 i026]()
: continue the test process with another observation,
We can rewrite the SPRT as follows:
• θn ≤ τ0 (n) : accept H0and terminate the test;
• θn ≥ τ1 (n) : accept H1and terminate the test;
• τ0 (n) < θn < τ1 (n) : continue the test process with another observation,
where
If the SPRT decides that a replica cluster of v does not exist, u restarts the SPRT with newly measured samples from v. However, if the SPRT decides that a replica cluster of v exists, u terminates the SPRT on v and isolates v from the network by stopping communication with v.
5. Analysis
In this section, we first describe the replica cluster detection accuracy of our proposed scheme and then analyze the resilience of our proposed scheme against replica cluster attacks. Next, we show how many observations on average are required to detect replica clusters. Finally, we provide an analysis on the energy consumption of our scheme.
5.1. Replica Cluster Detection Accuracy
In the SPRT, we define two types of errors as follows:
Since
β is the false negative probability, (1 −
β) is the replica cluster detection probability. According to [
12], the following inequality holds:
where
α’ and
β’ are user-configured false positive and false negative probabilities. Thus, replica cluster detection probability is bounded from below by
![Jsan 01 00153 i029]()
.
From Equation (5), we see that low user-configured false positive and false negative probabilities will result in a low false negative probability for the sequential test process, leading to high detection rates.
5.2. Resilience against Replica Cluster Attacks
Let us investigate how our proposed scheme tolerates against replica cluster attacks.
Lemma 5.1 Let γ denote the faction of the samples with H1 type out of n samples that node u receives from a replica cluster of node v. Given n samples, u detects a replica cluster of node v if u receives at least γ* × n samples with H1 type from a replica cluster of v such that ![Jsan 01 00153 i031]()
.
Proof 5.1 Since θn is the number of times that the sample with H1 type occurs in n samples, θn =γ × n holds. According to the SPRT, u detects a replica cluster of v if θn ≥ τ1 (n), which is rewritten as γ ≥γ* such that ![Jsan 01 00153 i031]() . Hence, if the number of samples with H1 type that u receives from a replica cluster of v is at least γ* × n, udetects a replica cluster of v
. Hence, if the number of samples with H1 type that u receives from a replica cluster of v is at least γ* × n, udetects a replica cluster of v.
Let us explore how
n affects
γ* when
α' =
β’ = 0.01,
p0 = 0.1, and
p1 = 0.9. As shown in
Figure 1, we see that
γ* gradually decreases as
n increases. This indicates that the SPRT requires the lower fraction of samples with
H1 types for replica cluster detection as the total number of samples increases. Putting it differently, the SPRT detects replica cluster attacks with the fewer number of samples as a replica cluster more actively makes a malicious impact on the network.
5.3. Average Number of Samples for Decision
Let
n denote the number of samples to terminate the SPRT. Since
n is changed with the types of samples, it is considered as a random variable with an expected value
E[
n]. According to [
12], we obtain
E[
n] as follows.
From this equation, we compute the expected numbers of n conditioned on the hypotheses H0 and H1 as follows:
Note that a sample in the SPRT corresponds to a time slot and thus E[n|H0] and E[n|H1] represent an average number of time slots to terminate the SPRT conditioned on the hypothesis H0 and H1, respectively. From Equation (7), given a value of p1, E[n|H1] increases as p0 rises. This means that p0 needs to be configured as a small value in order for replica clusters to be detected with a small number of samples. On the other hand, given a value of p0, E[n|H1] decreases as p1increases. This implies that the large value of p1 diminishes the number of claims required for replica cluster detection.
Figure 1.
The effects of n on γ*, which is the minimum fraction of samples with type H1 in n samples required for node u to detect a replica cluster of node v.
Figure 1.
The effects of n on γ*, which is the minimum fraction of samples with type H1 in n samples required for node u to detect a replica cluster of node v.
5.4. Energy Consumption
Since our scheme requires each sensor node to operate in monitor mode, each sensor node needs to receive all packets sent by its neighboring nodes. We compute the amount of energy that a senor node consumes to receive the packets. According to [
20], Mica2 sensor mote consumes 10 mA current to receive a byte. When battery voltage is 3 V and data rate is 19.2 Kbps, Mica2 takes
![Jsan 01 00153 i039]()
seconds to receive a byte. Thus, it consumes 0.03/2.4 × 10
3 J = 12.5
μ J to receive a byte. Based on this result, we compute the amount of energy depleted by a node when it receives the packets from its neighbors. For this calculation, we consider three cases of the packet size such as 12, 24, 36 bytes. As shown in
Figure 2, as the number of packets received by a node increases, the amount of energy consumed by a node also linearly increases. Given a number of received packets, we observe that the amount of energy consumption rises in line with an increase of packet size. From this observation, we see that packet size needs to be configured to be a small value in order to reduce energy consumption.
Figure 2.
Energy consumption vs. number of packets received by a node.
Figure 2.
Energy consumption vs. number of packets received by a node.
6. Simulation Study
In this section, we first describe our simulation environment and then present the simulation results.
6.1. Simulation Environment
We developed a simple simulation program to evaluate our proposed scheme. In our simulation, we have 1,000 sensor nodes and set
ρ = 0.01. We divide the entire time domain into 60 time slots such that a time slot duration is 60 simulation seconds and perform the simulation in units of time slots. We evaluate our scheme in two cases:
benign and
replica cluster. In benign case, a benign source node communicates with a number of destination nodes. In replica cluster case, a set of replica nodes with the same ID and secret keying materials forms a cluster, which communicates with a number of destination nodes. In both cases, we model the occurrence of the communication with a distinct destination node as a homogeneous Poisson process with rate parameter
λ, and thus the inter-occurrence times of distinct communications follow the exponential distribution. More specifically, the inter-occurrence time between two consecutive communications is calculated as
![Jsan 01 00153 i043]()
, where
U is a uniform random variate such that 0 ≤
U < 1. In benign case,
λ ranges from 0.02 to 0.1. In replica cluster case,
λ ranges from 0.2 to 0.4. We also set both the user-configured false positive threshold
α and the false negative threshold
β to 0.01, and we set the lower threshold
p0 and the upper threshold
p1 to 0.1 and 0.9, respectively. The rationale behind these configurations is discussed in
Section 5.
6.2. Simulation Results
We use the following metrics to evaluate the performance of our proposed scheme:
• Average Number of Samples is the average number of samples required for the SPRT to reach a correct decision.
• False Positive is the error probability that benign node is misidentified as a replica cluster.
• False Negative is the error probability that replica cluster is misidentified as a benign node.
We present the average results for 1,000 runs of the simulation in each configuration such that each run is executed for 60 time slots. For each run, we obtain each metric as the average of the results of the SPRTs that are performed. Note that the SPRT will restart (resp. terminate) if it accepts the null (resp. alternate) hypothesis H0 (resp. H1). Now we present our main findings.
First, we find that there are no false positives and no false negatives. Hence, a replica cluster is always detected and no benign node is misidentified as a replica cluster. This indicates that the SPRT comes to a decision with very high accuracy.
Second, we present the results of the average number of samples. For this purpose, we define
true negative as the case that a benign node is correctly determined to be a benign node. We also define
true positive as the case that a replica cluster is correctly determined to be a replica cluster. In the
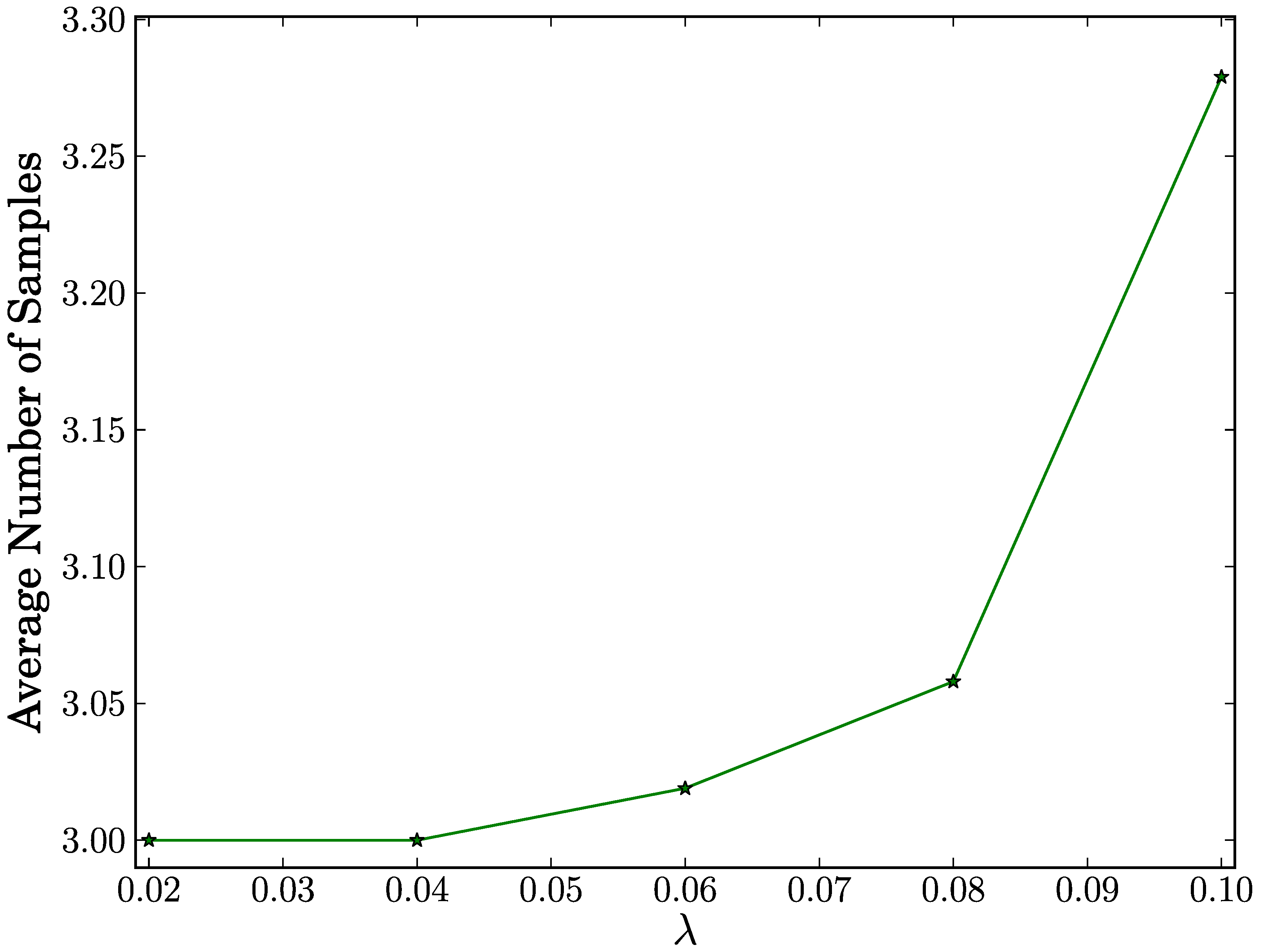
true negative case, as shown in
Figure 3, the average number of samples reaches its maximum of 3.279 for all configurations of
λ. This means that our proposed scheme requires less than four samples with an average in order to make a correct decision on a benign node. We also observe that a rise in
λ results in a very slight increase in the average number of samples. This indicates that the average number of samples increases very slightly in proportion to the number of distinct destination nodes.
In the
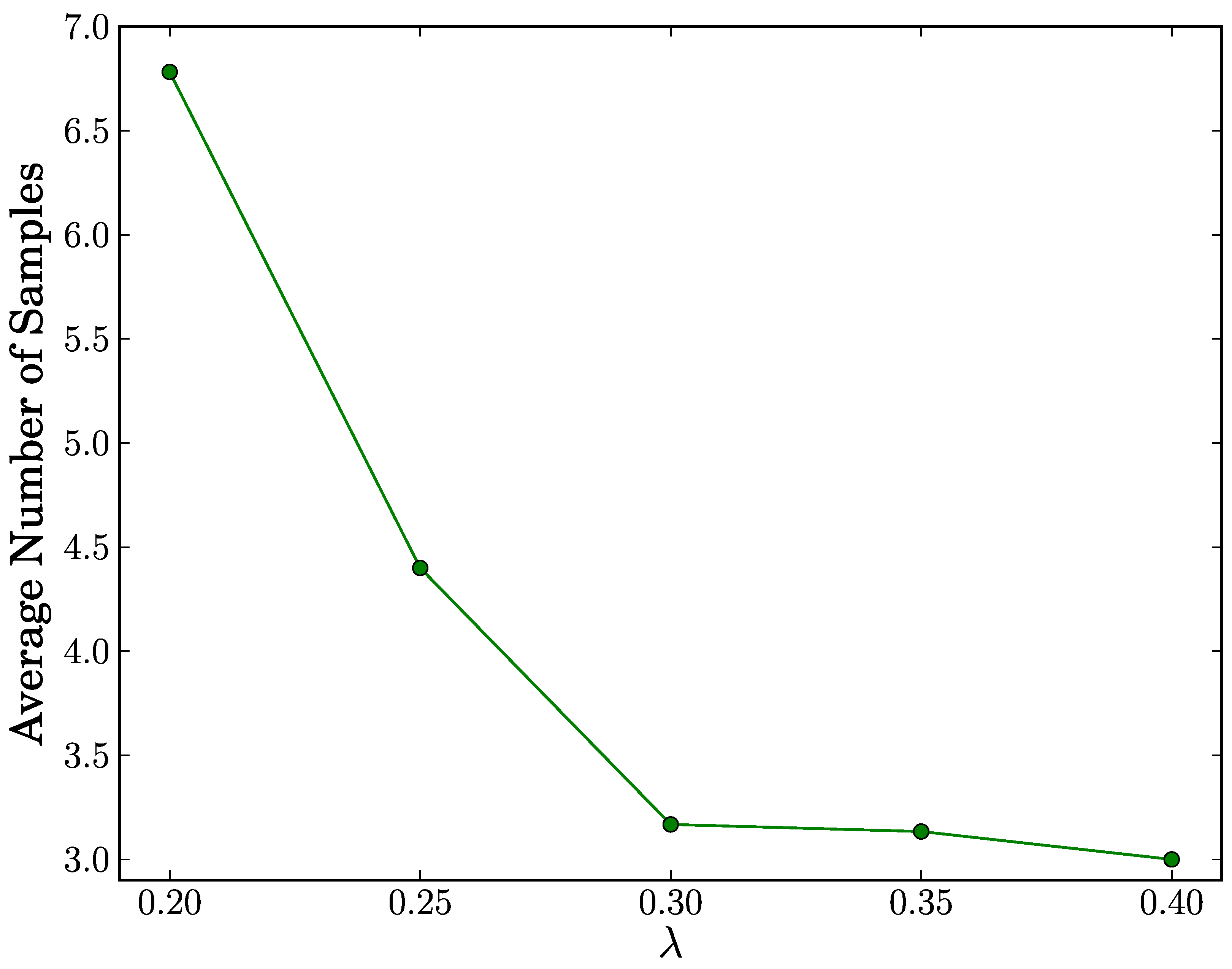
true positive case, as shown in
Figure 4, the average number of samples reaches its maximum of 6.782 for all configurations of
λ. This means that our proposed scheme achieves fast replica cluster detection with at most seven samples on average. Since a sample in the SPRT corresponds to a time slot and a time slot duration is 60 simulation seconds, the detection time will be at most 420 simulation seconds. Moreover, we observe that the average number of samples decreases as
λ increases. We infer from this observation that the higher values of
λ expedite the decision process to terminate in the acceptance of the alternate hypothesis
H1.
Finally,
Figure 5 shows the probability distribution of the number of samples in case of
true positive. In this distribution, we explore the cases of
λ = 0.2 and
λ = 0.25. In case of
λ = 0.2, we observe that in 69.4% of cases, the number of samples is at most seven. In case of
λ = 0.25, we observe that in 82.8% of cases, the number of samples is at most five. This means that the number of samples in most cases is below or very close to the average. As a result, our proposed scheme detects replica clusters with few samples in most cases.
Figure 3.
Average number of samples vs. λ in true negative case.
Figure 3.
Average number of samples vs. λ in true negative case.
Figure 4.
Average number of samples vs. λ in true positive case.
Figure 4.
Average number of samples vs. λ in true positive case.
Figure 5.
Probability distribution of the number of samples in true positive case.
Figure 5.
Probability distribution of the number of samples in true positive case.
7. Conclusions
In this paper, we introduce the replica cluster attacks and propose a replica cluster detection scheme using the Sequential Probability Ratio Test (SPRT). We also analytically show that our proposed scheme achieves robust replica cluster detection capability. Finally, we evaluate our proposed scheme through the simulation. The evaluation results show that it quickly stops replica cluster attacks without false negative or false positive errors.
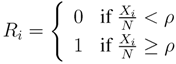
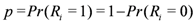
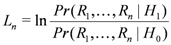
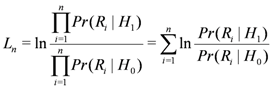
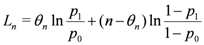
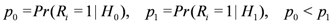
: accept H0 and terminate the test;
: accept H1 and terminate the test;
: continue the test process with another observation,
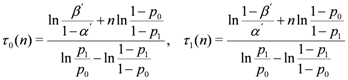
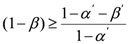
 .
. .
.  . Hence, if the number of samples with H1 type that u receives from a replica cluster of v is at least γ* × n, udetects a replica cluster of v.
. Hence, if the number of samples with H1 type that u receives from a replica cluster of v is at least γ* × n, udetects a replica cluster of v. 
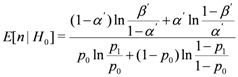
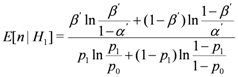

 seconds to receive a byte. Thus, it consumes 0.03/2.4 × 103 J = 12.5μ J to receive a byte. Based on this result, we compute the amount of energy depleted by a node when it receives the packets from its neighbors. For this calculation, we consider three cases of the packet size such as 12, 24, 36 bytes. As shown in Figure 2, as the number of packets received by a node increases, the amount of energy consumed by a node also linearly increases. Given a number of received packets, we observe that the amount of energy consumption rises in line with an increase of packet size. From this observation, we see that packet size needs to be configured to be a small value in order to reduce energy consumption.
seconds to receive a byte. Thus, it consumes 0.03/2.4 × 103 J = 12.5μ J to receive a byte. Based on this result, we compute the amount of energy depleted by a node when it receives the packets from its neighbors. For this calculation, we consider three cases of the packet size such as 12, 24, 36 bytes. As shown in Figure 2, as the number of packets received by a node increases, the amount of energy consumed by a node also linearly increases. Given a number of received packets, we observe that the amount of energy consumption rises in line with an increase of packet size. From this observation, we see that packet size needs to be configured to be a small value in order to reduce energy consumption.
 , where U is a uniform random variate such that 0 ≤ U < 1. In benign case, λ ranges from 0.02 to 0.1. In replica cluster case, λ ranges from 0.2 to 0.4. We also set both the user-configured false positive threshold α and the false negative threshold β to 0.01, and we set the lower threshold p0 and the upper threshold p1 to 0.1 and 0.9, respectively. The rationale behind these configurations is discussed in Section 5.
, where U is a uniform random variate such that 0 ≤ U < 1. In benign case, λ ranges from 0.02 to 0.1. In replica cluster case, λ ranges from 0.2 to 0.4. We also set both the user-configured false positive threshold α and the false negative threshold β to 0.01, and we set the lower threshold p0 and the upper threshold p1 to 0.1 and 0.9, respectively. The rationale behind these configurations is discussed in Section 5.