An Improved Identification Code for City Components Based on Discrete Global Grid System
Abstract
:1. Introduction
2. Method
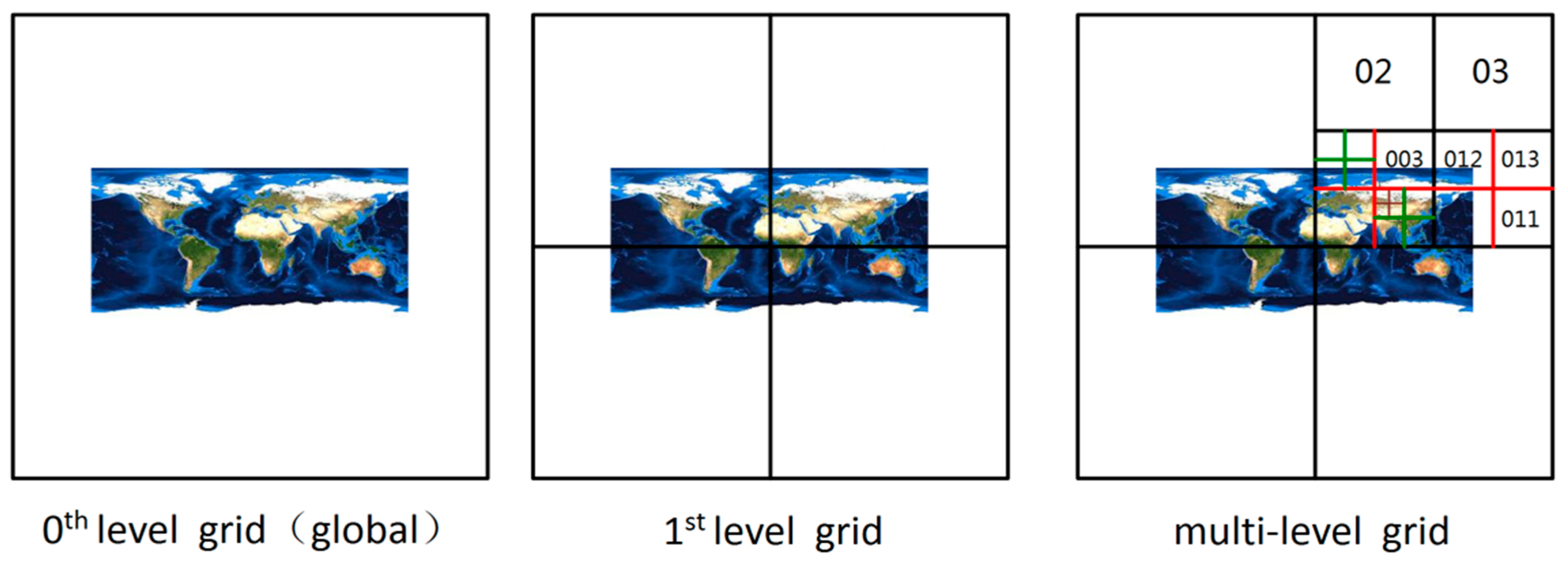
2.1. GeoSOT Grid Code
2.2. Identification Code of the City Component
- (1)
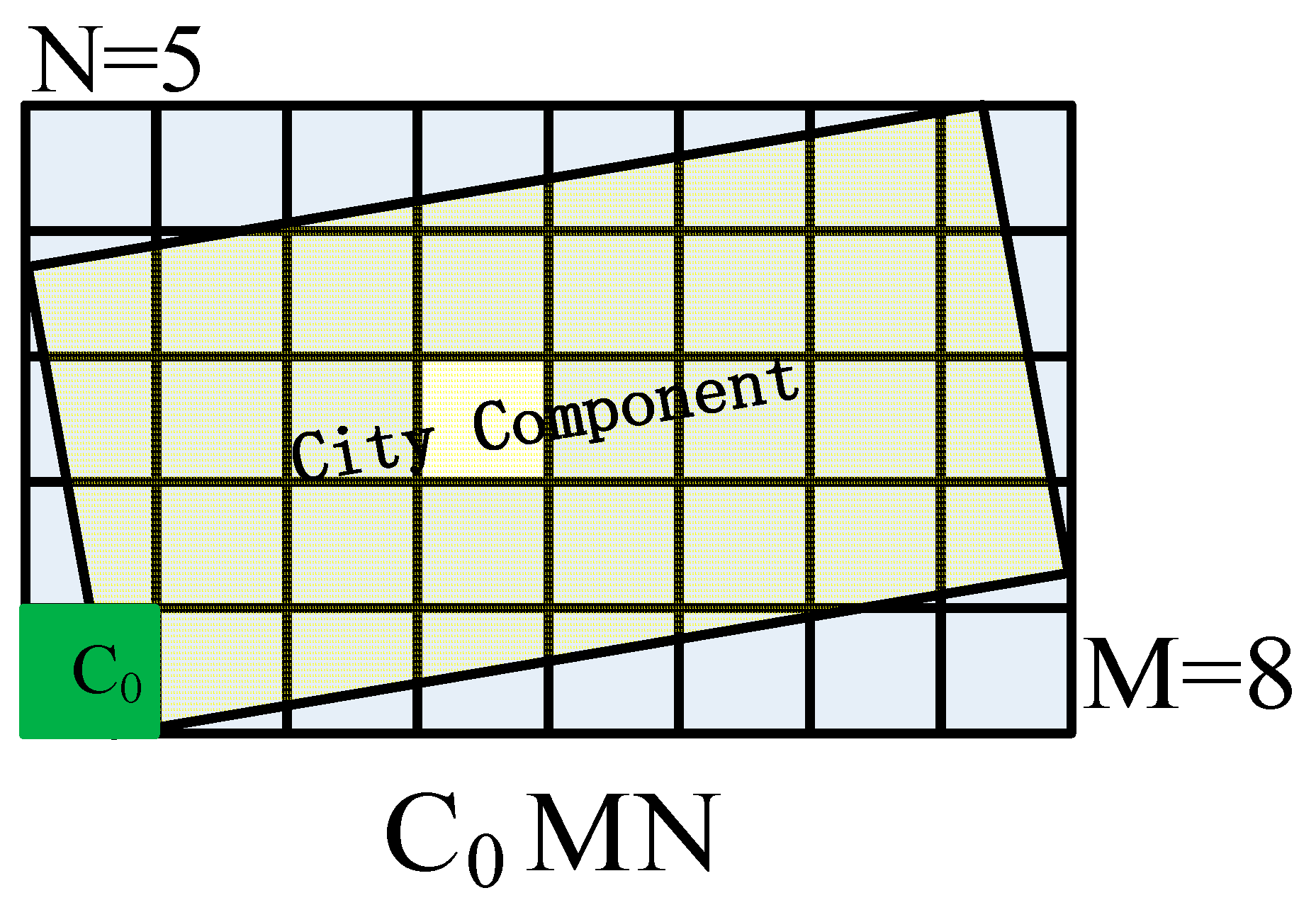
- The optimum grid level. The grid size at the level is and this is calculated by Equation (1).where , and and are the meridional length and zonal length of the component’s minimum bounding rectangle (MBR) (see Figure 2).
- (2)
- : let be the point closest to the Origin (0°, 0°) among the apexes of the component’s MBR, then the grid code of at the optimum grid level is . Specifically, the meridional code can be converted with longitude value by Equation (2), and the zonal code can be converted with latitude value through similar equations. Then, the meridional code and the zonal code are cross-integrated consecutively to form :
- (3)
- : for the two points closest to and farthest from the Origin (0°, 0°) among the apexes of the component’s MBR, whose grids at the optimum grid level are encoded with tag ends of and (). The meridional span code is calculated by Equation (3), and the zonal span code can be calculated by similar equations. For the identification code of point objects, may be omitted; for the identification code of polyline object and polygon object, is required.
3. Results and Discussion
3.1. Results of Encoding
3.2. Analysis of the Code
- (1)
- Universal utility across systems: Sequential code in the traditional method is a series of computer characters without any attributes of the component itself. As different users may specify different sequential codes for the same component, it is not conducive for accurate identification. In contrast, the grid code comes from the location information of the component, so different users may obtain the same identification code for the same city component. It is of universal utility across all of the systems and can facilitate operations between different departments in the unified management of multi-source city components.
- (2)
- Explicit expression of accurate location: The administrative division code in the traditional code usually represents a region with a large area and irregular shape. However, the discrete global grids of the same level share the same shape and size, which is consistent. Furthermore, the grid code can express more accurate spatial location information than the administrative division code. This helps in identifying city components effectively by their grid codes as required, and thereby might contribute to an improvement in the efficiency of a digital city management system.
- (3)
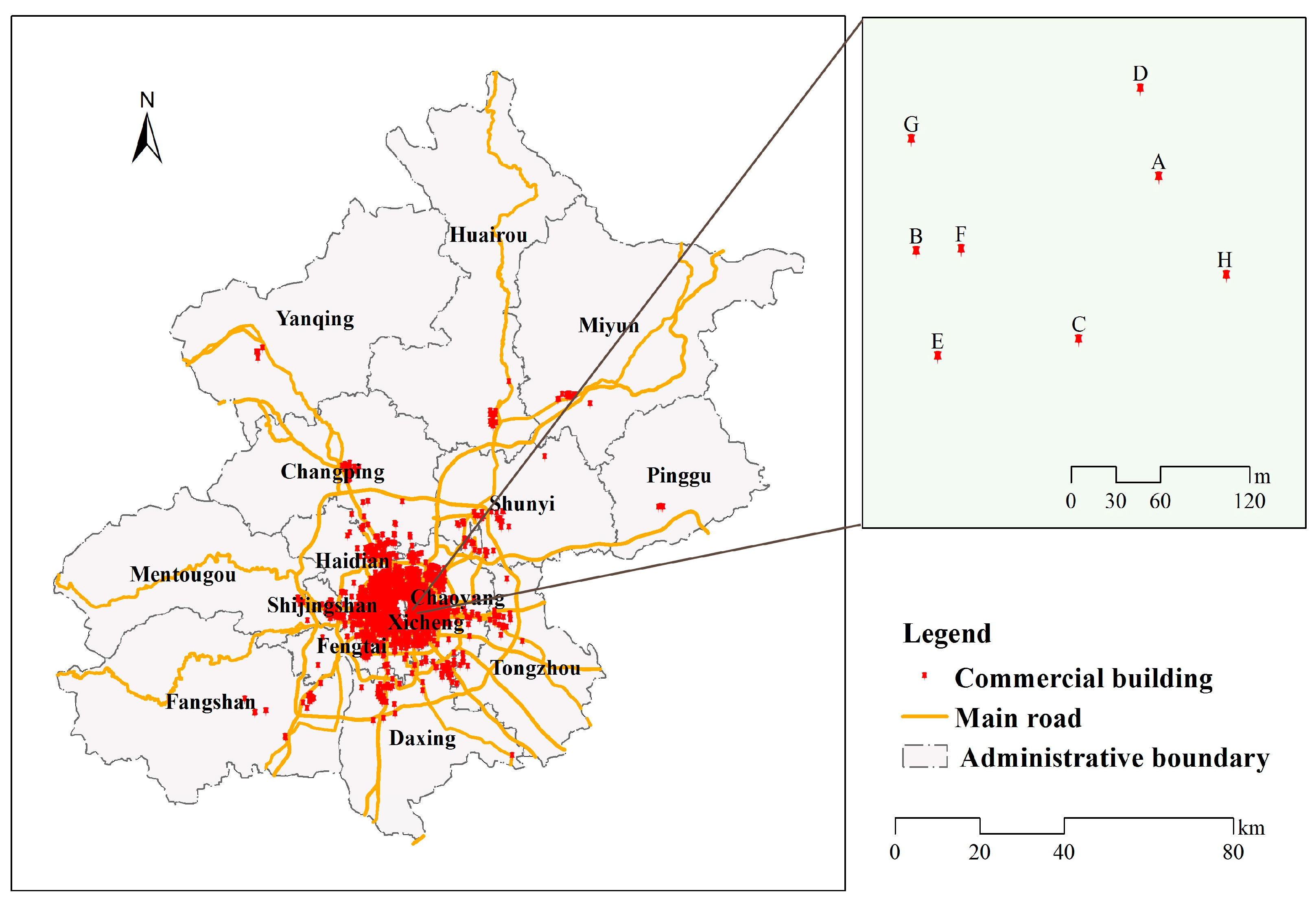
- Implicit expression of spatial relationships: Traditional codes offer hardly any useful information about spatial relationships. However, the discrete global grid system uses a unified subdivision and coding framework, so the grid code can indicate a simple spatial relationship between components [35]. Using Microsoft China (Point A in Figure 3) and the Daimler Tower (Point B in Figure 3), as examples, it can be seen that the codes of these two buildings were B9A33FDE7B and B9A33FDE4A, respectively. They were of the same length, but end with 7B and 4A, respectively. We made a simple inference of the spatial relationship between them according to their codes. For the spatial direction relationship, it was found that Microsoft China is located on the north-east side of the Daimler Tower, since 7 is greater than 4, and B is greater than A. For spatial distance relationship, since the code length was 10 characters, the grid size of this level was inferred to be approximately 48 m × 64 m. Their zonal distance is about three grids (144 m), and their meridional distance about one grid (64 m), which is broadly consistent with the actual distances (125 m and 49 m).
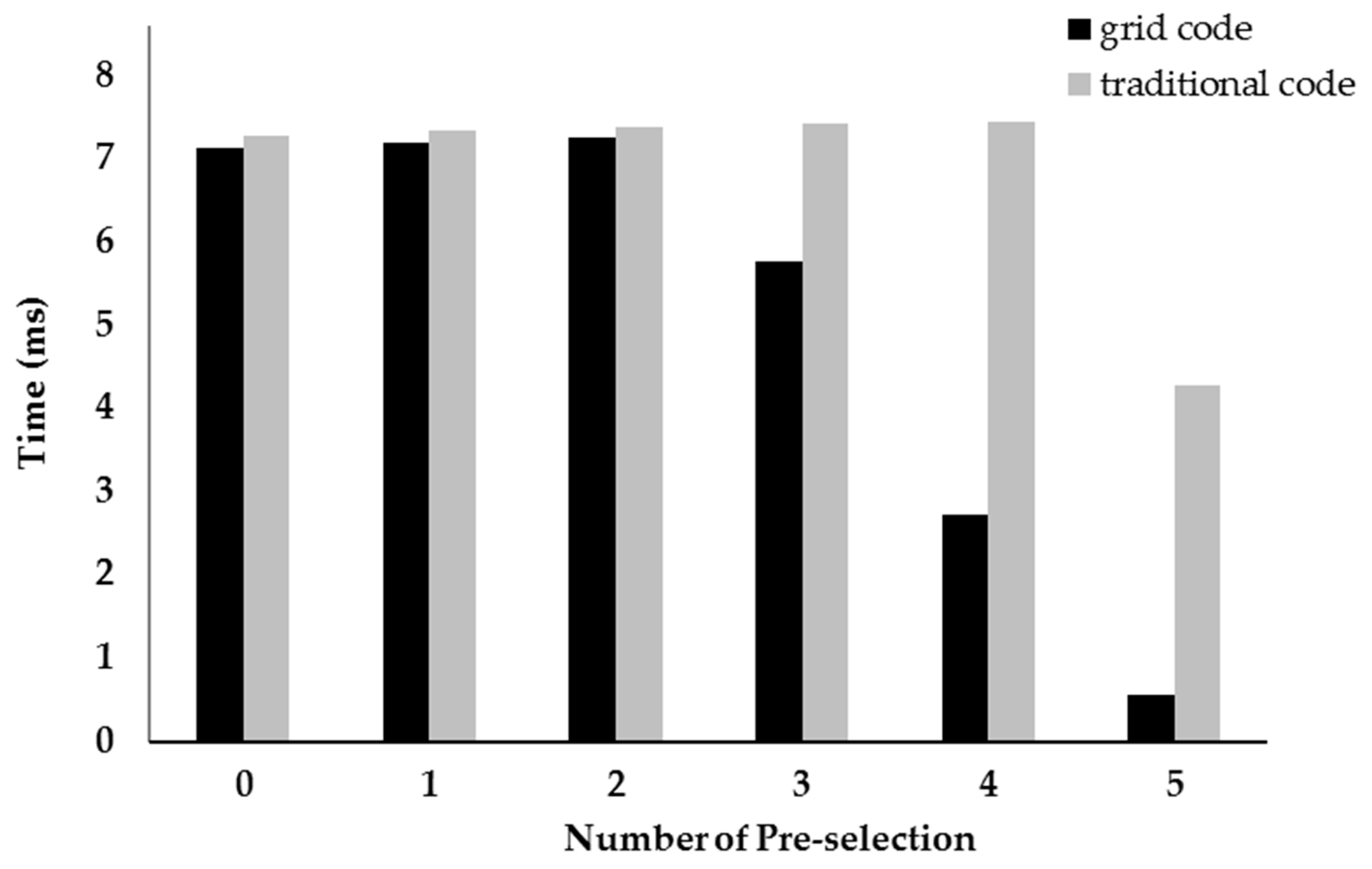
3.3. Comparison in Data Query
3.4. Performance in Geospatial Computation
3.5. Limitations and Prospects
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gong, J.; Wang, G. From digital city to smart city: New challenges to geographic information technology. J. Geomat. 2013, 38, 1–6. [Google Scholar]
- Li, S.; Wang, Y.; Chen, P.; Xu, X.; Cheng, C.; Chen, B. Spatiotemporal fuzzy clustering strategy for urban expansion monitoring based on time series of pixel-level optical and SAR images. IEEE J. STARS 2017, 99, 1–11. [Google Scholar] [CrossRef]
- Lederbogen, F.; Kirsch, P.; Haddad, L.; Streit, F.; Tost, H.; Schuch, P.; Wüst, S.; Pruessner, J.; Rietschel, M.; Deuschle, M.; et al. City living and urban upbringing affect neural social stress processing in humans. Nature 2011, 474, 498–501. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y. Digital collecting method discussion for municipal components in “grid” of urban management system. Beijing Surv. Mapp. 2010, 1, 59–62. [Google Scholar]
- Miao, Z.; Chen, Y.; Zeng, X.; Li, J. Integrating spatial and attribute characteristics of extended Voronoi diagrams in spatial patterning research: A case study of Wuhan City in China. ISPRS Int. J. Geo-Inf. 2016, 5, 120. [Google Scholar] [CrossRef]
- Li, D.; Li, Z.; Peng, M. The construction and application of Wuhan urban grid management and service system. Bull. Surv. Mapp. 2007, 32, 529–533. [Google Scholar]
- Cheng, B.; Li, C.; Fei, L.; Wang, J. Constructing the Geospatial Framework of Digital City. In Proceedings of the IEEE International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011. [Google Scholar]
- Xiao, Q.; Zou, Z. Design and implementation of urban-component mapping system. Eng. Surv. Mapp. 2011, 20, 42–45. [Google Scholar]
- Gao, P.; Wang, D.; Wu, Q. Information System for Digitized Supervision and Management of City; Part 2: Managed Component and Event; Standards Press of China: Beijng, China, 2013. [Google Scholar]
- Enserink, M. Are you ready to become a number? Science 2009, 323, 1662–1664. [Google Scholar] [CrossRef] [PubMed]
- Jörg, B.; Höllrigl, T.; Sicilia, M. Entities and Identities in Research Information Systems. In Proceedings of the International Conference on Current Research Information Systems, Prague, Czech Republic, 6–9 June 2012. [Google Scholar]
- Wang, J. Design and implementation on digitization investigation system of municipal component. Geomat. Spat. Inf. Technol. 2009, 32, 78–80. [Google Scholar]
- Li, S.; Gao, Y.; Fan, M. Research on an efficient method of city component census. Eng. Surv. Mapp. 2016, 25, 76–80. [Google Scholar]
- Liu, J. Components acquisition on the urban grid management. Geomat. Spat. Inf. Technol. 2009, 32, 98–101. [Google Scholar]
- Li, D. Is Geo-Services Ready? On generalized and Specialized Spatial Information Grid. In Proceedings of the ISPRS Workshop on Service and Application of Spatial Data Infrastructure, Hangzhou, China, 14–16 October 2005. [Google Scholar]
- Li, D.; Xiao, Z.; Zhu, X. Research on grid division and encoding of spatial information multi-grids. Acta Geod. Cartogr. Sin. 2006, 1, 52–56. [Google Scholar]
- Goodchild, M.; Yang, S. A hierarchical spatial data structure for global geographic information systems. Graph. Models Image Process. 1992, 54, 31–44. [Google Scholar] [CrossRef]
- White, D.; Kimerling, J.; Overton, W. Cartographic and geometric components of a global sampling design for environment monitoring. Cartogr. Geogr. Inf. Sci. 1992, 19, 5–22. [Google Scholar]
- White, D.; Kimerling, J.; Sahr, K.; Song, L. Comparing area and shape distortion on polyhedral-based recursive partitions of the sphere. Int. J. Geogr. Inf. Sci. 1998, 12, 805–827. [Google Scholar] [CrossRef]
- Kimerling, J.; Sahr, K.; White, D.; Song, L. Comparing geometrical properties of global grids. Cartogr. Geogr. Inf. Sci. 1999, 26, 271–288. [Google Scholar] [CrossRef]
- Sahr, K.; White, D.; Kimerling, J. Geodesic discrete global grid systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Vince, A.; Zheng, X. Arithmetic and Fourier transform for the PYXIS multi-resolution digital Earth model. Int. J. Digit. Earth 2009, 2, 59–79. [Google Scholar] [CrossRef]
- Tong, X.; Ben, J.; Liu, Y.; Zhang, Y. Modeling and expression of vector data in the hexagonal discrete global grid system. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-4/W2, 15–25. [Google Scholar] [CrossRef]
- Tong, X.; Ben, J.; Wang, Y.; Zhang, Y.; Pei, T. Efficient encoding and spatial operation scheme for aperture 4 hexagonal discrete global grid system. Int. J. Geogr. Inf. Sci. 2013, 27, 898–921. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Samavati, F.; Peterson, P. Categorization and conversions for indexing methods of discrete global grid systems. ISPRS Int. J. Geo-Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Zhai, W.; Yang, Z.; Wang, L.; Wu, F.; Cheng, C. The Non-sql Spatial Data Management Model in Big Data Time. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Li, S.; Cheng, C.; Chen, B.; Meng, L. Integration and management of massive remote-sensing data based on GeoSOT subdivision model. J. Appl. Remote Sens. 2016, 10, 034003. [Google Scholar] [CrossRef]
- Lu, N.; Cheng, C.; Jin, A.; Ma, H. An Index and Retrieval Method of Spatial Data Based on GeoSOT Global Discrete Grid System. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Jing, Y.; Cheng, C.; Zhang, B.; Zhai, W. Geographic Spatial Semantic Translation Method Using Subdivision Grid Coding. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Mahdavi-Amiri, A.; Bhojani, F.; Samavati, F. One-to-Two Digital Earth. In Proceedings of the International Symposium on Visual Computing, Crete, Greece, 29–31 July 2013. [Google Scholar]
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hexagonal connectivity maps for Digital Earth. Int. J. Digit. Earth 2015, 9, 750–769. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Alderson, T.; Samavati, F. A survey of digital earth. Comput. Graph. 2015, 53, 95–117. [Google Scholar] [CrossRef]
- Zhai, W.; Cheng, C. Vagueness in Spatial Data: A Grid-Coding Approach. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Cheng, C.; Tong, X.; Chen, B.; Zhai, W. A subdivision method to unify the existing latitude and longitude grids. ISPRS Int. J. Geo-Inf. 2016, 5, 161. [Google Scholar] [CrossRef]
- Chen, D.; Cheng, C.; Song, S.; Dong, F.; Chen, R. Research of Spatial Topological Relation Model Based on GeoSOT. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Hu, X.; Cheng, C. The Three-Dimensional Data Organization Method Based on GeoSOT-3D. In Proceedings of the IEEE International Conference on Geoinformatics, Kaohsiung, Taiwan, 25–27 June 2014. [Google Scholar]
- Sun, Z.; Cheng, C. True 3D modeling of radar detection range based on GeoSOT 3D. Acta Geod. Cartogr. Sin. 2017, 42, 144–148. [Google Scholar]
- Van, M.; Audigé, L.; Hanson, B.; Chanpman, J.; Hosman, A. What should an ideal spinal injury classification system consist of? A methodological review and conceptual proposal for future classifications. Eur. Spine J. 2010, 19, 1238–1249. [Google Scholar]
- Murphy, D.; Purschwitz, M.; Mahoney, B.; Hoskin, A. A proposed classification code for farm and agricultural injuries. Am. J. Public Health 1993, 83, 736–738. [Google Scholar] [CrossRef] [PubMed]
- Sahr, K. Location coding on icosahedral aperture 3 hexagon discrete global grids. Comput. Environ. Urban Syst. 2008, 32, 174–187. [Google Scholar] [CrossRef]
- Sahr, K. Hexagonal discrete global grid systems for geospatial computing. Arch. Photogramm. Cartogr. Remote Sens. 2011, 22, 363–376. [Google Scholar]
- Purss, M.; Gibb, R.; Samavati, F.; Peterson, P.; Rogers, J.; Ben, J.; Dow, C. Topic 21: Discrete Global Grid Systems Abstract Specification; Open Geospatial Consortium: Wayland, MA, USA, 2017. [Google Scholar]
- Dutton, G. Universal Geospatial Data Exchange via Global Hierarchical Coordinates. In Proceedings of the International Conference on Discrete Global Grids, Santa Barbara, CA, USA, 25–28 March 2000. [Google Scholar]
- Goodchild, M.F. Discrete Global Grids for Digital Earth. In Proceedings of the International Conference on Discrete Global Grids, Santa Barbara, CA, USA, 26–28 March 2000. [Google Scholar]
- Bernard, L.; Kanellopoulos, I.; Annoni, A.; Smits, P. The European geoportal––One step towards the establishment of a European Spatial Data Infrastructure. Comput. Environ. Urban Syst. 2005, 29, 15–31. [Google Scholar] [CrossRef]
- Čada, V.; Janečka, K. The strategy for the development of the infrastructure for spatial information in the Czech Republic. ISPRS Int. J. Geo-Inf. 2016, 5, 33. [Google Scholar] [CrossRef]
- Lin, B.; Zhou, L.; Xu, D.; Zhu, A.; Lu, G. A discrete global grid system for earth system modeling. Int. J. Geogr. Inf. Sci. 2017, 4, 1–27. [Google Scholar] [CrossRef]
| Level | Scale | Level | Scale | Level | Scale | Level | Scale |
|---|---|---|---|---|---|---|---|
| 1 | 256° | 9 | 1° | 17 | 16″ | 25 | 1/16″ |
| 2 | 128° | 10 | 32′ | 18 | 8″ | 26 | 1/32″ |
| 3 | 64° | 11 | 16′ | 19 | 4″ | 27 | 1/64″ |
| 4 | 32° | 12 | 8′ | 20 | 2″ | 28 | 1/128″ |
| 5 | 16° | 13 | 4′ | 21 | 1″ | 29 | 1/256″ |
| 6 | 8° | 14 | 2′ | 22 | 1/2″ | 30 | 1/512″ |
| 7 | 4° | 15 | 1′ | 23 | 1/4″ | 31 | 1/1024″ |
| 8 | 2° | 16 | 32″ | 24 | 1/8″ | 32 | 1/2048″ |
| Point | Name | Grid Code | Longitude | Latitude | Address |
|---|---|---|---|---|---|
| A | Microsoft China | B9A33FDE7B | 116.48299 | 39.99451 | No. 8 Wangjing Road |
| B | Daimler Tower | B9A33FDE4A | 116.48153 | 39.99407 | No. 8 Wangjing Road |
| C | Caterpillar Tower | B9A33FDE69 | 116.48251 | 39.99354 | No. 8 Wangjing Road |
| D | North Gate of Lei Shing Hong Plaza | B9A33FDE7C | 116.48288 | 39.99504 | No. 8 Wangjing Road |
| E | South Gate of Lei Shing Hong Plaza | B9A33FDE49 | 116.48166 | 39.99344 | No. 8 Wangjing Road |
| F | Lei Shing Hong Plaza A | B9A33FDE5A | 116.48180 | 39.99408 | No. 8 Wangjing Road |
| G | West Gate of Lei Shing Hong Plaza | B9A33FDE4B | 116.48150 | 39.99474 | No. 8 Wangjing Road |
| H | Lei Shing Hong Plaza C | B9A33FDEA5 | 116.48340 | 39.99392 | No. 8 Wangjing Road |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, K.; Cheng, C.; Hu, Y.; Fang, H.; Ji, Y.; Chen, B. An Improved Identification Code for City Components Based on Discrete Global Grid System. ISPRS Int. J. Geo-Inf. 2017, 6, 381. https://doi.org/10.3390/ijgi6120381
Qi K, Cheng C, Hu Y, Fang H, Ji Y, Chen B. An Improved Identification Code for City Components Based on Discrete Global Grid System. ISPRS International Journal of Geo-Information. 2017; 6(12):381. https://doi.org/10.3390/ijgi6120381
Chicago/Turabian StyleQi, Kun, Chengqi Cheng, Yi’na Hu, Huaqiang Fang, Yan Ji, and Bo Chen. 2017. "An Improved Identification Code for City Components Based on Discrete Global Grid System" ISPRS International Journal of Geo-Information 6, no. 12: 381. https://doi.org/10.3390/ijgi6120381
APA StyleQi, K., Cheng, C., Hu, Y., Fang, H., Ji, Y., & Chen, B. (2017). An Improved Identification Code for City Components Based on Discrete Global Grid System. ISPRS International Journal of Geo-Information, 6(12), 381. https://doi.org/10.3390/ijgi6120381




