An Efficient Parallel Algorithm for Multi-Scale Analysis of Connected Components in Gigapixel Images
Abstract
:1. Introduction
2. Background
2.1. Attribute Filters
2.2. Differential Attribute Profiles and the CSL Model
- convex, if ,
- concave, if ,
- flat, if .
2.3. Attribute Zone Decomposition
2.4. The DMP vs. the DAP
3. The Max-Tree Algorithm and the One-Pass Method
4. A Concurrent One-Pass Method
4.1. Parallel DAP Computation
4.2. Direct MOC Computation
| Algorithm 1 The filtering stage of the parallel Differential Attribute Profiles (DAP) algorithm |
procedure MaxTreeMakeDAP (Vp : Section; var node : Max-Tree; var out : DAP; lambda : integer[numscales]) for all v ∈ Vp do if not node[v].valid then w := v; for all scales i increasing order do while Par(w) ≠ ⊥ ⋀ not node[w].valid ⋀ node[w].area < lambda[i] do w := Par(w); end; ws[i] := w; (∗ temporary storage of for each scale ∗) if node[w].valid then for all scales j ≥ i do (∗ filtered node found ∗) val [j] := out[j][w]; end; else if node[w].area ≥ lambda[i] then (∗ w is filtered ∗) val[i] := out[i][w]; else (∗lambda[i] too large ∗) val[j] := 0; end; end; end; end; u := v; for all scales i increasing order do repeat if u ∈ Vp then for all scales j < i do out[j][u] := f [u]; end; for all scales j ≥ i do out[j][u] := val[j]; end; node[u].valid := true; end; u := node[u].parent; until u = ws[i]; end; if u ∈ Vp then (∗ Process ws[numscales − 1] ∗) for all scales j < i do out[j][u] := f [u]; end; node[u].valid := true; end; end; end; |
| Algorithm 2 The filtering stages of the parallel multi-scale opening characteristic (MOC) |
procedure NodeSetMOC (Vp : Section; var node : Max-Tree; current : integer; var maxDH, curScale : grayval; var outDH, outScale, outOrig : array[0, ..., N − 1]of pixel, lambda : integer[numscales] ); var scale, DH : grayval; if IsLevelRoot(node[current]) then (∗ compute scale and DH for current nodes ∗) scale := FindScale(node[current], lambda); DH := getDH(node[current]); end; if IsLevelRoot(node[current]) and scale = numscales then (∗ Initialize to out of scale range ∗) maxScale := numscales; maxDH := 0; curDH := 0; maxOrig := 0; curScale := numscales; else parent = node[current].parent; if not node[parent].valid then (∗ go into recursion to set parent values correctly ∗) NodeSetMOC(Vp, node, parent, maxDH, curScale, outDH, outScale, outOrig, lambda); else (∗ if the parent is valid, copy relevant values ∗) maxScale := outScale[parent]; maxDH := outDH[parent]; maxOrig := outOrig[parent]; curScale := node[parent].scale; curDH := node[parent].curDH; end if IsLevelRoot(node[current]) then (∗ if I have a level root, some things might change ∗) if scale = curScale then (∗ same scale class: add current pixel’s curDH ∗) curDH = curDH + curDH; else (∗ scale class change, update current scale and DH ∗) curDH = DH; curScale = scale; end; if curDH ≥ maxDH then (∗ If updated curDH is higher than or equal to the maximum DH found update maxDH, maxScale, and outOrig ∗) maxDH := curDH; maxScale := scale; outOrig = gval [current]; end; end; end; if current ∈ Vp then (∗ Store the information ∗) outScale[current] := maxScale; outDH[current] := maxDH; outOrig[current] := maxOrig; node[current].scale := curScale; node[current].curDH := curDH; node[current].valid := true end; end; |
| Algorithm 3 The final filtering stage of the parallel MOC |
procedure MaxTreeComputeMOC (Vp : Section; var outDH, outScale, outOrig : array[0, ..., N − 1]of pixel, lambda : integer[numscales] ); var curScale, maxScale, maxDH, curDH, maxOrig : grayval; for all v ∈ Vp do if not node[v].valid then NodeSetMOC(Vp, v, curDH, maxDH, maxScale, maxOrig, curScale, outDH, outScale, outOrig, lambda); end; end; end; |
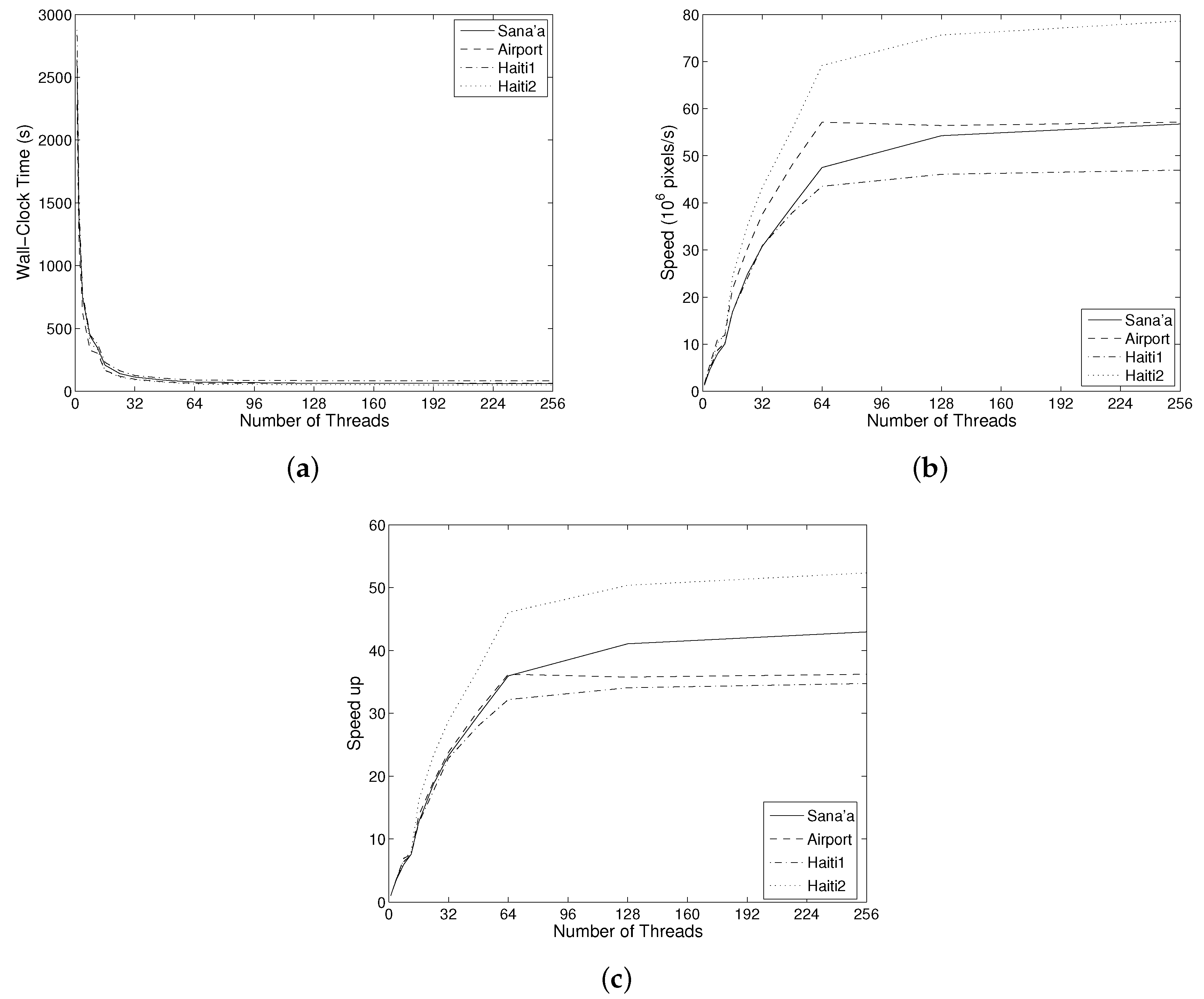
5. Experiments
5.1. Concurrent CSL Computation
- (1)
- Read image, and create inverted copy of image
- (2)
- Build Max-Tree from original image
- (3)
- Compute MOC
- (4)
- Build Min-Tree from inverted image
- (5)
- Build MCC
- (6)
- Combine MOC and MCC to final CSL
- (7)
- Write output
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bangham, J.A.; Ling, P.D.; Harvey, R. Scale-space from nonlinear filters. IEEE Trans. Pattern Anal. Machine Intell. 1996, 18, 520–528. [Google Scholar] [CrossRef]
- Bangham, J.A.; Chardaire, P.; Pye, C.J.; Ling, P.D. Multiscale nonlinear decomposition: The sieve decomposition theorem. IEEE Trans. Pattern Anal. Machine Intell. 1996, 18, 529–538. [Google Scholar] [CrossRef]
- Jackway, P.T.; Deriche, M. Scale-space properties of the multiscale morphological dilation-erosion. IEEE Trans. Pattern Anal. Machine Intell. 1996, 18, 38–51. [Google Scholar] [CrossRef]
- Koenderink, J.J. The structure of images. Biol. Cybernet. 1984, 50, 363–370. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wandell, B.A. Foundations of Vision; Sinauer Associates: Sunderland, MA, USA, 1995. [Google Scholar]
- Pesaresi, M.; Benediktsson, J. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Wilkinson, M.H.F.; Soille, P.; Pesaresi, M.; Ouzounis, G.K. Concurrent computation of differential morphological profiles on giga-pixel images. In Mathematical Morphology and Its Applications to Image and Signal Processing; Soille, P., Pesaresi, M., Ouzounis, G.K., Eds.; Springer: Berlin, Germany, 2011; pp. 331–342. [Google Scholar]
- Gimenez, D.; Evans, A.N. An evaluation of area morphology scale-spaces for colour images. Comput. Vis. Image Underst. 2008, 110, 32–42. [Google Scholar] [CrossRef]
- Salembier, P.; Wilkinson, M.H.F. Connected operators: A review of region-based morphological image processing techniques. IEEE Signal Process. Mag. 2009, 26, 136–157. [Google Scholar] [CrossRef]
- Salembier, P.; Serra, J. Flat zones filtering, connected operators, and filters by reconstruction. IEEE Trans. Image Process. 1995, 4, 1153–1160. [Google Scholar] [CrossRef] [PubMed]
- Ouzounis, G.K.; Soille, P. The Alpha-Tree Algorithm; Technical Report JRC74511; Publications Office of the European Union: ue Adolphe Fischer, Luxembourg, 2012. [Google Scholar]
- Ehrlich, D.; Kemper, T.; Blaes, X.; Soille, P. Extracting building stock information from optical satellite imagery for mapping earthquake exposure and its vulnerability. Nat. Hazards 2013, 68, 79–95. [Google Scholar] [CrossRef]
- Ouzounis, G.K. Automatic Extraction of Built-up Footprints from High Resolution Overhead Imagery through Manipulation of Alpha-Tree Data Structures. U.S. Patent 8682079 B1, 18 May 2014. [Google Scholar]
- Ouzounis, G.K.; Soille, P. Differential area profiles. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 4085–4088.
- Ouzounis, G.K.; Pesaresi, M.; Soille, P. Differential area profiles: Decomposition properties and efficient computation. IEEE Trans. Pattern Anal. Machine Intell. 2012, 34, 1533–1548. [Google Scholar] [CrossRef] [PubMed]
- Murra, M.D.; Benediktsson, J.; Waske, J.B.; Bruzzone, L. Morphological attribute profiles for the analysis of very high resolution images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- Murra, M.D.; Villa, A.; Benediktsson, J.; Chanussot, J.; Bruzzone, L. Classification of hyperspectral images by using extended morphological attribute profiles and independent component analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 541–545. [Google Scholar]
- Salembier, P.; Oliveras, A.; Garrido, L. Anti-extensive connected operators for image and sequence processing. IEEE Trans. Image Process. 1998, 7, 555–570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilkinson, M.H.F.; Gao, H.; Hesselink, W.H.; Jonker, J.E.; Meijster, A. Concurrent computation of attribute filters using shared memory parallel machines. IEEE Trans. Pattern Anal. Machine Intell. 2008, 30, 1800–1813. [Google Scholar] [CrossRef] [PubMed]
- Mura, M.D.; Benediktsson, J.A.; Bruzzone, L. Modelling structural information for building extraction with morphological attribute filters. Proc. SPIE 2009. [Google Scholar] [CrossRef]
- Breen, E.J.; Jones, R. Attribute openings, thinnings and granulometries. Comput. Vis. Image Underst. 1996, 64, 377–389. [Google Scholar] [CrossRef]
- Urbach, E.R.; Wilkinson, M.H.F. Shape-only granulometries and grey-scale shape filters. In Proceedings of the 2002 International Symposium on Mathematical Morphology (ISMM), Berlin, Germany, 20–21 June 2002; pp. 305–314.
- Urbach, E.R.; Roerdink, J.B.T.M.; Wilkinson, M.H.F. Connected shape-size pattern spectra for rotation and scale-invariant classification of gray-scale images. IEEE Trans. Pattern Anal. Machine Intell. 2007, 29, 272–285. [Google Scholar] [CrossRef] [PubMed]
- Gueguen, L.; Soille, P.; Pesaresi, M. Differential morphological decomposition segmentation: A multi-scale object based image representation. In Proceedings of the 20th International Confernece on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 938–941.
- Gueguen, L.; Pesaresi, M.; Soille, P. An interactive image mining tool handling gigapixel images. In Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 1581–1584.
- Akçay, H.G.; Aksoy, S. Automatic detection of geospatial objects using multiple hierarchical segmentations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2097–2111. [Google Scholar] [CrossRef] [Green Version]
- Murra, M.D.; Benediktsson, J.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Int. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Ouzounis, G.K.; Soille, P.; Pesaresi, M. Rubble detection from VHR aerial imagery data using differential morphological profiles. In Proceedings of the 34th International Symposium Remote Sensing of the Environment, Sydney, NSW, Australia, 10–14 April 2011.
- Gueguen, L.; Soille, P.; Pesaresi, M. Structure extraction and characterization from differential morphological profile. In Proceedings of the 7th Conference Image Information Mining, Sydney, NSW, Australia, 9–11 May 2011; pp. 53–57.
- Jin, X.; Davis, C.H. Automated building extraction from high-resolution satellite imagery in urban areas using structural, contextual, and spectral information. EURASIP J. Appl. Signal Process. 2005, 14, 2196–2206. [Google Scholar] [CrossRef]
- Shyu, C.R.; Scott, G.; Klaric, M.; Davis, C.H.; Palaniappan, K. Automatic object extraction from full differential morphological profile in urban imagery for efficient object indexing and retrievals. In Proceedings of the 3rd International Symposium Remote Sensing and Data Fusion Over Urban Areas (URBAN 2005), Tempe, AZ, USA, 13 March 2005.
- Pesaresi, M.; Ouzounis, G.K.; Gueguen, L. A new compact representation of morphological profiles: Report on first massive VHR image processing at the JRC. In Proceedings of SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 23–27 April 2012.
- Pesaresi, M.; Kanellopoulos, I. Detection of urban features using morphological based segmentation and very high resolution remotely sensed data. In Machine Vision and Advanced Image Processing in Remote Sensing; Springer: Berlin, Germany, 1999; pp. 271–284. [Google Scholar]
- Pesaresi, M.; Benediktsson, J.A. Image segmentation based on the derivative of the morphological profile. In Mathematical Morphology and Its Applications to Image and Signal Processing; Springer: Berlin, Germany, 2000; pp. 179–188. [Google Scholar]
- Beucher, S. Numerical residues. Image Vis. Comput. 2007, 25, 405–415. [Google Scholar] [CrossRef]
- Retornaz, T.; Marcotegui, B. Scene text localization based on the ultimate opening. In Proceedings of the International Symposium on Mathematical Morphology, Montreal, PQ, Canada, 21–22 October 2007; pp. 177–188.
- Hernández, J.; Marcotegui, B. Shape ultimate attribute opening. Image Vis. Comput. 2011, 29, 533–545. [Google Scholar] [CrossRef]
- Pesaresi, M.; Huadong, G.; Blaes, X.; Ehrlich, D.; Ferri, S.; Gueguen, L.; Halkia, M.; Kauffmann, M.; Kemper, T.; Lu, L.; et al. A global human settlement layer from optical HR/VHR RS data: Concept and first results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2102–2131. [Google Scholar] [CrossRef]
- Florczyk, A.J.; Ferri, S.; Syrris, V.; Kemper, T.; Halkia, M.; Soille, P.; Pesaresi, M. A new european settlement map from optical remotely sensed data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015. [Google Scholar] [CrossRef]
- Ehrlich, D.; Tenerelli, P. Optical satellite imagery for quantifying spatio-temporal dimension of physical exposure in disaster risk assessments. Nat. Hazards 2013, 68, 1271–1289. [Google Scholar] [CrossRef]
- Lu, L.; Guo, H.; Pesaresi, M.; Soille, P.; Ferri, S. Automatic recognition of built-up areas in China using CBERS-2B HR data. In Proceedings of 2013 Joint Urban Remote Sensing Event (JURSE), Sao Paulo, Brazil, 21–23 April 2013; pp. 65–68.
- Song, B.; Li, J.; Dalla Mura, M.; Li, P.; Plaza, A.; Bioucas-Dias, J.; Benediktsson, J.; Chanussot, J. Remotely sensed image classification using sparse representations of morphological attribute profiles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5122–5136. [Google Scholar] [CrossRef]
- Kemper, T.; Mudau, N.; Mangara, P.; Pesaresi, M. Towards an automated monitoring of human settlements in South Africa using high resolution SPOT satellite imagery. Int. Archi. Photogramm. Remote Sens. 2015, 40, 1389–1394. [Google Scholar] [CrossRef] [Green Version]
- Horvat, D.; Aalik, B.; Rupnik, M.; Mongus, D. Visualising the attributes of biological cells, based on human perception. In Human-Computer Interaction and Knowledge Discovery in Complex, Unstructured, Big Data; Springer: Berlin, Germany, 2013; pp. 386–399. [Google Scholar]
- Vincent, L. Greyscale area openings and closings, their efficient implementation and applications. In Proceedings of the EURASIP Workshop on Mathematical Morphology and Its Applications to Signal Processing, Barcelona, Spain, 12 May 1993; pp. 22–27.
- Maragos, P.; Ziff, R.D. Threshold superposition in morphological image analysis systems. IEEE Trans. Pattern Anal. Machine Intell. 1990, 12, 498–504. [Google Scholar] [CrossRef]
- Meijster, A.; Wilkinson, M.H.F. A comparison of algorithms for connected set openings and closings. IEEE Trans. Pattern Anal. Machine Intell. 2002, 24, 484–494. [Google Scholar] [CrossRef]
- Najman, L.; Couprie, M. Building the component tree in quasi-linear time. IEEE Trans. Image Process. 2006, 15, 3531–3539. [Google Scholar] [CrossRef] [PubMed]
- Menotti-Gomes, D.; Najman, L.; de Albuquerque Araújo, A. 1D Component tree in linear time and space and its application to gray-level image multithresholding. In Proceedings of 8th International Symposium on Mathematical Morphology (ISMM), Rio de Janeiro, Brazil, 10–13 October 2007; pp. 437–448.
- Berger, C.; Geraud, T.; Levillain, R.; Widynski, N.; Baillard, A.; Bertin, E. Effective component tree computation with application to pattern recognition in astronomical imaging. In Proceedings of the ICIP 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA; 2007; pp. 41–44. [Google Scholar]
- Wilkinson, M.H.F. A fast component-tree algorithm for high dynamic-range images and second generation connectivity. In Proceedings of the 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 1041–1044.
- Urbach, E.R.; Wilkinson, M.H.F. Efficient 2-D gray-scale morphological transformations with arbitrary flat structuring elements. IEEE Trans. Image Process. 2008, 17, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, M.H.F.; Moschini, U.; Ouzounis, G.K.; Pesaresi, M. Concurrent computation of connected pattern spectra for very large image information mining. In Proceedings of ESA-EUSC-JRC 8th Conference on Image Information Mining, Oberpfaffenhofen, Germany, 24–26 October 2012; pp. 21–25.
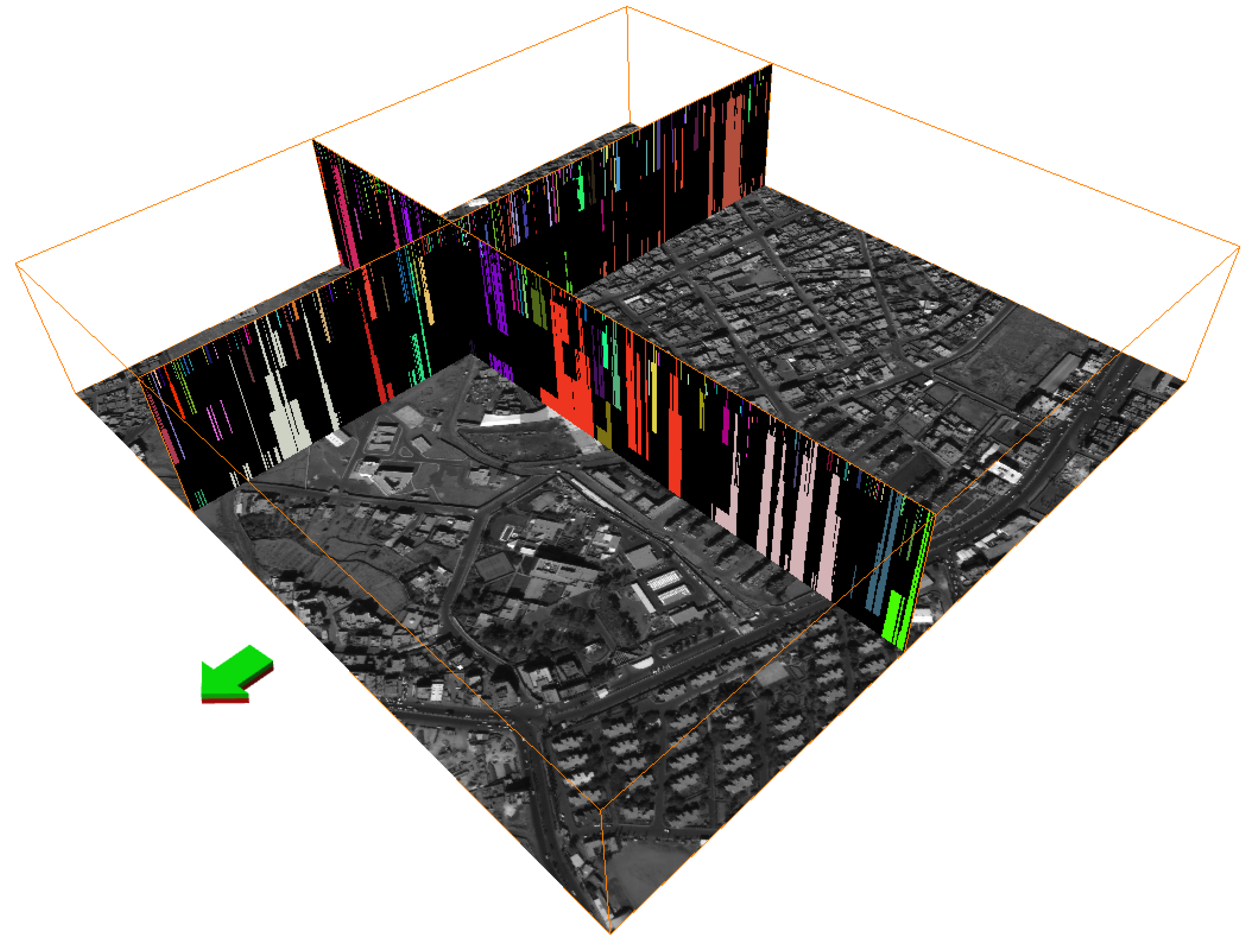



| Name | Size (× 106 Pixels) | Mean | Std. Dev. |
|---|---|---|---|
| Sana’a | 3482 | 121.78 | 75.57 |
| Airport | 3600 | 96.58 | 47.55 |
| Haiti1 | 3888 | 107.71 | 62.99 |
| Haiti2 | 3963 | 81.34 | 52.39 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilkinson, M.H.F.; Pesaresi, M.; Ouzounis, G.K. An Efficient Parallel Algorithm for Multi-Scale Analysis of Connected Components in Gigapixel Images. ISPRS Int. J. Geo-Inf. 2016, 5, 22. https://doi.org/10.3390/ijgi5030022
Wilkinson MHF, Pesaresi M, Ouzounis GK. An Efficient Parallel Algorithm for Multi-Scale Analysis of Connected Components in Gigapixel Images. ISPRS International Journal of Geo-Information. 2016; 5(3):22. https://doi.org/10.3390/ijgi5030022
Chicago/Turabian StyleWilkinson, Michael H.F., Martino Pesaresi, and Georgios K. Ouzounis. 2016. "An Efficient Parallel Algorithm for Multi-Scale Analysis of Connected Components in Gigapixel Images" ISPRS International Journal of Geo-Information 5, no. 3: 22. https://doi.org/10.3390/ijgi5030022






