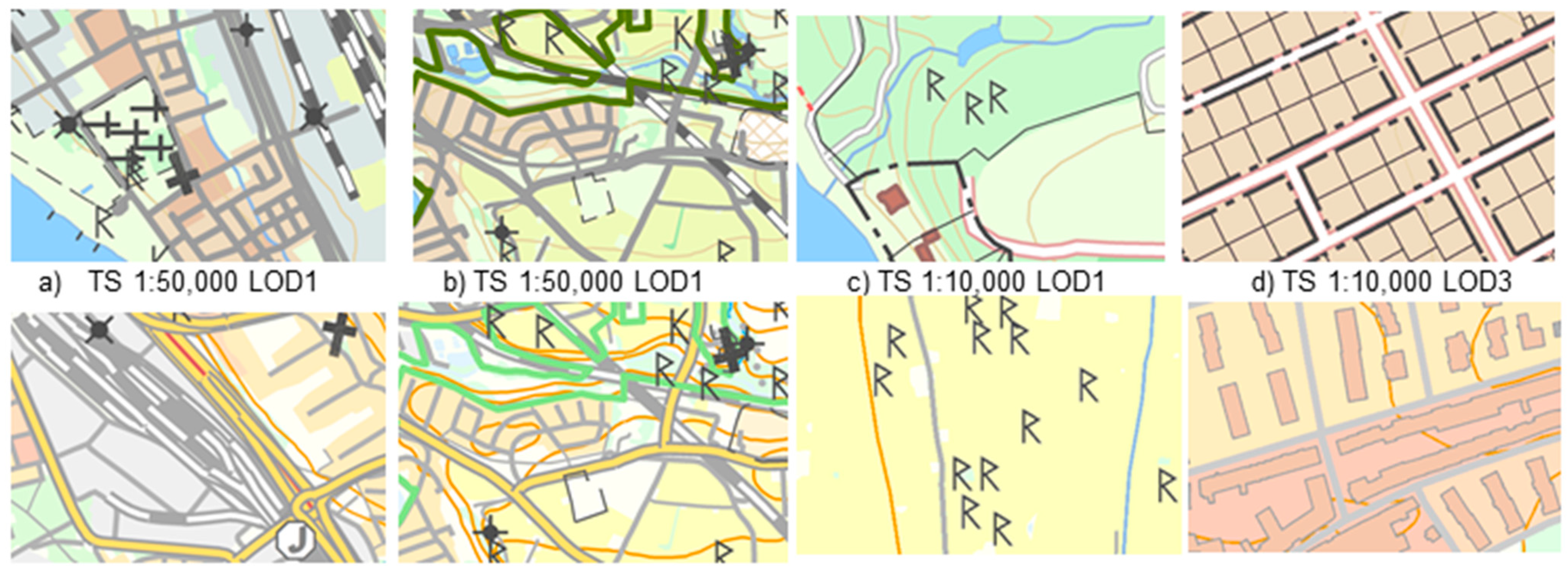
5.1. User Tests
The data acquisition process,
i.e., the user test, is important. In this study, we used a web-distributed test, which provided us with a large number of participants. This extensive material has been valuable when performing the described evaluations. However, every method has disadvantages. One disadvantage of our user test is that we were not able to observe or talk to the participants during the test. At the end of the test, we provided a comment box for which the participants were able to comment on the test or maps. However, only a few participants took advantage of this feature. Therefore, we do not know the attitudes of most of the participants towards the maps, which might have provided valuable qualitative data. Another disadvantage of user tests based on judgment is that they might answer differently than they would in real life [
61]. In future studies, it is therefore important to include other user test methods to reflect the different aspects of participants’ performances.
In the user studies we divided the participants into seven groups where the groups studied different maps. If there are biases between the groups this will potentially affect the classification of the map samples, especially since we used a single threshold value to distinguish between readable and non-readable maps. These circumstances are likely the reason that seemingly similar map samples are classified differently (see e.g., the map samples Trad10_GL1_04, Trad10_GL2_04 and Trad10_GL3_04 in the supplementary material).
In the user test, we used a scale of four possible answers, where we later classified two as readable and the other two as non-readable maps. In this way, we forced the user to decide whether the map was readable or not. Forcing the user to answer without a neutral choice is debatable, and we are aware that our choice of excluding a neutral choice might bias our results. Furthermore, we used the mean value of all answers to decide whether a map was readable or non-readable. We also tested with using the median values. The difference between these measures was fairly small. Five readable map samples (using mean values) where classified as non-readable using medians, and the same amount was misclassified in the other direction. All of the map samples that were classified differently using mean and medians had a perceived readability value between 2.41 and 2.58. In our study we preferred to use the mean value since it provided us with the possibility to use standard multiple linear regression with the (mean) perceived readability values as dependent variable (cf. Equation (11)).
5.2. Composites of Measures
There are no major differences between the results of the three composite methods (
Table 8). The percentage of correctly classified maps is mainly dependent on the ability or inability of the measures to explain readability. However, there are a few things that we should note. The threshold evaluation is appealing because it is conceptually easy and logical. If all the threshold constraints are met, then the map is simply classified as readable. A challenge of this method is setting the threshold. In this study, we set the threshold values according to a common formula for all measures (Equation (10)). We tested the threshold values through manual modifications to obtain a somewhat better result, but we preferred to continue with Equation (10) in the evaluation. In principle, it would also be possible to write an optimization routine to define the optimal threshold values (according to the map samples).
The results of
multiple linear regression (MLR) and
support vector machine (SVM) are similar (
Table 8). There are well-known methods for determining the regression parameters in MLR and the hyperplanes in SVM. One advantage of SVM is its ability to handle the situation in which training datasets only have information on whether the training map samples are readable or non-readable (a standard MLR requires numerical readability values). Additionally, the MLR method is likely more sensitive for outliers in the test data, which could be map samples with uncommon measurement values.
We also performed experiments with the artificial neural network Biased ARTMAP [
62,
63]. Biased ARTMAP is an unsupervised learning classification (clustering of map samples in measurement space) followed by supervised classification (determining whether each map sample cluster contains readable or non-readable map samples). However, the use of Biased ARTMAP produced significantly worse results than the other composite methods, possibly because Biased ARTMAP, and similar methods, relies on clusters in the input data. However, the readable/non-readable map samples do not form clusters in the measurement space (
cf. Figure 2) but rather determine the perceived readability by threshold values.
5.3. Evaluation of the Study
In our composite study (
Table 8), approximately 80% of the map samples were classified correctly based on the three best available measures. The accuracy was possibly limited by the following factors:
- (1)
The readability measures are inadequate.
- (2)
The symbol design was not good.
- (3)
The best composites methods were not used.
- (4)
We must consider the semantic aspects of map reading.
- (5)
We should have used fuzzy classification rather than crisp classification.
A short discussion of each of these factors is stated below.
One could argue that we included all relevant measures in this study. However, raster-based measures (e.g., [
12,
23]) and measures of complexity and graphical resolution (developed in e.g., [
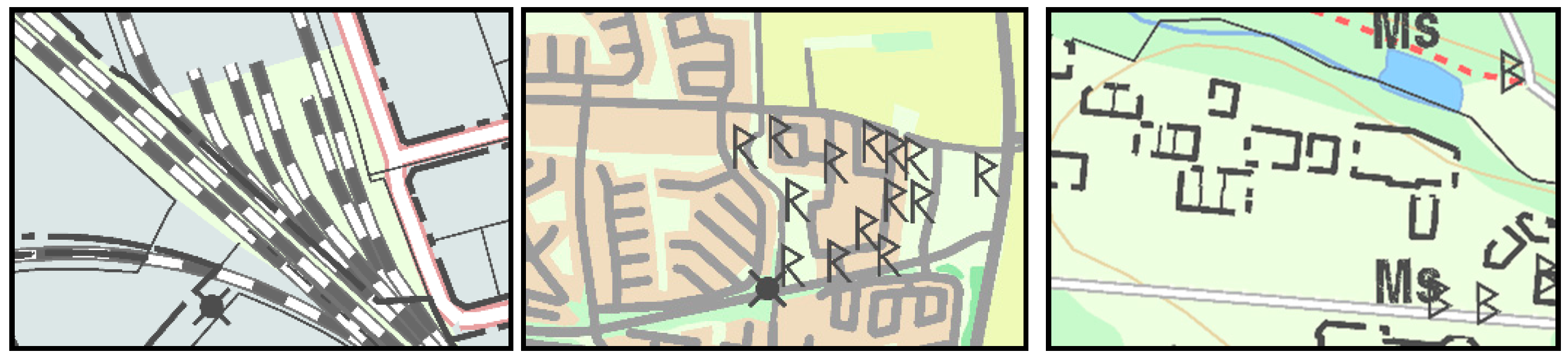
17]) are missing. Of course, we may still need to develop new measures that are missing in the literature. If we study map samples that were perceived as non-readable (by the participants) but classified as readable (by the measures), then we find samples with regions of dense lines (foremost railway lines) and point objects (
cf. Figure 5 and supplementary material). Here, we would need better measures to include these properties. One might also argue that the problem of the readability of these maps is not related to geometry but to the symbol style; hence, readability measures that better capture the symbol style are needed. It might also be so that the maps in
Figure 5 are perceived as non-readable because of that there are several similar objects in a neighborhood, which complicate the search for a spatial object (see e.g., [
5,
26]).
The design of the symbols is surely an important aspect of map readability. In our result we revealed that map samples including cadastre boundaries often were classified as non-readable. This is especially the case for small real-estates such as the right map in
Figure 5. In this case the chosen map symbol for the cadastre boundary is not appropriate for the size of the cadastre units.
Figure 5.
Maps that were often misclassified as readable: (left) maps with dense lines, (middle) maps with dense/overlapping symbols and (right) map with bad symbol types (of the cadastre boundaries).
Figure 5.
Maps that were often misclassified as readable: (left) maps with dense lines, (middle) maps with dense/overlapping symbols and (right) map with bad symbol types (of the cadastre boundaries).
An interesting research direction is to identify a pattern between misclassified maps and the properties of the map samples (
cf. supplementary material). We studied the relationships between the classification between the map samples and the outcomes of the study. A χ
2 test (with 5% significance) indicates that map samples that are dense and have dense lines is more likely to be misclassified (than map samples in general), but it is hard to make any clear conclusion. If we would have used a finer categorization of the properties of the map samples, we could perhaps have been able to identify the map samples in
Figure 5; however, our categorization (which occurred before the analysis) was too broad.
We can conclude that the three composite methods used provided similar results, despite the differing foundations of the methods. We can also conclude that composite methods based on clustering in measurement space, such as Biased ARTMAP [
62,
63], are not appropriate. Whether there are other composite methods that would provide substantially better results are, to the authors’ knowledge, not very likely.
The readability measures in this study are at the syntactic level (
cf. Section 2.5),
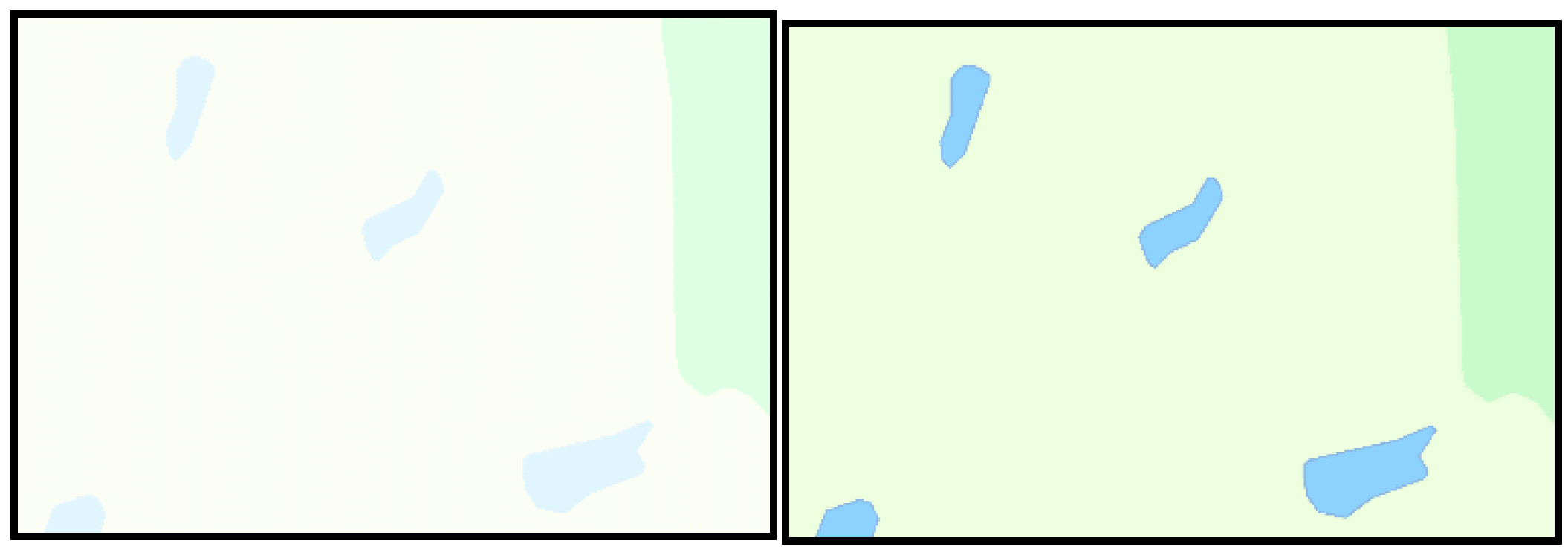
i.e., they measure graphical complexity. By studying the examples of misclassified map samples, we can observe the following. Map samples that are perceived as readable but classified as non-readable often cover a common geographic pattern (
Figure 6 and supplementary material). For map samples that cover more unusual geographic regions, the situation is often the opposite: the map samples are perceived as non-readable but classified as readable (
Figure 6 and supplementary material). Hence, it seems as that the map reader’s ability to interpret the map in a geographical context are important,
i.e., we cannot neglect the semantic aspects of the map samples when we study map reading. This result is indicated even though we deliberately chose map regions that did not contain strange geographic features (
cf. Section 3.2). One can argue that this result is an obvious result, e.g., it is well-established that readability of images in general is affected by the understanding of the context [
43].
Figure 6.
The two maps on the top are perceived as readable but are classified as non-readable; they both include a common geographic pattern. The two maps on the bottom are perceived as non-readable but are classified as readable; they both cover a more unusual geographic pattern.
Figure 6.
The two maps on the top are perceived as readable but are classified as non-readable; they both include a common geographic pattern. The two maps on the bottom are perceived as non-readable but are classified as readable; they both cover a more unusual geographic pattern.
Finally, in our study, we classified all the map samples as either readable or non-readable. By studying the perceived readability values for misclassified map samples (
cf. supplementary material), we can conclude that many misclassified map samples have a perceived readability value close to the threshold (as described in
Section 4.1, we used a perceived readability value of 2.5 as the threshold). One could experiment to see whether the use of a fuzzy classification scheme would improve the results, but this objective is outside the scope of our paper.