Effects of Pansharpening on Vegetation Indices
Abstract
:1. Introduction
2. Fast Pansharpening Algorithms
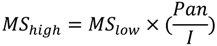
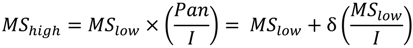
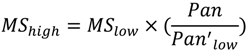
3. Effects of Pansharpening on Spatial Enhancement of Pansharpened Images

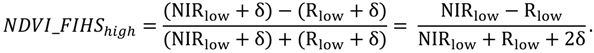
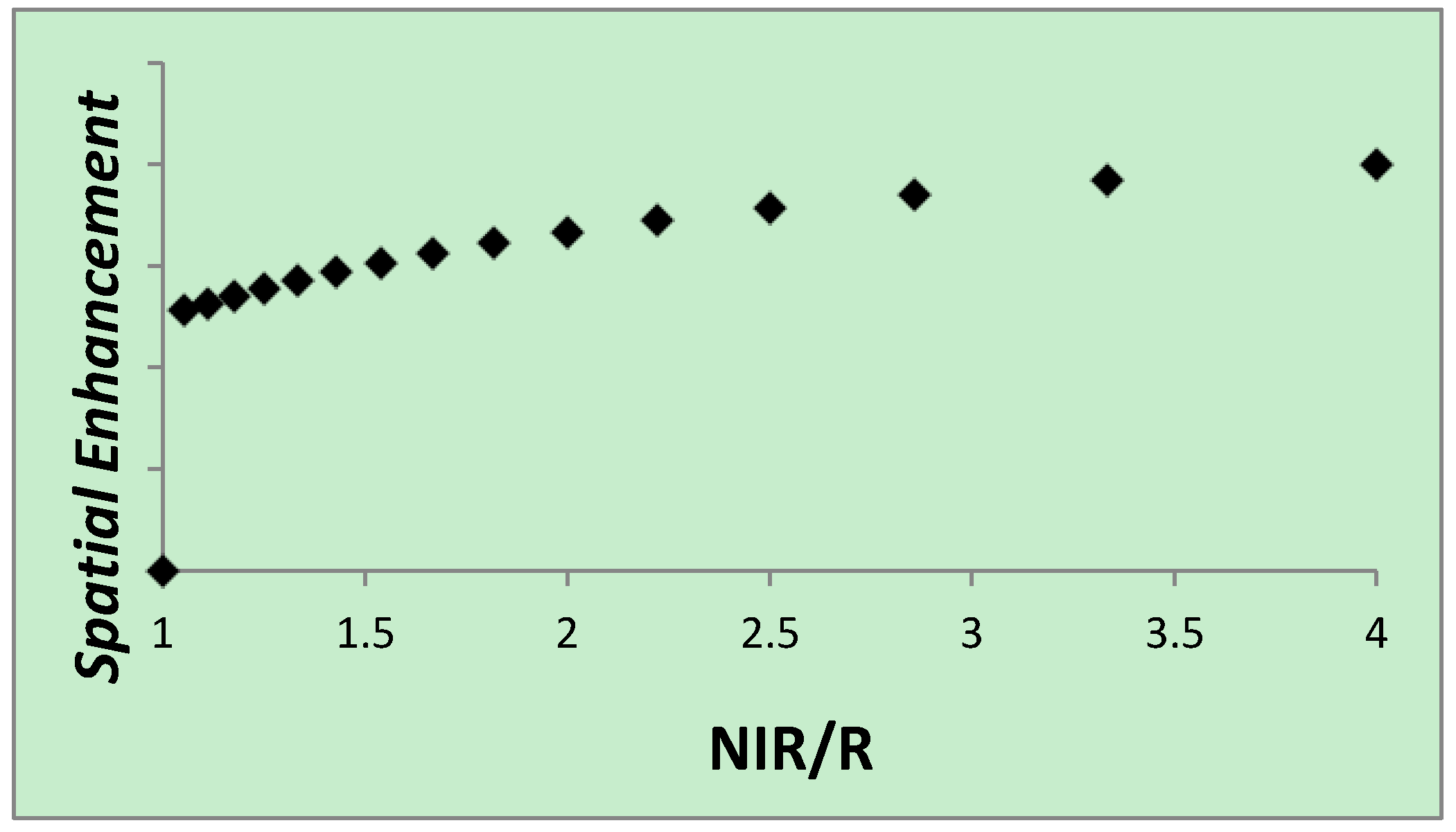
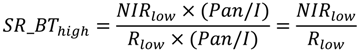
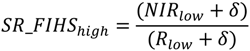
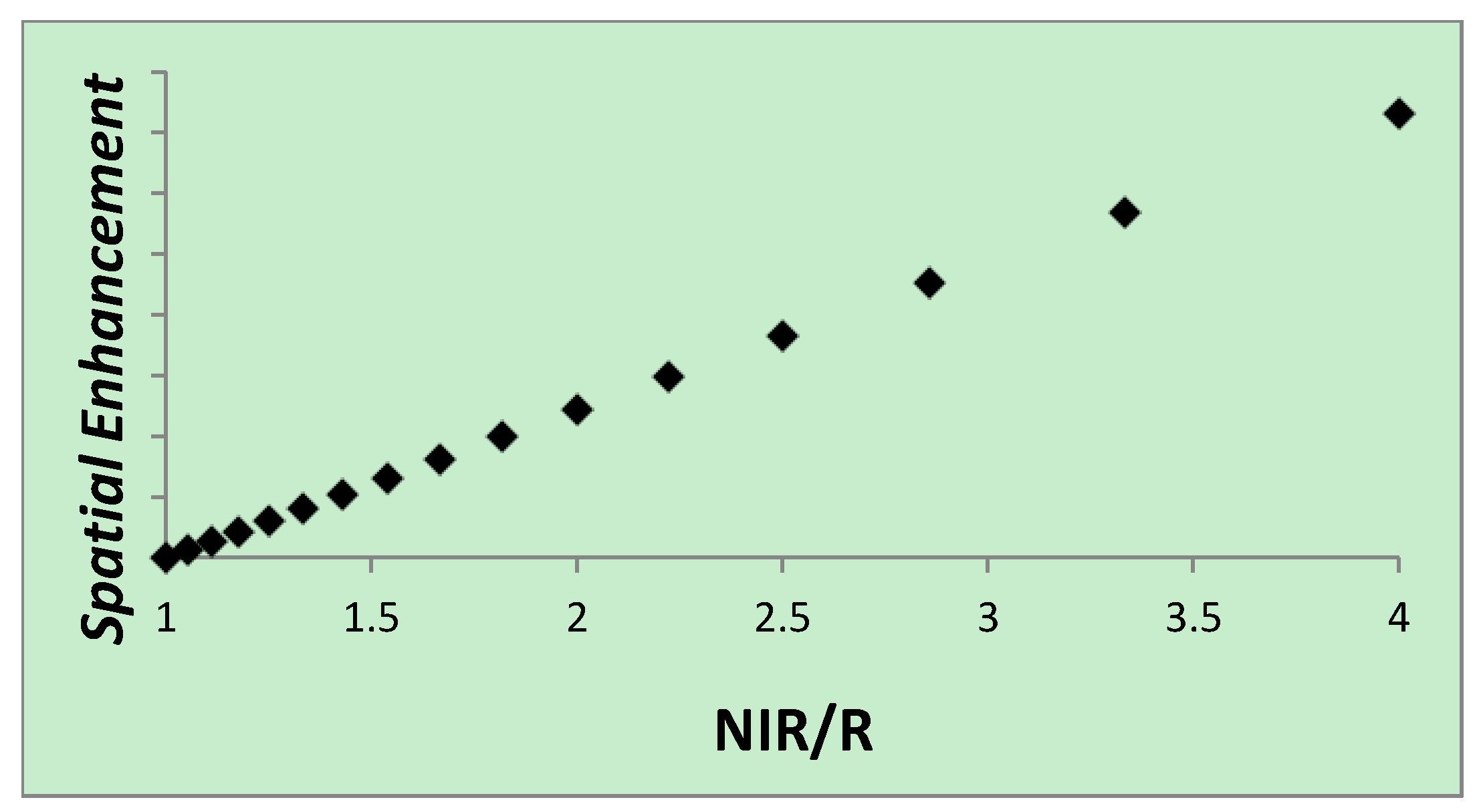
4. Methods
4.1. Study Area and Data

4.2. Image Pansharpening
4.3. Quantitative Evaluation of Pansharpened VI Images
5. Results and Discussion
5.1. Quantitative Evaluation of Pansharpened VI Images
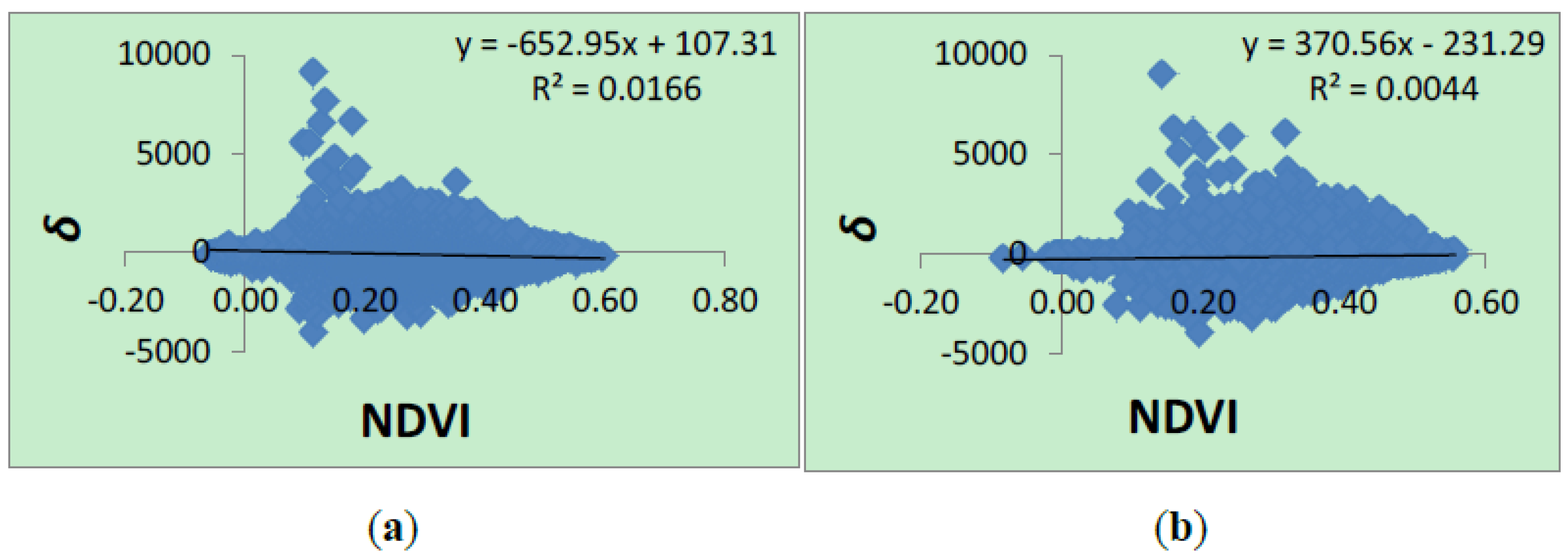
5.2. Spectral Quality of Pansharpened VI Images
| NDVI Image | Spectral Information | Bias | CC | MAE | RMSE |
|---|---|---|---|---|---|
| May | FIHS | −0.004 | 0.963 | 0.022 | 0.031 |
| AWT | 0.000 | 0.955 | 0.025 | 0.034 | |
| 60m | 0.000 | 0.946 | 0.027 | 0.037 | |
| November | FIHS | −0.004 | 0.953 | 0.021 | 0.029 |
| AWT | −0.001 | 0.954 | 0.021 | 0.030 | |
| 60m | −0.001 | 0.952 | 0.022 | 0.030 | |
| Difference (May–Nov.) | FIHS | −0.000 | 0.940 | 0.023 | 0.031 |
| AWT | −0.001 | 0.935 | 0.025 | 0.033 | |
| 60m | −0.001 | 0.925 | 0.026 | 0.035 |
| SR Image | Spectral Information | Bias | CC | MAE | RMSE |
|---|---|---|---|---|---|
| May | FIHS | 0.000 | 0.957 | 0.107 | 0.145 |
| AWT | 0.021 | 0.946 | 0.122 | 0.165 | |
| 60 m | 0.023 | 0.936 | 0.132 | 0.178 | |
| November | FIHS | −0.007 | 0.943 | 0.105 | 0.138 |
| AWT | −0.011 | 0.944 | 0.105 | 0.140 | |
| 60 m | −0.011 | 0.941 | 0.108 | 0.144 | |
| Difference (May-Nov.) | FIHS | 0.007 | 0.938 | 0.117 | 0.157 |
| AWT | 0.010 | 0.932 | 0.123 | 0.168 | |
| 60 m | 0.012 | 0.923 | 0.130 | 0.177 |

5.3. Spatial Quality of Pansharpened VI Images



5.4. Future Considerations for Pansharpening VI Images
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Lu, D.; Mausel, P.; Brondı́zio, E.; Moran, E. Relationships between forest stand parameters and Landsat TM spectral responses in the Brazilian Amazon Basin. For. Ecol. Manag. 2004, 198, 149–167. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar]
- Asner, G.P.; Wessman, C.A.; Schimel, D.S. Heterogeneity of savanna canopy structure and function from imaging spectrometry and inverse modeling. Ecol. Appl. 1998, 8, 1022–1036. [Google Scholar] [CrossRef]
- Goward, S.N.; Tucker, C.J.; Dye, D.G. North American vegetation patterns observed with the NOAA-7 advanced very high resolution radiometer. Vegetatio 1985, 64, 3–14. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Penuelas, J. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. Satellite-derived green vegetation fraction for the use in numerical weather prediction models. Adv. Sp. Res. 1997, 19, 477–480. [Google Scholar] [CrossRef]
- Johnson, B.; Tateishi, R.; Kobayashi, T. Remote sensing of fractional green vegetation cover using spatially-interpolated endmembers. Remote Sens. 2012, 4, 2619–2634. [Google Scholar] [CrossRef]
- Frequently Asked Questions about the Landsat Missions. Available online: http://landsat.usgs.gov/band_designations_landsat_satellites.php (accessed on 26 March 2014).
- Amro, I.; Mateos, J.; Vega, M.; Molina, R.; Katsaggelos, A.K. A survey of classical methods and new trends in pansharpening of multispectral images. EURASIP J. Adv. Signal Process. 2011, 79, 1–22. [Google Scholar]
- Johnson, B.A.; Tateishi, R.; Hoan, N.T. Satellite image pansharpening using a hybrid approach for object-based image analysis. ISPRS Int. J. GeoInf. 2012, 1, 228–241. [Google Scholar] [CrossRef]
- Johnson, B.A.; Tateishi, R.; Hoan, N.T. A hybrid pansharpening approach and multiscale object-based image analysis for mapping diseased pine and oak trees. Int. J. Remote Sens. 2013, 34, 6969–6982. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Benediktsson, J.A.; Aanaes, H. Classification of pansharpened urban satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 281–297. [Google Scholar] [CrossRef]
- Colditz, R.R.; Wehrmann, T.; Bachmann, M.; Steinnocher, K.; Schmidt, M.; Strunz, G.; Dech, S. Influence of image fusion approaches on classification accuracy: A case study. Int. J. Remote Sens. 2006, 27, 3311–3335. [Google Scholar] [CrossRef]
- Shackelford, A.K.; Davis, C.H. A hierarchical fuzzy classification approach for high-resolution multispectral data over urban areas. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1920–1932. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Capobianco, L.; Garzelli, A.; Marchesi, S.; Nencini, F. Analysis of the effects of pansharpening in change detection on VHR images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 53–57. [Google Scholar] [CrossRef]
- Bradley, B.A.; Jacob, R.W.; Hermance, J.F.; Mustard, J.F. A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite NDVI data. Remote Sens. Environ. 2007, 106, 137–145. [Google Scholar] [CrossRef]
- Vina, A.; Gitelson, A.A.; Rundquist, D.C.; Keydan, G.P.; Leavitt, B. Monitoring maize (Zea mays L.) phenology with remote sensing. Agron. J. 2004, 94, 1139–1147. [Google Scholar]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Dorsey, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1974; Volume 1, pp. 48–62.
- Birth, G.S.; McVey, G. Measuring the color of growing turf with a reflectance spectroradiometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Hassan, Q.K.; Bourque, C.P.-A.; Meng, F.-R. Application of Landsat-7 ETM+ and MODIS products in mapping seasonal accumulation of growing degree days at an enhanced resolution. J. Appl. Remote Sens. 2007, 1. [Google Scholar] [CrossRef]
- Hwang, T.; Song, C.; Bolstad, P.V.; Band, L.E. Downscaling real-time vegetation dynamics by fusing multi-temporal MODIS and Landsat NDVI in topographically complex terrain. Remote Sens. Environ. 2011, 115, 2499–2512. [Google Scholar] [CrossRef]
- Tu, T.-M.; Huang, P.S.; Hung, C.-L.; Chang, C.-P. A fast intensity-hue-saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II.Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Nuñez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1204–1211. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Tu, T.-M.; Su, S.-C.; Shyu, H.-C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- González-Audícana, M.; Otazu, X.; Fors, O.; Alvarez-Mozos, J. A low computational-cost method to fuse IKONOS images using the spectral response function of its sensors. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1683–1691. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar]
- Padwick, C.; Deskevich, M.; Pacifici, F.; Smallwood, S. Worldview-2 Pan-Sharpening. In Proceedings of the ASPRS 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010.
- Tu, T.-M.; Hsu, C.-L.; Tu, P.-Y.; Lee, C.-H. An adjustable pan-sharpening approach for IKONOS/QuickBird/GeoEye-1/WorldView-2 imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 125–134. [Google Scholar] [CrossRef]
- EarthExplorer. Available online: http://earthexplorer.usgs.gov/ (accessed on 26 March 2014).
- Spectral characteristics viewer. Available online: http://landsat.usgs.gov/tools_viewer.php (accessed on 26 March 2014).
- IGES Remote Sensing Toolbox. Available online: http://pub.iges.or.jp/modules/envirolib/view.php?docid=4943 (accessed on 26 March 2014).
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Lyon, J.G.; Yuan, D.; Lunetta, R.S.; Elvidge, C.D. A change detection experiment using vegetation indices. Photogramm. Eng. Remote Sens. 1998, 64, 143–150. [Google Scholar]
- Ehlers, M.; Klonus, S.; Johan Åstrand, P.; Rosso, P. Multi-sensor image fusion for pansharpening in remote sensing. Int. J. Image Data Fusion 2010, 1, 25–45. [Google Scholar] [CrossRef]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
- Pardo-Iguzquiza, E.; Rodrigues-Galiano, V.F.; Chica-Olmo, M.; Atkinson, P.M. Image fusion by spatially adaptive filtering using downscaling cokriging. ISPRS J. Photogramm. Remote Sens. 2011, 66, 337–346. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Johnson, B. Effects of Pansharpening on Vegetation Indices. ISPRS Int. J. Geo-Inf. 2014, 3, 507-522. https://doi.org/10.3390/ijgi3020507
Johnson B. Effects of Pansharpening on Vegetation Indices. ISPRS International Journal of Geo-Information. 2014; 3(2):507-522. https://doi.org/10.3390/ijgi3020507
Chicago/Turabian StyleJohnson, Brian. 2014. "Effects of Pansharpening on Vegetation Indices" ISPRS International Journal of Geo-Information 3, no. 2: 507-522. https://doi.org/10.3390/ijgi3020507






