Comparative Analysis of Spatial–Temporal Distribution between Traditional Taxi Service and Emerging Ride-Hailing
Abstract
:1. Introduction
2. Literature Review
3. Data Preparation
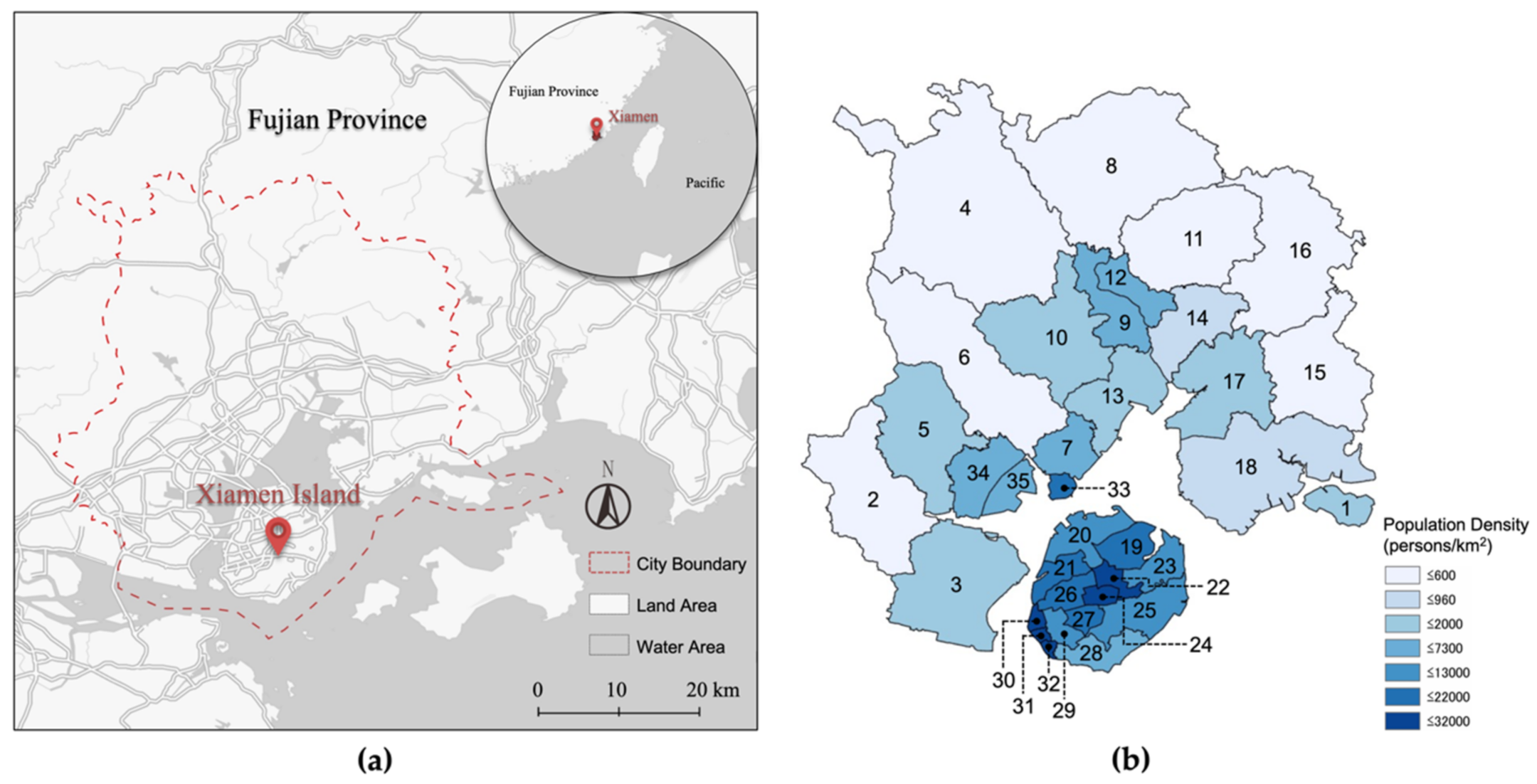
3.1. Xiamen City and Personal Mobility
3.2. Data Preparation
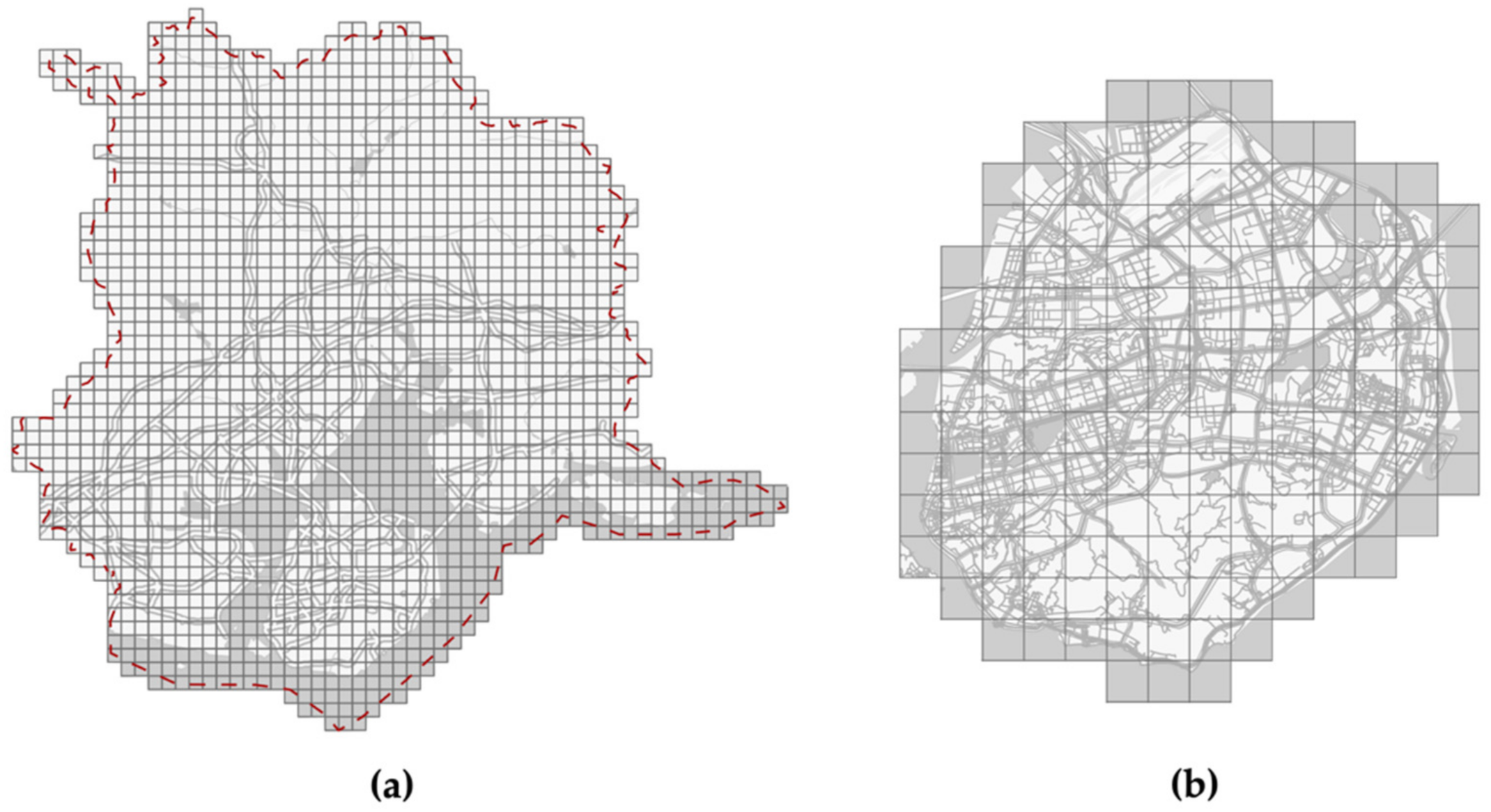
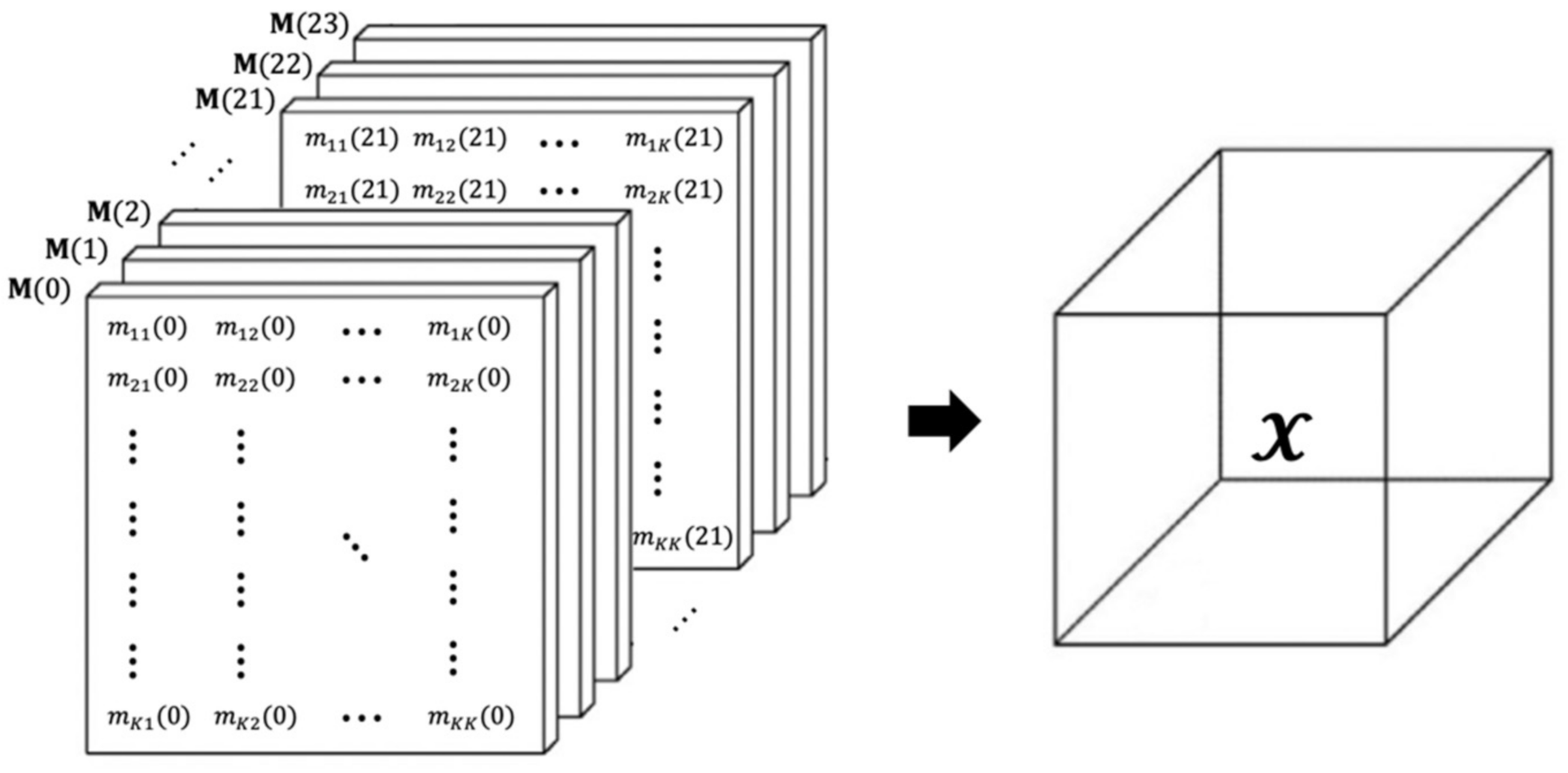
3.3. Uniform Cell Partition and ODT Tensor Establishment
4. Methods
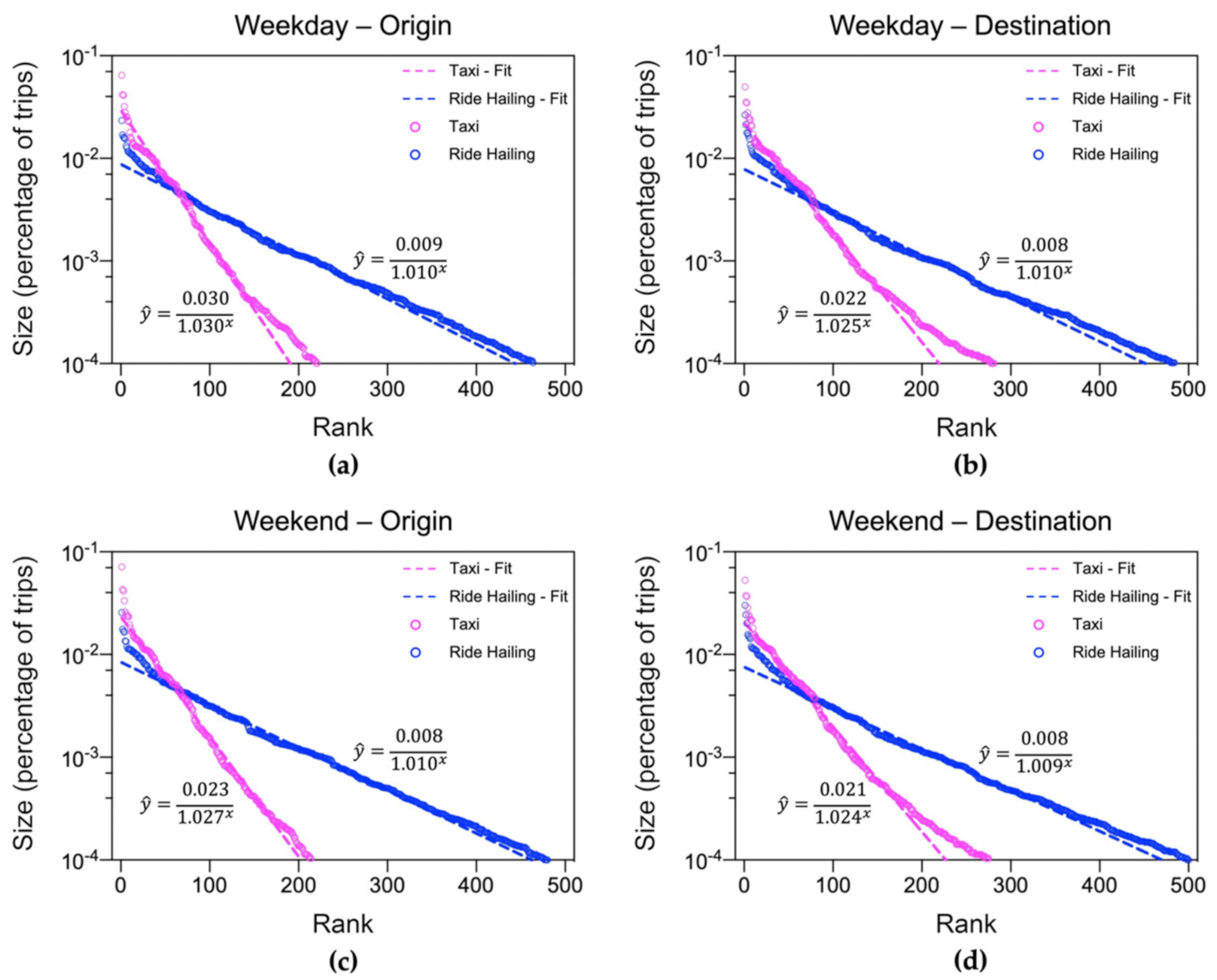
4.1. Rank–Size and Odds Ratio Analysis on Travel Demands
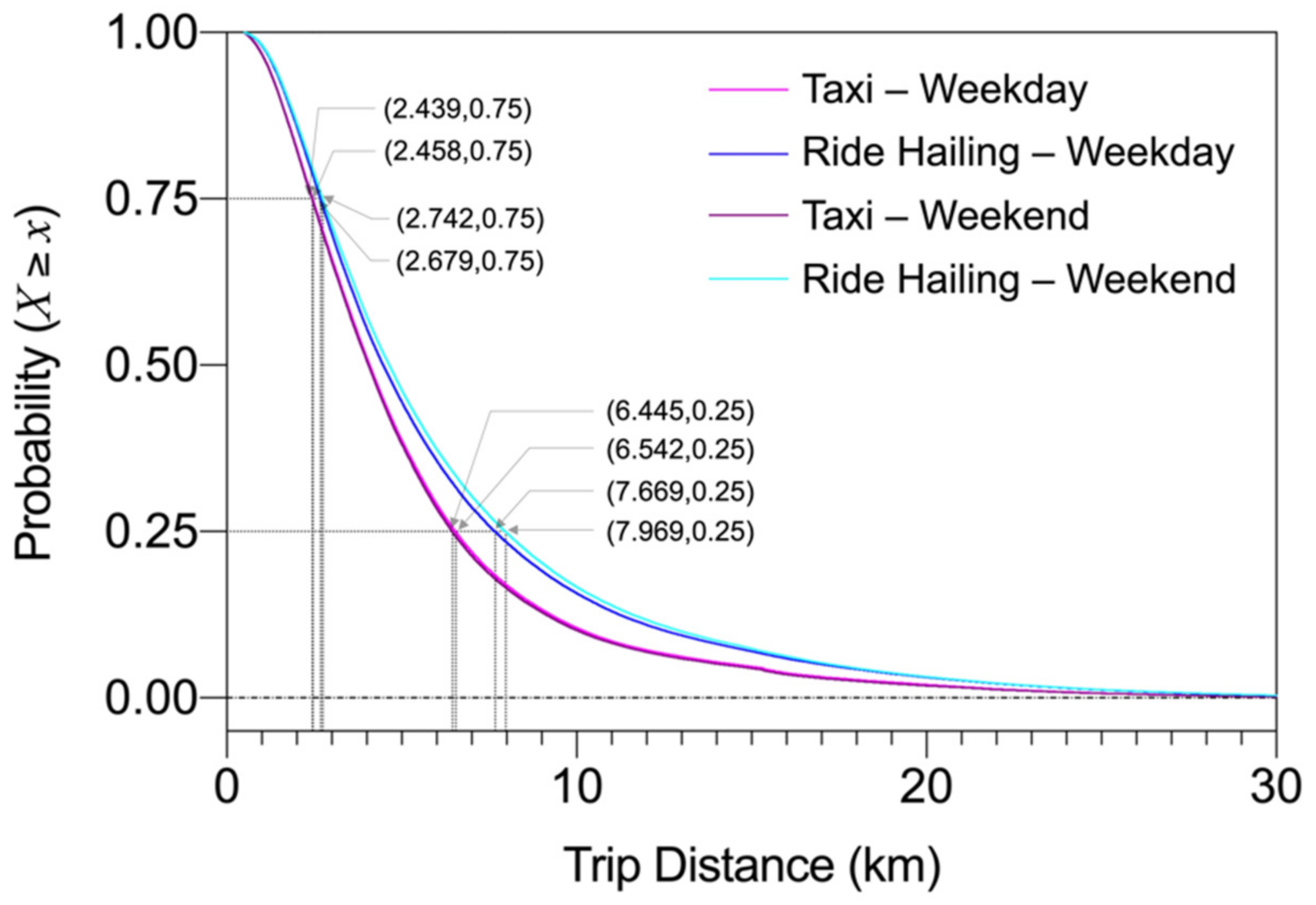
4.2. Statistics and Spatial Distribution of Trip Distances
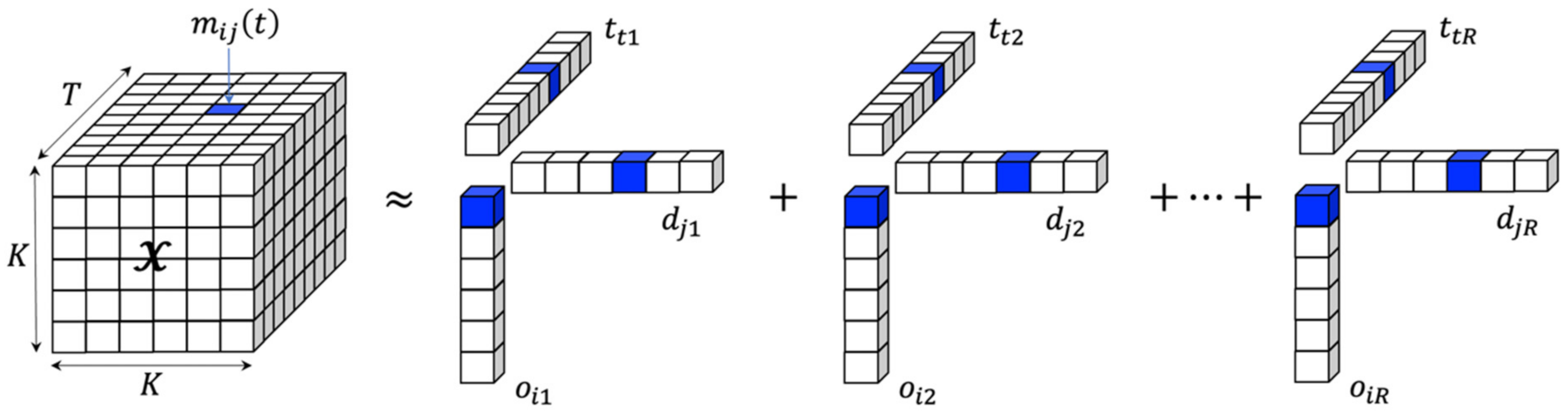
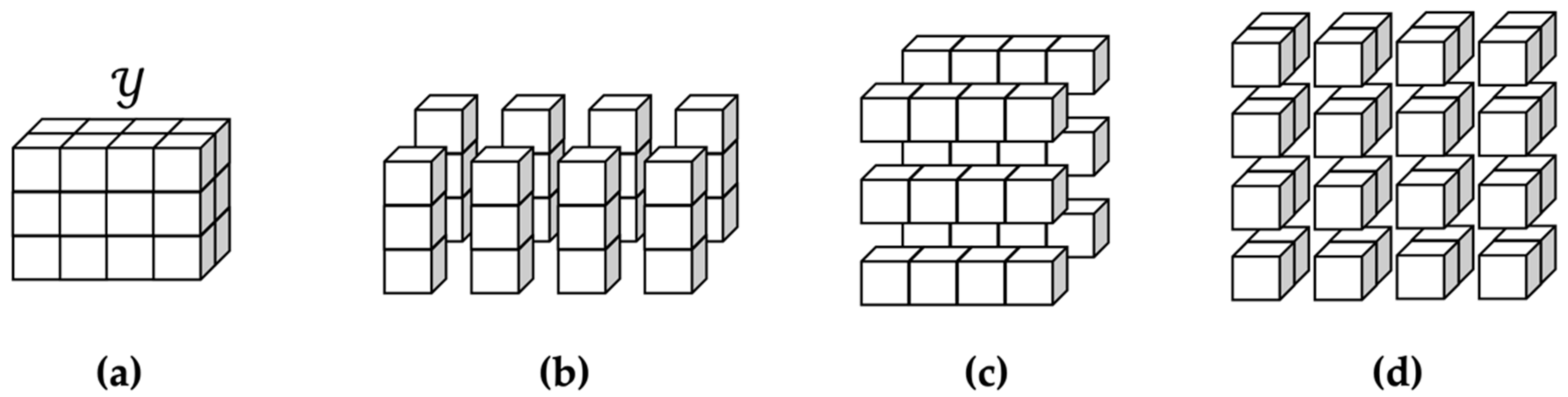
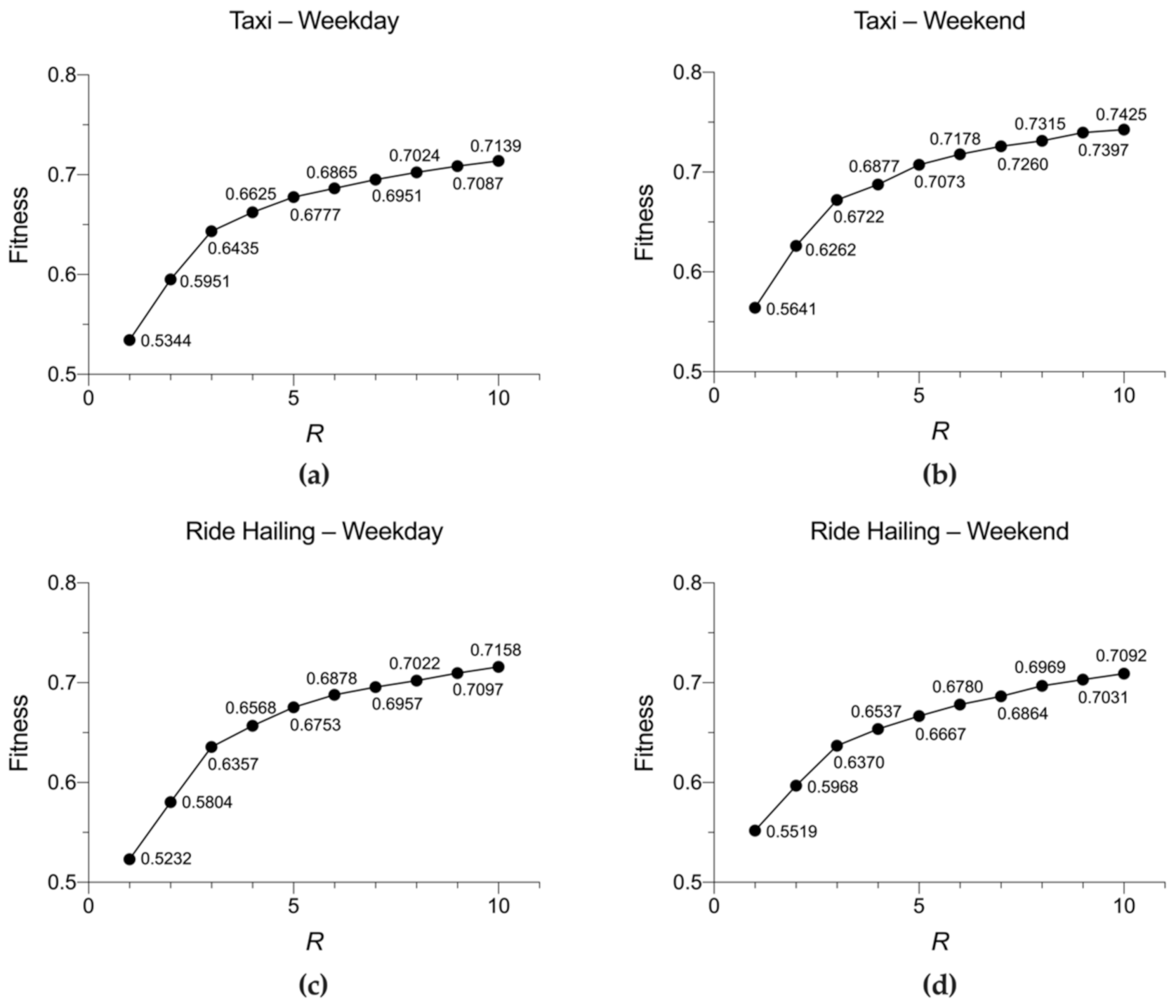
4.3. Factorization of ODT Tensor
5. Results
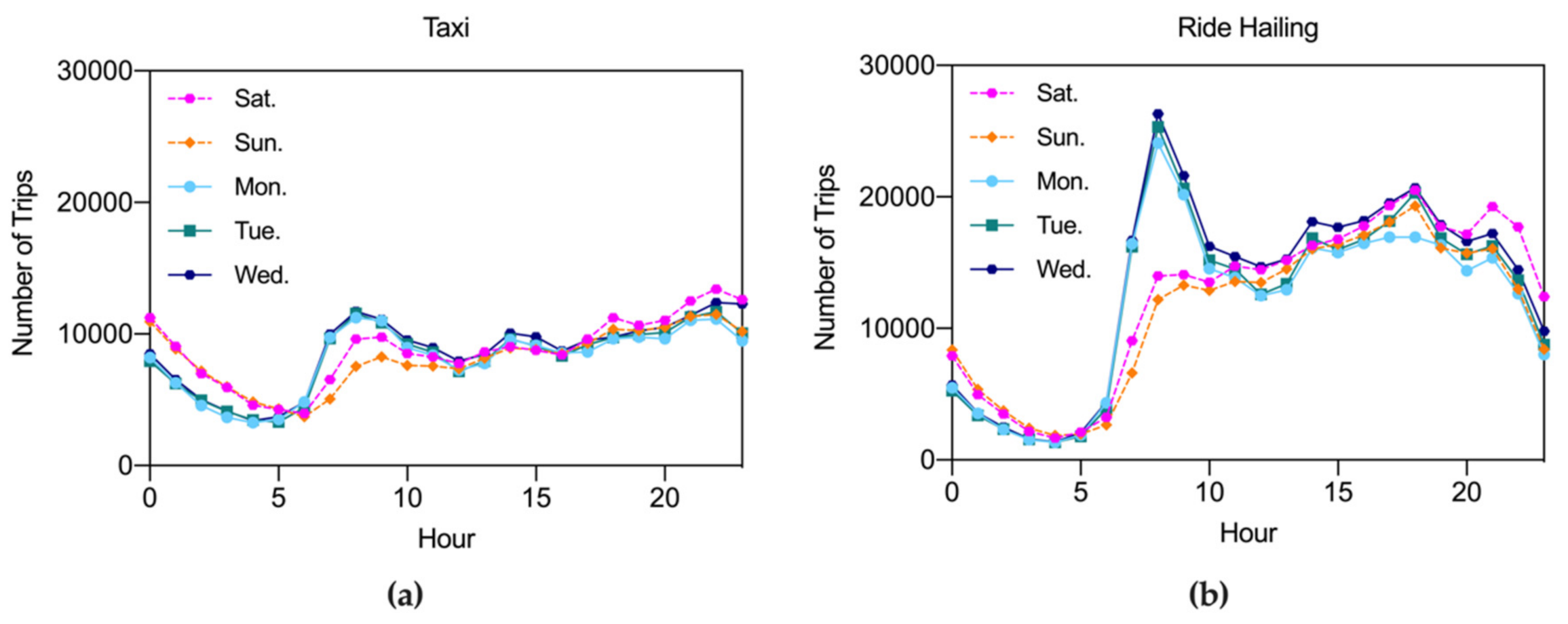
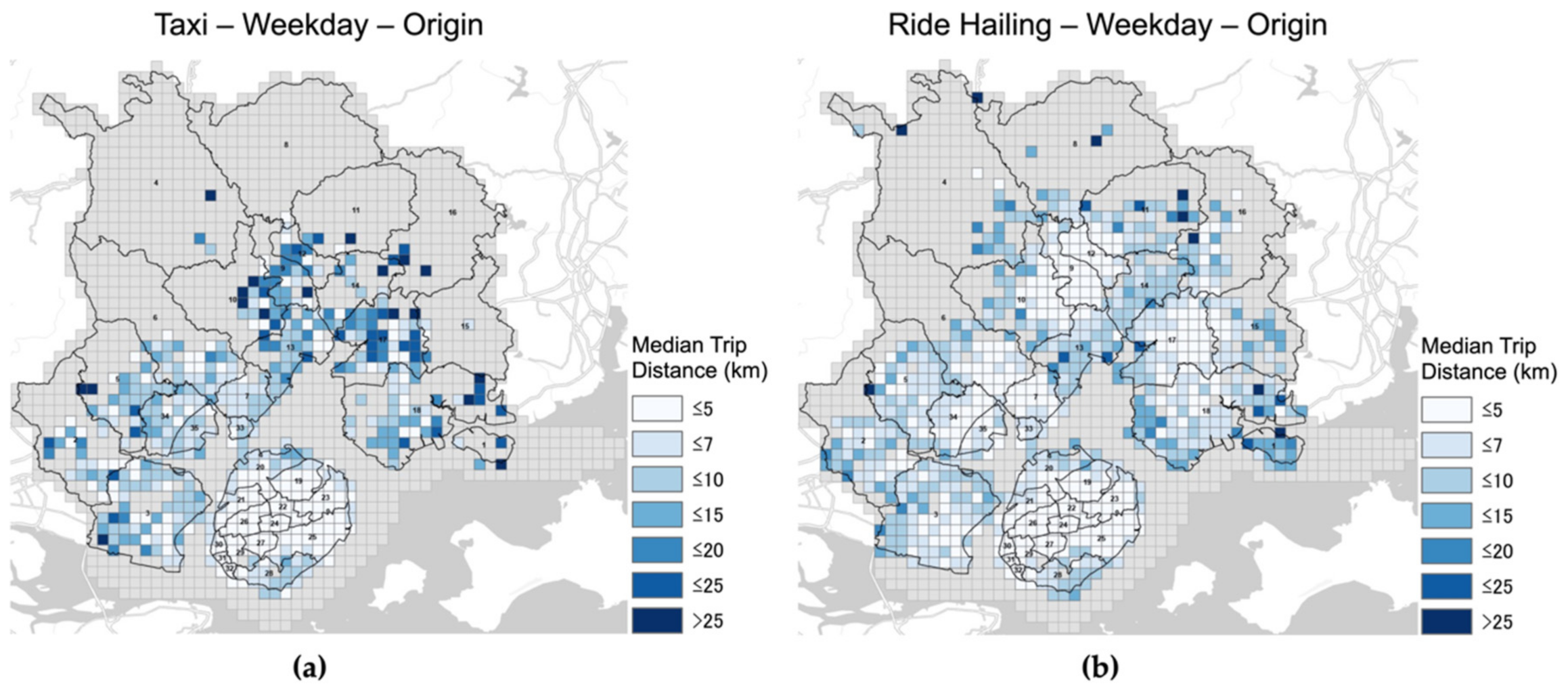
5.1. Spatial Differentiation of Travel Demands
5.2. Spatial Differentiation of Trip Distances
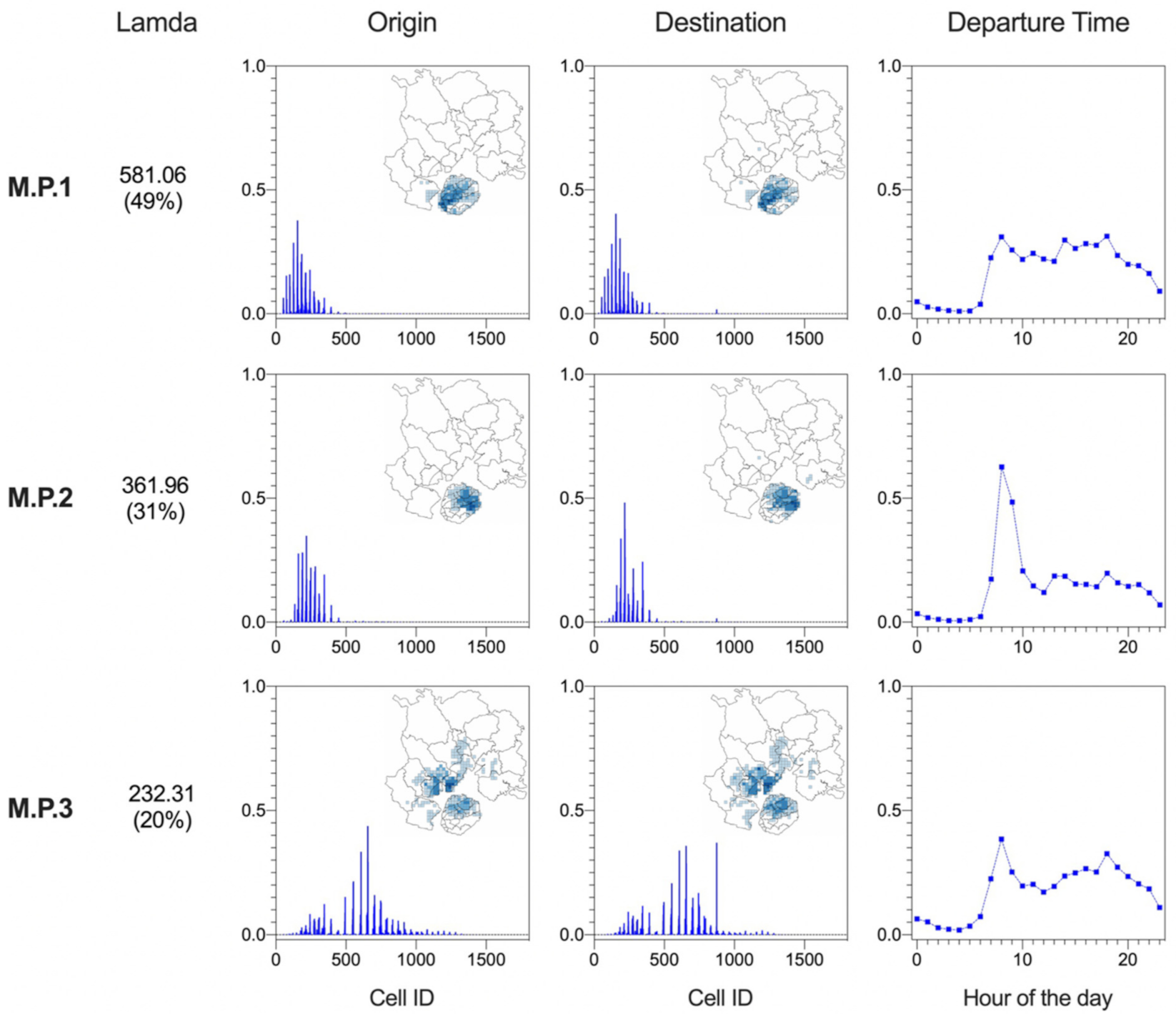
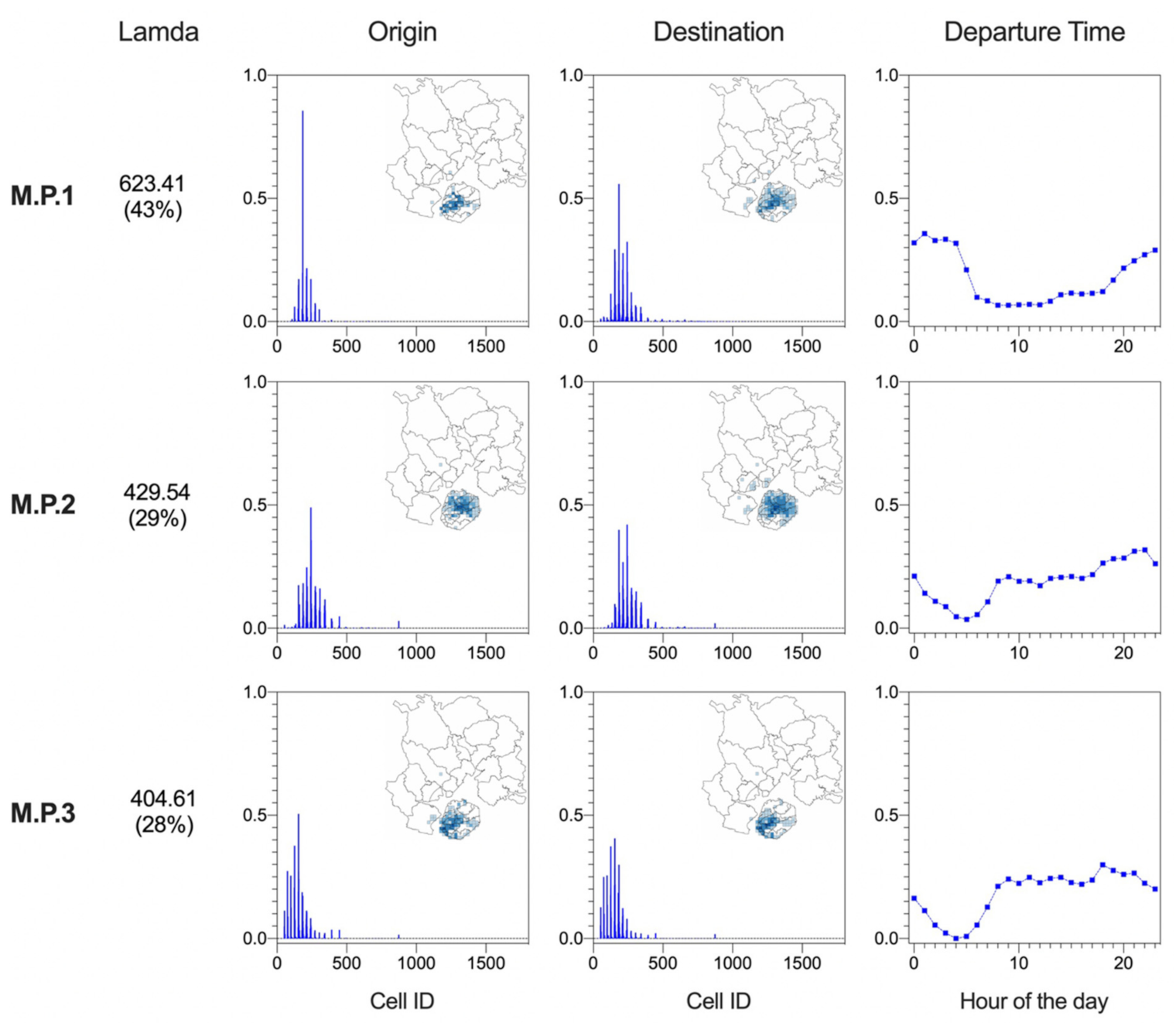
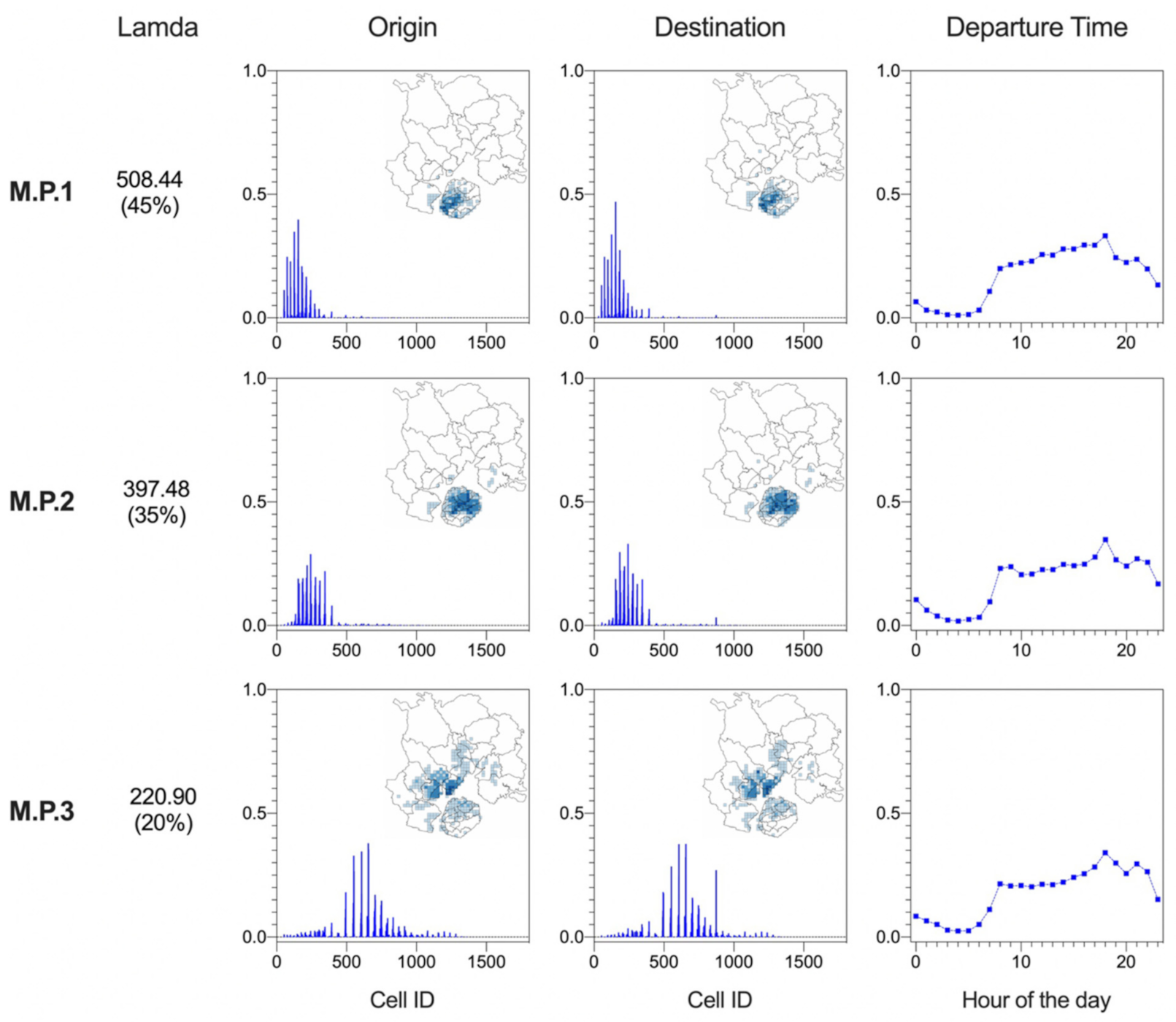
5.3. Meta-Patterns within the ODT Tensor
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Spatial Distribution of Travel Demands
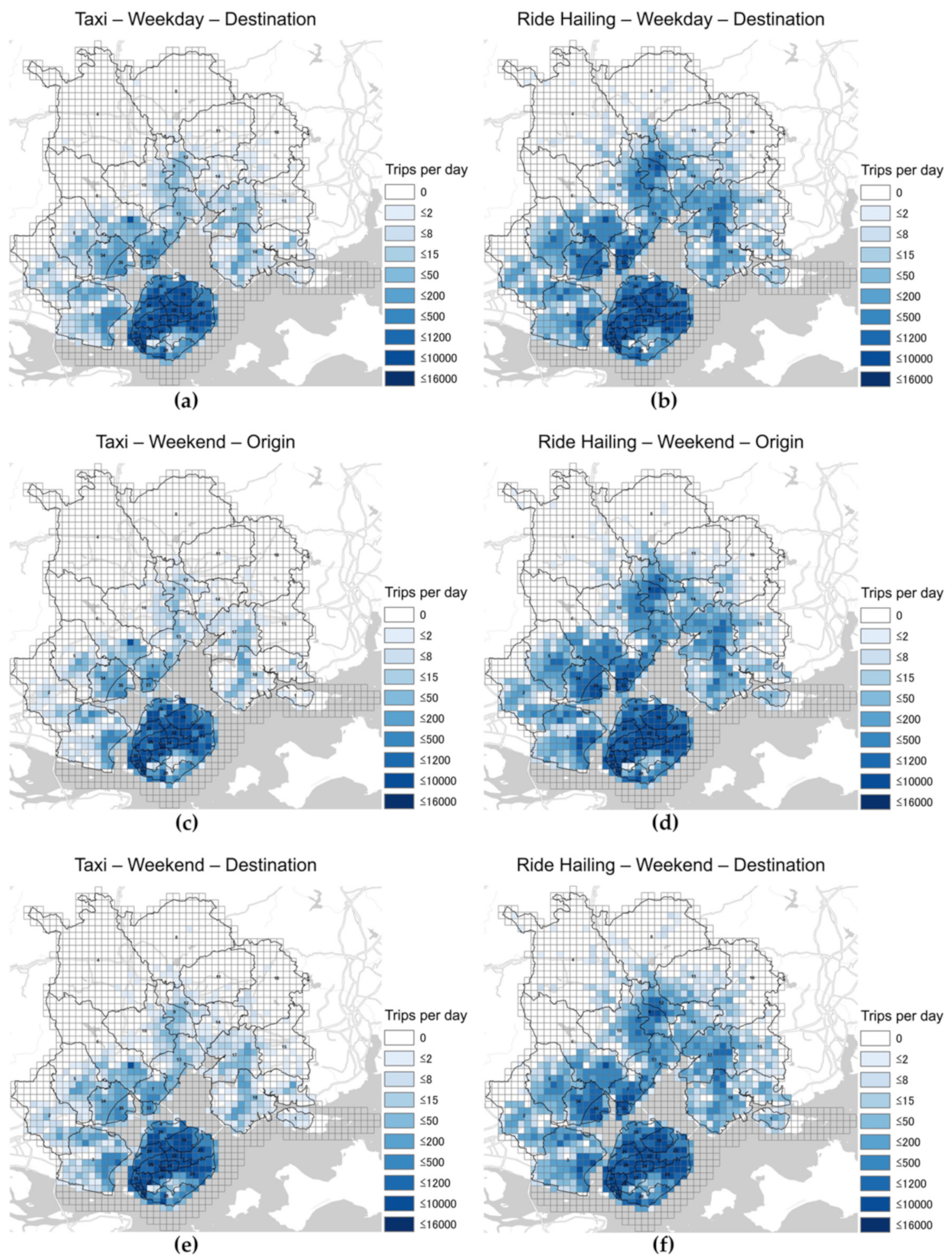
Appendix B. Spatial Distribution of Median Trip Distances

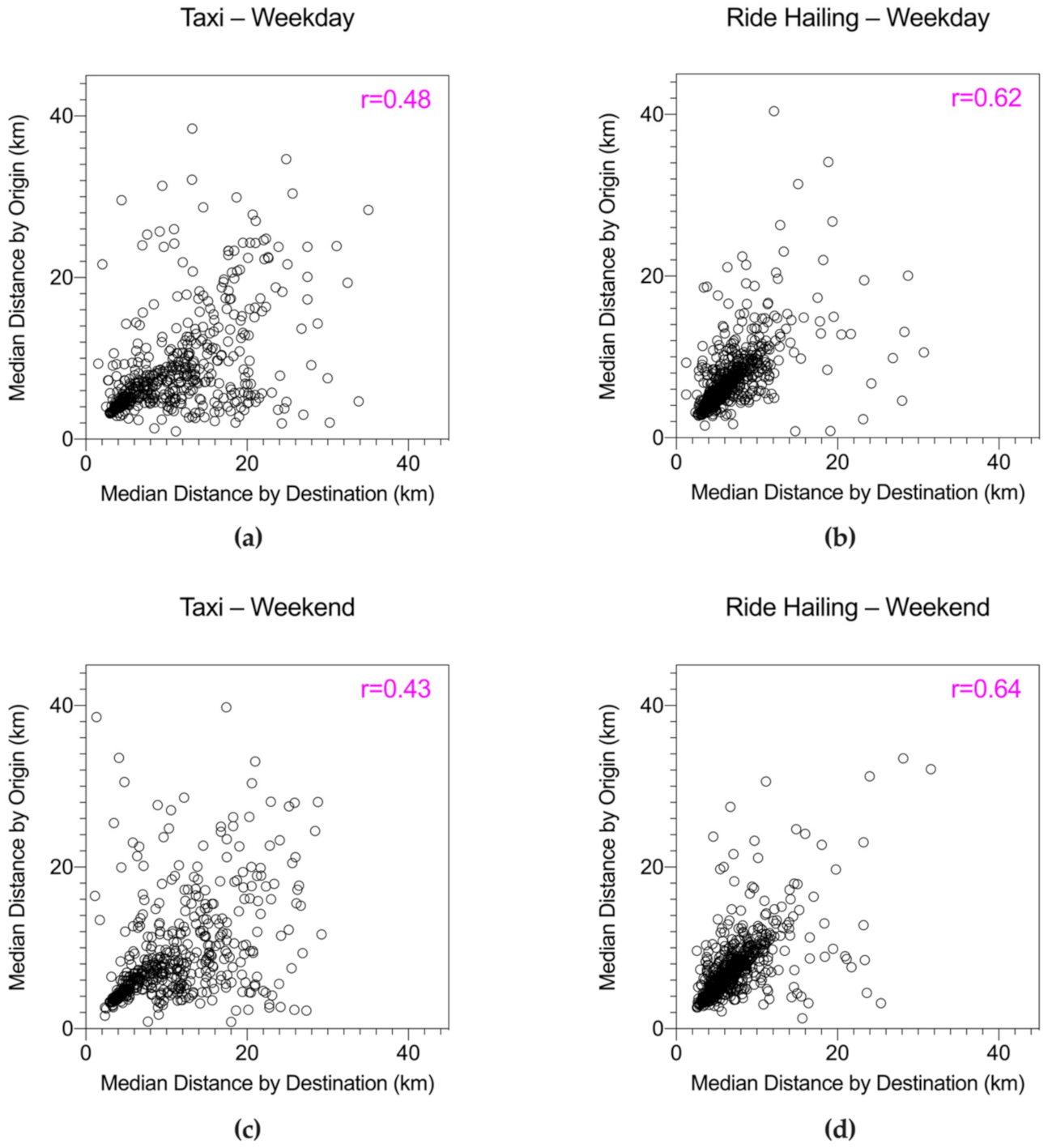
Appendix C. Correlations between Median Trip Distances
References
- Xiong, Z.; Li, J.; Wu, H. Understanding operation patterns of urban online ride-hailing services: A case study of Xiamen. Transp. Pol. 2021, 101, 100–118. [Google Scholar] [CrossRef]
- Nie, Y.M. How Can the Taxi Industry Survive the Tide of Ridesourcing? Evidence from Shenzhen, China. Transp. Res. Part C Emerg. Technol. 2017, 79, 242–256. [Google Scholar] [CrossRef]
- Rayle, L.; Dai, D.; Chan, N.; Cervero, R.; Shaheen, S. Just a Better Taxi? A Survey Based on a Comparison of Taxis, Transit, and Ridesourcing Services in San Francisco. Transp. Pol. 2016, 45, 168–178. [Google Scholar] [CrossRef] [Green Version]
- He, F.; Shen, Z.J.M. Modeling Taxi Services with Smartphone-based E-hailing Applications. Transp. Res. Part C Emerg. Technol. 2015, 58, 93–106. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Xiao, Y.; Gao, S. Urban Land Uses and Traffic “Source-sink Areas:” Evidence from GPS-enabled Taxi Data in Shanghai. Landscape Urban Plan. 2012, 106, 73–87. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, C.; Gao, S.; Xiao, Y.; Tian, Y. Understanding Intra-urban Trip Patterns from Taxi Trajectory Data. J. Geogr. Sys. 2012, 14, 463–483. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing Travel Patterns and City Structure with Taxi Trip Data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xu, Y.; Tu, W.; Ratti, C. Do Different Datasets tell the Same Story About Urban Mobility: A Comparative Study of Public Transit and Taxi Usage. J. Transp. Geogr. 2018, 70, 78–90. [Google Scholar] [CrossRef]
- Birant, D.; Kut, A. ST-DBSCAN: An Algorithm for Clustering Spatial–temporal Data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, S.; Biugila, N.; Wang, C.; Du, J.; Li, H. A Fast Clustering Algorithm Based on Pruning Unnecessary Distance Computations in DBSCAN for High-dimensional Data. Pattern Recog. 2018, 83, 375–387. [Google Scholar] [CrossRef]
- Kisilevich, S.; Mansmann, F.; Keim, D. P-DBSCAN: A Density-based Clustering Algorithm for Exploration and Analysis of Attractive Areas using Collections of Geo-tagged Photos. In Proceedings of the 1st International Conference and Exhibition on Computing for Geospatial Research & Application, Washington, DC, USA, 21–23 June 2010; pp. 1–4. [Google Scholar]
- Rocha, J.A.M.R.; Times, V.C.; Oliveira, G.; Alvares, L.O.; Bogorny, V. DB-SMoT: A Direction-Based Spatio-Temporal Clustering Method. In Proceedings of the 2010 5th IEEE International Conference Intelligent Systems, London, UK, 7–9 July 2010. [Google Scholar]
- Brunet, J.P.; Tamayo, P.; Golub, T.R.; Mesirov, J.P. Matrix Factorization for Molecular Pattern Recognition. Proc. Natl. Acad. Sci. USA 2004, 101, 4164–4169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Wang, Y.X.; Zhang, Y.J. Nonnegative Matrix Factorization: A Comprehensive Review. IEEE Trans. Knowl. Data Eng. 2012, 25, 1336–1353. [Google Scholar] [CrossRef]
- Guérin-pace, F. Rank-Size Distribution and the Process of Urban Growth. Urban Stud. 1995, 32, 551–562. [Google Scholar] [CrossRef]
- Smilde, A.; Bro, R.; Geladi, P. Multi-way Analysis: Applications in the Chemical Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Sidiropoulos, N.D.; Bro, R. On the uniqueness of multilinear decomposition of N-way arrays. J. Chemom. 2000, 14, 229–239. [Google Scholar] [CrossRef]
- Berge, J.M.F. The Typical Rank of Tall Three-way Arrays. Psychometrika 2000, 65, 525–532. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, Johns Hopkins Studies in the Mathematical Sciences; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Welling, M.; Weber, M. Positive Tensor Factorization. Pattern Recog. Ltrs. 2001, 22, 1255–1261. [Google Scholar] [CrossRef]
- Leike, A. Demonstration of the Exponential Decay Law using Beer Froth. Eur. J. Physics. 2001, 23, 21. [Google Scholar] [CrossRef] [Green Version]
- Wilson, T.J.; Lai, L.; Ban, Y.; Steven, X.G. Identification of Metagenes and their Interactions through Large-scale Analysis of Arabidopsis gene expression data. BMC Genomics. 2012, 13, 237. [Google Scholar] [CrossRef] [Green Version]
- Stad, J. Rank Is NP-Complete. J. Algor. 1990, 654, 644–654. [Google Scholar]
- Gujral, E.; Pasricha, R.; Yang, T.; Papalexakis, E.E. OCTEN: Online Compression-Based Tensor Decomposition. In Proceedings of the 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Le Gosier, Guadeloupe, 15–18 December 2019; pp. 455–459. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Lin, Y.; Geertman, S.; Hooimeijer, P.; Xu, W.T. Accessibility-based Equity of Public Facilities: A Case Study in Xiamen, China. Appl. Spat. Anal. Pol. 2021, 1–22. [Google Scholar] [CrossRef]
- Ding, Y.; Zhou, J.; Li, Y. Transit Accessibility Measures Incorporating the Temporal Dimension. Cities 2015, 46, 55–66. [Google Scholar]
- Duff, I.S.; Erisman, A.M.; Reid, J.K. Direct Methods for Sparse Matrices, 2nd ed.; Oxford University Press: New York, NY, USA, 2017; pp. 49–58. [Google Scholar]
- Lopez, C.; Leclercq, L.; Krishnakumari, P.; Chiabaut, N.; Van Lint, H. Revealing the day-to-day regularity of urban congestion patterns with 3D speed maps. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Gehrke, S.R.; Huff, M.P.; Reardon, T.G. Social and trip-level predictors of pooled ride-hailing service adoption in the Greater Boston region. Case Stud. Transp. Policy. 2021, 9, 1026–1034. [Google Scholar] [CrossRef]
- Alonso, B.; Barreda, R.; dell’Olio, L.; Ibeas, A. Modelling user perception of taxi service quality. Transp. Policy. 2018, 63, 157–164. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Miwa, T.; Morikawa, T. Comparative Analysis of Spatial–Temporal Distribution between Traditional Taxi Service and Emerging Ride-Hailing. ISPRS Int. J. Geo-Inf. 2021, 10, 690. https://doi.org/10.3390/ijgi10100690
Wang D, Miwa T, Morikawa T. Comparative Analysis of Spatial–Temporal Distribution between Traditional Taxi Service and Emerging Ride-Hailing. ISPRS International Journal of Geo-Information. 2021; 10(10):690. https://doi.org/10.3390/ijgi10100690
Chicago/Turabian StyleWang, Di, Tomio Miwa, and Takayuki Morikawa. 2021. "Comparative Analysis of Spatial–Temporal Distribution between Traditional Taxi Service and Emerging Ride-Hailing" ISPRS International Journal of Geo-Information 10, no. 10: 690. https://doi.org/10.3390/ijgi10100690





