Spatial Relations Using High Level Concepts
Abstract
:1. Introduction
2. Related Work
2.1. Implicit Spatial Information
2.2. Spatial Relations
 is contained within an object
is contained within an object  which in turn is contained within an object
which in turn is contained within an object  , it is straight forward to infer that
, it is straight forward to infer that  is contained within
is contained within  . Some spatial relations have a corresponding easily interpretable natural language expression which offers the potential for the linguistic interaction with spatial data [22,25,26]. Other applications of spatial relations include robotics and high-level computer vision [27]. Many sets of spatial relations have been proposed but the most predominant are the intersection models of Egenhofer [28,29] and the Region Connection Calculus (RCC) of Randell et al. [30]. Due to their ubiquitous nature we do not describe these in detail suffice to say that each consists entirely of binary topological relations and both sets are in fact equivalent. A detailed description of both these sets can be found in [31].
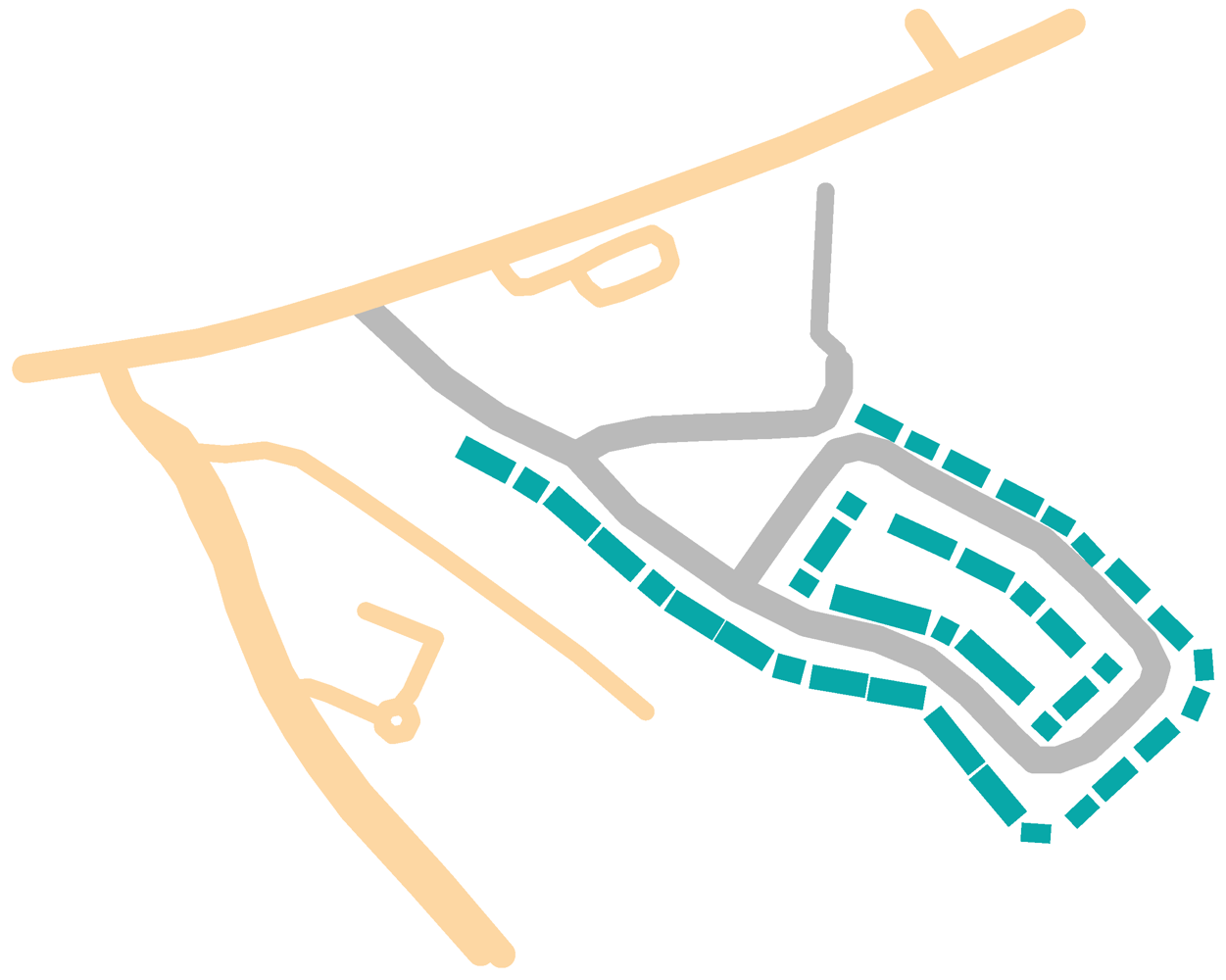
. Some spatial relations have a corresponding easily interpretable natural language expression which offers the potential for the linguistic interaction with spatial data [22,25,26]. Other applications of spatial relations include robotics and high-level computer vision [27]. Many sets of spatial relations have been proposed but the most predominant are the intersection models of Egenhofer [28,29] and the Region Connection Calculus (RCC) of Randell et al. [30]. Due to their ubiquitous nature we do not describe these in detail suffice to say that each consists entirely of binary topological relations and both sets are in fact equivalent. A detailed description of both these sets can be found in [31].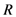 is nearly completely contained inside the object
is nearly completely contained inside the object 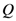 ; In (b) the object
; In (b) the object 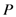 is between the objects
is between the objects 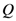 and
and 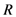 .
.
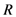 is nearly completely contained inside the object
is nearly completely contained inside the object 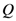 ; In (b) the object
; In (b) the object 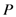 is between the objects
is between the objects 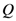 and
and 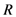 .
.
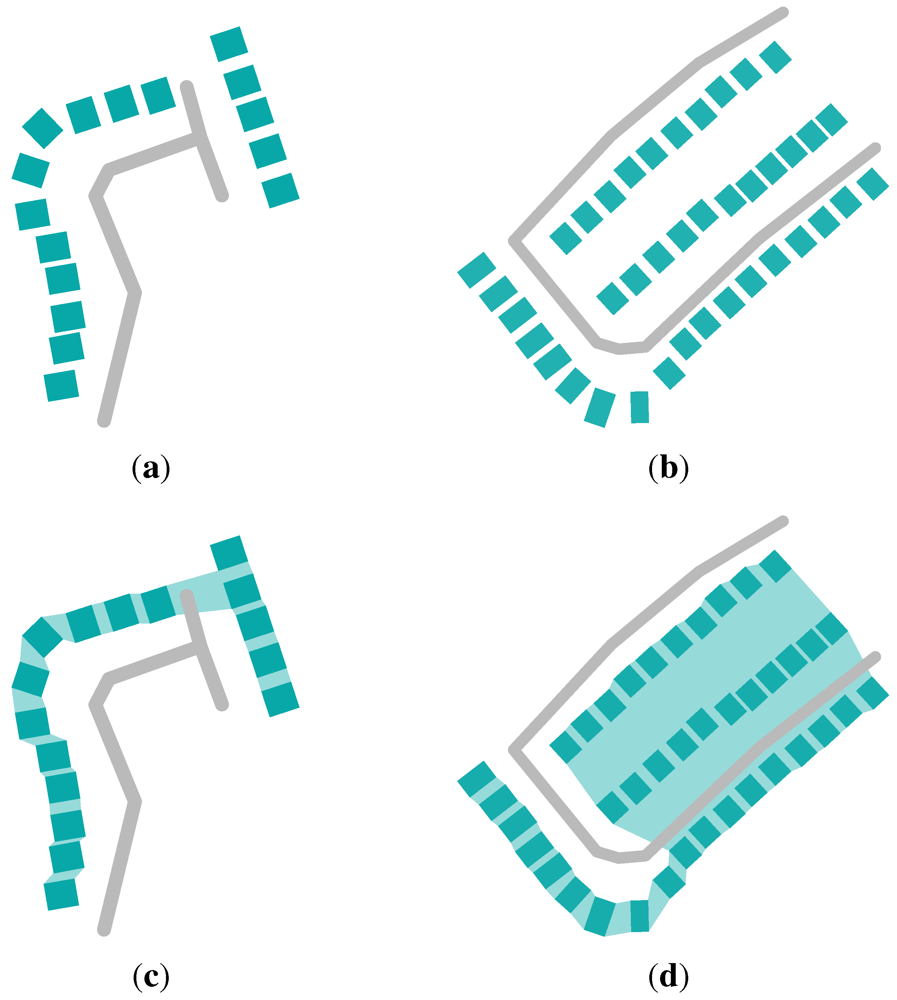
2.3. Map Generalisation
 and
and  . In order to merge these objects we define one possible connector to be the polygon
. In order to merge these objects we define one possible connector to be the polygon  which is represented by the grey region in Figure 3(b). The merger of the two polygons is then defined as the union of the polygons and the corresponding connector; the result of which is represented by the polygon
which is represented by the grey region in Figure 3(b). The merger of the two polygons is then defined as the union of the polygons and the corresponding connector; the result of which is represented by the polygon  in Figure 3(c).
in Figure 3(c).
3. Proposed Model
3.1. Generalisation Step
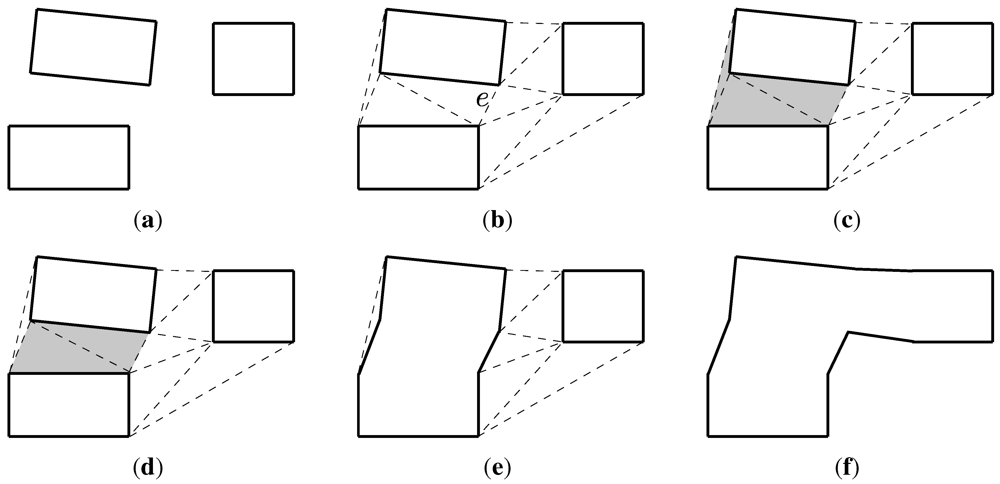
 , in this triangulation which connects two different polygons is determined; these polygons correspond to the spatially closest in the scene. In Figure 4(b) the edge
, in this triangulation which connects two different polygons is determined; these polygons correspond to the spatially closest in the scene. In Figure 4(b) the edge  is labeled. The two polygons adjacent to
is labeled. The two polygons adjacent to  and the corresponding set of connecting triangles are determined. This set of triangle is entitled
and the corresponding set of connecting triangles are determined. This set of triangle is entitled  . The set
. The set  corresponding to Figure 4(b) contains three triangles and is represented by the grey region in Figure 4(c). Next a subset of
corresponding to Figure 4(b) contains three triangles and is represented by the grey region in Figure 4(c). Next a subset of  , entitled
, entitled  , is obtained by removing those triangles which are not adjacent to
, is obtained by removing those triangles which are not adjacent to  and contain an edge of length greater than
and contain an edge of length greater than  times the length of
times the length of  .
.  corresponding to
corresponding to  in Figure 4(c) contains two polygons and is represented by the grey region in Figure 4(d).
in Figure 4(c) contains two polygons and is represented by the grey region in Figure 4(d).  and the two polygons adjacent to
and the two polygons adjacent to  are then merged to form a single polygon. The result of applying this step to Figure 4(d) is displayed in Figure 4(e). This process of identifying and merging two polygons is then iterated until a single polygon remains. The result of merging the three polygons in Figure 4(a) is displayed in Figure 4(f).
are then merged to form a single polygon. The result of applying this step to Figure 4(d) is displayed in Figure 4(e). This process of identifying and merging two polygons is then iterated until a single polygon remains. The result of merging the three polygons in Figure 4(a) is displayed in Figure 4(f).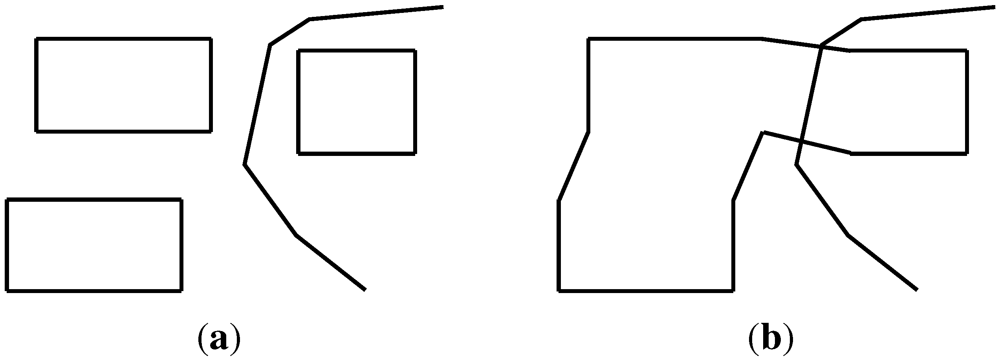
3.2. Inference Step
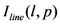 which determines the degree to which a line
which determines the degree to which a line  , corresponding to a road, enters a polygon
, corresponding to a road, enters a polygon  , corresponding to a housing estate.
, corresponding to a housing estate. 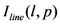 is leveraged by another function
is leveraged by another function  which determines the degree to which a point
which determines the degree to which a point 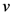 , which lies on
, which lies on  , enters
, enters  .
.  is a product of the functions
is a product of the functions  and
and  which measure the degree to which
which measure the degree to which 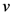 is surrounded by and close to the centroid of
is surrounded by and close to the centroid of  respectively. Having studied the spatial relation of enters in depth the authors believe both these attributes play a dominant role in its perception.
respectively. Having studied the spatial relation of enters in depth the authors believe both these attributes play a dominant role in its perception. we first generate a set
we first generate a set  of
of  rays where
rays where  is a ray with source
is a ray with source 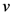 and direction
and direction  . For example in Figure 6 the set of rays for each corresponding point
. For example in Figure 6 the set of rays for each corresponding point 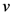 where
where  are illustrated. Let
are illustrated. Let  be a function which returns a value of
be a function which returns a value of  if
if  intersects
intersects  and returns a value of
and returns a value of  otherwise.
otherwise.  is computed using Equation (1).
is computed using Equation (1).
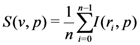
 takes values in the interval
takes values in the interval  . If
. If 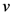 lies inside
lies inside  , and is completely surrounded by
, and is completely surrounded by  ,
,  will evaluate to
will evaluate to  ; this is the case for the points
; this is the case for the points 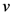 in Figure 6(a,c). If
in Figure 6(a,c). If 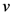 does not lie inside
does not lie inside  ,
,  will evaluate to a number less than or equal to
will evaluate to a number less than or equal to  indicating the degree to which
indicating the degree to which 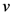 is surrounded by
is surrounded by  . This is the case for the point
. This is the case for the point 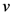 in Figure 6(b) where
in Figure 6(b) where  evaluates to
evaluates to  . In our implementation a value of 720 was assigned to the variable
. In our implementation a value of 720 was assigned to the variable  which was found to provide a fine enough resolution.
which was found to provide a fine enough resolution.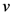 are represented by arrows.
are represented by arrows.  represents the centroid of each polygon.
represents the centroid of each polygon.
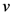 are represented by arrows.
are represented by arrows.  represents the centroid of each polygon.
represents the centroid of each polygon.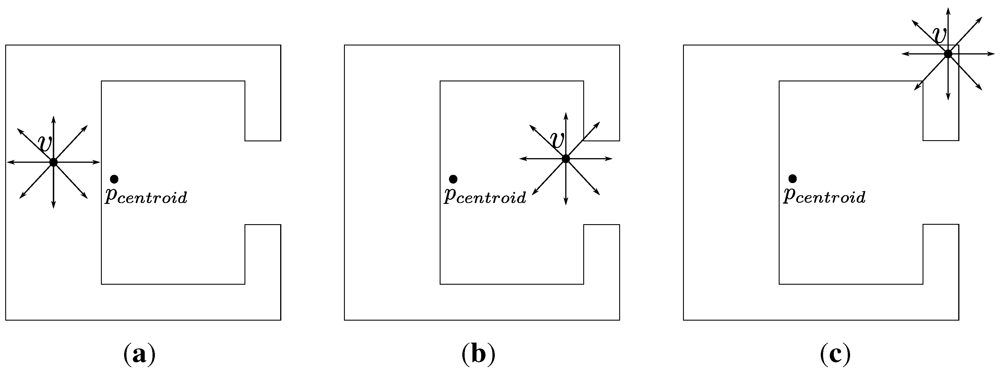
 we first compute the centroid, denoted
we first compute the centroid, denoted  , of
, of  . Next we compute the maximum distance, denoted
. Next we compute the maximum distance, denoted  , between
, between  and a point lying on the boundary of
and a point lying on the boundary of  . This is computed using Equation (2) where
. This is computed using Equation (2) where  is the set of vertices representing
is the set of vertices representing  .
.
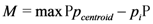
 be the distance between
be the distance between 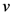 and
and  ; that is,
; that is,  .
.  is computed using Equation (3).
is computed using Equation (3).
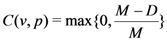
 takes values in the interval
takes values in the interval  . Specifically, if
. Specifically, if 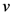 is equal to
is equal to  ,
,  will evaluate to
will evaluate to  . If the distance between
. If the distance between 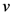 and
and  is less than
is less than  ,
,  will evaluate to a number in the interval
will evaluate to a number in the interval  decreasing with distance from
decreasing with distance from  . Otherwise
. Otherwise  will evaluate to
will evaluate to  . For example,
. For example,  corresponding to the scene in Figure 6(c) evaluates to a number close to
corresponding to the scene in Figure 6(c) evaluates to a number close to  because its distance from
because its distance from  is close to
is close to  . Meanwhile, due to the closer proximity of each
. Meanwhile, due to the closer proximity of each 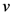 to the centroid of
to the centroid of  ,
,  corresponding to the scenes in Figure 6(a) and (b) evaluates to
corresponding to the scenes in Figure 6(a) and (b) evaluates to  and
and  respectively. Having computed
respectively. Having computed  and
and  we finally compute
we finally compute  using Equation (4).
using Equation (4).
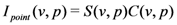
 takes values in the interval
takes values in the interval  .
.  approaches the value
approaches the value  as both function
as both function  and
and  approach the value
approach the value  . For example, the
. For example, the  values corresponding to the scenes in Figure 6(a–c) are 0.71 (
values corresponding to the scenes in Figure 6(a–c) are 0.71 (  ), 0.40 (
), 0.40 (  ) and 0.09 (
) and 0.09 (  ) respectively. We now turn our attention to computing the degree to which a line
) respectively. We now turn our attention to computing the degree to which a line  enters a polygon
enters a polygon  , that is
, that is 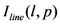 . Let
. Let  specify that the point
specify that the point 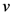 lies on the line
lies on the line  .
. 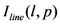 is defined by Equation (5).
is defined by Equation (5).
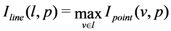
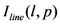 exactly represents a complex optimization problem for which we do not have a closed form solution. To overcome this difficulty we approximate this function using the following approach. We first select a set of points
exactly represents a complex optimization problem for which we do not have a closed form solution. To overcome this difficulty we approximate this function using the following approach. We first select a set of points  lying on
lying on  where the distance between two consecutive points
where the distance between two consecutive points  and
and  , measured in terms of distance along the line, is constant. In our implementation we assigned
, measured in terms of distance along the line, is constant. In our implementation we assigned  equal to the length of
equal to the length of  measured in meters to give a distance of one meter between consecutive points.
measured in meters to give a distance of one meter between consecutive points.4. Evaluation
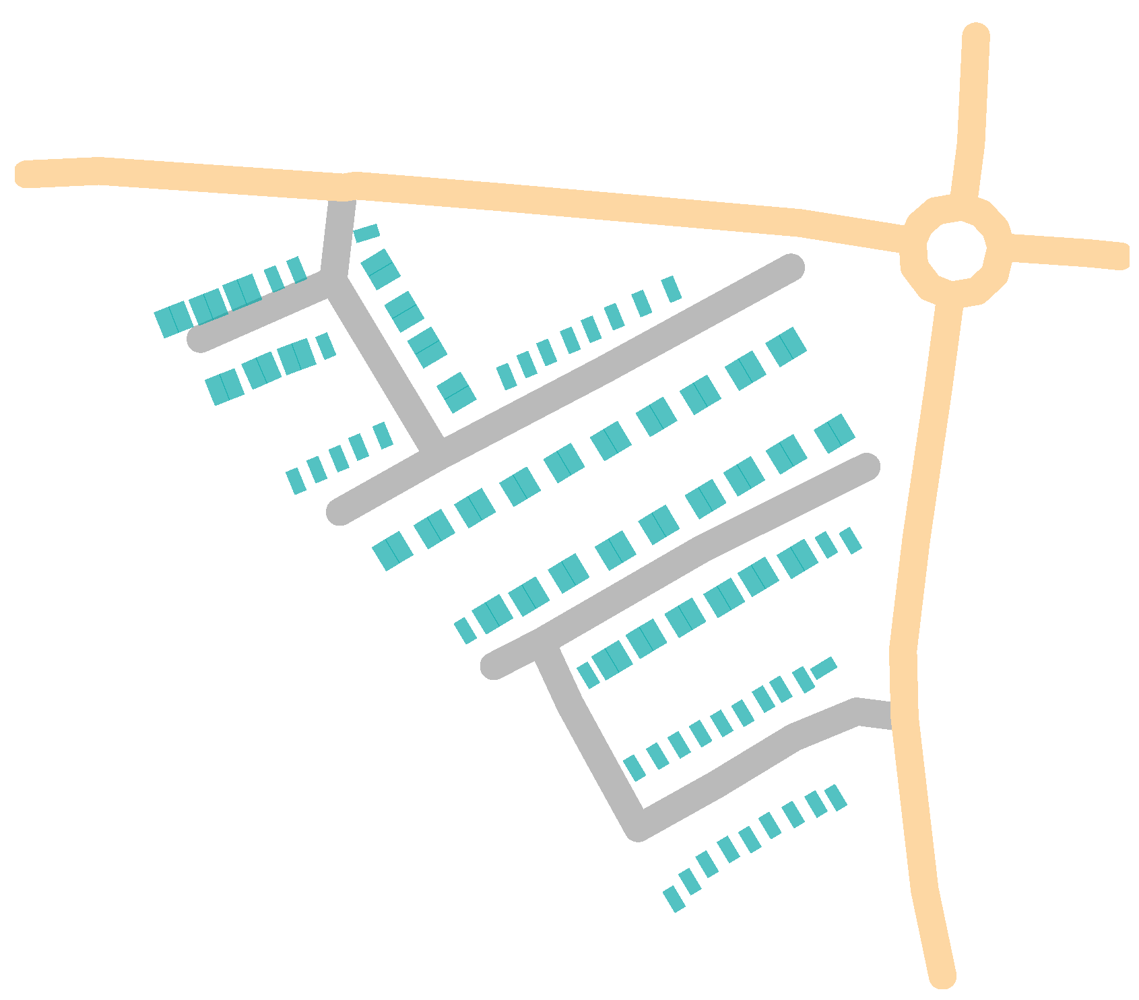
4.1. Spatial Data
4.2. Qualitative Evaluation
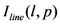 value listed under each sub-figure. This particular subset was chosen to demonstrate the behavior of the model. It is evident from this figure that, in all those scenes where there is a strong perception that the road enters the housing estate, a high
value listed under each sub-figure. This particular subset was chosen to demonstrate the behavior of the model. It is evident from this figure that, in all those scenes where there is a strong perception that the road enters the housing estate, a high 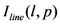 value (
value (  ) is assigned. Specifically these are the scenes Figure 9(a,c,e,f,i,k). On the other hand it is evident that all those scenes where there is a strong perception that the road does not enter the housing estate a low
) is assigned. Specifically these are the scenes Figure 9(a,c,e,f,i,k). On the other hand it is evident that all those scenes where there is a strong perception that the road does not enter the housing estate a low 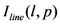 value (
value (  ) is assigned. Specifically these are the scenes Figure 9(b,d,g).
) is assigned. Specifically these are the scenes Figure 9(b,d,g).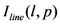 values.
values.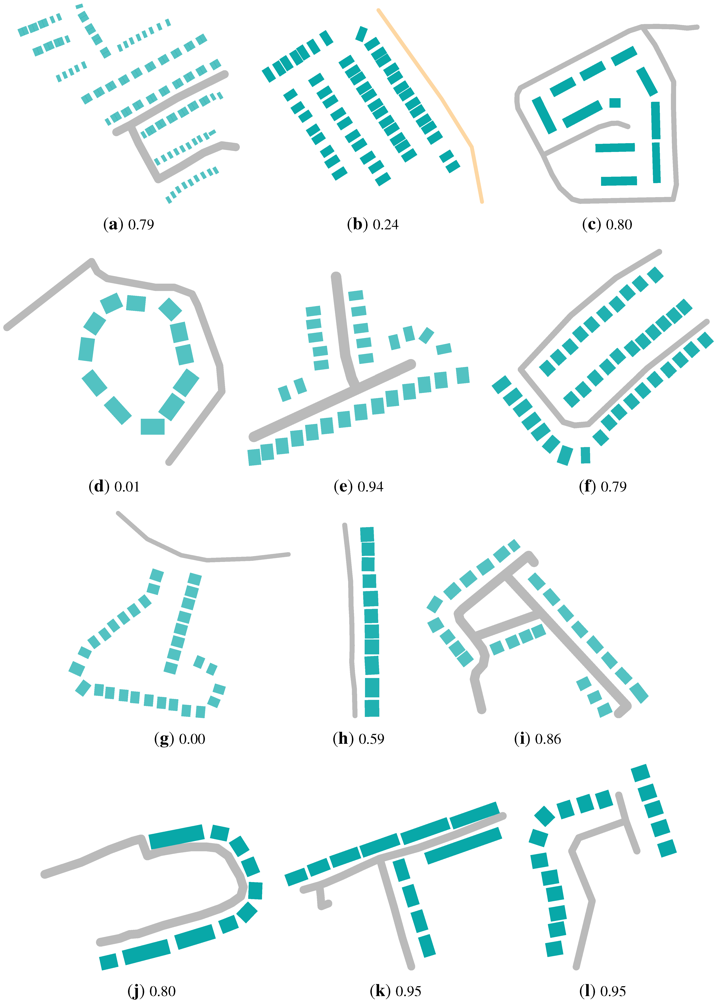
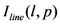 to each of these scenes. We argue that a scene may exhibit more than a single spatial relation.
to each of these scenes. We argue that a scene may exhibit more than a single spatial relation.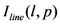 values of
values of  and
and  respectively. Despite a significantly higher value of
respectively. Despite a significantly higher value of 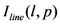 being assigned to Figure 9(l) relative to Figure 9(f), it is not evident that the relation of enters exists to a greater degree in Figure 9(l). This argument could also be applied to Figure 9(b,d). Determining how accurately the proposed model captures the degree to which the relation enters is present in a given scene would require a large scale behavioral study involving human subjects. As such, it is beyond the scope of this paper.
being assigned to Figure 9(l) relative to Figure 9(f), it is not evident that the relation of enters exists to a greater degree in Figure 9(l). This argument could also be applied to Figure 9(b,d). Determining how accurately the proposed model captures the degree to which the relation enters is present in a given scene would require a large scale behavioral study involving human subjects. As such, it is beyond the scope of this paper.4.3. Access Road Classification
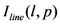 threshold of
threshold of  which was determined using the training set. That is, a road was classified as an access road if the corresponding
which was determined using the training set. That is, a road was classified as an access road if the corresponding 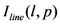 value was greater than
value was greater than  ; otherwise it was classified as a non-access road. On the test set
; otherwise it was classified as a non-access road. On the test set  classification accuracy was achieved. To demonstrate that
classification accuracy was achieved. To demonstrate that 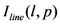 divides access and non-access roads into statistical significant groups an unbalanced analysis of variance (ANOVA) was performed [60]. It was found that the groups are statistical significant with
divides access and non-access roads into statistical significant groups an unbalanced analysis of variance (ANOVA) was performed [60]. It was found that the groups are statistical significant with  .
.5. Conclusions
Acknowledgments
References
- Murphy, G. The Big Book of Concepts; MIT Press: Boston, MA, USA, 2002. [Google Scholar]
- Walter, V.; Luo, F. Automatic interpretation of digital maps. ISPRS J. Photogramm. 2011, 66, 519–528. [Google Scholar] [CrossRef]
- Tryfona, N.; Egenhofer, M.J. Consistency among parts and aggregates: A computational model. Trans. GIS 1997, 1, 1–3. [Google Scholar]
- Price, R.; Tryfona, N.; Jensen, C.S. Modeling Topological Constraints in Spatial Part-Whole Relationships. In Proceedings of the 20th International Conference on Conceptual Modeling: Conceptual Modeling, Yokohama, Japan, 27–30 November 2001; pp. 27–40.
- Egenhofer, M.; Wilmsen, D. Changes in Topological Relations when Splitting and Merging Regions. In Proceedings of the 12th International Symposium on Spatial Data Handling, Vienna, Austria, 12–14 July 2006.
- Mackaness, W.; Edwards, G. The Importance of Modelling Pattern and Structure in Automated Map Generalization. In Proceedings of Joint Workshop on Multi-Scale Representations of Spatial Data, Ottawa, ON, Canada, 7–8 July 2002.
- Touya, G. A road network selection process based on data enrichment and structure detection. Trans. GIS 2010, 14, 595–614. [Google Scholar] [CrossRef]
- Werder, S.; Kieler, B.; Sester, M. Semi-Automatic Interpretation of Buildings and Settlement Areas in User-Generated Spatial Data. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 330–339.
- Butenuth, M.; Gösseln, G.; Tiedge, M.; Heipke, C.; Lipeck, U.; Sester, M. Integration of heterogeneous geospatial data in a federated database. ISPRS J. Photogramm. 2007, 62, 328–346. [Google Scholar] [CrossRef]
- Anders, K.; Fritsch, D. Automatics interpretation of digital maps for data revision. Int. Arch. Photogramm. Remote Sens. 1996, 31, 90–94. [Google Scholar]
- Lüscher, P.; Weibel, R.; Mackaness, W. Where is the Terraced House? On the Use of Ontologies for Recognition of Urban Concepts in Cartographic Databases. In Headway in Spatial Data Handling; Ruas, A., Gold, C., Eds.; Springer: Berlin, Germany, 2008; pp. 449–466. [Google Scholar]
- Regnault, N. Recognition of Building Clusters for Generalization. In Proceedings of the 7th International Symposium on Spatial Data Handling, Delft, The Netherlands, 12–16 August 1996; pp. 185–198.
- Yan, H.; Weibel, R.; Yang, B. A multi-parameter approach to automated building grouping and generalization. Geoinformatica 2008, 12, 73–89. [Google Scholar]
- Steinhauer, J.H.; Wiese, T.; Freksa, C.; Barkowsky, T. Recognition of Abstract Regions in Cartographic Maps. In Proceedings of the International Conference on Spatial Information Theory: Foundations of Geographic Information Science, Morro Bay, CA, USA, 19–23 September 2001; pp. 306–321.
- Qi, H.B.; Li, Z.L. An approach to building grouping based on hierarchical constraints. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2008, XXXVII, 449–454. [Google Scholar]
- Zhang, X.; Ai, T.; Stoter, J. Characterization and Detection of Building Patterns in Cartographic Data: Two Algorithms. In Advances in Spatial Data Handling and GIS; Shi, W., Yeh, A., Leung, Y., Zhou, C., Eds.; Springer: Berlin, Germany, 2012; pp. 93–107. [Google Scholar]
- Christophe, S.; Ruas, A. Detecting Building Alignments for Generalisation Purposes. In Advances in Spatial Data Handling; Richardson, D., van Oosterom, P., Eds.; Springer: Berlin, Germany, 2002; pp. 419–432. [Google Scholar]
- Mao, B.; Harrie, L.; Ban, Y. Detection and typification of linear structures for dynamic visualization of 3D city models. Comput. Environ. Urban Syst. 2012, 36, 233–244. [Google Scholar] [CrossRef]
- Luscher, P.; Weibel, R.; Burghardt, D. Integrating ontological modelling and Bayesian inference for pattern classification in topographic vector data. Comput. Environ. Urban Syst. 2009, 33, 363–374. [Google Scholar] [CrossRef] [Green Version]
- Haunert, J. Detecting Symmetries in Building Footprints by String Matching. In Advancing Geoinformation Science for a Changing World; Geertman, S., Reinhardt, W., Toppen, F., Eds.; Springer: Berlin, Germany, 2011; pp. 319–336. [Google Scholar]
- Egenhoger, M.J.; Franzosa, R.D. Point-set topological spatial relations. Int. J. Geogr. Inf. Syst. 1991, 5, 161–174. [Google Scholar] [CrossRef]
- Shariff, A.; Egenhofer, M.; Mark, D. Natural-language spatial relations between linear and areal objects: The topology and metric of english-language terms. Int. J. Geogr. Inf. Sci. 1998, 12, 215–246. [Google Scholar]
- Hernandez, D. Qualitative Representation of Spatial Knowledge; Springer: Berlin, Germany, 1994. [Google Scholar]
- Cohn, A.G.; Hazarika, S.M. Qualitative spatial representation and reasoning: An overview. Fundam. Inform. 2001, 46, 1–29. [Google Scholar]
- Riedemann, C. Matching Names and Definitions of Topological Operators. In Spatial Information Theory; Cohn, A., Mark, D., Eds.; Springer: Berlin, Germany, 2005; Volume 3693, pp. 165–181. [Google Scholar]
- Cai, G.; Wang, H.; MacEachren, A.; Fuhrmann, S. Natural conversational interfaces to geospatial databases. Trans. GIS 2005, 9, 199–221. [Google Scholar] [CrossRef]
- Sjoo, K.; Jensfelt, P. Functional Topological Relations for Qualitative Spatial Representation. In Proceedings of the International Conference on Advanced Robotics, Montevideo, Uruguay, 20–23 June 2011.
- Egenhofer, M. Reasoning about Binary Topological Relations. In Proceedings of the Second International Symposium on Advances in Spatial Databases, Zurich, Switzerland, 28–30 August 1991; pp. 143–160.
- Egenhofer, M. A Reference System for Topological Relations between Compound Spatial Objects. In Advances in Conceptual Modeling—Challenging Perspectives; Heuser, C., Pernul, G., Eds.; Springer: Berlin, Germany, 2009; Volume 5833, pp. 307–316. [Google Scholar]
- Randell, D.; Cui, Z.; Cohn, A. A Spatial Logic based on Regions and Connection. In Proceedings of the International Conference on Knowledge Representation and Reasoning, Cambridge, MA, USA, 16–29 October 1992; 92, pp. 165–176.
- Knauff, M.; Rauh, R.; Renz, J. A Cognitive Assessment of Topological Spatial Relations: Results from an Empirical Investigation. In Spatial Information Theory A Theoretical Basis for GIS; Hirtle, S., Frank, A., Eds.; Springer: Berlin, Germany, 1997; Volume 1329, pp. 193–206. [Google Scholar]
- Renz, J.; Rauh, R.; Knauff, M. Towards Cognitive Adequacy of Topological Spatial Relations. In Spatial Cognition II, Integrating Abstract Theories, Empirical Studies, Formal Methods, and Practical Applications; Springer-Verlag: London, UK, 2000; pp. 184–197. [Google Scholar]
- Klippel, A. Spatial information theory meets spatial thinking—Is topology the Rosetta Stone of spatial cognition? Ann. Assoc. Am. Geogr. 2012. [Google Scholar] [CrossRef]
- Mark, D.; Egenhofer, M. Modeling spatial relations between lines and regions: Combining formal mathematical models and human subjects testing. Cartogr. Geogr. Inf. Syst. 1994, 21, 195–212. [Google Scholar]
- Egenhofer, M.; Mark, D. Naive Geography. In Spatial Information Theory A Theoretical Basis for GIS; Frank, A., Kuhn, W., Eds.; Springer: Berlin, Germany, 1995; Volume 988, pp. 1–15. [Google Scholar]
- Clementini, E.; di Felice, P.; van Oosterom, P. A Small Set of Formal Topological Relationships Suitable for End-User Interaction. In Advances in Spatial Databases; Abel, D., Chin Ooi, B., Eds.; Springer: Berlin, Germany, 1993; Volume 692, pp. 277–295. [Google Scholar]
- Cai, G.; Wang, H.; MacEachren, A. Communicating Vague Spatial Concepts in Human-GIS Interactions: A Collaborative Dialogue Approach. In Spatial Information Theory. Foundations of Geographic Information Science; Kuhn, W., Worboys, M., Timpf, S., Eds.; Springer: Berlin, Germany, 2003. [Google Scholar]
- Zhan, F.B. A Fuzzy Set Model of Approximate Linguistic Terms in Descriptions of Binary Topological Relations between Simple Regions. In Applying Soft Computing in Defining Spatial Relations; Matsakis, P., Sztandera, L.M., Eds.; Physica-Verlag GmbH: Heidelberg, Germany, 2002; pp. 179–202. [Google Scholar]
- Bloch, I.; Colliot, O.; Cesar, R.M., Jr. On the ternary spatial relation “between”. IEEE Trans. Syst. Man Cybern. B Cybern. 2006, 36, 312–327. [Google Scholar] [CrossRef]
- Raubal, M. Cognitive engineering for geographic information science. Geogr. Compass 2009, 3, 1087–1104. [Google Scholar] [CrossRef]
- Sarjakoski, L. Chapter 2 Conceptual Models of Generalisation and Multiple Representation. In Generalisation of Geographic Information; Mackaness, W., Ruas, A., Sarjakoski, L., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; pp. 11–35. [Google Scholar]
- Weibel, R. Generalization of Spatial Data: Principles and Selected Algorithms. In Algorithmic Foundations of Geographic Information Systems; van Kreveld, M., Nievergelt, J., Roos, T., Widmayer, P., Eds.; Springer: Berlin, Germany, 1997; Volume 1340, pp. 99–152. [Google Scholar]
- Mackaness, W.A. Generalisation of Geographic Information: Cartographic Modelling and Applications; Mackaness, W.A., Ruas, A., Sarjakoski, L.T., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Jones, C.B.; Ware, J.M. Map generalization in the Web age. Int. J. Geogr. Inf. Sci. 2005, 19, 859–870. [Google Scholar] [CrossRef]
- Weibel, R. A Typology of Constraints to Line Simplification. In Proceedings of 7th International Symposium on Spatial Data Handling, Delft, The Netherlands, 12–16 August 1996; pp. 533–546.
- Regnauld, N.; Revell, P. Automatic amalgamation of buildings for producing ordnance survey 1:50,000 scale maps. Cartogr. J. 2007, 44, 239–250. [Google Scholar] [CrossRef]
- Haunert, J.; Wolff, A. Optimal and Topologically Safe Simplification of Building Footprints. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 192–201.
- Kieler, B.; Haunert, J.; Sester, M. Deriving scale-transition matrices from map samples for simulated annealing-based aggregation. Ann. GIS 2009, 15, 107–116. [Google Scholar] [CrossRef]
- Haunert, J.; Wolff, A. Area aggregation in map generalisation by mixed-integer programming. Int. J. Geogr. Inf. Sci. 2010, 24, 1871–1897. [Google Scholar] [CrossRef]
- Corcoran, P.; Mooney, P.; Winstanley, A.C. Planar and non-planar topologically consistent vector map simplification. Int. J. Geogr. Inf. Sci. 2011, 25, 1659–1680. [Google Scholar] [CrossRef]
- Jones, C.B. Geographical Information Systems and Computer Cartography; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Regnauld, N.; McMaster, R. A Synoptic View of Generalisation Operators. In Generalisation of Geographic Information; Mackaness, W., Ruas, A., Sarjakoski, L., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; pp. 37–66. [Google Scholar]
- Regnauld, N. Algorithms for the Amalgamation of Topographic Data. In Proceedings of the 21st International Cartographic Conference, Durban, South Africa, 10–16 August 2003.
- Ware, J.; Jones, C.; Bundy, G. A Triangulated Spatial Model for Cartographic Generalisation of Areal Objects. In Spatial Information Theory A Theoretical Basis for GIS; Frank, A., Kuhn, W., Eds.; Springer-Verlag: Berlin, Germany, 1995; Volume 988, pp. 173–192. [Google Scholar]
- Yang, L.; Zhang, L.; Ma, J.; Xie, J.; Liu, L. Interactive visualization of multi-resolution urban building models considering spatial cognition. Int. J. Geogr. Inf. Sci. 2011, 25, 5–24. [Google Scholar] [CrossRef]
- Li, Z.; Yan, H.; Ai, T.; Chen, J. Automated building generalization based on urban morphology and Gestalt theory. Int. J. Geogr. Inf. Sci. 2004, 18, 513–534. [Google Scholar] [CrossRef]
- Damen, J.; van Kreveld, M.; Spaan, B. High Quality Building Generalization by Extending the Morphological Operators. In Proceedings of the ICA Workshop on Generalization, Montpellier, France, 20–21 June 2008.
- Dupenois, M.; Galton, A. Assigning Footprints to Dot Sets: An Analytical Survey. In Spatial Information Theory; Hornsby, K., Claramunt, C., Denis, M., Ligozat, G., Eds.; Springer: Berlin, Germany, 2009; Volume 5756, pp. 227–244. [Google Scholar]
- Goodchild, M. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- DeGroot, M.; Schervish, M. Probability and Statistics, 4th ed; Pearson: London, UK, 2011. [Google Scholar]
- Zhang, X.; Ai, T.; Stoter, J.; Kraak, M.; Molenaar, M. Building pattern recognition in topographic data: Examples on collinear and curvilinear alignments. GeoInformatica 2013, in press. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Corcoran, P.; Mooney, P.; Bertolotto, M. Spatial Relations Using High Level Concepts. ISPRS Int. J. Geo-Inf. 2012, 1, 333-350. https://doi.org/10.3390/ijgi1030333
Corcoran P, Mooney P, Bertolotto M. Spatial Relations Using High Level Concepts. ISPRS International Journal of Geo-Information. 2012; 1(3):333-350. https://doi.org/10.3390/ijgi1030333
Chicago/Turabian StyleCorcoran, Padraig, Peter Mooney, and Michela Bertolotto. 2012. "Spatial Relations Using High Level Concepts" ISPRS International Journal of Geo-Information 1, no. 3: 333-350. https://doi.org/10.3390/ijgi1030333




