Model for Origin and Modification of Mass and Coupling Constant
Abstract
:1. Introduction
2. Field-Theory Model: Quantum Correction of Mass and Coupling Constant
2.1. Quantum Correction of Mass
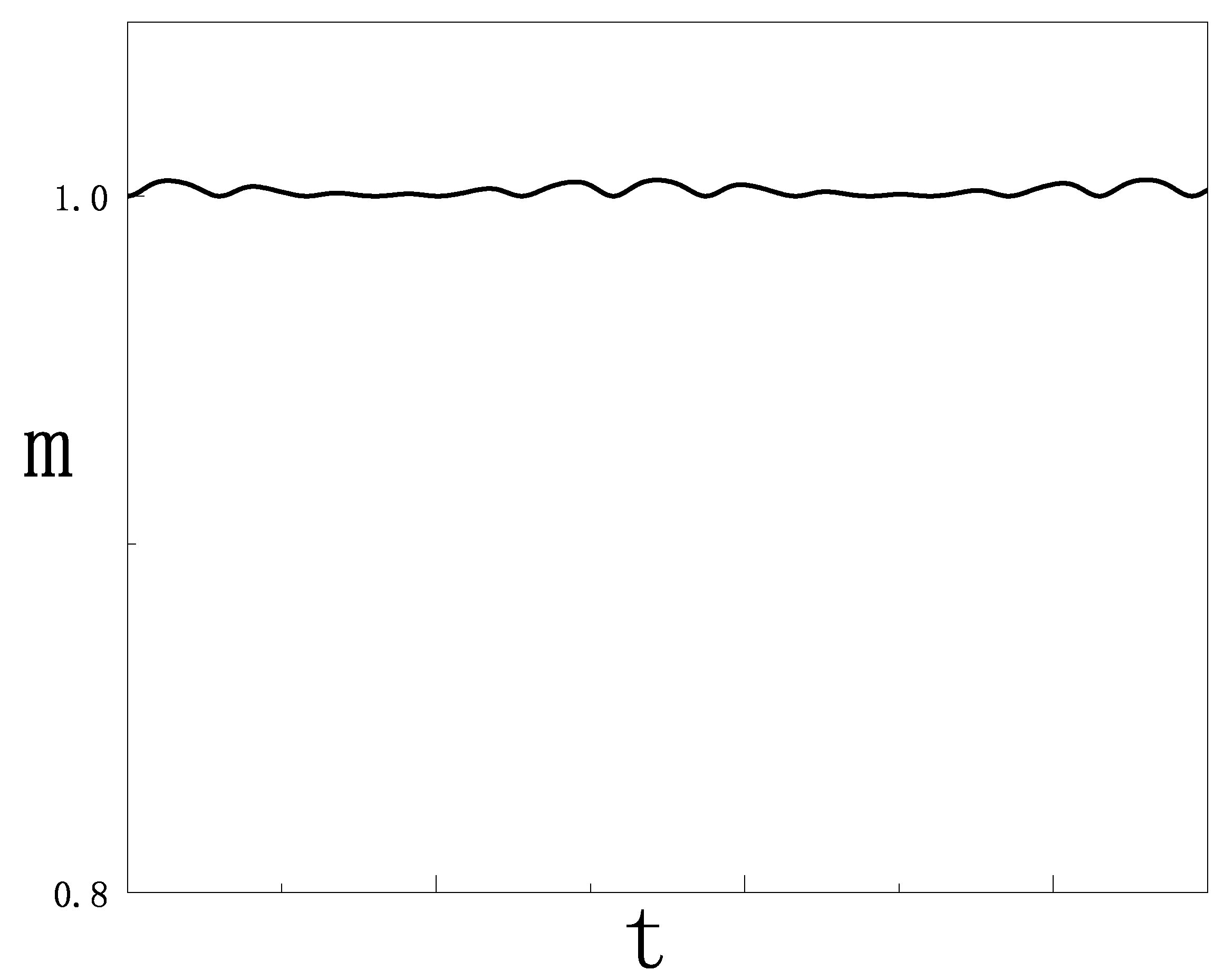
2.1.1. Model of Origin of Mass
2.1.2. Quantum Correction of Mass
2.2. Quantum Correction of Coupling Constant
2.2.1. Model of Origin of Coupling Constant
2.2.2. Quantum Correction of Coupling Constant
3. Mechanics Model: Quantum Correction of Mass and Coupling Constant
3.1. Quantum Correction of Mass
3.2. Quantum Correction of Coupling Constant
4. Discussions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dirac, P.A. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Teller, E. On the change of physical constants. Phys. Rev. 1948, 73, 801. [Google Scholar] [CrossRef]
- Jordan, P. Die physikalischen weltkonstanten. Naturwissenschaften 1937, 25, 513–517. [Google Scholar] [CrossRef]
- Jordan, P. The present state of Dirac’s cosmological hypothesis. Z. Phys. 1959, 157, 112–121. [Google Scholar] [CrossRef]
- Jordan, P. Schwerkraft und Weltall: Grundlagen der theoretischen Kosmologie; Vieweg: Braunschweig, Germany, 1952. [Google Scholar]
- Peracaula, J.S. The dynamics of vacuum, gravity and matter: Implications on the fundamental constants. arXiv 2023, arXiv:2308.13349. [Google Scholar]
- Nagata, R.; Chiba, T.; Sugiyama, N. WMAP constraints on scalar-tensor cosmology and the variation of the gravitational constant. Phys. Rev. D 2004, 69, 083512. [Google Scholar] [CrossRef]
- Wu, Y.S.; Wang, Z. Time variation of Newton’s gravitational constant in superstring theories. Phys. Rev. Lett. 1986, 57, 1978. [Google Scholar] [CrossRef]
- García-Berro, E.; Lorén-Aguilar, P.; Torres, S.; Althaus, L.G.; Isern, J. An upper limit to the secular variation of the gravitational constant from white dwarf stars. J. Cosmol. Astropart. Phys. 2011, 2011, 021. [Google Scholar] [CrossRef]
- Córsico, A.H.; Althaus, L.G.; García-Berro, E.; Romero, A.D. An independent constraint on the secular rate of variation of the gravitational constant from pulsating white dwarfs. J. Cosmol. Astropart. Phys. 2013, 2013, 032. [Google Scholar] [CrossRef]
- Garcia-Berro, E.; Kubyshin, Y.; Loren-Aguilar, P.; Isern, J. The variation of the gravitational constant inferred from the Hubble diagram of Type Ia supernovae. Int. J. Mod. Phys. D 2006, 15, 1163–1174. [Google Scholar] [CrossRef]
- Colaço, L.; Landau, S.; Gonzalez, J.; Spinelly, J.; Santos, G. Constraining a possible time-variation of the speed of light along with the fine-structure constant using strong gravitational lensing and Type Ia supernovae observations. J. Cosmol. Astropart. Phys. 2022, 2022, 062. [Google Scholar] [CrossRef]
- Gershteyn, M.L.; Gershteyn, L.I.; Gershteyn, A.; Karagioz, O.V. Experimental evidence that the gravitational constant varies with orientation. arXiv 2002, arXiv:physics/0202058. [Google Scholar]
- Lazaridis, K.; Wex, N.; Jessner, A.; Kramer, M.; Stappers, B.; Janssen, G.; Desvignes, G.; Purver, M.; Cognard, I.; Theureau, G.; et al. Generic tests of the existence of the gravitational dipole radiation and the variation of the gravitational constant. Mon. Not. R. Astron. Soc. 2009, 400, 805–814. [Google Scholar] [CrossRef]
- Müller, J.; Biskupek, L. Variations of the gravitational constant from lunar laser ranging data. Class. Quantum Gravity 2007, 24, 4533. [Google Scholar] [CrossRef]
- Ivashchuk, V.; Kobtsev, A. On exponential cosmological type solutions in the model with Gauss–Bonnet term and variation of gravitational constant. Eur. Phys. J. C 2015, 75, 1–12. [Google Scholar] [CrossRef]
- Fritzsch, H.; Sola, J. Matter non-conservation in the universe and dynamical dark energy. Class. Quantum Gravity 2012, 29, 215002. [Google Scholar] [CrossRef]
- Fritzsch, H.; Solà, J.; Nunes, R.C. Running vacuum in the Universe and the time variation of the fundamental constants of Nature. Eur. Phys. J. C 2017, 77, 1–16. [Google Scholar]
- Sola Peracaula, J. The cosmological constant problem and running vacuum in the expanding universe. Philos. Trans. R. Soc. A 2022, 380, 20210182. [Google Scholar] [CrossRef]
- Alvey, J.; Sabti, N.; Escudero, M.; Fairbairn, M. Improved BBN constraints on the variation of the gravitational constant. Eur. Phys. J. C 2020, 80, 1–6. [Google Scholar]
- Reuter, M.; Weyer, H. Running Newton constant, improved gravitational actions, and galaxy rotation curves. Phys. Rev. D 2004, 70, 124028. [Google Scholar] [CrossRef]
- Anber, M.M.; Donoghue, J.F. Running of the gravitational constant. Phys. Rev. D 2012, 85, 104016. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Emond, W.T.; Finelli, F.; Gumrukcuoglu, A.E.; Koyama, K.; Paoletti, D. A larger value for H0 by an evolving gravitational constant. arXiv 2020, arXiv:2004.11161. [Google Scholar] [CrossRef]
- Chen, Y.J.; Li, S.L.; Chen, Y.Z.; Li, W.D.; Dai, W.S. Gravitational constant model and correction. J. Math. Phys. 2022, 63, 112503. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Fine-structure constant: Is it really a constant? Phys. Rev. D 1982, 25, 1527. [Google Scholar] [CrossRef]
- Chamoun, N.; Landau, S.J.; Vucetich, H. Bekenstein model and the time variation of the strong coupling constant. Phys. Lett. B 2001, 504, 1–5. [Google Scholar] [CrossRef]
- Kolachevsky, N.; Matveev, A.; Alnis, J.; Parthey, C.; Steinmetz, T.; Wilken, T.; Holzwarth, R.; Udem, T.; Hänsch, T. Testing the stability of the fine structure constant in the laboratory. Space Sci. Rev. 2009, 148, 267–288. [Google Scholar] [CrossRef]
- Prestage, J.D.; Tjoelker, R.L.; Maleki, L. Atomic clocks and variations of the fine structure constant. Phys. Rev. Lett. 1995, 74, 3511. [Google Scholar] [CrossRef]
- Roberts, B.M.; Delva, P.; Al-Masoudi, A.; Amy-Klein, A.; Baerentsen, C.; Baynham, C.; Benkler, E.; Bilicki, S.; Bize, S.; Bowden, W.; et al. Search for transient variations of the fine structure constant and dark matter using fiber-linked optical atomic clocks. New J. Phys. 2020, 22, 093010. [Google Scholar] [CrossRef]
- Dzuba, V.; Flambaum, V. Atomic optical clocks and search for variation of the fine-structure constant. Phys. Rev. A 2000, 61, 034502. [Google Scholar] [CrossRef]
- Dzuba, V.; Flambaum, V. Highly charged ions for atomic clocks and search for variation of the fine structure constant. In Proceedings of the TCP 2014: 6th International Conference on Trapped Charged Particles and Fundamental Physics, Takamatsu, Japan, 1–5 December 2014; Springer: Cham, Switzerland, 2015; pp. 79–86. [Google Scholar]
- Webb, J.K.; Flambaum, V.V.; Churchill, C.W.; Drinkwater, M.J.; Barrow, J.D. Search for time variation of the fine structure constant. Phys. Rev. Lett. 1999, 82, 884. [Google Scholar] [CrossRef]
- Webb, J.; King, J.; Murphy, M.; Flambaum, V.; Carswell, R.; Bainbridge, M. Indications of a spatial variation of the fine structure constant. Phys. Rev. Lett. 2011, 107, 191101. [Google Scholar] [CrossRef] [PubMed]
- Truppe, S.; Hendricks, R.; Tokunaga, S.; Lewandowski, H.; Kozlov, M.; Henkel, C.; Hinds, E.; Tarbutt, M. A search for varying fundamental constants using hertz-level frequency measurements of cold CH molecules. Nat. Commun. 2013, 4, 2600. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, I.L.; Sola, J.; Espana-Bonet, C.; Ruiz-Lapuente, P. Variable cosmological constant as a Planck scale effect. Phys. Lett. B 2003, 574, 149–155. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J. On the possible running of the cosmological “constant”. Phys. Lett. B 2009, 682, 105–113. [Google Scholar] [CrossRef]
- Toms, D.J. Cosmological constant and quantum gravitational corrections to the running fine structure constant. Phys. Rev. Lett. 2008, 101, 131301. [Google Scholar] [CrossRef]
- Graham, N.; Quandt, M.; Weigel, H. Spectral Methods in Quantum Field Theory; Springer: Berlin/Heidelberg, Germany, 2009; Volume 777. [Google Scholar]
- Olver, F.W.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Barvinsky, A.; Vilkovisky, G. Beyond the Schwinger-DeWitt technique: Converting loops into trees and in-in currents. Nucl. Phys. B 1987, 282, 163–188. [Google Scholar] [CrossRef]
- Barvinsky, A.; Vilkovisky, G. Covariant perturbation theory (II). Second order in the curvature. General algorithms. Nucl. Phys. B 1990, 333, 471–511. [Google Scholar] [CrossRef]
- Barvinsky, A.; Vilkovisky, G. Covariant perturbation theory (III). Spectral representations of the third-order form factors. Nucl. Phys. B 1990, 333, 512–524. [Google Scholar] [CrossRef]
- Dai, W.S.; Xie, M. The number of eigenstates: Counting function and heat kernel. J. High Energy Phys. 2009, 2009, 033. [Google Scholar] [CrossRef]
- Pang, H.; Dai, W.S.; Xie, M. Relation between heat kernel method and scattering spectral method. Eur. Phys. J. C 2012, 72, 1–13. [Google Scholar] [CrossRef]
- Li, W.D.; Dai, W.S. Heat-kernel approach for scattering. Eur. Phys. J. C 2015, 75, 1–14. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Chen, Y.J.; Li, S.L.; Li, W.D.; Dai, W.S. Seeley–DeWitt expansion of scattering phase shift. Eur. Phys. J. Plus 2022, 137, 1140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-J.; Li, S.-L.; Liu, Y.-Y.; Gu, X.; Li, W.-D.; Dai, W.-S. Model for Origin and Modification of Mass and Coupling Constant. Universe 2023, 9, 426. https://doi.org/10.3390/universe9090426
Chen Y-J, Li S-L, Liu Y-Y, Gu X, Li W-D, Dai W-S. Model for Origin and Modification of Mass and Coupling Constant. Universe. 2023; 9(9):426. https://doi.org/10.3390/universe9090426
Chicago/Turabian StyleChen, Yu-Jie, Shi-Lin Li, Yuan-Yuan Liu, Xin Gu, Wen-Du Li, and Wu-Sheng Dai. 2023. "Model for Origin and Modification of Mass and Coupling Constant" Universe 9, no. 9: 426. https://doi.org/10.3390/universe9090426




