Geminga SNR: Possible Candidate of Local Cosmic-Ray Factory (II)
Abstract
:1. Introduction
2. Model Description
2.1. Propagation Model
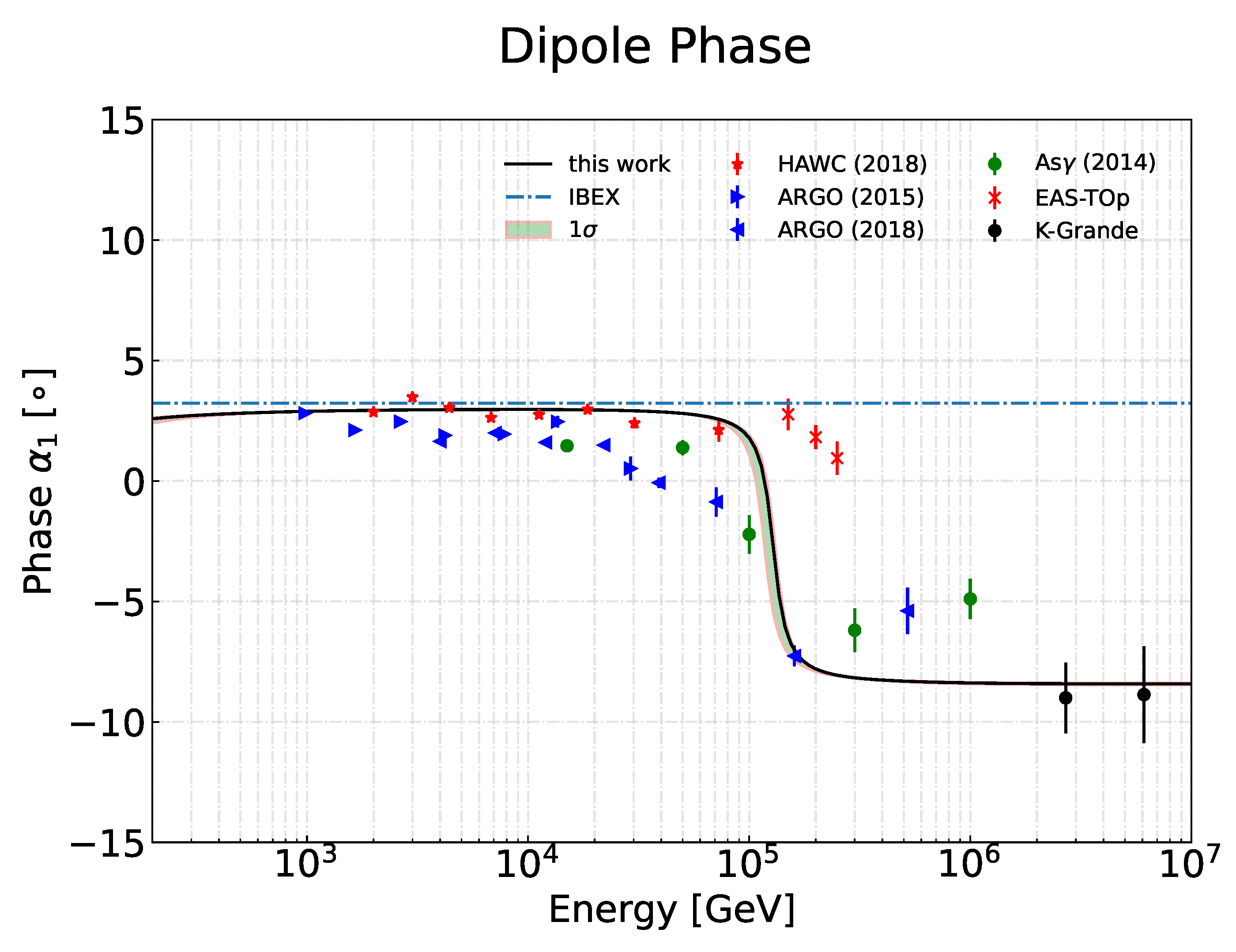
2.2. Anisotropic Diffusion
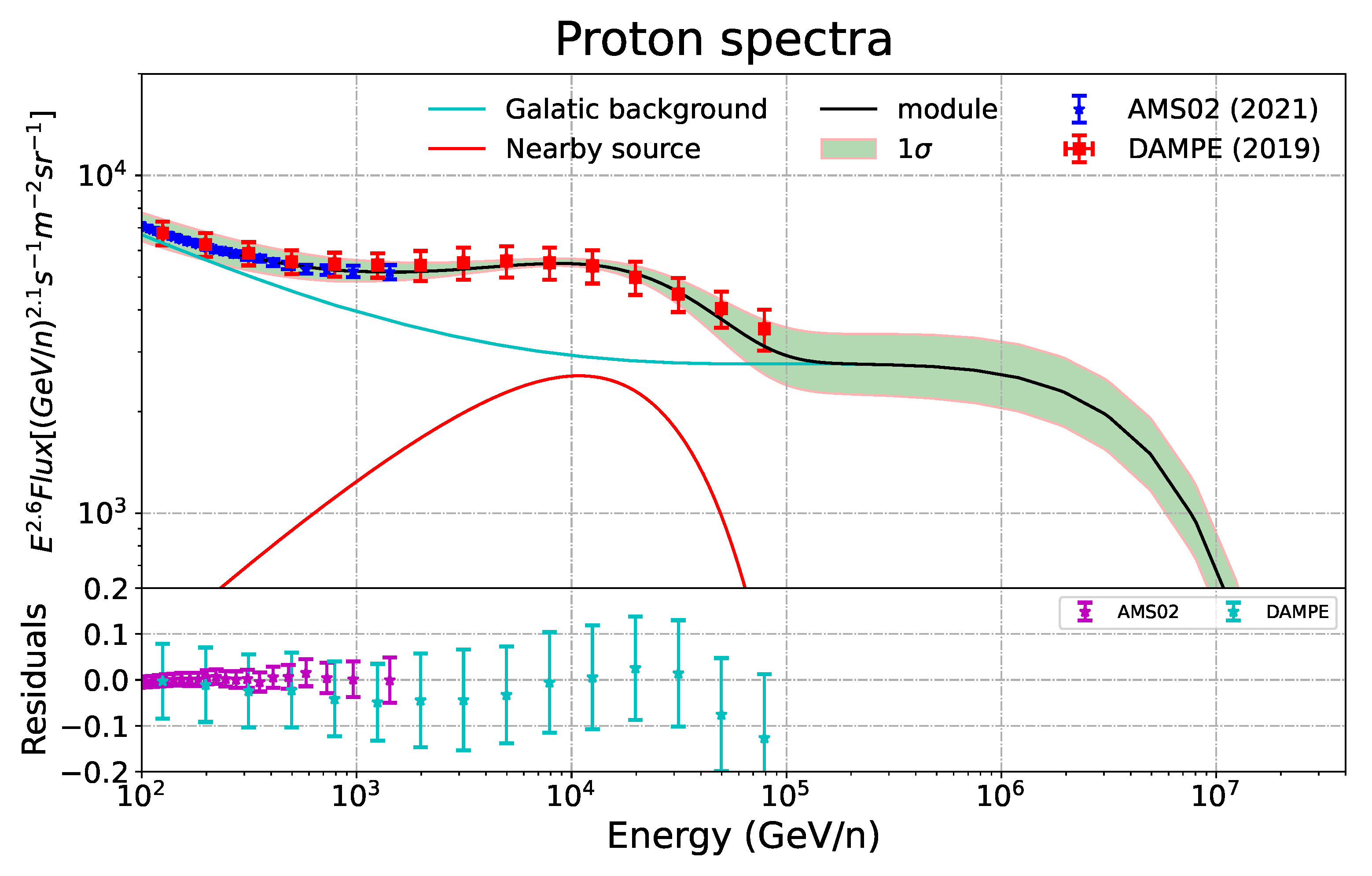
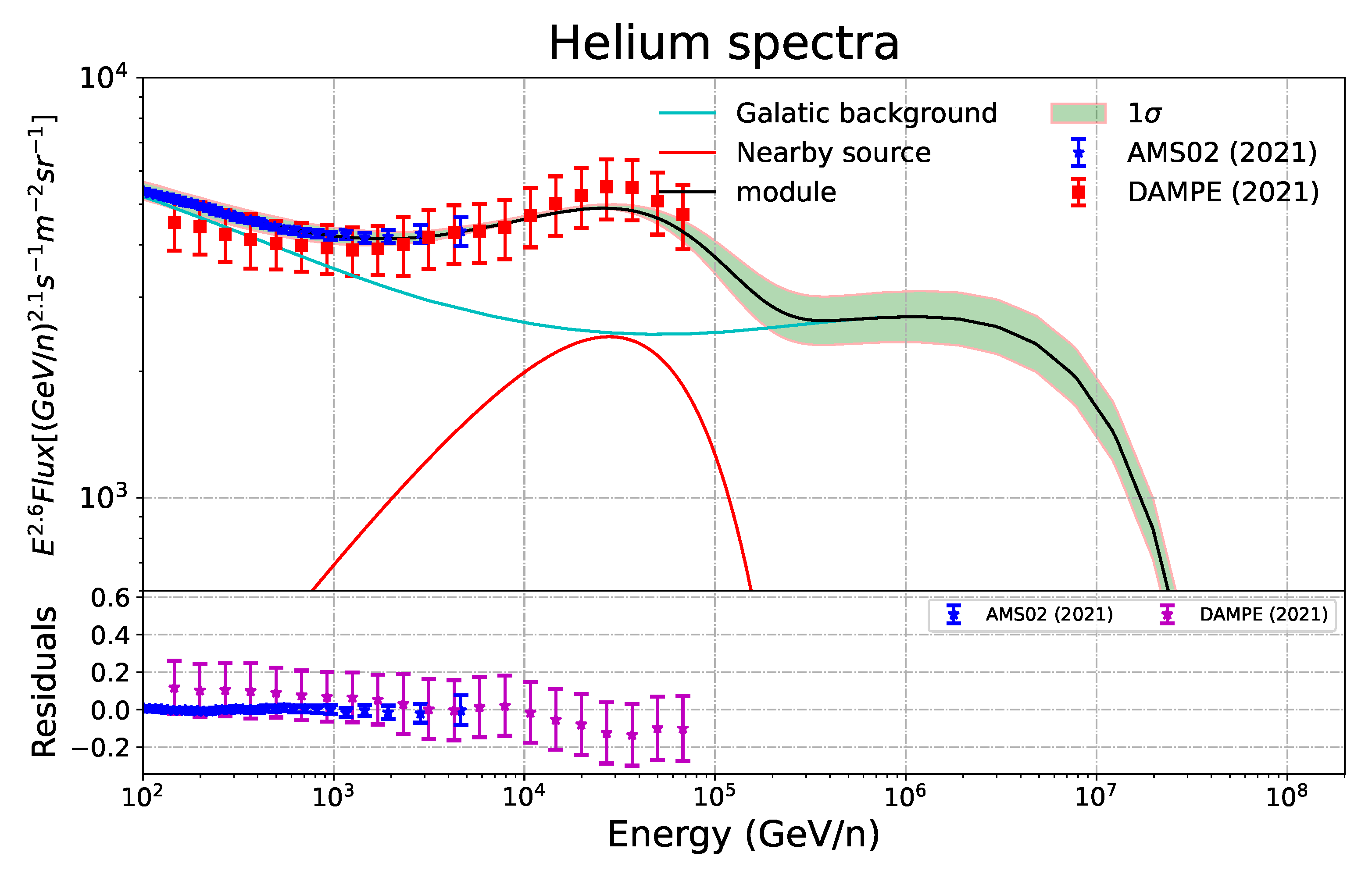
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baade, W.; Zwicky, F. Cosmic Rays from Super-novae. Contrib. Mt. Wilson Obs. 1934, 3, 79–83. [Google Scholar]
- Erlykin, A.D.; Wolfendale, A.W. A single source of cosmic rays in the range 1015–1016 eV. J. Phys. G Nucl. Phys. 1997, 23, 979–989. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Bottai, S.; et al. An anomalous positron abundance in cosmic rays with energies 1.5–100 GeV. Nature 2009, 458, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Battelino, M.; et al. Measurement of the Cosmic Ray e++e− Spectrum from 20 GeV to 1 TeV with the Fermi Large Area Telescope. Phys. Rev. Lett. 2009, 102, 181101. [Google Scholar] [CrossRef] [PubMed]
- Accardo, L.; Aguilar, M.; Aisa, D.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. High Statistics Measurement of the Positron Fraction in Primary Cosmic Rays of 0.5–500 GeV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2014, 113, 121101. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Electron and Positron Fluxes in Primary Cosmic Rays Measured with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2014, 113, 121102. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H.J.; Ahn, H.S.; Batkov, K.E.; Bashindzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; et al. Elemental energy spectra of cosmic rays from the data of the ATIC-2 experiment. Bull. Russ. Acad. Sci. Phys. 2007, 71, 494–497. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Bashinzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; Zatsepin, V.I.; et al. Energy spectra of abundant nuclei of primary cosmic rays from the data of ATIC-2 experiment: Final results. Bull. Russ. Acad. Sci. Phys. 2009, 73, 564–567. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Ahn, H.S.; Allison, P.S.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Boyle, P.J.; Childers, J.T.; Conklin, N.B.; Coutu, S.; et al. Cosmic-ray Proton and Helium Spectra from the First CREAM Flight. Astrophys. J. 2011, 728, 122. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA Measurements of Cosmic-Ray Proton and Helium Spectra. Science 2011, 332, 69. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Proton Flux in Primary Cosmic Rays from Rigidity 1 GV to 1.8 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 114, 171103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Helium Flux in Primary Cosmic Rays of Rigidities 1.9 GV to 3 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 115, 211101. [Google Scholar] [CrossRef]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bonechi, S.; Bongi, M.; et al. Direct Measurement of the Cosmic-Ray Proton Spectrum from 50 GeV to 10 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2019, 122, 181102. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.S.; Anderson, T.; Barrau, A.; Conklin, N.B.; Coutu, S.; Derome, L.; Han, J.H.; Jeon, J.A.; Kim, K.C.; Kim, M.H.; et al. Proton and Helium Spectra from the CREAM-III Flight. Astrophys. J. 2017, 839, 5. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. First results of the cosmic ray NUCLEON experiment. J. Cosmol. Astropart. Phys. 2017, 2017, 020. [Google Scholar] [CrossRef]
- An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; Chen, J.L.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar] [CrossRef] [PubMed]
- Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Becherini, Y.; Behera, B.; Bernlöhr, K.; Bochow, A.; Boisson, C.; et al. Probing the ATIC peak in the cosmic-ray electron spectrum with H.E.S.S. Astrophys. Process. 2009, 508, 561–564. [Google Scholar] [CrossRef]
- Borla Tridon, D. Measurement of the cosmic electron spectrum with the MAGIC telescopes. In Proceedings of the International Cosmic Ray Conference, Beijing, China, 11–18 August 2011; Volume 6, p. 47. [Google Scholar] [CrossRef]
- Staszak, D.; VERITAS Collaboration. Science Highlights from VERITAS. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 868. [Google Scholar] [CrossRef]
- DAMPE Collaboration; Ambrosi, G.; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bertucci, B.; Cai, M.S.; Chang, J.; Chen, D.Y.; et al. Direct detection of a break in the teraelectronvolt cosmic-ray spectrum of electrons and positrons. Nature 2017, 552, 63–66. [Google Scholar] [CrossRef]
- Blasi, P.; Amato, E. Diffusive propagation of cosmic rays from supernova remnants in the Galaxy. II: Anisotropy. J. Cosmol. Astropart. Phys. 2012, 2012, 011. [Google Scholar] [CrossRef] [Green Version]
- Ahlers, M. Deciphering the Dipole Anisotropy of Galactic Cosmic Rays. Phys. Rev. Lett. 2016, 117, 151103. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Bi, X.J.; Lin, S.J.; Wang, B.B.; Yin, P.F. Excesses of cosmic ray spectra from a single nearby source. Phys. Rev. D 2017, 96, 023006. [Google Scholar] [CrossRef]
- Liu, W.; Guo, Y.Q.; Yuan, Q. Indication of nearby source signatures of cosmic rays from energy spectra and anisotropies. J. Cosmol. Astropart. Phys. 2019, 2019, 010. [Google Scholar] [CrossRef]
- Qiao, B.Q.; Liu, W.; Guo, Y.Q.; Yuan, Q. Anisotropies of different mass compositions of cosmic rays. J. Cosmol. Astropart. Phys. 2019, 2019, 007. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Adams, F.C.; Christian, E.; Desiati, P.; Frisch, P.; Funsten, H.O.; Jokipii, J.R.; McComas, D.J.; Moebius, E.; Zank, G.P. Anisotropies in TeV Cosmic Rays Related to the Local Interstellar Magnetic Field from the IBEX Ribbon. J. Phys. Conf. Ser. 2015, 577, 012023. [Google Scholar] [CrossRef]
- Funsten, H.O.; DeMajistre, R.; Frisch, P.C.; Heerikhuisen, J.; Higdon, D.M.; Janzen, P.; Larsen, B.A.; Livadiotis, G.; McComas, D.J.; Möbius, E.; et al. Circularity of the Interstellar Boundary Explorer Ribbon of Enhanced Energetic Neutral Atom (ENA) Flux. Astrophys. J. 2013, 776, 30. [Google Scholar] [CrossRef]
- Effenberger, F.; Fichtner, H.; Scherer, K.; Büsching, I. Anisotropic diffusion of Galactic cosmic ray protons and their steady-state azimuthal distribution. Astrophys. Process. 2012, 547, A120. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 911–914. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P. Multimodal nested sampling: An efficient and robust alternative to Markov Chain Monte Carlo methods for astronomical data analyses. Mon. Not. R. Astron. Soc. 2008, 384, 449–463. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P.; Bridges, M. MULTINEST: An efficient and robust Bayesian inference tool for cosmology and particle physics. Mon. Not. R. Astron. Soc. 2009, 398, 1601–1614. [Google Scholar] [CrossRef] [Green Version]
- Tomassetti, N. Origin of the Cosmic-Ray Spectral Hardening. Astrophys. J. Lett. 2012, 752, L13. [Google Scholar] [CrossRef]
- Tomassetti, N. Cosmic-ray protons, nuclei, electrons, and antiparticles under a two-halo scenario of diffusive propagation. Phys. Rev. D 2015, 92, 081301. [Google Scholar] [CrossRef]
- Feng, J.; Tomassetti, N.; Oliva, A. Bayesian analysis of spatial-dependent cosmic-ray propagation: Astrophysical background of antiprotons and positrons. Phys. Rev. D 2016, 94, 123007. [Google Scholar] [CrossRef]
- Guo, Y.Q.; Tian, Z.; Jin, C. Spatial-dependent Propagation of Cosmic Rays Results in the Spectrum of Proton, Ratios of P/P, and B/C, and Anisotropy of Nuclei. Astrophys. J. 2016, 819, 54. [Google Scholar] [CrossRef]
- Liu, W.; Yao, Y.h.; Guo, Y.Q. Revisiting the Spatially Dependent Propagation Model with the Latest Observations of Cosmic-Ray Nuclei. Astrophys. J. 2018, 869, 176. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, W.; Yang, B.; Fu, X.D.; Xu, H.B.; Yao, Y.H.; Guo, Y.Q. Electron and positron spectra in three-dimensional spatial-dependent propagation model. Chin. Phys. C 2020, 44, 085102. [Google Scholar] [CrossRef]
- Zhang, P.p.; Qiao, B.q.; Liu, W.; Cui, S.w.; Yuan, Q.; Guo, Y.q. Possible bump structure of cosmic ray electrons unveiled by AMS-02 data and its common origin along with the nuclei and positron. J. Cosmol. Astropart. Phys. 2021, 2021, 012. [Google Scholar] [CrossRef]
- Guo, Y.Q.; Yuan, Q. Understanding the spectral hardenings and radial distribution of Galactic cosmic rays and Fermi diffuse γ rays with spatially-dependent propagation. Phys. Rev. D 2018, 97, 063008. [Google Scholar] [CrossRef]
- Green, D.A. Constraints on the distribution of supernova remnants with Galactocentric radius. Mon. Not. R. Astron. Soc. 2015, 454, 1517–1524. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, W.; Yuan, Q.; Hu, H.B.; Bi, X.J.; Wu, H.R.; Zhou, X.X.; Guo, Y.Q. Geminga SNR: Possible Candidate of the Local Cosmic-Ray Factory. Astrophys. J. 2022, 926, 41. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Cosmic ray nuclei, antiprotons and gamma rays in the galaxy: A new diffusion model. J. Cosmol. Astropart. Phys. 2008, 2008, 018. [Google Scholar] [CrossRef]
- Delahaye, T.; Lavalle, J.; Lineros, R.; Donato, F.; Fornengo, N. Galactic electrons and positrons at the Earth: New estimate of the primary and secondary fluxes. Astrophys. Process. 2010, 524, A51. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Becerril, A.; Belmont-Moreno, E.; et al. Observation of Anisotropy of TeV Cosmic Rays with Two Years of HAWC. Astrophys. J. 2018, 865, 57. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; Başeğmez-du Pree, S.; Bates, J.; et al. The Alpha Magnetic Spectrometer (AMS) on the international space station: Part II - Results from the first seven years. Phys. Rep. 2021, 894, 1–116. [Google Scholar] [CrossRef]
- Alemanno, F.; An, Q.; Azzarello, P.; Barbato, F.C.T.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Catanzani, E.; Chang, J.; Chen, D.Y.; et al. Measurement of the Cosmic Ray Helium Energy Spectrum from 70 GeV to 80 TeV with the DAMPE Space Mission. Phys. Rev. Lett. 2021, 126, 201102. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Cao, Z.; Catalanotti, S.; Chen, S.Z.; Chen, T.L.; Cui, S.W.; Dai, B.Z.; D’Amone, A.; et al. ARGO-YBJ Observation of the Large-scale Cosmic Ray Anisotropy During the Solar Minimum between Cycles 23 and 24. Astrophys. J. 2015, 809, 90. [Google Scholar] [CrossRef]
- Carvalho, B.B.; Bartoli, O.; Ferri, F.; Cesare, B.; Ferrero, S.; Remusat, L.; Capizzi, L.S.; Poli, S. Melt and fluid inclusions in migmatites: Unravelling anatexis and fluid regime of the deep crust. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 7–12 April 2019; p. 8044. [Google Scholar]
- Amenomori, M.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Cui, S.W.; Danzengluobu; Ding, L.K.; Feng, C.F.; Feng, Z.; et al. Northern Sky Galactic Cosmic Ray Anisotropy between 10 and 1000 TeV with the Tibet Air Shower Array. Astrophys. J. 2017, 836, 153. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Vittino, A.; Di Bernardo, G.; Di Mauro, M.; Ligorini, A.; Ullio, P.; Grasso, D. Cosmic-ray propagation with DRAGON2: I. numerical solver and astrophysical ingredients. J. Cosmol. Astropart. Phys. 2017, 2017, 015. [Google Scholar] [CrossRef]




| n | ||||||
|---|---|---|---|---|---|---|
| 4.66 | 0.54 | 0.62 | 0.1 | 4 | 6 | 5 |
| Parameter | 68% Limits | ||
|---|---|---|---|
| Background | |||
| Local source | |||
| [TV] | |||
| r [kpc] | |||
| t [kyr] | |||
| gl[] | |||
| gb [] | |||
| Anisotropy | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Guo, Y.; Zhou, X. Geminga SNR: Possible Candidate of Local Cosmic-Ray Factory (II). Universe 2023, 9, 93. https://doi.org/10.3390/universe9020093
Zhao B, Guo Y, Zhou X. Geminga SNR: Possible Candidate of Local Cosmic-Ray Factory (II). Universe. 2023; 9(2):93. https://doi.org/10.3390/universe9020093
Chicago/Turabian StyleZhao, Bing, Yiqing Guo, and Xunxiu Zhou. 2023. "Geminga SNR: Possible Candidate of Local Cosmic-Ray Factory (II)" Universe 9, no. 2: 93. https://doi.org/10.3390/universe9020093





