Thermodynamics of Hot Neutron Stars and Universal Relations
Abstract
:1. Introduction
2. Thermal Equilibrium in General Relativity
3. Binding Energy
4. Tidal Deformability
5. Rescaled Entropy
6. Results and Discussion
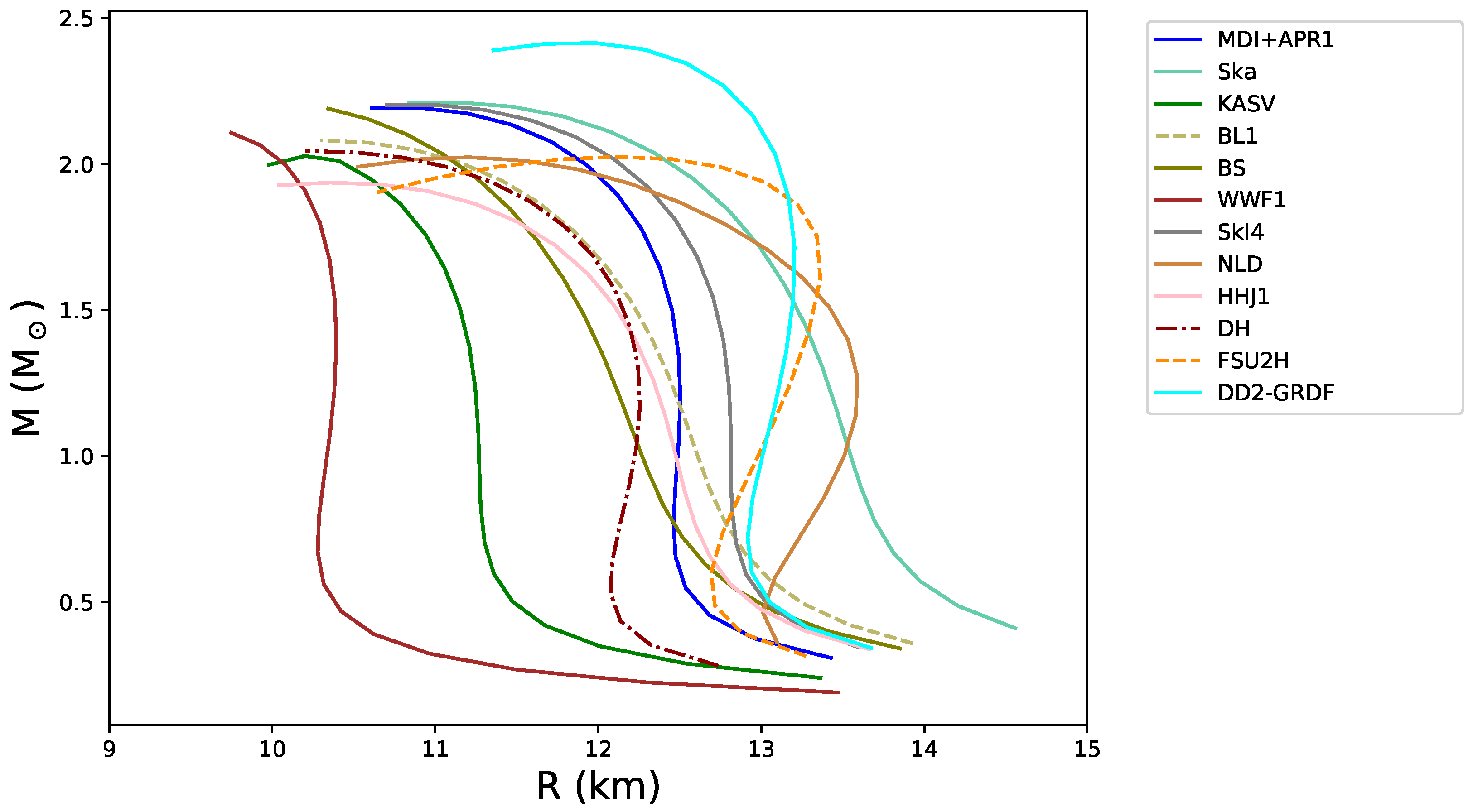
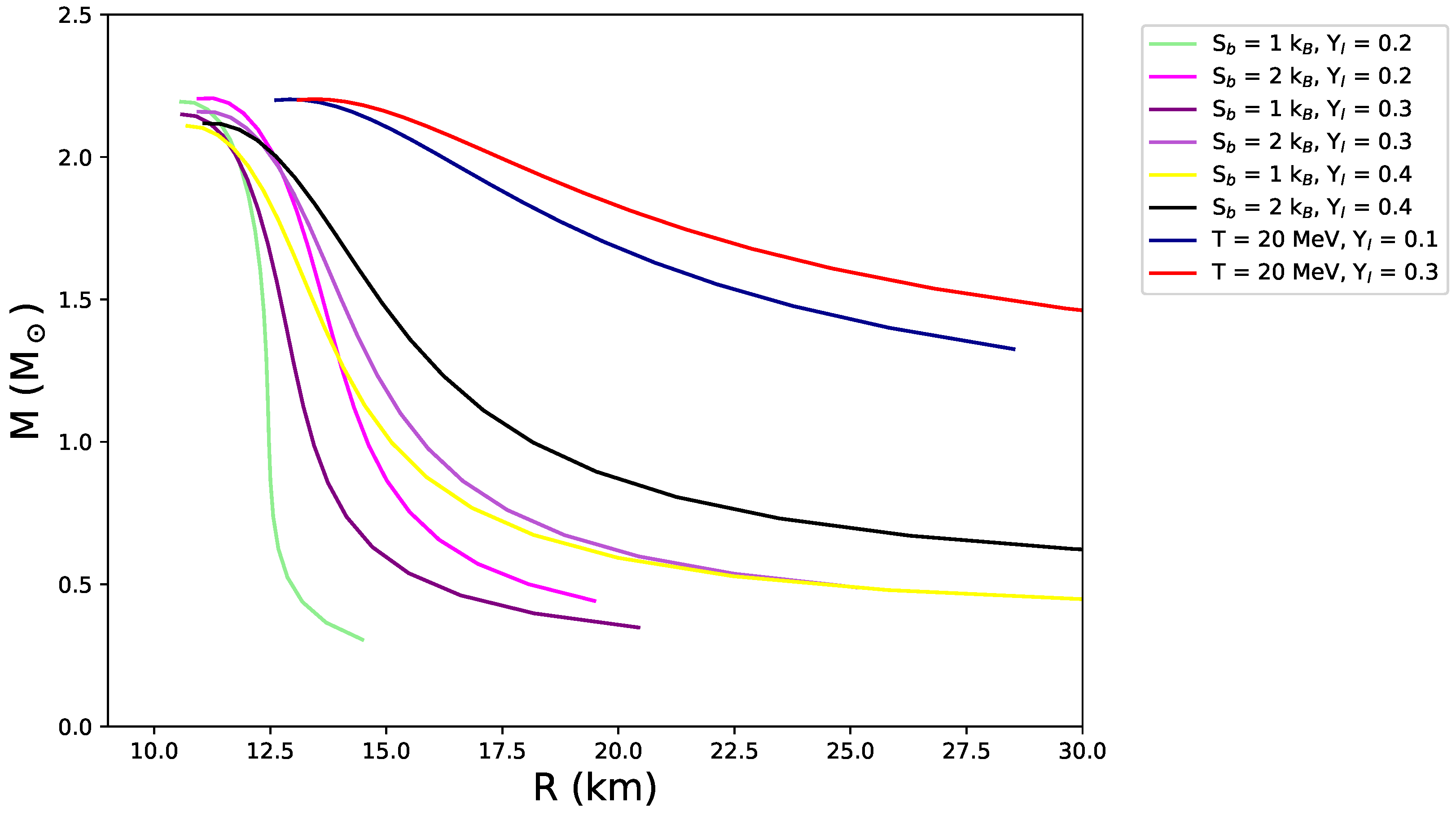
6.1. Hot Equations of State
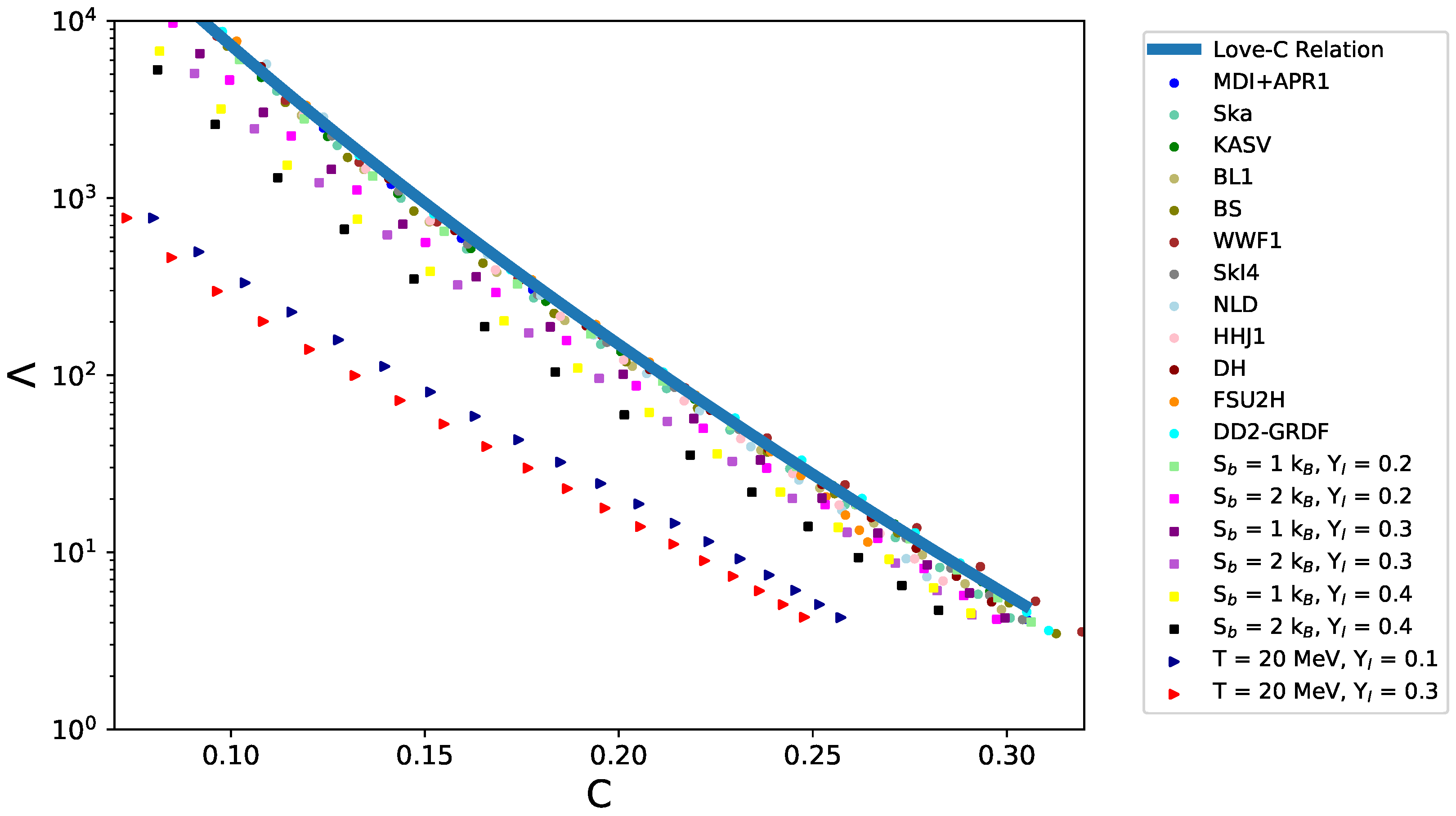
6.2. Rescaled Entropy vs. Compactness
6.3. Tidal Deformability vs. Compactness
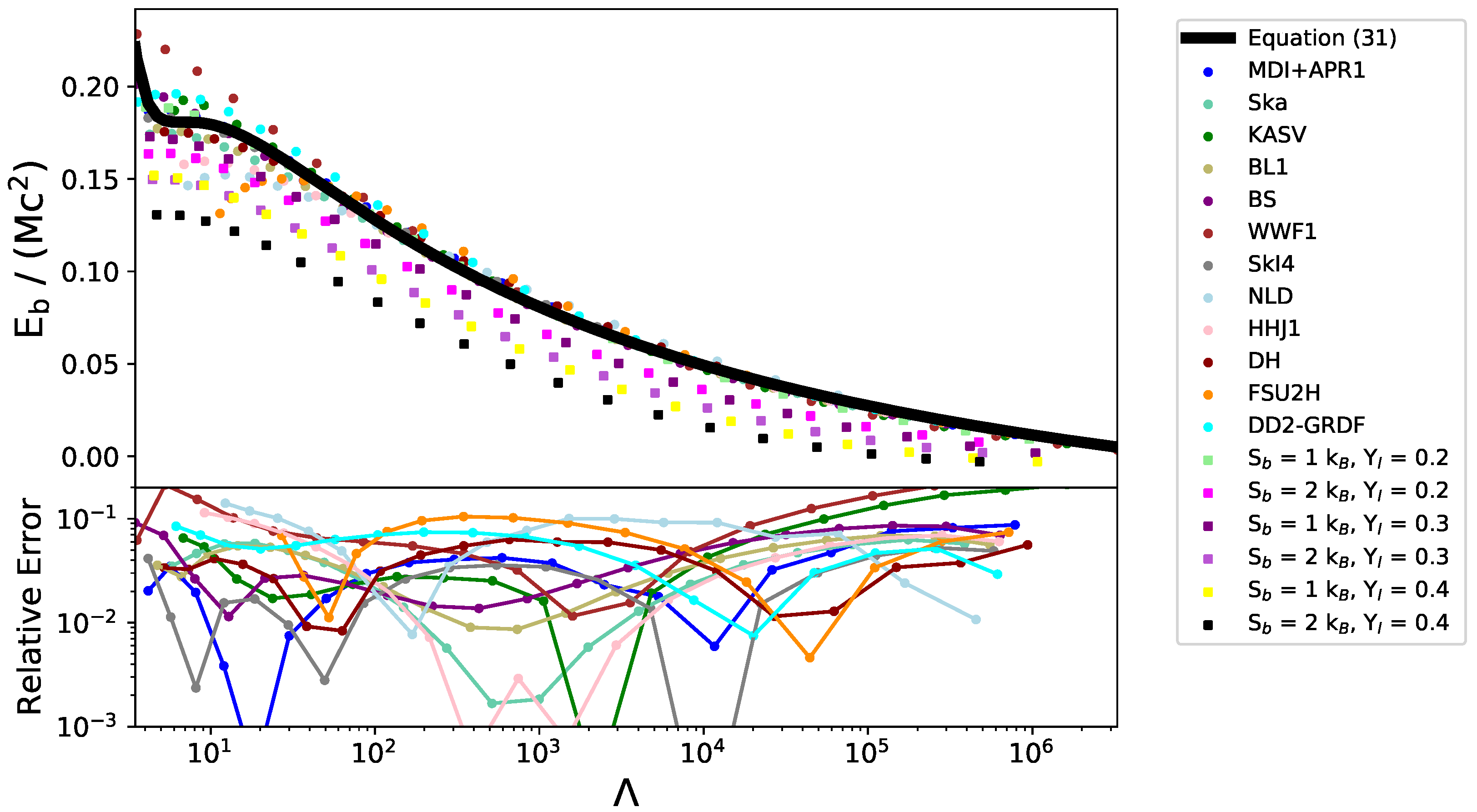
6.4. Binding Energy vs. Tidal Deformability
6.5. Binding Energy vs. Compactness
6.6. Binding Energy, Compactness and Tidal Deformability
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EOS | Equation of state |
| SN | Supernova |
| GW | Gravitational waves |
| BNS | Binary neutron stars |
| GR | General relativity |
| TE | Tolman–Ehrenfest |
| TOV | Tolman–Openheimer–Volkoff |
| MDI | Momentum-dependent interaction |
| LHS | Left-hand side |
| RHS | Right-hand side |
References
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Zel’dovich, Y.B.; Novikov, I.D. Stars and Relativity; Dover Publications INC.: Mineapolis, NY, USA, 1971. [Google Scholar]
- Weinberg, S. Gravitational and Cosmology: Principle and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Schutz, B.F. A First Course in General Relativity; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Schaffner-Bielich, J. Compact Star Physics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Lattimer, J.M.; Yahil, A. Analysis of the neutrino events from supernova 1987A. Astrophys. J. 1989, 340, 425–434. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J.; Bonasera, A. Tidal Heating and Mass Loss in Neutron Star Binaries: Implications for Gamma-Ray Burst Models. Astrophys. J. 1992, 397, 570. [Google Scholar] [CrossRef]
- Bildsten, L.; Cutler, C. Tidal Interactions of Inspiraling Compact Binaries. Astrophys. J. 1992, 400, 175. [Google Scholar] [CrossRef]
- Aras, P.; Weinberg, N.N. Urca reactions during neutron star inspiral. Mon. Not. R. Astron. Soc. 2019, 486, 1424. [Google Scholar] [CrossRef]
- Kochanek, C.S. Coalescing Binary Neutron Stars. Astrophys. J. 1992, 400, 175. [Google Scholar] [CrossRef]
- Lai, D. Resonant Oscillations and Tidal Heating in Coalescing Binary Neutron Stars. Mon. Not. R. Astron. Soc. 1994, 270, 611. [Google Scholar] [CrossRef]
- Reisenegger, A.; Goldreich, P. Excitation of Neutron Star Normal Modes during Binary Inspiral. Astrophys. J. 1994, 426, 688. [Google Scholar] [CrossRef]
- Ho, W.G.C.; Lai, D. Resonant Tidal Excitations of Rotating Neutron Stars in Coalescing Binaries. Mon. Not. R. Astron. Soc. 1994, 308, 153. [Google Scholar]
- Lai, D.; Wu, Y. Resonant Resonant Tidal Excitations of Inertial Modes in Coalescing Neutron Star Binaries. Phys. Rev. D 2006, 74, 024007. [Google Scholar] [CrossRef]
- Xu, W.; Lai, D. Resonant Tidal Excitation of Oscillation Modes in Merging Binary Neutron Stars: Inertial-Gravity Modes. Phys. Rev. D 2017, 96, 083005. [Google Scholar] [CrossRef]
- Tolman, R.C. On the use of the entropy principle in general relativity. Phys. Rev. 1930, 35, 896. [Google Scholar] [CrossRef]
- Tolman, R.C. On the weight of heat and thermal equilibrium in general relativity. Phys. Rev. 1930, 35, 904. [Google Scholar] [CrossRef]
- Tolman, R.C.; Ehrenfest, P. Temperature equilibrium in a static gravitational field. Phys. Rev. 1930, 36, 1791. [Google Scholar] [CrossRef]
- Tolman, R.C. Relativity Thermodynamics and Cosmology; Oxford University Press: New York, NY, USA, 1934. [Google Scholar]
- Sorkin, R.D.; Wald, R.M.; Jiu, Z.Z. Entropy of self-gravitating radiation. Gen. Relat. Grav. 1981, 13, 1127. [Google Scholar] [CrossRef]
- Gao, S. General maximum entropy principle for self-gravitating perfect fluid. Phys. Rev. D 2011, 84, 104023. [Google Scholar] [CrossRef]
- Gao, S. Addendum to “General maximum entropy principle for self-gravitating perfect fluid”. Phys. Rev. D 2012, 85, 027503. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Del Popolo, A.; Plastino, A.R. Thremodynamic equilibrium in general relativity. Phys. Rev. D 2019, 100, 104042. [Google Scholar] [CrossRef]
- Roupas, Z. Thermal mass limit of neutron cores. Phys. Rev. D 2015, 91, 023001. [Google Scholar] [CrossRef]
- Roupas, Z. Thermodynamical instabilities of perfect fluid spheres in General Relativity. Class. Quant. Grav. 2013, 30, 115018. [Google Scholar] [CrossRef]
- Oppenheim, K. Thermodynamics with long-range interactions: From Ising models to black holes. Phys. Rev. E 2003, 68, 016108. [Google Scholar] [CrossRef]
- Santiago, J.; Visser, M. Tolman temperature in a gravitational field. Eur. J. Phys. 2019, 40, 025604. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Temperature equilibrium in a stationary gravitational field. Phys. Rev. 1949, 76, 427. [Google Scholar] [CrossRef]
- Santiago, J.; Visser, M. Tolman-like temperature gradients in stationary spacetimes. Phys. Rev. D 2018, 98, 064001. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q: Unexpected Universal Relations for Neutron Stars and Quark Stars. Science 2013, 341, 6144. [Google Scholar] [CrossRef]
- Maselli, A.; Cardoso, V.; Gualtieri, L.; Pani, P. Equation-of-state-independent relations in neutron stars. Phys. Rev. D 2013, 88, 023007. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q anisotropically: Universal relations for compact stars with scalar pressure anisotropy. Phys. Rev. D 2015, 91, 123008. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate universal relations for neutron stars and quark stars. Phys. Rep. 2017, 681, 1–72. [Google Scholar] [CrossRef]
- Alexander, S.H.; Yagi, K.; Yunes, N. An entropy-area law for neutron stars near the black hole threshold. Class. Quant. Grav. 2019, 36, 015010. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Tan, H.; Dore, T.; Dexheimer, V.; Noronha-Hostler, J.; Yunes, N. Extreme matter meets extreme gravity: Ultraheavy neutron stars with phase transitions. Phys. Rev. D 2022, 105, 023018. [Google Scholar] [CrossRef]
- Martinon, G.; Maselli, A.; Gualtieri, L.; Ferrari, V. Rotating protoneutron stars: Spin evolution, maximum mass, and I-Love-Q relations. Phys. Rev. D 2014, 90, 064026. [Google Scholar] [CrossRef]
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I-Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef]
- Raduta, A.; Oertel, M.; Sedrakian, A. Proto-neutron stars with heavy baryons and universal relations. Mon. Not. R. Astron. Soc. 2020, 49, 914–931. [Google Scholar] [CrossRef]
- Khadkikar, S.; Raduta, A.R.; Oertel, M.; Sedrakian, A. Maximum mass of compact stars from gravitational wave events with finite-temperature equations of state. Phys. Rev. C 2021, 103, 055811. [Google Scholar]
- Reed, B.; Horowitz, C.J. Total energy in supernovae neutrinos and the tidal deformability and binding energy of neutron stars. Phys. Rev. D 2020, 102, 103011. [Google Scholar] [CrossRef]
- Klein, O. On the thermodynamic equilibrium in fluids in gravitational fields. Rev. Mod. Phys. 1949, 21, 531. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astroph. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hindeder, T. Constraining the Neutron Star Tidal Love Numbers with Gravitational Waves. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Hindeder, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic Tidal Properties of Neutron Stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Hindeder, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal Deformability of neutron stars with realistic equation of state and their gravitational wave signature in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love number of neutron and self-bound stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Carvajal, J.; Newton, W.G.; Li, B.A. Constraining the high-density behavior of the nuclear symmetry energy with the tidal polarizability of neutron stars. Phys. Rev. C 2013, 87, 015806. [Google Scholar] [CrossRef]
- Lackey, B.D.; Wade, L. Reconstructing the neutron star equation of state with gravitational wave detectors from a realistic population of inspiralling binary neutron stars. Phys. Rev. D 2013, 87, 015806. [Google Scholar] [CrossRef]
- Chakravarti, K.; Chakraborty, S.; Phukon, K.S.; Bose, S.; Sen Gupta, S. Constraining extra-spatial dimensions with observations of GW170817. Class. Quant. Grav. 2020, 37, 105004. [Google Scholar] [CrossRef]
- Koliogiannis, P.S.; Moustakidis, C.C. Effects of the equation of state on the bulk properties of maximally rotating neutron stars. Phys. Rev. C 2020, 101, 015805. [Google Scholar] [CrossRef]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J.M. Thermal properties of supernova matter: The bulk homogeneous phase. Phys. Rev. C 2014, 89, 065802. [Google Scholar] [CrossRef]
- Kurkela, A.; Fraga, E.S.; Schaffner-Bielich, J.; Vuorinen, A. Constraining Neutron Star Matter With Quantum Chromodynamics. Astrophys. J. 2014, 789, 127. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Koliogiannis, P.S.; Moustakidis, C.C. Thermodynamical Description of Hot, Rapidly Rotating Neutron Stars, Protoneutron Stars, and Neutron Star Merger Remnants. Astrophys. J. 2021, 912, 69. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Probing the Nuclear Equation of State from the Existence of a ∼2.6 M⊙ Neutron Star: The GW190814 Puzzle. Symmetry 2021, 13, 183. [Google Scholar] [CrossRef]
- Moustakidis, C.C.; Panos, C.P. Equation of state for β-stable hot nuclear matter. Phys. Rev. C 2008, 79, 045806. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F.D. A generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331. [Google Scholar] [CrossRef]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J.M. Thermal properties of hot and dense matter with finite range interactions. Phys. Rev. C 2015, 92, 025801. [Google Scholar] [CrossRef]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J. M. Degenerate limit thermodynamics beyond leading order for models of dense matter. Annal. Phys. 2015, 363, 533. [Google Scholar] [CrossRef]
- Wei, J.B.; Burgio, G.F.; Raduta, A.d.R.; Schulze, H.J. Hot neutron stars and their equation of state. Phys. Rev. C 2021, 104, 065806. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Schneider, A.S.; Constantinou, C.; Muccioli, B.; Prakash, M. Akmal-Pandharipande-Ravenhall equation of state for simulations of supernovae, neutron stars, and binary mergers. Phys. Rev. C 2019, 100, 025803. [Google Scholar] [CrossRef]
- Carbone, A.; Schwenk, A. Ab initio constraints on thermal effects of the nuclear equation of state. Phys. Rev. C 2019, 100, 025805. [Google Scholar] [CrossRef]
- Chesler, P.M.; Jokela, N.; Loeb, A.; Vuorinen, A. Finite-temperature equations of state for neutron star mergers. Phys. Rev. D 2019, 100, 066027. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127. [Google Scholar] [CrossRef]
- Goldman, I. New general-relativistic expression for the baryon number of a cold star. Phys. Rev. D 1989, 40, 327. [Google Scholar] [CrossRef]
- Goldman, I. Baryon number of a uniformly rotating cold star. Phys. Rev. D 1990, 42, 3386. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M. Neutron Stars, Lectures Delivered. In Proceedings of the 33rd Summer Institute on Particle Physics, (SSI 2005), Stony Brook, NY, USA, 25 July–5 August 2005. [Google Scholar]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. Mon. Not. Roy. Astron. Soc. 2016, 459, 646–656. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Thermal effects on tidal deformability in the last orbits of an inspiraling binary neutron star system. Phys. Let. B 2022, 832, 137267. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A Double Neutron Star System with a Large Mass Asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]


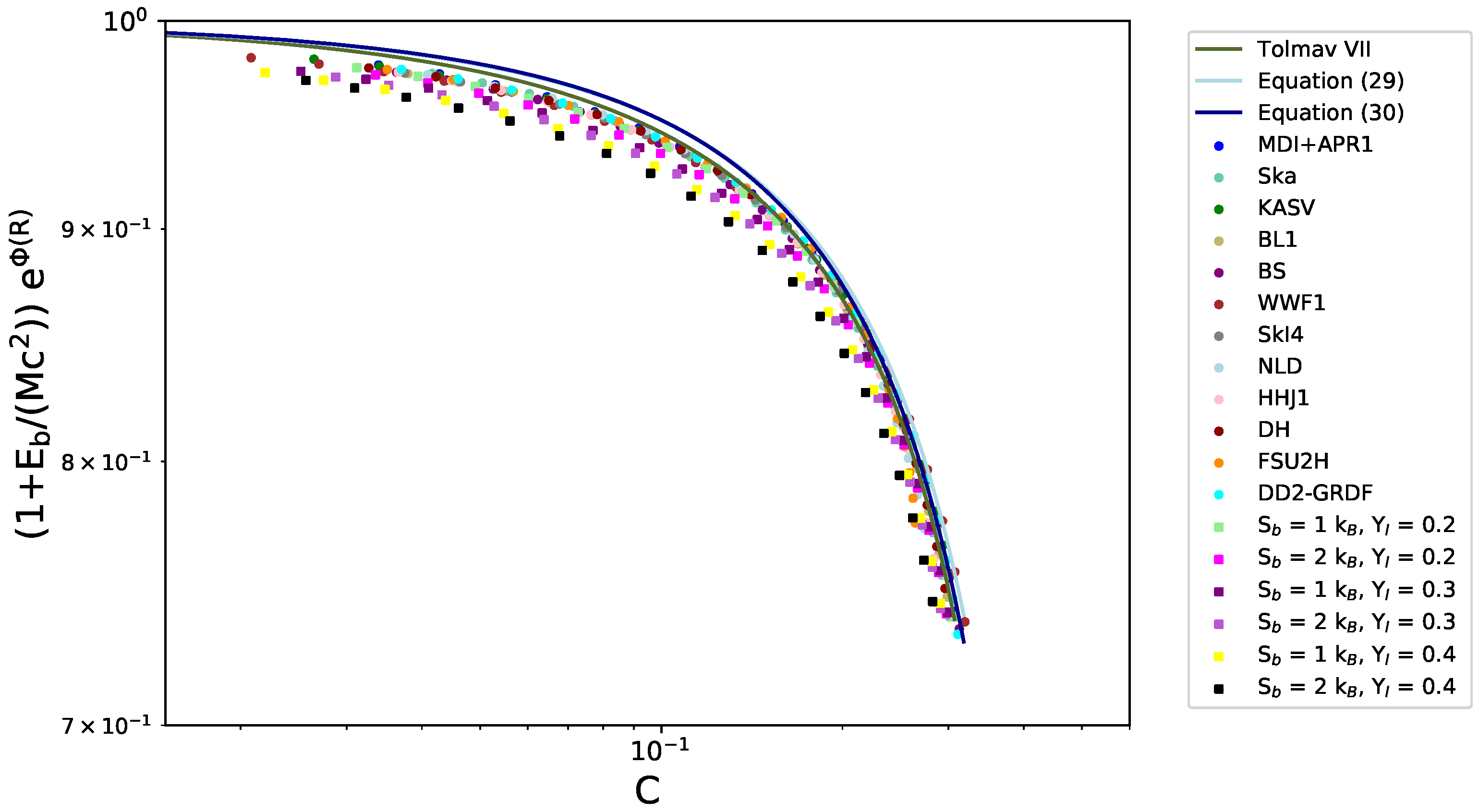
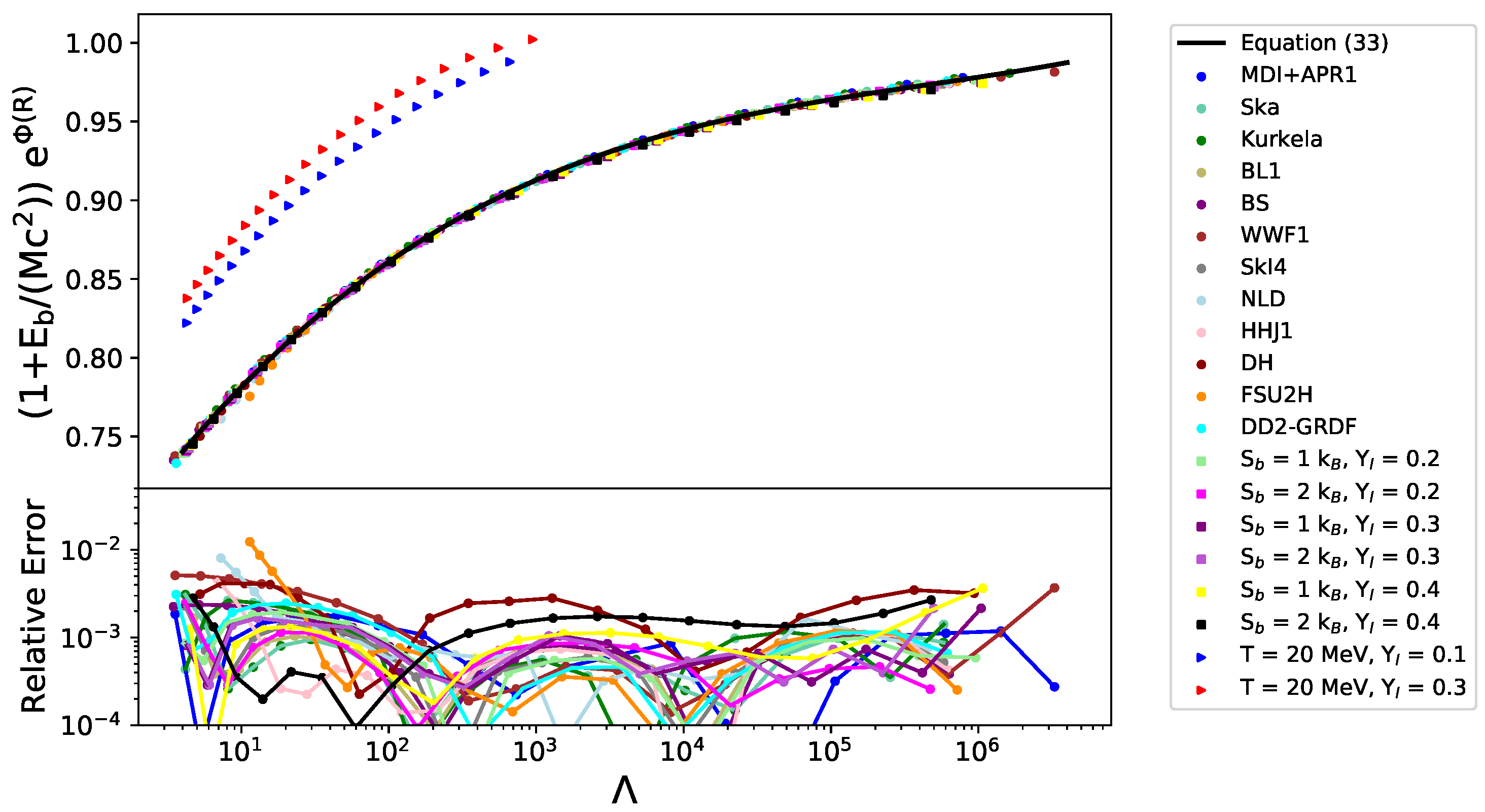
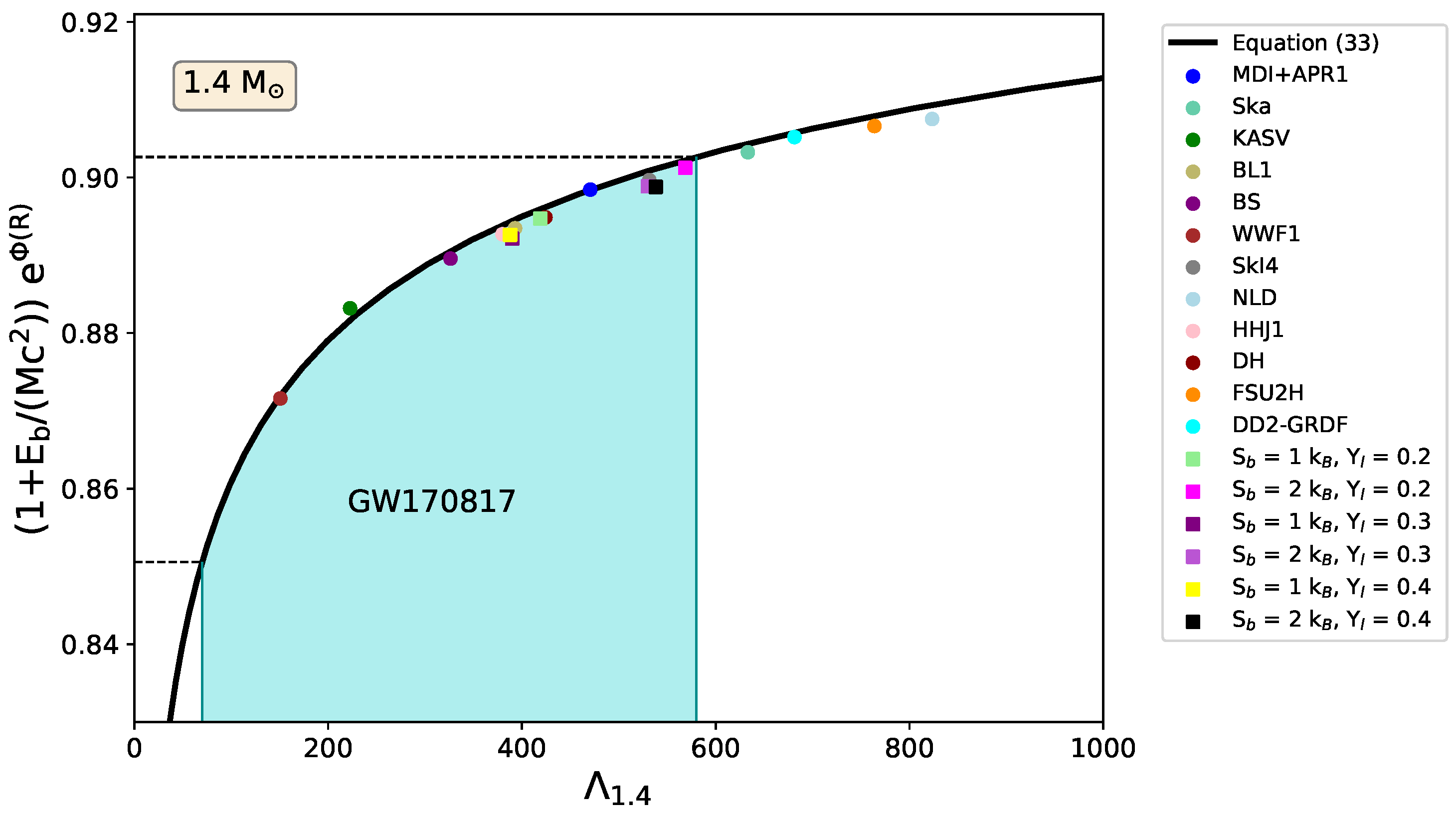
| −0.08399 | 1.52078 | −2.91006 | 1.85495 | 0.987 |
| 0.22350 | −0.02017 | 0.960 |
| 70 | ||
| 580 |
| 0.66656 | 0.05855 | −0.00402 | 0.00010 | 0.99969 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laskos-Patkos, P.; Koliogiannis, P.S.; Kanakis-Pegios, A.; Moustakidis, C.C. Thermodynamics of Hot Neutron Stars and Universal Relations. Universe 2022, 8, 395. https://doi.org/10.3390/universe8080395
Laskos-Patkos P, Koliogiannis PS, Kanakis-Pegios A, Moustakidis CC. Thermodynamics of Hot Neutron Stars and Universal Relations. Universe. 2022; 8(8):395. https://doi.org/10.3390/universe8080395
Chicago/Turabian StyleLaskos-Patkos, Pavlos, Polychronis S. Koliogiannis, Alkiviadis Kanakis-Pegios, and Charalampos C. Moustakidis. 2022. "Thermodynamics of Hot Neutron Stars and Universal Relations" Universe 8, no. 8: 395. https://doi.org/10.3390/universe8080395







