Fuzzy Instantons in Landscape and Swampland: Review of the Hartle–Hawking Wave Function and Several Applications

Abstract

The Euclidean path integral is well approximated by instantons. If instantons are dynamical, they will necessarily be complexified. Fuzzy instantons can have multiple physical applications. In slow-roll inflation models, fuzzy instantons can explain the probability distribution of the initial conditions of the universe. Although the potential shape does not satisfy the slow-roll conditions due to the swampland criteria, the fuzzy instantons can still explain the origin of the universe. If we extend the Euclidean path integral beyond the Hartle–Hawking no-boundary proposal, it becomes possible to examine fuzzy Euclidean wormholes that have multiple physical applications in cosmology and black hole physics.

1. Introduction: Preliminaries

In modern physics, understanding the nature of the origin of the universe is one of the most fundamental problems. Due to the singularity theorem [1], if we move backward in time and assume reasonable physical conditions, it appears that there must exist an initial singularity. At this singularity, all the laws of general relativity break down; hence, a quantum gravitational prescription is required.

To understand the initial singularity, the quantum gravitational description must be non-perturbative. The most conservative approach is to quantize the gravitational degrees of freedom as per the canonical quantization method [2]. Using this approach, one can obtain the quantized Hamiltonian constraint; or the so-called Wheeler–DeWitt equation. If we solve the equation, we can in principle obtain the probability for a given hypersurface and the corresponding field configurations.

One of the limitations of canonical quantization is that the probability depends on the selection of boundary conditions [3]. By selecting a certain boundary condition, one may or may not provide a reasonable probability distribution for the early universe. There is no fundamental principle that can be used to select the boundary condition; in principle, the boundary condition must be confirmed by the possible observational consequences [4].

1.1. Hartle–Hawking Wave Function

Now, we can ask what the most natural assumption regarding the boundary conditions of the universe is. It might be considered that the ground state wave function corresponds to the most natural choice of boundary conditions, although one potential problem with this is that the ground state is not defined in the context of quantum gravity. However, one may reasonably argue that the Euclidean path integral might be the ground state wave function of the Wheeler–DeWitt Equation [5]. The mathematical form, the so-called Hartle–Hawking wave function, is listed below (we use the convention $c=G=\hslash =1$):

$$\begin{array}{c}\hfill \mathsf{\Psi }\left[h_{\mu \nu },\psi \right]=\int \mathcal{D}{g}_{\mu \nu }\mathcal{D}\varphi e^{-S_{\mathrm{E}}\left[g_{\mu \nu },\varphi \right]},\end{array}$$

(1)

where $g_{\mu \nu }$ is the metric, $\varphi$ is a matter field, and $S_{\mathrm{E}}$ is the Euclidean action; we sum over all regular and compact Euclidean geometries and field configurations satisfying conditions $\partial g_{\mu \nu }=h_{\mu \nu }$ and $\partial \varphi =\psi$. One interesting feature of this wave function is that there is only one boundary (the final boundary) of the path integral; however, the path integral usually must have two boundaries (the initial and final boundaries). As the wave function has no initial boundary, it is known as the no-boundary wave function. Although there is no guarantee regarding the convergence of this path integral (this might diverge for Minkowski or anti-de Sitter background), it will still be useful in understanding the physics of de Sitter background.

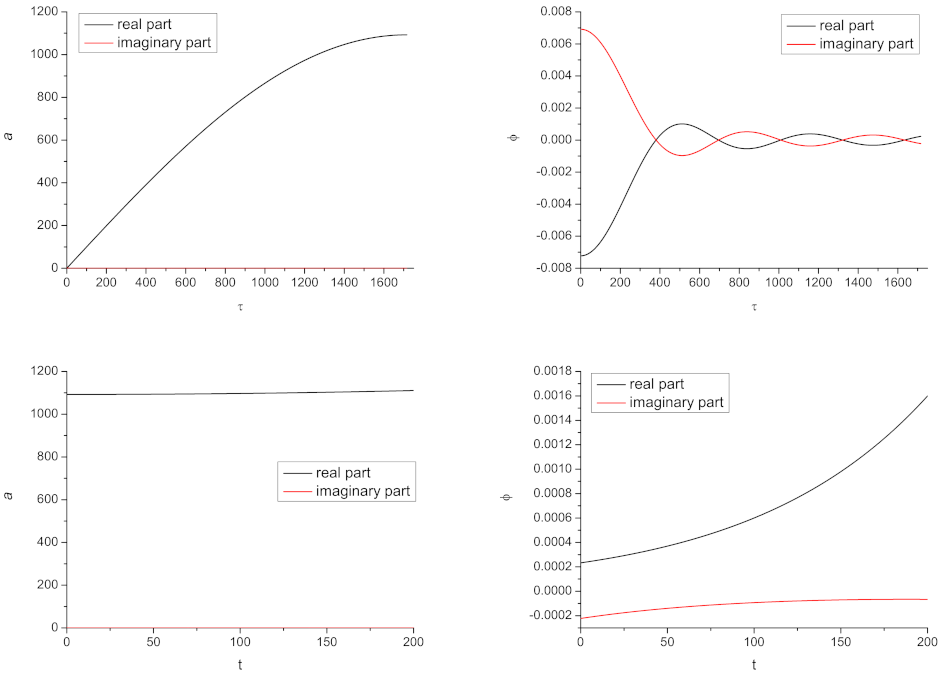
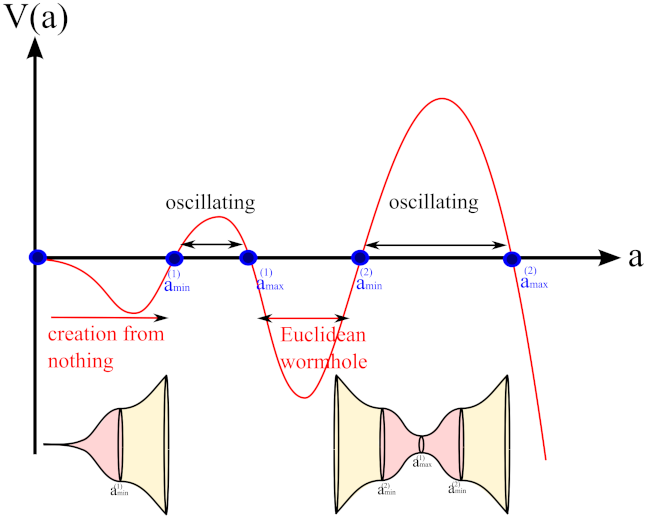
1.2. Steepest-Descent Approximation and Fuzzy Instantons

In cosmology, it is reasonable to assume $O(4)$-symmetry as follows:

$$\begin{array}{c}\hfill d{s}_{\mathrm{E}}^2=d{\tau }^2+a^2(\tau )d{\mathsf{\Omega }}_3^2,\end{array}$$

(2)

where $\tau$ is the Euclidean time, $d{\mathsf{\Omega }}_3^2$ is the 3-sphere, and $a(\tau )$ is the scale factor. In addition to this symmetry, if we impose the on-shell condition to the metric and matter field; or we restrict to instantons, we can approximate the wave function based on the steepest-descent approximation:

$$\begin{array}{c}\hfill \mathsf{\Psi }\left[b,\psi \right]\simeq \sum _{\mathrm{on}-\mathrm{shell}}{e}^{-S_{\mathrm{E}}^{\mathrm{on}-\mathrm{shell}}},\end{array}$$

(3)

where b and $\psi$ are the boundary values of $a(\tau )$ and $\varphi (\tau )$, respectively. Finally, the probability for each instanton is approximately:

$$\begin{array}{c}\hfill P\left[b,\psi \right]={\left|\mathsf{\Psi }\left[b,\psi \right]\right|}^2\simeq e^{-2\mathrm{Re}{S}_{\mathrm{E}}^{\mathrm{on}-\mathrm{shell}}},\end{array}$$

(4)

where

$$\begin{array}{c}\hfill S_{\mathrm{E}}^{\mathrm{on}-\mathrm{shell}}=\mathrm{Re}{S}_{\mathrm{E}}^{\mathrm{on}-\mathrm{shell}}+i\mathrm{Im}{S}_{\mathrm{E}}^{\mathrm{on}-\mathrm{shell}}.\end{array}$$

(5)

Due to the analyticity, at the point of the Wick-rotation $\tau ={\tau }_0+it$, we must impose the continuity of fields

$$\begin{array}{ccc}\hfill a(t=0)& =& a(\tau ={\tau }_0),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \varphi (t=0)& =& \varphi (\tau ={\tau }_0),\hfill \end{array}$$

(7)

as well as the Cauchy-Riemann conditions

$$\begin{array}{ccc}\hfill \dot{a}(t=0)& =& i\dot{a}(\tau ={\tau }_0),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \dot{\varphi }(t=0)& =& i\dot{\varphi }(\tau ={\tau }_0).\hfill \end{array}$$

(9)

therefore, in general, if the fields are dynamical, the on-shell solutions will be complex-valued; the instantons will be fuzzy. However, the boundary values b and $\psi$ must be real-valued [6]. In some sense, this is a type of boundary condition of the instantons. The reality at the boundary of the wave function is related to the classicality of the solution. Once the solution becomes classical, the probability must slowly vary along the steepest-descent path. If the solution is real-valued, or if the real component of each function is at least dominant over that of the imaginary part, the probability must slowly vary compared with the phase part, and hence the history will be sufficiently classical. Furthermore, the history should satisfy the classical equations of motion (e.g., the Hamilton–Jacobi equation). This condition can be summarized as follows:

$$\begin{array}{c}\hfill \left|{\nabla }_{\alpha }\mathrm{Re}{S}_{\mathrm{E}}\right|\ll \left|{\nabla }_{\alpha }\mathrm{Im}{S}_{\mathrm{E}}\right|,\end{array}$$

(10)

where $\alpha =a,\varphi$ is the canonical direction [7]. In many practical cases, this classicality condition can be easily demonstrated by verifying whether the real parts of the functions dominate the imaginary parts after the Wick-rotation and a sufficient Lorentzian time.

1.3. Scope of This Paper

The question that naturally arises is this: for which physical situations can the classicality condition be satisfied? The answer is that inflation is required to satisfy the classicality condition. This is very important: if our universe was created from the Hartle–Hawking wave function, a small amount of inflation is required [8]. However, there still remain several questions:

• Does the Hartle–Hawking wave function prefer sufficient inflation?
• Which type of inflation allows classicalization: slow-roll or fast-roll?
• Is the Hartle–Hawking wave function a unique choice for quantum cosmology; or can there be additional generalization from the Euclidean path integral approach?
• Is the Hartle–Hawking wave function compatible with the recent progress of quantum gravity?

In this study, we review several interesting developments about the Hartle–Hawking wave function and its potential applications. Furthermore, we answer a number of previous questions and provide certain possible future applications and research directions.

2. Fuzzy Instantons with Slow-Roll Inflation

The first issue is to obtain classicalized fuzzy instantons based on slow-roll inflation.

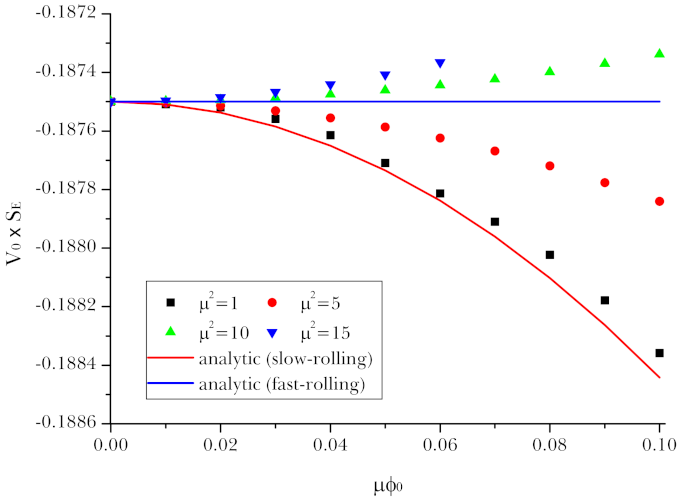
2.1. Simplest Model

To discuss the generic properties of slow-roll inflation and fuzzy instantons, we consider the following model [7]:

$$\begin{array}{c}\hfill S_{\mathrm{E}}=-\int d^{4}x\sqrt{+g}\left[\frac{1}{16\pi }\left(R-2\mathsf{\Lambda }\right)-\frac{1}{2}{\left(\nabla \mathsf{\Phi }\right)}^2-V\left(\mathsf{\Phi }\right)\right],\end{array}$$

(11)

where R is the Ricci scalar, $\mathsf{\Lambda }$ is the cosmological constant, $\mathsf{\Phi }$ is a scalar field, and

$$\begin{array}{c}\hfill V(\varphi )=\frac{1}{2}{m}^2{\mathsf{\Phi }}^2\end{array}$$

(12)

is the potential. For simplicity, one can define the metric and several other variables as follows:

$$\begin{array}{ccc}\hfill d{s}_{\mathrm{E}}^2& =& \frac{3}{\mathsf{\Lambda }}\left(d{\tau }^2+a^2(\tau )d{\mathsf{\Omega }}_3^2\right),\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \varphi & \equiv & \sqrt{\frac{4\pi }{3}}\mathsf{\Phi },\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \mu & \equiv & \sqrt{\frac{3}{\mathsf{\Lambda }}}m.\hfill \end{array}$$

(15)

The equations of motion are as follows:

$$\begin{array}{ccc}\hfill \ddot{a}+a+a\left(2{\dot{\varphi }}^2+{\mu }^2{\varphi }^2\right)& =& 0,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \ddot{\varphi }+3\frac{\dot{a}}{a}\dot{\varphi }-{\mu }^2\varphi & =& 0.\hfill \end{array}$$

(17)

These are two second-order differential equations but we will consider complexified instantons. Hence, each equation has two parts with one being the real part and the other being the imaginary part. Therefore, there are basically eight initial conditions (at $\tau =0$) that determine the solution; however, because of the Hamiltonian constraint, two of them are restricted. If we assume the no-boundary condition $a(\tau =0)=0$ with the Hamiltonian constraint, we must require that

$$\begin{array}{ccc}\hfill a(\tau =0)& =& 0,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill \dot{a}(\tau =0)& =& 1,\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill \dot{\varphi }(\tau =0)& =& 0.\hfill \end{array}$$

(20)

The above equations already fix six of the initial conditions. There are thus two free parameters $\mathrm{Re}\varphi (\tau =0)$ and $\mathrm{Im}\varphi (\tau =0)$, or we present

$$\begin{array}{c}\hfill \varphi (\tau =0)={\varphi }_0{e}^{i\theta },\end{array}$$

(21)

where both ${\varphi }_0$ and $\theta$ are real values (see a recent analytic review in [9]).

Physically, ${\varphi }_0$ corresponds to the initial condition of the inflaton field, i.e., the initial condition of an inflationary universe. Therefore, we will eventually examine the probability distribution as a function of ${\varphi }_0$. On the other hand, $\theta$ is merely a free parameter. This must be used to satisfy the boundary condition after the Wick-rotation (i.e., to achieve classicality). If we select an appropriate $\theta$, it may be possible that after the Wick-rotation $\tau ={\tau }_0+it$, the imaginary parts of both a and $\varphi$ will approach zero, and the real parts will dominate (e.g., see Figure 1 [10]). Therefore, in other words, $\theta$ is a tuning parameter for the classicality at a future infinity.

Then, one may ask what the role of $\theta$ is in detail [11]. To determine this, let us first assume slow-roll inflation given a classical background metric, i.e., ${\dot{\varphi }}^2\ll 1$, ${\mu }^2{\varphi }^2\ll 1$, and $\mathrm{Im}a\ll \mathrm{Re}a$. In this case, it can be stated that

$$\begin{array}{c}\hfill \mathrm{Re}a=C_a{e}^t+D_a{e}^{-t}\simeq C_a{e}^t,\end{array}$$

(22)

where $C_a$ and $D_a$ are integration constants. The equations of motion for the scalar fields are approximately

$$\begin{array}{ccc}\hfill \mathrm{Re}\ddot{\varphi }+3\mathrm{Re}\dot{\varphi }+{\mu }^2\mathrm{Re}\varphi & \simeq & 0,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill \mathrm{Im}\ddot{\varphi }+3\mathrm{Im}\dot{\varphi }+{\mu }^2\mathrm{Im}\varphi & \simeq & 0.\hfill \end{array}$$

(24)

Hence,

$$\begin{array}{ccc}\hfill \mathrm{Re}\varphi & \simeq & C_{\varphi }^{\mathrm{Re}}{e}^{-\frac{3}{2}t+\omega t}+D_{\varphi }^{\mathrm{Re}}{e}^{-\frac{3}{2}t-\omega t},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \mathrm{Im}\varphi & \simeq & C_{\varphi }^{\mathrm{Im}}{e}^{-\frac{3}{2}t+\omega t}+D_{\varphi }^{\mathrm{Im}}{e}^{-\frac{3}{2}t-\omega t},\hfill \end{array}$$

(26)

where $C_{\varphi }^{\mathrm{Re}}$, $D_{\varphi }^{\mathrm{Re}}$, $C_{\varphi }^{\mathrm{Im}}$, and $D_{\varphi }^{\mathrm{Im}}$ are constants, and

$$\begin{array}{c}\hfill {\omega }^2\equiv {\left(\frac{3}{2}\right)}^2-{\mu }^2.\end{array}$$

(27)

From these equations, we can easily obtain the following conclusion. If $\mu <3/2$, the solutions satisfy the over-damped motion. In other words, there are two linearly independent solutions with different exponents. Therefore, it is possible to select $\theta$ such as to make $C_{\varphi }^{\mathrm{Im}}\ll 1$ (and hence finely tune the integration constants). Then,

$$\begin{array}{c}\hfill \frac{\mathrm{Im}\varphi }{\mathrm{Re}\varphi }\simeq e^{-2\omega t}\to 0,\end{array}$$

(28)

and hence after the Wick-rotation, the solution will eventually satisfy the classicality conditions. On the other hand, if $\mu >3/2$, the solutions satisfy under-damped motion. For any choice of initial conditions, $\mathrm{Im}\varphi /\mathrm{Re}\varphi$ will be proportional to a trigonometric function, and hence,

$$\begin{array}{c}\hfill \frac{\mathrm{Im}\varphi }{\mathrm{Re}\varphi }\simeq \mathcal{O}\left(1\right).\end{array}$$

(29)

Therefore, the imaginary part and real part of the scalar field oscillate in a similar order.

One might query the consequences of this if there is no approach to classicalize a scalar field. Note that the imaginary part of the scalar field provides the negative kinetic term, indicating it is ghost-like. The energy of the scalar field will contribute to the matter content of the universe. If the imaginary part of the scalar field is of the same order as the real part even after the Wick-rotation, we cannot avoid the instability of the ghost-like imaginary part of the field. This is a catastrophic consequence, and we cannot physically allow this possibility. (However, for the possibility of observing restricted contributions from the ghost-like term, please refer to [12]).

For a generic scalar field potential V, the criterion for a classical universe is ${\mu }^2<9/4$, or

$$\begin{array}{c}\hfill \left|\frac{V^{″}}{V}\right|<6\pi .\end{array}$$

(30)

If $m^2/V<6\pi$, $\varphi =0$ (local minimum) can allow for a classical universe. If $m^2/V>6\pi$, there exists a cutoff ${\varphi }_{\mathrm{cutoff}}>0$ such that $\varphi >{\varphi }_{\mathrm{cutoff}}$ only allows for classical universes [7].

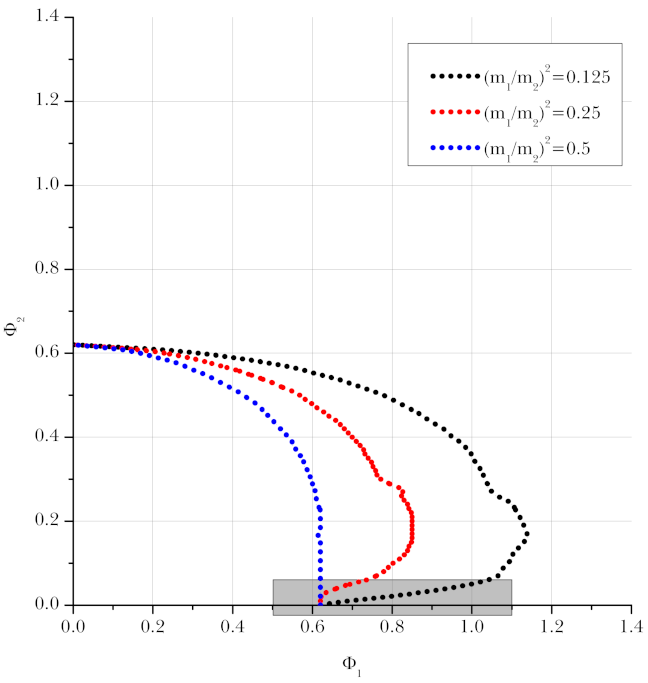
2.2. Probabilities and Preferences of Large e-Foldings

If one is able to construct a classical universe, it is possible to obtain the probability of that universe. For the slow-roll potential, the probability of a classical universe with the initial condition ${\varphi }_0$ is approximately

$$\begin{array}{c}\hfill logP\simeq \frac{3}{8V({\varphi }_0)}.\end{array}$$

(31)

Note that this is positive definite. Hence, the probability is exponentially enhanced. The most highly favored initial condition is a field value with the smallest possible potential. Considering the no-boundary proposal [8], this indicates that $\varphi \simeq {\varphi }_{\mathrm{cutoff}}$ corresponds to the most probable initial condition.

However, the limitation is that the e-foldings of the most probable initial condition are, in general, insufficient. For example, if we have a quadratic potential with $\mathsf{\Lambda }=0$, the most preferred e-folding number will be ∼0.62, while more than ∼50 e-foldings will be required [13].

There have been several proposals to resolve or understand this problem. First, the simplest suggestion is that the no-boundary proposal is simply wrong. For example, if we do not trust the steepest-descent approximation for theoretical reasons, we may obtain an alternative probability distribution [14]. Alternatively, if we begin from a new fundamental wave function, it is possible to obtain a different probability distribution that may prefer a large vacuum energy [3]. However, it is fair to say that there are still several theoretical arguments to support the consistency of the original approaches put forward by Hartle and Hawking [15]. Thus, we can consider several viable possibilities to rescue the Hartle–Hawking wave function [16]:

• We require a number of ad hoc terms to measure the probability. For example, Hartle, Hawking, and Hertog introduced the volume-weighting factor to the probability measure [8]. Consequently, there is competition between the volume-weighting component and the Euclidean probability component. If the vacuum energy is sufficiently large, the volume-weighting component is dominated, and large e-foldings are eventually preferred. However, this assumption cannot be justified from first principles. Furthermore, this leads to eternal inflation, while this eternal inflation goes beyond the scope of our understanding because of the infinite volume and subsequent quantum tunneling.
• Our universe began from $V\sim 1$ (Planck scale) vacuum energy. If this is the case, there are no significant probability differences between the cutoff and other field values. However, based on observational constraints, this Planck-scale inflation cannot be the primordial inflation of our universe.
• Unknown physical degrees of freedom are required. For example, if there exists a very long field space or a large number of fields that contribute to inflation [13], such degeneracy of the field space can compete with the Euclidean probability component. However, in multiple cases, this requires too many degrees of freedom. Hence, in terms of quantum field theory, these possibilities may be unnatural.
• Certain modifications of the theory of gravity can explain large e-foldings. For example, massive gravity models [17,18] could provide certain interesting possibilities; however, this approach goes beyond the regime of Einstein gravity.

2.3. Rescue from the Secondary Scalar Field

However, the most reasonable rescue is to probably introduce one additional massive field [11]. The primary idea is that the classicality condition requires the classicality of all fields not only the inflaton field but also the other matter fields. If this is not the case (i.e., if the only inflaton field is classicalized while the second field is not classicalized), the ghost-like modes of the secondary field cannot be controlled after the Wick-rotation. Hence, this possibility must be avoided.

For simplicity, let us consider the following model

$$\begin{array}{c}\hfill S_{\mathrm{E}}=-\int d^{4}x\sqrt{+g}\left[\frac{1}{16\pi }R-\frac{1}{2}{\left(\nabla {\mathsf{\Phi }}_1\right)}^2-\frac{1}{2}{\left(\nabla {\mathsf{\Phi }}_2\right)}^2-\frac{1}{2}{m}_1^2{\mathsf{\Phi }}_1^2-\frac{1}{2}{m}_2^2{\mathsf{\Phi }}_2^2\right],\end{array}$$

(32)

where $m_1$ and $m_2$ are mass parameters of ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$, respectively. In particular, we assume that $m_1\ll m_2$, and hence ${\mathsf{\Phi }}_1$ is the inflaton field and ${\mathsf{\Phi }}_2$ is only an assisting field. Similar to the previous section, one can select the metric ansatz as follows:

$$\begin{array}{c}\hfill d{s}_{\mathrm{E}}^2=\frac{1}{m_2^2}\left(d{\tau }^2+a^2(\tau )d{\mathsf{\Omega }}_3^2\right).\end{array}$$

(33)

Due to the slow-roll condition, the variation of ${\mathsf{\Phi }}_1$ is negligible along the field direction of ${\mathsf{\Phi }}_2$. Hence, it is possible to approximate that $(1/2)m_1{\mathsf{\Phi }}_1^2\simeq V_0$ is a constant; therefore, the classicality condition of the potential (Equation (30)) is

$$\begin{array}{c}\hfill \frac{m_2^2}{V_0}\simeq \frac{m_2^2}{\frac{1}{2}{m}_1^2{\mathsf{\Phi }}_1^2}\le 6\pi .\end{array}$$

(34)

The results of numerical investigation are consistent with this expectation (Figure 2 [11]). The shadowed box region becomes increasingly narrow as $m_1/m_2$ decreases. Hence, in the $m_1/m_2\ll 1$ limit, if ${\mathsf{\Phi }}_2\simeq 0$, the genuine cutoff of the ${\mathsf{\Phi }}_1$ direction will satisfy ${\mathsf{\Phi }}_1\gg 1$.

Now, we are required to ask what the most probable initial condition over the field space $({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2)$ is. The smallest potential energy is the most preferred initial condition. As we assumed $m_1\ll m_2$, the potential varies very sensitively along the ${\mathsf{\Phi }}_2$ direction. Hence, the initial conditions with ${\mathsf{\Phi }}_2\simeq 0$ must be the most preferred. If we assume ${\mathsf{\Phi }}_2\simeq 0$, the most probable initial condition of the ${\mathsf{\Phi }}_1$ direction is ${\mathsf{\Phi }}_{1,\mathrm{cutoff}}$. However, to classicalize the ${\mathsf{\Phi }}_2$ field, the following condition must be satisfied:

$$\begin{array}{c}\hfill \frac{m_2^2}{3\pi m_1^2}\le {\mathsf{\Phi }}_{1,\mathrm{cutoff}}^2,\end{array}$$

(35)

where the details regarding the constants on the left-hand-side are not extremely important. If there is a mass hierarchy $m_1\ll m_2$, the cutoff of ${\mathsf{\Phi }}_1$ will be sufficiently large while the initial condition of the inflaton field must have large e-foldings $\mathcal{N}$:

$$\begin{array}{c}\hfill \mathcal{N}\simeq \mathcal{O}\left(1\right)\times \frac{m_2^2}{m_1^2}.\end{array}$$

(36)

In this case, it is easy to make $\mathcal{N}$ greater than 50.

It might be asked why massive particles play an important role in the no-boundary wave functions, as per our physical intuitions, massive particles can be integrated out based on low energy effective theory. This is an interesting feature of Euclidean quantum gravity. Massive particles will have greater stability in Lorentzian signatures and lower stability in Euclidean signatures. If the Hartle–Hawking wave function is a fundamental prescription of quantum gravity, it must classicalize all fundamental fields, including the most massive (probably Planck-scale) particles. If the massive fields are not classicalized, there remains an imaginary degree of freedom, which is detrimental for providing a consistent description.

This idea is not limited to quadratic potential models. It might be interesting to apply it to realistic inflation models, in addition to models with various interactions among fields.

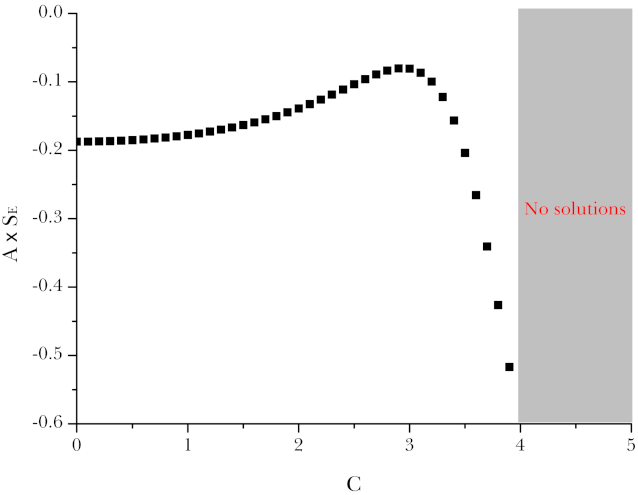
3. Fuzzy Instantons with Fast-Roll Potential

The second issue is to obtain classicalized fuzzy instantons even if the slow-roll condition is not guaranteed. Indeed, this issue has been highlighted in recent discussions in string theory.

3.1. Landscape vs. Swampland

To understand the cosmological constant problem and multiple fine-tuning issues regarding the universe, the cosmic landscape was a highly sophisticated hypothesis [19]. String theory allows for a wide variety (almost all possible) constants of nature, including the cosmological constant, as well as detailed shapes of the inflaton potential with these being referred to as the cosmic landscape. These possible parameter spaces are physically realized via eternal inflation and the quantum tunneling of bubble universes. Eventually, any fine-tuned parameters can be realized at a certain location in the multiverse.

Although there have been several criticisms of this approach, the most significant criticism was suggested by the string theory community [20]. As per the authors, the landscape where string theory is allowed is indeed a very restricted region among possible parameter spaces, e.g., it was conjectured that the inflaton potential must be restricted by

$$\begin{array}{ccc}\hfill \left|\frac{V^{″}}{V}\right|& >& \mathcal{O}(1),\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill \left|\frac{V^{\prime }}{V}\right|& >& \mathcal{O}(1),\hfill \end{array}$$

(38)

where these conditions are known as the swapland criteria. Of course, there are several subtle issues here. First, there is no fundamental proof of the criteria. Hence, the order-one constant is tricky to define. Perhaps slow-roll inflation can be marginally allowed [21]; however, there can be no fundamental cosmological constant if we seriously accept the swampland criteria.

In this study, we do not agree or disagree on the details of the swampland criteria. However, it has been established that they are harmful to the Hartle–Hawking proposal. In particular, there is a tension with Equation (30). On seeing more details, we may identify a run-away quintessence model, which is typical for string-inspired models [22]:

$$\begin{array}{c}\hfill V(\varphi )=A{e}^{-C\varphi }.\end{array}$$

(39)

For each point near ${\varphi }_0$, we can approximate the potential as

$$\begin{array}{c}\hfill V(\varphi )\simeq \frac{1}{2}A{C}^2{e}^{-C{\varphi }_0}{\left(\varphi -{\varphi }_0-\frac{1}{C}\right)}^2+\frac{A{e}^{-C{\varphi }_0}}{2}.\end{array}$$

(40)

Therefore, it is not surprising that $\varphi ={\varphi }_0$ has a classical history only if

$$\begin{array}{c}\hfill C^2\lesssim 3\pi .\end{array}$$

(41)

From numerical computations, we can confirm that $C\lesssim 4$ is the condition for the existence of a classical solution (Figure 3,22]). On the other hand, if $C>4$ happens, which is extremely natural for string-inspired models, there will be no classicalized instantons along the runaway direction. Hence, such a quintessence model is not compatible with the Hartle–Hawking wave function.

The question then arises as to whether, even in the context of the swampland criteria, there is any way to rescue the Hartle–Hawking wave function.

3.2. Rescue Using Hwang-Sahlmann-Yeom Instantons

Although the swampland criteria do not favor the local minimum of the potential, they do not exclude the unstable local maximum of the potential. We describe the hilltop potential near the hilltop ($\varphi =0$) as follows:

$$\begin{array}{c}\hfill V(\varphi )=V_0\left(1-\frac{1}{2}{\mu }^2{\varphi }^2\right).\end{array}$$

(42)

If $\mu \ll 1$, the slow-roll condition is satisfied; moreover, the usual fuzzy instanton can exist. On the other hand, if $\mu \gg 1$, which is more natural for string-inspired models, the slow-roll condition is no longer satisfied. Thus, close to the hilltop, the initial field values rapidly rise to the local maximum of the potential during the Euclidean time. By selecting proper initial conditions, one can obtain the fuzzy instantons close to the fast-rolling hilltop potentials [23] (for example, see Figure 4). We name these solutions Hwang-Shalmann-Yeom (HSY) instantons to contrast them with the slow-roll fuzzy instantons proposed by Hartle–Hawking–Hertog (HHH).

The physical difference is attributed to the probability (Figure 5 [22]). If $\mu \ll 1$, the probability is approximately

$$\begin{array}{c}\hfill log{P}_{\mathrm{HHH}}\simeq \frac{3}{8V_0\left(1-\frac{1}{2}{\mu }^2{\varphi }_0^2\right)}.\end{array}$$

(43)

On the other hand, if $\mu \gg 1$, the field quickly approaches the local maximum of the potential, and hence the dependence on the initial condition is negligible:

$$\begin{array}{c}\hfill log{P}_{\mathrm{HSY}}\simeq \frac{3}{8V_0}.\end{array}$$

(44)

Therefore, once there is a hilltop with $\mu \gg 1$, the probability of left-rolling and right-rolling are almost the same.

This HSY instanton can rescue the Hartle–Hawking wave function even in the context of the swampland because the classicalized universes can be created close to the narrow and unstable hilltop of the field space.

3.3. Cosmological Applications

If fuzzy instantons and the swampland criteria both exist in the context of the cosmic landscape, there can be multiple cosmological applications of HSY instantons [22].

• As per the moduli or dilaton stabilization issue, there is a probability competition between the stable and unstable directions. It may be that the only possible starting point from the no-boundary wave function is the hilltop of the potential. As per HSY instantons, there is no preference between left-rolling and right-rolling. Hence, given a reasonable probability, the moduli or dilaton stabilization can be explained using quantum cosmology [23].
• The universe starts from the local maximum rather than the local minimum. The cosmological constant depends on the local minimum; however, the probability of the HSY instanton depends on the local maximum. Therefore, although the cosmological constant varies from anti-de Sitter to de Sitter space, there may be no singular changes in the a priori probability because there is no singular change in the local maximum [22].
• HSY instantons can rescue the Hartle–Hawking wave function even in the context of the swampland criteria because classicalized universes can be created close to the narrow and unstable hilltop of the field space.

In terms of embedding a consistent inflation model with the swampland criteria and the trans-Planckian censorship conjecture, if we consider only a single-field inflation model, the no-boundary wave function will not be compatible with the criteria [21]. On the other hand, if we include one additional field, there may be the possibility of rescuing the no-boundary proposal. Alternatively, if the universe began from a hilltop of a very sharp potential, it can be explained from the no-boundary wave function. However, its smooth connection to a successful inflation model must be explained.

4. Extensions

In the previous sections, we examined the no-boundary proposal in a single scalar field model with Einstein gravity. However, in principle, there are possible additional extensions such as the following:

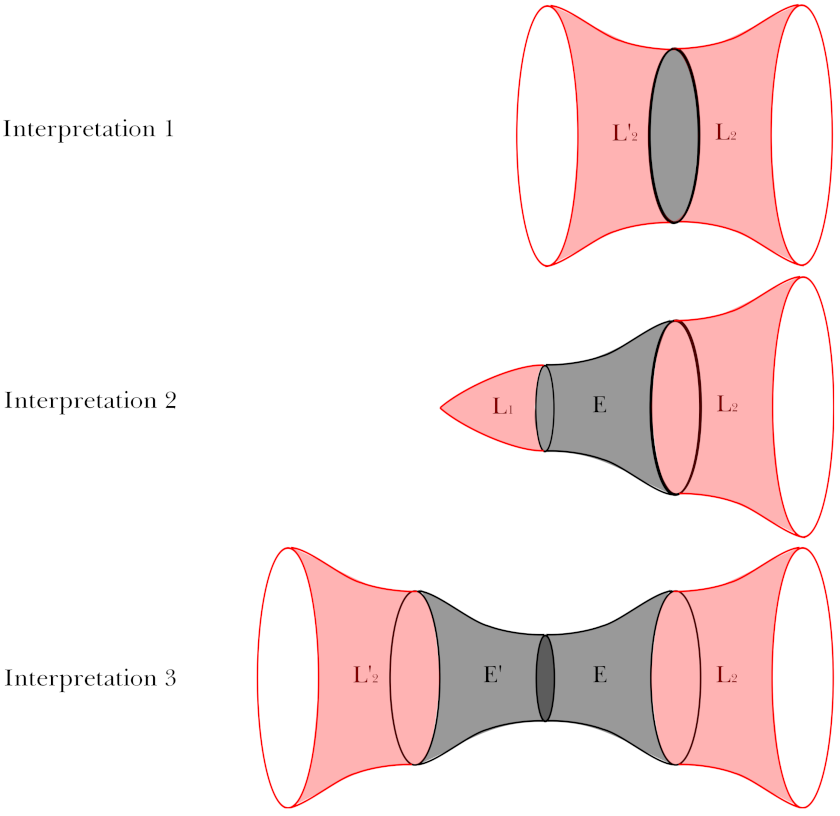
• The Euclidean path integral does not necessarily indicate the no-boundary proposal, which is a specific choice of the Euclidean path integral. In more generic cases, there can be two boundaries (initial and final boundaries). However, because of the ambiguity of time in quantum gravity, one may make the interpretation that two universes are created from nothing. These solutions are known as Euclidean wormholes (Figure 6 [24]).
• The theory can be extended by or embedded with quantum gravitational models. For example, string-inspired models can be used to introduce a number of additional terms, e.g., the Gauss–Bonnet term with dilaton coupling [25]. Furthermore, loop quantum cosmological models suggest the big bounce near the putative singularity [26]. These corrections suggest a new type of solution.

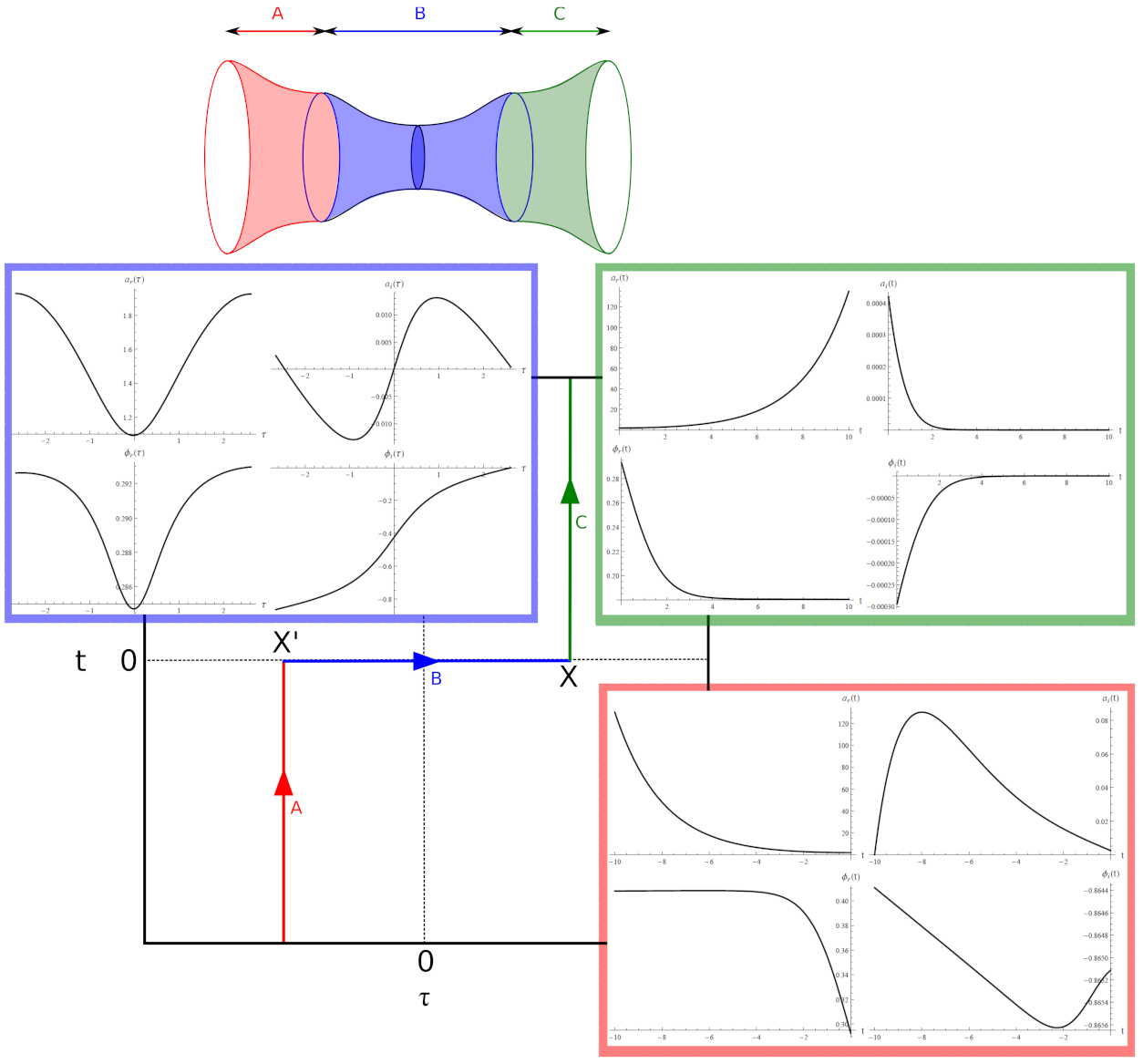
4.1. Fuzzy Euclidean Wormholes

As a simple extension, we consider fuzzy Euclidean wormholes in Einstein gravity [24]. Indeed, in terms of instantons, Euclidean wormholes are more natural than compact instantons. The intuitive reason for this is listed below [27].

Let us first consider a free scalar field model with an $O(4)$-symmetric metric ansatz. The following will then be the generic solution of the scalar field in a Lorentzian signature:

$$\begin{array}{c}\hfill \frac{d\varphi }{dt}=\frac{\mathcal{A}}{a^3}.\end{array}$$

(45)

Of course, due to classicality, $\mathcal{A}$ is a real-valued number. If we Wick-rotate this solution to Euclidean time, then we obtain

$$\begin{array}{c}\hfill \frac{d\varphi }{d\tau }=-i\frac{\mathcal{A}}{a^3}.\end{array}$$

(46)

Therefore, if the velocity of the scalar field is non-vanishing in Lorentzian signatures and if the solution is classical in Lorentzian signatures, it is necessary that the velocity of the scalar field must be purely imaginary in Euclidean signatures. However, purely imaginary scalar fields in Euclidean signatures are perfectly acceptable in terms of the formalism of the Euclidean path integral. Then, the corresponding Euclidean metric satisfies

$$\begin{array}{c}\hfill {\dot{a}}^2=1-\frac{a^2}{{\ell }^2}+\frac{a_0^4}{a^4},\end{array}$$

(47)

where $\ell \equiv \sqrt{3/\mathsf{\Lambda }}$ and $a_0^4=4\pi {\mathcal{A}}^2/3$.

If $a_0\ll \ell$, $\dot{a}$ has two zeros. Hence, the Euclidean solution has two turning points say $a_{\max }$ and $a_{\min }$. If we consider a solution that covers $a_{\max }$ to $a_{\min }$ to $a_{\max }$, this becomes the Euclidean wormhole solution where there are two boundaries arising from the solution, and the Wick-rotation can be applied for these two boundaries. The compact instantons are available only if $\mathcal{A}=0$, or when the velocity of the scalar field is zero. On the other hand, the non-compact instantons occur in more general situations when the Lorentzian solutions have non-trivial velocities.

What we have considered is the case in which the scalar field is free. The natural question that arises is what happens if we generalize to a specific inflation model. For this purpose, we can introduce the ansatz of the initial condition of the Euclidean wormholes as follows [27]:

$$\begin{array}{ccc}\hfill \mathrm{Re}a(0)& =& a_{\min }cosh\eta ,\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill \mathrm{Im}a(0)& =& a_{\min }sinh\eta ,\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill \mathrm{Re}\dot{a}(0)& =& \sqrt{\frac{4\pi }{3}}\frac{\mathcal{B}}{a_{\min }^2}\sqrt{sinh\zeta cosh\zeta },\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill \mathrm{Im}\dot{a}(0)& =& \sqrt{\frac{4\pi }{3}}\frac{\mathcal{B}}{a_{\min }^2}\sqrt{sinh\zeta cosh\zeta },\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill \mathrm{Re}\varphi (0)& =& {\varphi }_{0}cos\theta ,\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill \mathrm{Im}\varphi (0)& =& {\varphi }_{0}sin\theta ,\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill \mathrm{Re}\dot{\varphi }(0)& =& \frac{\mathcal{B}}{a_{\min }^3}sinh\zeta ,\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill \mathrm{Im}\dot{\varphi }(0)& =& \frac{\mathcal{B}}{a_{\min }^3}cosh\zeta ,\hfill \end{array}$$

(55)

where $a_{\min }$, $\mathcal{B}$, ${\varphi }_0$, $\eta$, $\zeta$, and $\theta$ are free parameters. However, these free parameters are not entirely free, but should satisfy the real-part and imaginary-part equations of the Hamiltonian constraint:

$$\begin{array}{ccc}\hfill 0& =& 1+\frac{8\pi }{3}{a}_{\min }^2\left(-V_{\mathrm{r}}+sinh2\eta V_{\mathrm{i}}\right)-\frac{4\pi {\mathcal{B}}^2}{3a_{\min }^4}\left(1+sinh2\zeta sinh2\eta \right),\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill 0& =& a_{\min }^6+\frac{{\mathcal{B}}^{2}sinh2\eta }{2\left(V_{\mathrm{r}}sinh2\eta +V_{\mathrm{i}}\right)},\hfill \end{array}$$

(57)

where $V_{\mathrm{r}}$ and $V_{\mathrm{i}}$ are the real and the imaginary part of $V(\varphi )$ at $\tau =0$. Based on these two equations, two parameters among the five free parameters are determined, say, $a_{\min }$ and $\eta$.

Now, the remaining free parameters are $\mathcal{B}$, ${\varphi }_0$, $\zeta$, and $\theta$. However, $\mathcal{B}$ determines the amplitude of the imaginary part of the scalar field, and hence the size of the wormhole throat. $\zeta$ is the parameter that determines the symmetry between the left and right sides of the wormhole. These two parameters do nothing but determine the shape of the wormhole. ${\varphi }_0$ corresponds to the initial field value of the solution. Therefore, the only tuning parameter that can be used to fulfill the classicality condition is $\theta$.

This situation is the same as the compact instanton case; however, there is a serious problem. In the compact instanton case, there is only one boundary (future boundary); hence, the classicality must be imposed given only one boundary. Using $\theta$, we can make one boundary classical. However, in the Euclidean wormhole case, there are two boundaries that we need to classicalize. In general, it is impossible to classicalize two boundaries at the same time.

However, there are a number of exceptional cases, e.g., let us consider the following potential:

$$\begin{array}{c}\hfill V(\varphi )=\frac{3}{8\pi {\ell }^2}\left(1+A{tanh}^2\frac{\varphi }{\alpha }\right),\end{array}$$

(58)

where ℓ, A, and $\alpha$ are free parameters (see Figure 7 [27]). This model provides a flat hilltop [28] that is consistent with the Starobinsky model [29], which is preferred by the recent Planck data analysis [30]. In this model, the scalar field at the end of the wormhole rolls down to the local minimum, and hence the primordial inflation is naturally terminated. By tuning $\theta$, we classicalize this end. On the other hand, it is not possible to tune the other end; however, if the scalar field rolls up to the hilltop, it is possible it will come to an automatic stop as long as the hilltop is sufficiently flat. If the field stops at the hilltop, the field will not be classicalized though the metric will be classicalized because the kinetic terms of the scalar field provide no contribution. Furthermore, because of the flat potential, there will be a local shift symmetry. By shifting the field along the complex direction, one can classicalize the field value at the hilltop. In any case, the point is that we can definitely classicalize one end; the other end is a little bit subtle, but the Euclidean action does not vary after the Wick-rotation at the hilltop. As we are observing only one universe, we do not require to worry about the details at the other end of the wormhole as long as the real part of the Euclidean action is bounded well.

In terms of this mechanism, we have three important comments:

• This mechanism cannot be applied to convex inflaton potential (e.g., quadratic potential). Therefore, the Euclidean wormhole selects the concave inflaton potential [27].
• For a given vacuum energy scale $V_0$ or ℓ, the probability of the Euclidean wormhole is larger than that of the compact instanton [24] because the maximum probability of the Euclidean wormhole is

  $$\begin{array}{c}\hfill logP\simeq \pi {\ell }^2\left(1+0.16{\left(\frac{a_0}{\ell }\right)}^{5/2}\right),\end{array}$$

  (59)

  where that of the compact instanton is $logP=\pi {\ell }^2$.
• For a given concave potential, there may be competition between the compact instantons and Euclidean wormholes. The largest probability of compact instantons occurs close to the cutoff, where it is generally larger than that of the Euclidean wormholes that appear only near the hilltop. On the other hand, if we assume a mechanism that enhances the large e-foldings (e.g., introducing a massive field direction), Euclidean wormholes will be more highly favored than compact instantons [28]. Therefore, as long as we assume that our universe experienced more than 50 e-foldings, a Euclidean wormhole with a concave potential will be preferred over compact instantons with convex or concave potentials.

In conclusion, Euclidean wormholes can interestingly answer the question of why our universe started from the concave part of a potential rather than the convex part? However, there is a point of warning that is worth remarking upon. For all computations of Euclidean wormholes, we implicitly assumed the ultraviolet(UV)-completion of the inflaton potentials. In general, the Euclidean wormhole requires the potential to have a flat direction. However, in the context of the swampland criteria, this might be an unjustifiable assumption. Identifying a sufficiently flat field direction within a UV-completed model would make an interesting future research topic.

4.2. Euclidean Wormholes in Gauss–Bonnet-Dilaton Gravity

If we consider the string theory as the UV-completion of quantum gravity, it is reasonable to include higher-order corrections of string-inspired models and observe their physical applications. The most famous model in this regard is known as Gauss–Bonnet-dilaton gravity:

$$\begin{array}{c}\hfill S=\int d^{4}x\sqrt{-g}\left(\frac{R}{16\pi }-\frac{1}{2}{\left(\nabla \varphi \right)}^2-V(\varphi )+\frac{1}{2}\xi (\varphi )R_{\mathrm{GB}}^2\right),\end{array}$$

(60)

where

$$\begin{array}{c}\hfill R_{\mathrm{GB}}^2=R_{\mu \nu \rho \sigma }{R}^{\mu \nu \rho \sigma }-4R_{\mu \nu }{R}^{\mu \nu }+R^2\end{array}$$

(61)

is the Gauss–Bonnet term, $\varphi$ is the dilaton field, and

$$\begin{array}{c}\hfill \xi (\varphi )=\lambda e^{-c\varphi }\end{array}$$

(62)

is the coupling function of the dilaton field. Note that $\lambda$ and c are model-dependent parameters.

Due to the corrections of the Gauss–Bonnet-dilaton term, although the null energy condition is satisfied, the null curvature condition is effectively violated. Equivalently, if we consider the Gauss–Bonnet-dilaton term as an effective contributor to matter, the null energy condition will be effectively violated. Accordingly, it is not surprising that a Lorentzian or Euclidean wormhole solution might exist [31].

To obtain a Euclidean wormhole solution, we consider the following initial condition at $\tau =0$ [32]:

$$\begin{array}{ccc}\hfill a(0)& =& \sqrt{\frac{3}{4\pi \left(2V_0-{\dot{\varphi }}^2(0)\right)}},\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill \dot{a}(0)& =& 0,\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill \varphi (0)& =& {\varphi }_0,\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill \dot{\varphi }(0)& =& 0,\hfill \end{array}$$

(66)

where $a(0)$ is obtained from the Hamiltonian constraint equation. By tuning ${\varphi }_0$, we must satisfy the boundary condition at $\tau ={\tau }_{\mathrm{end}}$:

$$\begin{array}{ccc}\hfill a({\tau }_{\mathrm{end}})& =& 0,\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill \dot{a}({\tau }_{\mathrm{end}})& =& -1,\hfill \end{array}$$

(68)

to achieve a regular end.

In general, this solution penetrates over a sharp potential barrier. Furthermore, because the volume is greater than that of the usual compact instanton, the probability is higher than that of the pure de Sitter instanton. Therefore, once there exists a string-inspired term, although there exists a potential barrier, it can be used to create a universe with a higher probability.

If we Wick-rotate at $\tau =0$, we can apply this solution to quantum cosmology [25]. However, if we extend the Euclidean time to $\tau <0$ and Wick-rotate the solution along the anisotropic direction, this can explain a (expanding) Lorentzian wormhole based on quantum tunneling [32]. The examination of the quantum tunneling of the Lorentzian wormhole is another interesting issue and requires further investigation.

4.3. Hartle–Hawking Wave Function with Loop Quantum Cosmology

For loop quantum gravity, we consider the generic quantum state that satisfies the (quantum) Hamiltonian constraint equation, in addition to the (quantum) momentum constraint equations. The generic states that satisfy the momentum constraint equations should follow the loop representations. Due to the loop representation, there must be a correction to the Hamiltonian constraint at the classical level [33]. By including these corrections, we can examine the effects of quantum gravity.

In general, it is believed that, in a cosmological context, the beginning of the universe can be explained by the big bounce. The Lorentzian dynamics of the scale factor satisfy the equation ${\dot{a}}^2+\mathcal{V}(a)=0$, where $\mathcal{V}(a)$ has a zero at a minimum value $a_{\min }$. This corresponds to the bouncing point of the universe [26]. However, there remains a conceptual question: As a goes to $a_{\min }$, the universe approaches the deep quantum regime, and it must be asked how we can select the arrow of time. It would seem strange if we were able to determine a definite direction for time even in this quantum gravitational regime.

Perhaps this conceptual tension might be explained if we introduce the Hartle–Hawking wave function [26]. To compute the Euclidean Lagrangian $L_{\mathrm{E}}$ from the loop quantum gravity modified Euclidean Hamiltonian $H_{\mathrm{E}}$, we follow the relation:

$$\begin{array}{c}\hfill L_{\mathrm{E}}=p_a\dot{a}-H_{\mathrm{E}},\end{array}$$

(69)

where $p_a$ is the canonical momentum of a. However, because of the Hamiltonian constraint, $H_{\mathrm{E}}=0$ in the on-shell level description. Therefore, the Euclidean action is simply

$$\begin{array}{c}\hfill S_{\mathrm{E}}=-\frac{3\pi }{2}\int a{\dot{a}}^{2}d\tau =-\frac{3\pi }{2}{\int }_0^{a_{\min }}a\sqrt{|\mathcal{V}(a)|}da.\end{array}$$

(70)

Interestingly, in Euclidean signatures, as a approaches to zero, $\mathcal{V}(a)$ approaches to zero. This indicates that the instanton explains the infinitely stretched solution as a function of $\tau$, although the probability is well-defined [34]. Except for this feature, the interpretation is the same as that of the usual Hartle–Hawking wave function. Therefore, close to the quantum bouncing point, the bouncing interpretation is not the only possible explanation, as a universe can be created from nothing (Figure 8 [26]). Furthermore, in certain parameter regimes, a Euclidean wormhole solution is possible. Accordingly, there is an ambiguity in defining the arrow of time around the quantum bouncing point; either a contracting phase bounces to an expanding phase or two expanding universes are created via a Euclidean wormhole solution.

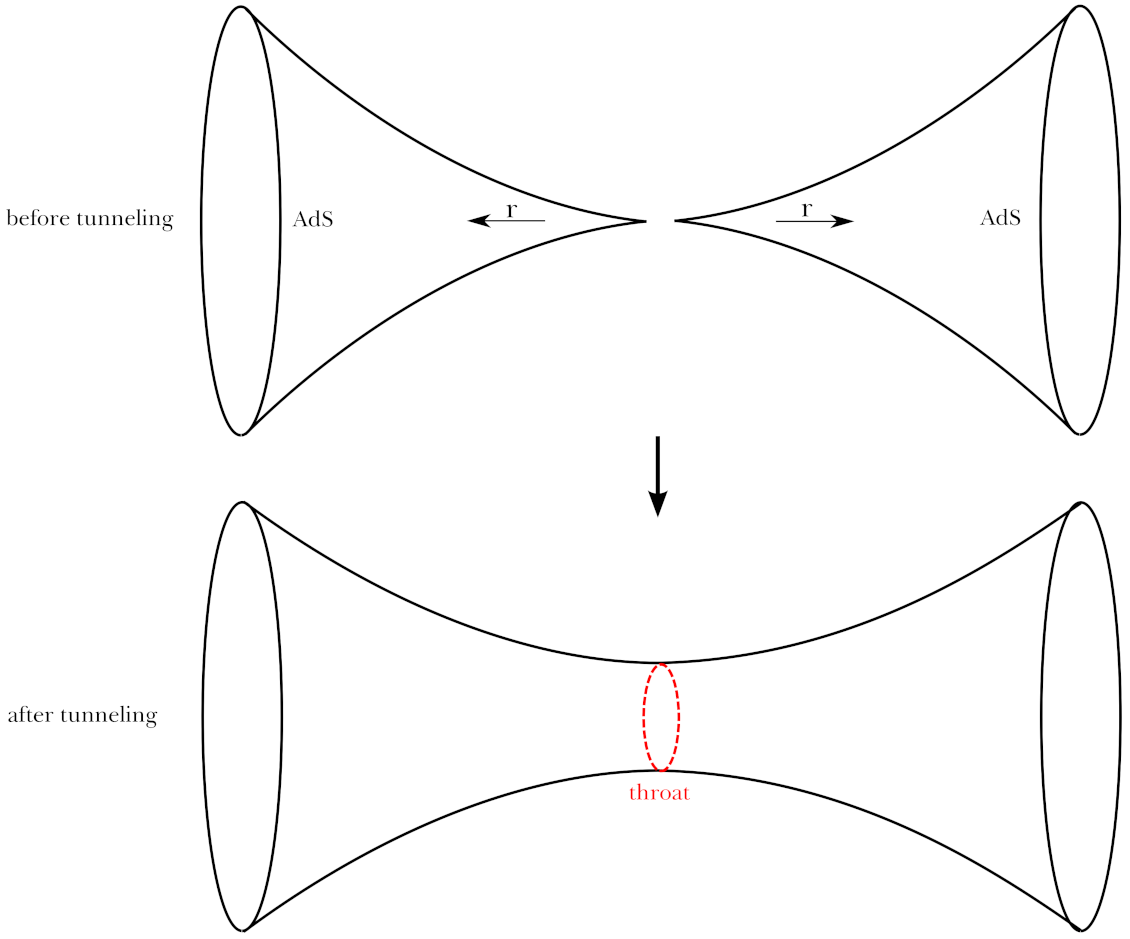
4.4. Fuzzy Instantons in Anti-De Sitter Space

Finally, we report a number of discussions of the anti-de Sitter space. Let us consider the following potential:

$$\begin{array}{c}\hfill V(\mathsf{\Phi })=V_0\left(-1-\frac{1}{2}{\mu }^2{\mathsf{\Phi }}^2+\lambda {\mathsf{\Phi }}^4\right).\end{array}$$

(71)

In the Euclidean domain, it is not surprising to have a complex-valued solution. Thus, we consider the following pure imaginary field: $\mathsf{\Phi }\to i\varphi$. Then, the potential is effectively

$$\begin{array}{c}\hfill U(\varphi )=V_0\left(-1+\frac{1}{2}{\mu }^2{\varphi }^2+\lambda {\varphi }^4\right),\end{array}$$

(72)

while the kinetic term has an opposite sign. Therefore, it is possible to determine a solution according to which the scalar field asymptotically approaches zero while there may exist a throat at the center [35].

One potential issue is whether the Euclidean action is well-defined or not. As the volume of Euclidean anti-de Sitter space is infinite, the Euclidean action itself is infinite. However, by subtracting to the pure anti-de Sitter background, one may obtain a finite action difference. The sufficient condition to obtain a finite action difference is that the field should approach zero sufficiently quickly near the infinity [36]. This can be achieved if we tune the shape of the potential [35].

If this finite action difference is allowed, this instanton can explain a case of tunneling from two separate anti-de Sitter spaces to a connected anti-de Sitter wormhole after the Wick-rotation (Figure 9 [35]). This solution satisfies the classicality at the time-like infinity. One potential question is whether any effects from the fuzzy core of the solution can reach a future infinity or not. However, in principle, this solution is embedded in the Euclidean path integral formalism. Therefore, we can very easily extend this technique to anti-de Sitter fuzzy Euclidean wormholes in a black hole background. After the Wick-rotation, this explains a Lorentzian (probably unstable) wormhole in anti-de Sitter space. The existence of this structure can then cause conceptual trouble with the ER = EPR conjecture [37]. We leave these interesting connections to the information loss paradox for future research [38,39].

5. Future Perspectives

In this study, we discussed various aspects of the fuzzy instantons of the Hartle–Hawking wave function.

First, we examined the slow-roll inflation models. Due to the fuzzy instanton analysis and classicality condition, the universe should experience a small amount of inflation. However, the amount is not sufficient, and we require several routes to rescue the Hartle–Hawking wave function to fit the observations. Perhaps the most natural approach is to introduce a massive field and impose the classicalization of all matter fields.

Second, we investigated the cases in which the slow-roll conditions break down. This is very natural from the point of view of a UV-completed theory such as string theory. However, a classical universe can be created even in these cases. We named these new types of solutions HSY instantons.

Third, we extended this to divergent situations, e.g., the Euclidean path integral formalism does not necessarily indicate that there is only one boundary. In principle, there can be two boundaries. This case is related to fuzzy Euclidean wormholes, which in de Sitter space can explain the preference of a concave inflaton potential. Fuzzy Euclidean wormholes in anti-de Sitter space may be related to the information loss paradox, in addition to a possible criticism of the ER=EPR conjecture. Furthermore, the no-boundary wave function can be applied to string-inspired models or loop quantum cosmology models. These models allow for Euclidean wormhole solutions.

There are several interesting possible directions for future research:

• Traditionally, we assumed cosmological landscapes and considered slow-roll inflation models. However, in recent discussions, models that are consistent with the swampland criteria might be more interesting. The Hartle–Hawking wave function is definitely useful for both problems, though it might be more interesting to provide possible observational consequences [40,41] that reveal issues related to the swampland criteria.
• Fuzzy Euclidean wormholes can be realized in various systems, but the application of the associated techniques might be complicated beyond Einstein gravity. This might include the Gauss–Bonnet-dilaton gravity model or the loop quantum cosmological model. Some fuzzy extensions of oscillating instantons are interesting [42]. In any case, this will be a challenging topic.
• Fuzzy instantons in anti-de Sitter backgrounds or black hole backgrounds are another interesting topic. This issue may cover a number of topics regarding Hawking radiation [43] as well as the information loss problem [44]. However, it is fair to say that it is not easy to impose the classicality condition at a future infinity if the symmetry is less than the $O(4)$-symmetry. The generalization of dynamical instantons in spherical symmetry will be an important topic.

In conclusion, the Euclidean path integral is approximated well by instantons. If the instantons are dynamical, they must be fuzzy or complexified. An investigation of dynamical wormholes is a challenging and fruitful future research topic. This is necessarily related to the study of fuzzy instantons not only in the context of cosmology but also in black hole physics. We leave these fascinating topics for future research.