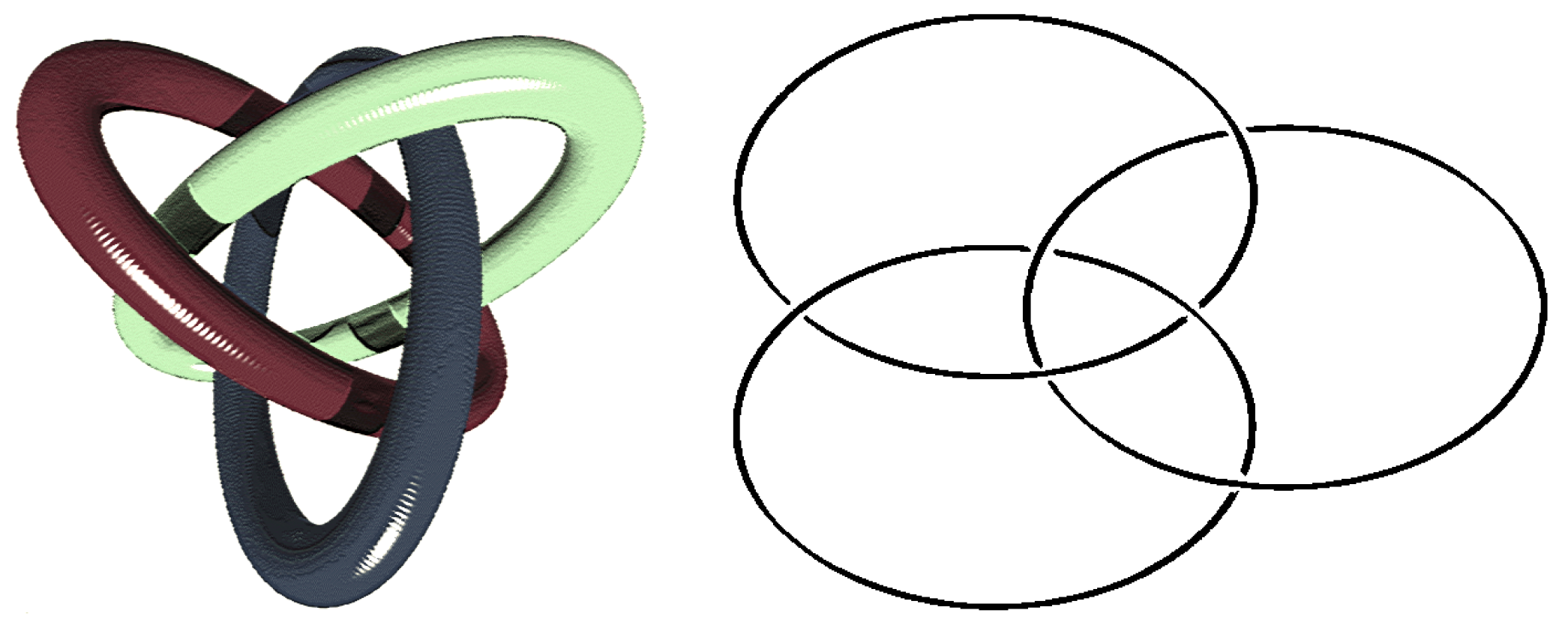1. Introduction
One hundred years after Einstein’s initial conception and formulation of the general theory of relativity, it still remains a vibrant subject of intense research and formidable depth. In this way, during all of these years, our understanding of gravitation in differential geometric terms is being continuously refined. We believe that one of the highest priorities of a centennial perspective on general relativity should be a careful re-examination of the validity domain of Einstein’s field equations. These equations constitute the irreducible kernel of general relativity and the possibility of retaining the form of Einstein’s equations, while concurrently extending their domain of validity is promising for shedding new light on old problems and guiding toward their effective resolution. These problems are primarily related to the following perennial issues: (a) the smooth manifold background of the theory; (b) the existence of singular loci in spacetime where the metric breaks down or the curvature blows up; and (c) the non-geometric nature of the second part of Einstein’s equations involving the energy-momentum tensor. It turns out that these problems are intrinsically related to each other and require a critical re-thinking of the initial assumptions referring to the domain of validity of Einstein’s equations.
In this communication, first of all, we would like to consider the problem of constructing distinguishable extensions of the smooth spacetime manifold solution space of Einstein’s equations incorporating singularities by taking into account recent developments in differential geometry. These developments pertain to the possible generalization of the technical framework of differential manifolds, on which the formalism and interpretation of general relativity is based on, to non-smooth or singular topological spaces by applying concepts and methods of sheaf theory and sheaf cohomology. In a nutshell, it turns out that all of the usual local constructions of differential geometry, re-interpreted sheaf-theoretically, do not require the notion of a global smooth manifold, but are based on much weaker conditions of an essentially cohomological nature. The physical interpretation of these findings, referring to appropriate extensions of Einstein’s equations over singular domains, is tantamount to the viable possibility of extending the covariant formulation of Einstein’s equations using continuous distribution-like or even non-smooth sheaves of coefficients for all of the involved tensorial physical quantities.
Second, we would like to show explicitly how certain generalized distribution-like solutions of partial differential equations, which fit appropriately in the above-mentioned sheaf-theoretic framework of differential geometry, bear significance in relation to obtaining singularity-free solutions of Einstein’s equations in extended domains. We scrutinize the generation of these distribution-like algebra sheaves of coefficients from a physical perspective and explain the means of their construction in terms of residue classes of sequences of smooth functions modulo the information of singular loci encoded in suitable ideals.
Finally, we consider the application of these distribution-like solution sheaves in geometrodynamics. The geometrodynamical formalism is very instructive in relation to the proposed extensions because it leads to the conclusion that active positive gravitational mass may emerge from purely topological considerations taking into account the constraints imposed by Einstein’s field equations in the vacuum. In this manner, we may re-assessfruitfully Wheeler’s insights referring to “mass without mass” and “charge without charge”, as well as re-evaluate the notion of wormhole solutions from a cohomological point of view. In this context, we propose to model topologically-circular boundaries of singular loci in three-dimensional space in terms of topological links. It turns out that there exists a universal topological link bearing the connectivity property of the Borromean rings. The cohomological expression of the Borromean link points to its physical interpretation as a higher order wormhole solution of the field equations.
2. General Relativity from the Perspective of Sheaf Theory
In the standard formulation of general relativity, the spacetime event structure is represented by means of a connected, four-dimensional real smooth manifold X. The chronogeometric relations on the event manifold X are expressed in terms of a pseudo-Riemannian metric of the Lorentzian signature, called the spacetime metric. The chronogeometric relations are not fixed kinematically a priori, like in all predecessor classical field theories, but they should be obtained dynamically in terms of the metric as a solution of Einstein’s field equations depending on the energy-momentum matter field distributions. In this manner, all of the pertinent chronogeometric relations defined on a four-dimensional smooth manifold, endowing it with the structure of a spacetime manifold, become variable. The dynamical constitution of these relations by means of the field equations requires the imposition of a compatibility requirement relating the metric tensor, which represents the spacetime geometry, with the affine connection, which represents the differential evolution of the gravitational field. A spacetime manifold is considered to be without singularities if the coefficients of the metric tensor field are smooth and the manifold X is geodesically complete with respect to the metric. In this case, all timelike geodesic curves can be extended to arbitrary length in the smooth spacetime manifold X. From a physical viewpoint, according to the above requirements, the notion of localization at a spacetime point-event is sensible only if the coefficients of the metric tensor field are smooth in an open neighborhood of this point.
Algebraically speaking, a real smooth manifold
X can be reconstructed entirely from the
-algebra
of smooth real-valued functions on it, and in particular, the points of
X are derived from the algebra
as the
-algebra homomorphisms
. This important observation in relation to general relativity has been first proposed and explicated by Geroch in the form of Einstein algebras [
1]. From a modern mathematical perspective, it is a consequence of the Gelfand representation theorem applied to the case of smooth manifolds [
2,
3]. In this way, manifold points constitute the
-spectrum of the algebra of smooth functions
, being isomorphic with the maximal ideals of this algebra. Notice that the
-algebra
is a commutative topological algebra that contains the field of real numbers
as a distinguished subalgebra, encapsulating the predominant physical assumption that our means of characterizing events is conducted by evaluations in the field of real numbers
.
The algebraic viewpoint is instructive because it makes clear that in the standard differential geometric setting of general relativity, all of the tensorial physical quantities are coordinatized by means of the commutative -algebra of globally-defined smooth real-valued functions . Hence, the background of the theory remains fixed as the -spectrum of the commutative topological algebra , supplying smooth coefficients for the coordinatization of physical quantities. The points of the manifold X, although not dynamically localizable degrees of freedom in general relativity, serve as the semantic information carriers of spacetime events. More precisely, the points are marked on a smooth manifold in terms of global evaluations of the smooth algebra in the field of real numbers. The subtlety of general relativity is exactly that manifold points are not dynamically localizable entities in the theory. More precisely, manifold points assume an indirect reference as indicators of spacetime events, only after the dynamical specification of chronogeometrical relations among them, as particular solutions of the generally covariant field equations. Clearly, the existence of singular loci in spacetime where the metric breaks down in terms of smooth function coefficients forbids the association of smooth manifold points with spacetime events. What remains is an emergent notion of an event horizon of a singular locus where spacetime information may be encoded appropriately.
The dynamical variability of the coefficients coordinatizing all tensorial physical quantities requires the action of a covariant differential operator to be applied upon them. This takes place via the notion of an affine connection, which is expressed as a covariant derivative acting on these smooth coefficients. The result of differentiation is encoded in -modules over the algebra , called modules of differential forms Ω and their duals , as well as their higher powers constructed by means of exterior algebra.
In the same algebraic context, the role of a metric geometry on a smooth manifold, as related to the above modules of differential forms and their duals in general relativity, pertains to the representability of spacetime events by points of the manifold, which in turn necessitates their coordinatization in terms of real numbers. This is tantamount to the requirement that all types of differentially-variable quantities should possess uniquely-defined dual types, such that their point-event representability can be made possible by means of real numbers. This is precisely the role of a geometry induced by a metric. Concretely, the spacetime metric assigns a unique dual to each differentially-variable quantity, by effecting an isomorphism between the modules Ω and , that is , such that .
The important thing to notice is that all of these constructions can be performed strictly locally, that is by using only sections defined in the neighborhood of points. This is an implication that differential geometric constructions should be expressed not in terms of global algebra coefficients, but in terms of sheaves of coefficients defined locally. Then, the task is to study the maximal extendibility of these constructions from the local to the global level, which is technically expressed via the theory of sheaf cohomology.
In the context of general relativity, the modeling of the dynamical variability, caused by the gravitational field by means of the Levi–Civita connection, from a local sheaf-theoretic perspective, is becoming even more relevant in view of the spacetime metric compatibility of this connection and the associated solution space of the theory. Einstein’s equations are formulated in terms of non-linear partial differential equations involving smooth functions, playing the role of local coefficients coordinatizing the metric tensor, the Ricci tensor and the scalar curvature. The solution of these equations in terms of the spacetime metric determines the local metrical properties of the spacetime manifold around any point, depending on the energy-momentum tensor. Notwithstanding this, all of the global cosmological predictions of the theory are obtained not from these local solutions of the field equations per se, but from the possibility of the continuation of some local solution to an extended region. The method of the continuation or extension of some solution from the local to the global level is mathematically of a sheaf-theoretic nature.
In view of the problem of singularities in general relativity, this is a clear warning that distribution-like sheaves of coefficients may be more appropriate for the continuation of some local solution over extended regions when the smooth ones become ill-defined over singular loci. It is a natural requirement that these sheaves of coefficients contain the standard smooth ones as a subalgebra, or equivalently, there is an algebra sheaf embedding of the smooth coefficients into the generalized ones. It is expected that distribution-like sheaves of coefficients can prevent the breaking down of the metric at singularities and, therefore, provide the means to extend the domain of validity of the field equations, under the proviso that the same tensorial equations can be re-expressed covariantly in terms of these generalized sheaves of coefficients.
3. Cohomological Conditions for Extending the Smooth Sheaf of Coefficients in General Relativity
Cohomology theory constitutes a sophisticated algebraic-topological method of assigning global invariants to a topological space in a homotopy-invariant way. The cohomology groups measure the global obstructions for extending sections from the local to the global level, for instance extending local solutions of a differential equation to a global solution. The differential geometric mechanism of smooth manifolds is essentially based on the set-up of the de Rham complex in terms of locally-defined smooth coefficients. In particular, de Rham cohomology measures the extent that closed differential forms fail to be exact and, thus, the obstruction to integrability. In this context, the central role is played by the lemma of Poincaré, according to which every closed differential form is locally exact in terms of smooth coefficients. The de Rham theorem asserts that the homomorphism from the de Rham cohomology ring to the differentiable singular cohomology ring, given by the integration of closed forms over differentiable singular cycles, is a ring isomorphism. The sheaf-theoretic understanding of this deep result came after the realization that both the de Rham cohomology and the differentiable singular cohomology are actually special isomorphic cases of sheaf cohomology. In particular, it has been also crystallized that the de Rham cohomology of a differential manifold depends only on the property of paracompactness of the underlying topological space. In turn, the paracompactness property, which is required in the definition of a differential manifold, can be also characterized cohomologically via the acyclic behavior of soft sheaves, like the sheaf of smooth functions. In other words, soft sheaves, namely sheaves whose sections over any closed subset can be extended to a global section, are acyclic over a paracompact topological space.
The re-interpretation and generalization of the standard de Rham cohomology theory on manifolds in sheaf-cohomological terms is physically significant, because it provides an intrinsic way to set up and solve differential equations expressing the dynamical variability of physical quantities. The concepts and technical tools of sheaf cohomology have been developed through the ground-breaking work of Grothendieck in geometry [
4,
5]. What should be initially kept in mind for physical applications is that the natural argument of a cohomology theory is a pair consisting of a topological space together with a sheaf of commutative algebras defined over it, rather than just a space.
It is instructive to include the basic definition characterizing the notion of a sheaf of sets on a topological space X, which also gives rise in a direct way to the notion of a sheaf of commutative algebras over X that we will employ in the sequel:
A presheaf
of sets on a topological space
X, consists of the following information:
- (I)
For every open set U of X, a set denoted by , and
- (II)
For every inclusion
of open sets of
X, a restriction morphism of sets in the opposite direction:
such that:
- (a)
= identity at for all open sets U of X.
- (b)
for all open sets . Usually, the following simplifying notation is used: .
A presheaf
of sets on a topological space
X is defined to be a sheaf if it satisfies the following two conditions, for every family
,
, of local open covers of
V, where
V open set in
X, such that
:
- (1)
Local identity axiom of sheaf:
Given with for all , then .
- (2)
Gluing axiom of sheaf:
Given
,
,
, such that:
for all
, then there exists a unique
, such that:
and
.
As a basic example, if denotes the presheaf that assigns to each open set the commutative algebra of all real-valued continuous functions on U, then is actually a sheaf. This is intuitively clear since the specification of a topology on X is solely used for the definition of the continuous functions on X. Thus, the continuity of each function can be determined locally. This means that continuity respects the operation of restriction to open sets and, moreover, that continuous functions can be amalgamated together in a unique manner, as is required for the satisfaction of the sheaf condition.
The realization that the natural argument of a cohomology theory is not only a space, but it is actually a pair consisting of a topological space together with a sheaf of commutative algebras localized over it, has given rise to the notion of a commutative locally -algebraized space, defined by means of a pair consisting of a topological space X and a sheaf of commutative -algebras on X, such that the restriction is a local commutative -algebra for any point . Regarding the possibility of extending consistently all of the standard local differential geometric constructions in the context of smooth manifolds to singular spaces, in terms of locally -algebraized spaces, where a suitable sheaf of commutative -algebras on X substitutes the smooth sheaf of -algebras , a full-grown theory has been recently developed, called Abstract Differential Geometry (ADG). This theory has shown that the standard differential-analytic tools of locally-Euclidean spaces and smooth manifolds leading to the formulation and solution of differential equations can be actually re-produced and generalized to non-smooth or singular topological spaces by means of sheaf cohomology. Equivalently, the suitability of a sheaf of commutative -algebras on an abstract topological space X for expressing the differential geometric mechanism in terms of these coefficients instead of the smooth ones is entirely determined only by the satisfaction of precise cohomological conditions pertaining to the characterization of the algebra sheaf . We note, in passing, that for the economy of symbols, we denote algebra sheaves by the same symbols as we used for the algebras before, since the difference is clear from the context.
The mathematical theory of ADG has been built rigorously by Mallios [
6,
7] (see also [
8]), based on critical prior work of Selesnick [
9]. The significance of ADG for physics has been also shown by an explicit reconstruction and generalization of the framework of the Maxwell and Yang–Mills gauge field theories in sheaf cohomological terms [
10,
11]; see also [
12,
13,
14]. An exposition of the basic didactics of ADG in relation to its physical applications has been presented by Raptis in [
15]. The basic method introduced for the generalization of the standard analytic tools of Classical Differential Geometry (CDG) consists of the following: Initially, a concept of CDG is suitable for the extension to a broader differential context (beyond the context of smooth manifolds) if it is liable to a process of sheaf-theoretic localization [
16]. In CDG, all of the differential geometric constructions require that the base space is a smooth manifold. The underlying reason is that the means of differentiation are lifted locally from the structure of a Euclidean space. In this way, the de Rham complex is fixed with respect to smooth coefficients, and all tensorial quantities are coordinatized in smooth terms. In ADG, the base space provides merely a topological basis of sheaf-theoretic localization, such that all of the pertinent differential geometric constructions can take place locally, whereas the latter are not subordinate to this topological basis, meaning that they are not dependent on any particular localization basis. Thus, the object of primary significance in ADG is not the base space itself, but the algebra sheaf of coefficients localized over it. The differentiation structure is built in the algebra sheaf of coefficients by means of the notion of a connection defined independently of any locally-Euclidean considerations. In this way, the associated de Rham complex can be satisfied by various possible algebra sheaves of coefficients modulo some well-defined cohomological conditions. We emphasize that the prominent role in the context of ADG is played by the algebra sheaf of coefficients, interpreted as a “functional coordinate arithmetic” [
14,
17] (see also [
18,
19,
20,
21,
22]), meaning that all geometric objects involved in the formalism are locally expressed in terms of its sections. In this way, an algebra sheaf of coefficients is not constrained ab initio to be a smooth one, restricting the geometric solution space within the spectrum of a smooth manifold. More generally, a suitable algebra sheaf of coefficients turns out to be an algebra sheaf of generalized functions, including distributions, defined by Rosinger in the context of solutions to non-linear partial differential equations [
23,
24].
Concerning general relativity, which is formulated using the CDG of smooth manifolds, the possibilities offered by ADG bear a remarkable physical significance. In particular, there arises the possibility of re-assessing the global problems of general relativity related to the existence of singularities, where the metric breaks down, from the perspective of appropriate generalized algebra sheaves of coefficients. In this manner, the validity of Einstein’s equations may be extended beyond differential manifolds, under the condition that the covariance properties of all tensorial physical quantities are maintained under these extensions, expressed in terms of the new sheaves of coefficients. From a physical viewpoint, this approach would allow one to obtain solutions in terms of distribution-like sheaves corresponding to non-punctual localization properties, which would nevertheless still satisfy the field equations. This clearly vindicates the following critical remark of Weyl [
25]: “While topology has succeeded fairly well in mastering continuity, we do not yet understand the inner meaning of the restriction to differential manifolds. Perhaps one day physics will be able to discard it”.
The possibility of obtaining extended admissible solution spaces in terms of generalized algebra sheaves of coefficients is based on the fact that the validity of the de Rham complex, in its sheaf-theoretic guise, is not restricted exclusively to the coordinatization of the tensorial physical quantities by smooth coefficients
, as is actually the case when the
-spectrum of the coefficients is a smooth manifold. Thus, we may consider distribution-like sheaves of coefficients satisfying the validity of the de Rham complex and, therefore, formulate and solve the field equations in terms of these distribution coefficients instead of the smooth ones. More precisely, this is the case if the following sequence of
-linear sheaf morphisms:
is a complex of
-vector space sheaves, identified as the sheaf-theoretic de Rham complex of
.
In this case, if the cohomological condition expressing the Poincaré Lemma,
is satisfied with respect to the algebra sheaf
and requiring that
is a soft algebra sheaf, viz. any section over any closed subset of
X can be extended to a global section, we obtain that the sequence:
is an exact sequence of
-vector space sheaves. Thus, the sheaf-theoretic de Rham complex of the algebra sheaf
constitutes an acyclic resolution of the constant sheaf
.
The physical interpretation of this fact is the following: First of all, the essential feature of the localization method, utilizing coefficients from algebra sheaves instead of global algebras, is that the sheaf-theoretic de Rham complex is actually an acyclic resolution of the constant sheaf of the reals coordinatizing the events. For instance, referring to the CDG of smooth manifolds, the de Rham complex, expressed in terms of local smooth coefficients and their differential forms of higher orders, provides such an acyclic resolution of the constant sheaf . What has been uncovered by ADG is that the smooth algebra sheaf is not unique in this respect. More concretely, any other soft algebra sheaf constituting an acyclic resolution of the constant sheaf is a viable source of coefficients for the coordinatization of the tensors, maintaining at the same time all of their covariance properties in terms of the new local coefficients. This crucial fact essentially questions the uniqueness of the role of local smooth coefficients for formulating the means of dynamical variability. In other words, it questions the unique role of smooth manifold geometric spectrums as domains of validity of the field equations.
The idea to address the problem of singularities from the perspective of ADG has been proposed already, for instance in [
11,
12]. More concretely, in particular relation to the issue of spacetime singularities, Mallios and Rosinger [
23,
24] have applied ADG using as an algebra sheaf of coefficients, a variety of the so-called “spacetime foam algebras”, and by Raptis [
26], building up on prior work by Mallios and Raptis [
27], using as a sheaf of coefficients “differential incidence algebras” defined over a locally-finite poset substitute of a continuous manifold.
Our present proposal constitutes a twist of perspective in comparison to these works, which is actually implemented by physical criteria of suitability going beyond the satisfaction of the cohomological conditions. Our quest is related to the possibility of using a particular type of a “spacetime foam algebra” as a kind of a distribution-like sheaf of coefficients, distinguished on physical grounds, for extending the domain of validity of Einstein’s field equations. For this purpose, from the whole variety of “spacetime foam algebras”, we distinguish only the “nowhere dense generalized function algebra” as bearing physical significance in relation to the field equations of general relativity. This is based on a physical criterion determining which properties should be characterized as intrinsic to the gravitational field and eventually deciding what should be generic with respect to its function or not. This physical criterion refers to the viable possibility of expressing the gravitational field sources via the instantiation of these generalized algebra sheaves of coefficients. Our rationale is based on the idea that in an intrinsically dynamically-variable theory, like general relativity, it should be the pertinent physical conditions or the sources of the field themselves that determine the type of these extensions as solutions to the field equations.
4. Coping with Spacetime Singularities: Conceptual and Technical Aspects
In the classical differential geometric formulation of general relativity, spacetime is represented as a connected, paracompact and Hausdorff four-dimensional
manifold
X, endowed with a pseudo-Riemannian metric of the Lorentzian signature, which is obtained as a solution of Einstein’s field equations. A spacetime manifold is considered to be without singularities if the coefficients of the metric tensor field are at least of class
and
X is geodesically complete with respect to the metric, meaning that all timelike geodesic curves can be extended to arbitrary length [
28,
29]. Consequently, a spacetime manifold is considered to be singular if there exist incomplete geodesic curves, or equivalently finite affine length geodesics that cannot be extended. A spacetime singularity delimits a locus where the behavior of the metric tensor coefficients become ill-defined with respect to the smooth characterization of the manifold. Usually, the singular locus is identified as a locus where the spacetime curvature blows up. We note that the localization at a spacetime point-event is meaningful if the metric coefficients are smooth, or at least of class
in a neighborhood of this point.
The usual way to cope with a spacetime singularity is to consider it as a singular spacetime boundary rather than a locus within spacetime. For instance, a spacetime boundary may be defined in terms of a set of incomplete curves
S. This takes place by the imposition of an appropriate equivalence relation ∼ on the set
S, such that the quotient set
is interpreted as the singular boundary of
X. The criterion of equivalence is determined by the choice of those equivalence classes, which are forced to play the role of ideal points in the extension of
X by
. There have been proposed various possible choices, for example Geroch’s “g-boundary” or Schmidt’s “b-boundary”, but it is always assumed that
X is topologically dense in
[
30,
31]. Following this approach, Heller and Sasin have shown that Einstein’s field equations can be formulated in the extension of
X by
, that is on
defined as an “Einstein structured space” [
32]. Actually, this is the Gelfand spectrum of a sheaf of Einstein algebras, which constitutes the sheaf-theoretic localization of an Einstein algebra, a notion proposed initially by Geroch in his attempt to re-formulate general relativity in algebraic terms without invoking directly a spacetime manifold background [
1]. In particular, it has been proven that the closed Friedmann world model and the Schwarzschild solution, combined with Schmidt’s “b-boundary” construction, fit nicely in the sheaf-theoretic context of an “Einstein structured space”. In turn, this has been a first indication that the validity of Einstein’s equations may be extended to bigger domains incorporating singular loci, which are not smooth manifolds anymore. It has been also pointed out that some sorts of singularities can also appear when there exists a transition to the quantum gravity regime. More concretely, the smooth manifold structure of spacetime can break down, and the possible validity of Einstein’s equations should be sought for in further extended and generalized non-smooth spectrums of appropriate sheaves of algebras, where the singularities are not necessarily forced to some type of spacetime boundary.
From a broader conceptual perspective, the issue of singularities in general relativity as impossibilities of extending smooth metric solutions of Einstein’s equations necessitates the coordinatization of all of the tensorial quantities by distributional coefficients effecting a type of topological coarse-graining over singular loci and, thus, localizing the point-event stratum in their terms. Under the proviso that these distributional coefficients form algebra sheaves fulfilling all of the required cohomological conditions, the means of extending local distributional solutions generalizes the standard method of extending timelike geodesic curves in a smooth manifold. The physical significance of this generalization is that the domain of validity of the field equations can be extended beyond the notion of a smooth manifold. Not only this, but additionally, these distinguishable extensions may be associated intrinsically with the gravitational field, under the constraint that sources of the field itself giving rise to singularities can be expressed topologically in the terms of distribution-like algebra sheaves.
In this state of affairs, the smoothness assumption can be retained, at best, only locally and certainly far from singular loci. Mathematically, there should exist an embedding of the algebra sheaf of smooth functions into a distribution-like algebra sheaf of coefficients qualified as a solution of the extended field equations. An illuminating way to think of the proposed approach in non-technical terms is that coping efficiently with singularities requires a process of folding out of the smooth point-event manifold background. This viewpoint has been emphasized by von Müller [
33], according to whom the process of folding out into a “statu-nascendi” level should be considered in the context of a whole new categorical apparatus qualifying its intrinsic characteristics in contradistinction to the event stratum. In this manner, we suggest that the existence of a distribution-like sheaf of coefficients as a solution of the field equations within an appropriately-extended domain characterized by some generic gravitational criterion paves the way for understanding the precise nature of this folding out of the smooth point-event stratum.
The possibility of extending the formulation of Einstein’s equations in the case of non-smooth spectrums using the sheaf-theoretic technique of localization in the context of ADG is of major significance. We note that non-smooth spectrums of algebra sheaves do not require the consideration of singularities as ideal points on the boundary of a smooth manifold. In other words, singular loci are allowed to be located, according to specific topological criteria, within a manifold. Of course, a natural requirement should be that the exclusion of singular loci would recast Einstein’s equation in the familiar form in terms of smooth coefficients. However, clearly in the case that Einstein’s equations become meaningfully extended over singular loci, then the coefficients of the metric and curvature tensors cannot be smooth any more. Therefore, from a smooth perspective, a singularity functions as an obstruction to the extension of a local solution to the field equations expressed in terms of smooth coefficients. Thus, more precisely, a singular locus plays the role of a cohomological obstruction to the extendibility of a local smooth solution. This criterion incorporates and generalizes sheaf-cohomologically the initial definition of singular behavior in terms of non-extendibility of geodesics. Essentially, the reason is that the notion of extendibility of local solutions is of a sheaf-theoretic nature, recalling for instance the well-known procedure of analytic continuation.
There are two important physical consequences emanating from the possibility of formulating Einstein’s equations in terms of generalized non-smooth sheaves of coefficients. The first is related to the natural question concerning the criterion of depicting a particular sheaf of algebras for this purpose. The second is related to a possible re-evaluation of the status of the energy-momentum source term in Einstein’s equations, which currently is not implemented by any process of geometrization.
Regarding the first, the required physical condition is the following: Since the formulation of Einstein’s equations can be extended over singular loci, it should precisely be the nature and specification of these singular loci that would determine the appropriate sheaf of coefficients, such that a solution can be expressed eventually in terms of these coefficients. In the non-singular case, we know already that a solution can be expressed in terms of smooth coefficients. In other words, we already know that if no singularity is present, the spacetime metric, obtained as a particular solution of the vacuum Einstein equations, for example, is always expressible in terms of smooth coefficients, i.e., in terms of the sheaf of algebras . Hence, we expect that in the presence of a particular type of a singular locus over which Einstein’s equations hold in terms of a distribution-like sheaf of coefficients, there exists a metric solution expressed in terms of these coefficients. Not only this, but additionally, since the knowledge of the metric solution is completely expressible in terms of these coefficients, considered as unknowns when plugged into the equations, the specification of a singular locus should force a corresponding algebra sheaf as the solution. In other words, the nature of a singular locus should determine the differentiability properties of a metric solution in the case that Einstein’s equations can be extended over this locus. As we stressed previously, the physical association of singular loci with sources of the gravitational field itself, giving rise to distinguishable extensions of the standard smooth manifold spacetime model of general relativity, implies that sources can be expressed topologically after all, if solutions of the field equations are expressed in terms of appropriate distribution-like algebra sheaves.
In this context, the physical significance of ADG is that it determines rigorously the criteria that these algebra sheaves of coefficients have to satisfy, such that Einstein’s equations can be satisfied over various sorts of singular loci, expressed in terms of these coefficients. Not surprisingly, these criteria are of a cohomological nature. Essentially, they determine viable algebra sheaves of coefficients by the requirement that they are soft, and thus acyclic, such that the validity of the de Rham complex remains intact. In turn, the basic idea is that the Poincaré lemma should remain in force, viz. closed differential forms expressed in these generalized coefficients should be locally exact as in the smooth case, so that the differential geometric mechanism can be extended over singularities without breaking down. We will present a general form of these algebra sheaves consisting of distribution-like coefficients in the sequel. According to Clarke, the answer to many of the problems related to singularities “involve detailed considerations of distributional solutions to Einstein’s equations, leading into an area that is only starting to be explored …” [
28]. We propose that the extension of the validity of Einstein’s equations over singular loci in terms of appropriate sheaves of algebras, which are generally non-smooth, sheds new light on the problem of singular behavior in general relativity.
Regarding the second physical consequence, it is instructive to remind that the energy-momentum source term in the smooth formulation of Einstein’s equations is not of any geometric nature. The energy-momentum tensor attributes the source of curvature entirely to matter (including the cosmological dark energy), as it does not incorporate the stress-energy associated with the gravitational field itself. There is an underlying assumption that spacetime is somehow empty unless it is filled in by matter, expressed in terms of the smooth coefficients of the energy-momentum tensor. This is the reason that when the energy-momentum part is zero, then the equations are called vacuum equations. Now, the validity of Einstein’s equations over singular domains in terms of generalized non-smooth algebra sheaves casts serious doubts on this assumption. Namely, the form of Einstein’s equations with the vanishing non-geometric second part may turn out to be the fundamental form of these equations. The reason is that sources of the gravitational field itself might be implemented in terms of non-smooth algebra sheaves, and thus, what is called a vacuum is not empty at all, precisely because it engulfs these sources. This idea is not actually as controversial as it sounds, if we take seriously into account that all classical experimental tests of general relativity involve a vanishing energy-momentum tensor, and thus, what they really verify is the equation
. This issue has been also pointed out and argued for extensively, from a non sheaf-theoretic point of view, by Vishwakarma [
34], who conducted a careful analysis based on the observational tests of the theory. In the sequel, we will discuss this issue in more detail from a geometrodynamical perspective in light of the particular form of distribution-like algebra sheaves.
5. Spacetime Extensions in Terms of Singularity-Free Distributional Algebra Sheaves
It is physically reasonable to expect that an admissible commutative algebra sheaf of coefficients in terms of which Einstein’s equations may be extended over a singular locus should be distribution-like. For example, we may think of a matter distribution confined to a submanifold of spacetime whose density is integrable over this submanifold. In the context of a linear field theory, this should be naturally modeled in terms of a linear distribution. Unfortunately, this is not possible in the context of general relativity, which is a non-linear theory. In other words, Schwarz’s linear distributions are not suitable candidates for expressing the information of singular loci.
The unsuitability of linear distributions rests on the fact that the space
they form is only a linear space, but it is not an algebra. This is characterized as the “Schwarz impossibility” and may be formulated as follows: There is no symmetric bilinear morphism:
so that
is the usual point-wise product of continuous functions, when
. Equivalently,
is not closed under any multiplication that extends the usual multiplication of continuous functions, where
V is an open subset
X. Since all of the involved arguments are of a local character, without loss of generality, we may simply consider
V as an open subset of
.
A physically natural way to bypass “Schwarz impossibility” is to assume the existence of an embedding morphism
, which embeds the vector space of distributions
as a vector subspace in
, where
is the quotient algebra:
and
is a subalgebra in
, for some index set Λ, whereas
is an ideal in
. This approach was initiated by Rosinger [
35,
36] and developed further in [
37,
38,
39,
40].
We will restrict ourselves to a certain subclass of this type of algebras, namely the unital, associative and commutative algebras of generalized functions, whose suitably-defined ideals can engulf algebraically the information of singular loci. These algebras, introduced by Rosinger [
36], have been formed in such a way as to express generalized solutions of non-linear partial differential equations. We may describe the generation of these algebras locally as follows:
Let
be an open set and
be a right-directed partial order on some specified index set Λ. That is, for all
λ,
μ∈Λ, there exists
ν∈Λ, such that
λ,
μ≤
ν. With respect to the usual componentwise operations,
is a unital and commutative algebra over the reals. We define the following ideal
in
, whose physical meaning will be described in the sequel:
In the above definition, we think of Γ as a singular locus in , characterized as a closed and nowhere dense subset relative to the open set , such that its complement in V is dense. The unital and commutative algebra contains smooth functions indexed by the set Λ and defined over V, to be thought of as diagrams or sequences of Λ-indexed smooth functions. The requirement of the right-directed partial order on the specified index set Λ, which is denoted by , is technically necessary in order that the above set forms actually an ideal in . Now, the ideal in includes all of these sequences of smooth functions that vanish asymptotically outside the singular locus Γ together with all of their partial derivatives. Therefore, intuitively speaking, the ideal of the form incorporates all of these sequences of smooth functions indexed by Λ whose support covers the singular locus Γ, whereas they vanish outside it. In this manner, the information of the singular locus Γ is encoded in the ideal in . Hence, the quotient commutative algebra is an algebra of residues of sequences of smooth functions modulo the singular information ideal .
A natural question in the above context refers to the requirement that the complement
of the singular locus Γ in
V should be dense. The necessity of this requirement can be understood by the fact that we wish to obtain an embedding
ι of the algebra of smooth functions
into the algebra of generalized functions
:
such that:
where
is the diagonal morphism with respect to Λ, defined for an open set
V as follows:
Hence, for every smooth function
ϕ in
, the diagonal image
of
ϕ in
is a sequence of smooth functions all identical to
ϕ, indexed by Λ. The embedding
ι is feasible according to the above, if and only if the ideal
satisfies the off diagonality condition:
Therefore, it remains to show that if the complement
of the singular locus Γ in
V is dense, according to the specification in (
6), then the ideal
actually satisfies the above off diagonality condition. Therefore, we suppose that
is dense in
V and consider a smooth function
χ in
. If
belongs to the ideal
, then the asymptotic vanishing condition in (
6) implies that
in
, and therefore, we must have
in
V because
is dense in
V by hypothesis. Thus, it follows that the ideal
satisfies the off diagonality condition (
9), as required.
Conclusively, there exists a canonical injective homomorphism of commutative algebras, or equivalently, an embedding
ι of the algebra of smooth functions
into the algebra of generalized functions
:
Furthermore, in view of (
6), it follows immediately that the partial differential operators:
satisfy the inclusion:
Thus, the standard partial derivative operators on
extend to
:
We conclude that the embedding of commutative algebras (
10) extends to an embedding of differential algebras. Therefore, the following diagram commutes:
We emphasize that the embedding (
10) preserves not only the algebraic structure of
, but also its differential structure. The off diagonality condition (
9) implies also the existence of an injective, linear morphism:
Therefore, the differential algebra
contains the space of distributions as a linear subspace; see [
38] (pp. 234–244), where those algebras that admit linear embeddings of distributions are characterized in terms of such off diagonality conditions. However, in contradistinction with (
10), the embedding (
13) does not commute with partial derivatives, and thus, the partial derivatives on
do not, in general, coincide with distributional derivatives, when restricted to
.
Finally, it is crucial to observe that a subset of a topological space is closed and nowhere dense if and only if it satisfies this condition locally. This is the key idea used to prove that the algebras of generalized functions
form actually sheaves of commutative algebras, which additionally, are soft and flasque or flabby [
23,
24]. Thus, they are characterized as cohomologically-appropriate sheaves of coefficients according to ADG. More precisely, the distribution-like soft algebra sheaves of the form
constitute an acyclic resolution of the constant sheaf of the reals coordinatizing the events. Thus, we conclude that the de Rham complex can be rigorously expressed in terms of these coefficients instead of the smooth ones, and consequently, Einstein’s equations can be formulated with respect to coefficients from the algebra sheaf
instead of the smooth ones from
. Consequently, the validity of Einstein’s equations can be extended over singular loci in a covariant manner by utilizing coefficients from the sheaf
for expressing all involved differential geometric tensorial quantities. Reciprocally, according to the intended physical interpretation of these algebra sheaves, pertaining to expressing sources of the gravitational field in terms of closed and nowhere dense subsets, the presence of a singular locus forces an algebra sheaf of the form
as coefficients with respect to which Einstein’s equations retain their validity over this locus and do not break down, like in the case of insisting to use indiscriminately-smooth coefficients.
For the sake of completeness, it is instructive to remind that the softness property of the sheaves of the form means that any section over any closed subset can be extended to a global section. Thus, these types of sheaves characterize cohomologically the topological property of paracompactness by means of acyclicity. Equivalently, soft sheaves are acyclic over a paracompact topological space. Moreover, sheaves of the form are not only soft, but they are flasque or flabby, as well, which is a local property. This means that the restriction morphism of sections in the sheaf definition is an epimorphism. Hence, in this case, we can always extend any local section by zero to obtain a global section of .
We may recapitulate by pointing out that the first basic idea involved in the construction of distribution-like algebra sheaves of coefficients, in their role to coordinatize solutions of non-linear partial differential equations, is to model a singular locus Γ in as a closed and nowhere dense subset relative to an open set , such that its complement in V is dense. The second basic idea is to express such a closed and nowhere dense singular locus as an ideal in an algebra sheaf constructed as an extension of the smooth one over a partially-ordered set. In this manner, the ideal expressing algebraically a singular locus contains diagrams of locally-defined smooth functions indexed by Λ whose support covers the singular locus Γ, whereas they vanish outside it. Then, it can be shown that the quotient commutative algebra sheaf is an algebra sheaf of residues of diagrams of smooth functions modulo the closed nowhere dense singular ideal .
It is instructive to emphasize that the algebra of global sections of the sheaf contains the space of Schwarz distributions only as a linear subspace and not as a commutative subalgebra. For example, Dirac’s delta, considered as a distribution, is represented in terms of a generalized function whose pertinent closed and nowhere dense set is an one-point set. It is well known that the square of the delta distribution is not a distribution itself, since the operation of point-wise multiplication of distributions is not well-defined in . Notwithstanding this fact, the representative generalized function may be unproblematically squared providing a legitimate generalized function without being a linear distribution itself. Clearly, by the rules of the construction of these commutative algebras of generalized functions, arbitrary nonlinear continuous operations may be applied to a generalized function giving another generalized function in the same algebra. In passing, it is also worth pointing out that the linear space of Schwarz distributions does not give rise to a flasque vector sheaf in contradistinction to the case of the embedding sheaf , a property that is crucial for the global extendibility of all standard local differential geometric constructions.
In the sequel, we are going to propose a concrete class of closed and nowhere dense sets modeling the boundaries of singular loci and forming a topological link in 3D space. Conceptually, this essentially means that the semantics of folding out a local smooth event stratum into a singular domain may be associated with the formation of some topological link configuration and its concomitant algebraic expression in terms of an algebra sheaf of the type . At the final stage, we have to examine if this algebra sheaf satisfies the cohomological conditions necessary for expressing the differential geometric mechanism of general relativity in these terms instead of the globally-smooth ones. This turns out to be actually the case, and therefore, algebra sheaves of the type can be used legitimately to express the metric solution of Einstein’s field equations extended now over singularities.
The important consequence is that we can retain not only the validity, but not the form and covariance property of Einstein’s equations even over singular loci. The reason is that all physical quantities can be still transformed according to a tensor law for any arbitrary admissible coordinate transformation. The difference in comparison to the smooth case is that the coordinates are allowed to be non-standard or non-smooth, while at the same time, all of the machinery of differential geometry can be applied with respect to them. In particular, while the coefficients of the tensorial physical quantities are non-smooth, all of the usual differential-geometric constructions can be carried out as in the smooth case. The only price to be paid for this generalization is the rejection of the fixed absolute smooth manifold background of the theory. We consider this fact as physically non-disturbing, since the essence of general relativity is in the covariant formulation and validity of Einstein’s equations and not on the existence of a smooth background manifold. In particular, what we gain from such a generalization is not only that Einstein’s equations can be extended covariantly over singular loci, but also that the solution of these equations in terms of coefficients from a sheaf of the form are free of singularities.
6. Topological Links in Geometrodynamics
According to the paradigm of geometrodynamics [
41], we may foliate a spacetime manifold
X into three-dimensional spacelike leaves
by utilizing an one-parameter family of embeddings
, such that
. In the geometrodynamical formulation, the three-dimensional Riemannian manifold
is thought of as dynamically evolving, where the corresponding metric at time
t,
, is derived by pulling back the spacetime metric
g via
. It is implicitly assumed that all three-dimensional spacelike leaves
are mutually disjoint, such that the Lorentzian manifold
represents
X, where the leaves of the considered foliation correspond to the constant time hypersurfaces.
The geometrodynamical picture is instructive for our purposes because it shows that active gravitational mass may emerge from purely topological considerations taking into account the constraints imposed by Einstein’s field equations in the vacuum [
42]. From a physical perspective, this may be interpreted in a novel way according to Wheeler’s insight referring to “mass without mass” [
43,
44] as follows: Localized configurations of topologically-singular loci in open sets of a spacetime manifold restricted to closed nowhere dense subsets amount to active gravitational mass/energy in their complementary open dense subsets. In particular, if we consider that the Lorentzian manifold
represents
X, the singular loci may be localized within the three-dimensional manifold Σ. In this context, if Σ has a non-trivial topology, Gannon’s theorem [
45] implies that spacetime is geodesically incomplete and, thus, singular. The simplest way to implement a non-trivial topology on Σ is via the hypothesis of non-simple connectivity. More precisely, the existence of singular loci in Σ, localized in closed nowhere dense subsets makes Σ a multiple-connected topological space and, thus, topologically different from
. We may recapitulate our conclusion up to now by asserting that the existence of singular loci in closed nowhere dense subsets of Σ, making it a multiply-connected topological space, implies active gravitational mass/energy in the complementary open dense subsets. Moreover, according to the “positive mass theorem” considered in the vacuum case, this gravitational mass/energy is non-zero and strictly positive. In passing, we would like to stress that Gannon’s theorem should be conceived of as a significant generalization of the Penrose–Hawking singularity theorems [
29], in the sense of replacing the usual geometric hypothesis of closed trapped surfaces in Σ by the more general applicable topological hypothesis of the non-simple connectivity of Σ.
In the same vein of ideas, we may also consider the system of Einstein–Maxwell equations without sources for the Maxwell field and, in this way, address from our perspective the alternative Wheeler’s insight referring to “charge without charge” [
43,
44]. This has been originally tied to the assumption that Σ is orientable and bears the standard wormhole topology, that is homotopically equivalent to
, such that the magnetic flux lines thread through the wormhole. In this case, the homology class of all two-spheres containing both of the wormhole mouths has zero charge, whereas the two individual wormhole mouths may be considered as having equal and opposite charges. In this context, a wormhole may be thought of in terms of a one-dimensional homology class in spacetime. From the general results of low-dimensional geometric topology [
46], we know that every homology class of a four-dimensional spacetime can be represented by an embedded submanifold. Using the geometrodynamic foliation, we may restrict this representation to Σ. In this manner, we can instantiate a higher-order wormhole solution, for example by considering an appropriate two-dimensional homology class.
We are going to outline a general method of generating these types of solutions guided by the form of the algebra sheaves incorporating gravitational properties defined on dense open sets of X and by restriction to dense open sets of Σ. For this purpose, we may consider a singular locus with boundary in or in its compactification , which is excised from or . We consider a singular locus as a singular disk cut off from , which may be visualized in terms of a cone whose apex is at infinity and whose base lies at the boundary of the singular locus. A singular disk of this form excised from gives rise to a two-dimensional relative homology class of , which may be interpreted according to the above as a two-dimensional embedded compact submanifold. The circular boundary of this singular disk is a closed and nowhere dense subset with respect to an open set of . Analogously, we may consider the excision of more than one singular disks from , such that their circular boundaries collectively define a closed and nowhere dense subset of an open set of . We propose to think of these circular singular boundaries as giving rise to topological links.
The notion of a topological link is based on the underlying idea of connectivity among a collection of topological circles, called simply loops [
47]. We consider that a loop is a tame closed curve. The property of tameness means that a closed curve can be deformed continuously and without self-intersections into a polygonal one, that is a closed curve formed by a finite collection of straight-line segments. Given this qualification, a loop is characterized by the following properties: First, it is a one-dimensional object. Second, it is bounded, meaning that it is contained in some sphere of sufficiently large radius. Third, a single cut at a point cannot separate a loop into two pieces, whereas any set of two cuts at two different points does separate a loop into two pieces. Moreover, a loop is called knotted if it cannot be continuously deformed into a circle without self-intersection. We only consider unknotted tame closed curves. A topological
N-link is a collection of
N loops, where
N is a natural number. Regarding the connectivity of a collection of N loops, the crucial property is the property of the splittability of the corresponding
N-link. We say that a topological
N-link is splittable if it can be deformed continuously, such that part of the link lies within
B and the rest of the link lies within
C, where
B,
C denote mutually-exclusive solid spheres (balls). Intuitively, the property of splittability of an
N-link means that the link can come at least partly apart without cutting. Complete splittability means that the link can come completely apart without cutting. On the other side, non-splittability means that not even one of the involved loops, or any pair of them, or any combination of them, can be separated from the rest without cutting.
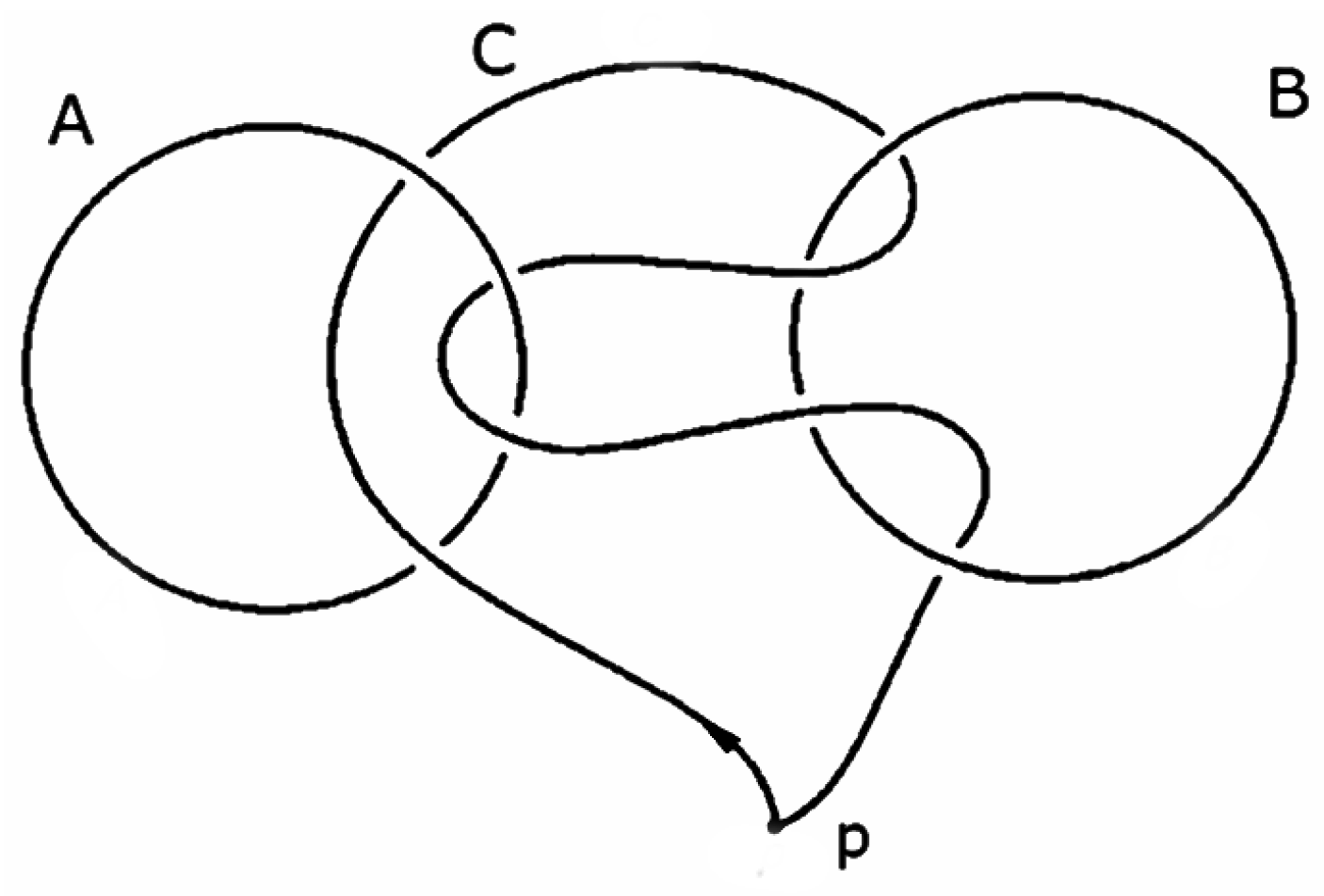
According to our hypothesis, a collection of circular singular boundaries defining a closed and nowhere dense subset of an open set of gives rise to a topological link in . We may now replace the loop components of such a topological link by open non-intersecting tubular neighborhoods such that the complement of the link in can be given by the structure of a three-dimensional compact and oriented manifold with a boundary. Clearly, this space is homologically equivalent to the original one since it is just its deformation retracted. Next, we may consider an ordering of the loops constituting the link, or equivalently, an ordering of their tubular neighborhoods . Then, if we take , , together with their ordering, we define the relative homology class that is represented by the compact oriented embedded submanifold whose two boundary components lie on the total boundary, that is the first one in and the second in . The orientation is defined as being negative on the first boundary component and positive on the second, so that we have a path from to in this case.
7. The Borromean Rings as a Universal Nowhere Dense Singular Link
According to the formalism of geometrodynamics, we consider the Lorentzian manifold as a representative of X, where the singularities are localized within the three-dimensional manifold Σ. We remind that, according to Gannon’s theorem, if Σ is multiple-connected as a topological space, then spacetime is geodesically incomplete. According to our previous analysis, a collection of circular singular boundaries defining a closed and nowhere dense subset of an open set of gives rise to a topological link in . Moreover, this implies the existence of active gravitational mass/energy in the complementary open dense subsets, which is non-zero and strictly positive.
In this context, it is important to examine if there exists a universal way via which we can obtain the three-dimensional manifold Σ by the information incorporated in a topological link in representing the singular boundaries, forming collectively a closed and nowhere dense subset. This sheds more light on the role of the algebra sheaves utilized to express gravitational properties defined on dense open sets of X and by restriction to dense open sets of Σ and is guiding in our quest of exploring generalized wormhole-types of solutions based on topological links and their associated homology classes.
It turns out that a universal way to obtain Σ by using a topological link in
representing the singular boundaries, according to the above, actually exists and is based on the notion of a universal topological link. In view of the type of solutions we are interested in, such a universal link is defined by the Borromean rings. In particular, using methods of geometric topology, it can be shown that any compact oriented three-dimensional manifold Σ without boundary can be obtained as the branched covering space of the three-sphere
with the branch set the Borromean rings [
48]. In this manner, the Borromean rings constitute a universal topological link.
The notion of a branched covering space is a generalization of the standard notion of a covering space, characterized as a local homeomorphism bearing the unique path lifting and homotopy lifting property [
49]. More precisely, a branched covering space of the three-sphere
is considered as a map from Σ to
such that this map is a covering space after we delete or exclude a locus of points, called the branched locus. The universality property says that Σ can be obtained in this way if the branched locus is formed by the Borromean rings, considered as a closed and nowhere dense set with respect to an open set in
in our setting. In a well-defined sense, this branched covering space provides the geometric representation of an algebra sheaf of the form
restricted to the three spatial dimensions, where the closed and nowhere dense subset formed by the Borromean rings is localized. We may extend this closed and nowhere dense subset to four dimensions by considering a timelike axis perpendicular to the Borromean rings, which plays the role of a three-fold symmetry axis of rotation.
The Borromean rings consist of three rings localized in , which are linked together in such a way that each of the rings lies completely over one of the other two, and completely under the other, as is shown in the pictures below:
This particular type of topological linking displayed by the Borromean rings is called the Borromean link and is characterized by the following distinguishing property: if any one of the rings is removed from the Borromean link, the remaining two come completely apart. It is important to emphasize that the rings should be modeled in terms of unknotted tame closed curves and not as perfectly circular geometric circles. The adjective topological means that they can be deformed continuously under the constraint that the particular type of linkage forming the Borromean configuration is preserved.
From the viewpoint of the theory of topological links, the Borromean link constitutes an interlocking family of three loops, such that if any one of them is cut at a point and removed, then the remaining two loops become completely unlinked [
47,
49,
50,
51,
52]. In more precise terms, the Borromean link is characterized topologically by the property of splittability as follows: The Borromean link is a non-splittable three-link (because it consists of three loops), such that every two-sub-link of this three-link is completely splittable. It is clear that it is a non-splittable three-link because not even one of the three loops, or any pair of them, can be separated from the rest without cutting. A two-sub-link is simply any sub-collection of two loops obtained by erasing the loop that does not belong to this sub-collection. Since the Borromean link is characterized by the property that if we erase any one of the three interlocking loops, then the remaining two loops become unlinked, it is clear that every two-sub-link of the non-splittable three-link is completely splittable.
![Universe 02 00017 i003]()
In our context, we conclude that if a triad of circular singular boundaries defining a closed and nowhere dense subset of an open set of
are connected in the form of the Borromean topological link, then Σ as a compact oriented three-dimensional manifold can be obtained as the branched covering space of the three-sphere
with the branch set these Borromean-linked boundaries. Based on these findings, we would like to explore their semantics in relation to the instantiation of a higher-order wormhole solution. For this purpose, we remind that the standard wormhole solution is thought of in terms of a one-dimensional homology class in a space homotopically equivalent to
. In our framework, we do not need to impose a particular topology on Σ ab initio, since it can now be derived universally as the branched covering space of
over the branch nowhere dense subset of singular boundaries forming a Borromean link. The fact that the Borromean link is a non-splittable three-link, such that every two-sub-link of this three-link is completely splittable, is characterized in homology theory by a non-vanishing triple Massey product, where all pairwise intersection products of one-dimensional homology classes vanish, reflecting the fact that the components of the Borromean link are not pairwise linked. If we denote the components of the Borromean link
by
, the triple Massey product [
49] is expressed as a two-dimensional cohomology class in the dense complement of
in
, that is it defines a non-trivial class in
.
8. Conclusions
The main purpose of this communication, one hundred years after Einstein’s formulation of the general theory of relativity, has been an invitation to re-think the validity domain of the field equations. The primary motivations emanate from three distinct sources: The first comes from Clarke’s assertion concerning the problem of singularities, according to which, the answers “involve detailed considerations of distributional solutions to Einstein’s equations, leading into an area that is only starting to be explored …”. The second comes from Weyl’s critical remark regarding the role of a background differential manifold, according to which, “while topology has succeeded fairly well in mastering continuity, we do not yet understand the inner meaning of the restriction to differential manifolds. Perhaps one day physics will be able to discard it”. The third comes from Wheeler’s ideas regarding the notions of “mass without mass” and “charge without charge” in the vacuum, which can be given a more precise mathematical formulation in topological terms.
The sheaf-theoretic re-formulation of the usual differential geometric framework of smooth manifolds points to the conclusion that there exist distinguishable extensions of the standard smooth manifold spacetime model of general relativity, which are utilized by appropriate extensions of the sheaf of coefficients parameterizing all tensorial physical quantities of the theory. The criteria of the suitability of these extensions are determined by sheaf-cohomological means and maintain the standard covariance properties of the theory in domains, including singular loci. We have presented and discussed in detail a concrete distribution-like sheaf of coefficients incorporating singularities in closed and nowhere dense subsets of an open set of a four-dimensional spacetime. An instructive way to think of these generalized algebra sheaves of coefficients refers to the role of a singularity as an obstruction to the existence of a solution to the field equations, expressed in terms of smooth coefficients. Thus, more generally, a singular locus may be thought of as a cohomological obstruction to the extendibility of a local smooth solution. This criterion incorporates and generalizes sheaf-cohomologically the initial definition of singular behavior in terms of the non-extendibility of geodesics. Essentially, the reason is that the notion of the extendibility of some local solution is of a sheaf-theoretic nature.
At a further stage involving the formalism of geometrodynamics, the existence of singular loci in closed and nowhere dense subsets of a spatial hypersurface, making it a multiply-connected topological space, implies active gravitational mass/energy in the complementary open dense subsets. Moreover, according to the “positive mass theorem” considered in the vacuum case, this gravitational mass/energy is non-zero and strictly positive. We show that it is enough for this purpose to consider singular boundaries forming closed and nowhere dense subsets and forcing a multiple-connected topology, which in turn implies that spacetime is geodesically incomplete. In view of expressing generalized wormhole solutions in this context, we propose that closed singular boundaries may form topological links. In this manner, using the results of geometric topology, we point out that the Borromean topological link is characterized as a universal link. Since this link is characterized cohomologically by a higher order invariant, it may be associated with a generalized wormhole model, which reinforces Wheeler’s ideas in geometrodynamics.
Finally, we express the hope that the proposed approach paves the way for a further technical and semantical refinement of the following two of Einstein’s fundamental insights in building up general relativity, which have not been addressed in satisfactory completeness up to the present:
“Under the influence of the ideas of Faraday and Maxwell the notion developed that the whole of physical reality could perhaps be represented as a field whose components depend on four space-time parameters. If the laws of this field are in general covariant, that is, are not dependent on a particular choice of coordinate system, then the introduction of an independent (absolute) space is no longer necessary. That which constitutes the spatial character of reality is then simply the four-dimensionality of the field. There is then no “empty” space, that is, there is no space without a field.”
“A field theory is not yet completely determined by the system of field equations. Should one admit the appearance of singularities? … It is my opinion that singularities must be excluded. It does not seem reasonable to me to introduce into a continuum theory points (or lines etc.) for which the field equations do not hold …”
In a nutshell, regarding the first, the utilization of distribution-like sheaves of coefficients extending the smooth one over singularities, and thus, extending the domain of validity of the field equations beyond globally-smooth manifolds, shows in agreement with geometrodynamics that active gravitational mass/energy may emerge from purely topological considerations taking into account the constraints imposed by the field equations in the vacuum. These topological considerations pertain to the modeling of singularities in terms of closed and nowhere dense sets, such that their complements who bear the induced active gravitational mass/energy are open and dense. In this manner, the vacuum can be legitimately considered as a structural quality of the field itself. Regarding the second, it is indeed unreasonable to consider singular loci in a continuum theory, where the field equations do not hold. The existence of distribution-like sheaves of coefficients provides precisely the means to bypass this problem by coordinatizing all of the tensorial quantities in their terms, extending the smooth ones and, therefore, extending the domain of validity of the field equations.