Asteroseismology of Compact Stars
Abstract
:1. Introduction
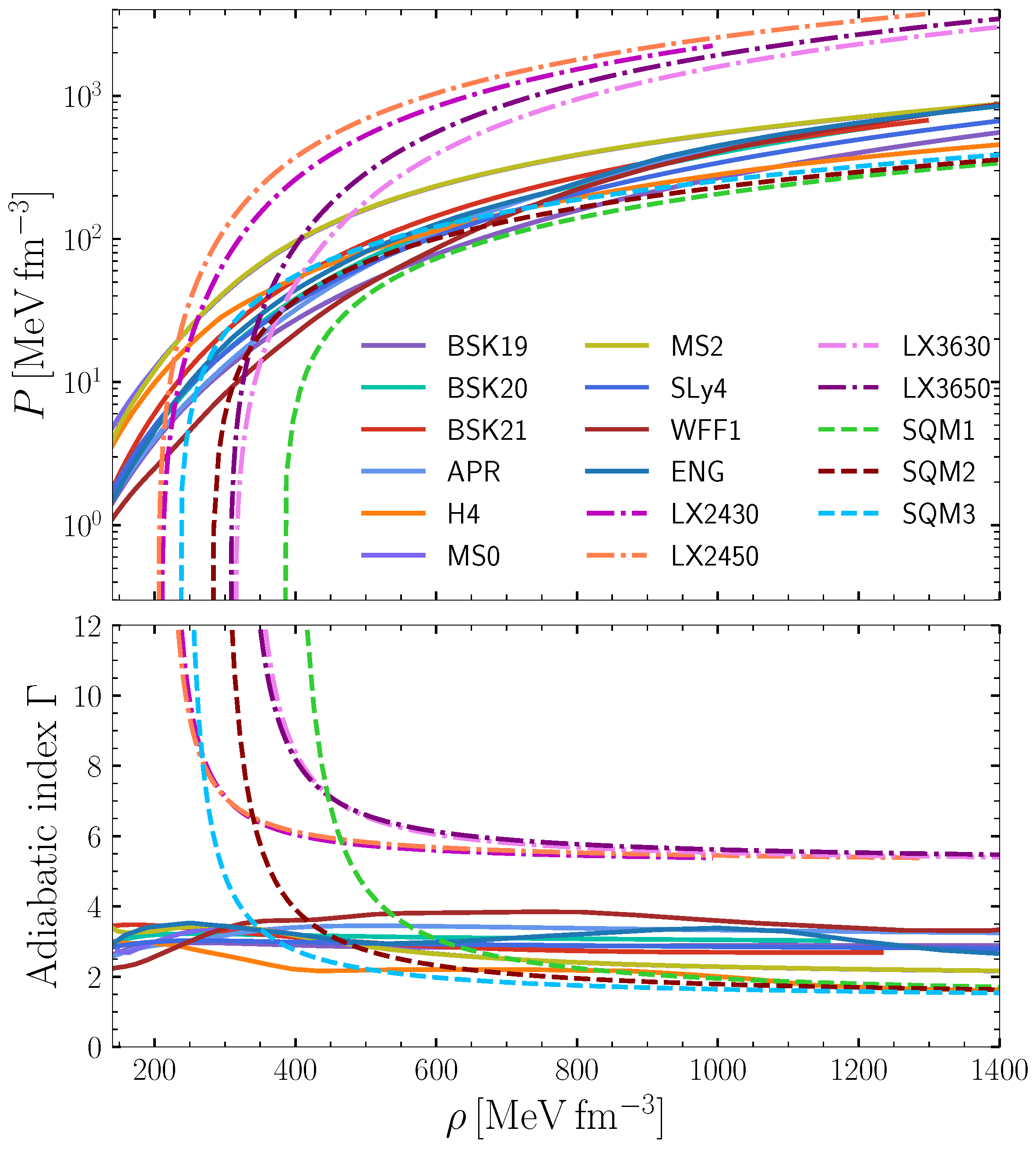
2. Equation of State of Compact Stars
2.1. Neutron Star
2.2. Quark Star
2.3. Strangeon Star
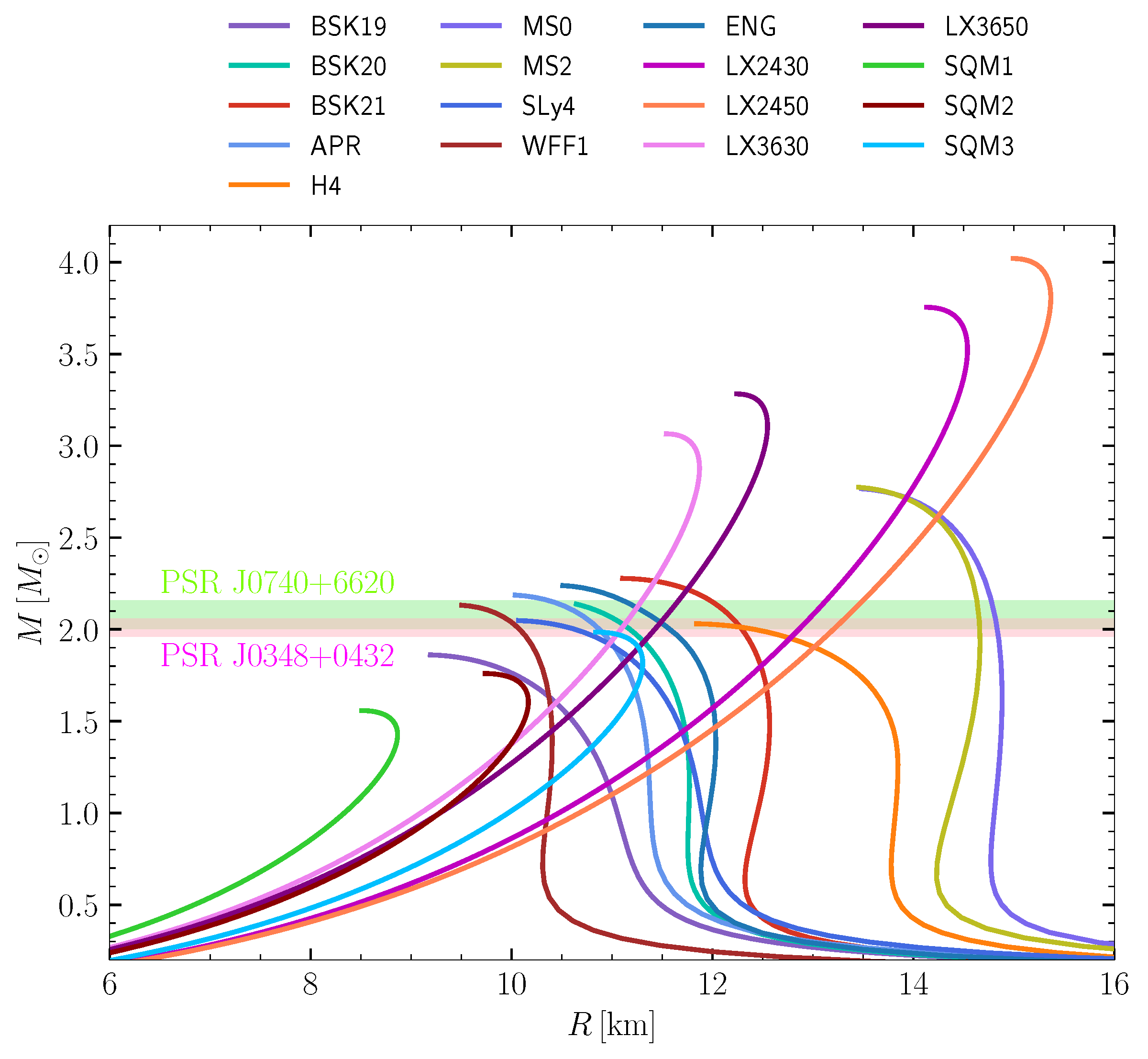
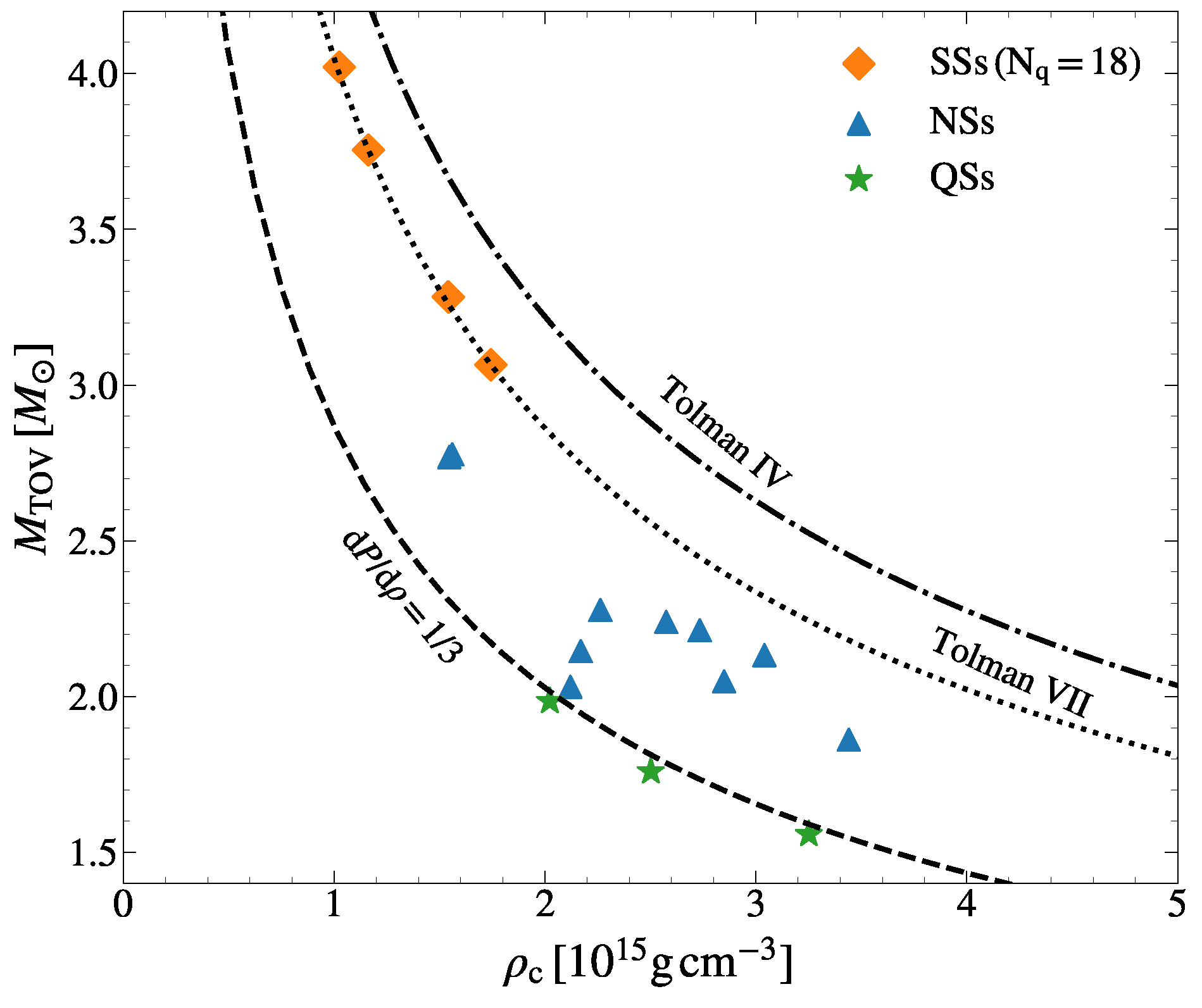
3. Global Structure of Compact Stars
4. Elastic Properties of Compact Stars
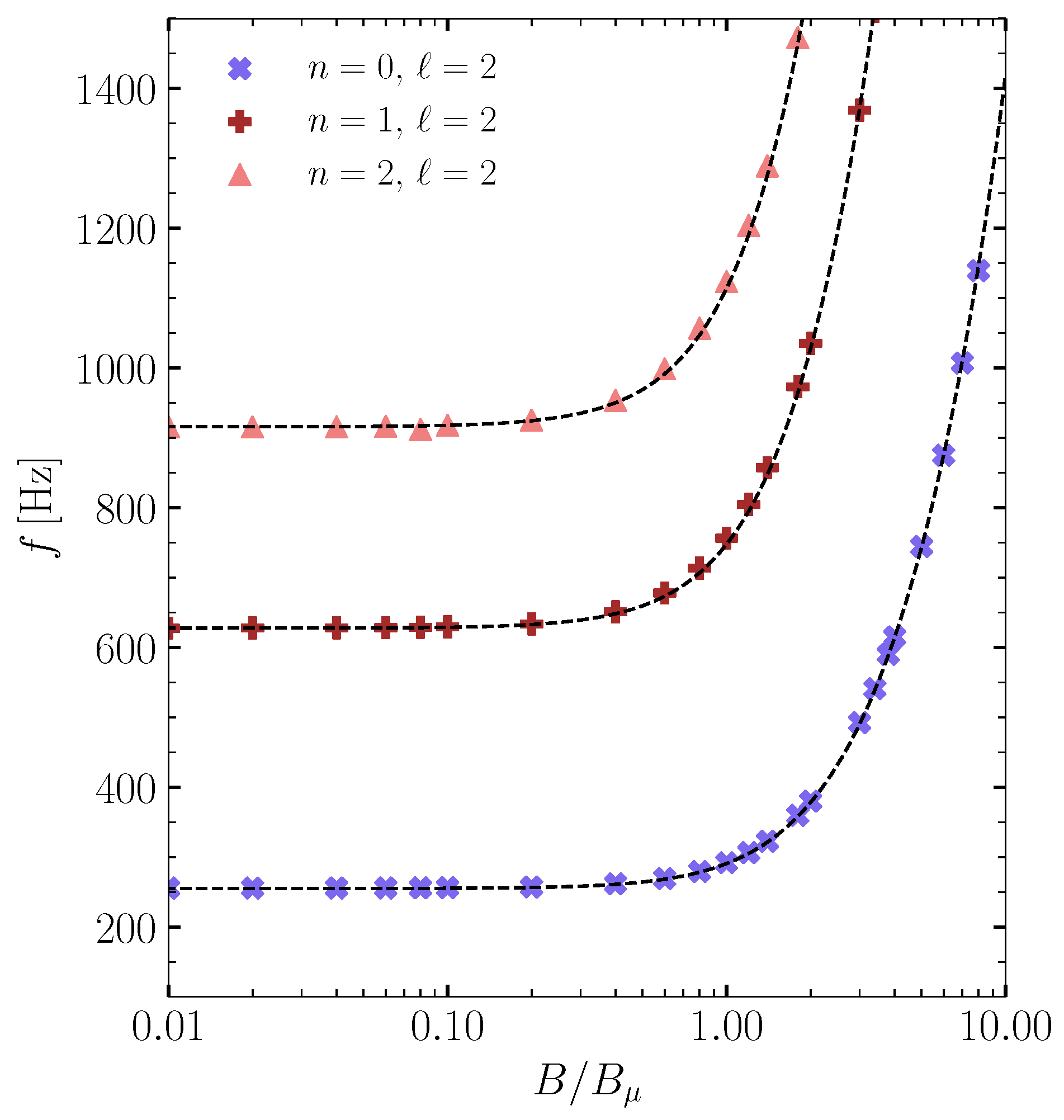
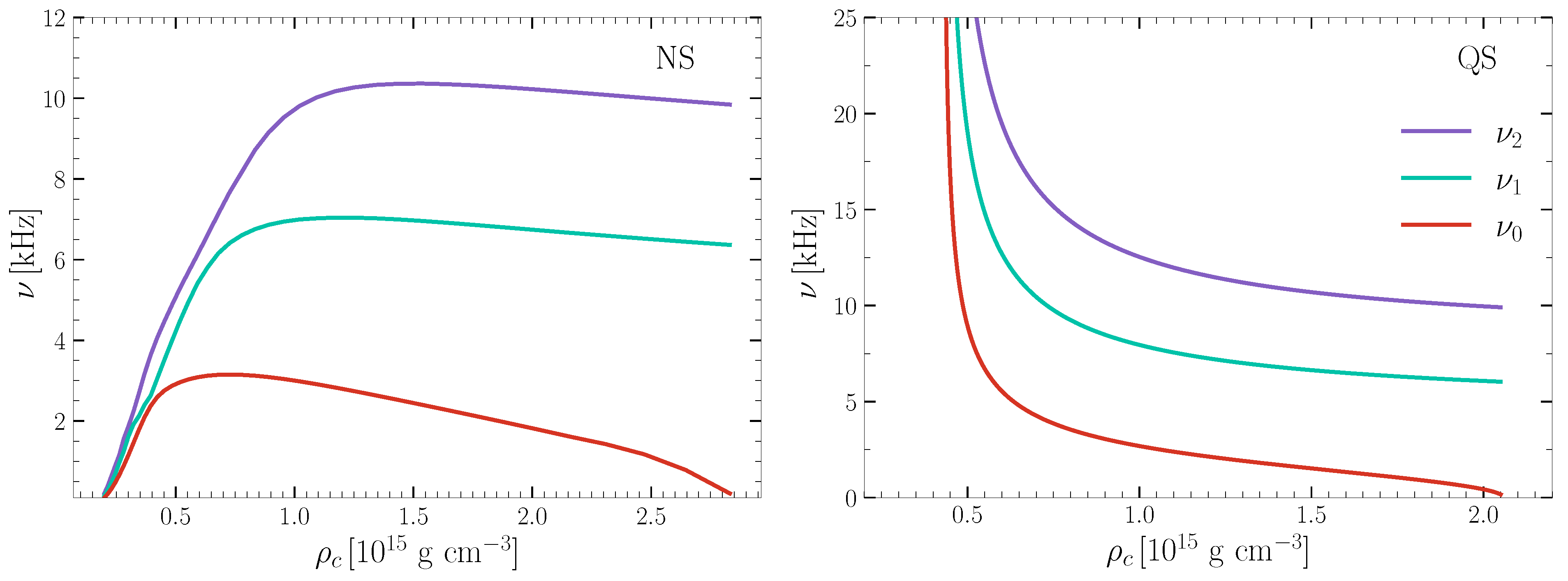
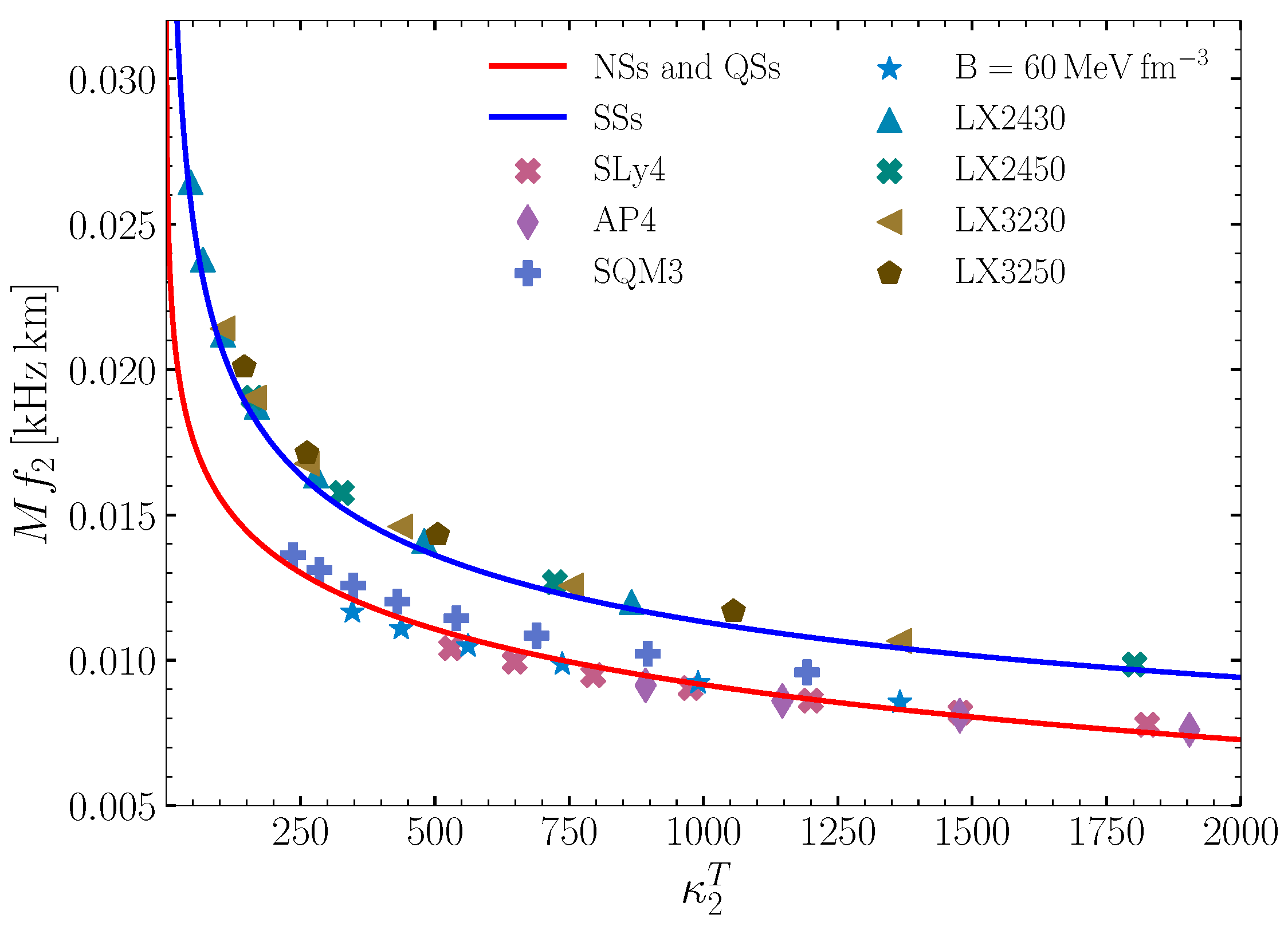
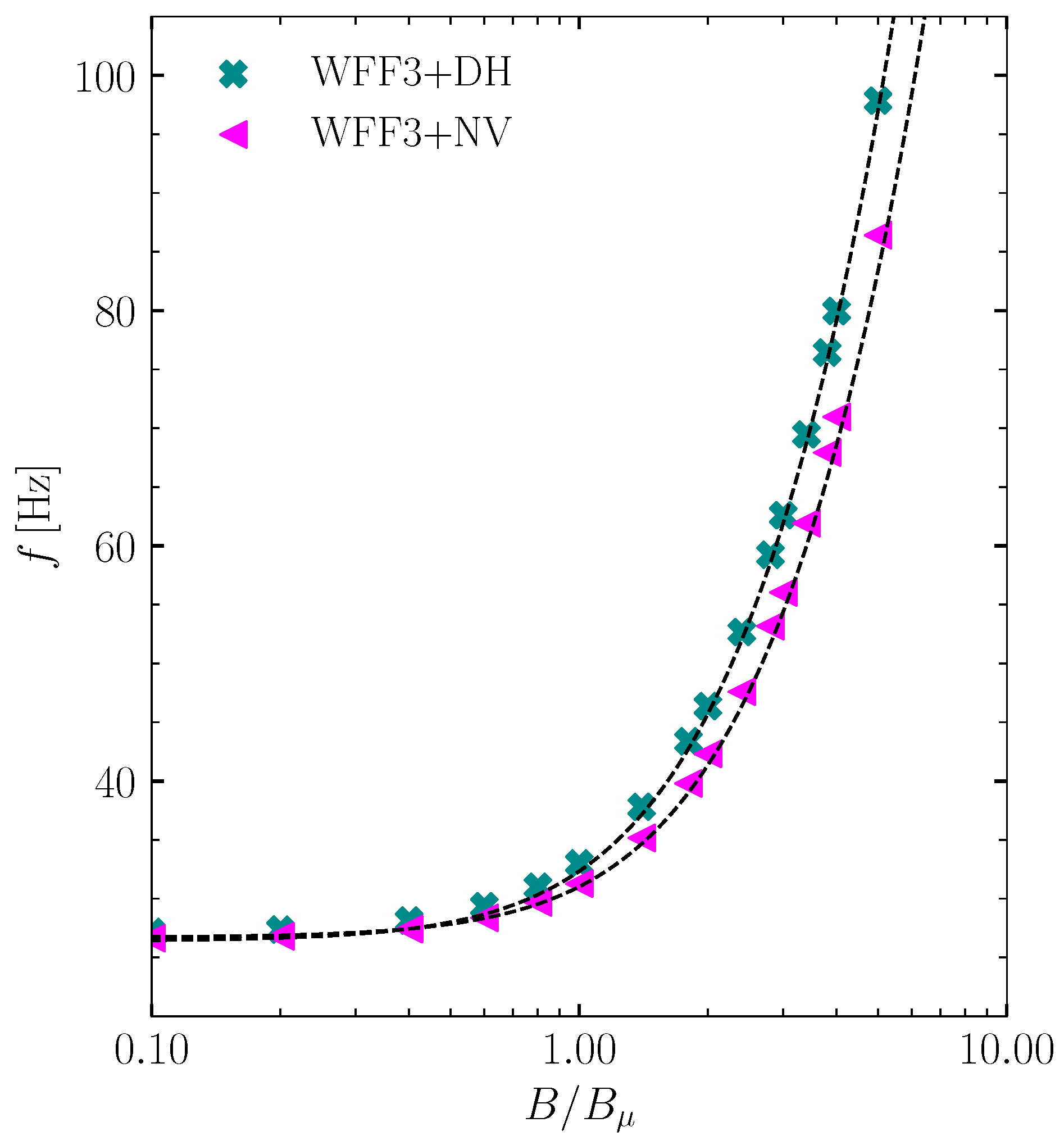
5. Asteroseismology of Compact Stars
5.1. Dynamical Stability of Compact Stars
5.2. Spheroidal Oscillations of Compact Stars
5.3. Torsional Oscillations of Compact Stars
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Hirvonen, J.; Komoltsev, O.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Strongly interacting matter exhibits deconfined behavior in massive neutron stars. Nat. Commun. 2023, 14, 8451. [Google Scholar] [CrossRef] [PubMed]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: New York, NY, USA, 2000. [Google Scholar]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Xu, R.X. Solid quark matter? Astrophys. J. 2003, 596, L59–L62. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007; Volume 326. [Google Scholar] [CrossRef]
- Alford, M.; Braby, M.; Paris, M.W.; Reddy, S. Hybrid stars that masquerade as neutron stars. Astrophys. J. 2005, 629, 969–978. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Y.; Xia, C.J.; Xu, R. Hybrid strangeon stars. Phys. Rev. D 2023, 108, 123031. [Google Scholar] [CrossRef]
- Xu, R.X.; Qiao, G.J.; Zhang, B. Psr 0943+10: A bare strange star? Astrophys. J. 1999, 522, L109. [Google Scholar] [CrossRef]
- Duncan, R.C. Global seismic oscillations in soft gamma repeaters. Astrophys. J. 1998, 498, L45. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Watts, A.L. Discovery of fast X-ray oscillations during the 1998 giant flare from SGR 1900+14. Astrophys. J. 2005, 632, L111–L114. [Google Scholar] [CrossRef]
- Ushomirsky, G.; Cutler, C.; Bildsten, L. Deformations of accreting neutron star crusts and gravitational wave emission. Mon. Not. R. Astron. Soc. 2000, 319, 902. [Google Scholar] [CrossRef]
- Haskell, B.; Jones, D.I.; Andersson, N. Mountains on Neutron Stars: Accreted vs. Non-Accreted crusts. Mon. Not. R. Astron. Soc. 2006, 373, 1423–1439. [Google Scholar] [CrossRef]
- Haskell, B.; Patruno, A. Are Gravitational Waves Spinning Down PSR J1023+0038? Phys. Rev. Lett. 2017, 119, 161103. [Google Scholar] [CrossRef]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Searches for Gravitational Waves from Known Pulsars at Two Harmonics in 2015–2017 LIGO Data. Astrophys. J. 2019, 879, 10, Erratum in Astrophys. J. 2020, 899, 170. [Google Scholar] [CrossRef]
- Ruderman, M. Neutron Starquakes and Pulsar Periods. Nature 1969, 223, 597–598. [Google Scholar] [CrossRef]
- Anderson, P.W.; Itoh, N. Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 1975, 256, 25–27. [Google Scholar] [CrossRef]
- Alpar, M.A.; Anderson, P.W.; Pines, D.; Shaham, J. Giant glitches and pinned vorticity in the VELA and other pulsars. Astrophys. J. 1981, 249, L29–L33. [Google Scholar] [CrossRef]
- Antonelli, M.; Montoli, A.; Pizzochero, P. Insights into the Physics of Neutron Star Interiors from Pulsar Glitches; World Scientific: Singapore, 2023. [Google Scholar] [CrossRef]
- Antonopoulou, D.; Haskell, B.; Espinoza, C.M. Pulsar glitches: Observations and physical interpretation. Rept. Prog. Phys. 2022, 85, 126901. [Google Scholar] [CrossRef]
- Zhou, A.Z.; Xu, R.X.; Wu, X.J.; Wang, N.; Hong, X.Y. Quakes in solid quark stars. Astropart. Phys. 2004, 22, 73–79. [Google Scholar] [CrossRef]
- Lai, X.Y.; Yun, C.A.; Lu, J.G.; Lü, G.L.; Wang, Z.J.; Xu, R.X. Pulsar Glitches in a Strangeon Star Model. Mon. Not. R. Astron. Soc. 2018, 476, 3303–3309. [Google Scholar] [CrossRef]
- Wang, W.; Lai, X.; Zhou, E.; Lu, J.; Zheng, X.; Xu, R. Pulsar glitches in a strangeon star model—II. The activity. Mon. Not. R. Astron. Soc. 2020, 500, 5336–5349. [Google Scholar] [CrossRef]
- Lai, X.Y.; Wang, W.H.; Yuan, J.P.; Lu, R.P.; Yue, H.; Xu, R.X. Pulsar glitch in a strangeon star model—III. The recovery. Mon. Not. R. Astron. Soc. 2023, 523, 3967–3973. [Google Scholar] [CrossRef]
- Li, H.B.; Kang, Y.; Hu, Z.; Shao, L.; Xia, C.J.; Xu, R.X. Quasi-periodic oscillations during magnetar giant flares in the strangeon star model. Mon. Not. R. Astron. Soc. 2023, 527, 855–862. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Adkins, P.W.; Albert, C.L.; Anders, J.F.; Aylward, A.T.; Baker, C.L.; Balsamo, E.R.; Bamford, W.A.; Benegalrao, S.S.; et al. The Neutron star Interior Composition Explorer (NICER): Design and development. In Proceedings of the Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. den Herder, J.W.A., Takahashi, T., Bautz, M., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9905, p. 99051H. [Google Scholar] [CrossRef]
- Baubock, M.; Psaltis, D.; Ozel, F. Effects of Spot Size on Neutron-Star Radius Measurements from Pulse Profiles. Astrophys. J. 2015, 811, 144. [Google Scholar] [CrossRef]
- Miller, M.C. The Case for psr J1614–2230 as a Nicer Target. Astrophys. J. 2016, 822, 27. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Bogdanov, S.; Grindlay, J.E.; Rybicki, G.B. Thermal X-rays from Millisecond Pulsars: Constraining the Fundamental Properties of Neutron Stars. Astrophys. J. 2008, 689, 407. [Google Scholar] [CrossRef]
- Watts, A.L.; Andersson, N.; Chakrabarty, D.; Feroci, M.; Hebeler, K.; Israel, G.; Lamb, F.K.; Miller, M.C.; Morsink, S.; Özel, F.; et al. Colloquium: Measuring the neutron star equation of state using X-ray timing. Rev. Mod. Phys. 2016, 88, 021001. [Google Scholar] [CrossRef]
- Haskell, B.; Bejger, M. Astrophysics with continuous gravitational waves. Nat. Astron. 2023, 7, 1160–1170. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Yunes, N.; Miller, M.C.; Yagi, K. Gravitational-wave and X-ray probes of the neutron star equation of state. Nat. Rev. Phys. 2022, 4, 237–246. [Google Scholar] [CrossRef]
- Andersson, N. Gravitational waves from instabilities in relativistic stars. Class. Quant. Grav. 2003, 20, R105. [Google Scholar] [CrossRef]
- Andersson, N.; Ferrari, V.; Jones, D.I.; Kokkotas, K.D.; Krishnan, B.; Read, J.S.; Rezzolla, L.; Zink, B. Gravitational waves from neutron stars: Promises and challenges. Gen. Rel. Grav. 2011, 43, 409–436. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schutz, B.F. W-modes: A New family of normal modes of pulsating relativistic stars. Mon. Not. R. Astron. Soc. 1992, 255, 119. [Google Scholar] [CrossRef]
- McDermott, P.N.; van Horn, H.M.; Hansen, C.J. Nonradial Oscillations of Neutron Stars. Astrophys. J. 1988, 325, 725. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Zhou, E.P.; Zhou, X.; Li, A. Constraints on interquark interaction parameters with GW170817 in a binary strange star scenario. Phys. Rev. D 2018, 97, 083015. [Google Scholar] [CrossRef]
- Miao, Z.; Li, A.; Zhu, Z.; Han, S. Constraining hadron-quark phase transition parameters within the quark-mean-field model using multimessenger observations of neutron stars. Astrophys. J. 2020, 904, 103. [Google Scholar] [CrossRef]
- Yu, H.; Weinberg, N.N. Dynamical tides in coalescing superfluid neutron star binaries with hyperon cores and their detectability with third generation gravitational-wave detectors. Mon. Not. Roy. Astron. Soc. 2017, 470, 350–360. [Google Scholar] [CrossRef]
- Lau, S.Y.; Yagi, K. Probing hybrid stars with gravitational waves via interfacial modes. Phys. Rev. D 2021, 103, 063015. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, C.; Xia, C.; Zhou, E.; Ma, Y. Probing phase transitions in neutron stars via the crust-core interfacial mode. Phys. Rev. D 2023, 107, 083023. [Google Scholar] [CrossRef]
- Zavlin, V.E.; Pavlov, G.G. Modeling neutron star atmospheres. In Proceedings of the 270th WE-Heraeus Seminar on Neutron Stars, Pulsars and Supernova Remnants, Bad Honnef, Germany, 21–25 January 2002; pp. 262–272. [Google Scholar]
- Potekhin, A.Y. Atmospheres and radiating surfaces of neutron stars. Phys. Usp. 2014, 57, 735–770. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Pethick, C.J.; Ravenhall, D.G. Matter at large neutron excess and the physics of neutron-star crusts. Ann. Rev. Nucl. Part. Sci. 1995, 45, 429–484. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Rel. 2008, 11, 10. [Google Scholar] [CrossRef]
- Rezzolla, L.; Pizzochero, P.; Jones, D.I.; Rea, N.; Vidaña, I. (Eds.) The Physics and Astrophysics of Neutron Stars; Springer: Cham, Switzerland, 2018; Volume 457. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Caplan, M.E.; Horowitz, C.J. Colloquium: Astromaterial science and nuclear pasta. Rev. Mod. Phys. 2017, 89, 041002. [Google Scholar] [CrossRef]
- Haskell, B.; Andersson, N.; Jones, D.I.; Samuelsson, L. Are neutron stars with crystalline color-superconducting cores relevant for the LIGO experiment? Phys. Rev. Lett. 2007, 99, 231101. [Google Scholar] [CrossRef]
- Pereira, J.P.; Bejger, M.; Tonetto, L.; Lugones, G.; Haensel, P.; Zdunik, J.L.; Sieniawska, M. Probing elastic quark phases in hybrid stars with radius measurements. Astrophys. J. 2021, 910, 145. [Google Scholar] [CrossRef]
- Lindblom, L. Spectral Representations of Neutron-Star Equations of State. Phys. Rev. D 2010, 82, 103011. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic theory of superconductivity. Phys. Rev. 1957, 106, 162. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Lin, L.M. Torsional oscillations of crystalline color-superconducting hybrid stars: Possible sources for Advanced LIGO? Phys. Rev. D 2013, 88, 124002. [Google Scholar] [CrossRef]
- Lau, S.Y.; Leung, P.T.; Lin, L.M. Tidal deformations of compact stars with crystalline quark matter. Phys. Rev. D 2017, 95, 101302. [Google Scholar] [CrossRef]
- Lai, X.Y.; Xu, R.X. Quark stars composed of Lennard-Jones matter. Mon. Not. R. Astron. Soc. 2009, 398, 31. [Google Scholar] [CrossRef]
- Lai, X.Y.; Gao, C.Y.; Xu, R.X. H-cluster stars. Mon. Not. R. Astron. Soc. 2012, 431, 3282–3290. [Google Scholar] [CrossRef]
- Lai, X.; Xu, R. Quark-Cluster Stars: The Structure. In Proceedings of the International Journal of Modern Physics Conference Series; World Scientific: Singapore, 2013; Volume 23, pp. 213–222. [Google Scholar] [CrossRef]
- Xu, R.X. 1E 1207.4-5209: A Low-mass bare strange star? Mon. Not. R. Astron. Soc. 2005, 356, 359–370. [Google Scholar] [CrossRef]
- Yue, Y.L.; Cui, X.H.; Xu, R.X. Is psr b0943+10 a low-mass quark star? Astrophys. J. 2006, 649, L95–L98. [Google Scholar] [CrossRef]
- Zhu, W.W.; Xu, R.X. GCRT J1745-3009: A precessing radio pulsar? Mon. Not. R. Astron. Soc. 2006, 365, L16. [Google Scholar] [CrossRef]
- Lai, X.; Xia, C.; Xu, R. Bulk strong matter: The trinity. Adv. Phys. X 2023, 8, 2137433. [Google Scholar] [CrossRef]
- Wang, W.Y.; Yang, Y.P.; Niu, C.H.; Xu, R.; Zhang, B. Magnetospheric Curvature Radiation by Bunches as Emission Mechanism for Repeating Fast Radio Bursts. Astrophys. J. 2022, 927, 105. [Google Scholar] [CrossRef]
- Wang, W.Y.; Jiang, J.C.; Lu, J.; Xu, H.; Xu, J.; Lee, K.; Liu, J.; Xu, R. Repeating fast radio bursts: Coherent circular polarization by bunches. Sci. China Phys. Mech. Astron. 2022, 65, 289511. [Google Scholar] [CrossRef]
- Lai, X.Y.; Yu, Y.W.; Zhou, E.P.; Li, Y.Y.; Xu, R.X. Merging Strangeon Stars. Res. Astron. Astrophys. 2018, 18, 024. [Google Scholar] [CrossRef]
- Lai, X.Y.; Zhou, E.P.; Xu, R.X. Strangeons constitute bulk strong matter: Test using GW 170817. Eur. Phys. J. A 2019, 55, 60. [Google Scholar] [CrossRef]
- Lai, X.Y.; Xia, C.J.; Yu, Y.W.; Xu, R.X. Merging strangeon stars II: The ejecta and light curves. Res. Astron. Astrophys. 2021, 21, 250. [Google Scholar] [CrossRef]
- Gao, Y.; Lai, X.Y.; Shao, L.; Xu, R.X. Rotation and deformation of strangeon stars in the Lennard-Jones model. Mon. Not. R. Astron. Soc. 2022, 509, 2758–2779. [Google Scholar] [CrossRef]
- Li, H.B.; Gao, Y.; Shao, L.; Xu, R.X.; Xu, R. Oscillation modes and gravitational waves from strangeon stars. Mon. Not. R. Astron. Soc. 2022, 516, 6172–6179. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron star structure and the equation of state. Astrophys. J. 2001, 550, 426. [Google Scholar] [CrossRef]
- Fantina, A.F.; Chamel, N.; Pearson, J.M.; Goriely, S. Neutron star properties with unified equations of state of dense matter. Astron. Astrophys. 2013, 559, A128. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Ultimate energy density of observable cold matter. Phys. Rev. Lett. 2005, 94, 111101. [Google Scholar] [CrossRef] [PubMed]
- Mogliacci, S.; Andersen, J.O.; Strickland, M.; Su, N.; Vuorinen, A. Equation of State of hot and dense QCD: Resummed perturbation theory confronts lattice data. J. High Energy Phys. 2013, 12, 055. [Google Scholar] [CrossRef]
- Fraga, E.S.; Kurkela, A.; Vuorinen, A. Interacting quark matter equation of state for compact stars. Astrophys. J. Lett. 2014, 781, L25. [Google Scholar] [CrossRef]
- Fraga, E.S.; Kurkela, A.; Vuorinen, A. Neutron star structure from QCD. Eur. Phys. J. A 2016, 52, 49. [Google Scholar] [CrossRef]
- Kurkela, A.; Vuorinen, A. Cool quark matter. Phys. Rev. Lett. 2016, 117, 042501. [Google Scholar] [CrossRef]
- Ghiglieri, J.; Kurkela, A.; Strickland, M.; Vuorinen, A. Perturbative Thermal QCD: Formalism and Applications. Phys. Rept. 2020, 880, 1–73. [Google Scholar] [CrossRef]
- Ogata, S.; Ichimaru, S. First-principles calculations of shear moduli for Monte Carlo-simulated Coulomb solids. Phys. Rev. A 1990, 42, 4867–4870. [Google Scholar] [CrossRef]
- Strohmayer, T.; Ogata, S.; Iyetomi, H.; Ichimaru, S.; van Horn, H.M. The Shear Modulus of the Neutron Star Crust and Nonradial Oscillations of Neutron Stars. Astrophys. J. 1991, 375, 679. [Google Scholar] [CrossRef]
- Farouki, R.T.; Hamaguchi, S. Thermal energy of the crystalline one-component plasma from dynamical simulations. Phys. Rev. E 1993, 47, 4330–4336. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, C.J.; Hughto, J. Molecular Dynamics Simulation of Shear Moduli for Coulomb Crystals. arXiv 2008, arXiv:0812.2650. [Google Scholar]
- Baiko, D.A. Shear modulus of neutron star crust. Mon. Not. R. Astron. Soc. 2011, 416, 22. [Google Scholar] [CrossRef]
- Mannarelli, M.; Rajagopal, K.; Sharma, R. The Rigidity of crystalline color superconducting quark matter. Phys. Rev. D 2007, 76, 074026. [Google Scholar] [CrossRef]
- Ippolito, N.D.; Nardulli, G.; Ruggieri, M. Self-consistent evaluation of quark masses in three flavor crystalline color superconductivity. J. High Energy Phys. 2007, 04, 036. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Ruoff, J. Radial oscillations of relativistic stars. Astron. Astrophys. 2001, 366, 565. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley-VCH: New York, NY, USA, 1983. [Google Scholar]
- Chandrasekhar, S. Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Phys. Rev. Lett. 1964, 12, 114–116. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Astrophys. J. 1964, 140, 417–433, Erratum in Astrophys. J. 1964, 140, 1342. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Cowling, T.G. The non-radial oscillations of polytropic stars. Mon. Not. R. Astron. Soc. 1941, 101, 367. [Google Scholar] [CrossRef]
- Sotani, H.; Yasutake, N.; Maruyama, T.; Tatsumi, T. Signatures of hadron-quark mixed phase in gravitational waves. Phys. Rev. D 2011, 83, 024014. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Buonanno, A.; Lehner, L.; Broeck, C.V.D.; Ajith, P.; Ghosh, A.; Chatziioannou, K.; Pani, P.; Puerrer, M.; Sotiriou, T.; et al. Extreme gravity and fundamental physics. Bull. Am. Astron. Soc. 2019, 51, 251. [Google Scholar]
- Kalogera, V.; Sathyaprakash, B.S.; Bailes, M.; Bizouard, M.-A.; Buonanno, A.; Burrows, A.; Colpi, M.; Evans, M.; Fairhurst, S.; Hild, S.; et al. The Next Generation Global Gravitational Wave Observatory: The Science Book. arXiv 2021, arXiv:2111.06990. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Constraining the p-Mode–g-Mode Tidal Instability with GW170817. Phys. Rev. Lett. 2019, 122, 061104. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration; KAGRA Collaboration; Abbott, R.; Abe, H.; Acernese, F.; Ackley, K.; Adhikari, N.; Adhikari, R.X.; Adkins, V.K.; et al. First joint observation by the underground gravitational-wave detector KAGRA with GEO 600. Prog. Theor. Exp. Phys. 2022, 2022, 063F01. [Google Scholar] [CrossRef]
- Abe, H.; Akutsu, T.; Ando, M.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Bae, S.; Bajpai, R.; Cannon, K.; et al. The Current Status and Future Prospects of KAGRA, the Large-Scale Cryogenic Gravitational Wave Telescope Built in the Kamioka Underground. Galaxies 2022, 10, 63. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Nagar, A.; Balmelli, S.; Dietrich, T.; Ujevic, M. Quasiuniversal properties of neutron star mergers. Phys. Rev. Lett. 2014, 112, 201101. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Nagar, A.; Dietrich, T.; Damour, T. Modeling the Dynamics of Tidally Interacting Binary Neutron Stars up to the Merger. Phys. Rev. Lett. 2015, 114, 161103. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T.; Nagar, A. Modeling the complete gravitational wave spectrum of neutron star mergers. Phys. Rev. Lett. 2015, 115, 091101. [Google Scholar] [CrossRef]
- Chakravarti, K.; Andersson, N. Exploring universality in neutron star mergers. Mon. Not. R. Astron. Soc. 2020, 497, 5480–5484. [Google Scholar] [CrossRef]
- Shao, L.; Yagi, K. Neutron stars as extreme laboratories for gravity tests. Sci. Bull. 2022, 67, 1946–1949. [Google Scholar] [CrossRef] [PubMed]
- Piro, A.L. Shear waves and giant flare oscillations from soft gamma-ray repeaters. Astrophys. J. 2005, 634, L153–L156. [Google Scholar] [CrossRef]
- Samuelsson, L.; Andersson, N. Neutron Star Asteroseismology. Axial Crust Oscillations in the Cowling Approximation. Mon. Not. R. Astron. Soc. 2007, 374, 256–268. [Google Scholar] [CrossRef]
- Sotani, H.; Kokkotas, K.D.; Stergioulas, N. Torsional Oscillations of Relativistic Stars with Dipole Magnetic Fields. Mon. Not. R. Astron. Soc. 2007, 375, 261–277. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Fiks, V.; Fabrocini, A. Equation of state for dense nucleon matter. Phys. Rev. C 1988, 38, 1010–1037. [Google Scholar] [CrossRef] [PubMed]
- Negele, J.W.; Vautherin, D. Neutron star matter at sub-nuclear densities. Nucl. Phys. A 1973, 207, 298–320. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Piro, A.L.; Bildsten, L. Neutron star crustal interface waves. Astrophys. J. 2005, 619, 1054–1063. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. Astrophys. J. 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Jaikumar, P.; Reddy, S.; Steiner, A.W. The Strange star surface: A Crust with nuggets. Phys. Rev. Lett. 2006, 96, 041101. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.-B.; Gao, Y.; Shao, L.; Xu, R.-X. Asteroseismology of Compact Stars. Universe 2024, 10, 157. https://doi.org/10.3390/universe10040157
Li H-B, Gao Y, Shao L, Xu R-X. Asteroseismology of Compact Stars. Universe. 2024; 10(4):157. https://doi.org/10.3390/universe10040157
Chicago/Turabian StyleLi, Hong-Bo, Yong Gao, Lijing Shao, and Ren-Xin Xu. 2024. "Asteroseismology of Compact Stars" Universe 10, no. 4: 157. https://doi.org/10.3390/universe10040157