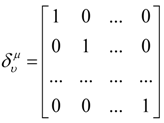
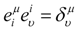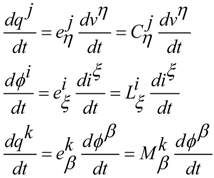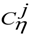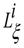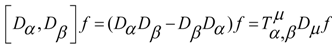Beyond an Input/Output Paradigm for Systems: Design Systems by Intrinsic Geometry
Abstract
:1. Introduction
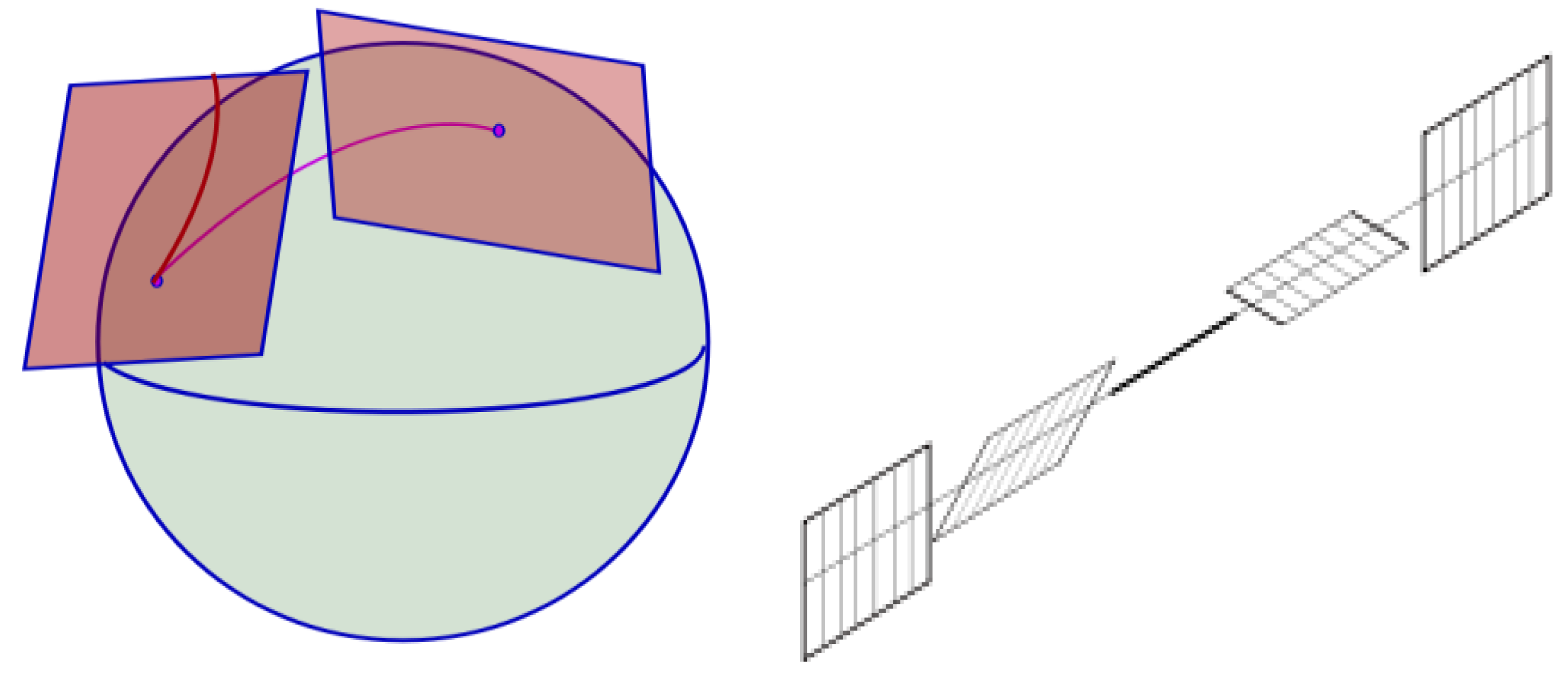
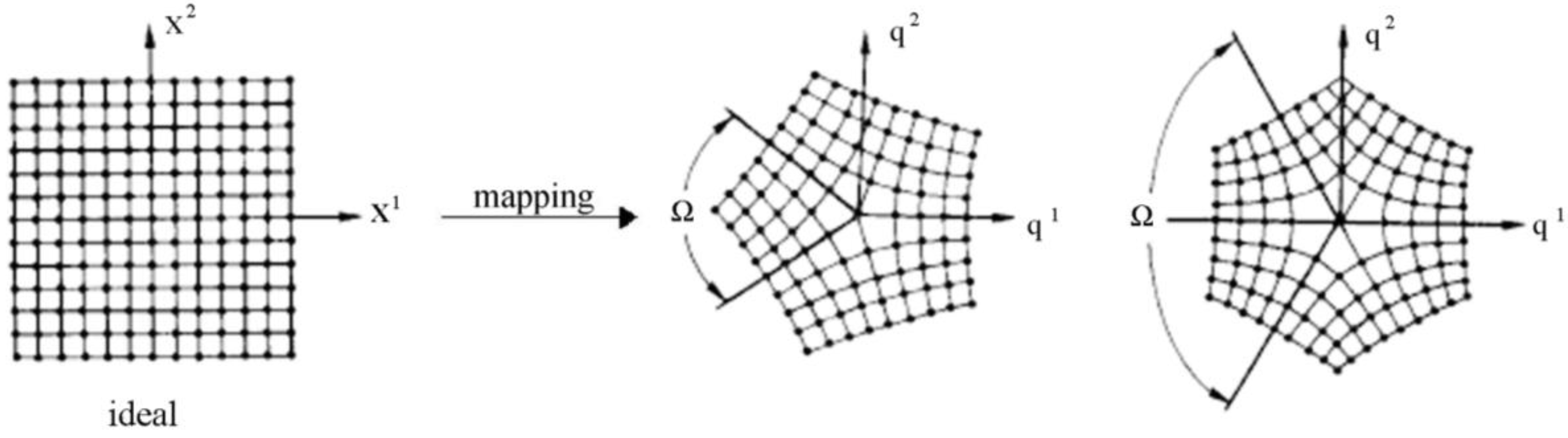
2. Local Intrinsic Geometry Used to Map Global Intrinsic Geometry
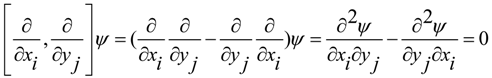
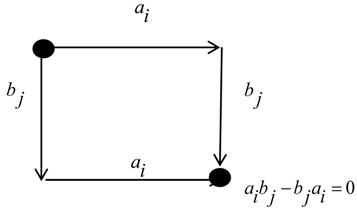
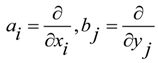
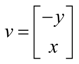
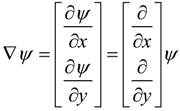
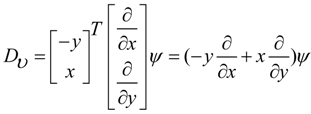
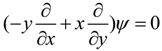
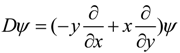 .
.
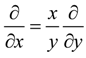
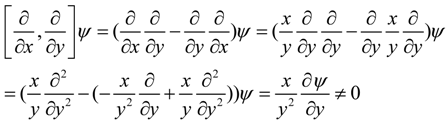
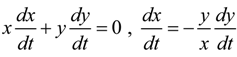
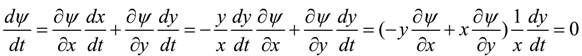
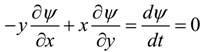
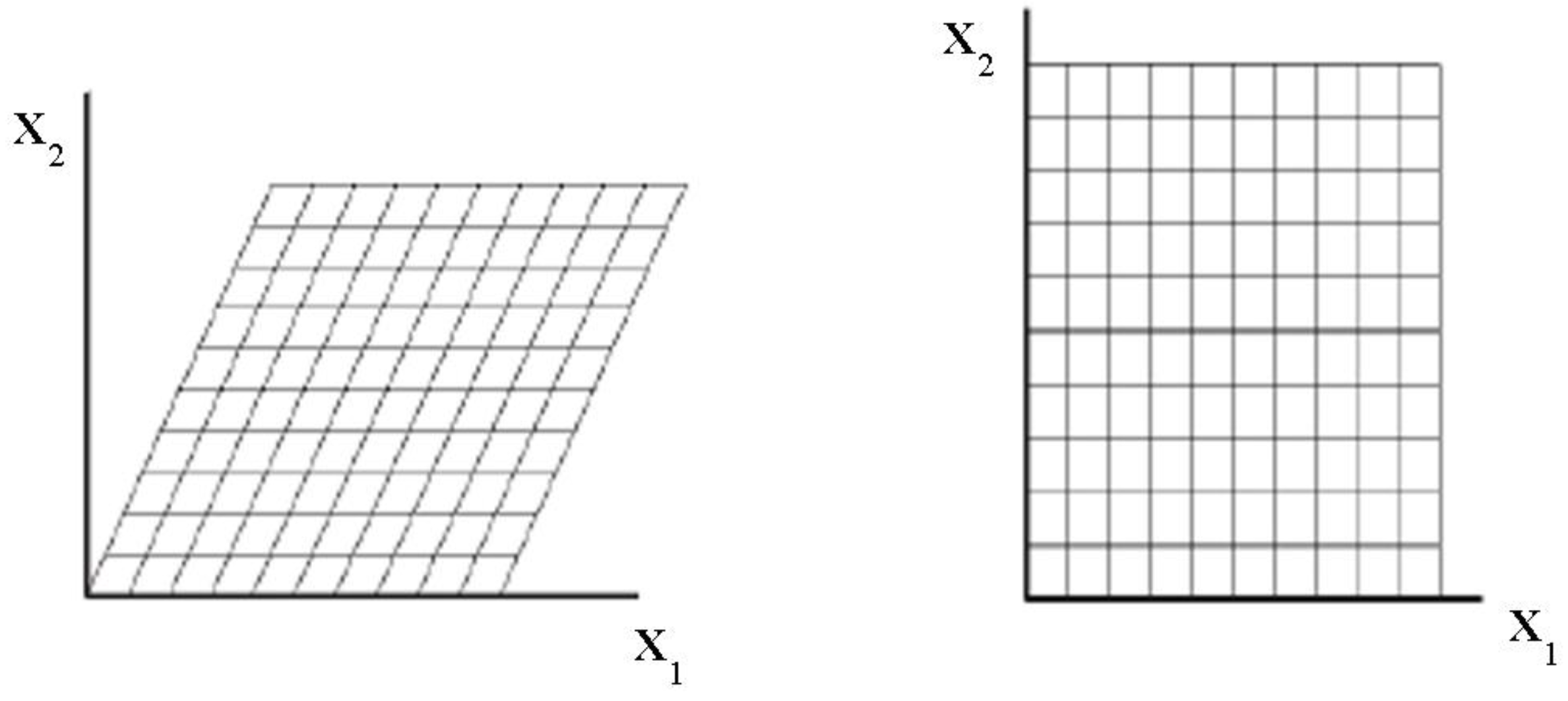
2.1. Change of Intrinsic Geometry by Moving Reference
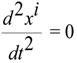
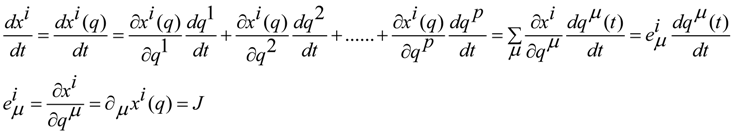
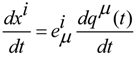
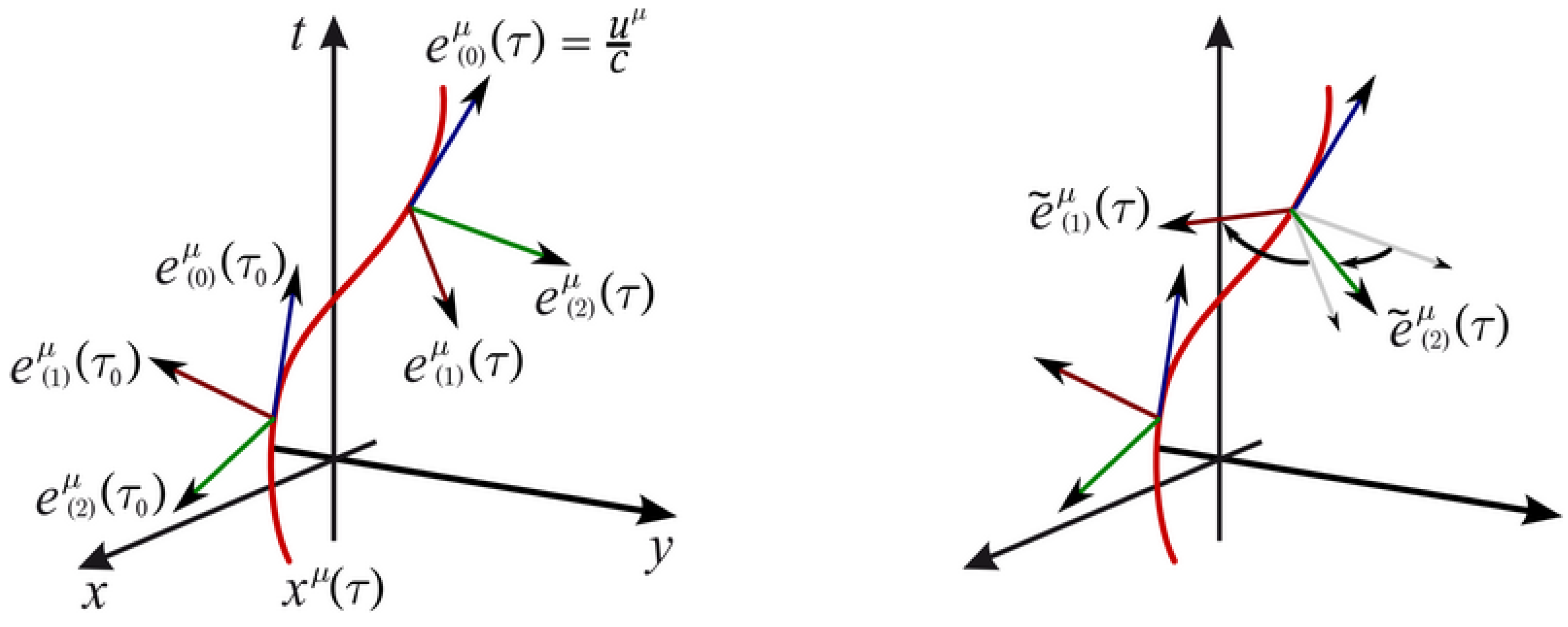
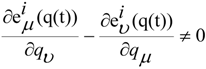
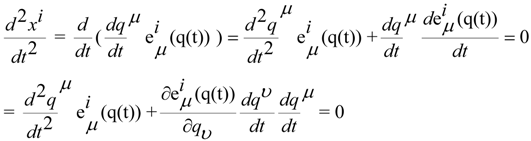
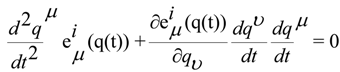
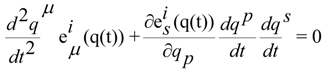
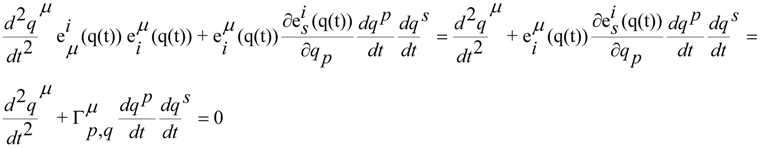
 . Because the previous equation can be written in this way
. Because the previous equation can be written in this way
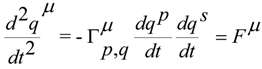

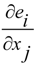 as the linear combination of the basis
as the linear combination of the basis
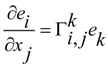
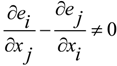
 are not commutative in the index
are not commutative in the index  we have that
we have that  are not Christoffel symbols but are simple connections with torsion
are not Christoffel symbols but are simple connections with torsion  . Now, we have
. Now, we have
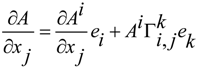
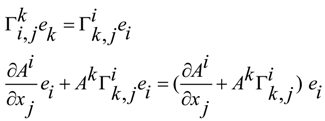
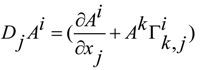
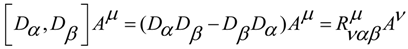
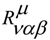 is the Riemann tensor curvature.
is the Riemann tensor curvature.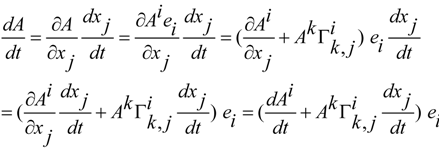
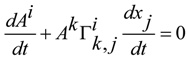
2.2. Electrical Circuit and Moving Reference
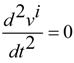
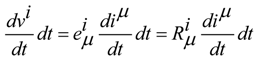
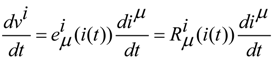
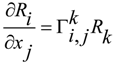
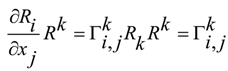
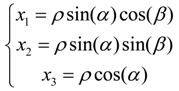

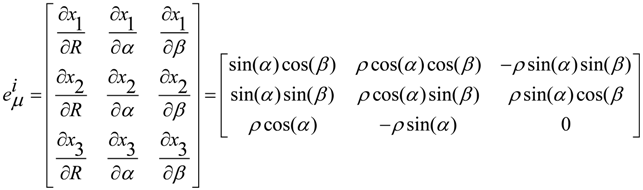

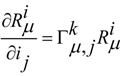
 is ordinary resistors, while the other is sources of voltages vβ controlled by current iα in other circuits by the proportional value
is ordinary resistors, while the other is sources of voltages vβ controlled by current iα in other circuits by the proportional value 

2.3. Deformation and Displacement in Media with Defects for Rotation (Disclination) and Translation (Dislocation)
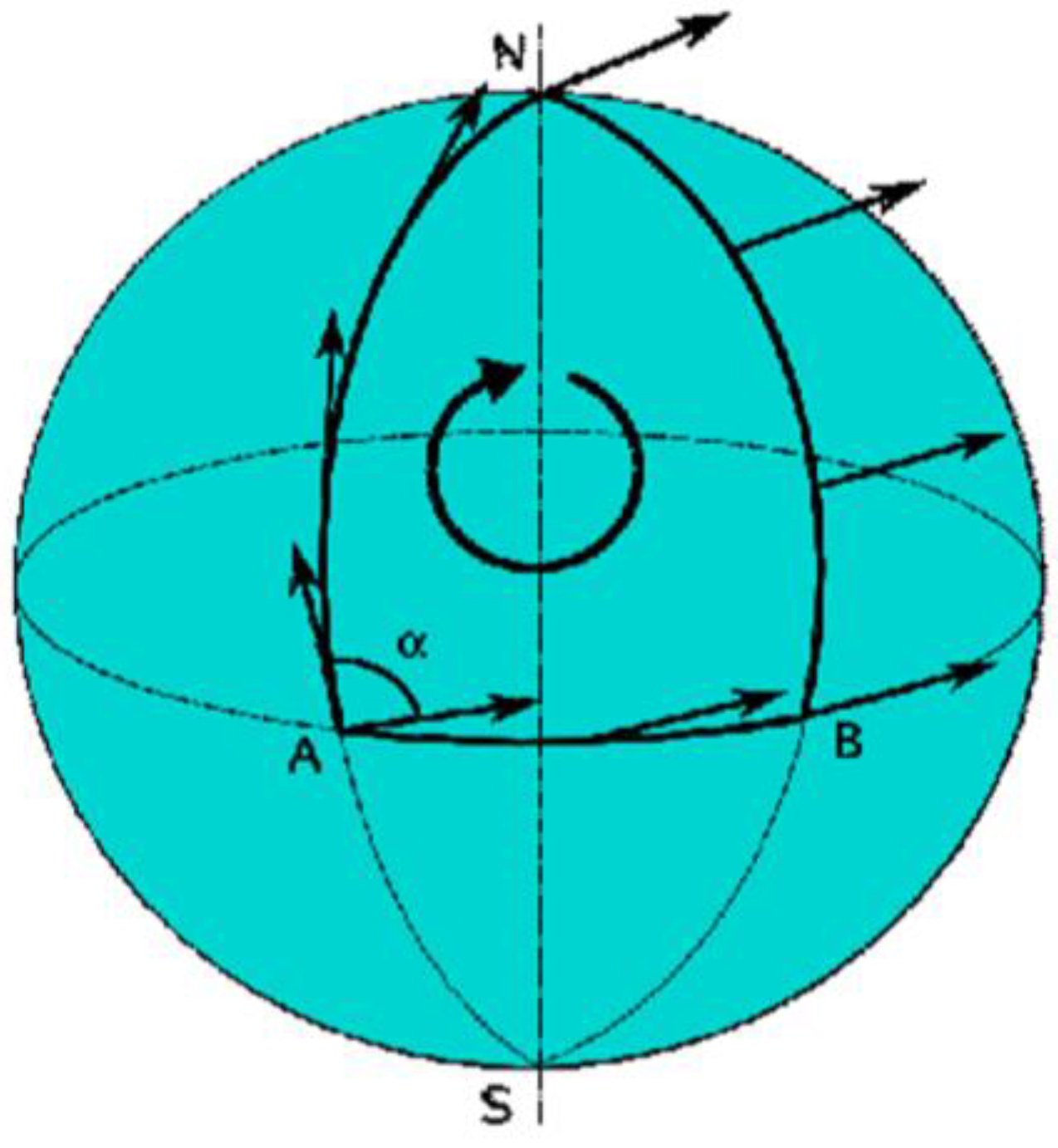
 where s is the displacement vector (Figure 8).
where s is the displacement vector (Figure 8).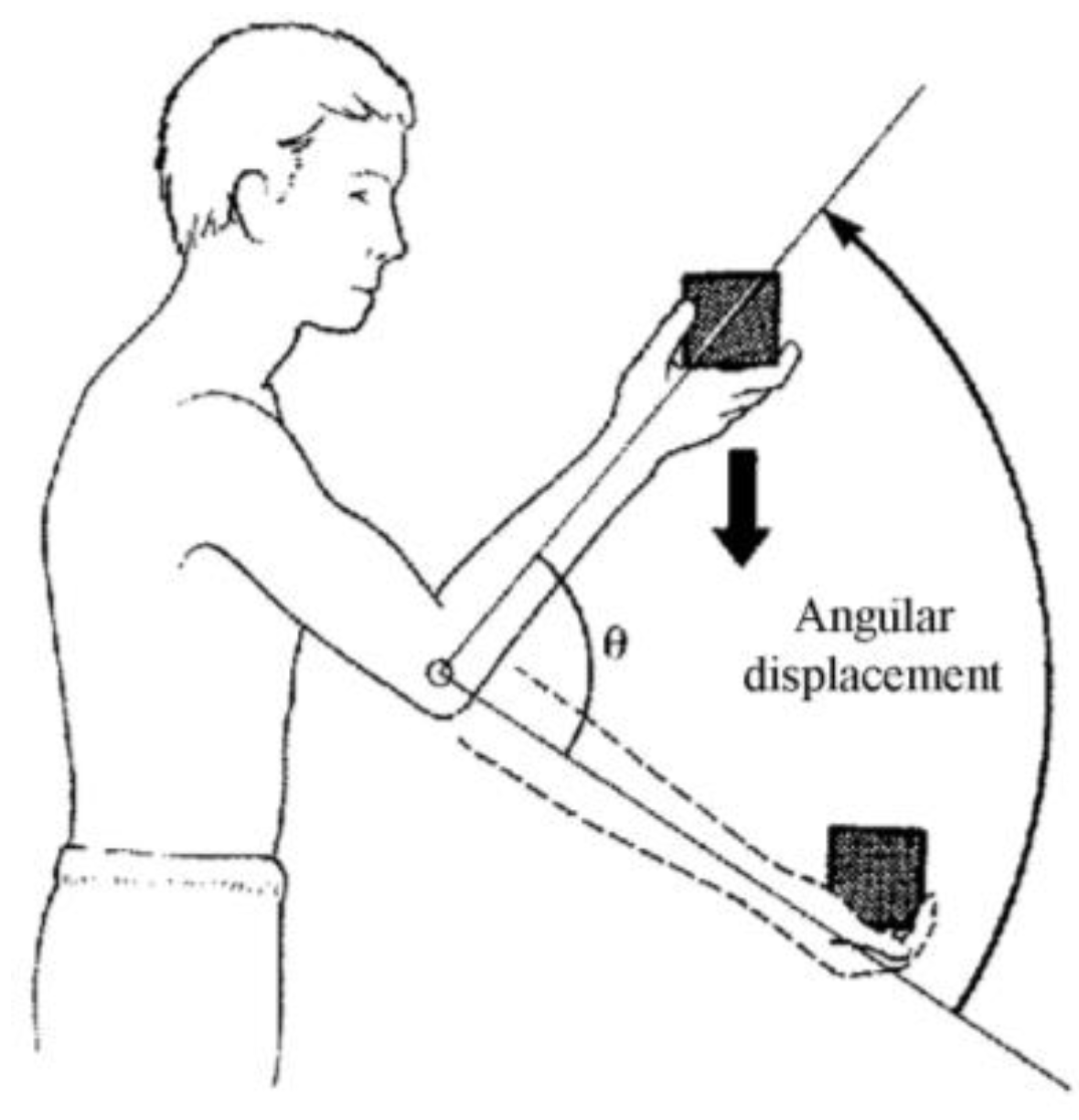
 we can compute the affine connection
we can compute the affine connection  in this way
in this way  . Now, when
. Now, when  , we have curvature and metric gα,β = (eα)T (eβ) but no torsion. When
, we have curvature and metric gα,β = (eα)T (eβ) but no torsion. When  , we have the torsion
, we have the torsion
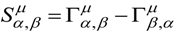
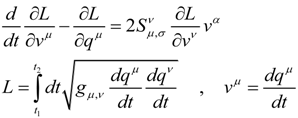
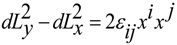
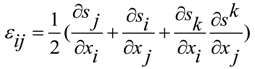
- (1)
- The deformed elements fit perfectly or they do not. In the latter case, we must apply a further deformation to re-compact the body. In the first case, we speak of a compatible deformation.
- (2)
- In the second case, we have an incompatible deformation. Let us imagine that during the deformation the coordinates are dragged with the medium. In the compatible deformation, the internal or intrinsic observer cannot see any difference as the Galileo internal observer for inertial system. In the incompatible deformation, the internal observer notices a change in the number of particles along a cycle in the medium as excess of holes or particles. The internal point of view is useful to find an incompatible deformation, due to the presence of defects. Mathematically, an incompatible deformation corresponds to the non-integrability of the differential form dsj where sj is the displacement. The non-integrability means that the displacement field sj (x) is multivalued, and thus discontinuities or defects arise when passing from one point to another. This fact is expressed by,
 is the torsion tensor. The torsion is given by Figure 11.
is the torsion tensor. The torsion is given by Figure 11.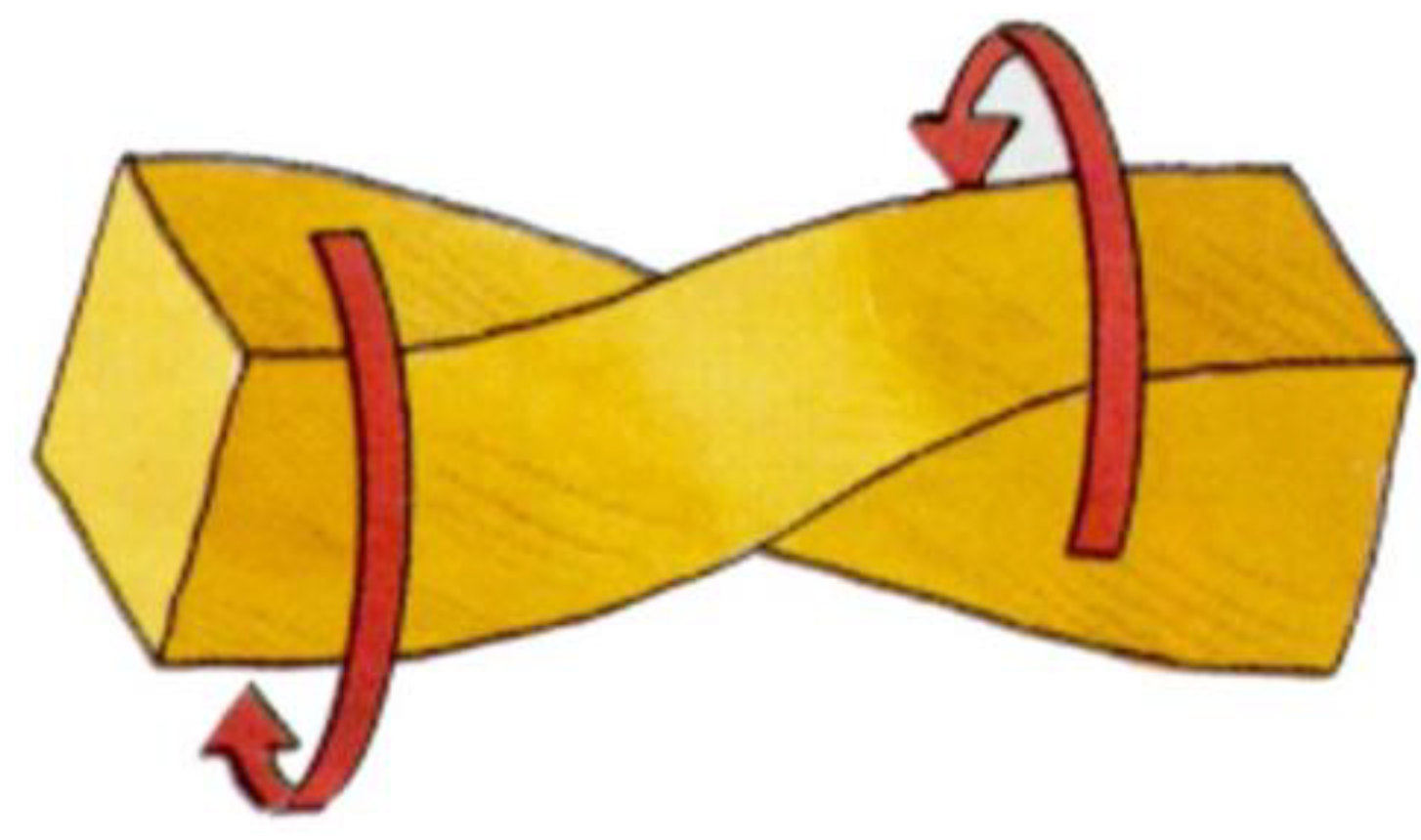

3. Incompatible Condition for Commutators and Wave Field Control by Active Secondary Sources
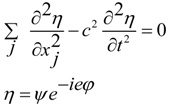
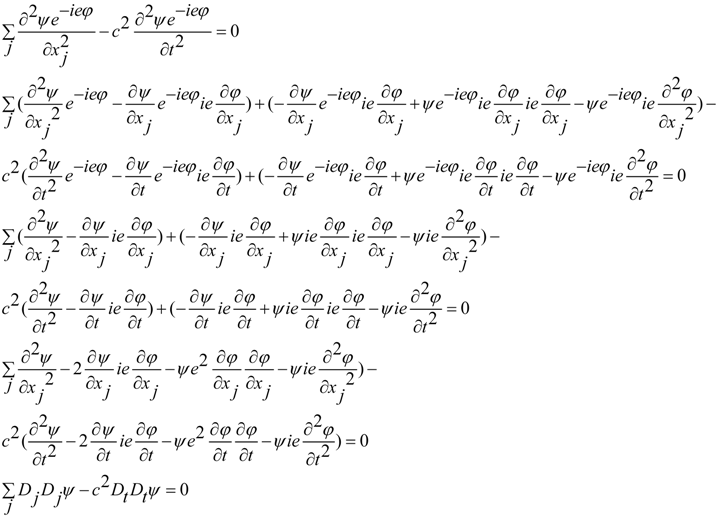
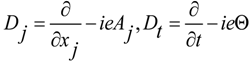
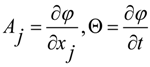

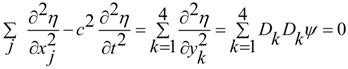
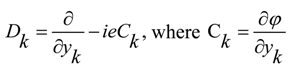
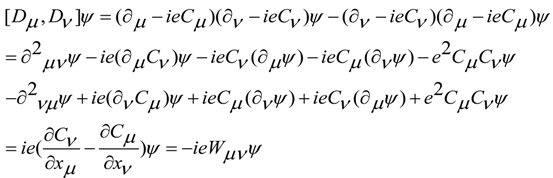
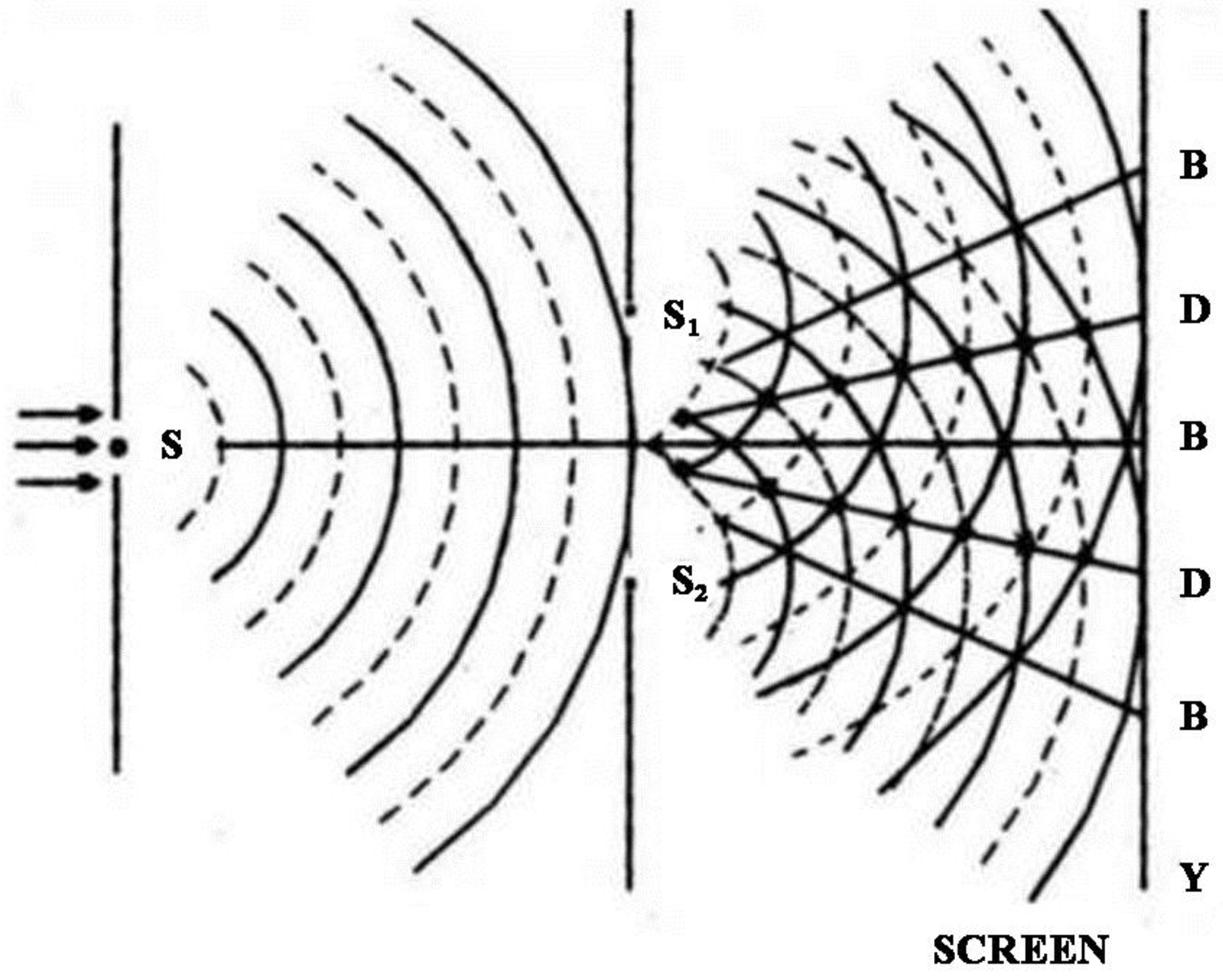
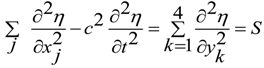
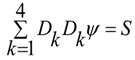
 we have
we have
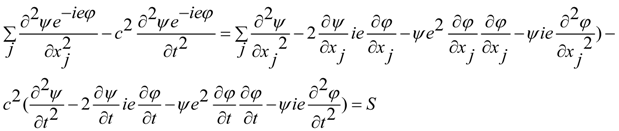
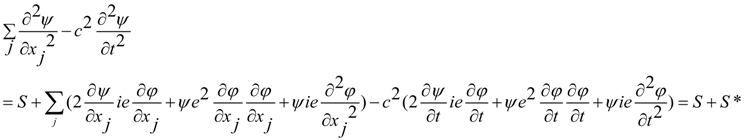
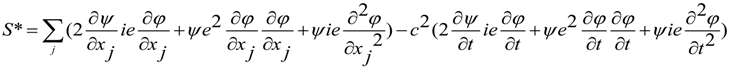
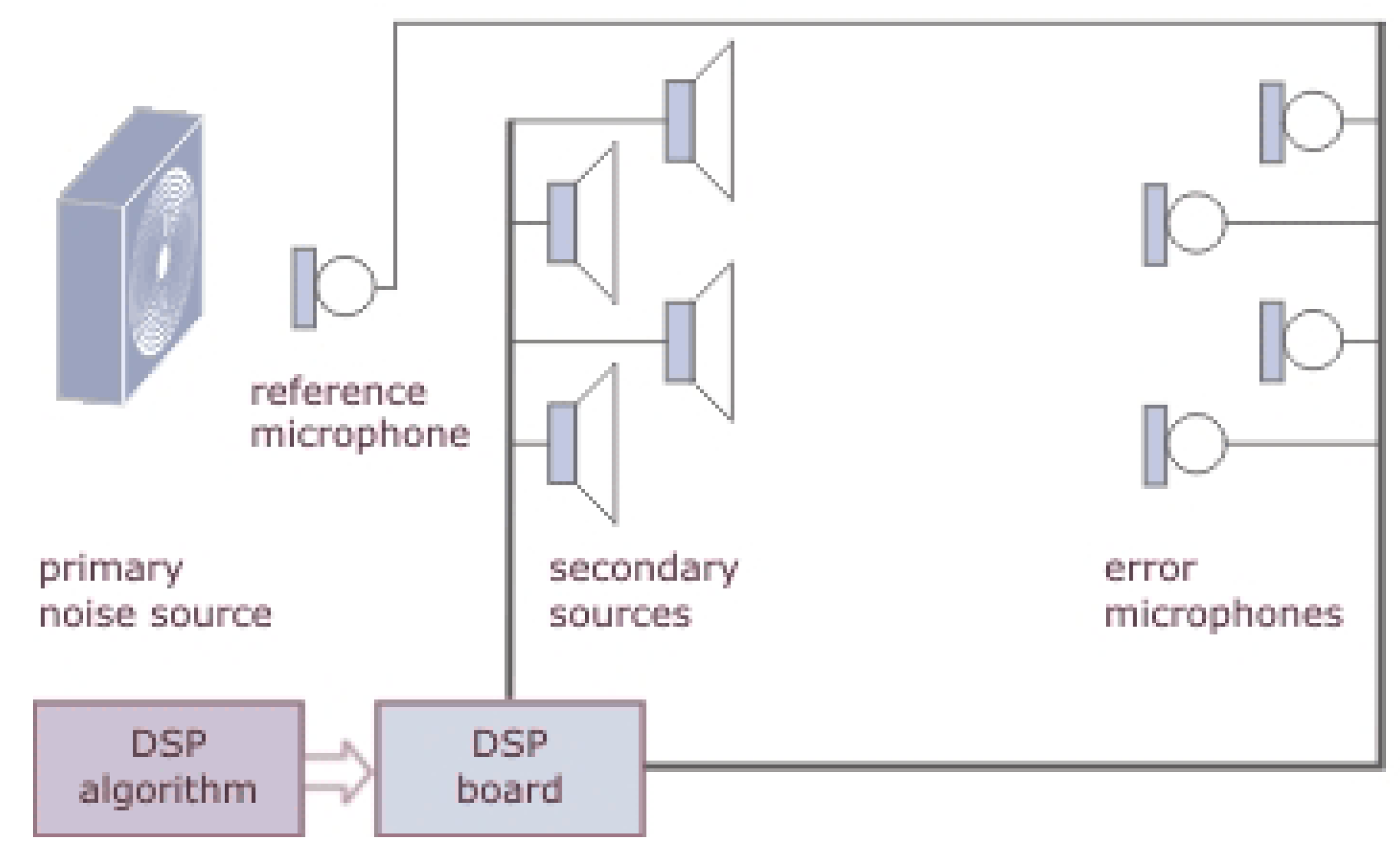
4. Schrödinger and Maxwell Equations Commutators and Incompatible Equations
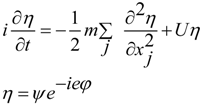
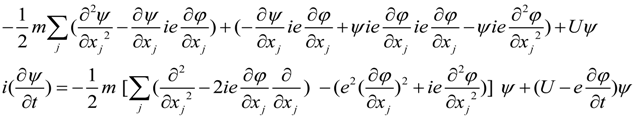
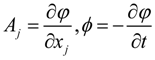
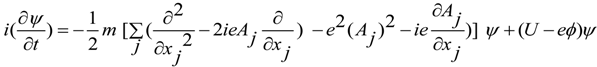
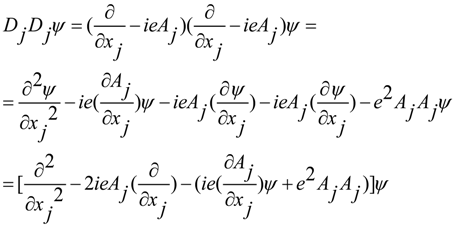
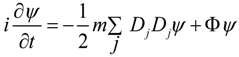
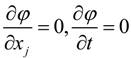
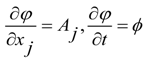
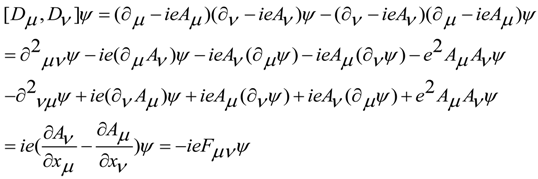
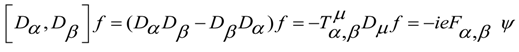
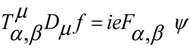
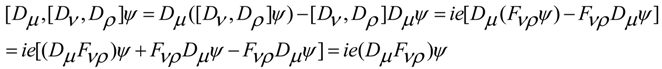
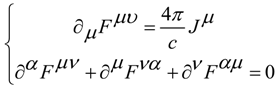
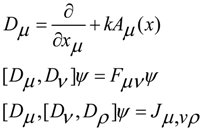
5. Dynamic Equations with Torsion in Non-Conservative Gravity Maxwell-Like Equations
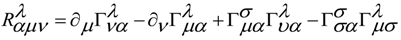
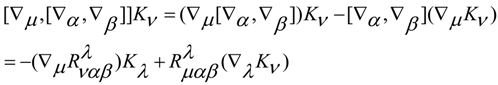
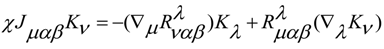

6. Conclusions
- (a)
- The description of a suitable substratum and its global and local properties on invariance;
- (b)
- The field potentials are compensative fields defined by a gauge covariant derivative. They share the global invariance properties with the substratum;
- (c)
- The calculation of the commutators of the covariant derivatives in (b) provides the relations between the field strength and the field potentials;
- (d)
- The Jacobi identity applied to commutators provides the dynamic equations satisfied by the field strength and the field potentials;
- (e)
- The commutator between the covariant derivatives (b) and the commutator (c) (triple Jacobian commutator) fixes the relations between field strength and field currents.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Caianello, E. Quantum and other physics as systems theory. La Rivista del Nuovo Cimento 1992, 15, 1–65. [Google Scholar]
- Kozma, R.; Pino, R.E.; Pazienza, G.E. Advances in Neuromorphic Memristor Science and Applications; Springer: Berlin, Germany, 2012. [Google Scholar]
- Resconi, G.; Licata, I. Geometry for a brain. Optimal control in a network of adaptive memristor. Adv. Studies Theor. Phys. 2013, 7, 479–513. [Google Scholar]
- Ruggero, M.L.; Tartaglia, A. Einstein—Cartan theory as a theory of defects in space-time. Am. J. Phys. 2003, 71, 1303–1313. [Google Scholar] [CrossRef]
- Kleinert, H. Gauge Fields in Condensed Matter, Volume II: Stresses and Defects; World Scientific: Singapore, 1989. [Google Scholar]
- Jessel, M. Acoustique Theorique. Propagation et holophonie; Masson: Paris, France, 1973. [Google Scholar]
- Jessel, M.; Resconi, G. A general system logical theory. Int. J. Gen. Syst. 1986, 12, 159–182. [Google Scholar] [CrossRef]
- Vuksanovic, B.; Nikolic, D. Multichannel Active Noise Control in Open Spaces. In Proceedings of ICCC 2004, Zakopane, Poland, 25–28 May 2004.
- Russer, P. The Geometric Representation of Electrodynamics by Exterior Differential Forms. In Proceedings of the TELSIKS 2013, Nis, Serbia, 16–19 October 2013.
- Mignani, R.; Pessa, E.; Resconi, G. Non-conservative gravitational equation. Gen. Relat. Gravit. 1997, 29, 1049–1073. [Google Scholar] [CrossRef]
- Mignani, R.; Pessa, E.; Resconi, G. Electromagnetic-like generation of unified-Gauge theories. Phys. Essay 1999, 12, 62–79. [Google Scholar] [CrossRef]
- Hamani Daouda, M.; Rodrigues, M.E.; Houndjo, M.J.S. New black holes solutions in a Modified Gravity. ISRN Astron. Astrophys. 2011, 2011. [Google Scholar] [CrossRef]
- Licata, I. Methexis, mimesis and self duality: Theoretical physics as formal systems. Versus 2014, 118, 119–140. [Google Scholar]
- Aitchinson, I.J.R.; Hey, A.J.G. Gauge Theories in Particle Physics: A Practical Introduction, 4th ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Resconi, G.; Marcer, P.J. A novel representation of quantum cybernetics using Lie algebras. Phys. Lett. A 1987, 125, 282–290. [Google Scholar] [CrossRef]
- Fatmi, H.A.; Marcer, P.J.; Jessel, M.; Resconi, G. Theory of cybernetic and intelligent machine based on Lie commutators. Int. J. Gen. Syst. 1990, 16, 123–164. [Google Scholar] [CrossRef]
- Resconi, G. Geometry of Knowledge for Intelligent Systems; Springer: Berlin, Germany, 2013. [Google Scholar]
- Licata, I.; Resconi, G. Information as Environment Changings. Classical and Quantum Morphic Computation. Methods, Models, Simulation and Approaches. Toward A General Theory of Change; Minati, G., Pessa, E., Abram, M., Eds.; World Scientific: Singapore, 2012; pp. 47–81. [Google Scholar]
- Licata, I. Beyond turing: Hypercomputation and quantum morphogenesis. Asian Pacif. Math. Newsl. 2012, 2, 20–24. [Google Scholar]
- Kleinert, H. Nonabelian Bosonization as a nonholonomic transformations from Flat to Curved field space. Ann. Phys. 1997, 253, 121–176. [Google Scholar] [CrossRef]
- De Witt, B.; Nicolai, H.; Samtleben, H. Gauged Supergravities, Tensor Hierarchies and M-theory. 2008. Available online: http://arxiv.org/pdf/0801.1294.pdf (accessed on 22 July 2014).
- Mukhi, S. Unravelling the Novel Higgs Mechanism in (2+1)d Chern-Simons Theories. J. High Energy Phys. 2011, 83. [Google Scholar] [CrossRef]
Appendix A
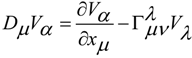
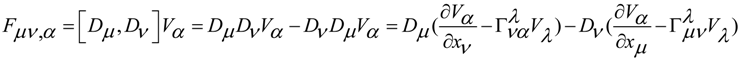
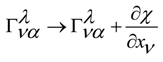
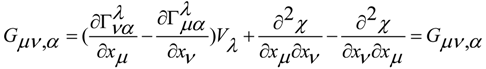
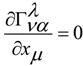
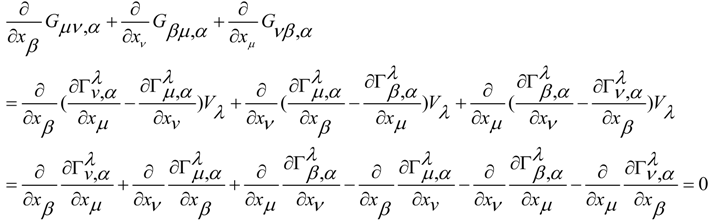
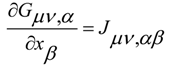
 in a non-linear material where we have complex non-linear phenomena inside the virtual material that represents the vacuum. In the previous equations, in the free field of the medium the Proca terms Γρ Γλ , the Chern-Simons terms ( ∂ν Γρ ) Γλ and the Maxwell-like terms ( ∂ν Γρ ) ( ∂μ Γλ ) are present. So, we have the mass terms, the topologic terms and the electromagnetic-like field terms. We can model the gravitational wave with torsion as a particle in a non-linear medium which gives the mass of the particle, in a way that can be compared to usual SSB processes of the standard model, for an orientation in extensive literature [20,21,22].
in a non-linear material where we have complex non-linear phenomena inside the virtual material that represents the vacuum. In the previous equations, in the free field of the medium the Proca terms Γρ Γλ , the Chern-Simons terms ( ∂ν Γρ ) Γλ and the Maxwell-like terms ( ∂ν Γρ ) ( ∂μ Γλ ) are present. So, we have the mass terms, the topologic terms and the electromagnetic-like field terms. We can model the gravitational wave with torsion as a particle in a non-linear medium which gives the mass of the particle, in a way that can be compared to usual SSB processes of the standard model, for an orientation in extensive literature [20,21,22].© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Resconi, G.; Licata, I. Beyond an Input/Output Paradigm for Systems: Design Systems by Intrinsic Geometry. Systems 2014, 2, 661-686. https://doi.org/10.3390/systems2040661
Resconi G, Licata I. Beyond an Input/Output Paradigm for Systems: Design Systems by Intrinsic Geometry. Systems. 2014; 2(4):661-686. https://doi.org/10.3390/systems2040661
Chicago/Turabian StyleResconi, Germano, and Ignazio Licata. 2014. "Beyond an Input/Output Paradigm for Systems: Design Systems by Intrinsic Geometry" Systems 2, no. 4: 661-686. https://doi.org/10.3390/systems2040661