1. Introduction
Vladimir Fock (1898–1974) was undoubtedly one of the greatest personalities of Soviet theoretical physics. His technical and conceptual contributions to the theory of general relativity (although he did not like to call it this way, Relativistic Theory of Gravitation was his favourite name, in agreement with H. Bondi [
1,
2]), to both classical and relativistic QM and the quantum field theory (think of the spaces that bear his name) are widely known [
3].
Fock was a protagonist of the construction of QM and its dissemination in the USSR. He participated in the “defence” of this theory and, in particular, of the “Copenhagen interpretation”, from the attacks by Soviet ideologues, often playing his card in advance and always successfully. However, he was also an acute critic of the contradictions and half-truths of the Bohr school “from inside”, and he had an important impact on its evolution. It is not possible, in this short note, to retrace the steps of his itinerary and the interested reader is referred to other works [
4,
5,
6,
7].
This work focuses on what can undoubtedly be considered the goal of Fock’s philosophical reflection on the foundations of QM, with particular reference to the non-relativistic QM. This goal is represented by the article entitled “Quantum Physics and Philosophical Problems”, published in Foundations of Physics in 1971. The article is the English version of papers published in Russian at about the same time [
8,
9,
10].
In this article, Fock analyses the difference between classical and quantum measurement procedures, and introduces the awe-inspiring concept of “relativity with respect to the means of observation”, which we will focus on later. One must remember that Fock was a supporter of dialectical materialism by conviction, not by chance (as we know from reading his private papers) and the article contains several points of reference to that doctrine (For example, at page 303: “We see once more that even the electron is inexhaustible”. Only two references are listed and the first is “Materialism and Empiriocriticism” by V. Lenin). However, even a rather rapid reading of the article clearly demonstrates the substantial immunity to this type of philosophy, apart from the author’s strong fascination for the same. The text, in fact, never refers to the fundamental aspect of Diamat, that is the supposed dialectical relationship (or “dialectical contradiction”) between things or events, for example between the preparation and the detection of a micro-object.
It can be assumed that the “dialectical materialism” was, in Fock’s mind and most likely that of other Soviet physicists, nothing more than a synonym for “realism”, i.e., affirmation of the existence of an objective world beyond the observations. We will come back to the significance of objectivity for Fock later on.
The remainder of this note is organised as follows. In
Section 2, we will examine the central concepts of Fock’s work, introducing his “relativity with respect to the means of observation”. In
Section 3, Fock’s “relativity” is reviewed focusing on the aspect of time reversal invariance of the microscopic component of the experiment (micro-process or micro-object). When this invariance is made explicit, it allows a reinterpretation of Fock’s proposal which does not differ—at least in substance—from the “transactional” proposal presented by Cramer a decade later. In
Section 4, we re-examine the question of collapse and its physical meaning under different viewpoints. Finally, in
Section 5, we introduce the Born rule by using the transactional approach, which can be considered the most recent fruit of Fock’s philosophy and Cramer’s physics.
2. The Relativity to the Means of Observation
Fock assumes a fundamental distinction between
apparatuses of observation/measurement, which are physical systems described by classical laws, and
micro-objects, described by quantum laws. At a classical level the choice of the measuring apparatus can affect the observed object, perturbing its physical quantities but, at least in principle, this perturbation is always eliminable by means of definite correction procedures. For example, the trajectory of a falling object can be vertical in a reference system and parabolic in another; it is actually the same process described with different coordinates. In QM this issue is more complex (hereinafter the sentences in italic are reported from [
8]):
…the very possibility of observing such micro-processes presupposes the presence of definite physical conditions that may be intimately connected with the nature of the phenomenon itself. The fixation of these physical conditions does not only determine a reference system, but also requires a more detailed physical specification.
Therefore, the physical process should not be considered “in itself”, but always in relation to these conditions. We can note that this statement admits a profound implication: the wavefunction of a system is indeed relative to a statistical ensemble which is not a set of intrinsically identical micro-objects; it is instead a set of identical preparations (or detections) of the micro-object in a defined experimental setup. The legacy of controversy with D. Blokhintsev is here evident; Blokhintsev had previously supported the exactly opposite point of view, at a distance from operationality.
Both the measurement apparatuses and micro-objects are subject to the uncertainty principle. However, the uncertainties of the physical quantities that describe the status of the apparatus are much greater than their minimum values that appear in the Heisenberg inequalities; hence, the operation of the measuring apparatus is in fact classical. The language used for the measurements is therefore that of classical physics. It is at this level that Fock’s “realism” emerges. Fock does not deny the objective reality of the micro-processes, but states that their characterization is only possible through experimental operations that imply the use of apparatuses, which are also objectively existing physical entities. This characterization is summarized in the wavefunction, which is hence related to the preparation of the micro-object; it remains the same regardless of the choice of the next measurement setup, and it is precisely in this sense that it constitutes an “objective” characteristic of the micro-process.
At this point, Fock observes that the “complementary” characteristics of the processes/quantum objects illustrated in detail by Bohr appear:
(…) only under different and incompatible conditions, while under attainable conditions they manifest themselves only partially, in a “milder” form (e.g., approximate localization, allowed by the Heisenberg relations in coordinate space and in momentum space).
There is no sense in considering simultaneous manifestations of complementary properties in their sharp form; this is the reason why the notion of “wave-corpuscular dualism” is self-consistent and devoid of contradictions.
Using a more modern language, we can say that the corpuscular behaviour only occurs during the emission or absorption of a micro-object, while the wave-like behaviour occurs during the propagation of the micro-object; this means that the two aspects are never in opposition to each other because they occur at different
moments in time. The meaning of the passage by Fock, however, is different: it is not possible to exactly measure conjugated variables that enter into the same uncertainty inequality. Likewise, it is impossible to conduct experiments where the same micro-object simultaneously interferes with itself (wave-like behaviour) and does not interfere with itself (corpuscle behaviour). Thus, a micro-object prepared in a certain way gives rise to different behaviours when, after its preparation, it interacts with different apparatuses. This is the principle of “relativity with respect to the means of observation”. We underline the pertinence of the term
relativity: also in Einstein theory, actually, space and time find their sense as “theatre of coordinates” in a set of measurement procedures that the inertial observers share. At this point, Fock introduces his fundamental distinction between
initial experiment,
final experiment and
complete experiment
. The initial experiment includes the preparation of the micro-object, for instance of a beam of electrons of a given energy, and the conditions subsequent to this preparation, for instance, the passage of the beam through a crystal; this fixes the properties of the micro-object that will be explored in a subsequent
final experiment. In Fock’s words, the initial experiment refers to
the future, the final experiment to
the past. An important fact of Nature, that Fock mentions explicitly, is that once the initial experiment has been fixed, the final experiment can still be selected in a variety of different ways. The ensemble of an initial experiment and a final experiment
actually performed is referred to as a complete experiment. It is the result of the complete experiment which should be compared with the theoretical prediction:
The problem of the theory is thus to characterize the initial state of a system in such a way that it would be possible to deduce from it the probability distributions for any given type of final experiment. This would give a complete description of the potentialities contained in the initial experiment.
So Fock interprets the wavefunction “collapse” with the usual image of the passage from potency into act. This transition is not a choice between different pre-existing possibilities, but an actual creation of previously inexistent features. Although Fock never use the term “creation”, it should be acknowledged that the concept is surprising for a dialectical materialist!
Fock does not explain the existence of probability distributions for the results of a given final experiment in place of classical Laplacian determinism, and simply states that it “necessarily” derives from relativity to the means of observation. In fact, he postulates the Born rule.
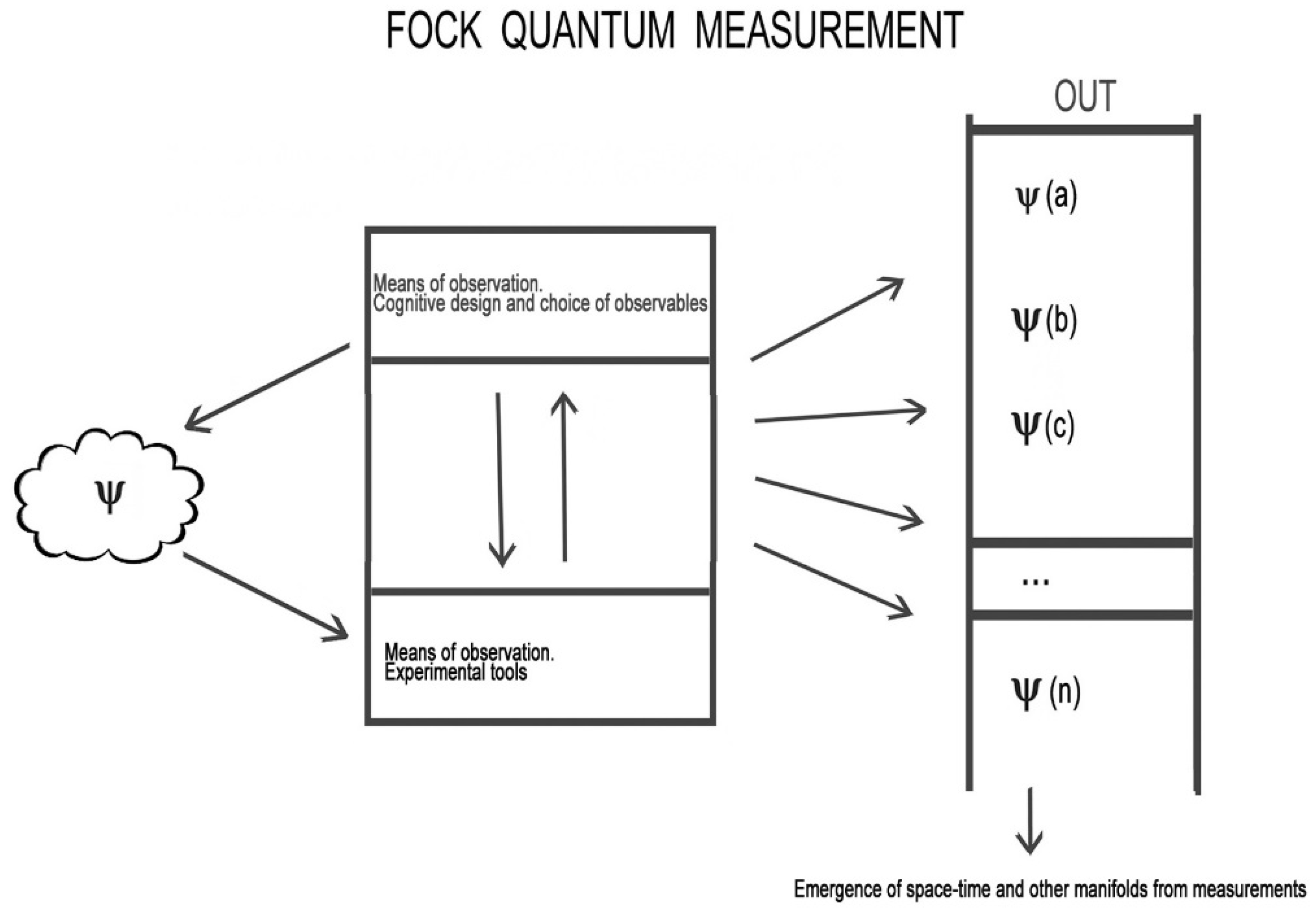
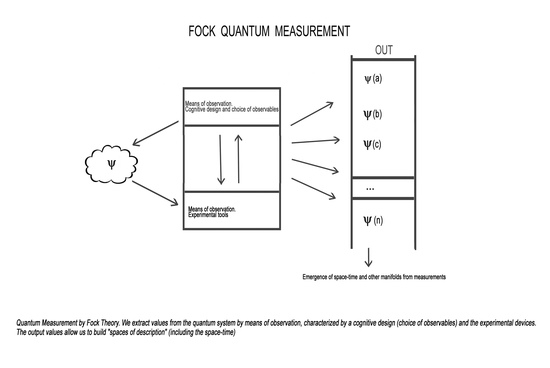
A further aspect worthy of note is the following: since the probability distribution of a given final experiment is derivable (at least in principle) by the wavefunction associated with the preparation during the initial experiment (If we wanted to take the actualisation concept seriously, we would have to view the initial wavefunction as a sort of “archetype” or, by using a language closer to the new theoreticians of quantum information, an atemporal cosmic code, as in J. A. Wheeler “It from Bit”), it will also depend on the value of the parameters that appear in this wavefunction. Some of these parameters may have nothing to do with positions or motions in space, so the completely new idea of non-spatiotemporal degrees of freedom is introduced. This category includes quantities such as the spin, isospin and strangeness. Following in Bohr’s footsteps, Fock elaborates a much more radical position, close to the Heisenberg’s one, and shifts the interpretative axis from the
naive wave/particle dualism to the revolutionary idea of a logics of quantum events (
Figure 1).
Figure 1.
Fock quantum measurement.
Figure 1.
Fock quantum measurement.
Before closing this Section it seems useful to highlight an objection by Selleri [
11] to the principle of relativity to the means of observation. Selleri considers a variant of the double-slit experiment in which two semi-transparent detectors are positioned behind the two slits. Each of the two detectors allows the particle to pass undisturbed with a probability
p, or is activated—detecting the passage—with probability 1-
p. The distribution of the impacts on the rear screen will hence be the weighted average of three distributions: one (without interference fringes) relating to events in which the first detector has been activated, one (also without fringes) relating to events in which the other detector has been activated, and finally one (with interference fringes) relating to the passages during which neither of the two detectors were triggered. Therefore, with the same measurement apparatus, comments Selleri, it is possible to have behaviours of the micro-object during its propagation that are particle-like (absence of self-interference) and wave-like (presence of self-interference). This disproves the position of Fock according to whom it is the apparatus that determines the behaviour of the micro-object.
Selleri’s position does not, in our opinion, take into account the clear distinction that Fock makes between initial experiment and final experiment. In the setup proposed by Selleri, the final experiment is always the same (the impact of the particle on the rear screen) but we are in presence of three distinct initial experiments. In the first experiment, the particle is prepared in the source and is then passed through the first detector; in the second experiment, the particle is prepared in the source and is then passed through the second detector; in the third experiment, the particle is prepared in the source and then passed through both detectors. So, the particle propagates itself as a corpuscle in the first two cases, and as a wave in the third case. These two possibilities never occur simultaneously in the same complete experiment.
3. From Fock to Cramer
Let us consider the complete experiment during which a micro-object is prepared in the state associated with the wavefunction Ψ and detected in the final state Φ. The “passage from potency into act” is a metaphor that Fock applies to the process Ψ → Φ, but could just as well be applied to the reverse process Φ * → Ψ * on the advanced conjugated wavefunctions.
In fact, due to the substantial reversibility in time of the micro-processes, this metaphor must be applicable in both ways, if it is acceptable to apply it in one of them. This means that the detection is the initial event that induces in the past—in the presence of appropriate physical conditions (initial experiment by Fock)—the preparation of the micro-object in a certain state, by means of a “collapse”. The complete experiment of Fock is then described by the ordered pair (Ψ, Φ), and this pair contains all the information related to the history of the micro-object: there is no longer any “quantum randomness”. This appears when only one of the two terms of the pair is fixed, and so the other takes on different values with different probabilities. Probabilities which, as expressed by the Born rule, are standard Kolmogorovian probabilities.
A final experiment of a given complete experiment can serve as an initial experiment of a second complete experiment; this may give rise to a causal chain (…, Ψ) (Ψ, Φ) (Φ, …) in which the ordinary time-oriented formulation of the principle of causality applies between the individual pairs of the chain, but not within each pair. To find out more about this aspect, one can consider this sequence as a sequence of pairs …, u)(u, … where u = Ψ, Φ and so on. Each of these pairs represents a single collapse event which includes both an emission of the advanced wavefunction u * towards the past [u)] and the emission of the delayed wavefunction u towards the future [(u]. The emission of u * represents the closing of the previous final experiment, the emission of u represents the opening of the next initial experiment.
It is clear that this variation in Fock’s conceptual model directly introduces the quantum nonlocality (about which Fock could not have a clear view from his historical horizon), and goes very close to the “transactional interpretation” of QM formulated by Cramer 10 years later (In transactional language, the emission of u * is the result of the collapse of the advanced wavefunction coming from the final experiment, whilst the emission of u is the result of the collapse of the delayed wavefunction coming from the initial experiment) [
12,
13,
14].
A complementary reading to the transactional version is also possible: the emission of u * can be seen as the destruction of the u state in some kind of “vacuum” or “void”, while the emission of u can be seen as the creation of u starting from this same “void”. It is easy to see that this scheme reproduces the cognitive (or informational) arrow of time. In fact, the “void” can be equated to a subject who perceives qualia u (u * = annihilation of u that “enters into the vacuum”) and acts by projecting the content u (emission of u which “exits from the vacuum”). The well-known scheme is therefore reproduced according to which the past is what is perceived, while the future is that upon which is possible to act. In more physical terms, the past is the time domain from which signals are received; the future is the complementary time domain, to which one can send signals.
One can notice that the “void” thus introduced, overshadowed by the quantum formalism but not explicitly represented by it, is outside both time and space. Its “subjectivity” is therefore of a non-individualized cosmic nature. It is this entity of background the environment of the various pairs u)(u, and the interface or connection between them. We have to therefore use a non-spatiotemporal interface, from which the temporal (and possibly spatio-temporal) order derives as an emergent property. The vision of the single pair (Ψ, Φ) as a four-dimensional reality that emerges from a diachronic process bidirectional in time, proposed by Cramer and the “hylozoistic” vision in terms of pairs u)(u associated to a void-subject are complementary and compatible. They are related to each other like the vase and the two faces of the famous Gestalt figure.
An important aspect is that the representation of the action of the background (the “void”) does not require Hamiltonian operators, because it is in fact a form of vertical causality that connects the manifest physical reality with a different, unmanifest and timeless state of that same reality. In the usual quantum formalism, this action is however represented by the projector | u><u |. It transforms the ket | u’> into a new ket proportional to | u>, and acts in a similar way on the bra <u’ |; in both cases a representation of the quantum leap u’ → u is given. The initial and final extremes of a transaction hence consist of real quantum leaps, such as the decay of a nucleus or the ionization of an atom. Fock’s reasoning, restricted to measurement apparatuses and procedures, can therefore be generalized in relation to any process enclosed within real quantum leaps. So, vice versa, there is never an entanglement between the base states of the micro-object and those of the apparatus in a measurement process; a conclusion that leads to the elimination of the same premise on which the measurement theory, from Von Neumann onwards, has always been based.
A photon impinging on a photographic plate is localized as a quantum leap, consisting in the reduction of a single molecule of silver halide in the emulsion. The determination of the state occurs at this micro-interaction level, while the rest of the measuring chain is classical: the subsequent photographic process leads to the fixation of the darkening of a single halide granule, the one which the reduced molecule belongs to. The subsequent scan of the plate can do nothing but detect that granule as a separate pre-existing object with pre-existing properties (e.g., darkening).
A major limitation that the interpretation of Fock shares with that of Copenhagen is hence superseded, namely the ambiguity on the nature of the wavefunction collapse and the conditions under which it occurs (measurement processes only?). The reduction process does, in fact, become objective, and identified in real quantum leaps.
The problem of the origin of randomness in QM therefore returns to the problem of the randomness of quantum leaps. However, any solution to this problem would invariably require the definition of an ontology to support the QM formalism, and a deliberately minimalist interpretation such as that proposed by Fock does not take such problems into consideration.
Yet, due to its minimalism, Fock’s proposal can be very useful for all those using the theory (especially non-relativistic) in application domains such as molecular physics, solid state, etc. which require a clear and simple metatheoretical reference. They are, in fact, interested in a clear and direct connection with the experiments and, in this respect, Fock’s proposal is without doubt excellent.
4. The Theories of Collapse: From a “Freak” Postulate to a New Physics
Since the early QM axiomatic formulations the state vector collapse got a status similar to the parallel postulate in Euclidean Elements. Just like that, it has been necessary that a new physical view took place to eliminate its ambiguities. We can here just give a short survey of the essential steps of such a complex topic.
It is well known the controversy on the hidden variable theories, solved by the J. Bell clarifying work [
15,
16] and the collateral debate on the QM “without observers” [
17,
18]. At first, the concept of “particle localization” was given special attention because of the De Broglie motion dogma which invoked the necessity not to renounce to precise space-temporal images able to make clear “what we are speaking of”.
In the meantime, a more physical research line, based on the thermodynamics of the relation between the microphysics (of the measured entities) and the macrophysics (of the measurement apparatus) was taking shape. An irreversible passage during the measurement process was the core of this idea. In other words, the measurement tools transfer their interaction with the quantum objects in the macroscopic world, so fixing the obtained information in an irreversible way. Such quantum theory of measurement was based on ergodic considerations which made it possible to build up an equation able to operate a selection between the states of the microscopic system and those of the tool, formalized by an opportune Hamiltonian. We remember here the fundamental results by the Milan-Brescia group (P. Caldirola, A. Loinger, M. Prosperi, P. Bocchieri) [
19,
20]. Also, in this case, we can observe that the definition of the micro-observables is the semi-classical one suggested by the Schrödinger equation, so heavily conditioned by epistemological assumptions related to the concept of “particle”.
An interesting filiation of these ideas has been proposed in the GRW theory since 1985. It is a very ambitious idea because it aims to solve the QM macroscopic ambiguities by introducing a spontaneous localization time, linked to both the space-time structure and the number of constituents in the system [
21,
22]. Beyond the question of micro-objectivation, the GRW theory shifts the collapse from the sphere of the measurement processes to the physical environment itself. As is known, the interest for the emerging of the macroscopicity is central also in the thermal QFT where it is possible to consider the environment as a “measurement tool” with respect to the possible histories of the quantum system (see e.g., [
23]). The developments of GRW theory and the transactional approach have suggested far too radical ideas, such as the emerging of space-time starting from Relativistic GRW flash nets (Tumulka) or non-local transactions [
14,
24,
25,
26,
27]. Such reading of the “spontaneous collapse”—or R-processes, using the R. Penrose terminology—is, patently, no more an internal debate in QM foundations, but a new working hypothesis regarding, for example, the radical role of non-locality in Quantum Cosmology. Recently, the authors have proposed a Big-Bang description as nucleation by vacuum via R processes in a De Sitter space [
28,
29,
30].
In a more general way, and in accordance with the Fock view here analyzed, an R process is not only a localization process, but also the bootstrap of a physical event from a pre-spatial and a-temporal structure, which logically precedes the Heisenberg dynamic vacuum of QFT. The idea if a pre-geometric structure of this kind comes out from the quantum gravity’s deep exigencies as well as from other kinds of causal nets discretization, such as Q-Ticks [
31].
5. R Processes and Born Rule
Let us analyze shortly the born rule by using the notion of transaction as a non-local bootstrap mechanism for R processes. For this reading of the
quantum jump, see [
32]. It is clear that such elementary situation is closer to the particle physics than to many-body situations, and so it is unsatisfying to interpret the born rule as an expression of the thermodynamic equilibrium in a phase space of positions [
33]. The theoretical approach here proposed is more general and includes the thermal equilibrium situations as a particular case.
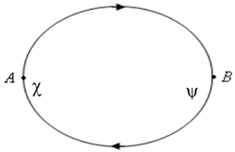
Let us consider two pure quantum states ψ and χ. What we mean here with “pure quantum state” is a quality or a set of qualities which can be directly created/annihilated in a quantum jump. These states can be graphically represented by dots:
The creation of a pure state can be represented by an oriented segment exiting the dot of the state:
alternatively, by the de Beauregaard symbols
׀ ψ),
׀ χ).
The annihilation of a pure state can be represented by an oriented segment entering the dot representing that state:
Alternatively, by the de Beauregard symbols (ψ
׀, (χ
׀.
If a segment exit one of the two states to enter the other one, then the two states will be connected:
The Graph (1) can be read in two different ways corresponding to two different kinds of connections. When we read it from left to right (i.e., following the same direction of the segment) we will see the creation of ψ followed by the destruction of χ. Such a process is expressed by the de Beauregard formalism (that has to be read from right to left) by the form (χ ׀ ψ).
When we read it from right to left (in the opposite direction to the segment), we will see the destruction of χ followed by the creation of ψ that in de Beauregard formalism corresponds to ׀ ψ)(χ ׀.
We can thereby connect the dots by many oriented segments. So, we will have more complex graphs than (1), such as the loop:
The observations we made for Graph (1) are the same for Graph (2) or for more complex ones. We will assume that a graph, whatever complex, is always one-way: in the same directions of the arrows or in the opposite one. In other words, we impose that mixed two-way paths are meaningless. A set of loops following the arrows’ direction will thus correspond to the transaction [
26,
27] whose extremes are the creation of ψ and the destruction of χ (or
vice versa, depending on the sign of energy of the states associated with these qualities). A set of loops following the opposite direction of the arrows will correspond to the projection of the state χ on the state ψ.
In the references [
26,
27,
34], as for the loops following the arrows’ direction, it is shown that the transaction (χ
׀ ψ) is associated with a complex number, called the transaction amplitude, which is represented by the form < χ
׀ ψ > in the ordinary Dirac formalism. The probability to close a transaction given one of its extremes is proportional to the squared module of the amplitude and such result is the Born rule. So, the same conclusions has to be applied to the process of projection | ψ )( χ | because the two processes have the same loop structure and only a different direction. (This projection appears together with its inverse. The correct time orientation is however fixed by the sign of the energy). Thus:
In other words: by destroying the incoming state χ, the probability to get an outgoing state ψ is equal to the probability to get an incoming state ψ for a transaction ending with the destruction of the state χ. Thus, the Born rule shows a
dual structure that makes it possible to express it with reference to both transactions and projections. It is possible to show that such approach naturally leads to the Feynman path integrals [
27].
Obviously, The Born Rule, introduced in this way, refers to projective measurements on pure states. Anyway, the result of the initial experiment may consist also in a mix of pure states represented by a density matrix. The result of the final experiment can be the eigenstate of a certain observable. In the absence of a post-selection, we get an ensemble of transactions having the same initial preparation represented by the mix and different final experiments corresponding to the output of the different eigenstates. Consequently, the statistical mean of the obtained values for the observable is equal to the trace (on the eigenstates of that observable) of the product of the density matrix and the observable itself.
On the other hand, if we take into consideration not just a single transaction, but a couple of connected transactions T1 and T2 (such that the final experiment of T1 coincides with the initial experiment of T2) and we select the output states from the initial experiment of T1 (pre-selection) and the final experiment of the T2 (post-selection), respectively, then the Born Rule takes the form of the well-known ABL Rule [
35].
Under such conditions, if the quantum system under consideration is made of two subsystems weakly coupled and the intermediate projective measurement is taken only on the states of one of them, it is possible—under opportune conditions—to get a “weak” measurement of the other system’s state [
36]. This one undergoes an induced projection whose only effect is a bias in the following time evolution. Such scheme has been used in some recent experiments of great interest (see, for example, [
37,
38]).
A statement ascribed to L. Bragg says: “everything in the future is a wave, everything in the past is a particle”; The R processes provide this sentence with a new and immediate logical meaning. When only one of the transaction’s extremes is fixed, a wide range of possibilities is still open as for the closing of the other extreme, they are compatible with the system’ symmetries and the conservation laws and each of them is associated with an amplitude. For the symmetry of the temporal inversion, it is true also when the opposite extreme is fixed. Fixing both extremes means to look at the whole process of manifestation/demanifestation of the single qualities as the expression of a fundamental non-locality, of which that the more traditional EPR-GHZ phenomena are particular cases.
The passage from an extreme to the other one can take place, as we have seen, through complex chains involving various groups of qualities. Thus, the Born rule expresses both the possibility to close a transaction given one of its extremes (the complete Fock experiment) and the probability to find what concatenation of two transactions is individuated by a R process (in Fock’s terms: the result of a final experiment followed by a given outgoing of an initial experiment). It is, in any case, an emergent aspect of non-locality.
Contrary to what may appear at first sight, an interpretation based on the R processes does not elude the debate on the foundations, but expands it instead. Actually, the wave/particle dualism seems structurally unable to include the non-local features clearly emerged from the experiments in the 80s, to such an extent that it stimulated a new critical debate on Copenhagen Interpretation [
39]. Putting the R processes at the core means introducing
ab initio the non-locality at the heart of QM: a quantum “object” is, after all, a system described by the Feynman Path Integrals [
34,
40] and it is thus the emerging of locality from a non-local background that requires a new meta-theory of QM. The recent debate on Afshar experiment clearly shows that no point of the formalism is thrown into crisis, but its “restrictive” interpretations are [
41].
Such few notes should be sufficient to explain that the relativity with respect to measurement is in no way to be regarded as a sort of relativism or “weak” ontology.
So, our treatment goes beyond the “minimalist” original Fock’s aims, by characterizing it in a “strong” sense which opens the current debate on the emergent reality of micro-processes
6. Conclusions
The relativity with respect to the means of observation therefore remains, in our opinion, a most useful concept for the teaching of QM and for a correct understanding of its physical meaning, at least as far as the non-relativistic domain is concerned. When the advanced propagation of the conjugated wavefunction is taken into account, this approach broadly overlaps the concept of transaction introduced by Cramer later on. We can conclude by stating that this extension of Fock’s proposal, which appears to be very natural, leads to an objective view of the collapse that removes the classical measurement apparatuses from their privileged position and opens a reflection on the R processes’ role in fundamental physics. Instead of a world dissolving in measurements—as the Bohr critics feared—it is just the fidelity to measurements that reveals to us the deep structure of quantum events.
The Fock generation had to face a complicated systemic and epistemological problem: how can we define the objectivity of micro-phenomena considering they are strongly dependent on initial and boundary conditions (see
Section 2)? Is the measurement apparatus’s purpose to make them “real”? Therefore, what is a measurement apparatus? We agree that such questions can find their answers in defining a general ontological scenario, which is still an open debate. That generation had so to adopt necessarily “minimalist” approaches. As contemporary scientists, we re-adopt these approaches with different aims, focusing on the contemporary challenges of QM (non-locality).
In particular, if compared to the “Copenhagen interpretation”, the Fock proposal seems more naturally oriented towards a time symmetric vision of the quantum process. This topic has been strongly sustained by Y. Aharonov and his school. The development of this research initially led to a detailed debate on the statistics of the pre- and post-selected processes, then to the innovative field of the “weak measurements” which are the object of intense experimental research and the subject of debate. In this paper, we tried to develop the Fock thought in the direction of the transactional approach proposed by Cramer in the 80s and still used nowadays. In doing so, we have deliberately stepped a bit towards ontology, going beyond the “minimalism” of the original Fock approach. We find that such passage is made clear in the second part of the paper when we refer to the objective reduction programs and the transactions as an emergent phenomenon.
The interest from the systemic viewpoint is connected to the general discussion on the measurement processes. As it is well known in the study of complex systems, the observer and the observed are a model dependent dipolar entity, closely linked to what we want to observe. In the theory here presented, all the observables arise from a process depending both on the system’s logic and the way we obtain information about it. The space-time itself takes on emergent features in such scenario: the relational theatre originates from its actors!
In this sense, we seem that the Fock reflection is exemplary and paradigmatic for the system and emergence theories.