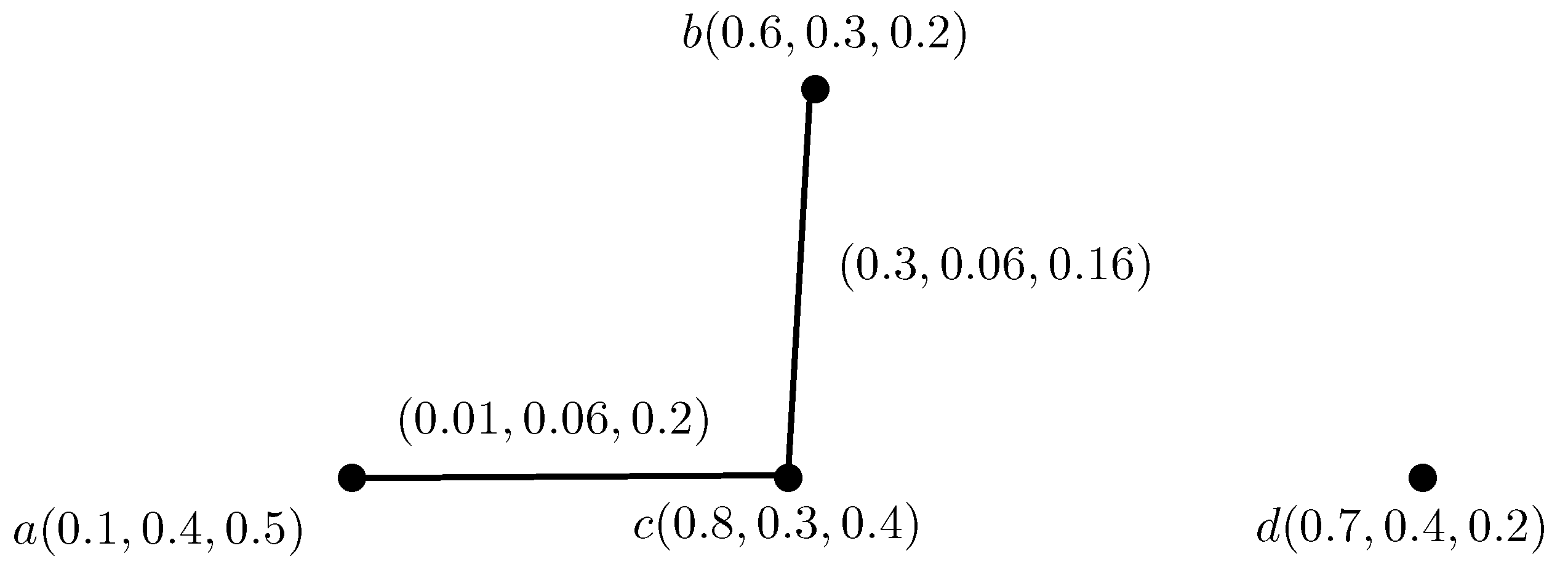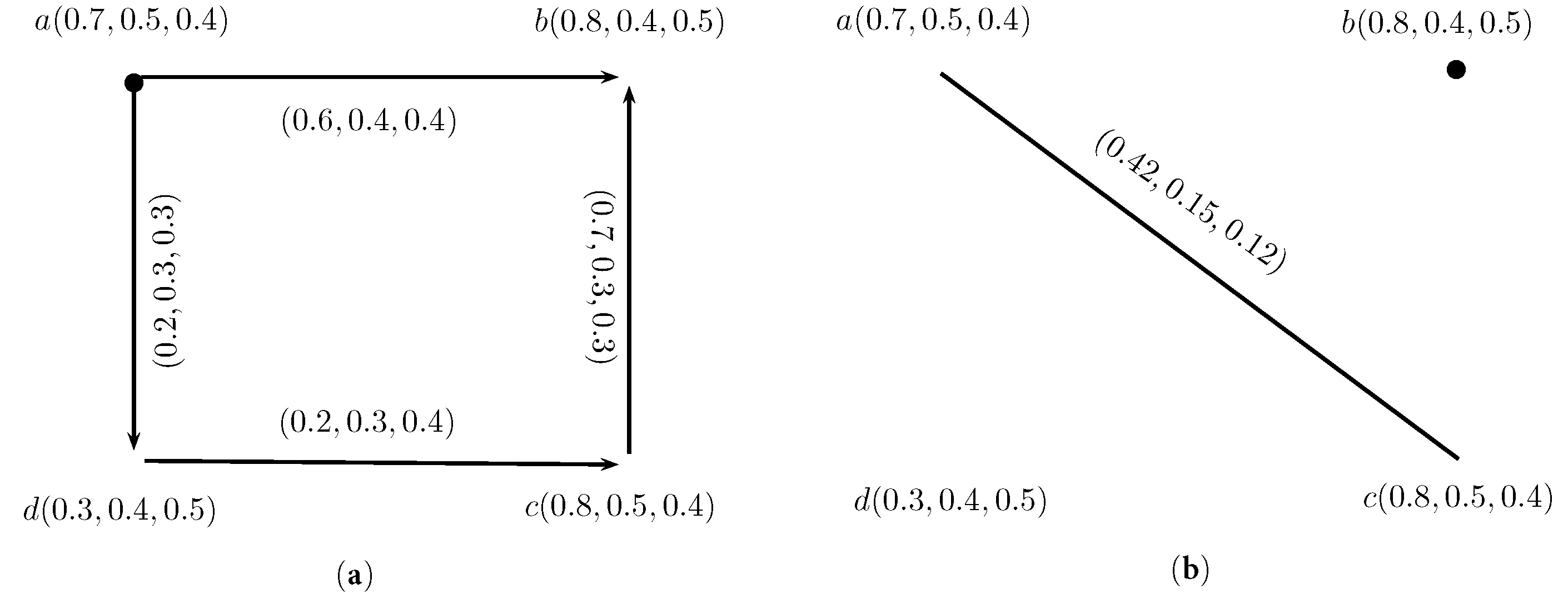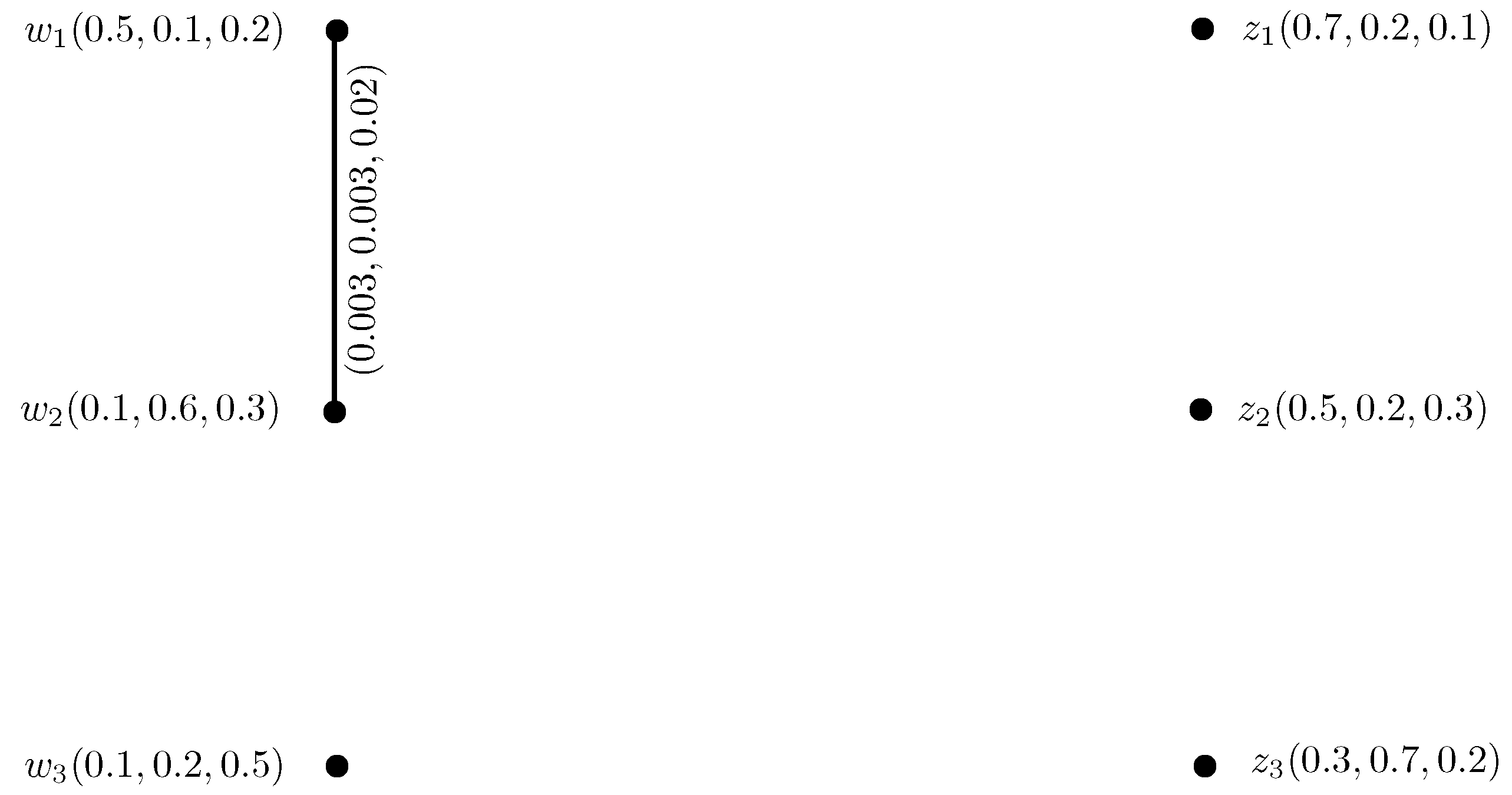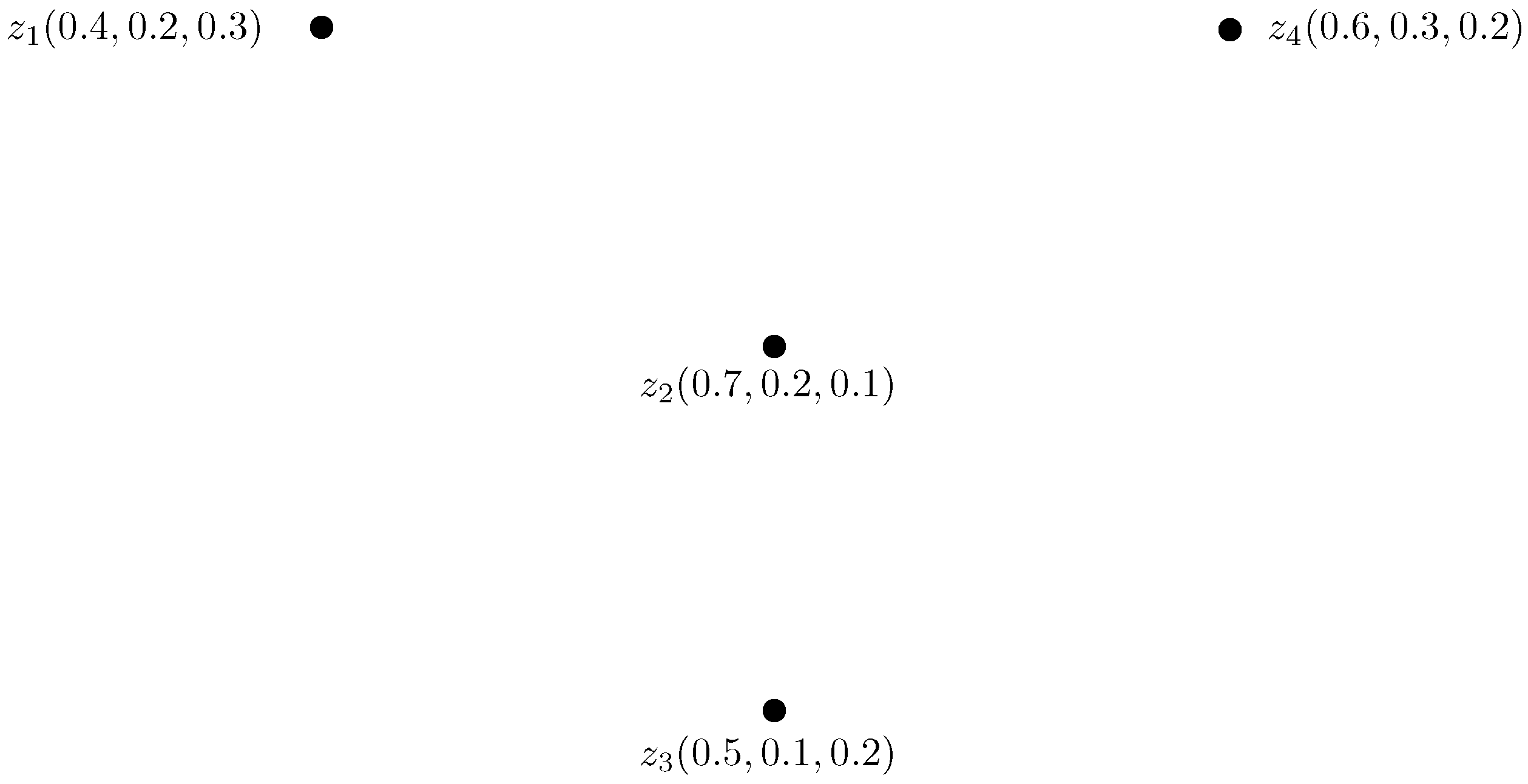1. Introduction
Euler [
1] introduced the concept of graph theory in 1736, which has applications in various fields, including image capturing, data mining, clustering and computer science [
2,
3,
4,
5]. A graph is also used to develop an interconnection between objects in a known set of objects. Every object can be illustrated by a vertex, and interconnection between them can be illustrated by an edge. The notion of competition graphs was developed by Cohen [
6] in 1968, depending on a problem in ecology. The competition graphs have many utilizations in solving daily life problems, including channel assignment, modeling of complex economic, phytogenetic tree reconstruction, coding and energy systems.
Fuzzy set theory and intuitionistic fuzzy sets theory are useful models for dealing with uncertainty and incomplete information. However, they may not be sufficient in modeling of indeterminate and inconsistent information encountered in the real world. In order to cope with this issue, neutrosophic set theory was proposed by Smarandache [
7] as a generalization of fuzzy sets and intuitionistic fuzzy sets. However, since neutrosophic sets are identified by three functions called truth-membership
, indeterminacy-membership
and falsity-membership
, whose values are the real standard or non-standard subset of unit interval
. There are some difficulties in modeling of some problems in engineering and sciences. To overcome these difficulties, Smarandache in 1998 [
8] and Wang et al. [
9] in 2010 defined the concept of single-valued neutrosophic sets and their operations as a generalization of intuitionistic fuzzy sets. Yang et al. [
10] introduced the concept of the single-valued neutrosophic relation based on the single-valued neutrosophic set. They also developed kernels and closures of a single-valued neutrosophic set. The concept of the single-valued intuitionistic neutrosophic set was proposed by Bhowmik and Pal [
11,
12].
The valuable contribution of fuzzy graph and generalized structures has been studied by several researchers [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22]. Smarandache [
23] proposed the notion of the neutrosophic graph and separated them into four main categories. Wu [
24] discussed fuzzy digraphs. Fuzzy
m-competition and
p-competition graphs were introduced by Samanta and Pal [
25]. Samanta et al. [
26] introduced
m-step fuzzy competition graphs. Dhavaseelan et al. [
27] defined strong neutrosophic graphs. Akram and Shahzadi [
28] introduced the notion of a single-valued neutrosophic graph and studied some of its operations. They also discussed the properties of single-valued neutrosophic graphs by level graphs. Akram and Shahzadi [
29] introduced the concept of neutrosophic soft graphs with applications. Broumi et al. [
30] proposed single-valued neutrosophic graphs and discussed some properties. Ye [
31,
32,
33] has presented several novel concepts of neutrosophic sets with applications. In this paper, we first introduce the concept of intuitionistic neutrosophic competition graphs. We then discuss
m-step intuitionistic neutrosophic competition graphs. Further, we describe applications of intuitionistic neutrosophic competition graphs in ecosystem and career competition. Finally, we present our developed methods by algorithms.
Our paper is divided into the following sections: In
Section 2, we introduce certain competition graphs using the intuitionistic neutrosophic environment. In
Section 3, we present applications of intuitionistic neutrosophic competition graphs in ecosystem and career competition. Finally,
Section 4 provides conclusions and future research directions.
2. Intuitionistic Neutrosophic Competition Graphs
We have used standard definitions and terminologies in this paper. For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44].
Definition 1. [38] Let X be a fixed set. A generalized intuitionistic fuzzy set I of X is an object having the form I=, where the functions and define the degree of membership and degree of non-membership of an element , respectively, such that: This condition is called the generalized intuitionistic condition.
Definition 2. [11] An intuitionistic neutrosophic set (IN-set) is defined as , , , , where:for all, , such that: Definition 3. [12] An intuitionistic neutrosophic relation (IN-relation) is defined as an intuitionistic neutrosophic subset of , which has of the form:where , and are intuitionistic neutrosophic subsets of satisfying the conditions: - 1.
one of these , , , and , is greater than or equal to ,
- 2.
.
Definition 4. An intuitionistic neutrosophic graph (IN-graph) , h, (in short ) on X (vertex set) is a triplet such that:
- 1.
, , ,
- 2.
, , ,
- 3.
, for all ,
where,denote the truth-membership, indeterminacy-membership and falsity-membership of an element and: denote the truth-membership, indeterminacy-membership and falsity-membership of an element , (edge set). We now illustrate this with an example.
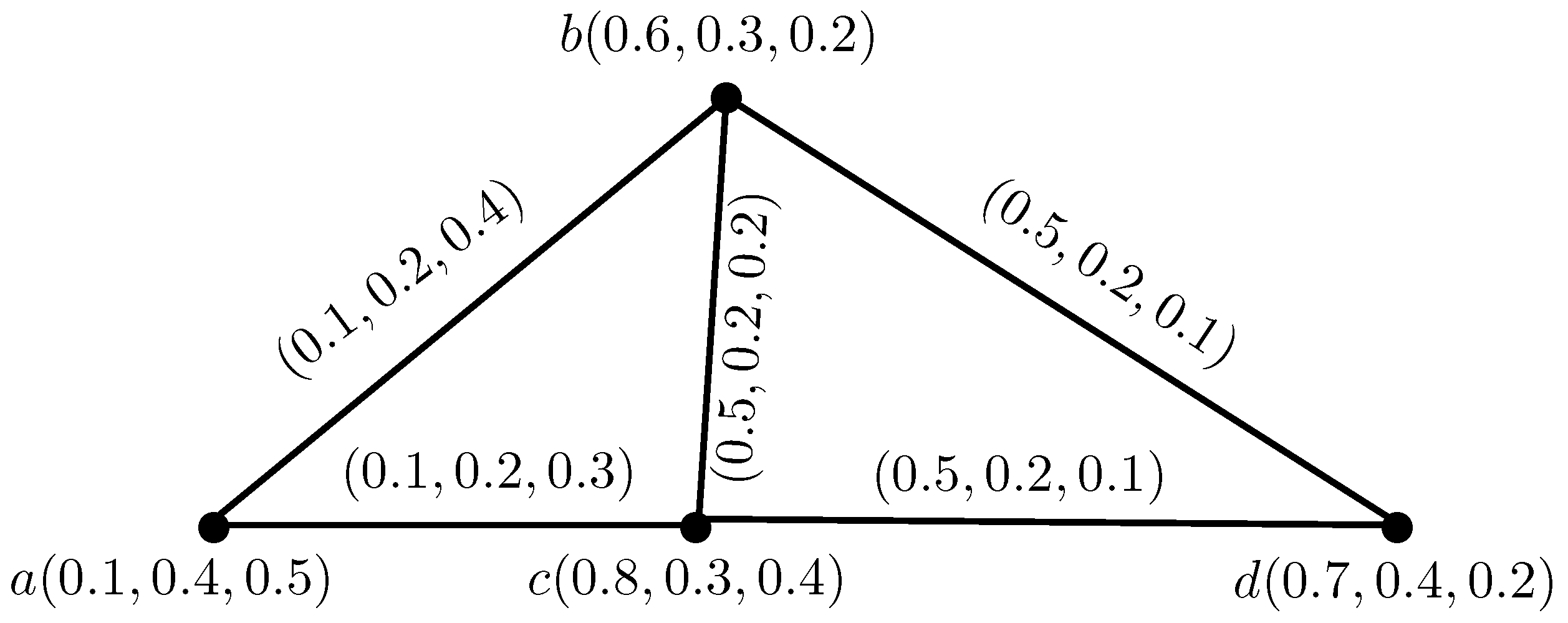
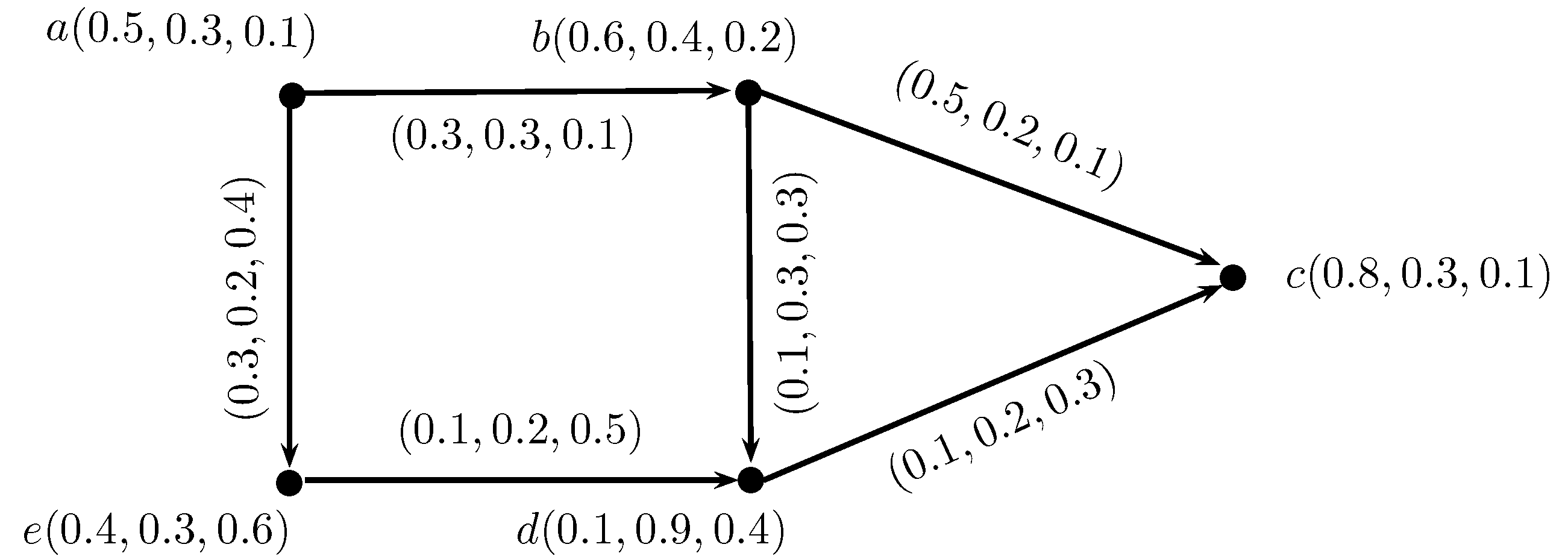
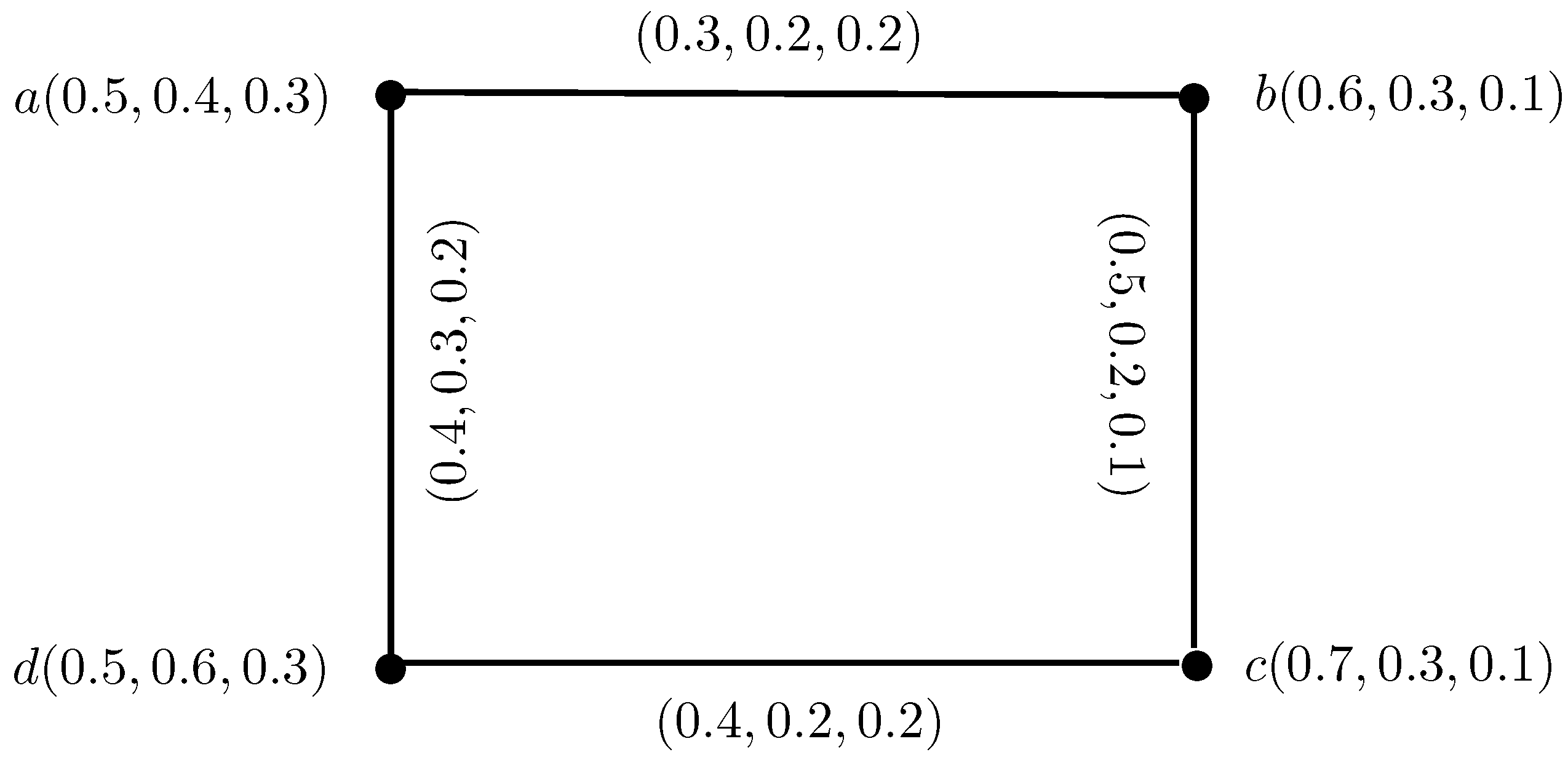
Example 1. Consider IN-graph on non-empty set X, as shown in Figure 1. Definition 5. Let be an intuitionistic neutrosophic digraph (IN-digraph), then intuitionistic neutrosophic out-neighborhoods (IN-out-neighborhoods) of a vertex w are an IN-set:where,such that defined by , defined by and defined by . Definition 6. Let be an IN-digraph, then the intuitionistic neutrosophic in-neighborhoods (IN-in-neighborhoods) of a vertex w are an IN-set:where, such that defined by , defined by and defined by . Example 2. Consider , h, to be an IN-digraph, such that, , b, c, d, , a, , , , (b, , , , (c, , , , (d, , , , (e, , , and , , , , , , , , , , , , , , , , , , , , , , , , as shown in Figure 2. Then, , , , , , , , , , , , , , and a, , , , b, , , , (d, , , . Similarly, we can calculate IN-out and in-neighborhoods of the remaining vertices.
Definition 7. The height of an IN-set , , , is defined as: For example, the height of an IN-set , , , , , , , , , , , in , b, is , , .
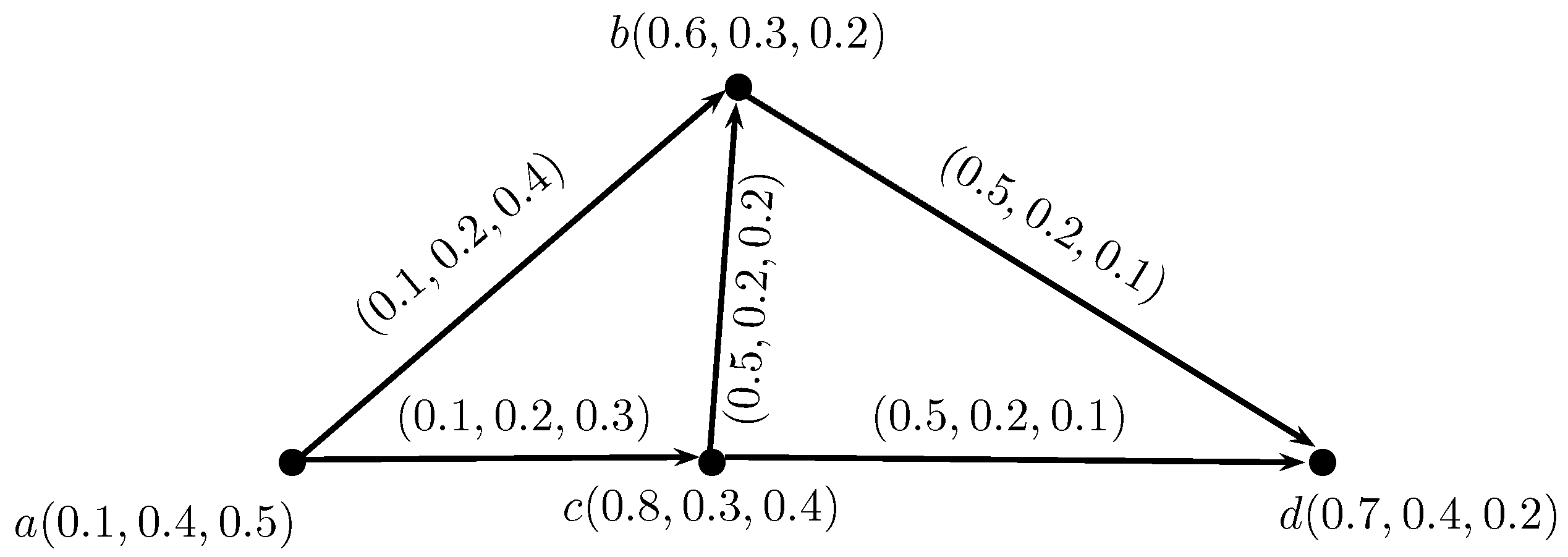
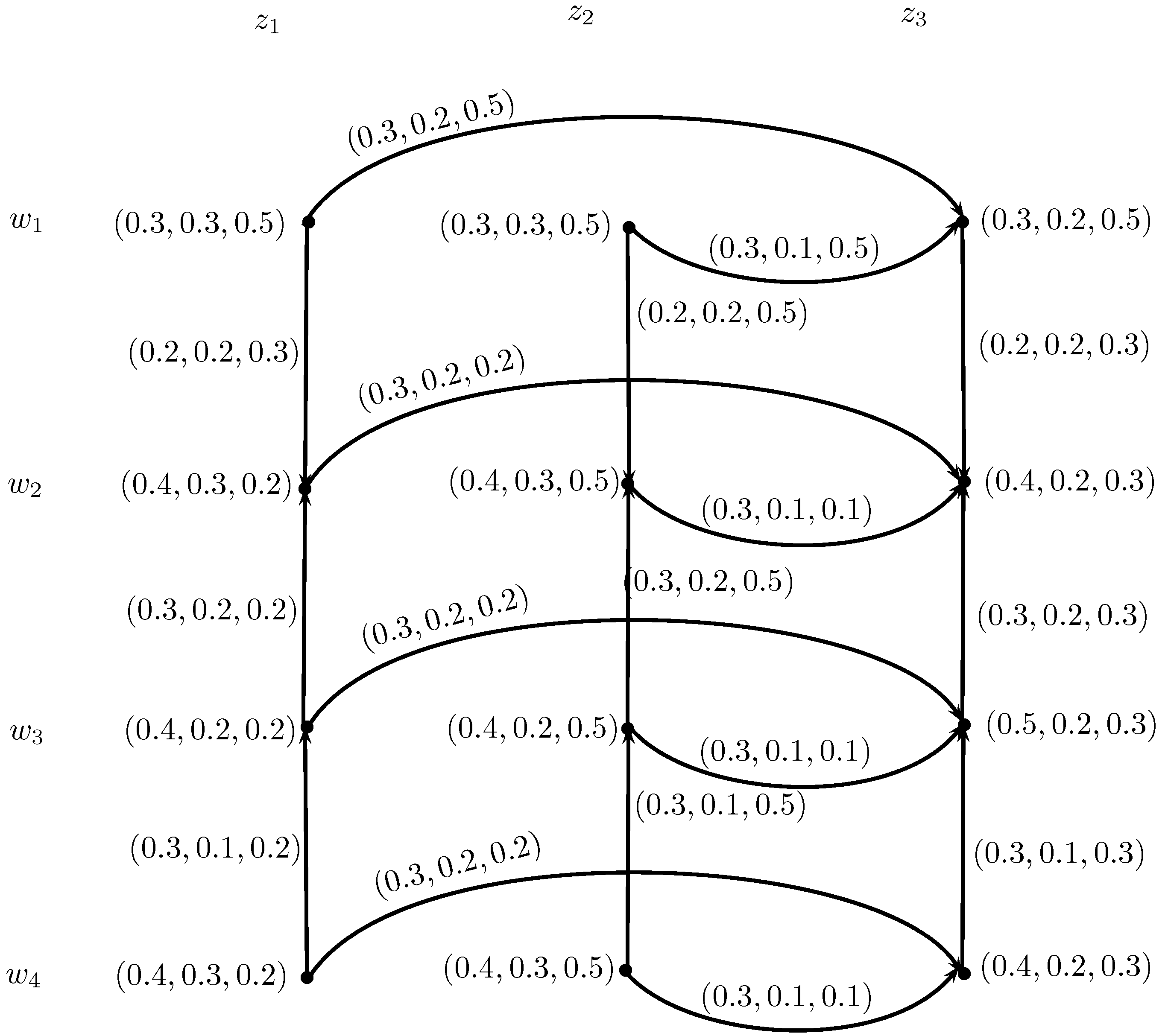
Definition 8. An intuitionistic neutrosophic competition graph (INC-graph) of an IN-digraph , h, is an undirected IN-graph X, h, , which has the same intuitionistic neutrosophic set of vertices as in and has an intuitionistic neutrosophic edge between two vertices w, in if and only if is a non-empty IN-set in . The truth-membership, indeterminacy-membership and falsity-membership values of edge , in are: Example 3. Consider , h, to be an IN-digraph, such that, , b, c, , , , , , , , , , , , , , , , , and , , , , , , , , , , , , , , , , , , , , as shown in Figure 3. By direct calculations, we have Table 1 and Table 2 representing IN-out and in-neighborhoods, respectively. Therefore, there is an edge between two vertices in INC-graph , whose truth-membership, indeterminacy-membership and falsity-membership values are given by the above formula.
Definition 9. For an IN-graph , h, , where , , and , , , then an edge , , w, z is called independent strong if: Otherwise, it is called weak.
Theorem 1. Suppose is an IN-digraph. If contains only one element of , then the edge , of is independent strong if and only if: Proof. Suppose,
is an IN-digraph. Suppose
,
,
q,
, where
,
q and
r are the truth-membership, indeterminacy-membership and falsity-membership values of either the edge
,
or the edge
,
, respectively. Here,
Therefore, the edge
,
in
is independent strong if and only if
,
and
. Hence, the edge
,
of
is independent strong if and only if:
☐
We illustrate the theorem with an example as shown in
Figure 5.
Theorem 2. If all the edges of an IN-digraph are independent strong, then:for all edges , in . Proof. Suppose all the edges of IN-digraph
are independent strong. Then:
for all the edges
,
in
. Let the corresponding INC-graph be
.
Case (1): When for all w, , then there does not exist any edge in between w and z. Thus, we have nothing to prove in this case.
Case (2): When
, let
,
,
,
,
,
,
,
, …,
,
,
,
, where
,
and
are the truth-membership, indeterminacy-membership and falsity-membership values of either
or
for
, 2, …, l, respectively. Therefore,
Obviously,
and
and
for all edges
show that:
therefore,
and:
Hence, , , and for all edges , in . ☐
Theorem 3. Let , and , be two INC-graph of IN-digraphs , and , , respectively. Then, where, is an IN-graph on the crisp graph , and are the crisp competition graphs of and , respectively. is an IN-graph on such that:
- 1.
- 2.
, ,
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
Proof. Using similar arguments as in Theorem 2.1. [
39], it can be proven. ☐
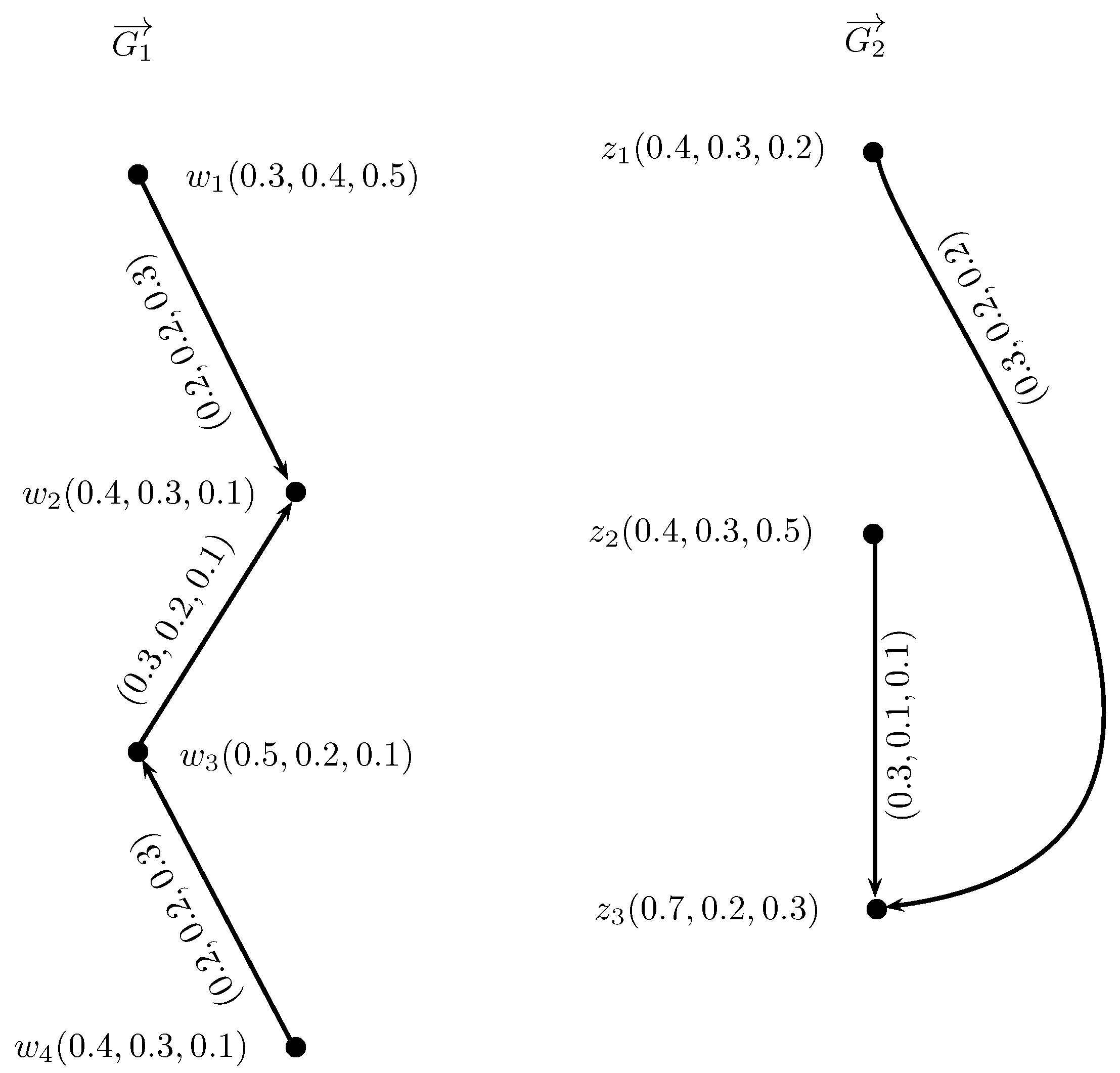
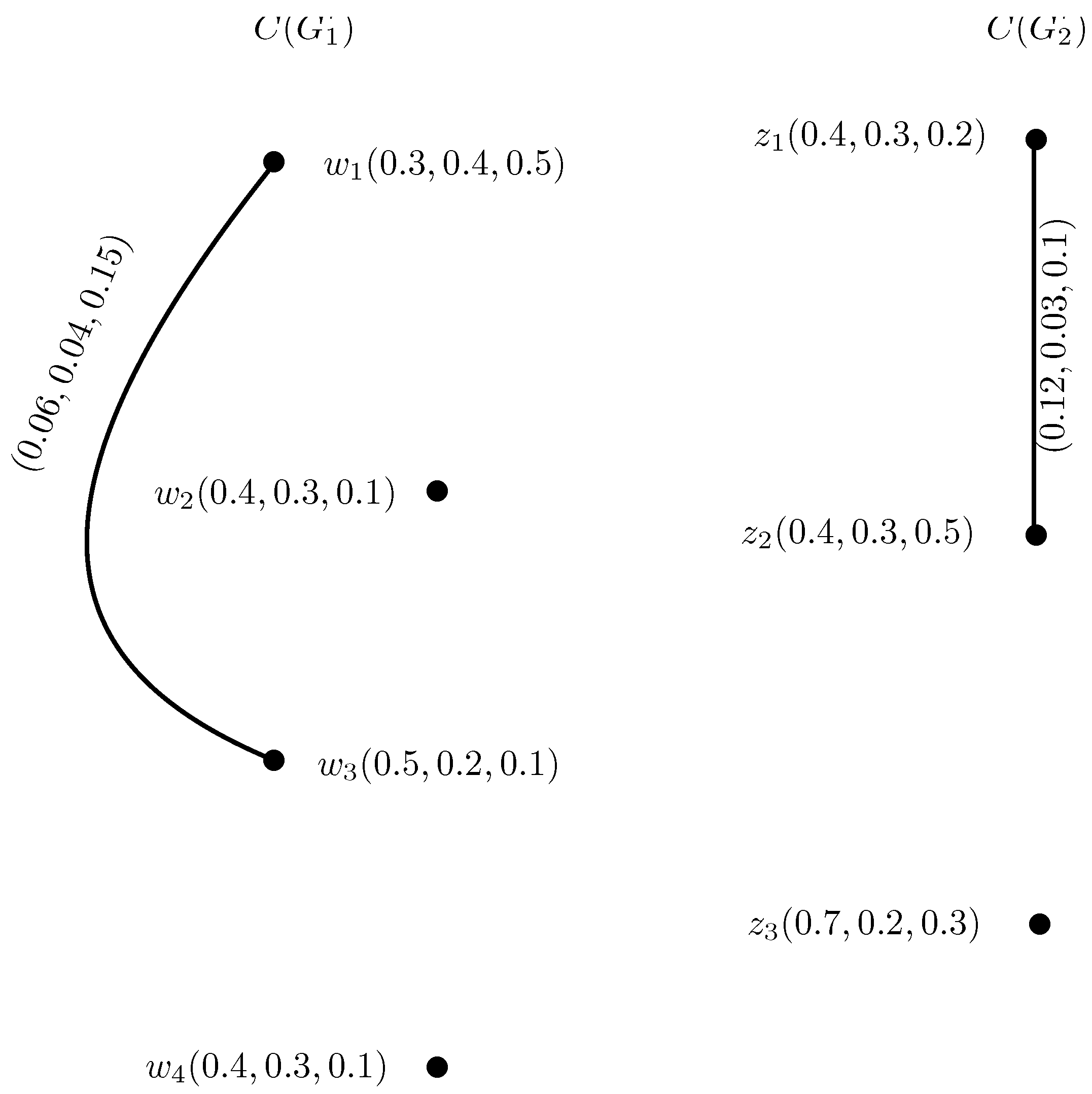
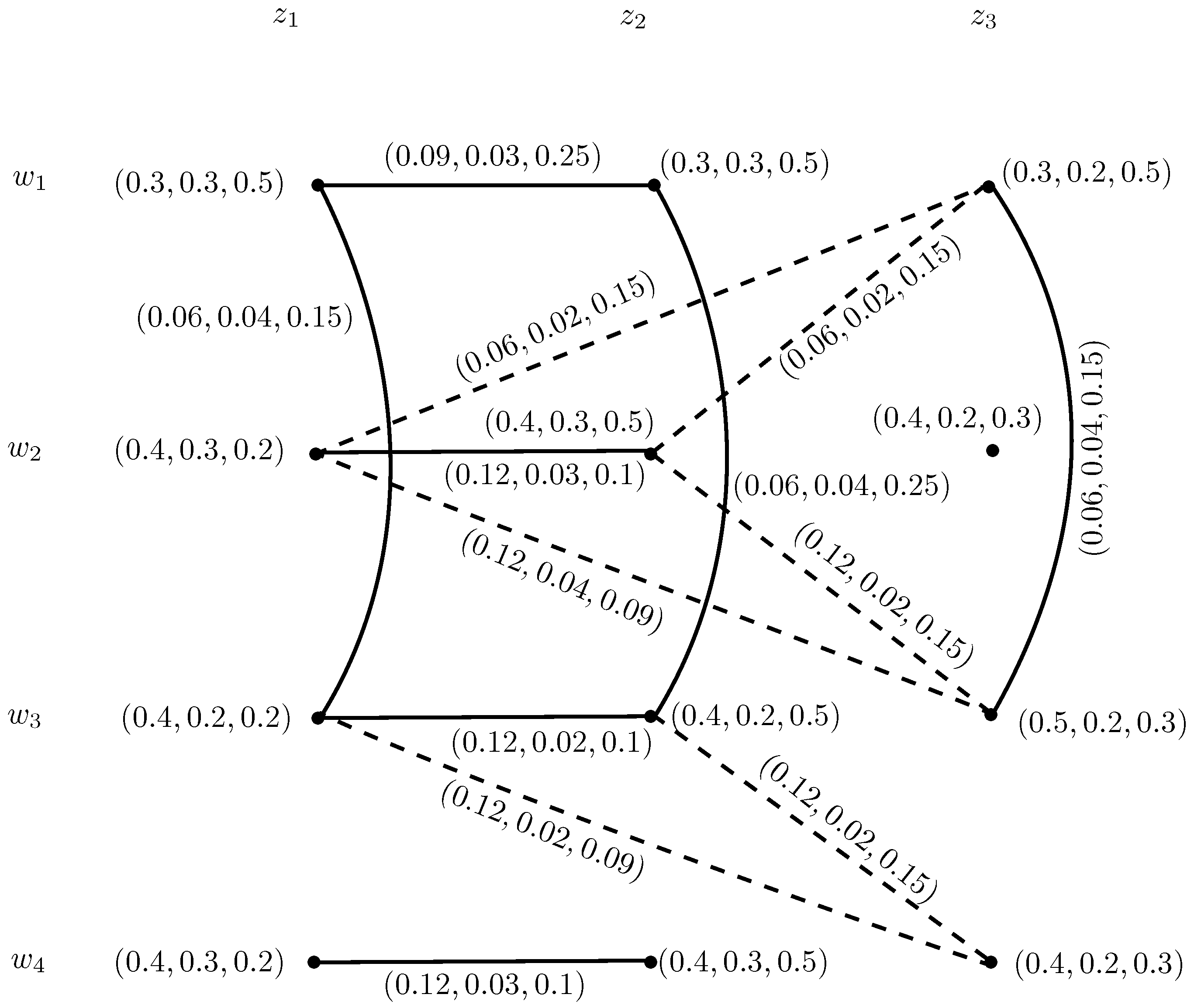
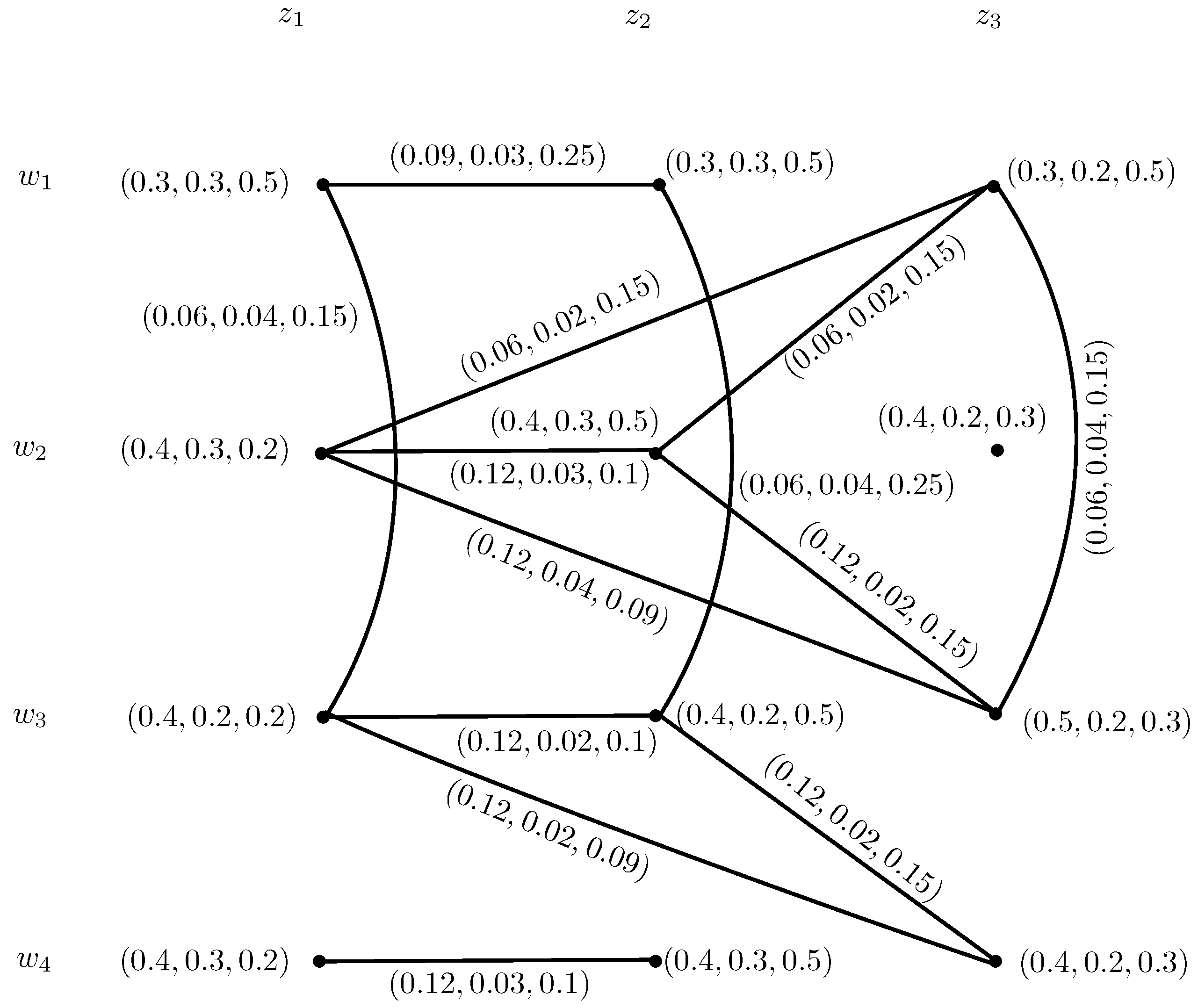
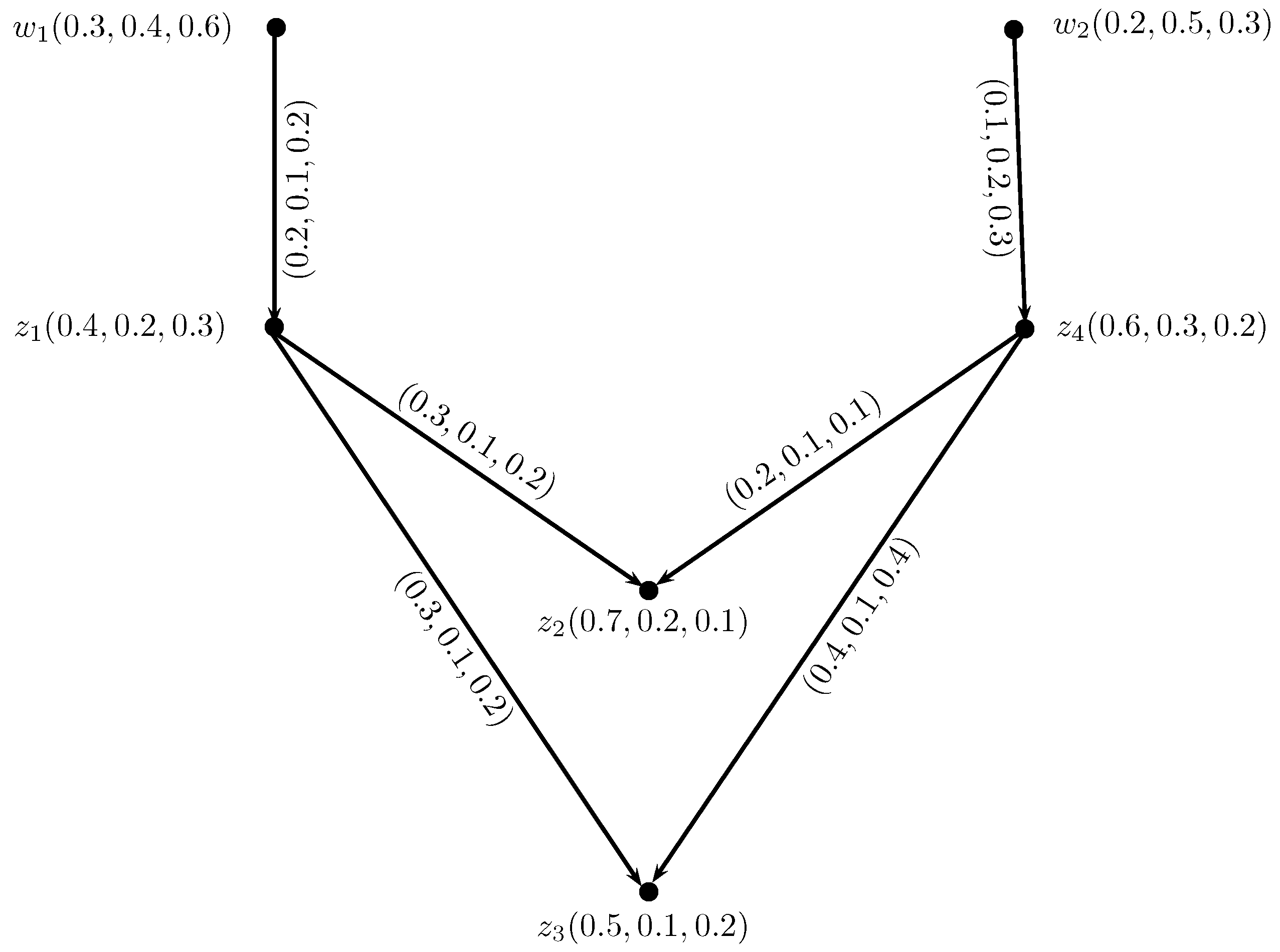
Example 4. Consider , , and , , to be two IN-digraphs, respectively, as shown in Figure 6. The intuitionistic neutrosophic out and in-neighborhoods of and are given in Table 3 and Table 4. The INC-graphs and are given in Figure 7. We now construct the INC-graph , , where , , and , , , from and using Theorem . We obtained two sets of edges by using Condition . The truth-membership, indeterminacy-membership and falsity-membership of edges can be calculated by using Conditions to as, All the truth-membership, indeterminacy-membership and falsity-membership degrees of adjacent edges of and are given in Table 5. The INC-graph obtained by using this method is given in Figure 8 where solid lines indicate part of INC-graph obtained from , and the dotted lines indicate the part of . The Cartesian product of IN-digraphs and is shown in Figure 9. The IN-out-neighborhoods of are calculated in Table 6. The INC-graphs of are shown in Figure 10. It can be seen that from Figure 8 and Figure 10. Definition 10. The intuitionistic neutrosophic open-neighborhood of a vertex w of an IN-graph , h, is IN-set , , , , where,and defined by , , defined by , and defined by , . For every vertex , the intuitionistic neutrosophic singleton set, , , , , such that: , , defined by , and , respectively. The intuitionistic neutrosophic closed-neighborhood of a vertex w is . Definition 11. Suppose , h, is an IN-graph. The single-valued intuitionistic neutrosophic open-neighborhood graph of is an IN-graph , h, , which has the same intuitionistic neutrosophic set of vertices in and has an intuitionistic neutrosophic edge between two vertices w, in if and only if is a non-empty IN-set in . The truth-membership, indeterminacy-membership and falsity-membership values of the edge , are given by: Definition 12. Suppose , h, is an IN-graph. The single-valued intuitionistic neutrosophic closed-neighborhood graph of is an IN-graph , h, , which has the same intuitionistic neutrosophic set of vertices in and has an intuitionistic neutrosophic edge between two vertices w, in if and only if is a non-empty IN-set in . The truth-membership, indeterminacy-membership and falsity-membership values of the edge , are given by: Example 5. Consider , h, to be an IN-graph, such that , b, c, , , , , , , , , , , , , , , , , , and , , , , , , , , , , , , , , , , as shown in Figure 11. Then, corresponding intuitionistic neutrosophic open and closed-neighborhood graphs are shown in Figure 12. Theorem 4. For each edge of an IN-graph , there exists an edge in .
Proof. Suppose
,
is an edge of an IN-graph
,
h,
. Suppose
,
h,
is the corresponding closed neighborhood of an IN-graph. Suppose
w,
and
w,
. Then,
w,
. Hence,
Thus, for each edge , in IN-graph , there exists an edge , in . ☐
Definition 13. The support of an IN-set , , , in X is the subset of X defined by:and is the number of elements in the set. We now discuss p-competition intuitionistic neutrosophic graphs.
Suppose p is a positive integer. Then, p-competition IN-graph of the IN-digraph , h, is an undirected IN-graph , h, , which has the same intuitionistic neutrosophic set of vertices as in and has an intuitionistic neutrosophic edge between two vertices w, z in if and only if . The truth-membership value of edge , in is , ; the indeterminacy-membership value of edge , in is , ; and the falsity-membership value of edge , in is , where .
The three-competition IN-graph is illustrated by the following example.
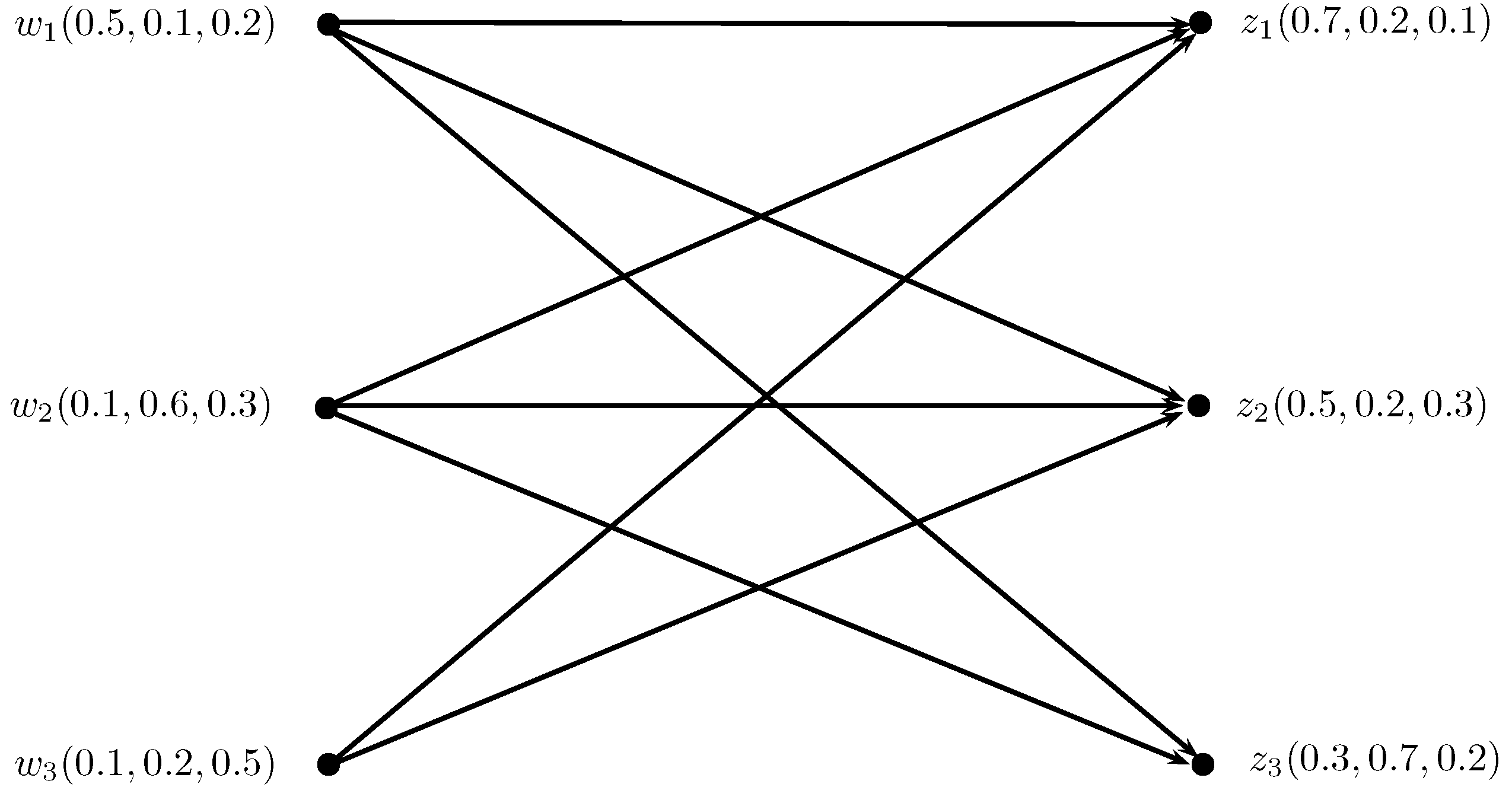
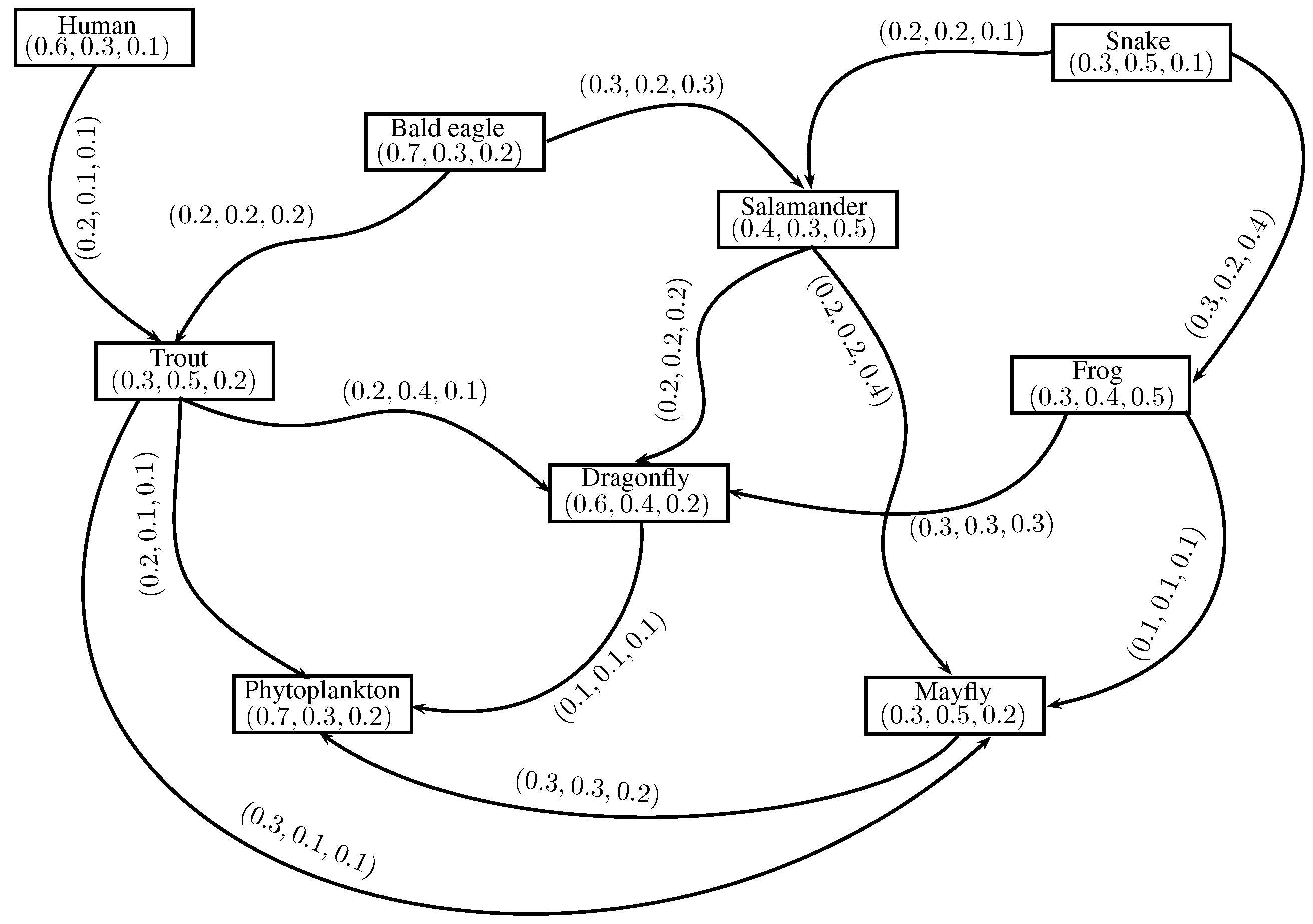
Example 6. Consider , h, to be an IN-digraph, such that , , , , , , , , , , , , , , , , , , , , , , , , , , , , , and , , , , , , , , , , , , , , , , , , , , , , , as shown in Figure 13. Then, , , , , , , , , , , , , , , , , , , , , , , , and , , , , , , , . Therefore, , , , , , , , , , , , , , , , , , , , and , , , , , , , . Now, . For , , , , and , . As shown in Figure 14. We now define another extension of INC-graph known as the m-step INC-graph.
: a directed intuitionistic neutrosophic path of length m from z to w.
: single-valued intuitionistic neutrosophic m-step out-neighborhood of vertex z.
: single-valued intuitionistic neutrosophic m-step in-neighborhood of vertex z.
: m-step INC-graph of the IN-digraph .
Definition 14. Suppose , h, is an IN-digraph. The m-step IN-digraph of is denoted by , h, where the intuitionistic neutrosophic set of vertices of is the same as the intuitionistic neutrosophic set of vertices of and has an edge between z and w in if and only if there exists an intuitionistic neutrosophic directed path in .
Definition 15. The intuitionistic neutrosophic m-step out-neighborhood of vertex z of an IN-digraph , h, is IN-set: there exists a directed intuitionistic neutrosophic path of length m from z to w, , , , , and , are defined by , , is an edge of , , , is an edge of and , , is an edge of , respectively. Definition 16. The intuitionistic neutrosophic m-step in-neighborhood of vertex z of an IN-digraph , h, is IN-set: there exists a directed intuitionistic neutrosophic path of length m from w to z, , , , , and , are defined by , , is an edge of , , , is an edge of and , , is an edge of , respectively. Definition 17. Suppose , h, is an IN-digraph. The m-step INC-graph of IN-digraph is denoted by , h, , which has the same intuitionistic neutrosophic set of vertices as in and has an edge between two vertices w, in if and only if is a non-empty IN-set in . The truth-membership value of edge , in is , ; the indeterminacy-membership value of edge , in is , ; and the falsity-membership value of edge , in is , .
The two-step INC-graph is illustrated by the following example.
Example 7. Consider , h, is an IN-digraph, such that, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , and , , , , , , , , , , , , , , , , , , , , and , , , , as shown in Figure 15. Then, , , , , , , , and , , , , , , , . Therefore, , , , , , , , . Thus, , and . This is shown in Figure 16. Definition 18. The intuitionistic neutrosophic m-step out-neighborhood of vertex z of an IN-digraph , h, is IN-set: there exists a directed intuitionistic neutrosophic path of length m from z to w, , , , , and , are defined by , , , is an edge of , , , , is an edge of and , , , is an edge of , respectively. Definition 19. Suppose , h, is an IN-graph. Then, the m-step intuitionistic neutrosophic neighborhood graph (IN-neighborhood-graph) is defined by , h, , where , , , , , , , , , and are such that: Theorem 5. If all the edges of IN-digraph , h, are independent strong, then all the edges of are independent strong.
Proof. Suppose , h, is an IN-digraph and , h, is the corresponding m-step INC-graph. Since all the edges of are independent strong, then , and . Then, , or , or , , or , or and , or , or .
Hence, the edge , is independent strong in . Since, , is taken to be the arbitrary edge of , thus all the edges of are independent strong. ☐