Leak Location of Pipeline with Multibranch Based on a Cyber-Physical System
Abstract
:1. Introduction
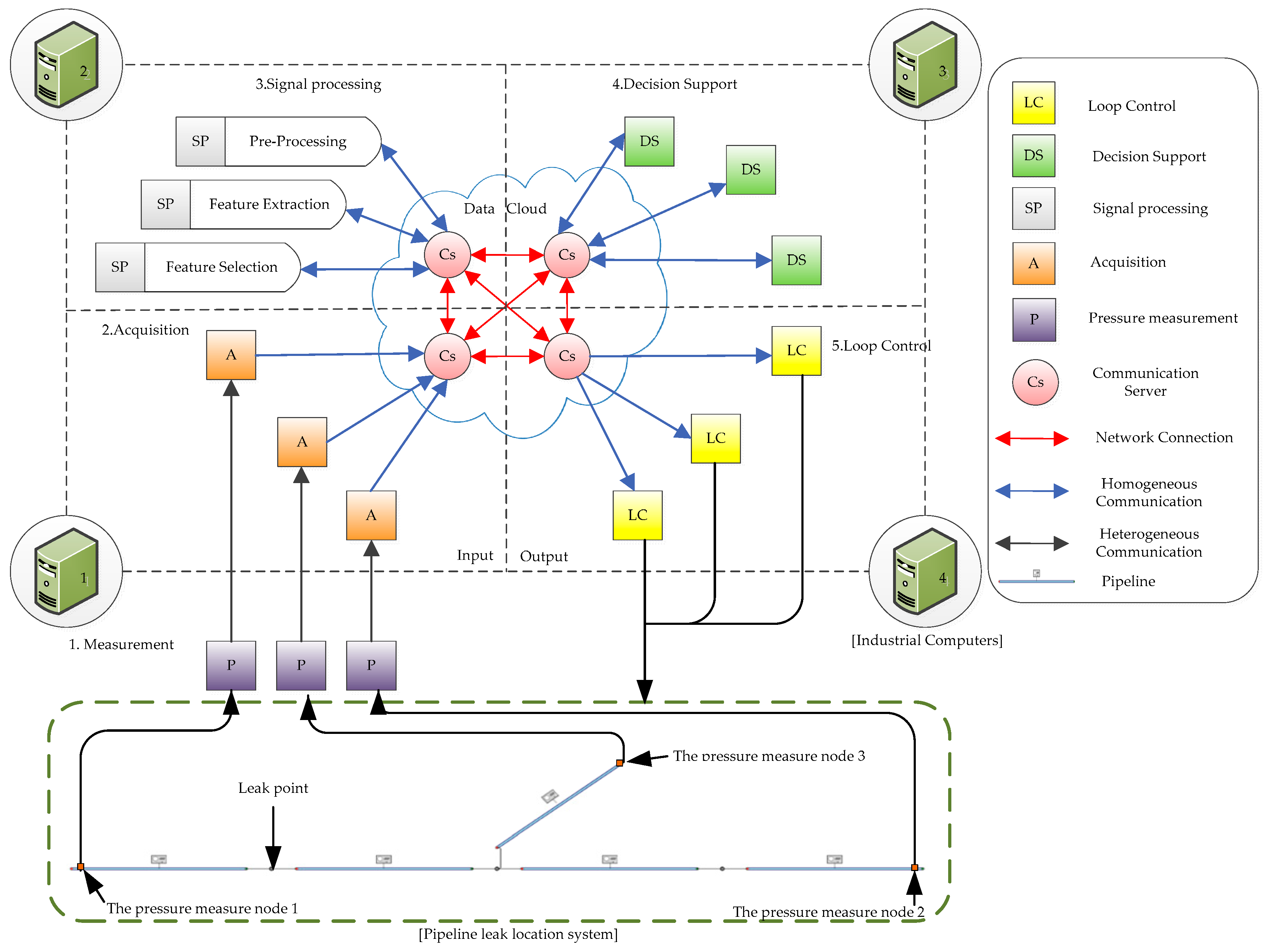
2. Cyber-Physical Leak Location System Design
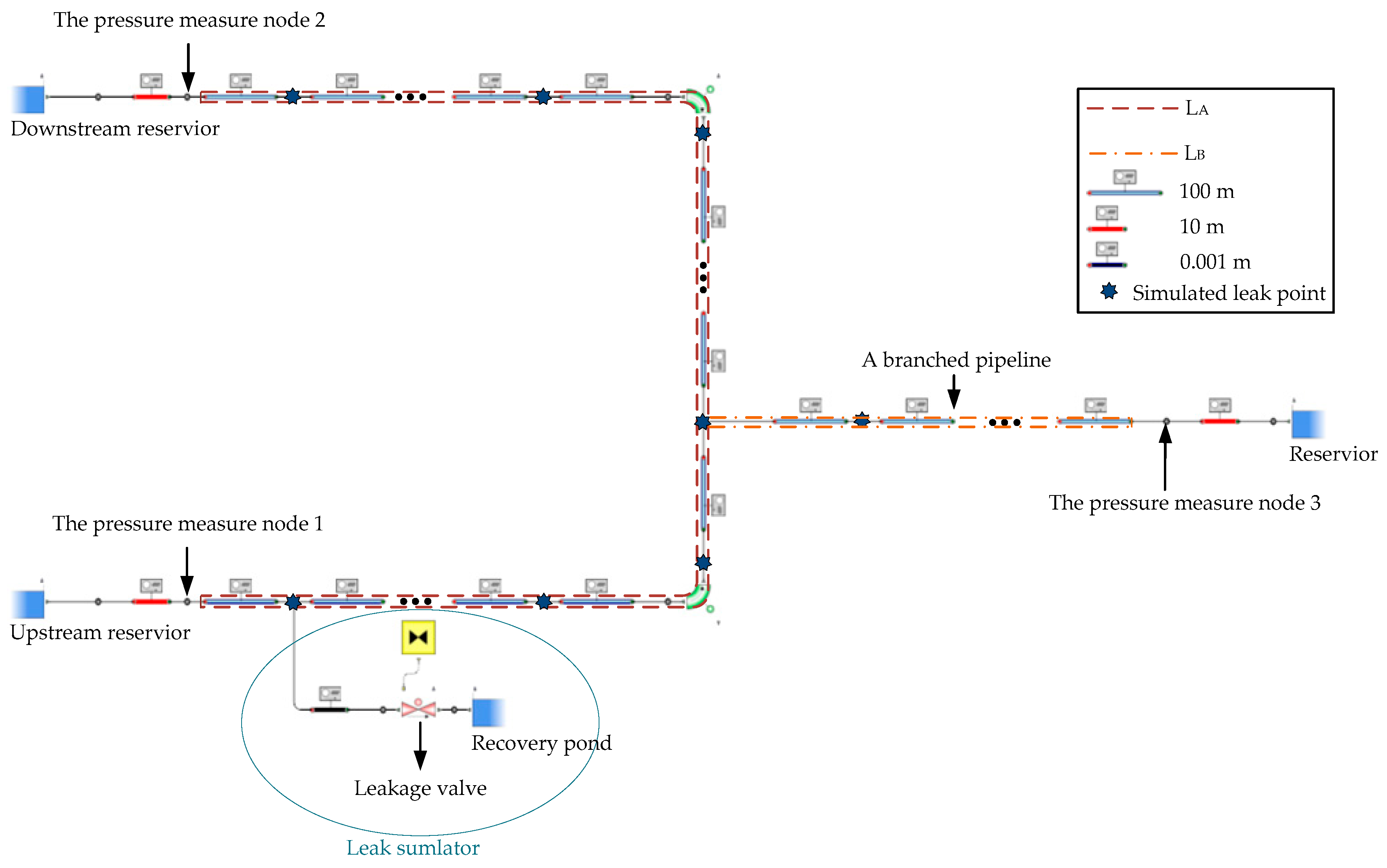
3. Leak Location Method of Pipeline with Multibranch
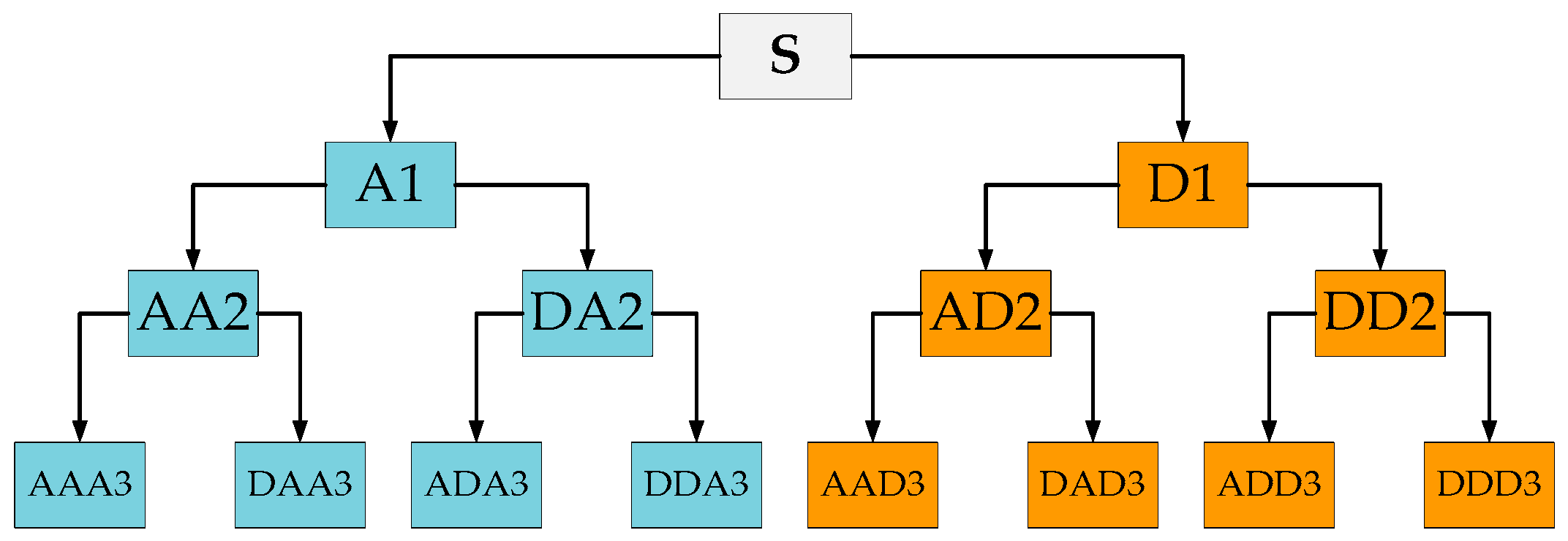
3.1. Wavelet Packet Analysis
3.2. Improved Twin Support Vector Machine
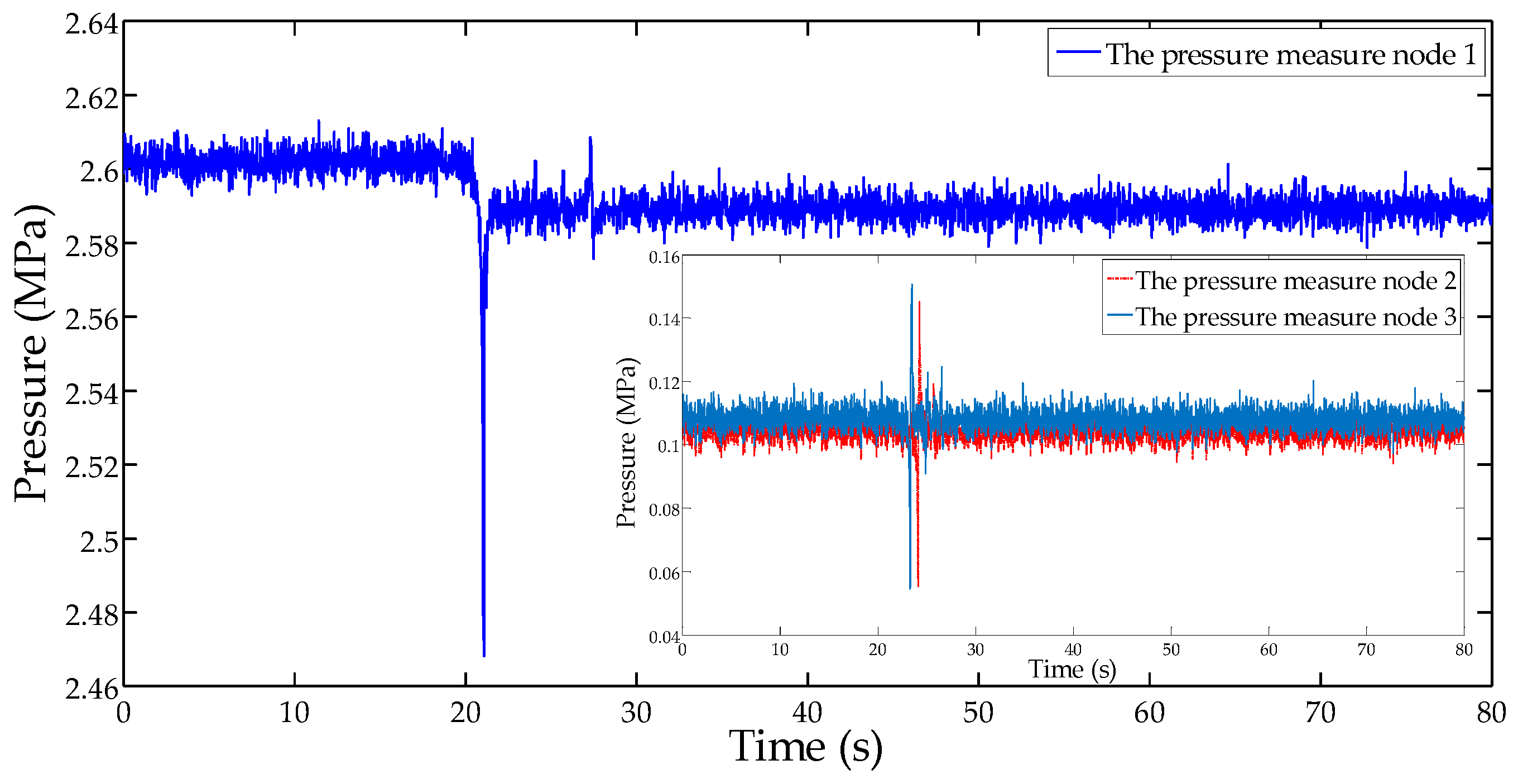
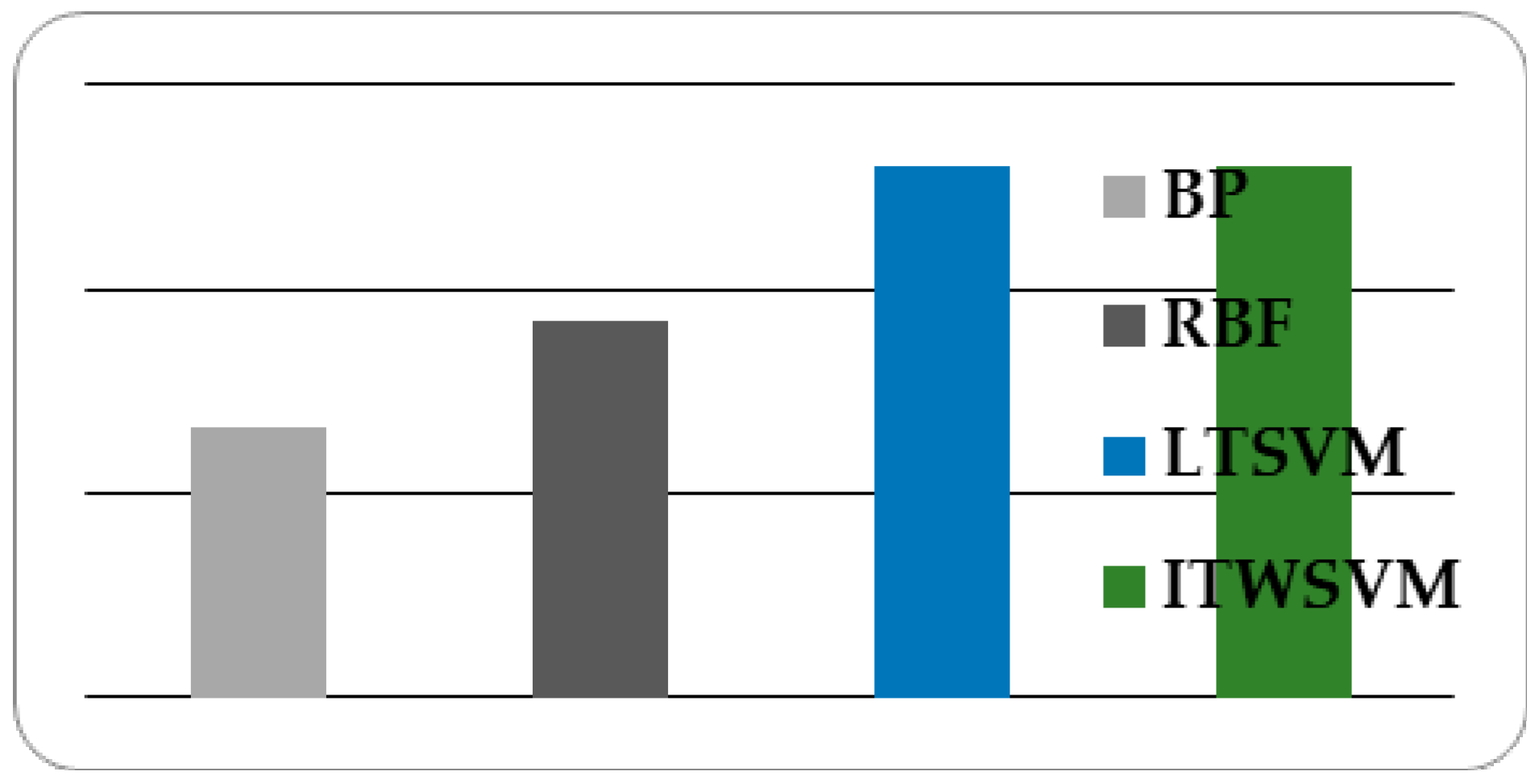
4. Simulation and Analysis
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Murvay, P.; Silea, I. A survey on gas leak detection and localization techniques. J. Loss Prev. Process Ind. 2012, 25, 966–973. [Google Scholar] [CrossRef]
- Datta, S.; Sarkar, S. A review on different pipeline fault detection methods. J. Loss Prev. Process Ind. 2016, 41, 97–106. [Google Scholar] [CrossRef]
- Verde, C.; Torres, L. Modeling and Monitoring of Pipelines and Networks: Advanced Tools for Automatic Monitoring and Supervision of Pipelines; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Liang, W.; Zhang, L. A wave change analysis (WCA) method for pipeline leak detection using Gaussian mixture model. J. Loss Prev. Process Ind. 2012, 25, 60–69. [Google Scholar] [CrossRef]
- Liu, J.; Su, H.; Ma, Y.; Wang, G.; Wang, Y.; Zhang, K. Chaos characteristics and least squares support vector machines based online pipeline small leakages detection. Chaos Solitons Fractals 2016, 91, 656–669. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Q.; Wen, J.; Wang, F. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement 2014, 55, 434–443. [Google Scholar] [CrossRef]
- Mandal, S.K.; Chan, F.T.S.; Tiwari, M.K. Leak detection of pipeline: An integrated approach of rough set theory and artificial bee colony trained SVM. Expert Syst. Appl. 2012, 39, 3071–3080. [Google Scholar] [CrossRef]
- Qu, Z.; Feng, H.; Zeng, Z.; Zhuge, J.; Jin, S. A SVM-based pipeline leakage detection and pre-warning system. Measurement 2010, 43, 513–519. [Google Scholar] [CrossRef]
- Ni, L.; Jiang, J.; Pan, Y. Leak location of pipelines based on transient model and PSO-SVM. J. Loss Prev. Process Ind. 2013, 26, 1085–1093. [Google Scholar] [CrossRef]
- Lang, X.; Li, P.; Hu, Z.; Ren, H.; Li, Y. Leak detection and location of pipelines based on LMD and least squares twin support vector machine. IEEE Access 2017, 5, 8659–8668. [Google Scholar] [CrossRef]
- Verde, C.; Torres, L.; González, O. Decentralized scheme for leaks’ location in a branched pipeline. J. Loss Prev. Process Ind. 2016, 43, 18–28. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Leak detection in water-filled small-diameter polyethylene pipes by means of acoustic emission measurements. Appl. Sci. 2017, 7, 2. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Automatic leak detection in buried plastic pipes of water supply networks by means of vibration measurements. Shock Vib. 2015, 2015, 165304. [Google Scholar] [CrossRef]
- Yazdekhasti, S.; Piratla, K.R.; Atamturktur, S.; Khan, A. Experimental evaluation of a vibration-based leak detection technique for water pipelines. Struct. Infranstruct. Eng. 2017. [Google Scholar] [CrossRef]
- Junie, P.; Dinu, O.; Eremia, C.; Stefanoiu, D.; Petrescu, C.; Savulescu, I. A WSN based monitoring system for oil and gas transportation through pipelines. IFAC Proc. Vol. 2012, 45, 1796–1801. [Google Scholar] [CrossRef]
- Yuan, X.; Anumba, C.J.; Parfitt, M.K. Cyber-physical systems for temporary structure monitoring. Autom. Constr. 2016, 66, 1–14. [Google Scholar] [CrossRef]
- Morgan, J.; O’Donnell, G.E. Cyber-physical process monitoring systems. J. Intell. Manuf. 2015. [Google Scholar] [CrossRef]
- Lei, D.; Yang, L.; Xu, W.; Zhang, P.; Huang, Z. Experimental study on alarming of concrete micro-crack initiation based on wavelet packet analysis. Constr. Build. Mater. 2017, 149, 716–723. [Google Scholar] [CrossRef]
- Shao, Y.; Chen, W.; Zhang, J.; Wang, Z.; Deng, N. An efficient weighted Lagrangian twin support vector machine for imbalanced data classification. Pattern Recogn. 2014, 47, 3158–3167. [Google Scholar] [CrossRef]
- Zhang, X. Study on the Algorithms for some Optimization Problems and Applications. Ph.D. Thesis, Xidian University, Xi’an, China, 2011. [Google Scholar]
- Jeong, U.; Kim, Y.H.; Kim, J.; Kim, T.; Kim, S.J. Experimental evaluation of permanent magnet probe flowmeter measuring high temperature liquid sodium flow in the ITSL. Nucl. Eng. Des. 2013, 265, 566–575. [Google Scholar] [CrossRef]
- Chen, J.; Pan, S. A descent method for a reformulation of the second-order cone complementarity problem. J. Comput. Appl. Math. 2008, 213, 547–558. [Google Scholar] [CrossRef]
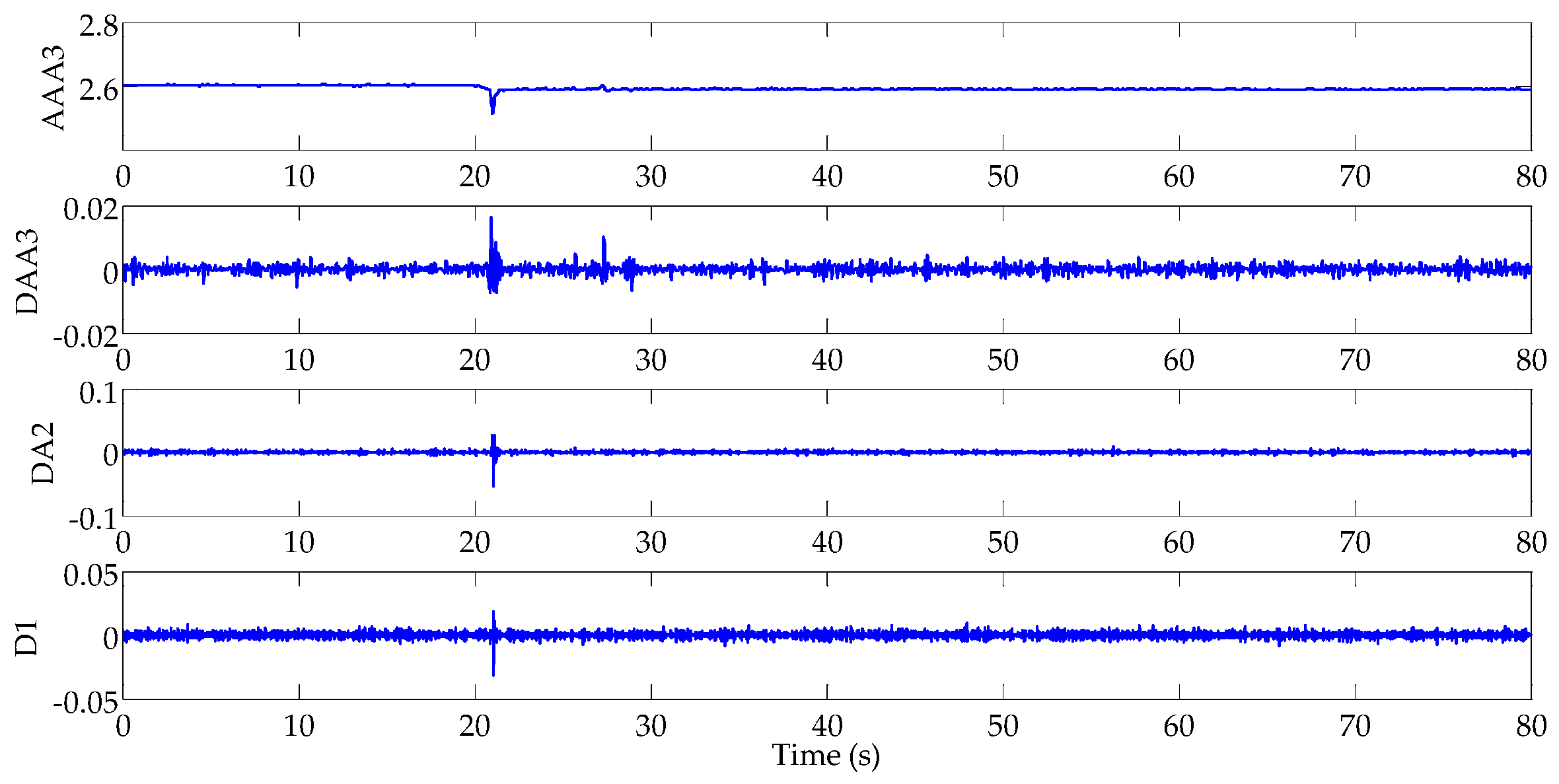
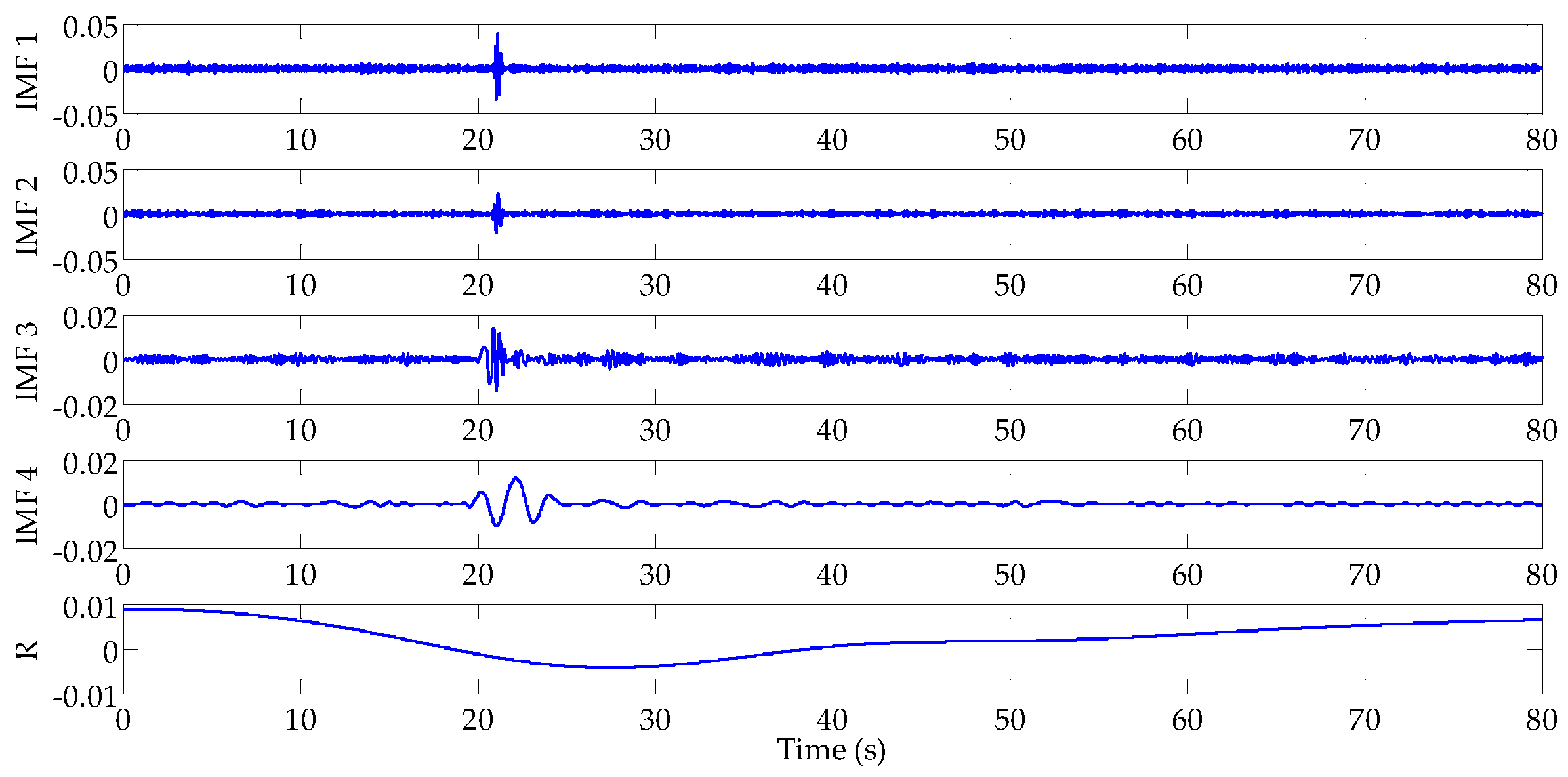
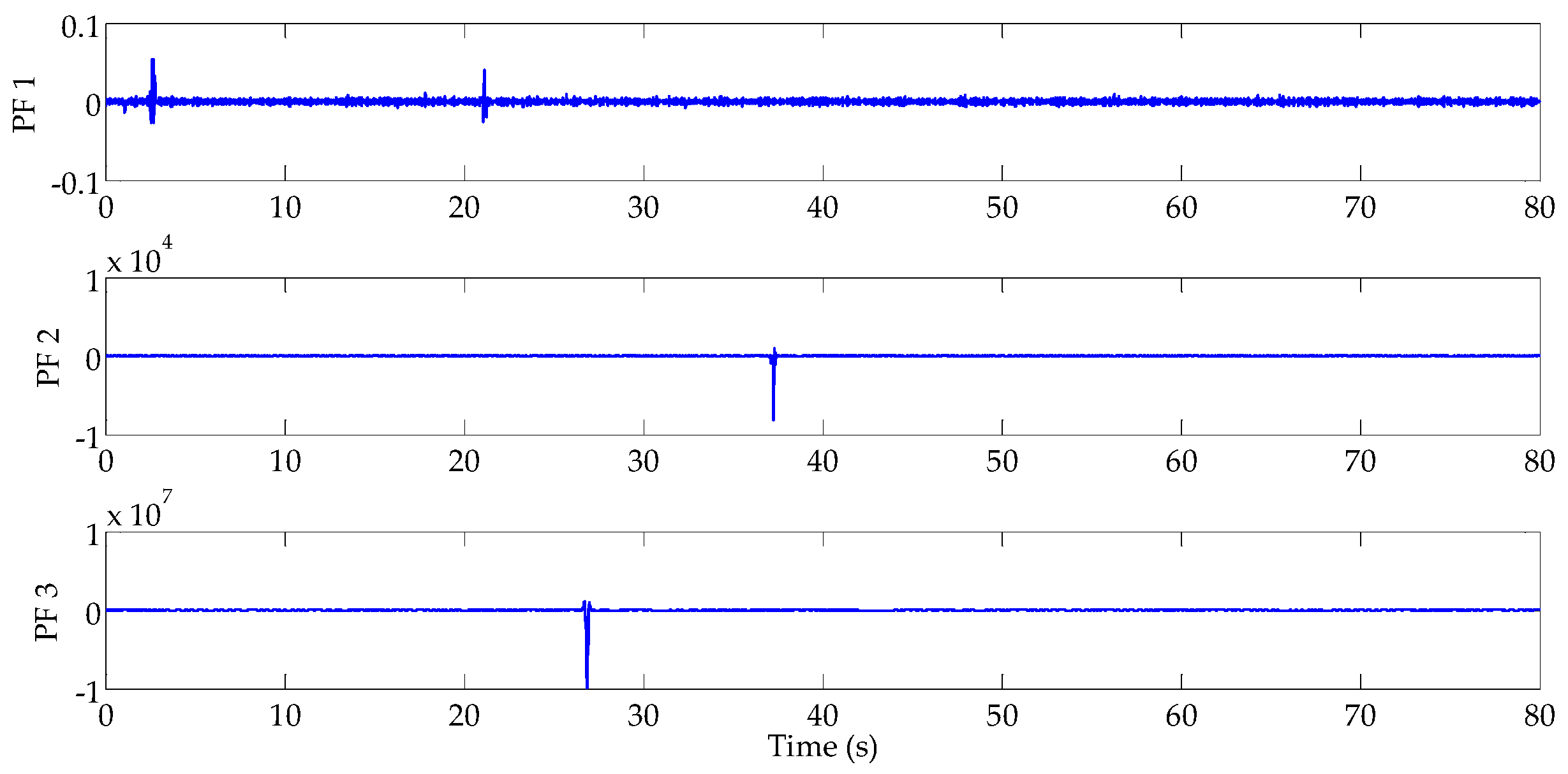
| Leakage Position | Signal Singular Point of Pressure Measure Node 1 (s) | Signal Singular Point of Pressure Measure Node 2 (s) | Signal Singular Point of Pressure Measure Node 3 (s) |
|---|---|---|---|
| 100 m from upstream | 21.06 | 24.1 | 23.3 |
| 500 m from upstream | 21.38 | 23.78 | 22.98 |
| 1000 m from upstream | 21.78 | 23.38 | 22.58 |
| 1500 m from upstream | 22.18 | 22.98 | 22.18 |
| 2000 m from upstream | 22.58 | 22.58 | 21.78 |
| 2500 m from upstream | 22.98 | 22.18 | 22.18 |
| 3000 m from upstream | 23.38 | 21.78 | 22.58 |
| 3500 m from upstream | 23.78 | 21.38 | 22.98 |
| 4000 m from upstream | 24.06 | 20.98 | 23.42 |
| 500 m from branch junction | 22.98 | 22.98 | 21.38 |
| 1000 m from branch junction | 23.62 | 23.42 | 20.98 |
| Method | Computation (s) | Accuracy (%) |
|---|---|---|
| BP | 5.43 | 83.2 |
| RBF | 1.82 | 88.4 |
| LTSVM | 5.262 | 96.06 |
| The proposed method | 0.267 | 96.06 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, X.; Li, P.; Li, Y.; Ren, H. Leak Location of Pipeline with Multibranch Based on a Cyber-Physical System. Information 2017, 8, 113. https://doi.org/10.3390/info8040113
Lang X, Li P, Li Y, Ren H. Leak Location of Pipeline with Multibranch Based on a Cyber-Physical System. Information. 2017; 8(4):113. https://doi.org/10.3390/info8040113
Chicago/Turabian StyleLang, Xianming, Ping Li, Yan Li, and Hong Ren. 2017. "Leak Location of Pipeline with Multibranch Based on a Cyber-Physical System" Information 8, no. 4: 113. https://doi.org/10.3390/info8040113





