Information Mining from Heterogeneous Data Sources: A Case Study on Drought Predictions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data Sources
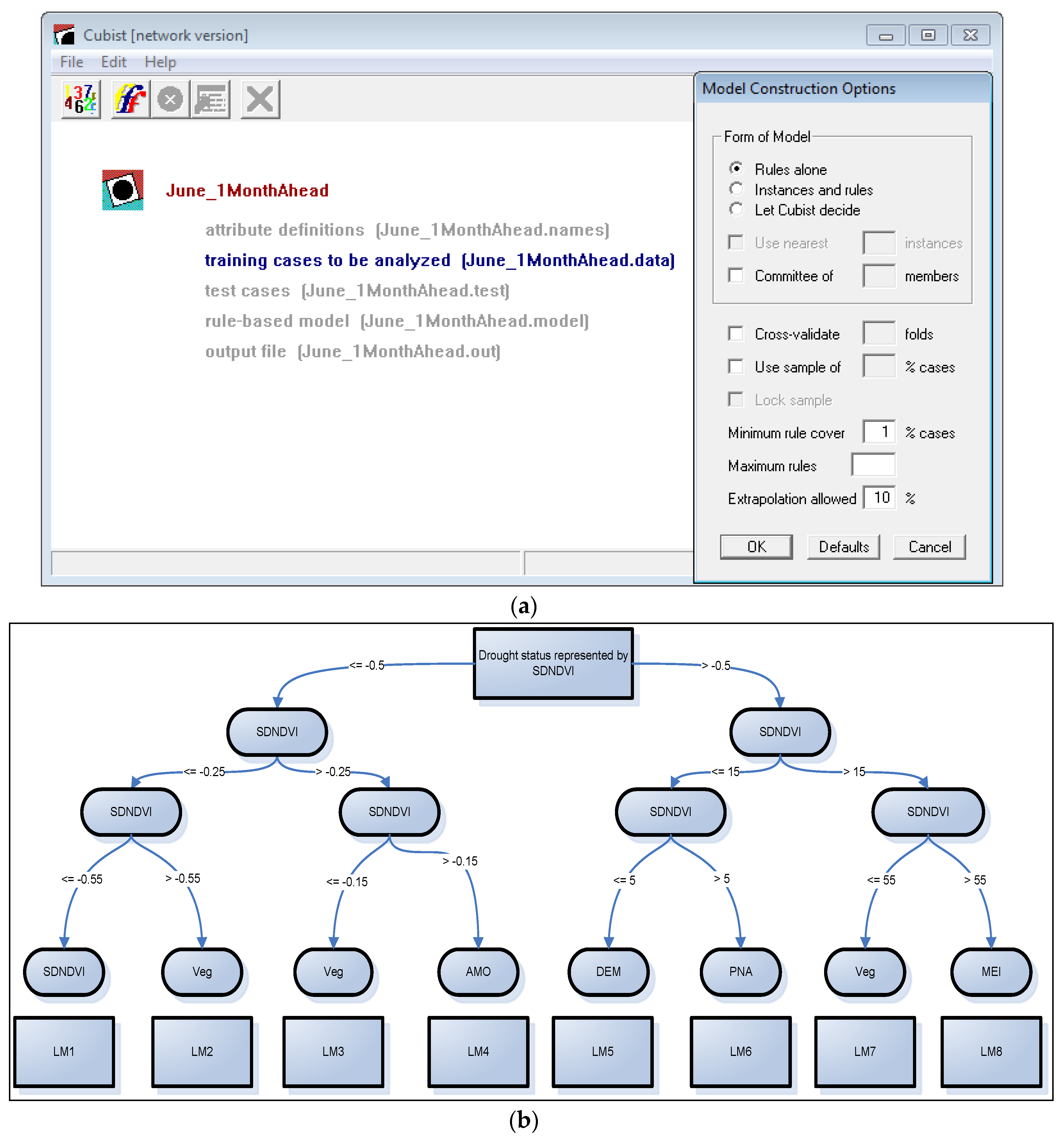
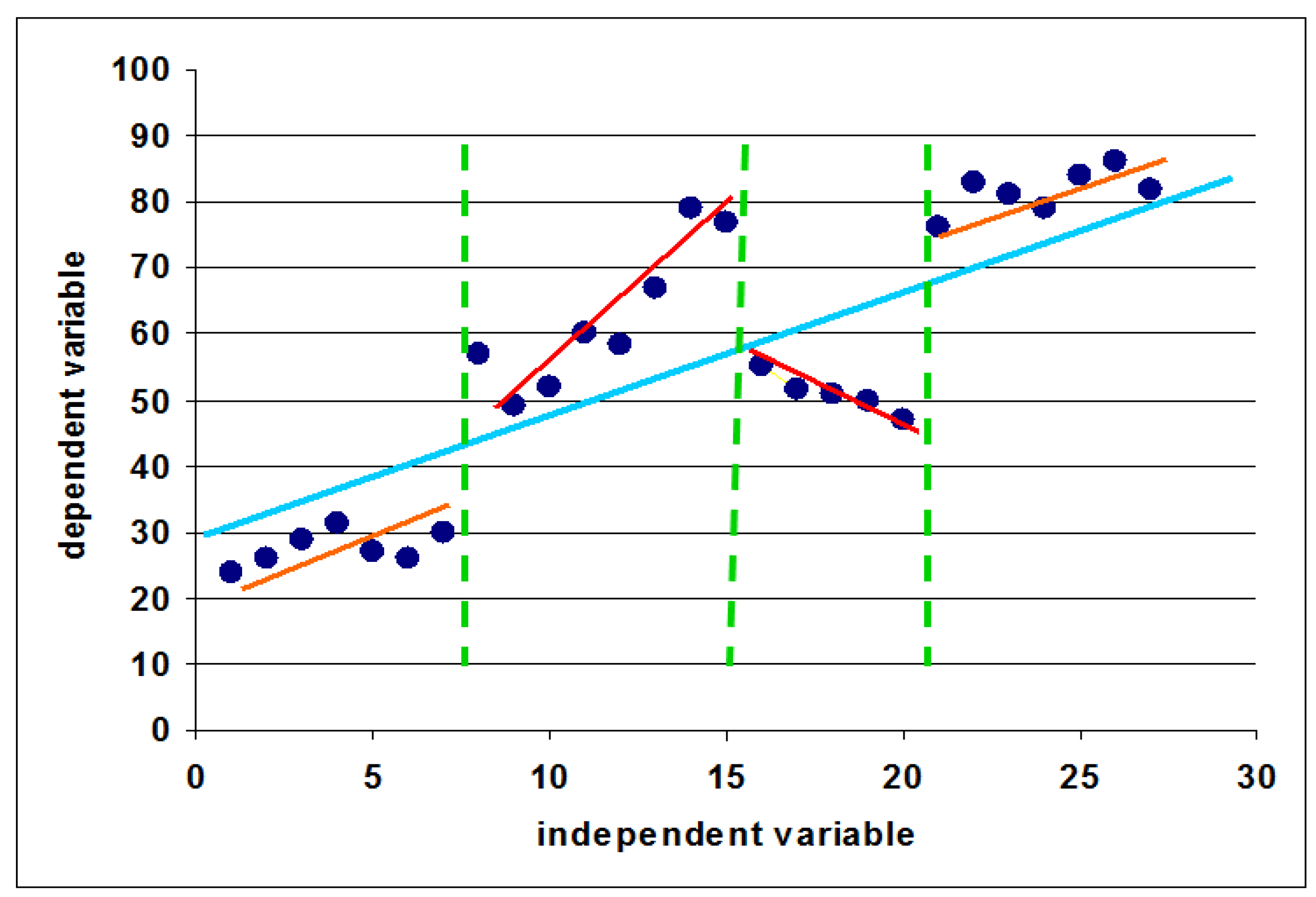
2.2. Classification and Regression Tree Modeling
2.3. Accuracy Assessment
3. Results and Discussions
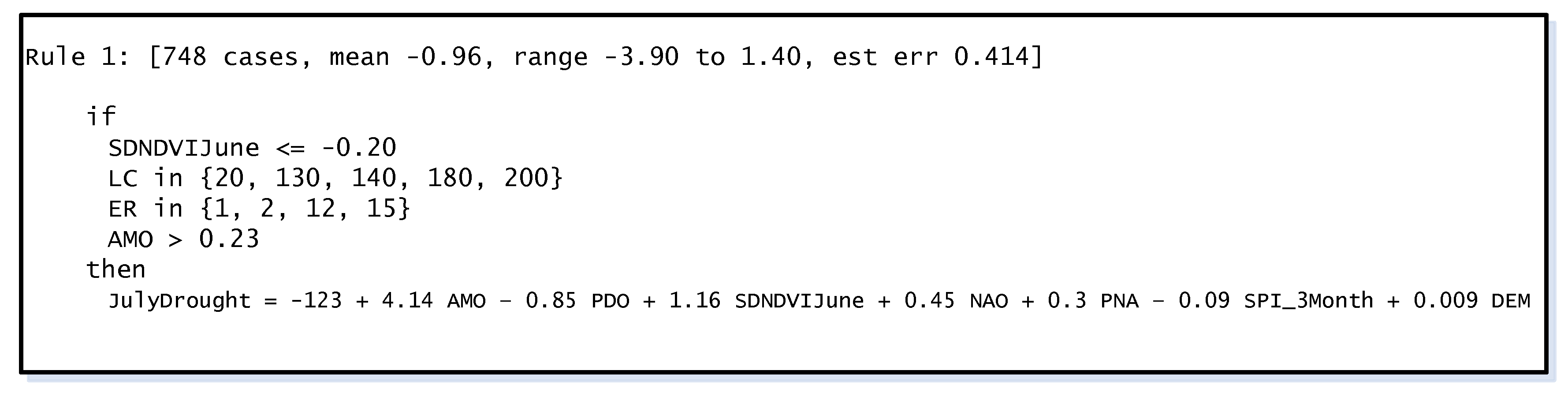
3.1. CART Model Trees for Drought Predictions
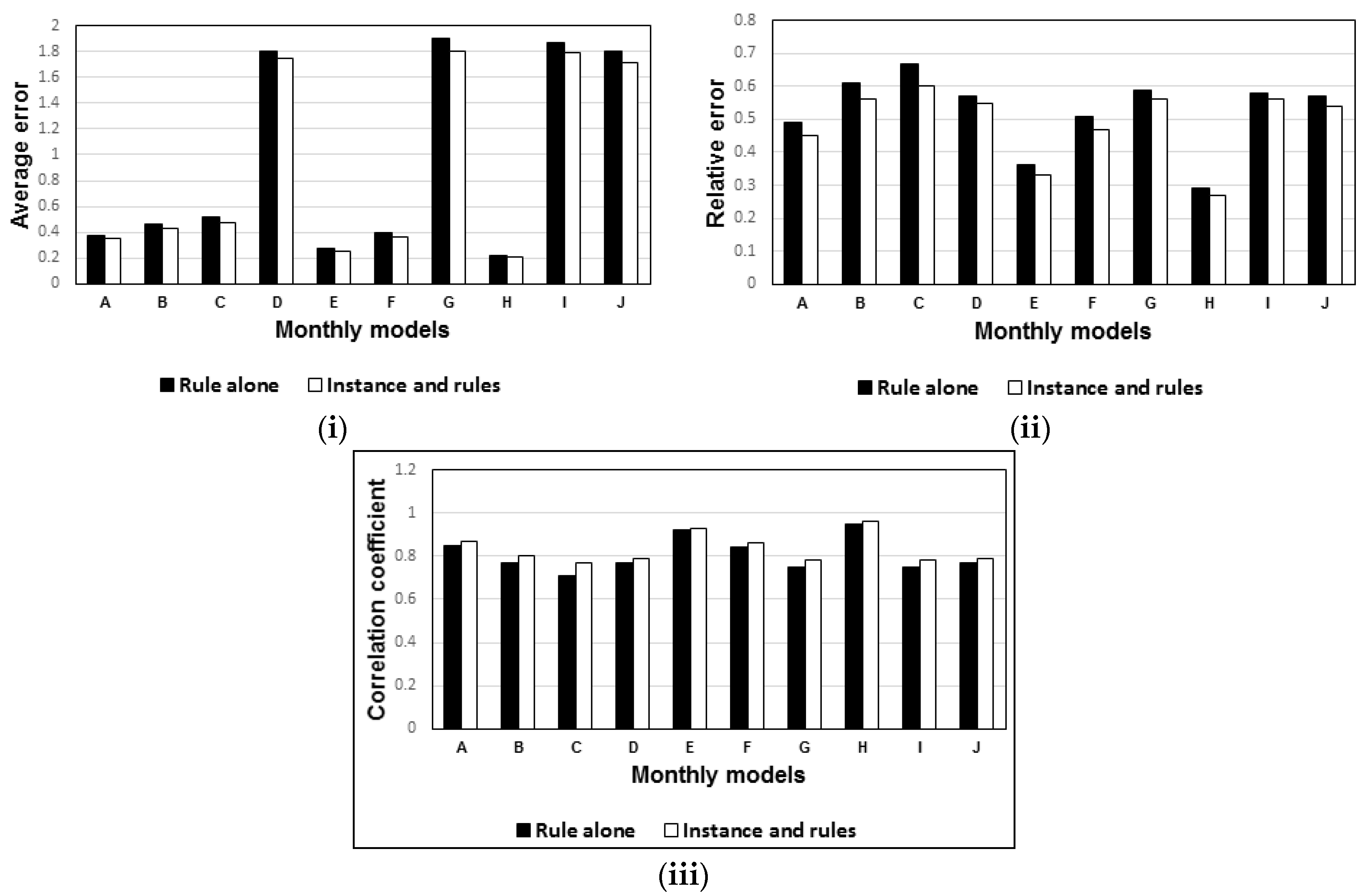
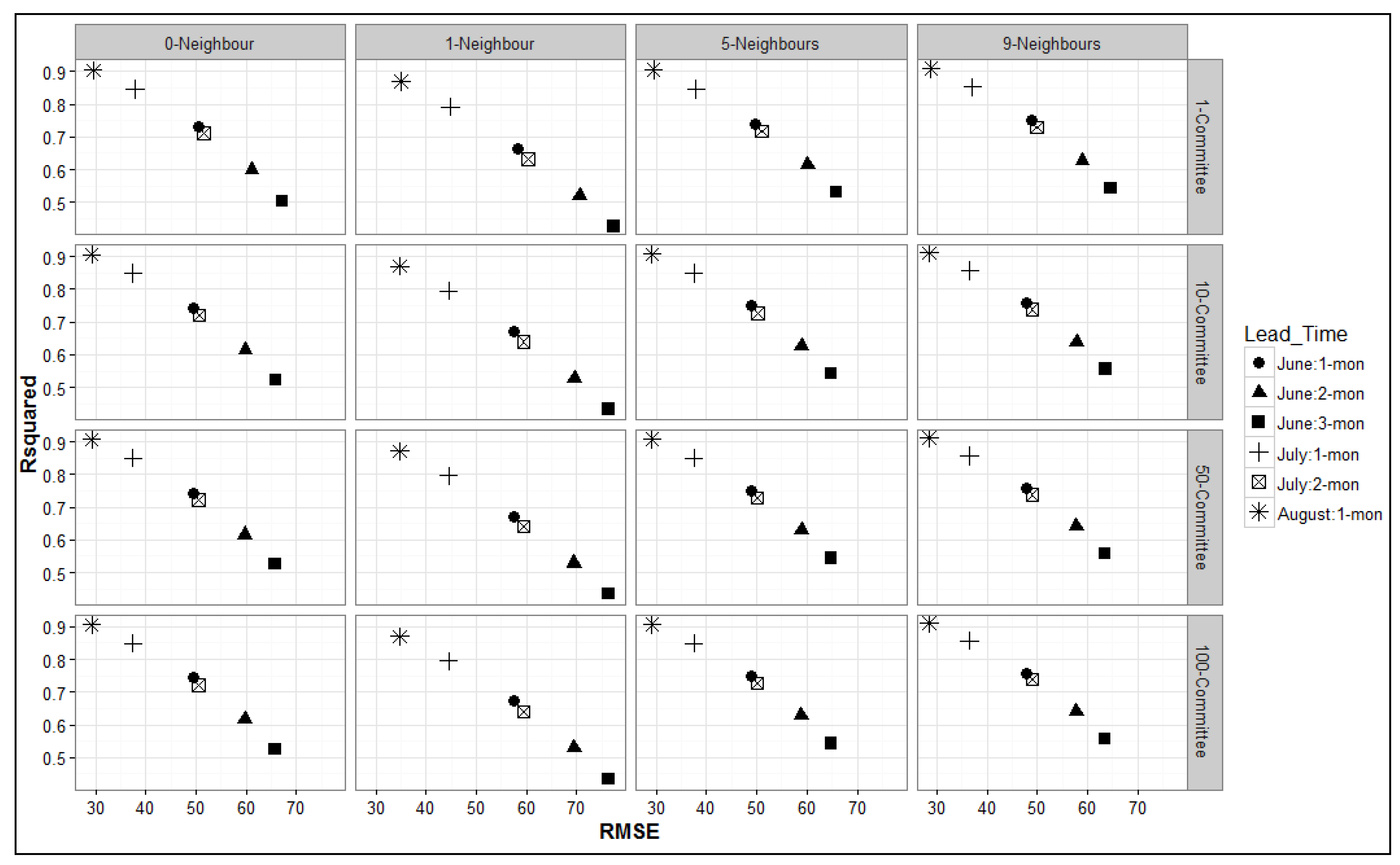
3.2. Model Performance Evaluations
3.3. Percentage Splits for Training and Testing
4. Conclusions
- The “instance and rules” models significantly increased the performance of the drought model compared to the “rules alone” model. For further performance enhancement of the models, the instance-and-rules model can be combined with ensemble models.
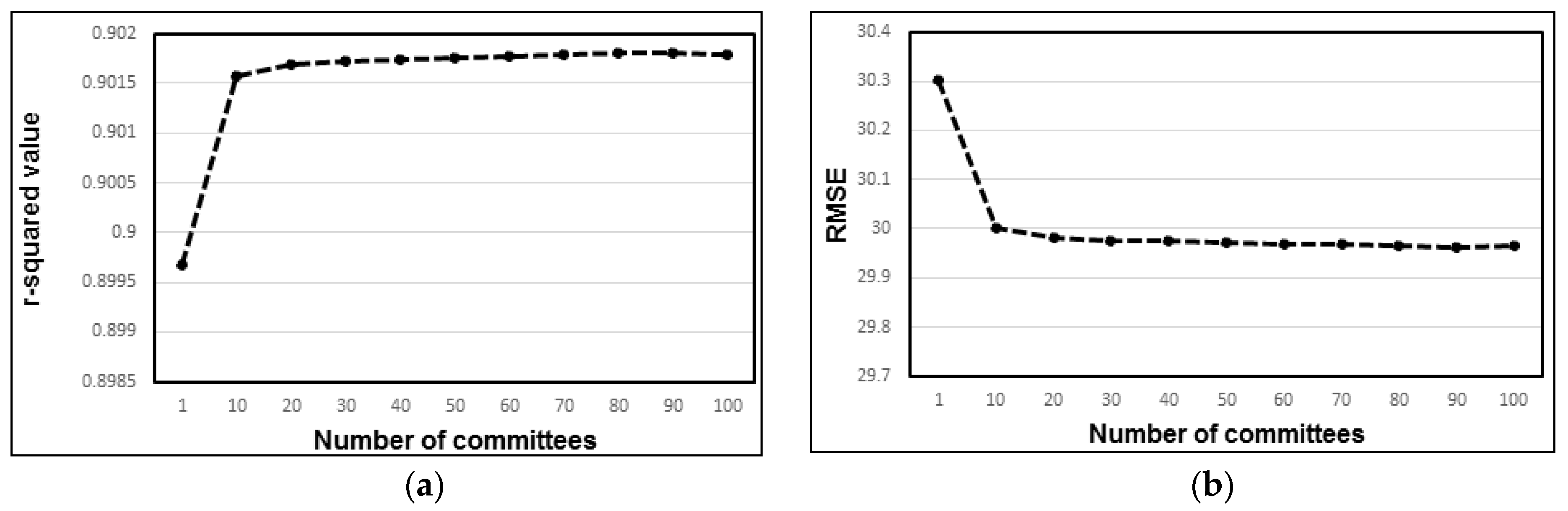
- When using ensemble model options, it was confirmed that the highest average r-squared value was obtained for the model with 30 committees. There was no gain in performance when additional committees were added to the models. RMSE consistently decreased for models with one to 30 committees but remained the same for all models with more than 30 committees. Therefore, it is imperative to use 30 committee models for future experiments employing committee models.
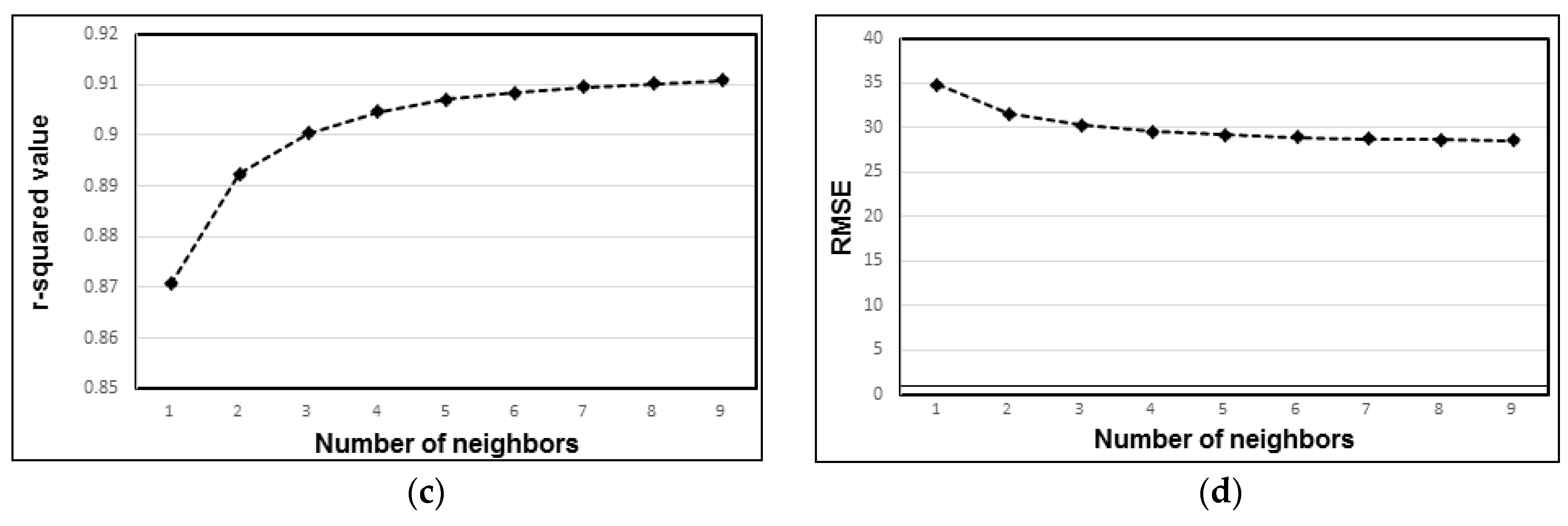
- For ensemble models, the r-squared value increased consistently with up to seven neighbors, with r-squared values remaining constant when any additional neighbors were considered. RMSE also decreased with up to seven neighbors but remained constant when additional neighbors were considered. Therefore, the optimum threshold for the highest model accuracy is the use of seven neighbors.
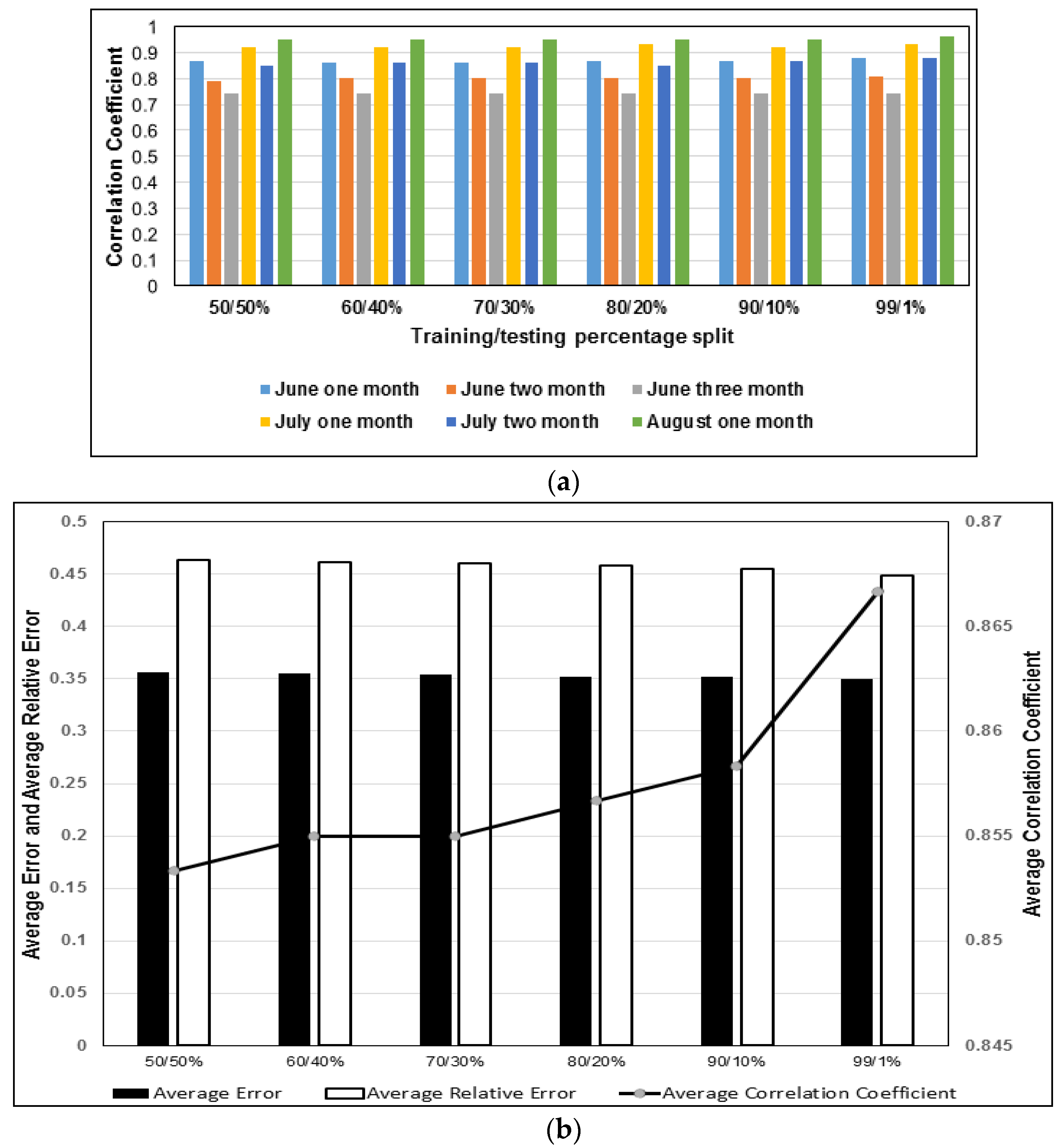
- In the iterative experiment to determine the best training/testing data split (i.e., 50/50%, 60/40%, 70/30%, 80/20%, 90/10%, or 99/1%), the CC results revealed a consistent increase as split percentage changed from 50/50% to 99/1%. For the practical implementation of regression tree modeling of drought, accuracy was higher when the original data set was split 90/10% into training and testing data sets.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Negash, S.; Gray, P. Business Intelligence. In Handbook on Decision Support Systems; Burstein, F., Holsapple, C., Eds.; Springer: Heidelberg, Germany, 2008; Volume 2, pp. 175–193. [Google Scholar]
- Langseth, J.; Vivatrat, N. Why Proactive Business Intelligence is a Hallmark of the Real-Time Enterprise: Outward Bound. Intell. Enterp. 2003, 5, 34–41. [Google Scholar]
- Ali, M.; Bosse, T.; Hindriks, K.V.; Hoogendoorn, M.; Jonker, C.M.; Treur, J. Recent Trends in Applied Artificial Intelligence. In Proceedings of the 26th International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems (IEA/AIE 2013), Amsterdam, The Netherlands, 17–21 June 2013. [Google Scholar]
- Hor, C. Extracting Knowledge From Substations for Decision Support. IEEE Trans. Power Deliv. 2005, 20, 595–602. [Google Scholar] [CrossRef]
- Nonaka, I. A Dynamic Theory of Organizational Knowledge Creation. Organ. Sci. 1994, 5, 14–37. [Google Scholar] [CrossRef]
- Dienes, Z.; Perner, J. A theory of implicit and explicit knowledge. Behav. Brain Sci. 1999, 22, 735–808. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Kamber, M. Data Mining: Concepts and Techniques, 2nd ed.; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2006. [Google Scholar]
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. The KDD process for extracting useful knowledge from volumes of data. Commun. ACM 1996, 39, 27–34. [Google Scholar] [CrossRef]
- Jackson, J. Data Mining: A Conceptual Overview. Commun. Assoc. Inf. Syst. 2002, 8, 267–296. [Google Scholar]
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. Knowledge Discovery and Data Mining: Towards a Unifying Framework. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96 AAAI), Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 82–88. [Google Scholar]
- Miller, H.J.; Han, J. Geographic Data Mining and Knowledge Discovery; Taylor & Francis: London, UK, 2001. [Google Scholar]
- UNCCD. United Nations Convention to Combat Desertification, Article 1; United Nations: Bonn, Germany, 1999. [Google Scholar]
- Dai, A. Drought under global warming: A review. Adv. Rev. Natl. Center Atmos. Res. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Wilhite, D. Drought and Water Crisis: Science, Technology and Management Issues; Taylor & Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Masih, I.; Maskey, S.; Mussá, F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- EM-DAT. EM-DAT: The International Disaster Database. Available online: http://www.emdat.be/ (accessed on 22 August 2015).
- Kumar, V.; Panu, U. Predictive assessment of severity of agricultural droughts based on agro-climatic factors. J. Am. Water Resour. Assoc. 1997, 33, 1255–1264. [Google Scholar] [CrossRef]
- Leilah, A.A.; Al-Khate, S.A. Statistical analysis of wheat yield under drought conditions. J. Arid Environ. 2005, 61, 483–496. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Durdu, O.F. Application of linear stochastic models for drought forecasting in the Buyuk Menderes river basin, western Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 1145–1162. [Google Scholar] [CrossRef]
- Modarres, R. Streamflow drought time series forecasting. Stoch. Environ. Res. Risk Assess. 2007, 21, 223–233. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought forecasting based on the remote sensing data using. ARIMA Models. ARIMA Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Fernandez, C.; Vega, J.A.; Fonturbel, T.; Jimenez, E. Streamflow drought time series forecasting: A case study in a small watershed in North West Spain. Stoch. Environ. Res. Risk Assess. 2009, 23, 1063–1070. [Google Scholar] [CrossRef]
- Lohani, V.K.; Loganathan, G.V. An early warning system for drought management using the palmer drought index. J. Am. Water Resour. Assoc. 1997, 33, 1375–1386. [Google Scholar] [CrossRef]
- Paulo, A.A.; Ferreira, E.; Coelho, C.; Pereira, L.S. Drought class transition analysis through Markov and Loglinear models, an approach to early warning. Agric. Water Manag. 2005, 77, 59–81. [Google Scholar] [CrossRef]
- Cancelliere, A.; Mauro, G.D.; Bonaccorso, B.; Rossi, G. Drought forecasting using the Standardized Precipitation Index. Water Resour. Manag. 2007, 21, 801–819. [Google Scholar] [CrossRef]
- Steinemann, A. Drought indicators and triggers: A stochastic approach to evaluation. J. Am. Water Resour. Assoc. 2003, 39, 1217–1233. [Google Scholar] [CrossRef]
- Banik, P.; Mandal, A.; Rahman, M.S. Markov chain analysis of weekly rainfall data in determining drought-proneness. Discret. Dyn. Nat. Soc. 2002, 7, 231–239. [Google Scholar] [CrossRef]
- Ochola, W.O.; Kerkides, P. A Markov chain simulation model for predicting critical wet and dry spells in Kenya: Analysing rainfall events in the Kano plains. Irrig. Drain. 2003, 52, 327–342. [Google Scholar] [CrossRef]
- Moreira, E.E.; Paulo, A.A.; Pereira, L.S.; Mexia, J.T. Analysis of SPI drought class transitions using loglinear models. J. Hydrol. 2006, 331, 349–359. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtinb, V.; Bagherzadehc, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using feed-forward recursive neural network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Kim, T.; Valdes, J. A nonlinear model for drought forecasting based on conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R.; Singh, V.P. Drought forecasting using a hybrid stochastic and neural network model. J. Hydrol. Eng. 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Bacanli, U.G.; Firat, M.; Dikbas, E.F. Adaptive Neuro-Fuzzy Inference System for drought forecasting. Stoch. Environ. Res. Risk Assess. 2009, 23, 1143–1154. [Google Scholar] [CrossRef]
- Pongracz, R.; Bogardi, I.; Duckstein, L. Application of fuzzy rule-based modeling technique to regional drought. J. Hydrol. 1999, 224, 100–114. [Google Scholar] [CrossRef]
- Balling, J.; Goodrich, G.B. Analysis of drought determinants for the Colorado River Basin. Clim. Chang. 2007, 82, 179–194. [Google Scholar] [CrossRef]
- Steinemann, A. Using climate forecasts for drought management. J. Appl. Meteorol. Climatol. 2006, 75, 1353–1361. [Google Scholar] [CrossRef]
- Farokhnia, A.; Morid, S.; Byun, H.R. Application of global SST and SLP data for drought forecasting on Tehran plain using data mining and ANFIS techniques. Theor. Appl. Climatol. 2011, 104, 71–81. [Google Scholar] [CrossRef]
- Dhanya, C.T.; Nagesh, K.D. Data mining for evolution of association rules for droughts and floods in India using climate inputs. J. Geophys. Res. 2009, 114, 1–15. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A. Spatiotemporal drought forecasting using nonlinear models. In Proceedings of the EGU General Assembly 2010, Vienna, Austria, 2–7 May 2010. [Google Scholar]
- Tadesse, T.; Wilhite, D.; Harms, S.; Hayes, M.; Goddard, S. Drought Monitoring Using Data Mining Techniques: A Case Study for Nebraska, USA. Nat. Hazards 2004, 33, 137–159. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Demisse, G.B.; Tadesse, T.; Solomon, A. Drought Spatial Object Prediction Approach using Artificial Neural Network. Geoinform. Geostat. Overv. 2015, 3, 1–7. [Google Scholar]
- Demisse, G.B. Knowledge Discovery From Satellite Images for Drought Monitoring. Ph.D. Thesis, Addis Ababa University, Addis Ababa, Ethiopia, 2013. [Google Scholar]
- Andreadis, K.M.; Clark, E.A.; Wood, A.W.; Hamlet, A.F.; Lettenmaier, D.P. Twentieth-century drought in the conterminous United States. J. Hydrometeorol. 2005, 6, 985–1001. [Google Scholar] [CrossRef]
- Dubrovsky, M.; Svoboda, M.D.; Trnka, M.; Hayes, M.J.; Wilhite, D.A.; Zalud, Z.; Hlavinka, P. Application of relative drought indices in assessing climate-change impacts on drought conditions in Czechia. Theor. Appl. Climatol. 2008, 96, 155–171. [Google Scholar] [CrossRef]
- NOAA. DROUGHT: Monitoring Economic, Environmental, and Social Impacts. Available online: http://www.ncdc.noaa.gov/news/drought-monitoring-economic-environmental-and-social-impacts (accessed on 4 January 2016).
- Sheffield, J.; Wood, E.F. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim. Dyn. 2008, 31, 79–105. [Google Scholar] [CrossRef]
- UCS. Causes of Drought: What’s the Climate Connection? Union of Concerned Scientists (UCS). Available online: http://www.ucsusa.org/global_warming/science_and_impacts/impacts/causes-of-drought-climate-change-connection.html#.VprO5k98wRI (accessed on 10 December 2016).
- National Meteorological Services Agency (NMSA). Assessment of Drought in Ethiopia; Meteorological Research Reports Series, No. 2; NMSA: Addis Ababa, Ethiopia, 1996.
- EMA. Ethiopian Mapping Agency (EMA). Available online: http://www.ema.gov.et/ (accessed on 22 December 2016).
- FEWSNET. Normalized Difference Vegetation Index, Product Documentation. Available online: http://earlywarning.usgs.gov/fews/africa/web/readme.php?symbol=nd (accessed on 20 June 2011).
- Holben, B.N. Characteristics of maximum-value composite images from temporal data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- USGS. USGS—Earth Resources Observation and Science (EROS) Center-Elevation Data. Available online: http://eros.usgs.gov/#/Find_Data/Products_and_Data_Available/gtopo30/hydro/africa (accessed on 1 September 2011).
- Ecodiv.org. Atlas of the Potential Vegetation of Ethiopia. Available online: http://ecodiv.org/atlas_ethiopia/index.html (accessed on 1 September 2011).
- ESA. European Space Agency, Global Land Cover Map. Available online: http://ionia1.esrin.esa.int/index.asp (accessed on 10 November 2011).
- GLCF. Global Land Cover Facility. Available online: http://www.landcover.org/aboutUs/ (accessed on 20 December 2010).
- NOAA. National Oceanic and Atmospheric Administration, Climate Indices: Monthly Atmospheric and Ocean Time Series. Available online: http://www.esrl.noaa.gov/psd/data/climateindices/list/ (accessed on 1 September 2011).
- Enfield, D.B.; Mestas-Nunez, A.M.; Trimble, P.J. The Atlantic multidecadal oscillation and it’s relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation and relationships to regional temperature and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.D.; Jonsson, T.; Wheeler, D. Extension to the North Atlantic Oscillation using early instrumental pressure observations from Gibraltar and South-West Iceland. Int. J. Climatol. 1997, 17, 1433–1450. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. Measuring the strength of ENSO—How does 1997/98 rank? Weather Forecast. 1998, 53, 315–324. [Google Scholar] [CrossRef]
- Frank, I.; Kalivas, J.; Kowalski, B. Partial Lease Square Solutions for Multicomponent Analysis. Lab. Chemom. 1983, 55, 1800–1804. [Google Scholar]
- Tadesse, M.; Sha, N.; Vannucci, M. Bayesian Variable Selection in Clustering HighDimensional Data. J. Am. Stat. Assoc. 2005, 100, 602–617. [Google Scholar] [CrossRef]
- Pierna, J.; Dardenne, P. Soil parameter quantification by NIRS as a Chemometric challenge at ‘Chimiométrie 2006’. Chemom. Intell. Lab. Syst. 2008, 91, 94–98. [Google Scholar] [CrossRef]
- Xu, Q.; Daszykowski, M.; Walczak, B.; Daeyaert, F.; Jonge, M.R.; Koymans, H.; Lewi, P.J.; Vinkers, H.M.; Janssen, P.A.; Heeres, J.; et al. Multivariate adaptive regression splines—Studies of HIV reverse transcriptase inhibitors. Chemom. Intell. Lab. Syst. 2004, 72, 27–34. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rulequest. An Overview of Cubist. Available online: http://www.rulequest.com/cubistwinhtml (accessed on 20 September 2015).
- Tadesse, T.; Wardlow, B.D.; Hayes, M.J.; Svoboda, M.D. The Vegetation Outlook (VegOut): A New Method for Predicting Vegetation Seasonal Greenness. GIScience Remote Sens. 2010, 47, 25–52. [Google Scholar] [CrossRef]
- Brown, J.F.; Wardlow, B.D.; Tadesse, T.; Hayes, M.J.; Reed, B.C. The Vegetation Drought Response Index (VegDRI): A New Integrated Approach for Monitoring Drought Stress in Vegetation. GIScience Remote Sens. 2008, 45, 16–46. [Google Scholar] [CrossRef]
- Tadesse, T.; Demisse, G.; Zaitchik, B.; Dinku, T. Satellite-based hybrid drought monitoring tool for prediction of vegetation condition in Eastern Africa: A case study for Ethiopia. Water Resour. Res. 2014, 50. [Google Scholar] [CrossRef]
- Berhan, G.; Shawndra, H.; Tadesse, T.; Solomon, A. Drought Prediction System for Improved Climate Change Mitigation. IEEE Transs Geosci. Remote Sens. 2014, 52, 4032–4037. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A. Regression rules as a tool for predicting soil properties from infrared reflectance spectroscopy. Chemom. Intell. Lab. Syst. 2008, 94, 72–79. [Google Scholar] [CrossRef]
- Shao, Q.; Rowe, R.C.; York, P. Investigation of an artificial intelligence technology-Model trees Novel applications for an immediate release tablet formulation database. Eur. J. Pharm. Sci. 2007, 31, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Loh, W.Y.; Shih, Y.S. Split selection methods for classification trees. Stat. Sin. 1997, 7, 815–840. [Google Scholar]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings of the AI 92 (Adams & Sterling, Eds.), Hobart, Australia, 16–18 November 1992; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
- Hullermeier, E. Possibilistic instance-based learning. Artif. Intell. 2003, 148, 335–383. [Google Scholar] [CrossRef]
- Aha, D.W. Lazy Learning. Artif. Intell. Rev. 1997, 11, 7–10. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J. Diagn. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Witten, I.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Elsevier: San Francisco, CA, USA, 2011. [Google Scholar]
- Henderson, B.L.; Bui, E.N.; Moran, C.J.; Simon, D.A.P. Australia-wide predictions of soil properties using decision trees. Geoderma 2005, 124, 383–398. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Kvalseth, T.O. Cautionary note about R 2. Am. Stat. 1985, 39, 279–285. [Google Scholar] [CrossRef]
- Cheung, W.H.; Senay, G.; Singh, A. Trends and spatial distribution of annual and seasonal rainfall in Ethiopia. Int. J. Climatol. 2008, 28, 1723–1734. [Google Scholar] [CrossRef]
- Korecha, D.; Barnston, A.G. Predictability of June–September Rainfall in Ethiopia. Mon. Weather Rev. 2006, 135, 628–650. [Google Scholar] [CrossRef]
- Segele, Z.T.; Lamb, P.J. Characterization and variability of Kiremt rainy season over Ethiopia. Meteorol. Atmos. Phys. 2005, 89, 153–180. [Google Scholar] [CrossRef]
- Seleshi, Y.; Zanke, U. Recent Changes In Rainfall and Rainy Days In Ethiopia. Int. J. Climatol. 2004, 24, 973–983. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Oza, N.C. Ensemble Data Mining Methods; NASA Ames Research Center: Moffett Field, CA, USA, 2004.
- Fortmann-Roe, S. Understanding the Bias-Variance Tradeoff. Available online: http://scott.fortmann-roe.com/docs/BiasVariance.html (accessed on 14 October 2016).
- Ruefenacht, B.; Hoppus, A.; Caylor, J.; Nowak, D.; Walton, J.; Yang, L.; Koeln, G. Analysis of Canopy Cover and Impervious Surface Cover of Zone 41; San Dimas Technology & Development Center: San Dimas, CA, USA, 2002. [Google Scholar]
| DEM | SDNDVI | LC | AWC | ER | SPI | PDO | AMO | NAO | PNA | MEI |
|---|---|---|---|---|---|---|---|---|---|---|
| 598 | −0.40 | 200 | 97.5 | 2 | 0.21 | 0.68 | 0.243 | −0.07 | −0.53 | 0.068 |
| 700 | −0.40 | 110 | 56.42857 | 2 | 0.72 | −1.47 | −0.11 | −0.82 | −0.92 | 1.005 |
| 2850 | 0.00 | 14 | 123.5 | 6 | 0.48 | 0.68 | 0.243 | −0.07 | −0.53 | 0.068 |
| 524 | 0.00 | 30 | 175 | 2 | 0.86 | 2.36 | −0.027 | 0.99 | 2.10 | 1.700 |
| 258 | −0.10 | 30 | 157.7778 | 1 | 1.28 | 1.10 | −0.10 | 0.56 | −1.18 | −0.221 |
| 1697 | 0.30 | 14 | 159.5 | 6 | 1.07 | 1.10 | −0.10 | 0.56 | −1.18 | −0.221 |
| 572 | −0.40 | 110 | 127.7778 | 2 | 0.33 | 0.18 | −0.299 | −0.42 | −0.36 | −0.152 |
| 1876 | −0.70 | 30 | 158.3334 | 6 | −1.39 | 0.89 | −0.226 | 1.22 | 0.39 | 0.394 |
| 1106 | −0.20 | 110 | 33.33334 | 2 | −1.32 | −0.44 | 0.015 | −0.03 | −1.19 | −0.219 |
| 1213 | 0.00 | 130 | 91.5 | 2 | 1.38 | 0.46 | −0.194 | 1.52 | −1.36 | 0.807 |
| 1567 | 0.20 | 110 | 197.5 | 5 | 0.17 | 1.10 | −0.100 | 0.56 | −1.18 | −0.221 |
| 422 | −0.20 | 30 | 157.7778 | 2 | −2.54 | −1.3 | 0.222 | 1.12 | 0.43 | −0.500 |
| 1182 | 0.10 | 110 | 159.5 | 2 | −0.59 | 0.74 | 0.197 | 0.88 | 1.31 | −1.187 |
| 1612 | 0.20 | 20 | 175 | 6 | −0.17 | 0.18 | −0.299 | −0.42 | −0.36 | −0.152 |
| 1589 | −0.60 | 20 | 91.5 | 5 | −0.03 | 0.46 | −0.194 | 1.52 | −1.36 | 0.807 |
| 3159 | 0.50 | 110 | 170 | 9 | 1.32 | 1.10 | −0.100 | 0.56 | −1.18 | −0.221 |
| 2835 | 0.10 | 20 | 65.55556 | 6 | −0.41 | 1.26 | −0.125 | 0.2 | 1.36 | 0.952 |
| 1385 | 0.20 | 20 | 144.5 | 5 | −0.57 | 1.27 | 0.396 | 0.13 | 0.90 | 0.177 |
| 908 | 0.20 | 200 | 88 | 2 | 1.82 | 1.10 | −0.100 | 0.56 | −1.18 | −0.221 |
| Attribute | Attribute Usage in the If-Conditions | Attribute Usage in the Regression Model | Rank |
|---|---|---|---|
| AMO | 83% | 54% | 2 |
| MEI | 81% | 23% | 7 |
| ER | 72% | 36% | 6 |
| DEM | 61% | 52% | 4 |
| PDO | 51% | 87% | 1 |
| SPI | 50% | 61% | 5 |
| AWC | 40% | 39% | 8 |
| LC | 35% | 35% | 9 |
| SDNDVI | 32% | 100% | 3 |
| PNA | 13% | 12% | 10 |
| NAO | 0% | 24% | 11 |
| Model | MAD | RE | CC |
|---|---|---|---|
| June one-month outlook | 0.3750 | 0.49 | 0.85 |
| June two-month outlook | 0.46488 | 0.61 | 0.77 |
| June three-month outlook | 0.51748 | 0.67 | 0.71 |
| June four-month outlook | 1.79753 | 0.57 | 0.77 |
| July one-month outlook | 0.27255 | 0.36 | 0.92 |
| July two-month outlook | 0.39691 | 0.51 | 0.84 |
| July three-month outlook | 1.89925 | 0.59 | 0.75 |
| August one-month outlook | 0.22184 | 0.29 | 0.95 |
| August two-month outlook | 1.86404 | 0.58 | 0.75 |
| September one-month outlook | 1.80224 | 0.57 | 0.77 |
| Monthly Outlooks | Percentage Splits | |||||
|---|---|---|---|---|---|---|
| 50/50% | 60/40% | 70/30% | 80/20% | 90/10% | 99/1% | |
| June one-month | 0.365 | 0.367 | 0.365 | 0.363 | 0.363 | 0.361 |
| June two-month | 0.4408 | 0.4386 | 0.4354 | 0.4336 | 0.4398 | 0.4392 |
| June three-month | 0.4886 | 0.487 | 0.4901 | 0.4851 | 0.4912 | 0.4999 |
| July one-month | 0.2622 | 0.2623 | 0.2625 | 0.258 | 0.2592 | 0.2497 |
| July two-month | 0.3672 | 0.3655 | 0.3658 | 0.3625 | 0.3501 | 0.3424 |
| August one-month | 0.2118 | 0.2091 | 0.2082 | 0.2095 | 0.2077 | 0.2044 |
| Average | 0.355933 | 0.354917 | 0.3545 | 0.35195 | 0.351833 | 0.349433 |
| Maximum | 0.4886 | 0.487 | 0.4901 | 0.4851 | 0.4912 | 0.4999 |
| Minimum | 0.2118 | 0.2091 | 0.2082 | 0.2095 | 0.2077 | 0.2044 |
| Standard deviation | 0.09537 | 0.095348 | 0.095776 | 0.094646 | 0.097163 | 0.101541 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demisse, G.B.; Tadesse, T.; Atnafu, S.; Hill, S.; Wardlow, B.D.; Bayissa, Y.; Shiferaw, A. Information Mining from Heterogeneous Data Sources: A Case Study on Drought Predictions. Information 2017, 8, 79. https://doi.org/10.3390/info8030079
Demisse GB, Tadesse T, Atnafu S, Hill S, Wardlow BD, Bayissa Y, Shiferaw A. Information Mining from Heterogeneous Data Sources: A Case Study on Drought Predictions. Information. 2017; 8(3):79. https://doi.org/10.3390/info8030079
Chicago/Turabian StyleDemisse, Getachew B., Tsegaye Tadesse, Solomon Atnafu, Shawndra Hill, Brian D. Wardlow, Yared Bayissa, and Andualem Shiferaw. 2017. "Information Mining from Heterogeneous Data Sources: A Case Study on Drought Predictions" Information 8, no. 3: 79. https://doi.org/10.3390/info8030079






