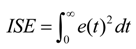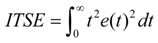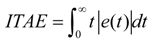Multivariable PID Decoupling Control Method of Electroslag Remelting Process Based on Improved Particle Swarm Optimization (PSO) Algorithm
Abstract
:1. Introduction
2. Technique Flowchart and Mathematics Model of ESR Process
2.1. Technique Flowchart
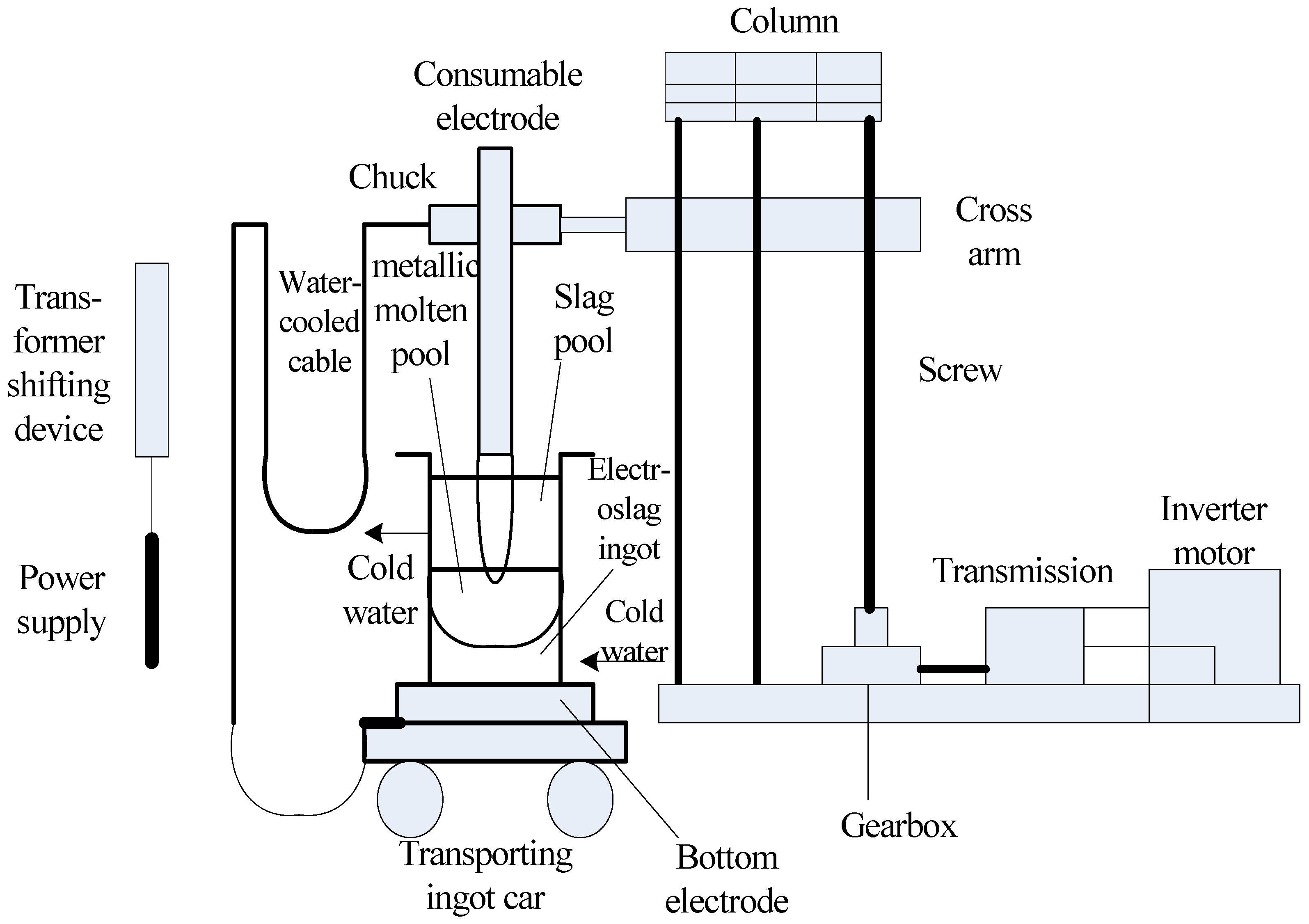
- (1)
- Melting slag stage. It includes an opening stage to make slag and slag melting with low power by using the lower voltage and current. Because the slag pool has not been formed, there will be large current fluctuations. When the slag pool is formed, the current becomes stable. The slag will be melted until all slag materials have been added. From now on, slag melting will be put under a high power to melt all slag and keep a certain temperature.
- (2)
- Exchange electrodes. They will be finished by the movement of the robot arm, which should be finished in no more than five minutes to avoid the solidification of the melted electroslag. After the completion of the electrode exchange, because there will large heat absorption after the cold metal electrodes are inserted into the electroslag pool, the normal casting should not begin. To achieve the melting speed required by the steel casting technique, the current set-point must be increased.
- (3)
- Casting stage. The electrode melting velocity in the normal casting stage is the key factor of deciding the solidification of steel ingot. So the biggest allowed electrode melting velocity of the electroslag furnace may be concluded in accord with the related formulas.
- (4)
- Feeding stage. The main function of the feeding stage is to remove the pit on the top of the ingot caused by the solidification.
2.2. Mathematic Model
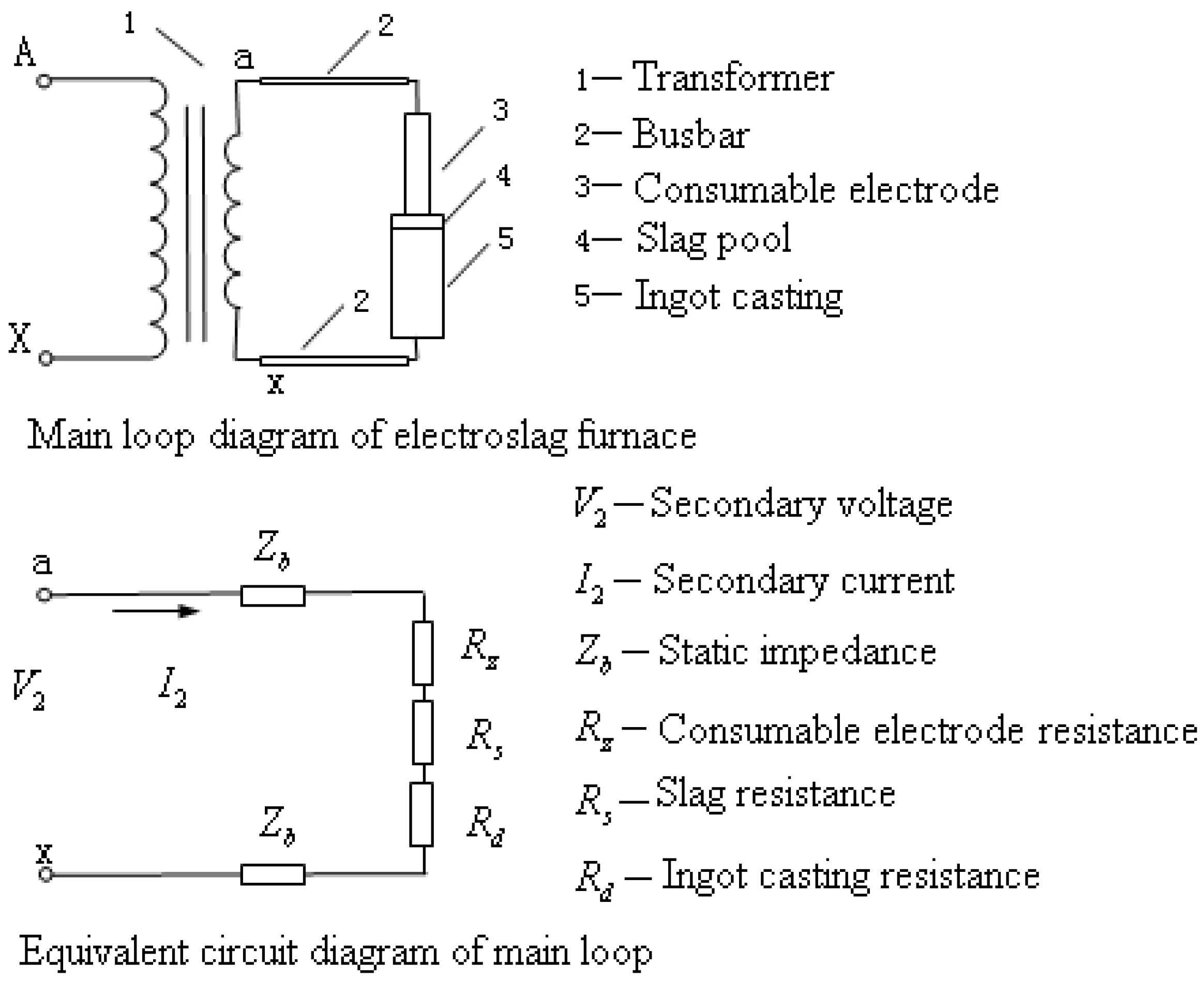
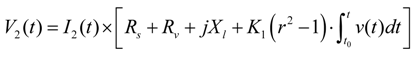
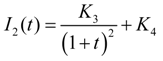
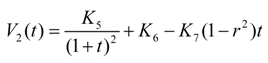
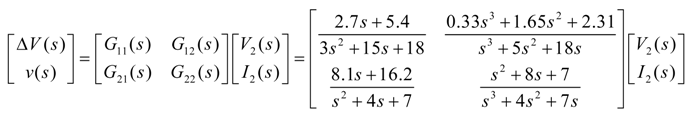
3. Self-Tuning of Multivariable PID Controller Parameters Based on IPSO
3.1. Multivariable PID Control Strategy
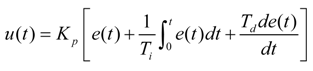
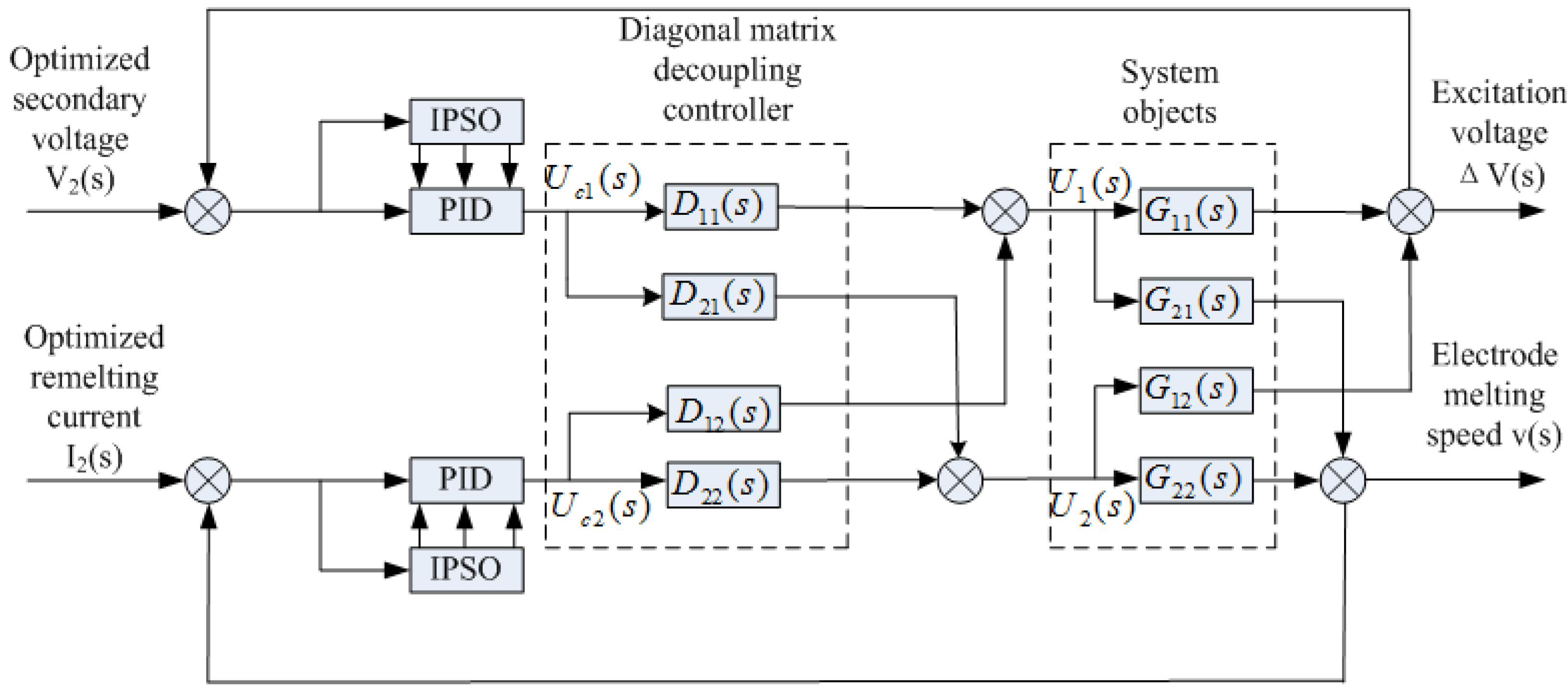
3.2. Diagonal Matrix Decoupling
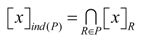
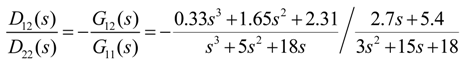
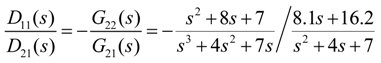
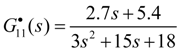
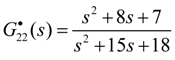
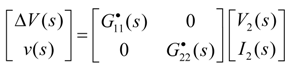
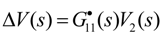
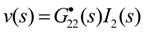
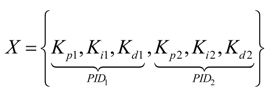
- (1)
- Integral of squared error (ISE)
- (2)
- Integral of time squared error (ITSE)
- (3)
- Integral of absolute error (IAE)
- (4)
- Integral of time multiplied by absolute error (ITAE)
3.3. Particle Swarm Optimization Algorithm
3.4. Adaptive Chaotic Migration Mutation Operator
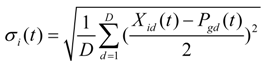
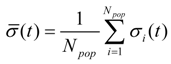
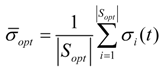
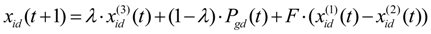

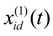 ,
, 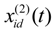 ,
, 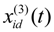 are different random individuals in the particle swarm Sopt, λ is the migration factor, F is the scale factor, t is the current iteration and T is the maximum iteration number.
are different random individuals in the particle swarm Sopt, λ is the migration factor, F is the scale factor, t is the current iteration and T is the maximum iteration number.3.5. Algorithmic Procedure
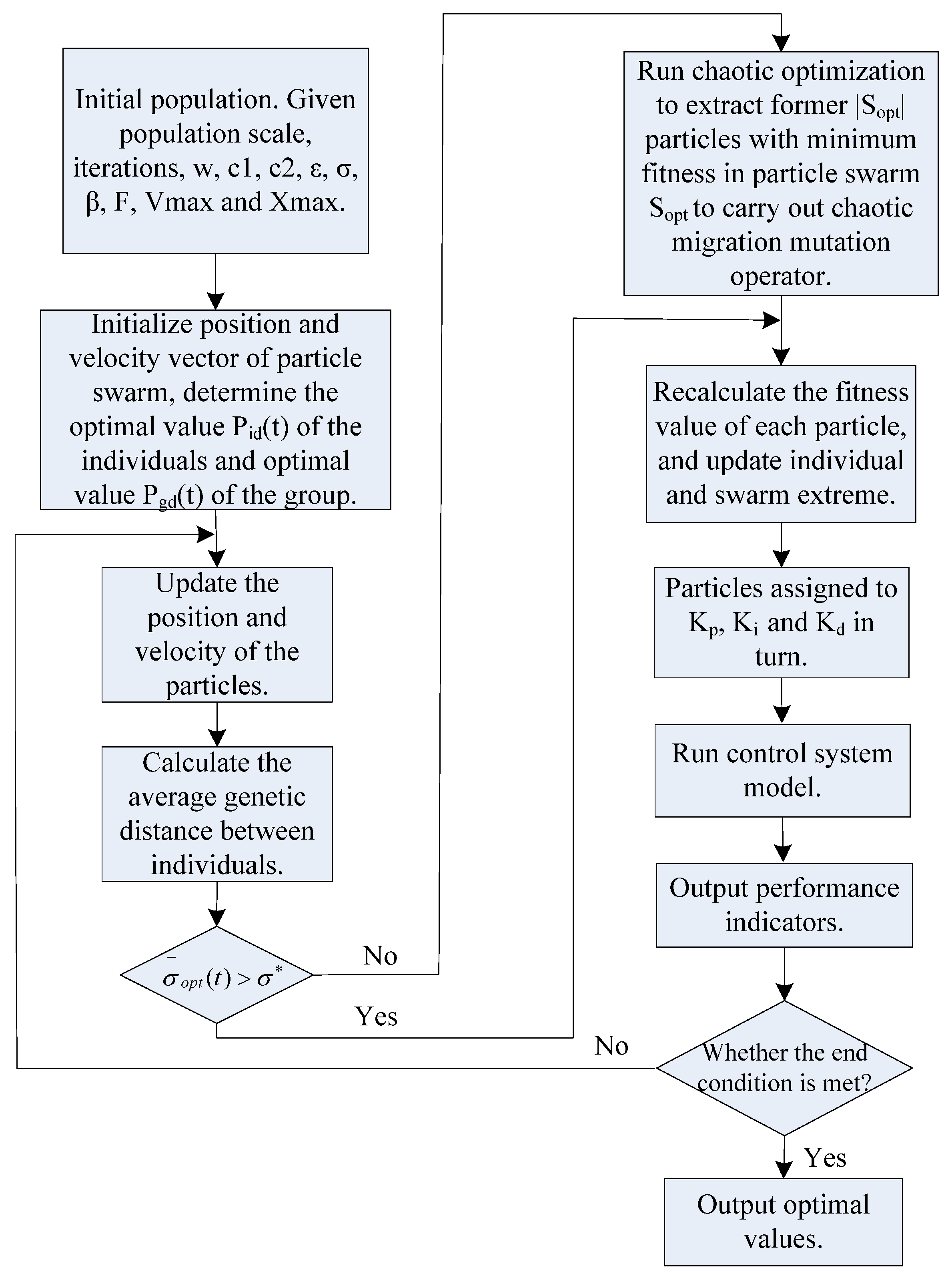
- (1)
- Initialization population. Initialize the population size, random positions, particle velocities, inertia weights, learning factor, collection valve value, chaos perturbation range [−β,β], scale factor F, maximum iteration number, the particle’s position range [−xmax,xmax] and the particle flight speed range [−vmax,vmax].
- (2)
- Calculate the fitness of each particle, and determine the optimal value Pid(t) of each particle and the optimal value Pgd(t) of the whole particle swarm.
- (3)
- According to Equations (19) and (20), the particle’s position and velocity are updated. Then update the individual optimal value Pid(t) of the particle and the optimal values Pgd(t) of particle swarm.
- (4)
- Equations (21)–(23) are utilized to calculate the average distance σopt (t) between particles. Then compare σopt (t) and σ*. If σopt (t) > σ*, go to step 5. If σopt (t) ≤ σ*, judge whether the optimal termination condition is satisfied or not. If it is met, the optimization process is finished and output the optimal results. Otherwise, return to step 2.
- (5)
- According to Equations (24) and (25), the chaotic optimization is processed. Extract the former |Sopt| particle with minimum fitness to take the place of the individuals in the original particle swarm Sopt. According to Equations (26) and (27), the chaotic migration mutation operation is carried out. After the mutation operation, return to step 2.
4. Simulation Experiments
4.1. Input-Output Characteristics of ESR Process
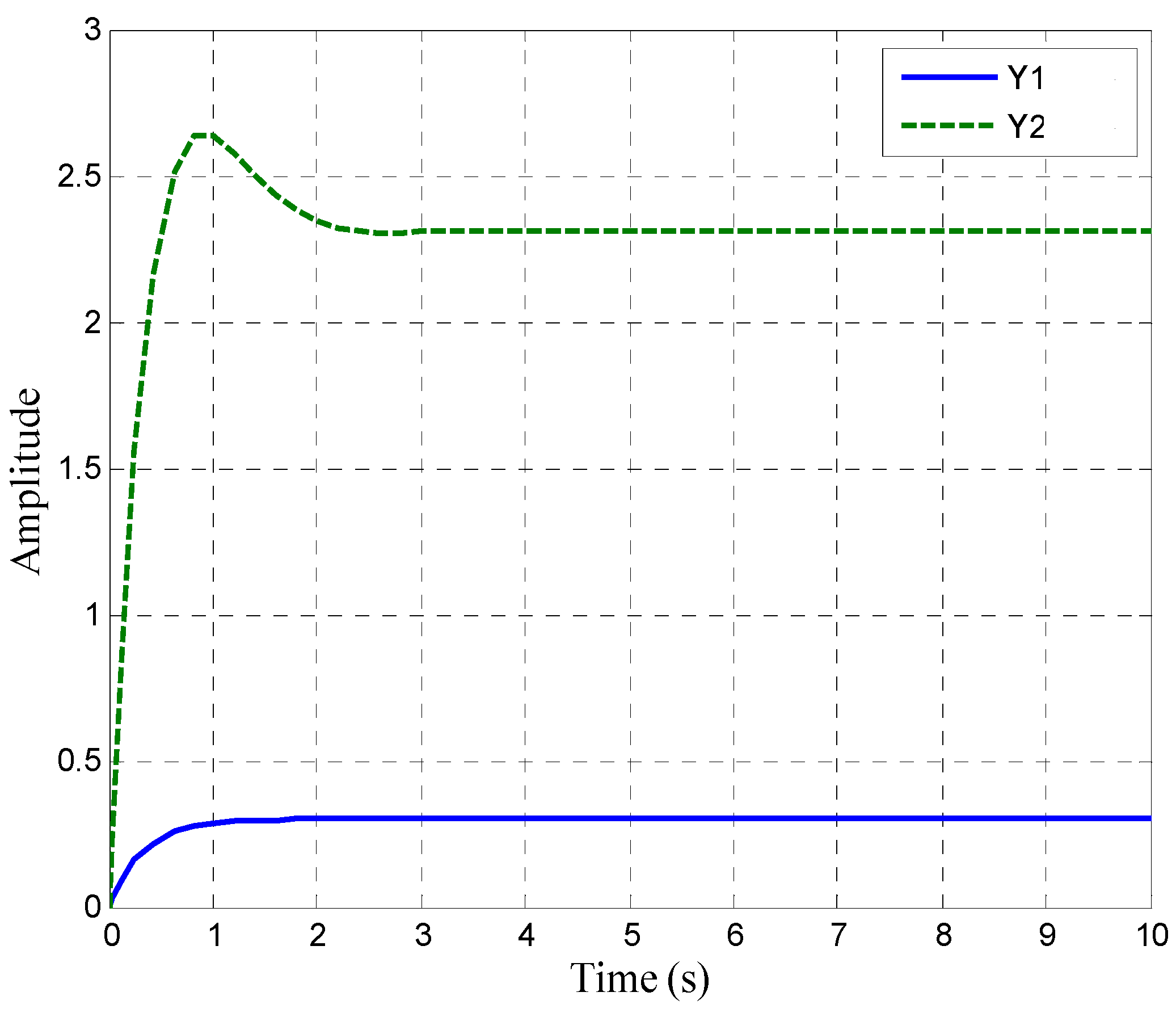
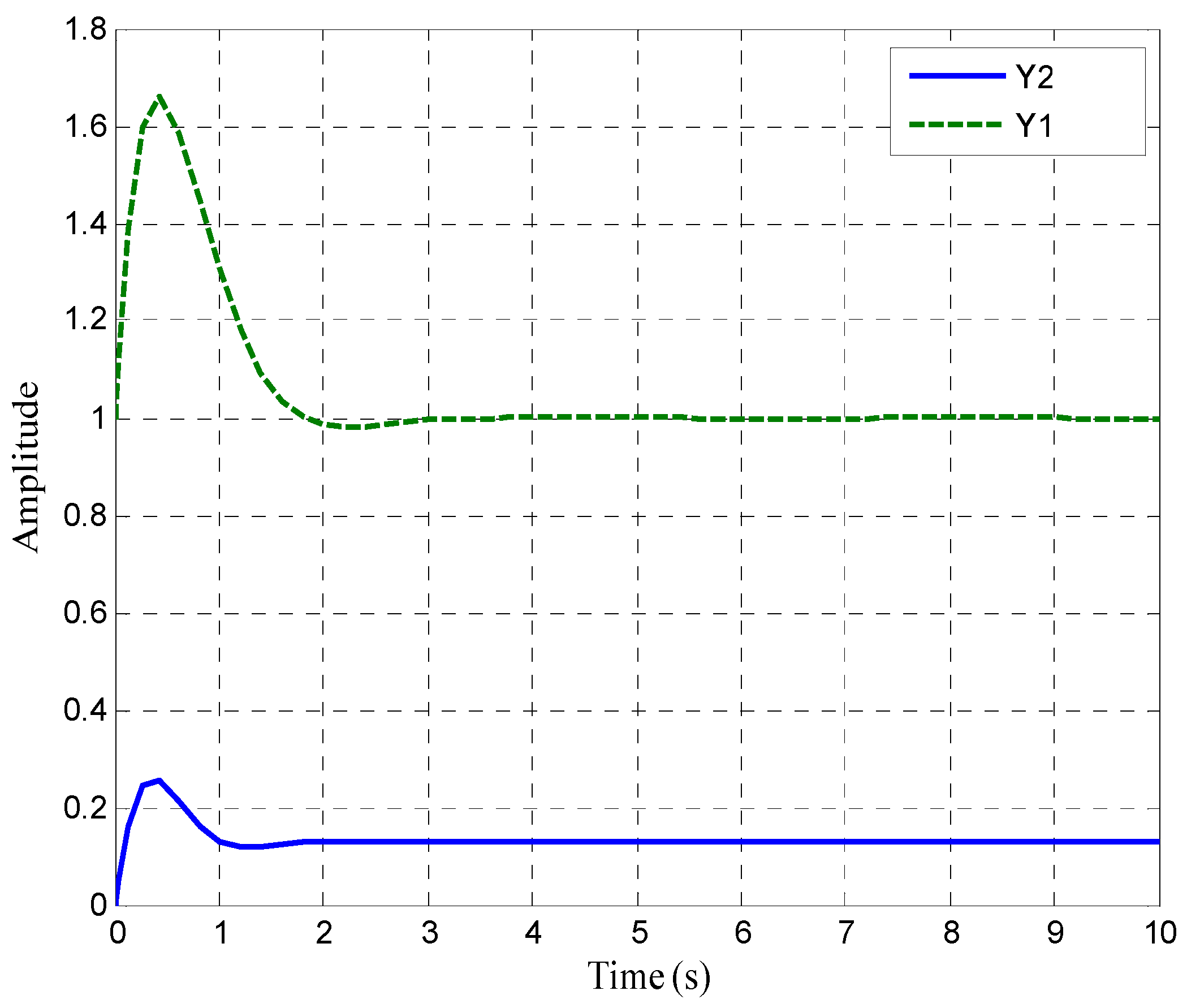
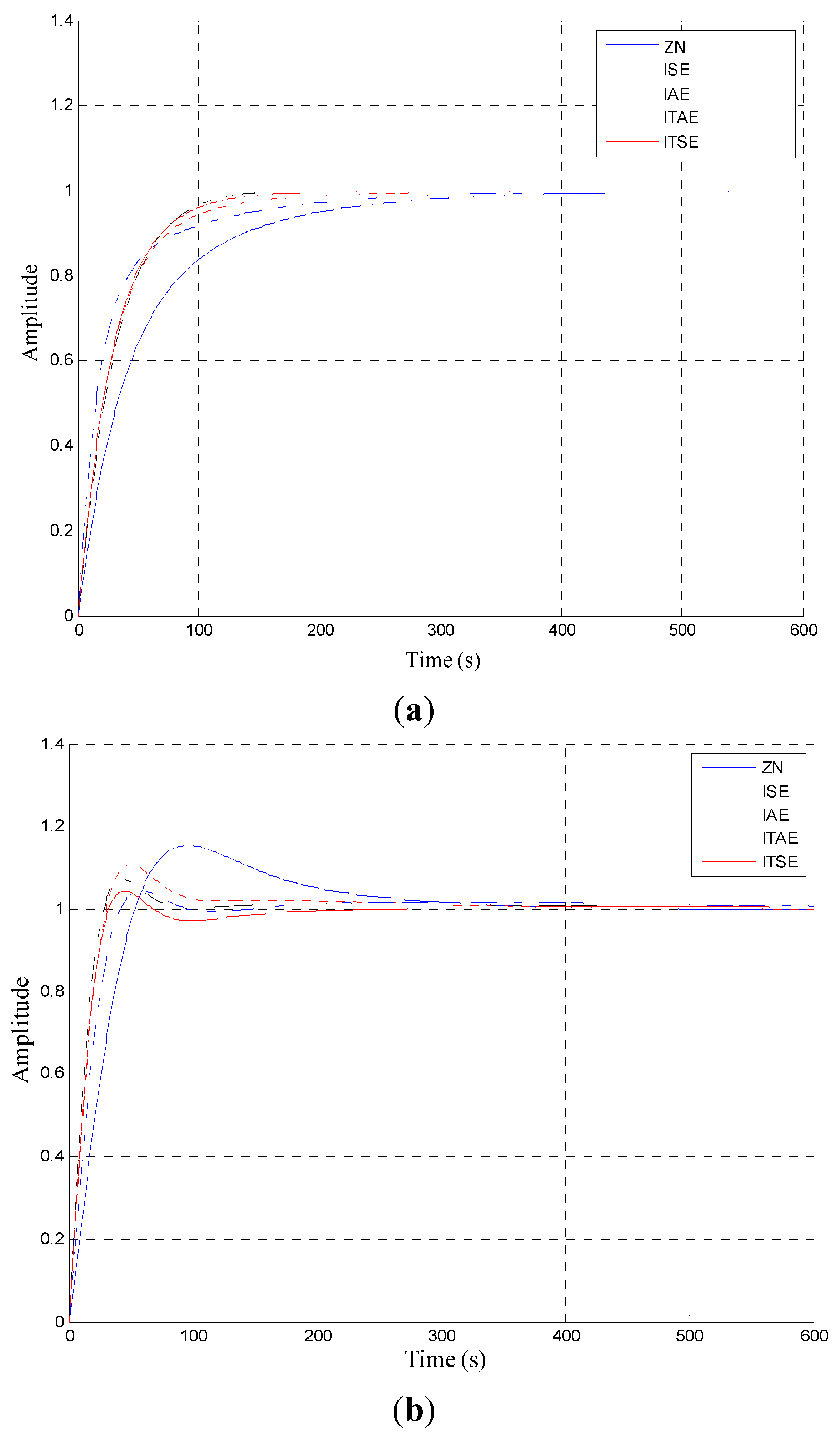
4.2. PID Controller Optimized by IPSO Algorithm
| PID Parameters | System 1 | System 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZN | ISE | IAE | ITAE | ITSE | ZN | ISE | IAE | ITAE | ITSE | |
| Kp | 4.61 | 4.94 | 7.59 | 8.75 | 8.59 | 4.61 | 7.21 | 3.20 | 7.21 | 7.86 |
| Ki | 5.90 | 7.58 | 9.70 | 9.70 | 9.22 | 5.90 | 1.63 | 3.49 | 8.7 | 1.26 |
| Kd | 0.85 | 0.60 | 1.61 | 1.61 | 1.29 | 0.85 | 0.33 | 0.09 | 0.09 | 0.42 |
| Performance Indices | System 1 | System 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZN | ISE | IAE | ITAE | ITSE | ZN | ISE | IAE | ITAE | ITSE | |
| Overshoot (%) | 0.32 | 0.25 | 0.27 | 0.23 | 0.43 | 2.44 | 2.40 | 1.93 | 1.43 | 1.60 |
| Tr (s) | 0.87 | 0.75 | 0.64 | 0.60 | 0.71 | 0.94 | 0.88 | 0.79 | 0.60 | 0.68 |
| Ts (s) | 1.24 | 0.96 | 1.01 | 0.81 | 0.87 | 4.32 | 4.01 | 4.11 | 3.50 | 3.97 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cao, F.; Wang, W.; Wang, J.-S. Intelligent optimal setting control of electroslag remelting process based on knowledge mining and case-based reasoning. Inf. Control 2010, 39, 114–119. (in Chinese). [Google Scholar]
- Li, B.; Wang, F.; Shan, M. Numerical Analysis of Electromagnetic Field in an Electroslag Remelting Process with Three-Phases Electrodes. In CFD Modeling and Simulation in Materials Processing; MNastac, L., Zhang, L., Thomas, B.G., Sabau, A., Ei-Kaddah, N., Powell, A.C., Combeau, H., Eds.; Wiley: Hoboken, NJ, USA, 2012; pp. 131–138. [Google Scholar]
- Weber, V.; Jardy, A.; Dussoubs, B.; Ablitzer, D.; Rybéron, S.; Schmitt, V.; Hans, S.; Poisson, H. A comprehensive model of the electroslag remelting process: Description and validation. Metall. Mater. Trans. B 2009, 40, 271–280. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.-C.; Wang, J.-B. Analysis and application of two principles for ESR furnace swing control. Metall. Ind. Autom. 2006, 2, 53–55. (in Chinese). [Google Scholar]
- Li, W.-Z.; Jia, X.-H.; Wang, J.-C.; Lin, Y.-S. Improvement of consarc ESR furnace control system. J. Iron Steel Res. 2007, 19, 99–101. (in Chinese). [Google Scholar]
- Zhao, L.-L.; Song, J.-C.; Liu, X.-H.; Liu, H.-Y. Intelligent control study based on genetic algorithm for electroslag remelting process. Mach. Electron. 2008, 5, 16–19. (in Chinese). [Google Scholar]
- Ren, W.; Zheng, X.-F.; Jiang, L.-X. Fuzzy adaptive PID control for electrode regulating system of electroslag furnace. Metall. Ind. Autom. 2006, 1, 15–18. (in Chinese). [Google Scholar]
- Jin, Y.C.; Ryu, K.H.; Sung, S.W.; Lee, J.; Lee, I.-B. PID auto-tuning using new model reduction method and explicit PID tuning rule for a fractional order plus time delay model. J. Process Control 2014, 24, 113–128. [Google Scholar] [CrossRef]
- Dey, C.; Mudi, R.K. An improved auto-tuning scheme for PID controllers. ISA Trans. 2009, 48, 396–409. [Google Scholar] [CrossRef]
- Jin, Q.B.; Hao, F.; Wang, Q. A multivariable IMC-PID method for non-square large time delay systems using NPSO algorithm. J. Process Control 2013, 23, 649–663. [Google Scholar] [CrossRef]
- Sarkar, B.K.; Mandal, P.; Saha, R.; Mookherjee, S.; Sanyal, D. GA-optimized feedforward-PID tracking control for a rugged electrohydraulic system design. ISA Trans. 2013, 52, 853–861. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Wang, W. Self-tuning of PID parameters based on particle swarm optimization. Control Decis. 2005, 20, 73–76. (in Chinese). [Google Scholar]
- Xiong, W.; Xu, B.; Zhou, Q. Study on optimization of PID parameter based on improved PSO. Comput. Eng. 2005, 31, 41–43. (in Chinese). [Google Scholar]
- Cao, F.; Wang, W. Harmony search based particle swarm optimisation approach for optimal PID control in electroslag remelting process. Int. J. Model. Identif. Control 2012, 15, 20–27. [Google Scholar] [CrossRef]
- Wang, D.-Y.; He, G.-Q.; Song, W.-M.; Kang, Y.-J.; Liu, J.-Z. Study and application on intelligent control of the ESR process. Ind. Heat. 2005, 34, 42–45. (in Chinese). [Google Scholar]
- Ahn, S.; Beaman, J.J.; Williamson, R.L.; Melgaard, D.K. Model-Based control of electroslag remelting process using unscented kalman filter. J. Dyn. Syst. Meas. Control 2010, 132. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 760–766.
- Wang, F.; Yu, P.L.H.; Cheung, D.W. Combining technical trading rules using particle swarm optimization. Expert Syst. Appl. 2014, 41, 3016–3026. [Google Scholar] [CrossRef]
- Cheng, S.; Shi, Y.; Qin, Q. A study of normalized population diversity in particle swarm optimization. Int. J. Swarm Intell. Res. 2013, 4, 1–34. [Google Scholar] [CrossRef]
- Ren, Z.; San, Z.; Chen, J. Improved particle swarm optimization and its application research in tuning of PID parameters. J. Syst. Simul. 2006, 18, 2870–2873. (in Chinese). [Google Scholar]
- Che, L.; Cheng, Z. Hybrid discrete differential evolution with a self-adaptive penalty function for constrained engineering optimization. J. Mech. Eng. 2011, 47, 141–151. (in Chinese). [Google Scholar]
- Hu, W.; Xu, F. Self-tuning of PID parameters based on improved particle swarm optimization. Appl. Res. Comput. 2012, 29, 1791–1794. (in Chinese). [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, J.-S.; Ning, C.-X.; Yang, Y. Multivariable PID Decoupling Control Method of Electroslag Remelting Process Based on Improved Particle Swarm Optimization (PSO) Algorithm. Information 2014, 5, 120-133. https://doi.org/10.3390/info5010120
Wang J-S, Ning C-X, Yang Y. Multivariable PID Decoupling Control Method of Electroslag Remelting Process Based on Improved Particle Swarm Optimization (PSO) Algorithm. Information. 2014; 5(1):120-133. https://doi.org/10.3390/info5010120
Chicago/Turabian StyleWang, Jie-Sheng, Chen-Xu Ning, and Yang Yang. 2014. "Multivariable PID Decoupling Control Method of Electroslag Remelting Process Based on Improved Particle Swarm Optimization (PSO) Algorithm" Information 5, no. 1: 120-133. https://doi.org/10.3390/info5010120
APA StyleWang, J.-S., Ning, C.-X., & Yang, Y. (2014). Multivariable PID Decoupling Control Method of Electroslag Remelting Process Based on Improved Particle Swarm Optimization (PSO) Algorithm. Information, 5(1), 120-133. https://doi.org/10.3390/info5010120