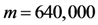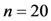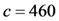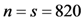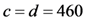Lightweight Proofs of Retrievability for Electronic Evidence in Cloud
Abstract
:1. Introduction
2. Related Work
3. An Electronic Evidence Preservation Center in Cloud
3.1. Center Management Area (CMA)
3.2. Classification Preservation Area (CPA)
3.3. Archive Storage Area (ASA)
 in the cloud. These servers will store all chunks of the evidence file, and each chunk is split into some blocks. In FG-PoR schemes, each block has a corresponding tag, and all blocks and tags will be stored in the ASA. The ASA will provide safe, reliable, efficient storage services for massive electronic evidence in the cloud. When the CMA asks the CPA about the integrity of a stored evidence file, the CPA will query the metadata for the locations of the desired chunks and construct proofs of retrievability to prove that the file is intact and retrievable.
in the cloud. These servers will store all chunks of the evidence file, and each chunk is split into some blocks. In FG-PoR schemes, each block has a corresponding tag, and all blocks and tags will be stored in the ASA. The ASA will provide safe, reliable, efficient storage services for massive electronic evidence in the cloud. When the CMA asks the CPA about the integrity of a stored evidence file, the CPA will query the metadata for the locations of the desired chunks and construct proofs of retrievability to prove that the file is intact and retrievable.3.4. Evidence Recovery Area (ERA)
 , and uses hash function to check the integrity of the evidence file. Then it sends the evidence to the CMA, and further forwards it to the LAU. The CMA could also check the integrity of the evidence file by running verifying algorithm VeriResp( ). If the ERA or the CMA has found some error data blocks of the evidence matrix, the ERA will use the retrieved algorithm RetrData( ) to recover these data blocks.
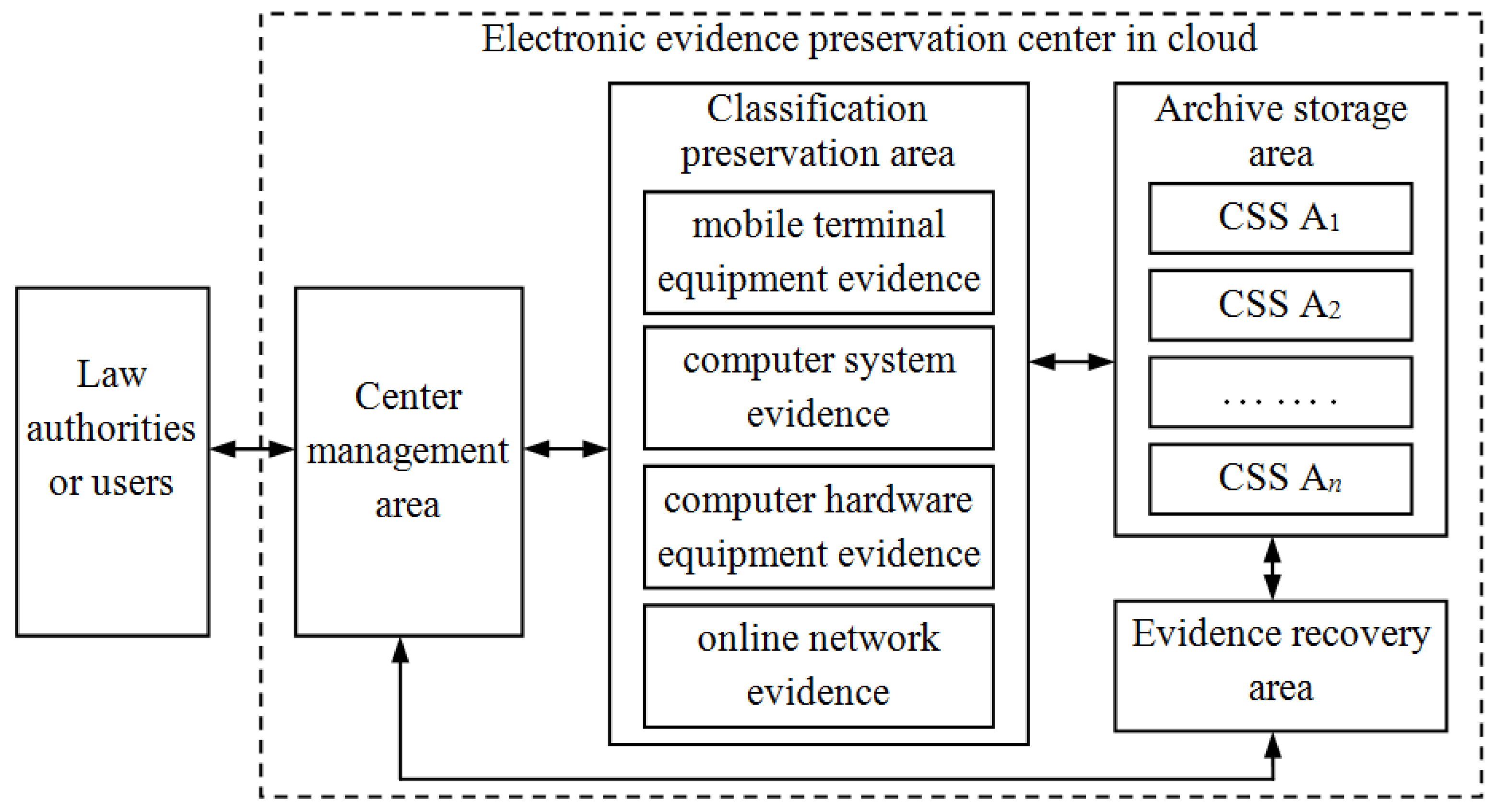
, and uses hash function to check the integrity of the evidence file. Then it sends the evidence to the CMA, and further forwards it to the LAU. The CMA could also check the integrity of the evidence file by running verifying algorithm VeriResp( ). If the ERA or the CMA has found some error data blocks of the evidence matrix, the ERA will use the retrieved algorithm RetrData( ) to recover these data blocks.4. Proofs of Retrievability for Electronic Evidence
 and will send it to the ASA to store. The CMA will send challenge message Chal( ) to the CPA so as to make regular checks on the integrity and availability of electronic evidence at appropriate intervals. The CPA will query the metadata for the locations of the challenged chunks and compute response values to send back to the CMA. When the CMA has found out some data blocks are incorrect, it will tell the information to the ERA, then the ERA uses retrieved algorithm RetrData( ) to recover electronic evidence. When all incorrect data blocks have been recovered, the ERA will send them back to the ASA again.
and will send it to the ASA to store. The CMA will send challenge message Chal( ) to the CPA so as to make regular checks on the integrity and availability of electronic evidence at appropriate intervals. The CPA will query the metadata for the locations of the challenged chunks and compute response values to send back to the CMA. When the CMA has found out some data blocks are incorrect, it will tell the information to the ERA, then the ERA uses retrieved algorithm RetrData( ) to recover electronic evidence. When all incorrect data blocks have been recovered, the ERA will send them back to the ASA again.4.1. Notation and Preliminaries
 be an electronic evidence file: it is divided into
be an electronic evidence file: it is divided into  chunks, and each chunk is split into
chunks, and each chunk is split into  blocks:
blocks:  , where each block
, where each block  . These evidence blocks may be expressed in the following matrix form
. These evidence blocks may be expressed in the following matrix form
 KeyGen( ). This algorithm is run by the CMA to generate public key
KeyGen( ). This algorithm is run by the CMA to generate public key  and private key
and private key  .
. TagSigGen
TagSigGen  . This algorithm is run by the CMA. It takes as input the private key
. This algorithm is run by the CMA. It takes as input the private key  and the evidence blocks set
and the evidence blocks set  , and outputs the tags set
, and outputs the tags set  and signatures set
and signatures set  .
. RespGen
RespGen  . This algorithm is run by the CPA. It takes as input the evidence blocks subset
. This algorithm is run by the CPA. It takes as input the evidence blocks subset  and the tags subset
and the tags subset  , and returns a response value
, and returns a response value  as output. It will query the ASA whether the ASA is actually storing all evidence blocks intact or not.
as output. It will query the ASA whether the ASA is actually storing all evidence blocks intact or not. VeriResp
VeriResp  . This algorithm is run by the CMA. It takes as input the public key
. This algorithm is run by the CMA. It takes as input the public key  , the response value
, the response value  and signatures subset
and signatures subset  , It will output 1 if the integrity of all evidence blocks is verified, otherwise will output 0.
, It will output 1 if the integrity of all evidence blocks is verified, otherwise will output 0. VeriHash(H,H′). This algorithm is run by the ERA. It takes as input two sets of hash values of evidence blocks
VeriHash(H,H′). This algorithm is run by the ERA. It takes as input two sets of hash values of evidence blocks  and H′.
and H′.  is saved previously, and H′ is computed when it is needed. If
is saved previously, and H′ is computed when it is needed. If  and H′ are equal, outputs 1, otherwise outputs 0.
and H′ are equal, outputs 1, otherwise outputs 0. RetrData(Ω′, S′). This algorithm is run by the ERA. It takes as input the set of tags Ω′ and the set of signatures S′ of the error evidence blocks returned from the ASA, and outputs the correct evidence blocks
RetrData(Ω′, S′). This algorithm is run by the ERA. It takes as input the set of tags Ω′ and the set of signatures S′ of the error evidence blocks returned from the ASA, and outputs the correct evidence blocks  .
.4.2. Nyberg-Rueppel Signature Scheme
 , a prime factor
, a prime factor  of
of  , and an element
, and an element  of order
of order  . The signer’s private key is a random element
. The signer’s private key is a random element  , while the corresponding public key is
, while the corresponding public key is  .
. , the signer selects
, the signer selects  at random and computes
at random and computes  and
and  as follows:
as follows:
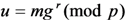
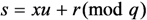
 is the signature of the message
is the signature of the message  . The signer sends the message
. The signer sends the message  and the signatures
and the signatures  to the receiver.
to the receiver. and the signatures
and the signatures  , to verify the validity of a signature, it checks that the following equality holds:
, to verify the validity of a signature, it checks that the following equality holds:
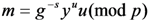
4.3. Finer Grained Proofs of Retrievability (FG-PoR)
4.3.1. Key Generation
 . Chooses two primes
. Chooses two primes  and
and  ,
,  is a factor of
is a factor of  , and an element
, and an element  of order
of order  . Chooses a secret random element
. Chooses a secret random element  , and sets
, and sets  . Chooses a secret key
. Chooses a secret key  ,
,  is the length of the key
is the length of the key  . Thus the secret key is
. Thus the secret key is  and the public key is
and the public key is  .
.4.3.2. Tags and Signatures Generation
 , the CMA runs the TagSigGen( ) algorithm to create a tag
, the CMA runs the TagSigGen( ) algorithm to create a tag  and a signature
and a signature  for each block
for each block  as
as

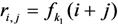
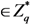
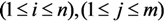 ,
, 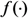 is a pseudo-random function. The tags set may be expressed in the following matrix form
is a pseudo-random function. The tags set may be expressed in the following matrix form
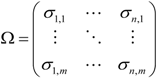
 and the set of corresponded tags
and the set of corresponded tags  to the CPA; the CPA categorizes the chunks and sends all blocks to the ASA, and only saves metadata of the chunks on it. Then the CMA computes
to the CPA; the CPA categorizes the chunks and sends all blocks to the ASA, and only saves metadata of the chunks on it. Then the CMA computes 
 and sends hash values set
and sends hash values set  to the ERA. Finally, the CMA deletes all copies of
to the ERA. Finally, the CMA deletes all copies of  ,
,  and
and  . It preserves only signatures set
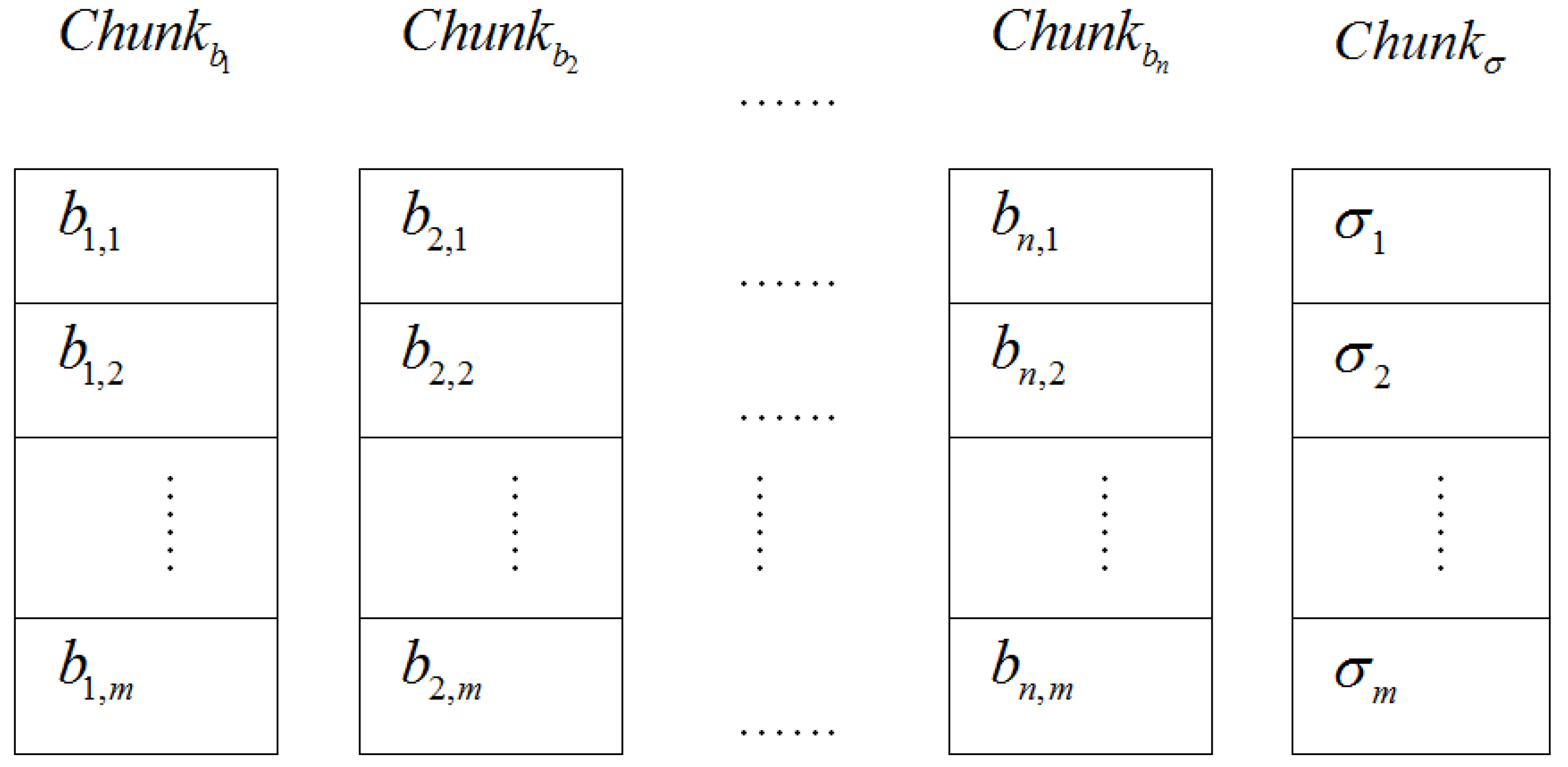
. It preserves only signatures set  and metadata of the evidence file on its own storage. The storage distribution of the electronic evidence blocks and their tags on the CSS of the ASA is given in Figure 3.
and metadata of the evidence file on its own storage. The storage distribution of the electronic evidence blocks and their tags on the CSS of the ASA is given in Figure 3.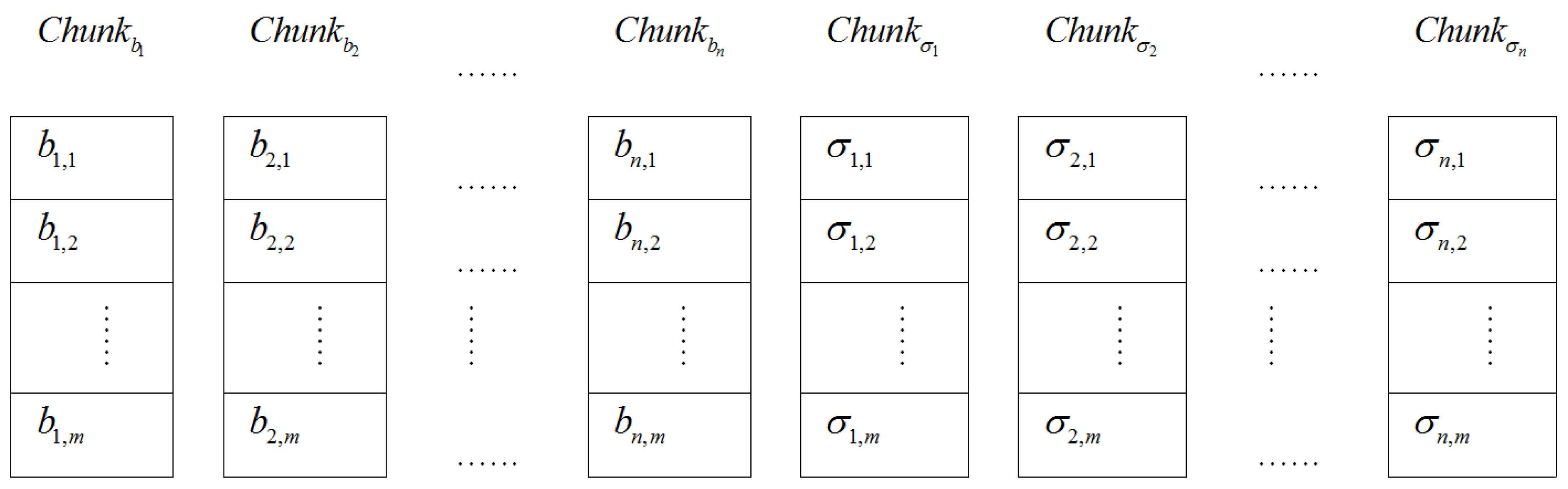
4.3.3. Challenge Choice
 , where
, where  is the identity number of the evidence file
is the identity number of the evidence file  , and it may be expressed as
, and it may be expressed as  .
.  is the number of challenged columns of the evidence matrix,
is the number of challenged columns of the evidence matrix,  .
.  is the number of challenged rows of the evidence matrix,
is the number of challenged rows of the evidence matrix,  .
.  are three fresh keys and are chosen randomly for each challenge.
are three fresh keys and are chosen randomly for each challenge. 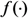 be a pseudo-random function,
be a pseudo-random function,  be a pseudo-random permutation. At each challenge, both the CMA and the CPA use key
be a pseudo-random permutation. At each challenge, both the CMA and the CPA use key  to generate indices of challenged columns
to generate indices of challenged columns 
 , also use key
, also use key  to generate indices of challenged rows
to generate indices of challenged rows 
 . They further use key
. They further use key  to derive
to derive  coefficients
coefficients 
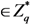 ,
,  ,
,  .
.4.3.4. Response Generation
 and corresponded tags
and corresponded tags  in Section 4.3.2. Grounded on indices of challenged columns and rows
in Section 4.3.2. Grounded on indices of challenged columns and rows  ,
,  , the CPA chooses subset of evidence blocks
, the CPA chooses subset of evidence blocks  and subset of tags
and subset of tags  from the ASA by querying the metadata of evidence chunks, then it generates response values
from the ASA by querying the metadata of evidence chunks, then it generates response values  based on
based on  and
and  .
. and the subset of tags
and the subset of tags  may be expressed in the following matrix form
may be expressed in the following matrix form
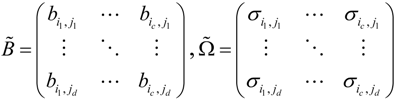
 are as follows
are as follows

 as a proof that the ASA possesses electronic evidence
as a proof that the ASA possesses electronic evidence  , finally the CPA sends
, finally the CPA sends  to the CMA.
to the CMA.4.3.5. Response Verification
 from the CPA, it takes out indices of challenged columns
from the CPA, it takes out indices of challenged columns  , challenged rows
, challenged rows  , and coefficients
, and coefficients  . Then the CMA chooses the subset of signatures
. Then the CMA chooses the subset of signatures  from the set of signatures
from the set of signatures  which has been saved previously. Further, the CMA computes
which has been saved previously. Further, the CMA computes
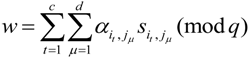
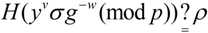
 . Otherwise, the verify algorithm returns 0.
. Otherwise, the verify algorithm returns 0.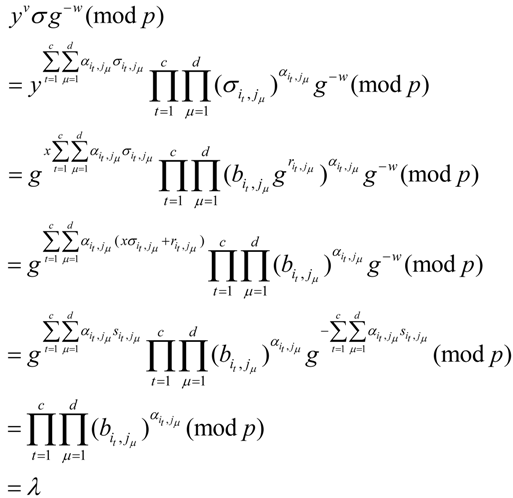
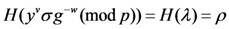
4.3.6. Evidence Retrieve
 , it sends a request message Requ
, it sends a request message Requ  to the CMA. The CMA will forward message Requ
to the CMA. The CMA will forward message Requ  to the CPA and the ERA. The ERA queries the chunks and the blocks of the evidence file from the ASA. After the ERA has got feedback message
to the CPA and the ERA. The ERA queries the chunks and the blocks of the evidence file from the ASA. After the ERA has got feedback message  , it will use hash function to compute the hash value of each element of evidence matrix
, it will use hash function to compute the hash value of each element of evidence matrix  to get the set
to get the set  . Each element of the set
. Each element of the set  is calculated as following
is calculated as following
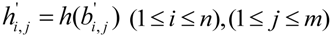
 with
with  , which has been saved in Section 4.3.2. If
, which has been saved in Section 4.3.2. If  , then
, then  , it means that all evidence blocks are intact. If one or several hash values of the set are not equal, then this means that these evidence blocks may have been altered in network transmitting or on the ASA storage. In Section 4.3.5, when the verify algorithm returns 0, it shows also that some evidence blocks may be incorrect in the ASA.
, it means that all evidence blocks are intact. If one or several hash values of the set are not equal, then this means that these evidence blocks may have been altered in network transmitting or on the ASA storage. In Section 4.3.5, when the verify algorithm returns 0, it shows also that some evidence blocks may be incorrect in the ASA. , in order to get original evidence block
, in order to get original evidence block  , the ERA queries its tag
, the ERA queries its tag  from the ASA, and asks the CMA to send back corresponding signature
from the ASA, and asks the CMA to send back corresponding signature  . As long as tag
. As long as tag  and
and  are not damaged, the ERA will use RetrData( ) algorithm to recover evidence block
are not damaged, the ERA will use RetrData( ) algorithm to recover evidence block 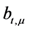
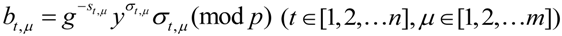
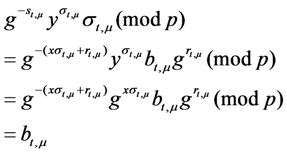
4.4. More Lightweight Proofs of Retrievability (ML-PoR)
4.4.1. Key Generation
 and the public key is
and the public key is  .
.4.4.2. Tags and Signatures Generation
 be a pseudo-random function, the CMA uses secret key
be a pseudo-random function, the CMA uses secret key  to derive random sequence
to derive random sequence
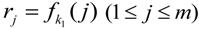
 , the CMA computes
, the CMA computes

 as
as
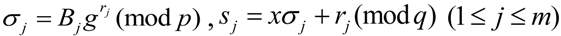
 as
as
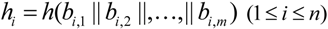
4.4.3. Challenge Choice
 . Both the CMA and the CPA use
. Both the CMA and the CPA use  keyed with
keyed with  to generate indices of challenged rows
to generate indices of challenged rows 
 , and use
, and use  keyed with
keyed with  to derive coefficients
to derive coefficients 

 .
.4.4.4. Response Generation
 and the subset of tags
and the subset of tags  to computes
to computes
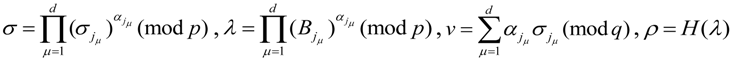
 as a proof that the ASA possesses electronic evidence
as a proof that the ASA possesses electronic evidence  , and the CPA sends response values
, and the CPA sends response values  to the CMA.
to the CMA.4.4.5. Response Verification
 from the CPA, it chooses the subset of signatures
from the CPA, it chooses the subset of signatures  from the set of signatures
from the set of signatures  and computes
and computes
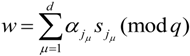

4.4.6. Evidence Retrieve
 from the ASA, it uses hash function to compute hash value of each column of evidence matrix
from the ASA, it uses hash function to compute hash value of each column of evidence matrix  to get
to get 

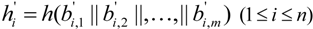
 with
with  , if
, if  , then
, then  , so this means that all evidence blocks are intact. If one or several hash values are not equal, then it means that some column vectors of evidence matrix have been altered in network transmitting or on the ASA storage.
, so this means that all evidence blocks are intact. If one or several hash values are not equal, then it means that some column vectors of evidence matrix have been altered in network transmitting or on the ASA storage.
 , it means tth column elements
, it means tth column elements  have been altered. To recover
have been altered. To recover  , the ERA queries the ASA to get the set of tags
, the ERA queries the ASA to get the set of tags  . As long as the set of tags
. As long as the set of tags  is not damaged, the ERA will use
is not damaged, the ERA will use  and the set of signatures
and the set of signatures  to recover
to recover  .
.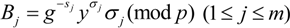
 , other elements are intact. So the ERA further computes following equation to recover
, other elements are intact. So the ERA further computes following equation to recover 
 .
.
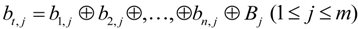
5. Security and Performance Analysis
 , so it adds extra computation costs. To reduce explaining duplication, for security analysis, we will only focus on the FG-PoR scheme. For performance analysis, we will consider both the FG-PoR scheme and ML-PoR scheme.
, so it adds extra computation costs. To reduce explaining duplication, for security analysis, we will only focus on the FG-PoR scheme. For performance analysis, we will consider both the FG-PoR scheme and ML-PoR scheme.5.1. Security Analysis
 and
and  of order
of order  , and set
, and set  , compute
, compute  . It is pointed out that no probabilistic algorithm could solve DLP with non-negligible advantage within polynomial time.
. It is pointed out that no probabilistic algorithm could solve DLP with non-negligible advantage within polynomial time. is a random oracle, by the definition of a random oracle, the CSA can guess hash values
is a random oracle, by the definition of a random oracle, the CSA can guess hash values  on the premise
on the premise  with only negligible probability.
with only negligible probability. , but the CSA has lost evidence blocks
, but the CSA has lost evidence blocks  , where
, where  , so the CSA forges evidence blocks
, so the CSA forges evidence blocks  to replace
to replace  , and computes
, and computes
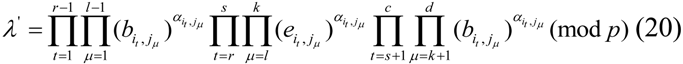
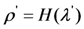 .
.  is stored perfectly in the CSA, the subset of challenge tags
is stored perfectly in the CSA, the subset of challenge tags  is also stored perfectly. Though some evidence blocks are forged, the values of
is also stored perfectly. Though some evidence blocks are forged, the values of  based on the subset of challenge tags
based on the subset of challenge tags  are no change.
are no change. .
. , he computes the value of
, he computes the value of  , and verifies the relation
, and verifies the relation  whether it is true or not. In Section 4.3.5, we have proved the relation
whether it is true or not. In Section 4.3.5, we have proved the relation
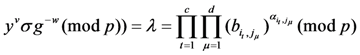
 true, unless the CSA can solve the random oracle. This means it can find hash values
true, unless the CSA can solve the random oracle. This means it can find hash values  and
and  to let
to let  on the premise
on the premise  , but this is not feasible [18]. In view of this, the CMA thinks that evidence blocks have been altered on the CSA.
, but this is not feasible [18]. In view of this, the CMA thinks that evidence blocks have been altered on the CSA. ,
,  and
and  be the malicious CSA’s forged evidence block, corresponded tag and signature, and
be the malicious CSA’s forged evidence block, corresponded tag and signature, and  ,
,  and
and  be the expected values from an honest CSS. If the forged values
be the expected values from an honest CSS. If the forged values  ,
,  and
and  make the equation true, then we can find a solution to the DLP.
make the equation true, then we can find a solution to the DLP. ,
,  and
and  satisfy the following equation
satisfy the following equation
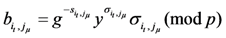
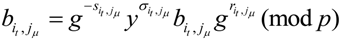
 , then have
, then have  ,
,  and
and  satisfy the following equation
satisfy the following equation
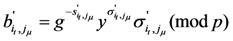
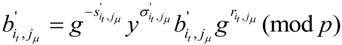
 , otherwise
, otherwise  , which contradicts our assumption.
, which contradicts our assumption.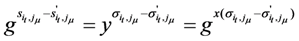
 and
and  , have
, have  ,
,  . Therefore we have found a solution to DLP
. Therefore we have found a solution to DLP  .
. .
. to generate tag
to generate tag  for each evidence block
for each evidence block  . Then it uses random number
. Then it uses random number  to blind tag
to blind tag  to get signature
to get signature  . Even if the contents of two evidence blocks are the same, they have different indices, so their tags and signatures are different. It avoids evidence blocks of different indices having the same tags and signatures.
. Even if the contents of two evidence blocks are the same, they have different indices, so their tags and signatures are different. It avoids evidence blocks of different indices having the same tags and signatures. to the CSA, including key
to the CSA, including key  . The CSA uses pseudo-random permutation
. The CSA uses pseudo-random permutation  keyed with
keyed with  to generate indices of challenged columns
to generate indices of challenged columns  and keyed with
and keyed with  to generate indices of challenged rows
to generate indices of challenged rows  . In each challenge, the key
. In each challenge, the key  are different, so
are different, so  and
and  are different, finally, challenged subset of evidence blocks
are different, finally, challenged subset of evidence blocks  are not the same.
are not the same. keyed with
keyed with  to derive coefficients
to derive coefficients  , and uses coefficients
, and uses coefficients  to generate response values. In each challenge,
to generate response values. In each challenge,  is chosen randomly, so coefficients
is chosen randomly, so coefficients  are derived randomly. Moreover, challenged subset of evidence blocks
are derived randomly. Moreover, challenged subset of evidence blocks  are not the same, and then response values
are not the same, and then response values  of each challenge are not the same. It avoids the CSA to use its own expected challenge blocks to calculate the response values, or using previous response values instead of response values is needed in this challenge.
of each challenge are not the same. It avoids the CSA to use its own expected challenge blocks to calculate the response values, or using previous response values instead of response values is needed in this challenge. has been altered in the CSA, he will ask the CSA to send back the set of tags
has been altered in the CSA, he will ask the CSA to send back the set of tags  . Assume evidence block
. Assume evidence block  is incorrect; the ERA takes
is incorrect; the ERA takes  from the set of signatures
from the set of signatures  , and uses following equation to recover
, and uses following equation to recover 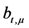
5.2. Performance Analysis
 as challenge values and sends them to the storage server. Moreover, the storage server returns
as challenge values and sends them to the storage server. Moreover, the storage server returns  as response values to the verifier, so communication costs of [11](Section 6) are the highest in the five schemes. The communication costs of DEMC-PDP, FG-PoR and ML-PoR are roughly equivalent.
as response values to the verifier, so communication costs of [11](Section 6) are the highest in the five schemes. The communication costs of DEMC-PDP, FG-PoR and ML-PoR are roughly equivalent. ,
,  and random coefficient
and random coefficient  in the five schemes. To tags and signatures generation, response generation and response verification three steps, the computation costs of five schemes are listed in Table 1. In Table 1, the operation symbols denote meaning: H: hash function operation; A: addition operation; M: multiplication operation; E: exponentiation operation; P: pairing operation; X: xor operation
in the five schemes. To tags and signatures generation, response generation and response verification three steps, the computation costs of five schemes are listed in Table 1. In Table 1, the operation symbols denote meaning: H: hash function operation; A: addition operation; M: multiplication operation; E: exponentiation operation; P: pairing operation; X: xor operation| Communication, Computation and Storage Costs | DEMC-PDP [10] | PEMC-PDP [10] | [11](Section 6) | FG-PoR | ML-PoR |
|---|---|---|---|---|---|
| Communication costs of challenge values | 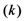 | 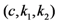 | 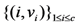 | 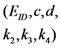 | 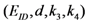 |
| Communication costs of response values |  | 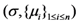 | 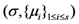 | 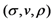 | 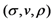 |
| Computation costs of tags and signatures generation | 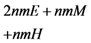 | 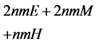 | 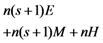 |  | 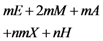 |
| Computation costs of response generation |  |  | 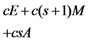 |  | 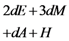 |
| Computation costs of response verification |  | 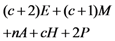 | 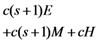 | 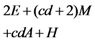 |  |
| Storage costs of file blocks and tags | 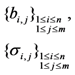 | 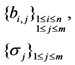 | 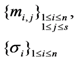 | 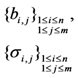 |  |
| Computation costs of encoding and decoding | No | No | Yes | No | No |
 , each has 1024 bits,
, each has 1024 bits,  is a 160-bit prime. Given an 80 MB evidence file
is a 160-bit prime. Given an 80 MB evidence file  that has 640,000 data blocks, each block is 1 Kbits (1024 bits). The parameters of five schemes are described as follows:
that has 640,000 data blocks, each block is 1 Kbits (1024 bits). The parameters of five schemes are described as follows:
- the number of file blocks is
;
- the number of copies is
;
- the number of challenged blocks is
.
- [11]( Section 6):
- the number of file blocks is 640,000;
- the number of encoded blocks is 32,400;
- the number of columns is the same as the number of rows in matrix
;
- the number of challenged columns
.
- Our FG-PoR, ML-PoR:
- the number of file blocks is 640,000;
- the number of columns is the same as the number of rows in matrix
;
- the number of challenged columns is the same as the number of challenged rows
.
 to achieve a high probability of assurance.
to achieve a high probability of assurance.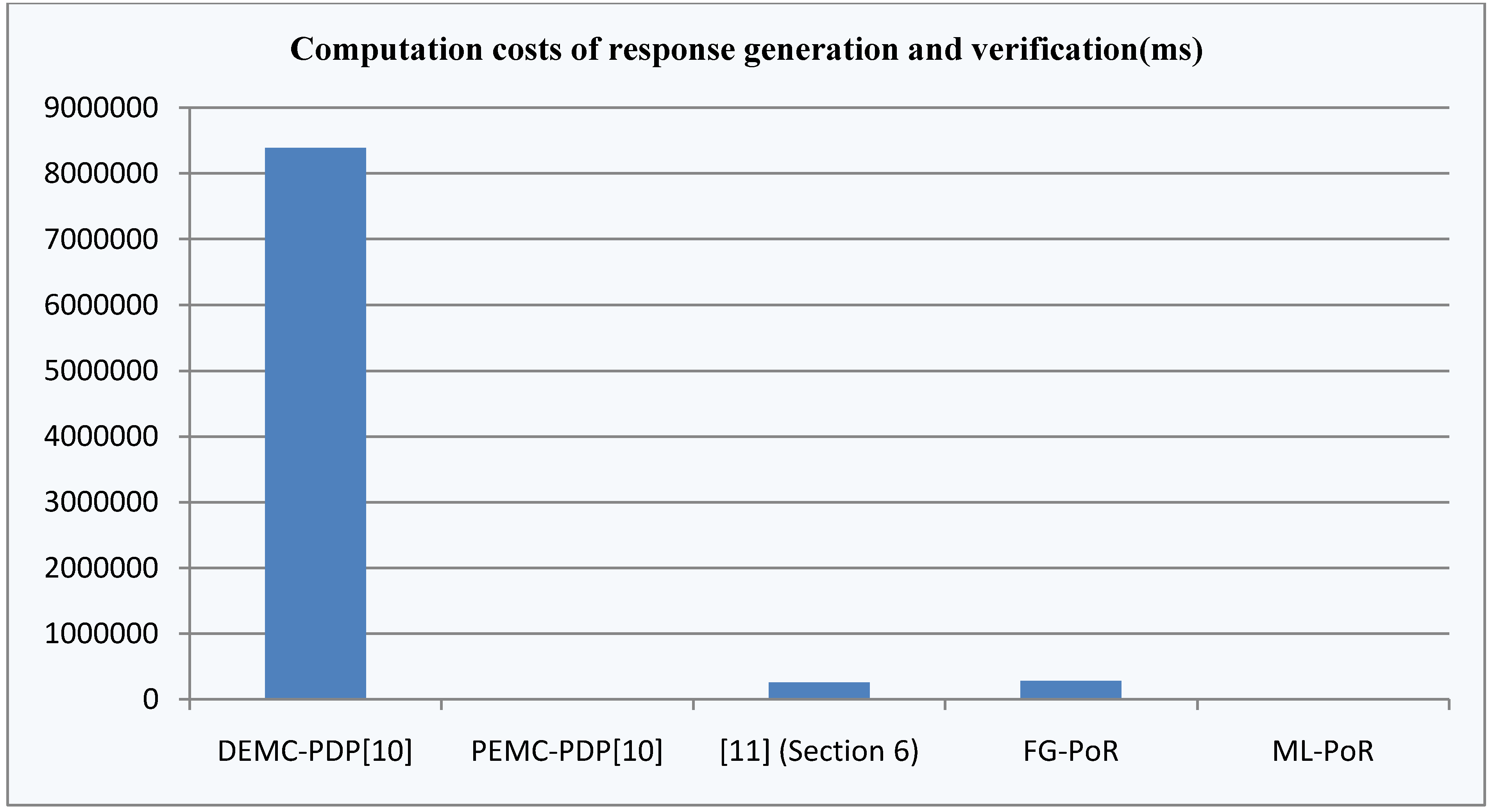
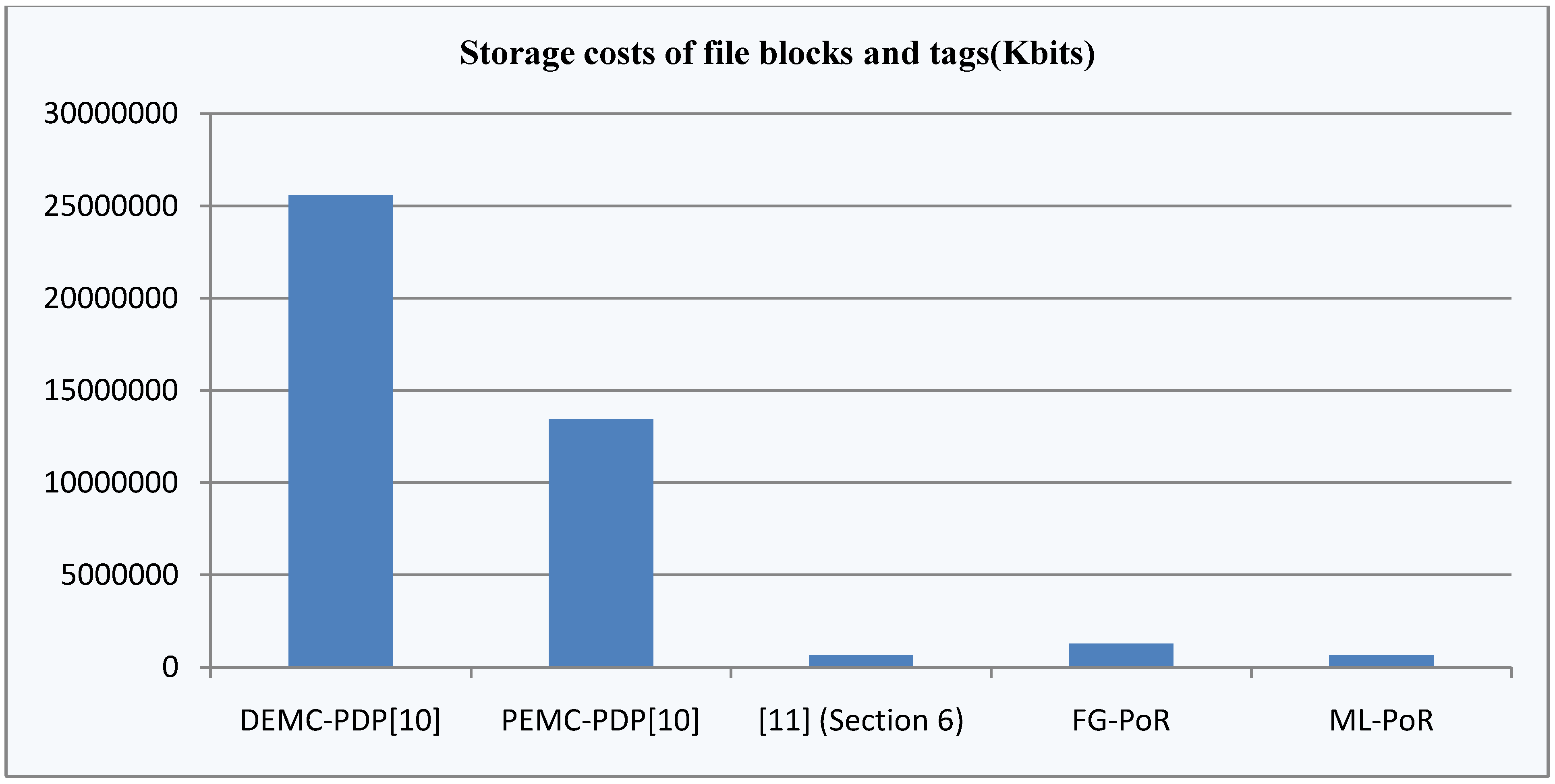
 sectors. It provides provable data possession and data recovery dual functions, but its erasure of codes adds extra computation costs and storage costs, so the total costs of [11](Section 6) are higher than our FG-PoR and ML-PoR. DEMC-PDP [10] and PEMC-PDP [10] use multi-replication technology to achieve provable data possession and data recovery functions, but storage costs are too high. Also, the computation costs of DEMC-PDP [10] are the highest of the five schemes. Our ML-PoR generates only a tag to each row of evidence matrix, rather than generating a tag to each element of evidence matrix. Therefore, it reduces computation costs and storage costs compared to that of the FG-PoR. In overall performance, ML-PoR is superior to the other four schemes.
sectors. It provides provable data possession and data recovery dual functions, but its erasure of codes adds extra computation costs and storage costs, so the total costs of [11](Section 6) are higher than our FG-PoR and ML-PoR. DEMC-PDP [10] and PEMC-PDP [10] use multi-replication technology to achieve provable data possession and data recovery functions, but storage costs are too high. Also, the computation costs of DEMC-PDP [10] are the highest of the five schemes. Our ML-PoR generates only a tag to each row of evidence matrix, rather than generating a tag to each element of evidence matrix. Therefore, it reduces computation costs and storage costs compared to that of the FG-PoR. In overall performance, ML-PoR is superior to the other four schemes.6. Conclusions
Acknowledgments
Conflict of Interest
References
- Chen, L.; Mai, Y.H.; Huang, C.H.; Dong, Z.X.; Shi, W.M.; Song, X.L. Computer Forensics Technology (in Chinese); Wuhan University Press: Wuhan, China, 2007. [Google Scholar]
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing; Special Publication 800–145. National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011. Available online: http://csrc.nist.gov/publications/nistpubs/800-145/SP800-145.pdf (accessed on 20 March 2013 ).
- Kent, K.; Chevalier, S.; Grance, T.; Dang, H. Guide to Integrating Forensic Techniques into Incident Response; Special Publication 800–86. National Institute of Standards and Technology: Gaithersburg, MD, USA, 2006. Available online: http://cybersd.com/sec2/800-86Summary.pdf (accessed on 26 June 2013).
- Wang, C.; Wang, Q.; Ren, K.; Lou, W.J. Ensuring data storage security in cloud computing. In Proceedings of the 2009 17th International Workshop on Quality of Service (IWQos’09), Charleston, SC, USA, 13–15 July 2009; pp. 1–9.
- Taylor, M.; Haggerty, J.; Gresty, D.; Hegarty, R. Digital evidence in cloud computing systems. Comput. Law Secur. Rev. 2010, 26, 304–308. [Google Scholar]
- Ateniese, G.; Burns, R.; Curtmola, R.; Herring, J.; Kissner, L.; Peterson, Z.; Song, D. Provable data possession at untrusted stores. In Proceedings of the 14th Association for Computing Machinery (ACM) Conference on Computer and Communications Security, Alexandria, VA, USA, 29 October–2 November 2007; pp. 598–609.
- Juels, A.; Kaliski, B.S. PORs: Proofs of retrievability for large files. In Proceedings of the 14th Association for Computing Machinery (ACM) Conference on Computer and Communications Security, Alexandria, VA, USA, 29 October–2 November 2007; pp. 584–597.
- Bowers, K.D.; Juels, A.; Oprea, A. HAIL: A high-availability and integrity layer for cloud storage. In Proceeding of the 16th Association for Computing Machinery (ACM) conference on Computer and Communications Security, New York, NY, USA, 9–13 November 2009; pp. 187–198.
- Curtmola, R.; Khan, O.; Burns, R.; Ateniese, G. MR-PDP: Multiple-replica provable data possession. In Proceedings of the 28th International Conference on Distributed Computing Systems, Beijing, China, 17–20 June 2008; pp. 411–420.
- Barsoum, A.F.; Hasan, M.A. Provable possession and replication of data over cloud servers. Available online: http://cacr.uwaterloo.ca/techreports/2010/cacr2010-32.pdf (accessed on 20 June 2013).
- Shacham, H.; Waters, B. Compact proofs of retrievability. In Proceedings of the 14th International Conference on the Theory and Application of Cryptology and Information Security: Advances in Cryptology, Melbourne, Australia, 7–11 December 2008; Springer-Verlag: Melbourne, Australia, 2008; pp. 90–107. [Google Scholar]
- Wang, Q.; Wang, C.; Ren, K.; Lou, W.J. Enabling public auditability and data dynamics for storage security in cloud computing. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 847–859. [Google Scholar] [CrossRef]
- Wolthusen, S.D. Overcast: Forensic discovery in cloud environments. In Proceedings of the Fifth International Conference on IT Security Incident Management and IT Forensics, Stuttgart, Germany, 15–17 September 2009; pp. 3–9.
- Grispos, G.; Storer, T.; Glisson, W.B. Calm before the storm: The challenges of cloud computing in digital forensics. Int. J. Digit. Crime Forensics 2012, 4, 28–48. [Google Scholar] [CrossRef]
- Birk, D.; Wegener, C. Technical issues of forensic investigations in cloud computing environments. In Proceedings of the 6th International Workshop on Systematic Approaches to Digital Forensic Engineering, Oakland, CA, USA, 26 May 2011; pp. 1–10.
- Nyberg, K.; Rueppel, R.A. A new signature scheme based on the DSA giving message recovery. In Proceedings of the 1st Association for Computing Machinery (ACM) Conference on Computer and Communications Security, Fairfax, VA, USA, 3–5 November 1993; pp. 58–61.
- Camenisch, J.L.; Piveteau, J.M.; Stadler, M.A. Blind signatures based on the discrete logarithm problem. In Advances in Cryptology—EUROCRYPT’94: Workshop on the Theory and Application of Cryptographic Techniques Perugia, Italy, May 9–12, 1994. Proceedings; De Santis, A., Ed.; Springer: Berlin and Heidelberg, Germany, 1995; pp. 428–432. [Google Scholar]
- Liu, F.F.; Gu, D.W.; Lu, H.N.; Long, B.; Li, X.H. Reducing computational and communication complexity for dynamic provable data possession. China Commun. 2011, 8, 67–75. [Google Scholar]
- Wang, Y.J.; Sun, W.D.; Zhou, S.; Pei, X.Q.; Li, X.Y. Key technologies of distributed storage for cloud computing. J. Softw. 2012, 23, 962–986. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Song, X.; Deng, H. Lightweight Proofs of Retrievability for Electronic Evidence in Cloud. Information 2013, 4, 262-282. https://doi.org/10.3390/info4030262
Song X, Deng H. Lightweight Proofs of Retrievability for Electronic Evidence in Cloud. Information. 2013; 4(3):262-282. https://doi.org/10.3390/info4030262
Chicago/Turabian StyleSong, Xiuli, and Hongyao Deng. 2013. "Lightweight Proofs of Retrievability for Electronic Evidence in Cloud" Information 4, no. 3: 262-282. https://doi.org/10.3390/info4030262
APA StyleSong, X., & Deng, H. (2013). Lightweight Proofs of Retrievability for Electronic Evidence in Cloud. Information, 4(3), 262-282. https://doi.org/10.3390/info4030262