Seven Means, Generalized Triangular Discrimination, and Generating Divergence Measures
Abstract
:1. Introduction
 ,
,  ,
,
 , let us consider two groups of measures:
, let us consider two groups of measures: ,
,
 ,
,
 .
.
- (i)
;
- (ii)
.
 ,
,

 .
.
 ,
,  and
and  are respectively known as triangular discrimination, Hellingar’s divergence and symmetric chi-square divergence. These measures allow the following inequalities among the measures.
are respectively known as triangular discrimination, Hellingar’s divergence and symmetric chi-square divergence. These measures allow the following inequalities among the measures. .
.

 .
.

 . The measure
. The measure  is generalized J-divergence extensively studied in Taneja [2,3]. It admits the following particular cases:
is generalized J-divergence extensively studied in Taneja [2,3]. It admits the following particular cases:- (i)
;
- (ii)
;
- (iii)
.


 . The measure
. The measure  known as generalized arithmetic and geometric mean divergence. It also admits the following particular cases:
known as generalized arithmetic and geometric mean divergence. It also admits the following particular cases:- (i)
;
- (ii)
;
- (iii)
;
- (iv)
.
 ,
,  and
and  . The non-negativity of the arithmetic-geometric mean divergence,
. The non-negativity of the arithmetic-geometric mean divergence,  is based on the well-known arithmetic and geometric means, i.e., we can write it as
is based on the well-known arithmetic and geometric means, i.e., we can write it as
 ,
,
 and
and  are arithmetic and geometric means respectively. Moreover, the measure
are arithmetic and geometric means respectively. Moreover, the measure  can also be written in terms of arithmetic mean
can also be written in terms of arithmetic mean .
.
2. Seven Means
 be two positive numbers. Eves [4] studied the geometrical interpretation of the following seven means:
be two positive numbers. Eves [4] studied the geometrical interpretation of the following seven means:
- Arithmetic mean:
;
- Geometric mean:
;
- Harmonic mean:
;
- Heronian mean:
;
- Contra-harmonic mean:
;
- Root-mean-square:
;
- Centroidal mean:
.
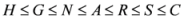
 , where
, where  stands for any of the above seven means, then we have
stands for any of the above seven means, then we have
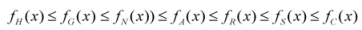
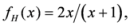
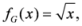
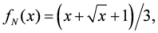

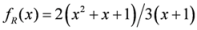 ,
, 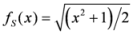 and
and 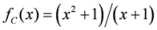 ,
,  ,
, 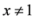 . In all cases, we would have equality sign if
. In all cases, we would have equality sign if 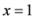 , i.e.,
, i.e., 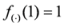 .
.  and
and  , the means
, the means  ,
,  ,
,  ,
,  and
and  may also be written in terms of the means
may also be written in terms of the means  and
and  .
. 2.1. Inequalities among Differences of Means
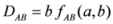
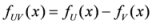 , with
, with 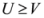 . Thus, according to (3), the inequality (1) admits 21 non-negative differences. These differences satisfy some simple inequalities given by the following pyramid:
. Thus, according to (3), the inequality (1) admits 21 non-negative differences. These differences satisfy some simple inequalities given by the following pyramid:
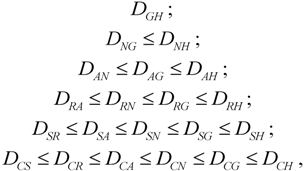
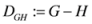 ,
, 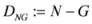 , etc. After simplifications, we have the following equalities among some of these measures:
, etc. After simplifications, we have the following equalities among some of these measures:
- (i)
;
- (ii)
;
- (iii)
.
 and
and  are the well know triangular discsrimination [5] and Hellinger’s distance [6] given by
are the well know triangular discsrimination [5] and Hellinger’s distance [6] given by  and
and  respectively. Not all the measures appearing in the above pyramid (4) are convex in the pair
respectively. Not all the measures appearing in the above pyramid (4) are convex in the pair  . Recently, the author [7] has proved the following theorem for the convex measures.
. Recently, the author [7] has proved the following theorem for the convex measures. 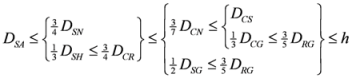
 be a convex and differentiable function satisfying
be a convex and differentiable function satisfying  . Consider a function
. Consider a function
 ,
,  ,
,
 is convex in
is convex in  . Additionally, if
. Additionally, if  , then the following inequality hold:
, then the following inequality hold:
 .
.
 be two convex functions satisfying the assumptions:
be two convex functions satisfying the assumptions:
- (i)
,
;
- (ii)
and
are twice differentiable in
;
- (iii)
- there exists the real constants
such that
and
,
,
for allthen we have the inequalities:
,
for all, where the function
is as defined in Lemma 2.1.
2.2. Generalized Triangular Discrimination
 consider the following measure generalizing triangular discrimination
consider the following measure generalizing triangular discrimination

 ,
,
 ,
,
 ,
,


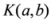 (reference Jain and Srivastava [10]),
(reference Jain and Srivastava [10]),  (reference Kumar and Johnson [11]) and
(reference Kumar and Johnson [11]) and  , the latter being symmetric to
, the latter being symmetric to  measure [12].
measure [12].  will be considered here for the first time. The generalization (6) considered above is little different from the one considered by Topsoe [13]:
will be considered here for the first time. The generalization (6) considered above is little different from the one considered by Topsoe [13]:
 .
.
 ,
,  , where
, where
 .
.
 is given by
is given by
 ,
,
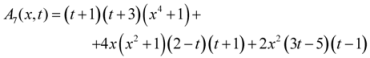
 when the function is positive. But for at least
when the function is positive. But for at least  ,
,  ,
, 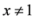 , we have
, we have  . Also, we have
. Also, we have  . Thus according to Lemma 1.1, the measure
. Thus according to Lemma 1.1, the measure  is convex for all
is convex for all  ,
,  . Testing individually to fix
. Testing individually to fix  , we can check the convexity for other measures as well, for example
, we can check the convexity for other measures as well, for example  ,
,  is convex.
is convex. with respect to
with respect to  , we have
, we have
 .
.
 ,
,  . This proves that the function
. This proves that the function  is monotonically increasing with respect to
is monotonically increasing with respect to  . This gives
. This gives
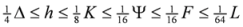
 and
and  . Thus combining Equations (5) and (8), we have
. Thus combining Equations (5) and (8), we have
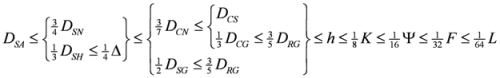
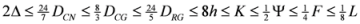
3. New Inequalities
3.1. First Stage
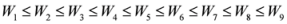
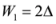 ,
, 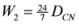 ,
, 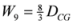 , etc. We can write
, etc. We can write
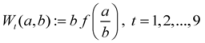
,
,
,
,
,
,
,
,
and.
,
,
,
,
,
;
,
,
and.
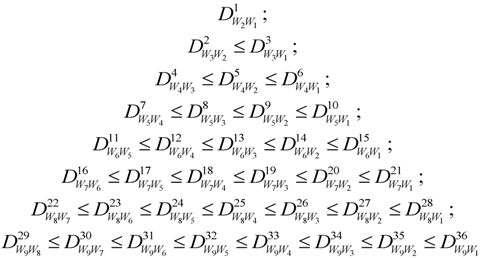
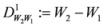 ,
, 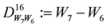 , etc. After simplifications, we have equalities among first four lines of the pyramid:
, etc. After simplifications, we have equalities among first four lines of the pyramid: 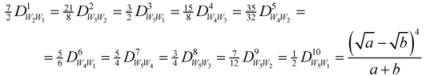
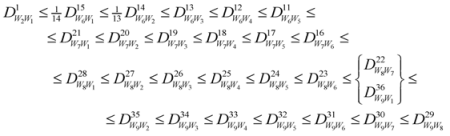
 : We shall apply two approaches to prove this result.
: We shall apply two approaches to prove this result.
 ,
,
 ,
, 

 .
.
 . In order to prove the result, we need to show that
. In order to prove the result, we need to show that  . By considering the difference
. By considering the difference  , we have
, we have


 ,
,
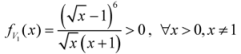
 , we get the required result.
, we get the required result. : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 



 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 ,
,
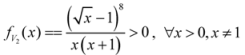
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 ,
,
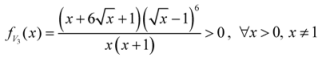
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
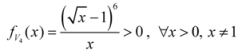
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 


 ,
,
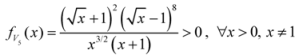
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
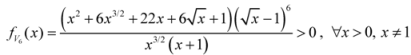
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
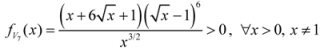
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
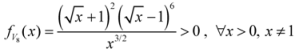
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
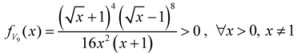
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
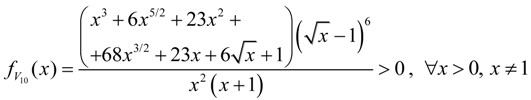
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
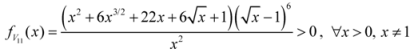
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
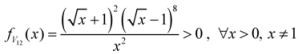
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
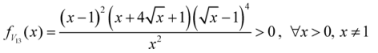
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 

 ,
,
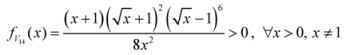
- (i)
;
- (ii)
;
- (iii)
;
- (iv)
;
- (v)
;
- (vi)
;
- (vii)
;
- (viii)
;
- (ix)
;
- (x)
;
- (xi)
;
- (xii)
.
3.1.1. Reverse Inequalities
- (i)
- (ii)
- (iii)
;
- (iv)
.
3.2. Second Stage
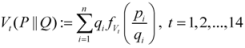
 ,
, 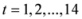 are given by (16)–(29) respectively. In all the cases we have
are given by (16)–(29) respectively. In all the cases we have  ,
, 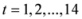 . By the application of Lemma 2.1, we can say that the above 14 measures are convex. We may try to connect 14 measures given in (30) through inequalities.
. By the application of Lemma 2.1, we can say that the above 14 measures are convex. We may try to connect 14 measures given in (30) through inequalities. 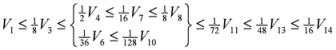
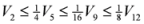
,
,
,
,
,
,
,
,
,
,
,
- and
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
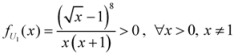
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
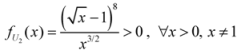
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
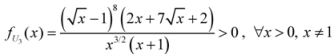
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 .
.
 . Let us consider now, and
. Let us consider now, and
 ,
,
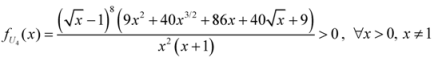
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,

 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
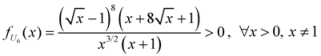
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
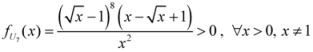
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
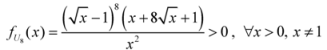
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
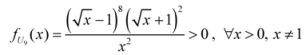
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
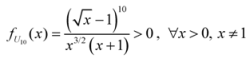
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
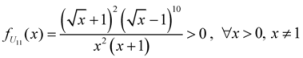
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
3.3. Third Stage
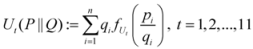
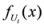 ,
, 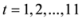 are given by (33)–(43) respectively. In all the cases, we have
are given by (33)–(43) respectively. In all the cases, we have  ,
, 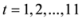 . By the application of Lemma 2.1, we can say that the above 11 measures are convex. Here follows the second derivatives of the functions (33)–(43), applied frequently in the next theorem.
. By the application of Lemma 2.1, we can say that the above 11 measures are convex. Here follows the second derivatives of the functions (33)–(43), applied frequently in the next theorem.
,
,
,
,
,
,
,
,
,
- and
.
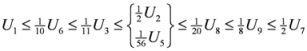
 ,
, 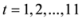 .
.  : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
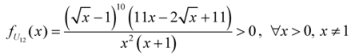
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
,
 ,
,
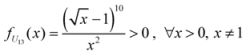
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
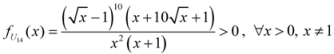
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
3.4. Forth Stage
 to
to  . This comparison is given in the theorem below. Here below are the second derivatives of the functions given by (46)–(58).
. This comparison is given in the theorem below. Here below are the second derivatives of the functions given by (46)–(58). ,
,
 ,
,
 .
.
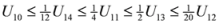
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 ,
,
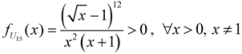
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 : Let us consider a function
: Let us consider a function  . After simplifications, we have
. After simplifications, we have
 ,
, 
 .
.
 given by
given by
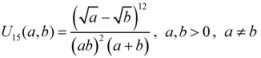
3.5. Equivalent Expressions
- Measures appearing in Theorem 3.2. We can write
,
,
,
,
,
,
,
,
,
,
.
- Measures appearing in Theorems 3.3 and 3.4. We could write
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
4. Generating Divergence Measures and Exponential Representations
4.1. First Generalization of Triangular Discrimination
 , let us consider the following measures
, let us consider the following measures
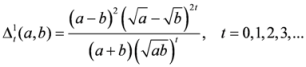
 ,
,
 ,
,


 .
.
 . Now we will prove its convexity. We can write
. Now we will prove its convexity. We can write  ,
,  , where
, where
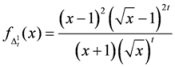
 is given by
is given by
 ,
,
 .
.
 ,
,  ,
, 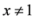 , we have
, we have  . Also we have
. Also we have  . In view of Lemma 1.1, the measure
. In view of Lemma 1.1, the measure  is convex for all
is convex for all  ,
,  .
. 

 ,
,
 are the constants. For simplicity we will choose,
are the constants. For simplicity we will choose,




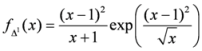
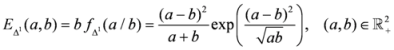
4.2. Second Generalization of Triangular Discrimination
 , let us consider the following measures
, let us consider the following measures
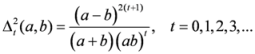

 .
.
 . Now we will prove its convexity. We can write
. Now we will prove its convexity. We can write  ,
,  , where
, where
 .
.
 is given by
is given by
 ,
,
 .
.
 ,
,  ,
, 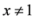 , we have
, we have  . Also we have
. Also we have  . In view of Lemma 2.1, the measure
. In view of Lemma 2.1, the measure  is convex for all
is convex for all  ,
,  .
.  is given by
is given by
 .
.
4.3. First Generalization of the Measure ![Information 04 00198 i116]()
 , let us consider the following measures
, let us consider the following measures
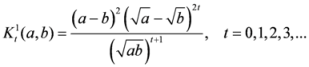
,
,
- and
.
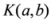 given by (3). We will prove now its convexity. We might write
given by (3). We will prove now its convexity. We might write  ,
,  , where
, where
 .
.
 is given by
is given by
 ,
,
 .
.
 ,
,  ,
, 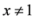 , we have
, we have  . Also we have
. Also we have  . In view of Lemma 1.1, the measure
. In view of Lemma 1.1, the measure  is convex for all
is convex for all  ,
,  .
.  is given by
is given by
 .
.
4.4. Second Generalization of the Measure ![Information 04 00198 i116]()
 , let us consider the following measures
, let us consider the following measures
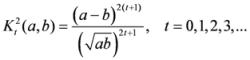

 .
.
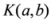 given by (1.3). We will now prove its convexity. We can write
given by (1.3). We will now prove its convexity. We can write  ,
,  , where
, where
 .
.
 is given by
is given by
 ,
,
 .
.
 ,
,  ,
, 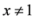 , we have
, we have  . Also we have
. Also we have  . In view of Lemma 1.1, the measure
. In view of Lemma 1.1, the measure  is convex for all
is convex for all  ,
,  .
.  is given by
is given by
 .
.
4.5. Generalization of Hellingar’s Discrimination
 , let us consider the following measures
, let us consider the following measures
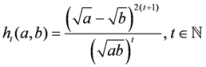
,
,
,
- and
.
 ,
,  , where
, where
 .
.
 is given by
is given by
 ,
,
 .
.
 ,
,  ,
, 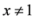 , we have
, we have  . Also
. Also  . In view of Lemma 2.1, the measure
. In view of Lemma 2.1, the measure  is convex for all
is convex for all  ,
,  .
.  is given by
is given by
 .
.
4.6. New Measure
 , let us consider the following measures
, let us consider the following measures
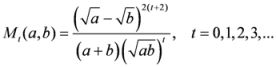
,
,
,
- and
.
 ,
,  , where
, where
 .
.
 is given by
is given by
 ,
,
 .
.
 ,
,  ,
, 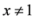 , we have
, we have  . Also we have
. Also we have  . In view of Lemma 2.1, the measure
. In view of Lemma 2.1, the measure  is convex for all
is convex for all  ,
,  .
.  is given by
is given by
 .
.
- (i)
- The first 10 measures appearing in the second pyramid (13) represents the same measure (14) and is same as
. The last measure given by (51) is the same as
. The measure (51) is the only one that appears in all the four parts of the Theorem 3.4. Both these measures generate the interesting measure shown in (60).
- (ii)
- (iii)
- Following the similar lines of (54) and (55), the exponential representation of the principal measure
appearing in (6) is given by
Acknowledgements
References and notes
- Taneja, I.J. Refinement inequalities among symmetric divergence measures. Austr. J. Math. Anal. Appl. 2005, 2, 1–23. [Google Scholar]
- Taneja, I.J. New developments in generalized information measures. In Advances in Imaging and Electron Physics; Hawkes, P.W., Ed.; Elsevier Publisher: New York, NY, USA, 1995; Volume 91, pp. 37–135. [Google Scholar]
- Taneja, I.J. On symmetric and non-symmetric divergence measures and their generalizations. In Advances in Imaging and Electron Physics; Hawkes, P.W., Ed.; Elsevier Publisher: New York, NY, USA, 2005; Volume 138, pp. 177–250. [Google Scholar]
- Eves, H. Means appearing in geometrical figures. Math. Mag. 2003, 76, 292–294. [Google Scholar]
- LeCam, L. Asymptotic Methods in Statistical Decision Theory; Springer: New York, NY, USA, 1986. [Google Scholar]
- Hellinger, E. Neue Begründung der Theorie der quadratischen Formen von unendlichen vielen Veränderlichen. J. Reine Aug. Math. 1909, 136, 210–271. [Google Scholar]
- Taneja, I.J. Inequalities having seven means and proportionality relations. 2012. Available online: http://arxiv.org/abs/1203.2288/ (accessed on 7 April 2013).
- Taneja, I.J.; Kumar, P. Relative information of type s, Csiszar’s f-divergence, and information inequalities. Inf. Sci. 2004, 166, 105–125. [Google Scholar] [CrossRef]
- Taneja, I.J. Refinement of inequalities among means. J. Combin. Inf. Syst. Sci. 2006, 31, 357–378. [Google Scholar]
- Jain, K.C.; Srivastava, A. On symmetric information divergence measures of Csiszar’s f-divergence class. J. Appl. Math. Stat. Inf. 2007, 3, 85–102. [Google Scholar]
- Kumar, P.; Johnson, A. On a symmetric divergence measure and information inequalities. J. Inequal. Pure Appl. Math. 2005, 6, 1–13. [Google Scholar]
- Taneja, I.J. Bounds on triangular discrimination, harmonic mean and symmetric chi-square divergences. J. Concr. Appl. Math. 2006, 4, 91–111. [Google Scholar]
- Topsoe, F. Some inequalities for information divergence and related measures of discrimination. IEEE Trans. Inf. Theory 2000, 46, 1602–1609. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Sunde, J.; Buse, C. New inequalities for jefferys divergence measure. Tamsui Oxf. J. Math. Sci. 2000, 16, 295–309. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Taneja, I.J. Seven Means, Generalized Triangular Discrimination, and Generating Divergence Measures. Information 2013, 4, 198-239. https://doi.org/10.3390/info4020198
Taneja IJ. Seven Means, Generalized Triangular Discrimination, and Generating Divergence Measures. Information. 2013; 4(2):198-239. https://doi.org/10.3390/info4020198
Chicago/Turabian StyleTaneja, Inder Jeet. 2013. "Seven Means, Generalized Triangular Discrimination, and Generating Divergence Measures" Information 4, no. 2: 198-239. https://doi.org/10.3390/info4020198























































































































































