Implementation of Classical Communication in a Quantum World
Abstract
:1. Introduction
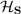 ; in addition, they typically explicitly specify the “prepared” quantum state
; in addition, they typically explicitly specify the “prepared” quantum state 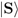 with which the observers interact, for example by an expression such as “
with which the observers interact, for example by an expression such as “  ” where
” where 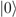 and
and 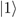 are basis vectors and “A” and “B” name Alice and Bob, respectively. The “local operations” are generally dealt with cursorily: Alice and Bob are said to measure spin or polarization, for example, with the details of the apparatus used to do so, if any are given, relegated to the Methods section. The “classical communication” between Alice and Bob is rarely discussed at all. Understanding LOCC in physical terms, however, requires not just understanding the quantum state being observed, but understanding both the “local operations” and the “classical communication” as physical processes.
are basis vectors and “A” and “B” name Alice and Bob, respectively. The “local operations” are generally dealt with cursorily: Alice and Bob are said to measure spin or polarization, for example, with the details of the apparatus used to do so, if any are given, relegated to the Methods section. The “classical communication” between Alice and Bob is rarely discussed at all. Understanding LOCC in physical terms, however, requires not just understanding the quantum state being observed, but understanding both the “local operations” and the “classical communication” as physical processes. 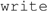 and
and  methods—as well as a semantics for that data structure that renders the message meaningful. These requirements are independent of whether Alice and Bob are human beings or non-human information-processing machines; two computers attached to the internet must share a communication protocol (e.g.,
methods—as well as a semantics for that data structure that renders the message meaningful. These requirements are independent of whether Alice and Bob are human beings or non-human information-processing machines; two computers attached to the internet must share a communication protocol (e.g., 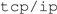 ) and must share assumptions about both the syntax and semantics of the data structures employed to encode transmitted messages.
) and must share assumptions about both the syntax and semantics of the data structures employed to encode transmitted messages. 2. Preliminaries
2.1. Assumption: Quantum Theory is Universal
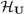 comprising a collection of quantum degrees of freedom. The universe is moreover, as assumed by Everett [9], not part of anything else; it is an isolated quantum system. The evolution of the universal quantum state
comprising a collection of quantum degrees of freedom. The universe is moreover, as assumed by Everett [9], not part of anything else; it is an isolated quantum system. The evolution of the universal quantum state 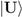 , therefore, satisfies a Schrödinger equation
, therefore, satisfies a Schrödinger equation 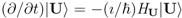 , where HU is a deterministic universal Hamiltonian. This assumption rules out any objective non-unitary “collapse” of
, where HU is a deterministic universal Hamiltonian. This assumption rules out any objective non-unitary “collapse” of 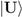 ; it amounts to the adoption of what Landsman [10] calls “stance 1” regarding quantum theory, a stance that is realist about quantum states, and therefore demands an explanation for the appearance of classicality. All available experimental evidence is consistent with this universality assumption [11]. Alice, Bob, the systems that they observe and the systems that they employ to encode classical communications are, on this assumption, all collections of quantum degrees of freedom evolving under the action of the universal Hamiltonian HU.
; it amounts to the adoption of what Landsman [10] calls “stance 1” regarding quantum theory, a stance that is realist about quantum states, and therefore demands an explanation for the appearance of classicality. All available experimental evidence is consistent with this universality assumption [11]. Alice, Bob, the systems that they observe and the systems that they employ to encode classical communications are, on this assumption, all collections of quantum degrees of freedom evolving under the action of the universal Hamiltonian HU. 2.2. Consequence: Measurements are Actions by POVMs
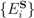 is a POVM representing a measurement of the state of some quantum system S, then each component
is a POVM representing a measurement of the state of some quantum system S, then each component 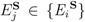 is a Hilbert-space automorphism on
is a Hilbert-space automorphism on 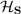 , i.e.,
, i.e., 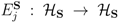 ; one can also write
; one can also write 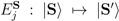 , where in general
, where in general 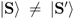 . Given the assumption of universality, it is clear that any such automorphism must be implemented by the unitary physical propagator
. Given the assumption of universality, it is clear that any such automorphism must be implemented by the unitary physical propagator 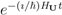 acting on the universal Hilbert space
acting on the universal Hilbert space 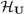 , and hence on
, and hence on 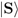 as a collection of components of some universal state
as a collection of components of some universal state 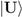 . Hence a measurement can be thought of as a physical action by a POVM, as emphasized for example by Fuchs’ [18] depiction of a POVM as an observer’s prosthetic hand.
. Hence a measurement can be thought of as a physical action by a POVM, as emphasized for example by Fuchs’ [18] depiction of a POVM as an observer’s prosthetic hand. 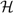 . Each component Πj of a von Neumann projection {Πi} projects any state
. Each component Πj of a von Neumann projection {Πi} projects any state 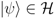 onto a basis vector
onto a basis vector 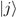 of
of 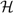 . If the set {
. If the set { 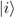 } of images of the components of {Πi} is complete in the sense of spanning
} of images of the components of {Πi} is complete in the sense of spanning 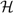 , one can write
, one can write 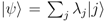 for states
for states 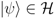 . In this case a general Hermitian observable M can be written
. In this case a general Hermitian observable M can be written 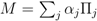 where αj is the jth possible observable outcome of M acting on
where αj is the jth possible observable outcome of M acting on 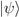 . Hence from an observer’s point of view, what a projection {Πi} produces is not just a new state vector, but a real outcome value αj; {Πi} is not just a Hilbert-space automorphism, but is also a mapping from
. Hence from an observer’s point of view, what a projection {Πi} produces is not just a new state vector, but a real outcome value αj; {Πi} is not just a Hilbert-space automorphism, but is also a mapping from 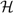 to the set of real outcome values of some observable of interest.
to the set of real outcome values of some observable of interest. 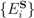 can be thought of as a mapping from
can be thought of as a mapping from 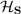 to a set of real outcome values with two caveats. First, the components of a general POVM are not necessarily orthogonal and hence do not, in general, all project to the same basis. Second, any finite observer can explicitly represent, and hence can physically encode in a classical memory or communication medium, values with at most some finite number N of bits. Hence from an observer’s point of view, a component
to a set of real outcome values with two caveats. First, the components of a general POVM are not necessarily orthogonal and hence do not, in general, all project to the same basis. Second, any finite observer can explicitly represent, and hence can physically encode in a classical memory or communication medium, values with at most some finite number N of bits. Hence from an observer’s point of view, a component 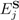 of a general POVM
of a general POVM 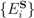 is not just an automorphism on
is not just an automorphism on 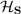 ; it is also a mapping
; it is also a mapping 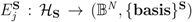 , where
, where 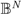 is the set of binary codes of length N and {basis}S is the set of bases of
is the set of binary codes of length N and {basis}S is the set of bases of 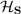 [3]. Indeed, any collection
[3]. Indeed, any collection 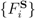 of mappings
of mappings 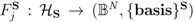 for which the probabilities P(αj) of obtaining real outcome values αj ∈
for which the probabilities P(αj) of obtaining real outcome values αj ∈ 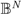 sum to unity, and for which each of the components
sum to unity, and for which each of the components 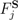 is implementable by the unitary physical propagator
is implementable by the unitary physical propagator 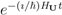 acting on the universal Hilbert space
acting on the universal Hilbert space 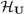 must be positive semi-definite (to yield real outcome values), normalized (to yield well-defined probabilities) and be a collection of Hilbert-space automorphisms (to be implementable by
must be positive semi-definite (to yield real outcome values), normalized (to yield well-defined probabilities) and be a collection of Hilbert-space automorphisms (to be implementable by 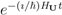 ); hence such a collection must be a POVM. The POVM formalism thus represents the extraction of classical information from quantum systems in the only way that it can be represented while maintaining consistency with the universality assumption.
); hence such a collection must be a POVM. The POVM formalism thus represents the extraction of classical information from quantum systems in the only way that it can be represented while maintaining consistency with the universality assumption. 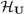 of its set of obtainable outcome values. Such a specification would, for any particular POVM and hence any particular Hilbert space, require scientific investigation of the physical system represented by that Hilbert space to be complete. Classical theorems [19,20] restricting the completeness of system identification strongly suggest that such completeness is infeasible in principle. Hence explicitly-specified POVMs can at best be viewed as predictively-adequate approximations based on experimental investigations carried out thus far; in practice such POVMs are available only for systems with small numbers of (known or stipulated) degrees of freedom.
of its set of obtainable outcome values. Such a specification would, for any particular POVM and hence any particular Hilbert space, require scientific investigation of the physical system represented by that Hilbert space to be complete. Classical theorems [19,20] restricting the completeness of system identification strongly suggest that such completeness is infeasible in principle. Hence explicitly-specified POVMs can at best be viewed as predictively-adequate approximations based on experimental investigations carried out thus far; in practice such POVMs are available only for systems with small numbers of (known or stipulated) degrees of freedom. 2.3. Consequence: Observers must Identify the Systems They Observe
Nothing is said in this definition, or in the surrounding discussion [4,5], about how observers are able to “access” a physical system “without prior knowledge” of such state variables as its location, size or shape, and without “prior agreement” about which item in their shared environment constitutes the system of interest. To find the identification of physical systems by observers treated explicitly, one must look to cybernetics, where unique identification of even classical finite-state machines (FSMs) by finite sequences of finite observations is shown to be impossible in principle [19,20], or to the cognitive neuroscience of perception, where the identification in practice of individual systems over extended periods of time is recognized as a computationally-intensive heuristic process [21,22,23].“A property of a physical system is objective when it is:
3. Decompositional Equivalence and Its Consequences
3.1. Assumption: Our Universe Exhibits Decompositional Equivalence
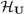 by specifications of tensor product structures. Call this symmetry decompositional equivalence [3]. Stated formally, decompositional equivalence is the assumption that if a TPS S ⊗ E = S′ ⊗ E′ = U, then the dynamics HU = HS + HE + HS−E = HS′ + HE′ + HS′ − E′, where S and S′ are arbitrarily chosen collections of physical degrees of freedom, E and E′ are their respective “environments” and HS − E and HS′ − E′ are, respectively, the S − E and S′ − E′ interaction Hamiltonians. Such equivalence of TPSs of
by specifications of tensor product structures. Call this symmetry decompositional equivalence [3]. Stated formally, decompositional equivalence is the assumption that if a TPS S ⊗ E = S′ ⊗ E′ = U, then the dynamics HU = HS + HE + HS−E = HS′ + HE′ + HS′ − E′, where S and S′ are arbitrarily chosen collections of physical degrees of freedom, E and E′ are their respective “environments” and HS − E and HS′ − E′ are, respectively, the S − E and S′ − E′ interaction Hamiltonians. Such equivalence of TPSs of 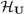 can be alternatively expressed in terms of the linearity of HU: If HU =∑ij Hij where the indices i and j range without restriction over all quantum degrees of freedom within
can be alternatively expressed in terms of the linearity of HU: If HU =∑ij Hij where the indices i and j range without restriction over all quantum degrees of freedom within 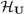 , decompositional equivalence is the assumption that the interaction matrix elements (
, decompositional equivalence is the assumption that the interaction matrix elements ( 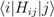 do not depend on the labels assigned to collections of degrees of freedom by specifications of TPSs. Decompositional equivalence is thus consistent with the general philosophical position of microphysicalism (for a recent review, see [29]), but involves no claims about explanatory reduction, and indeed no claims about explanation at all; it requires only that emergent properties of composite objects exactly supervene, as a matter of physical fact, on the fundamental interactions of the microscale components of those objects.
do not depend on the labels assigned to collections of degrees of freedom by specifications of TPSs. Decompositional equivalence is thus consistent with the general philosophical position of microphysicalism (for a recent review, see [29]), but involves no claims about explanatory reduction, and indeed no claims about explanation at all; it requires only that emergent properties of composite objects exactly supervene, as a matter of physical fact, on the fundamental interactions of the microscale components of those objects. 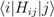 do not depend on specifications of TPSs. This is an assumption that the pairwise interaction Hamiltonians Hij are not just independent of where and when the degrees of freedom labeled by i and j interact, but are also independent of any other classical information that might be included in the specification of a reference frame from which the interaction of i and j might be observed. As such, it is similar in spirit to Tegmark’s “External Reality Hypothesis (ERH)” that “there exists an external physical reality completely independent of us humans” ([30] p. 101). If taken literally, however, the ERH violates energy conservation, as it allows human beings to behave arbitrarily without affecting “external physical reality” and vice-versa. The assumption of decompositional equivalence, on the other hand, does not involve, entail, or allow decoupling of observers or any other systems from their environments; any evidence that energy is not conserved, or evidence that energy is conserved but not additive would be evidence that decompositional equivalence is not satisfied in our universe. Were our universe to fail in fact to satisfy decompositional equivalence, any shift in specified system boundaries—any change in the TPS of
do not depend on specifications of TPSs. This is an assumption that the pairwise interaction Hamiltonians Hij are not just independent of where and when the degrees of freedom labeled by i and j interact, but are also independent of any other classical information that might be included in the specification of a reference frame from which the interaction of i and j might be observed. As such, it is similar in spirit to Tegmark’s “External Reality Hypothesis (ERH)” that “there exists an external physical reality completely independent of us humans” ([30] p. 101). If taken literally, however, the ERH violates energy conservation, as it allows human beings to behave arbitrarily without affecting “external physical reality” and vice-versa. The assumption of decompositional equivalence, on the other hand, does not involve, entail, or allow decoupling of observers or any other systems from their environments; any evidence that energy is not conserved, or evidence that energy is conserved but not additive would be evidence that decompositional equivalence is not satisfied in our universe. Were our universe to fail in fact to satisfy decompositional equivalence, any shift in specified system boundaries—any change in the TPS of 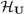 —could be expected to alter fundamental physical laws or their dynamical outcomes; in such a universe, the notions of “fundamental physical laws” and “well-defined dynamics” would be effectively meaningless. It is, therefore, assumed in what follows that decompositional equivalence is in fact satisfied in our universe U, and hence that the dynamics HU is independent of system boundaries.
—could be expected to alter fundamental physical laws or their dynamical outcomes; in such a universe, the notions of “fundamental physical laws” and “well-defined dynamics” would be effectively meaningless. It is, therefore, assumed in what follows that decompositional equivalence is in fact satisfied in our universe U, and hence that the dynamics HU is independent of system boundaries. 3.2. Consequence: System-Environment Decoherence can have No Physical Consequences
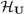 , select eigenstates of the S − E interaction HS−E. Such environmentally-mediated superselection or einselection [33,34] assures that observations of S that are mediated by information transfer through E will reveal eigenstates of HS−E; in the canonical example, observations of macroscopic objects mediated by information transfer through the ambient visible-spectrum photon field reveal eigenstates of position. From this perspective, it is the quantum mechanism of einselection that underlies the classical notion that the “environment” of a system—whether this refers to the ambient environment or to an experimental apparatus—objectively encodes the physical state of the system, where “objectively” has the sense given in the Ollivier–Poulin–Zurek definition [4,5] quoted in Section 2.3.
, select eigenstates of the S − E interaction HS−E. Such environmentally-mediated superselection or einselection [33,34] assures that observations of S that are mediated by information transfer through E will reveal eigenstates of HS−E; in the canonical example, observations of macroscopic objects mediated by information transfer through the ambient visible-spectrum photon field reveal eigenstates of position. From this perspective, it is the quantum mechanism of einselection that underlies the classical notion that the “environment” of a system—whether this refers to the ambient environment or to an experimental apparatus—objectively encodes the physical state of the system, where “objectively” has the sense given in the Ollivier–Poulin–Zurek definition [4,5] quoted in Section 2.3. 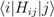 , between any pair of degrees of freedom i and j within U. An arbitrary boundary shift, in other words, has no physical consequences. In particular, a boundary shift that transforms S ⊗ E into an alternative TPS S′ ⊗ E′ has no physical consequences for the values of matrix elements (
, between any pair of degrees of freedom i and j within U. An arbitrary boundary shift, in other words, has no physical consequences. In particular, a boundary shift that transforms S ⊗ E into an alternative TPS S′ ⊗ E′ has no physical consequences for the values of matrix elements ( 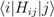 where i and j are degrees of freedom within the intersection E ∩ E′, and hence has no physical consequences for states of E ∩ E′ or for the classical information that such states encode. The encodings within E ∩ E′ of arbitrary states of S and S′, and hence of einselected pointer states of S and S′ are, therefore, entirely independent of the boundaries of these systems, and hence entirely independent of the Hamiltonians HS−E and HS′−E′ defined at those boundaries. The encoding of information about S in E is, in other words, entirely a result of the action of HU = ∑ij Hij , and is entirely independent of specified system boundaries or “emergent” system-environment interactions definable at such specified boundaries.
where i and j are degrees of freedom within the intersection E ∩ E′, and hence has no physical consequences for states of E ∩ E′ or for the classical information that such states encode. The encodings within E ∩ E′ of arbitrary states of S and S′, and hence of einselected pointer states of S and S′ are, therefore, entirely independent of the boundaries of these systems, and hence entirely independent of the Hamiltonians HS−E and HS′−E′ defined at those boundaries. The encoding of information about S in E is, in other words, entirely a result of the action of HU = ∑ij Hij , and is entirely independent of specified system boundaries or “emergent” system-environment interactions definable at such specified boundaries. 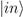 of the molecules within the voxel, with a decoherence time at room temperature and pressure of substantially less than 10−20 s [35], and as einselecting
of the molecules within the voxel, with a decoherence time at room temperature and pressure of substantially less than 10−20 s [35], and as einselecting 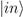 as an eigenstate of position within the fluid at all subsequent times. Such einselection prevents the wavefunction
as an eigenstate of position within the fluid at all subsequent times. Such einselection prevents the wavefunction 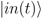 from spreading into a macroscopically-extended spatial superposition, just as decoherence and einselection by interplanetary dust, gasses and radiation prevent the wavefunction of Hyperion from doing so [36]. Does the state of the fluid outside the stipulated voxel objectively encode the position of the continuously-deforming voxel boundary at which this einselection takes place? Could observers with no prior knowledge of the stipulated voxel boundary determine its position by observing the state of the fluid? Obviously they could not.
from spreading into a macroscopically-extended spatial superposition, just as decoherence and einselection by interplanetary dust, gasses and radiation prevent the wavefunction of Hyperion from doing so [36]. Does the state of the fluid outside the stipulated voxel objectively encode the position of the continuously-deforming voxel boundary at which this einselection takes place? Could observers with no prior knowledge of the stipulated voxel boundary determine its position by observing the state of the fluid? Obviously they could not. 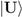 can, in this case, be considered to be a pure quantum state with von Neumann entropy of zero at all times. This situation is in stark contrast to that of a universe in which decompositional equivalence is violated, i.e., a universe in which the dynamics do depend on system boundaries, either via a physical process of “wave-function collapse” driven by measurement or a physical and therefore ontological “emergence” of bounded systems driven by decoherence. In this latter kind of universe, entanglement is physically destroyed by decoherence and von Neumann entropy objectively increases. A countervailing physical process that creates entanglement, either between measurements or in regions of weak decoherence, and hence decreases von Neumann entropy must be postulated to prevent such a universe from solidifying into an objectively classical system, a kind of system that our universe demonstrably is not.
can, in this case, be considered to be a pure quantum state with von Neumann entropy of zero at all times. This situation is in stark contrast to that of a universe in which decompositional equivalence is violated, i.e., a universe in which the dynamics do depend on system boundaries, either via a physical process of “wave-function collapse” driven by measurement or a physical and therefore ontological “emergence” of bounded systems driven by decoherence. In this latter kind of universe, entanglement is physically destroyed by decoherence and von Neumann entropy objectively increases. A countervailing physical process that creates entanglement, either between measurements or in regions of weak decoherence, and hence decreases von Neumann entropy must be postulated to prevent such a universe from solidifying into an objectively classical system, a kind of system that our universe demonstrably is not. 3.3. Consequence: Identification of Systems by Observers is Intrinsically Ambiguous
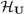 , and hence in the TPS of U, over which the POVM is defined. This can only be the case if the POVM is not defined over one component of a fixed TPS, but rather over all of
, and hence in the TPS of U, over which the POVM is defined. This can only be the case if the POVM is not defined over one component of a fixed TPS, but rather over all of 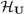 .
. 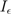 such that:
such that:
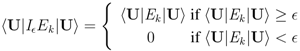
 . Defining any POVM {Ei} over all of
. Defining any POVM {Ei} over all of 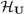 as in (1) renders the definition of “system” implicit: A system S is whatever returns finite outcome values
as in (1) renders the definition of “system” implicit: A system S is whatever returns finite outcome values 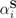 when acted upon by some POVM
when acted upon by some POVM 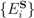 composed with
composed with 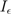 . The detectable degrees of freedom of such a system are, at some time t, the degrees of freedom in the inverse images
. The detectable degrees of freedom of such a system are, at some time t, the degrees of freedom in the inverse images 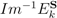 of the components
of the components 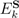 for which
for which  at t.
at t.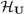 will satisfy (1) for any given
will satisfy (1) for any given 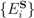 ; the collections of quantum degrees of freedom represented by the “system” components of these TPSs will be indistinguishable in principle by an observer deploying
; the collections of quantum degrees of freedom represented by the “system” components of these TPSs will be indistinguishable in principle by an observer deploying 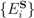 . Observations in any universe satisfying decompositional equivalence thus satisfy a symmetry, called “observable-dependent exchange symmetry” in [38]: Any two systems S and T for which a POVM
. Observations in any universe satisfying decompositional equivalence thus satisfy a symmetry, called “observable-dependent exchange symmetry” in [38]: Any two systems S and T for which a POVM 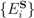 returns identical sets of outcome values when composed with
returns identical sets of outcome values when composed with 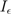 can be exchanged arbitrarily without affecting observations carried out using
can be exchanged arbitrarily without affecting observations carried out using 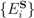 . To borrow an example from [38], many distinct radioactive sources may appear identical to an observer equipped only with a Geiger counter. It is shown in [38] that all observational consequences of the no-cloning theorem, the Kochen–Specker theorem and Bell’s theorem follow from observable-dependent exchange symmetry. Decompositional equivalence is sufficient, therefore, for the universe to appear quantum-mechanical, not classical, to finite observers whose means of collecting classical information can be represented by POVMs.
. To borrow an example from [38], many distinct radioactive sources may appear identical to an observer equipped only with a Geiger counter. It is shown in [38] that all observational consequences of the no-cloning theorem, the Kochen–Specker theorem and Bell’s theorem follow from observable-dependent exchange symmetry. Decompositional equivalence is sufficient, therefore, for the universe to appear quantum-mechanical, not classical, to finite observers whose means of collecting classical information can be represented by POVMs. 4. Decoherence as Semantics
4.1. Decoherence as Implemented by a POVM
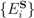 can be defined as a mapping:
can be defined as a mapping:
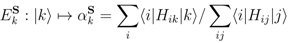
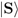 in
in 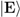 . It thus takes the slogan “decoherence is continuous measurement by the environment” literally.
. It thus takes the slogan “decoherence is continuous measurement by the environment” literally.  . In this case, O can be considered the “system” and ∪k(Im−1Ek) ⊂ U where
. In this case, O can be considered the “system” and ∪k(Im−1Ek) ⊂ U where  can be considered the “environment” in (2); the Hamiltonian Hik then characterizes the observer-environment interaction, and encodes classical information—the outcome values αk—about ∪k(Im−1Ek) into
can be considered the “environment” in (2); the Hamiltonian Hik then characterizes the observer-environment interaction, and encodes classical information—the outcome values αk—about ∪k(Im−1Ek) into 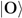 . Hence (2) provides a general definition of decoherence as the deployment of a POVM by an observer. For observers embedded in a relatively static environment, for which the total observer-environment interaction ∑ik Hik is nearly constant, (2) is reasonably interpreted as defining a single, continuously-deployed POVM. For observers embedded in highly-variable environments that nonetheless exhibit some periodicity, as most human observers are, it is reasonable to view (2) as describing the deployment of not one but a periodic sequence of POVMs, each normalized over a subset of the environmental degrees of freedom with which O interacts. As such a sequence must be finite for a finite observer, a finite observer can only be viewed as decohering his, her or its environment in a finite number of ways. Hence unlike the “environment as witness”, a finite observer as witness can physically encode the states of at most a finite number of distinct “systems”. Because the POVMs encoded by finite observers are limited in their resolution by
. Hence (2) provides a general definition of decoherence as the deployment of a POVM by an observer. For observers embedded in a relatively static environment, for which the total observer-environment interaction ∑ik Hik is nearly constant, (2) is reasonably interpreted as defining a single, continuously-deployed POVM. For observers embedded in highly-variable environments that nonetheless exhibit some periodicity, as most human observers are, it is reasonable to view (2) as describing the deployment of not one but a periodic sequence of POVMs, each normalized over a subset of the environmental degrees of freedom with which O interacts. As such a sequence must be finite for a finite observer, a finite observer can only be viewed as decohering his, her or its environment in a finite number of ways. Hence unlike the “environment as witness”, a finite observer as witness can physically encode the states of at most a finite number of distinct “systems”. Because the POVMs encoded by finite observers are limited in their resolution by 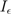 , each of the distinct “systems” representable by a finite observer is in fact an equivalence class under observable-dependent exchange symmetry.
, each of the distinct “systems” representable by a finite observer is in fact an equivalence class under observable-dependent exchange symmetry. 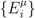 . The detectable outcome values produced by these POVMs have non-overlapping inverse images; hence they all mutually commute. If these POVMs are regarded as all acting at each of a sequence of times ti, their outcomes at those times can be considered to be a sequence of real vectors
. The detectable outcome values produced by these POVMs have non-overlapping inverse images; hence they all mutually commute. If these POVMs are regarded as all acting at each of a sequence of times ti, their outcomes at those times can be considered to be a sequence of real vectors 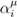 . These vectors form a consistent decoherent history of the Sµ at the ti, in the sense defined by Griffiths [8]. In a universe in which decoherence is an informational process, the number of such consistent decoherent histories and hence the number of “classical realms” [40] is limited only by the number of distinct sets of subspaces of
. These vectors form a consistent decoherent history of the Sµ at the ti, in the sense defined by Griffiths [8]. In a universe in which decoherence is an informational process, the number of such consistent decoherent histories and hence the number of “classical realms” [40] is limited only by the number of distinct sets of subspaces of 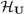 , i.e., is combinatorial in the number of degrees of freedom of
, i.e., is combinatorial in the number of degrees of freedom of 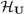 . Each of these histories, as a discrete time sequence of real vectors, can be regarded as a sequential sample of the state transitions of a classical finite state machine (FSM; [19]). As shown by Moore [20], no finite sequence of observations of an FSM is sufficient to uniquely identify the FSM; hence no finite sample of any decoherent history is sufficient to identify the TPS boundaries at which the POVMs contributing to the history are defined, confirming the observable-dependent exchange symmetry of observations in a universe satisfying decompositional equivalence.
. Each of these histories, as a discrete time sequence of real vectors, can be regarded as a sequential sample of the state transitions of a classical finite state machine (FSM; [19]). As shown by Moore [20], no finite sequence of observations of an FSM is sufficient to uniquely identify the FSM; hence no finite sample of any decoherent history is sufficient to identify the TPS boundaries at which the POVMs contributing to the history are defined, confirming the observable-dependent exchange symmetry of observations in a universe satisfying decompositional equivalence. 4.2. Decoherence Defines a Virtual Machine
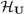 to the space of classical virtual machines, i.e., by a diagram such Figure 1; as such a mapping takes quantum states to classical information, it can be represented as a POVM {Ei}. The requirement that this diagram commutes is the requirement that the action of the physical propagator
to the space of classical virtual machines, i.e., by a diagram such Figure 1; as such a mapping takes quantum states to classical information, it can be represented as a POVM {Ei}. The requirement that this diagram commutes is the requirement that the action of the physical propagator 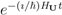 eacting from tn to tn+1 is represented, by the mapping {Ei}, as a classical state transition from the nth to the (n + 1)th state of some virtual machine V. This commutativity requirement is fully equivalent to the commutativity requirement that defines consistency of observational histories of U (e.g., [8] Equation 10.20). Hence an evolution HU is consistent under a decoherence mapping {Ei} if it can be interpreted as an implementation of a classical virtual machine.
eacting from tn to tn+1 is represented, by the mapping {Ei}, as a classical state transition from the nth to the (n + 1)th state of some virtual machine V. This commutativity requirement is fully equivalent to the commutativity requirement that defines consistency of observational histories of U (e.g., [8] Equation 10.20). Hence an evolution HU is consistent under a decoherence mapping {Ei} if it can be interpreted as an implementation of a classical virtual machine. 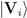 of a virtual machine V implemented by U. Commutativity of this diagram assures that the decoherence mapping {Ei} is consistent.
of a virtual machine V implemented by U. Commutativity of this diagram assures that the decoherence mapping {Ei} is consistent.
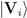 of a virtual machine V implemented by U. Commutativity of this diagram assures that the decoherence mapping {Ei} is consistent.
of a virtual machine V implemented by U. Commutativity of this diagram assures that the decoherence mapping {Ei} is consistent. 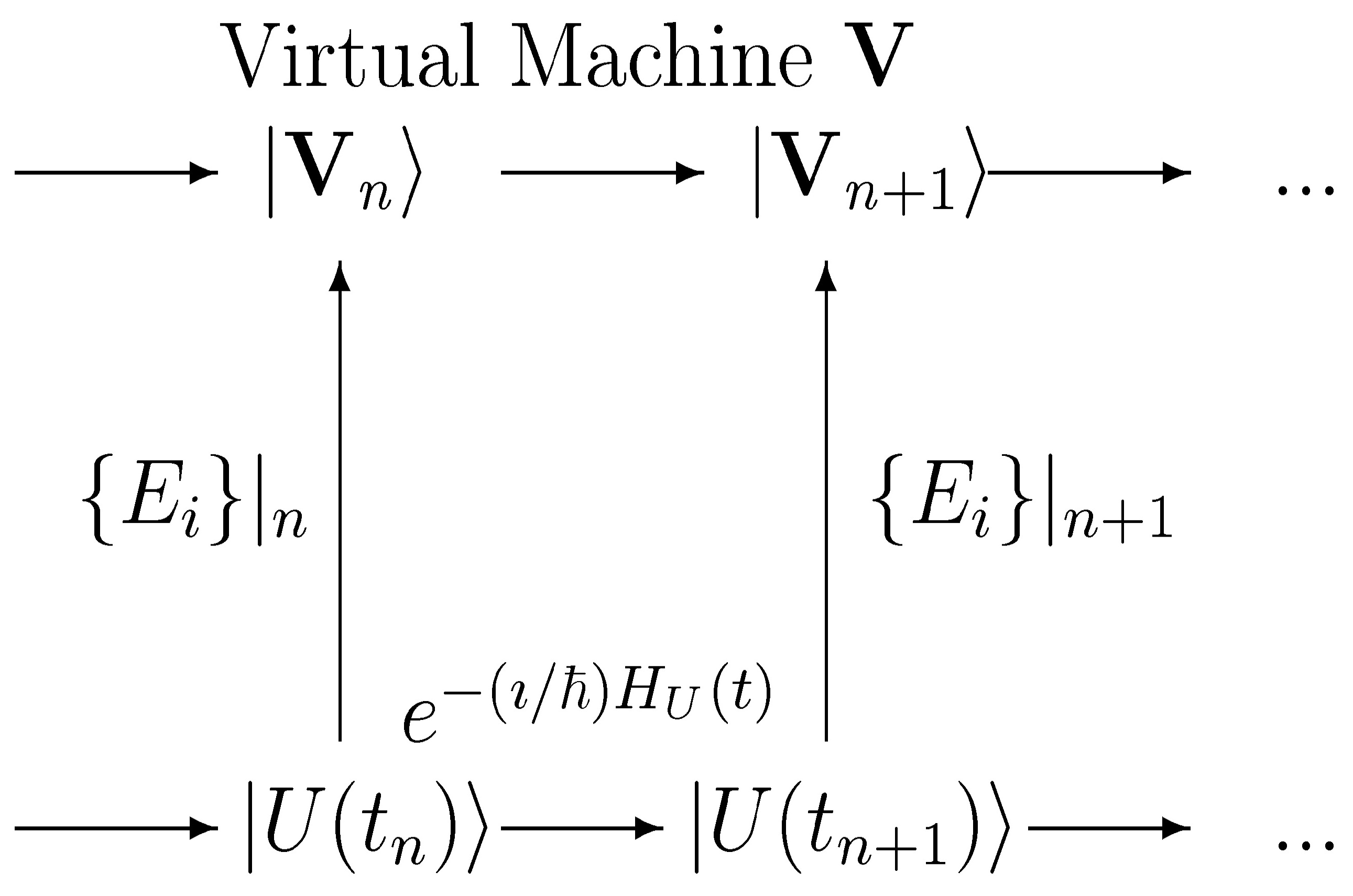
5. Observation as Entanglement
5.1. Classical Communication is Regressive
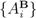 ” and Bob’s POVM for acquiring information from Alice “
” and Bob’s POVM for acquiring information from Alice “ 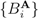 ”, and suppose that these POVMs are deployed at some time t0. Clearly the same question can be asked at t0 as at t2 and t1, and clearly it cannot be answered by postulating yet another agreement, another classical communication, and another deployment of POVMs. The same kind of regress infects any simple joint assumption by Alice and Bob that they are observing the same system, an assumption that must be communicated to be effective. Any instance of measurement under LOCC conditions, in other words, requires the postulation of a priori classical communication between the observers, and hence requires that the observers themselves be regarded as classically objective a priori. Minimal quantum mechanics with decompositional equivalence provides no mechanism by which such a priori classical objectivity can be achieved; hence minimal quantum mechanics with decompositional equivalence does not support LOCC. At best, minimal quantum mechanics with decompositional equivalence supports the appearance of LOCC in cases in which observers agree to treat their observations as observations of the same system.
”, and suppose that these POVMs are deployed at some time t0. Clearly the same question can be asked at t0 as at t2 and t1, and clearly it cannot be answered by postulating yet another agreement, another classical communication, and another deployment of POVMs. The same kind of regress infects any simple joint assumption by Alice and Bob that they are observing the same system, an assumption that must be communicated to be effective. Any instance of measurement under LOCC conditions, in other words, requires the postulation of a priori classical communication between the observers, and hence requires that the observers themselves be regarded as classically objective a priori. Minimal quantum mechanics with decompositional equivalence provides no mechanism by which such a priori classical objectivity can be achieved; hence minimal quantum mechanics with decompositional equivalence does not support LOCC. At best, minimal quantum mechanics with decompositional equivalence supports the appearance of LOCC in cases in which observers agree to treat their observations as observations of the same system. 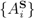 and
and 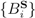 Bob by Alice and Bob, respectively. (A) Alice and Bob receive POVM selection instructions from a classical source. (B) Alice and Bob jointly observe the production of S and agree that their selected POVMs identify it.
Bob by Alice and Bob, respectively. (A) Alice and Bob receive POVM selection instructions from a classical source. (B) Alice and Bob jointly observe the production of S and agree that their selected POVMs identify it.
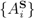 and
and 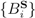 Bob by Alice and Bob, respectively. (A) Alice and Bob receive POVM selection instructions from a classical source. (B) Alice and Bob jointly observe the production of S and agree that their selected POVMs identify it.
Bob by Alice and Bob, respectively. (A) Alice and Bob receive POVM selection instructions from a classical source. (B) Alice and Bob jointly observe the production of S and agree that their selected POVMs identify it.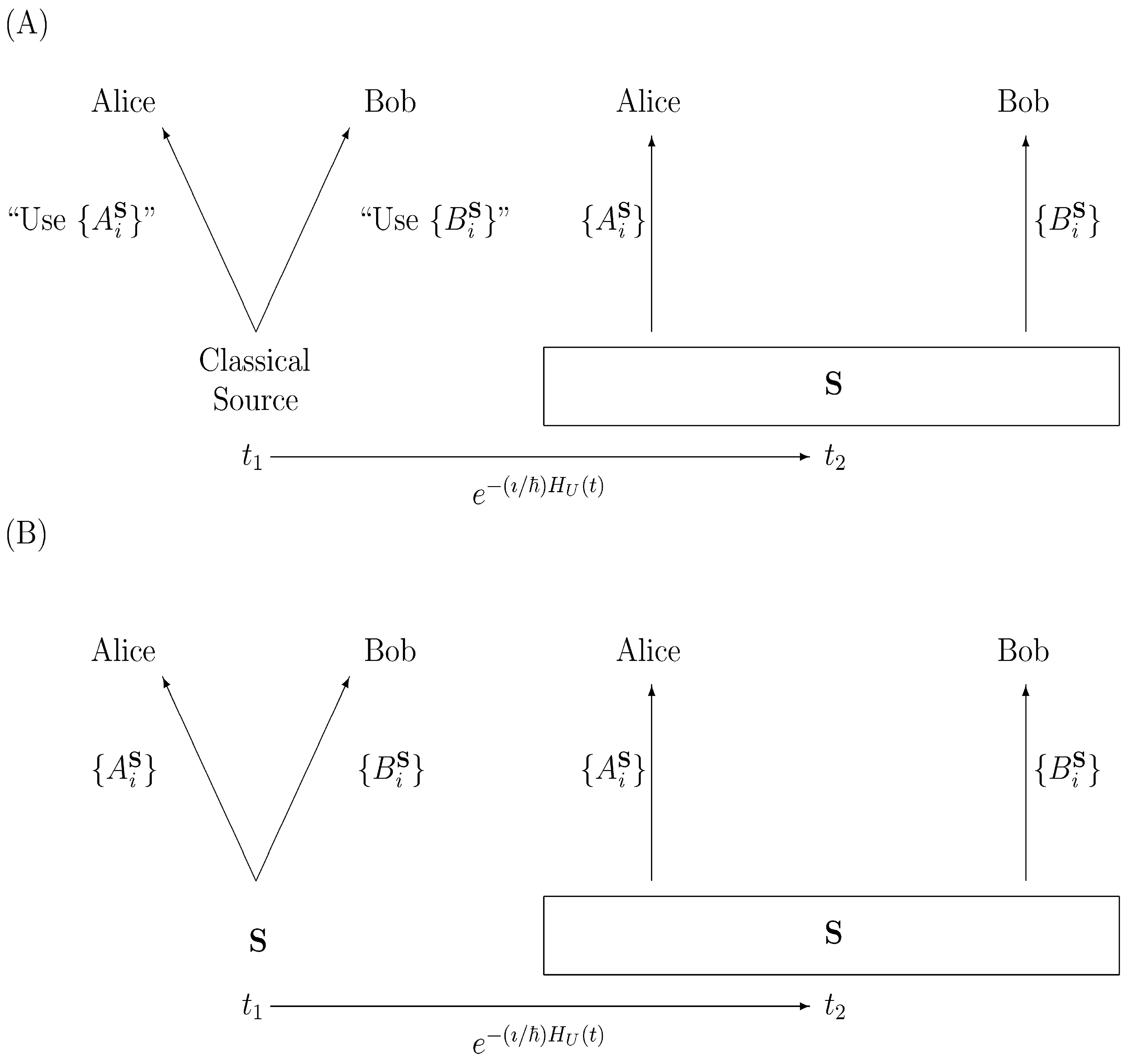
5.2. Memory is Communication
5.3. Implementation of POVMs by HU
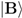 . If Alice is to regard a state
. If Alice is to regard a state 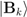 of Bob as a report, i.e., as classically encoding a state
of Bob as a report, i.e., as classically encoding a state 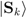 of some identified external system S, it must be possible, at least in principle, for her to establish that a counterfactual-supporting classical correlation—a classical correlation that exists whether observed or not—between
of some identified external system S, it must be possible, at least in principle, for her to establish that a counterfactual-supporting classical correlation—a classical correlation that exists whether observed or not—between 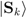 and
and 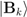 is maintained by the B − S interaction and hence, given decompositional equivalence, by HU. The action of HU maintains a counterfactual-supporting classical correlation between states of S and B just in case S and B are entangled; if the correlation that is maintained is perfect, S and B must be monogamously entangled. Whether joint states of two identified systems appear to be entangled is, however, dependent on the choice of basis and hence the POVM deployed to determine their joint states [46,47,48,49,50]. Bob’s state
is maintained by the B − S interaction and hence, given decompositional equivalence, by HU. The action of HU maintains a counterfactual-supporting classical correlation between states of S and B just in case S and B are entangled; if the correlation that is maintained is perfect, S and B must be monogamously entangled. Whether joint states of two identified systems appear to be entangled is, however, dependent on the choice of basis and hence the POVM deployed to determine their joint states [46,47,48,49,50]. Bob’s state 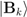 is, therefore, a classical encoding of
is, therefore, a classical encoding of 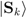 for Alice only if she deploys a POVM that projects
for Alice only if she deploys a POVM that projects 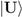 onto a Hilbert-space bases in which
onto a Hilbert-space bases in which 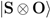 is entangled, and is a perfectly classical encoding if this apparent entanglement is monogamous.
is entangled, and is a perfectly classical encoding if this apparent entanglement is monogamous. 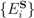 to identify S” is, therefore, just to say that O and S are entangled by the action of HU on the quantum degrees of freedom that implement O and S: Observation is entanglement. The existence of such entanglement is an objective fact that is, in a universe satisfying decompositional equivalence, independent of the boundaries of S and O. Whether S and O appear to be entangled to a third-party observer, however, is not an objective fact; it rather depends on the POVM employed by that observer to extract classical information from the degrees of freedom implementing S and O. Hence while the classical correlation between S and O is “real”—i.e., physical, a result of the action of HU—whether it appears classical to third parties is virtual, i.e., dependent on semantic interpretation. All public communication is, therefore, nonfungible or “unspeakable” in the sense defined in [51]: The information communicated is always strictly relative to a POVM—a “reference frame” in the language of [51]—that is not specified by HU and cannot be assumed without circularity. Any publicly-communicable classical description of the world is, therefore, intrinsically logically circular.
to identify S” is, therefore, just to say that O and S are entangled by the action of HU on the quantum degrees of freedom that implement O and S: Observation is entanglement. The existence of such entanglement is an objective fact that is, in a universe satisfying decompositional equivalence, independent of the boundaries of S and O. Whether S and O appear to be entangled to a third-party observer, however, is not an objective fact; it rather depends on the POVM employed by that observer to extract classical information from the degrees of freedom implementing S and O. Hence while the classical correlation between S and O is “real”—i.e., physical, a result of the action of HU—whether it appears classical to third parties is virtual, i.e., dependent on semantic interpretation. All public communication is, therefore, nonfungible or “unspeakable” in the sense defined in [51]: The information communicated is always strictly relative to a POVM—a “reference frame” in the language of [51]—that is not specified by HU and cannot be assumed without circularity. Any publicly-communicable classical description of the world is, therefore, intrinsically logically circular. 6. Conclusions
References
- Nielsen, M.A.; Chaung, I.L. Quantum Information and Quantum Computation; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Landauer, R. Information is a physical entity. Physica A 1999, 263, 63–67. [Google Scholar] [CrossRef]
- Fields, C. If physics is an information science, what is an observer? Information 2012, 3, 92–123. [Google Scholar]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Objective properties from subjective quantum states: Environment as a witness. Phys. Rev. Lett. 2004, 93, 220401:1–220401:4. [Google Scholar]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Environment as a witness: Selective proliferation of information and emergence of objectivity in a quantum universe. Phys. Rev. A 2005, 72, 042113:1–042113:21. [Google Scholar]
- Blume-Kohout, R.; Zurek, W.H. Quantum Darwinism: Entanglement, branches, and the emergent classicality of redundantly stored quantum information. Phys. Rev. A 2006, 73, 062310:1–062310:21. [Google Scholar]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Griffiths, R.B. Consistent Quantum Theory; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Everett, H., III. “Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Landsman, N.P. Between classical and quantum. In Handbook of the Philosophy of Science: Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Elsevier: Amsterdam, the Netherland, 2007; pp. 417–553. [Google Scholar]
- Schlosshauer, M. Experimental motivation and empirical consistency of minimal no-collapse quantum mechanics. Ann. Phys. 2006, 321, 112–149. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, F. An analog analogue of a digital quantum computation. Phys. Rev. A 1996, 57, 2403–2406. [Google Scholar] [CrossRef]
- Briegel, H.J.; Browne, D.E.; Dür, W.; Raussendorf, R.; van den Nest, M. Measurement-based quantum computation. Nat. Phys. 2009, 5, 19–26. [Google Scholar]
- Aaronson, S. NP-complete problems and physical reality. Available online: http://arxiv.org/abs/quant-ph/0502072 (accessed on 6 December 2012).
- Wallace, D. Philosophy of quantum mechanics. In The Ashgate Companion to Contemporary Philosophy of Physics; Rickles, D., Ed.; Ashgate Publisher: Aldershot, UK, 2008; pp. 16–98. [Google Scholar]
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Fuchs, C.A. QBism: The perimeter of quantum Bayesianism. Available online: http://arxiv.org/abs/1003.5209 (accessed on 6 December 2012).
- Ashby, W.R. An Introduction to Cybernetics; Chapman and Hall: London, UK, 1956. [Google Scholar]
- Moore, E.F. Gedankenexperiments on sequential machines. In Autonoma Studies; Shannon, C.W., McCarthy, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1956; pp. 129–155. [Google Scholar]
- Rips, L.; Blok, S.; Newman, G. Tracing the identity of objects. Psychol. Rev. 2006, 133, 1–30. [Google Scholar]
- Scholl, B.J. Object persistence in philosophy and psychology. Mind Lang. 2007, 22, 563–591. [Google Scholar] [CrossRef]
- Fields, C. The very same thing: Extending the object token concept to incorporate causal constraints on individual identity. Adv. Cogn. Psychol. 2012, 8, 234–247. [Google Scholar]
- Zurek, W.H. Decoherence, einselection and the existential interpretation (the rough guide). Philos. Trans. R. Soc. A 1998, 356, 1793–1821. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel-Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Abenm, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. Combined results of searches for the standard model Higgs boson in pp collisions at √s = 7 TeV. Phys. Lett. B 2012, 710, 26–48.
- Fields, C. A model-theoretic interpretation of environmentally-induced superselection. Int. J. Gen. Syst. 2012, 41, 847–859. [Google Scholar] [CrossRef]
- Hu, B.L. Emergence: Key physical issues for deeper philosophical inquiries. J. Phys. Conf. Ser. 2012, 361. [Google Scholar] [CrossRef]
- Tegmark, M. The mathematical universe. Found. Phys. 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum theory. Rev. Mod. Phys. 2004, 76, 1267–1305. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherenceand the Quantum to Classical Transition; Springer: Berlin, Germany, 2007. [Google Scholar]
- Zurek, W.H. Pointer basis of the quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 1981, 24, 1516–1525. [Google Scholar] [CrossRef]
- Zurek, W.H. Environment-induced superselection rules. Phys. Rev. D 1982, 26, 1862–1880. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, D. The emergence of classical properties through interaction with the environment. Z. Phys. B 1985, 59, 223–243. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, chaos, quantum-classical correspondence, and the algorithmic arrow of time. Phys. Scr. 1998, 76, 186–198. [Google Scholar] [CrossRef]
- Brune, M.; Haglet, E.; Dreyer, J.; Maitre, X.; Maali, A.; Wunderlich, C.; Raimond, J.M.; Haroche, S. Observing the progressive decoherence of the meter in a quantum measurement. Phys. Rev. Lett. 1996, 77, 4887–4890. [Google Scholar]
- Fields, C. Bell’s theorem from Moore’s theorem. Int. J. Gen. Syst. Available online: http://arxiv.org/abs/1201.3672 (accessed on 10 December 2012). in press.
- Zeh, D. The problem of conscious observation in quantum mechanical description. Found. Phys. Lett. 2000, 13, 221–233. [Google Scholar] [CrossRef]
- Hartle, J.B. The quasiclassical realms of this quantum universe. Found. Phys. 2008, 41, 982–1006. [Google Scholar] [CrossRef]
- Tanenbaum, A.S. Structured Computer Organization; Prentice Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Hopcroft, J.E.; Ullman, J.D. Introduction to Automata, Languages and Computation; Addison-Wesley: Boston, MA, USA, 1979. [Google Scholar]
- Wallace, D. Decoherence and ontology. In Many Worlds? Everett, Quantum Theory and Reality; Saunders, S., Barrett, J., Kent, A., Wallace, D.D., Eds.; Oxford University Press: Oxford, UK, 2010; pp. 53–72. [Google Scholar]
- Tegmark, M. Many worlds in contex. In Many Worlds? Everett, Quantum Theory and Reality; Saunders, S., Barrett, J., Kent, A., Wallace, D.D., Eds.; Oxford University Press: Oxford, UK, 2010; pp. 553–581. [Google Scholar]
- Scully, R.J.; Scully, M.O. The Demon and the Quantum: From the Pythagorean Mystics to Maxwell’s Demon and Quantum Mystery; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Zanardi, P. Virtual quantum subsystems. Phys. Rev. Lett. 2001, 87, 077901:1–077901:4. [Google Scholar]
- Zanardi, P.; Lidar, D.A.; Lloyd, S. Quantum tensor product structures are observable-induced. Phys. Rev. Lett. 2004, 92, 060402:1–060402:4. [Google Scholar]
- de la Torre, A.C.; Goyeneche, D.; Leitao, L. Entanglement for all quantum states. Eur. J. Phys. 2010, 31, 325–332. [Google Scholar]
- Harshman, N.L.; Ranade, K.S. Observables can be tailored to change the entanglement of any pure state. Phys. Rev. A 2011, 84, 012303:1–012303:4. [Google Scholar]
- Thirring, W.; Bertlmann, R.A.; Köhler, P.; Narnhofer, H. Entanglement or separability: The choice of how to factorize the algebra of a density matrix. Eur. Phys. J. D 2011, 64, 181–196. [Google Scholar]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555–609. [Google Scholar]
- Bohr, N. The quantum postulate and the recent developments of atomic theory. Nature 1928, 121, 580–590. [Google Scholar]
- Zurek, W.H. Relative states and the environment: Einselection, envariance, quantum darwinism, and the existential interpretation. Available online: http://arxiv.org/abs/0707.2832 (accessed on 10 December 2012).
- Castagnoli, G. Quantum correlation between the selection of the problem and that of the solution sheds light on the mechanism of the speed up. Phys. Rev. A 2010, 82, 052334:1–052334:8. [Google Scholar]
- Castagnoli, G. Probing the mechanism of the quantum speed-up by time-symmetric quantum mechanics. Available online: http://128.84.158.119/abs/1107.0934v9 (accessed on 10 December 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fields, C. Implementation of Classical Communication in a Quantum World. Information 2012, 3, 809-831. https://doi.org/10.3390/info3040809
Fields C. Implementation of Classical Communication in a Quantum World. Information. 2012; 3(4):809-831. https://doi.org/10.3390/info3040809
Chicago/Turabian StyleFields, Chris. 2012. "Implementation of Classical Communication in a Quantum World" Information 3, no. 4: 809-831. https://doi.org/10.3390/info3040809




