Research of Feature Extraction Method Based on Sparse Reconstruction and Multiscale Dispersion Entropy
Abstract
:1. Introduction
2. Methodology
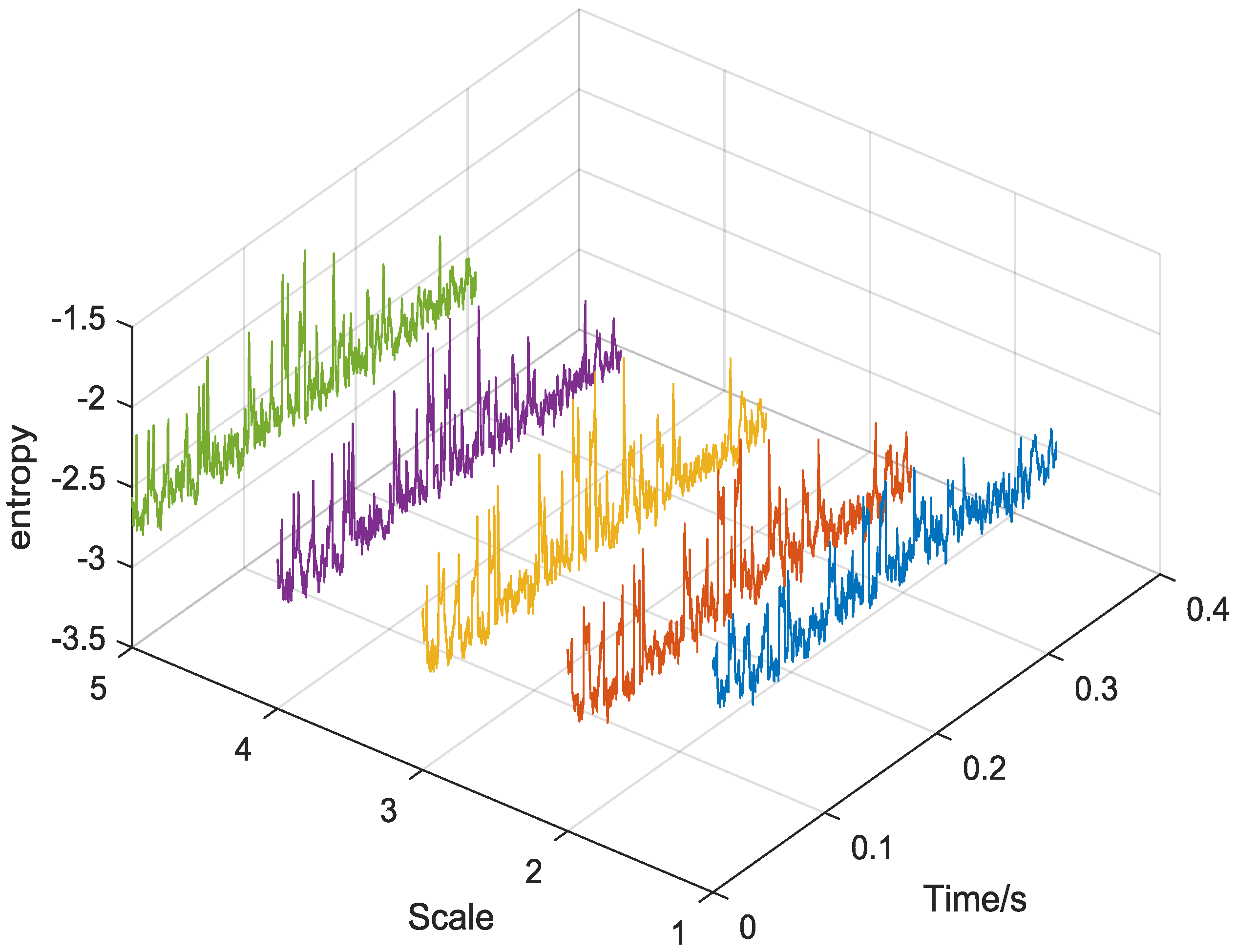
2.1. Multiscale Dispersion Entropy Based on RMS (MDErms)
2.2. Locality Preserving Projections (LPP)
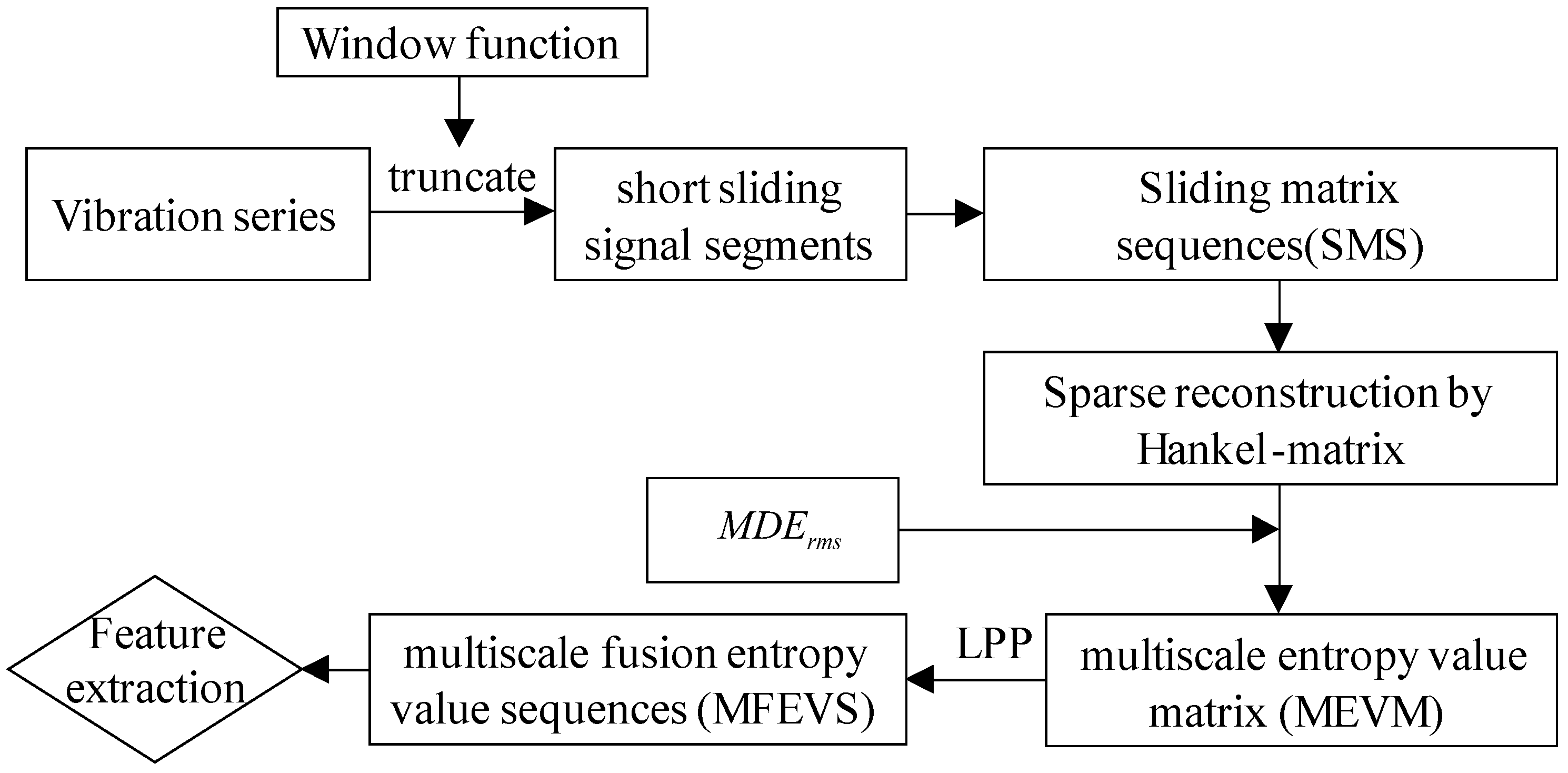
3. Fault Feature Extraction Technique
3.1. Sliding Matrix Sequences (SMS) Truncation and Sparse Reconstruction
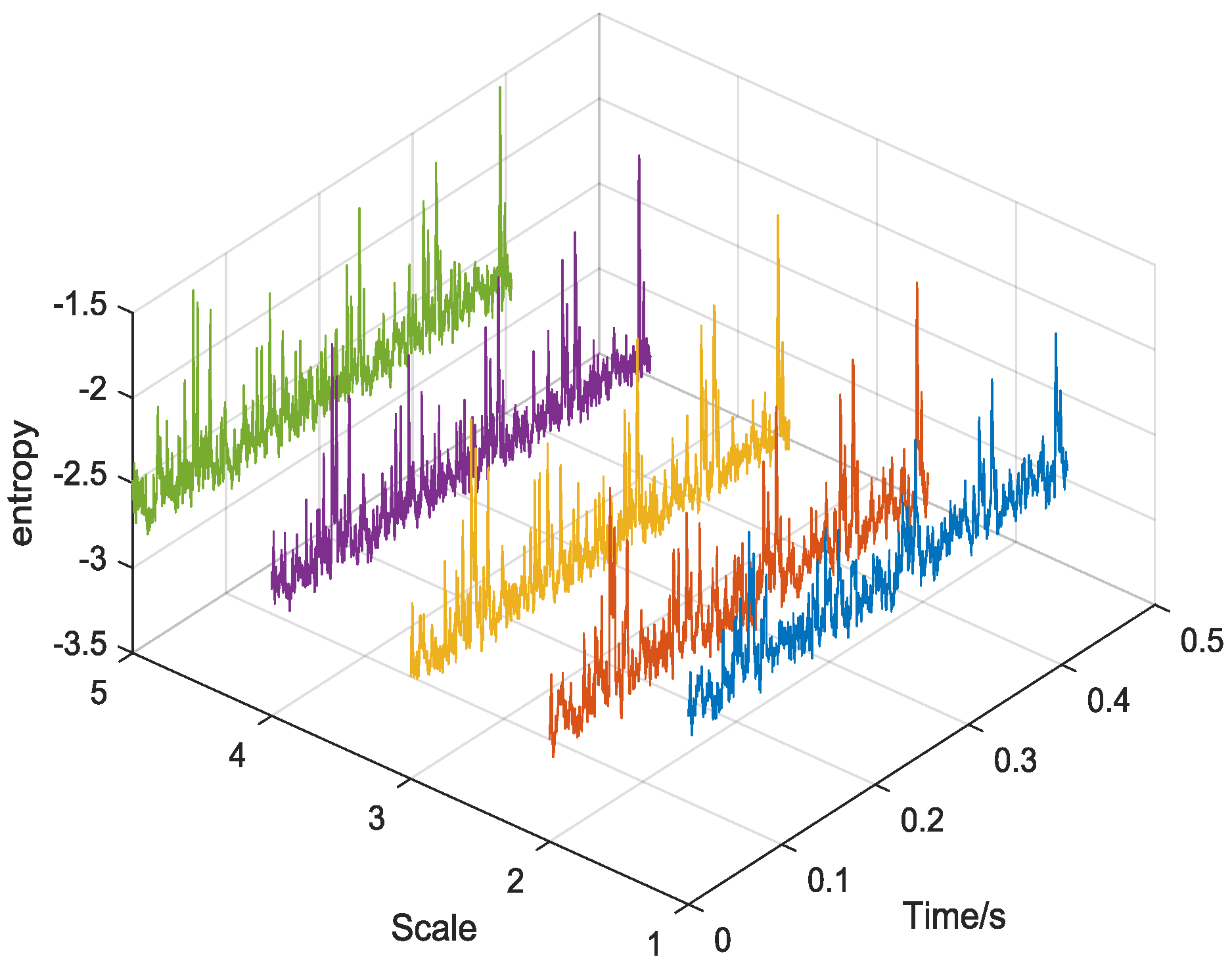
3.2. Feature Extraction with MFEVS
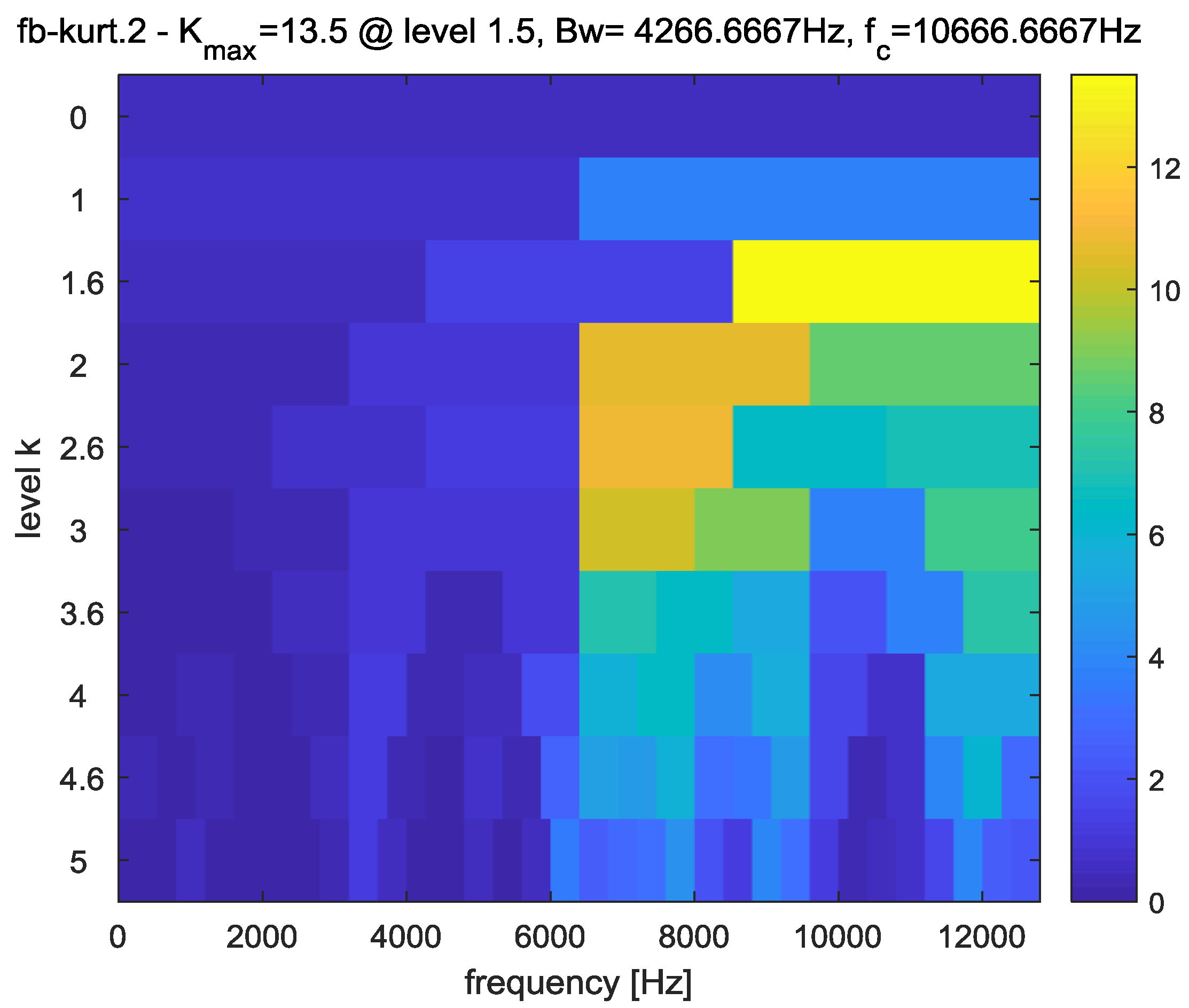
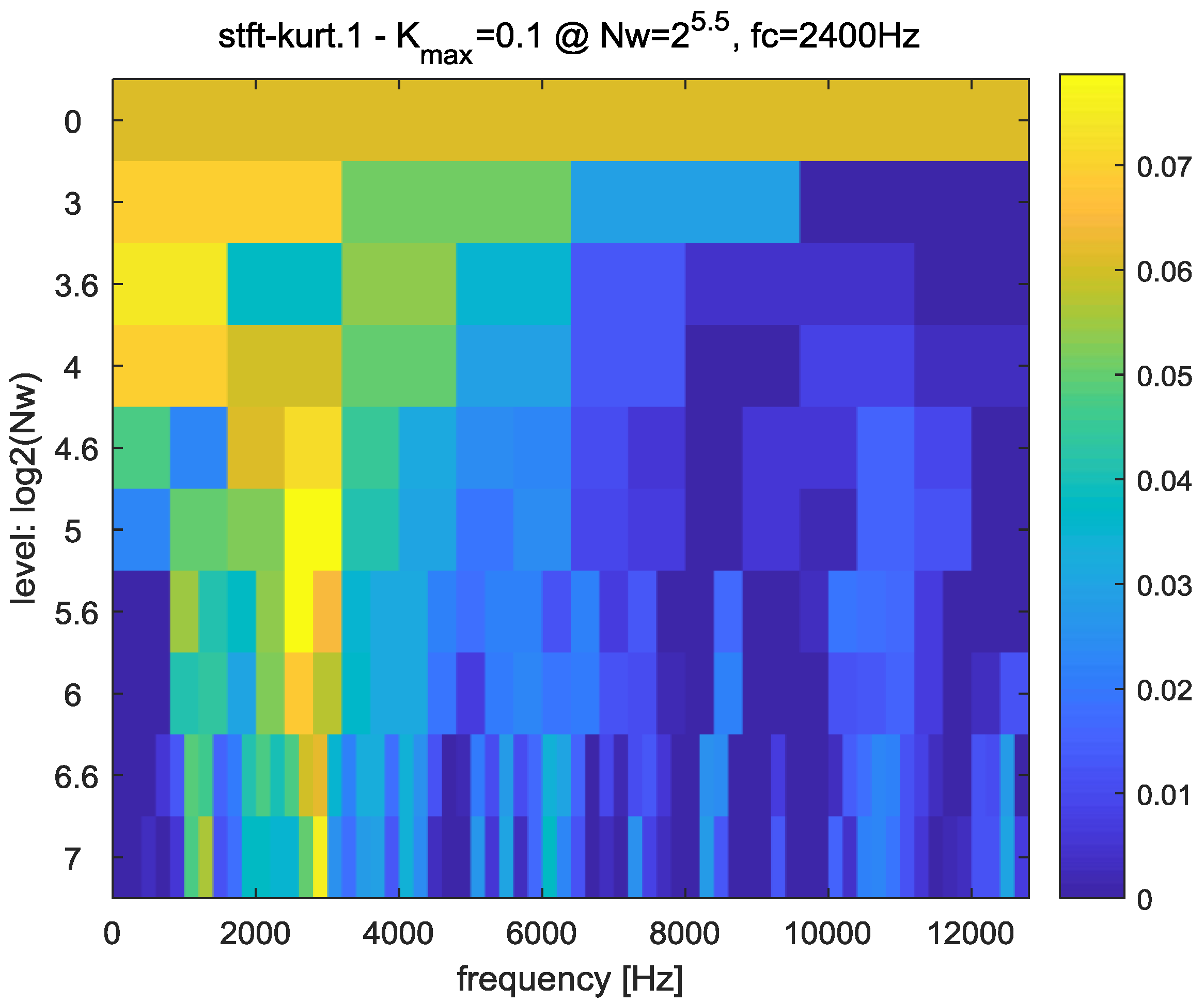
3.3. FIR Bandpass Filter Design
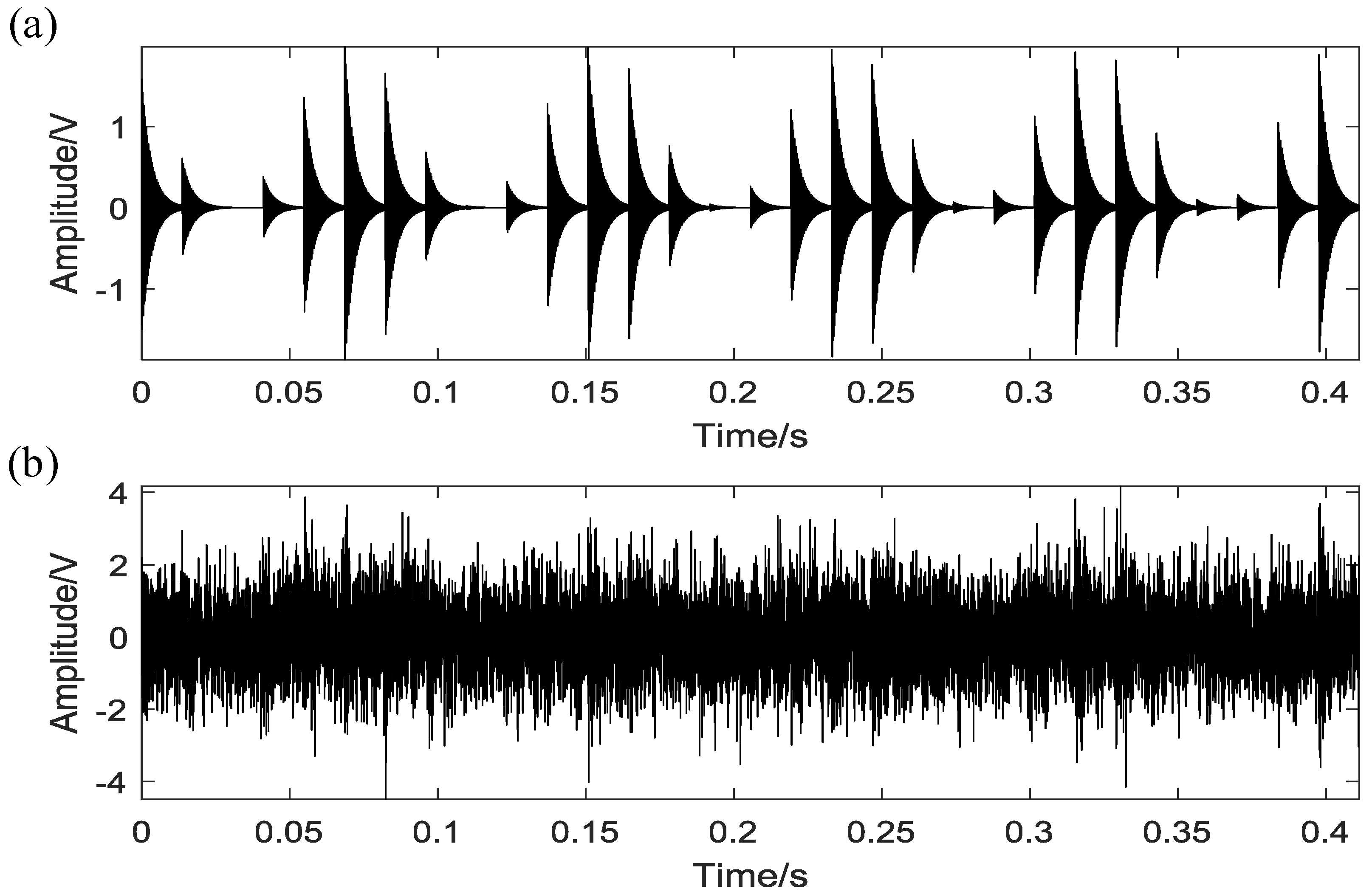
4. Simulation Study
5. Experiment Validation
5.1. Test Rig Instruction
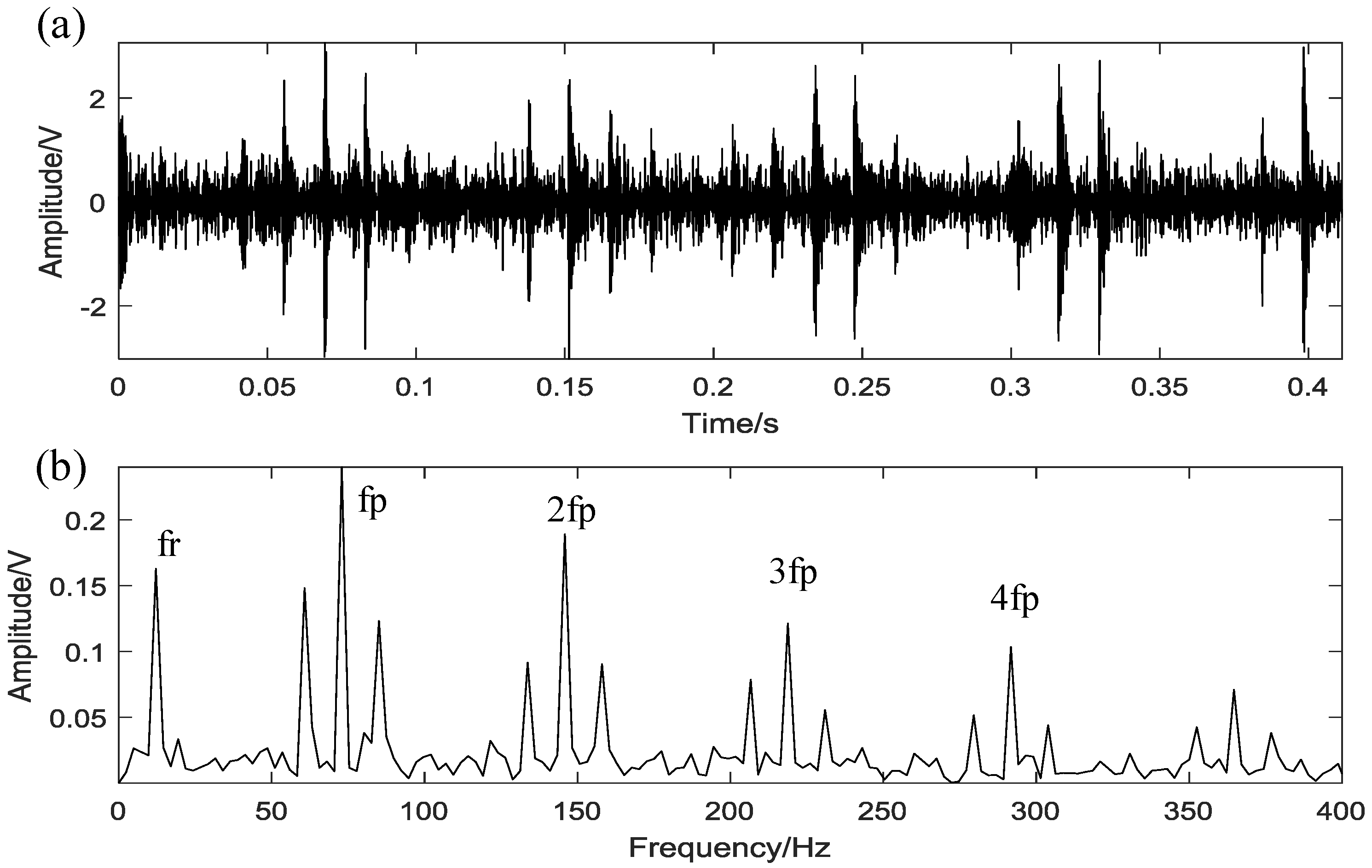
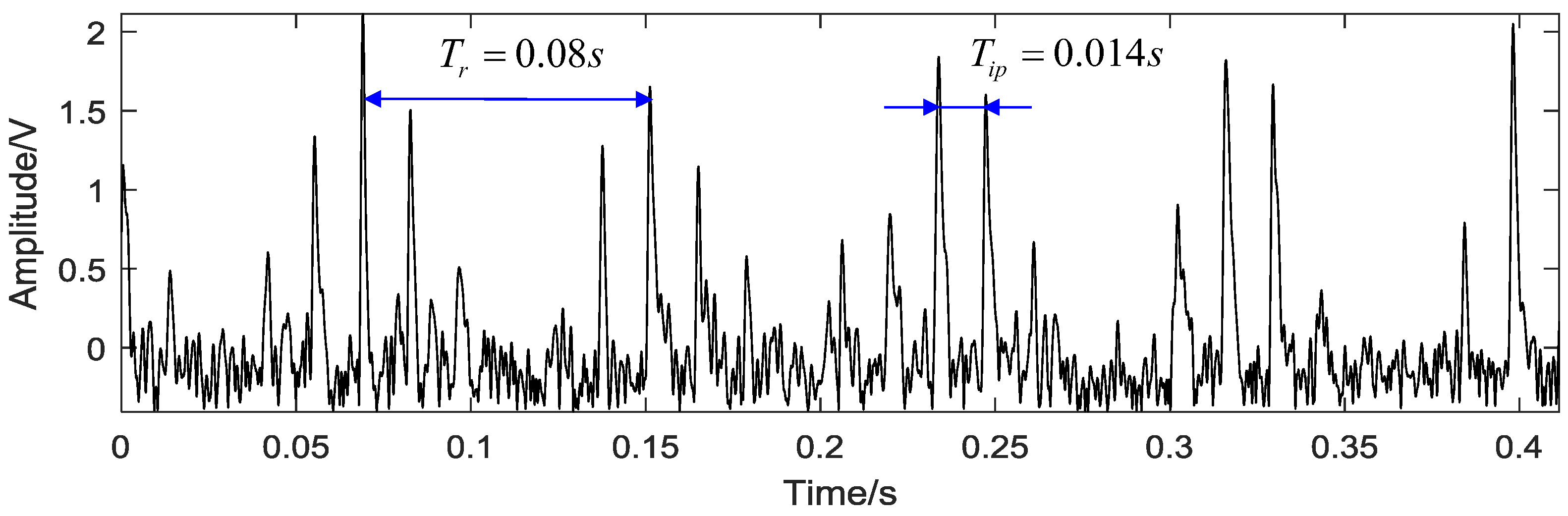
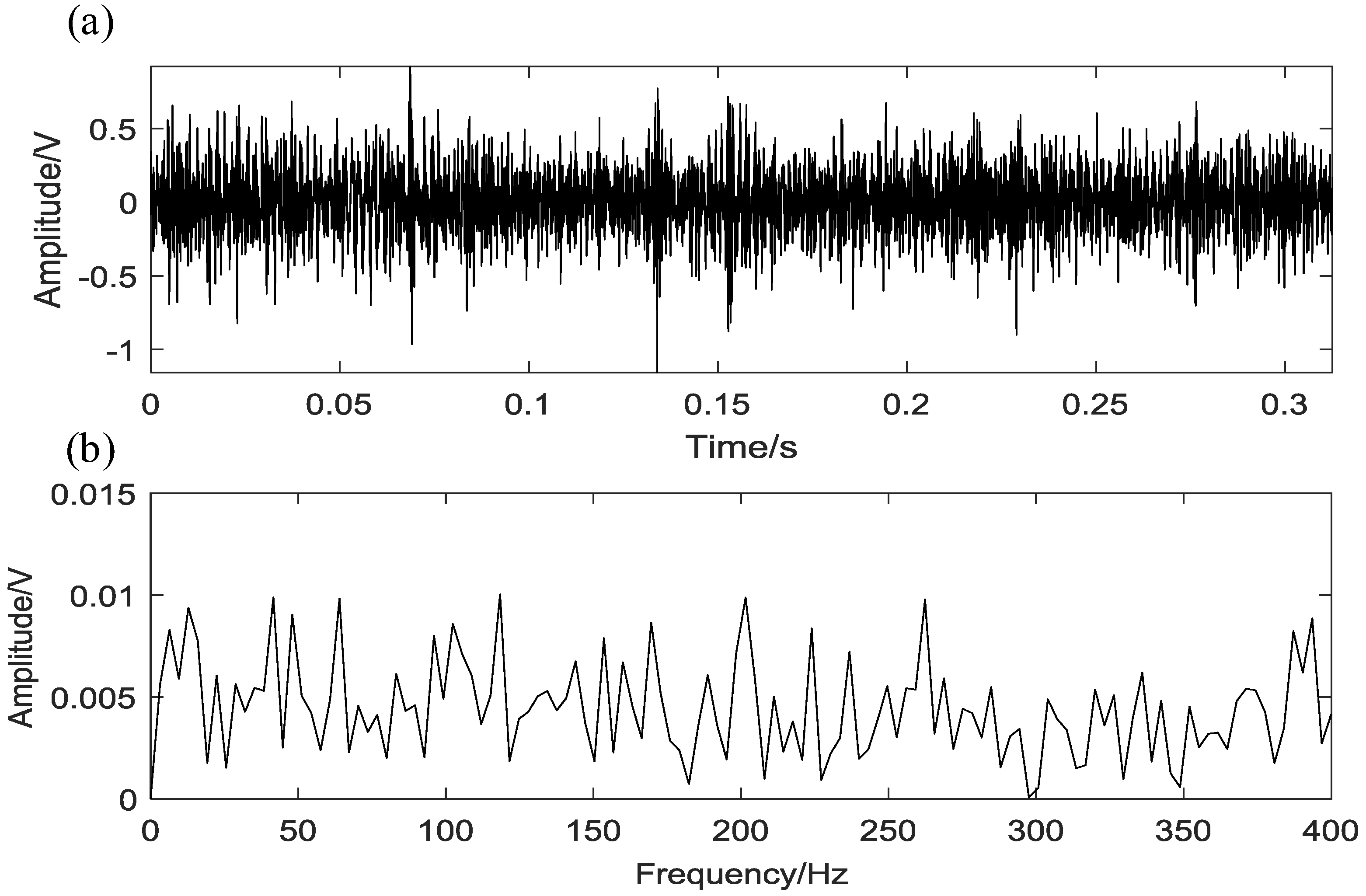
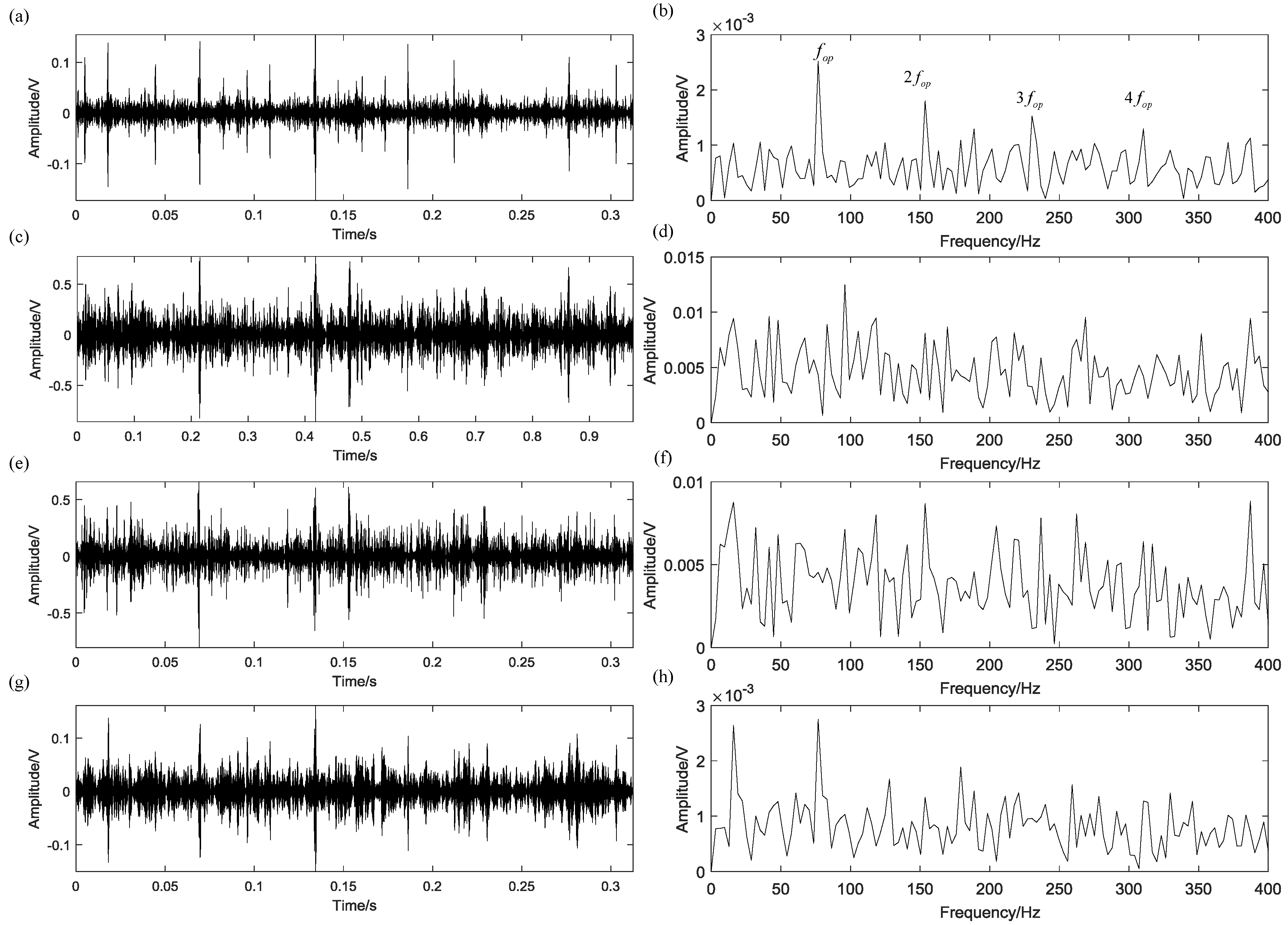
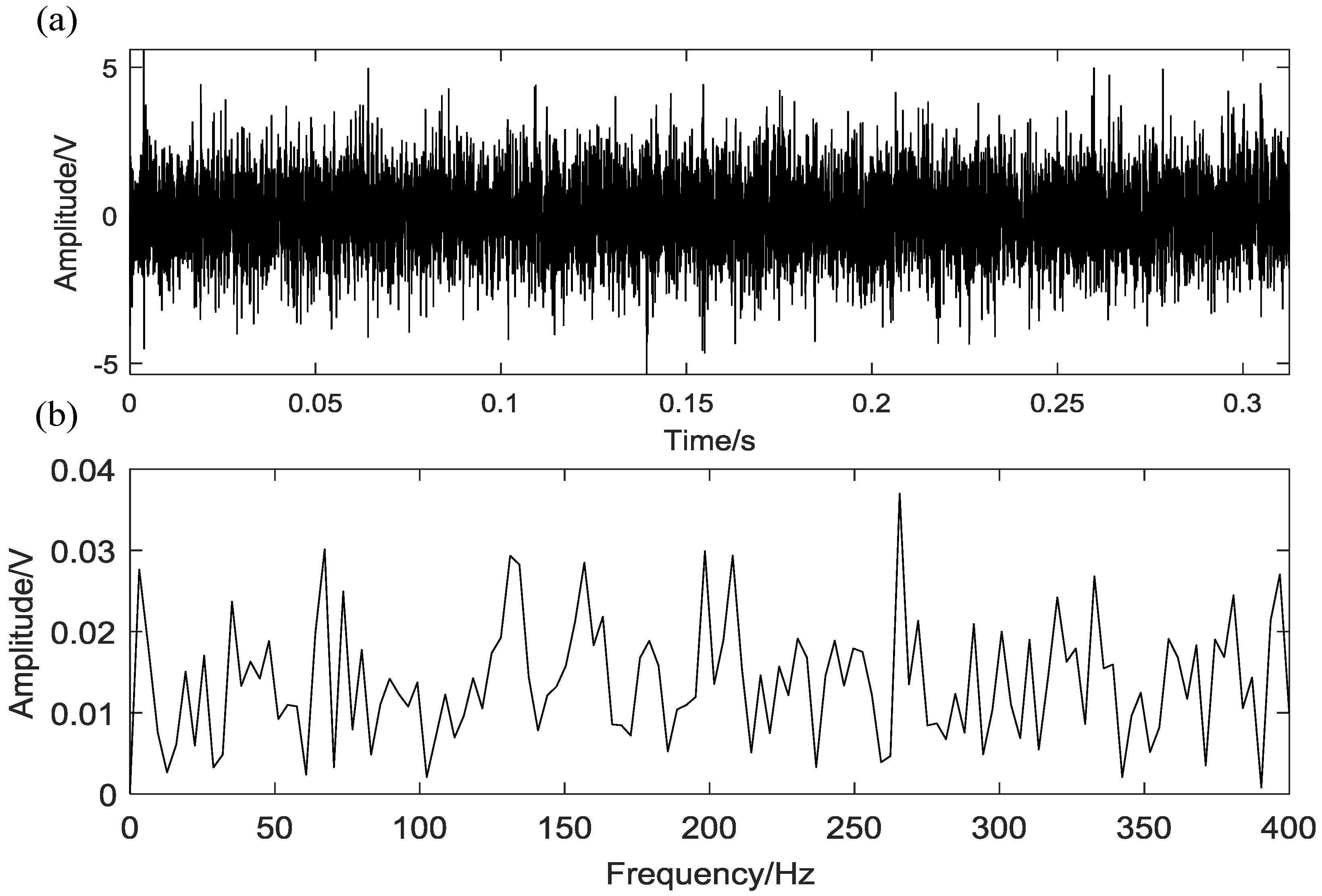
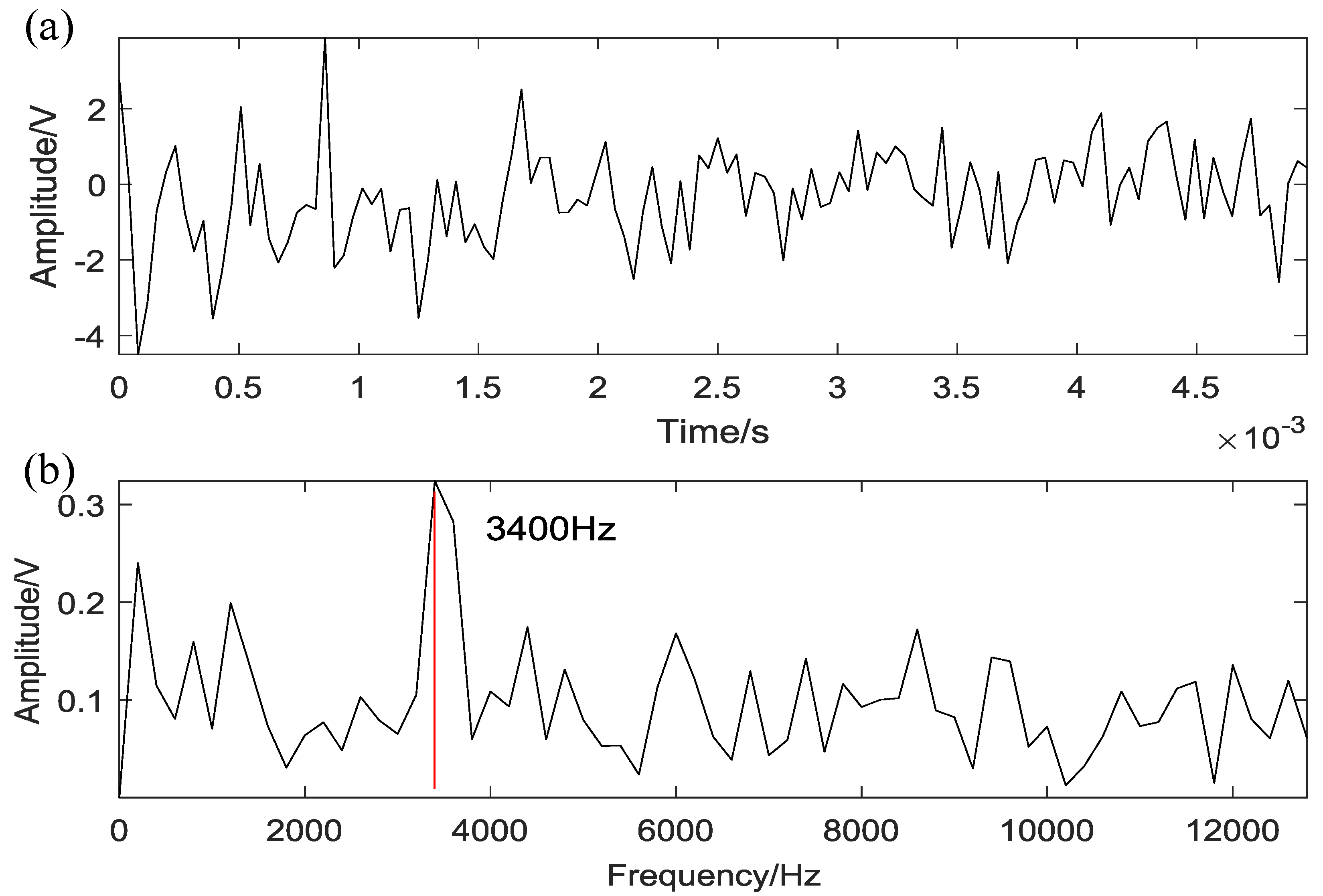
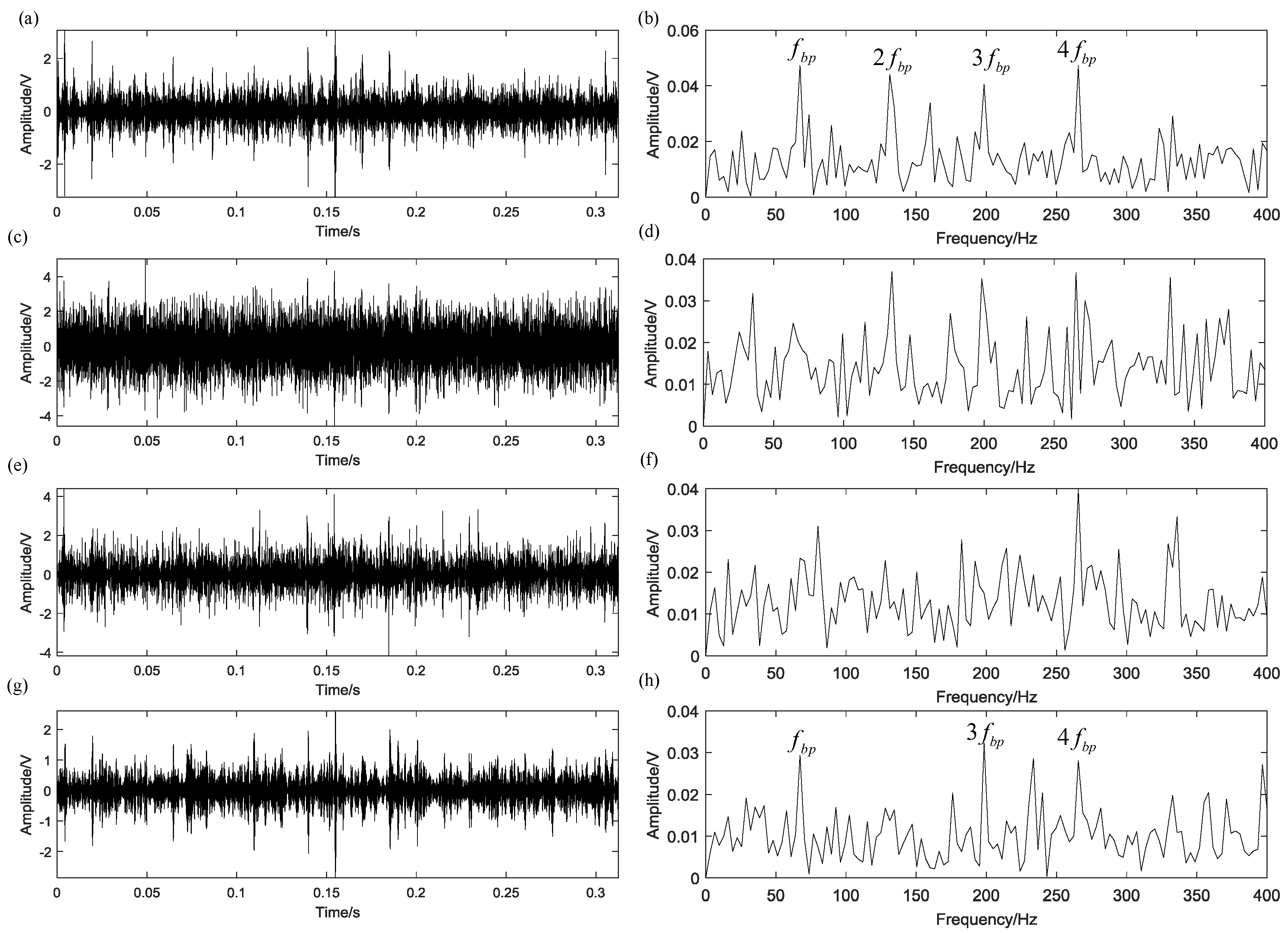
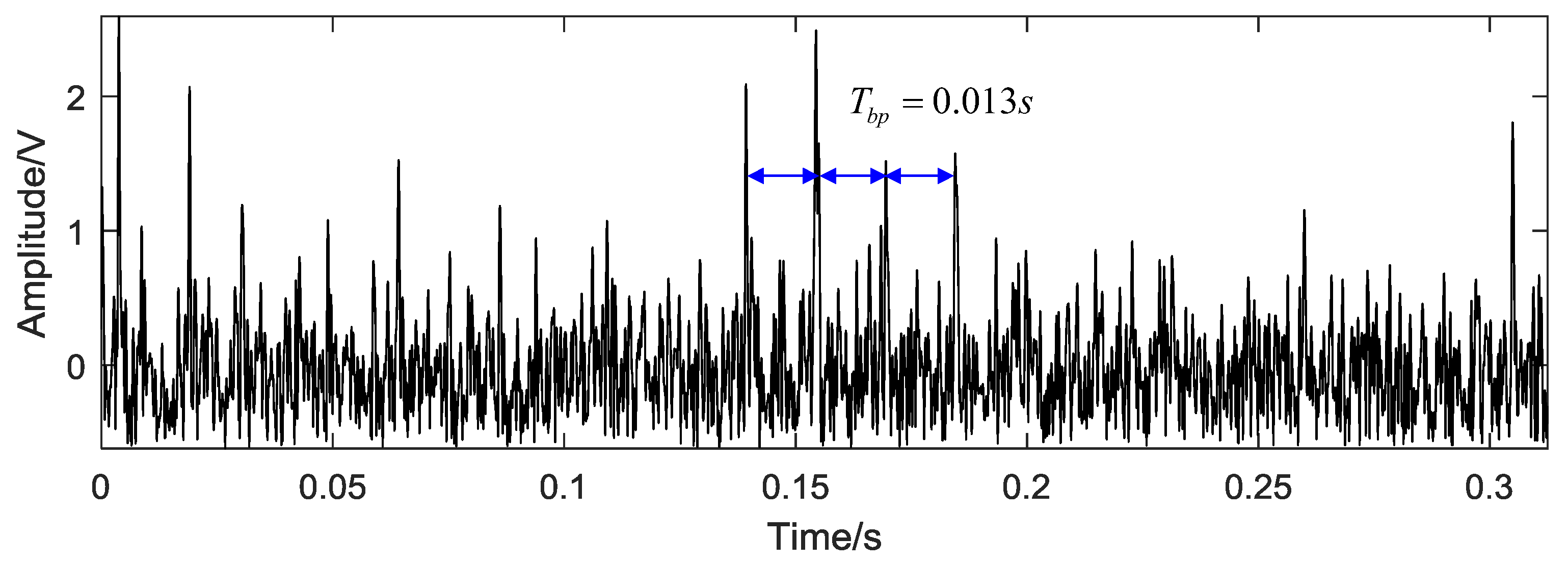
5.2. Case 1: Bearing Outer Race Fault
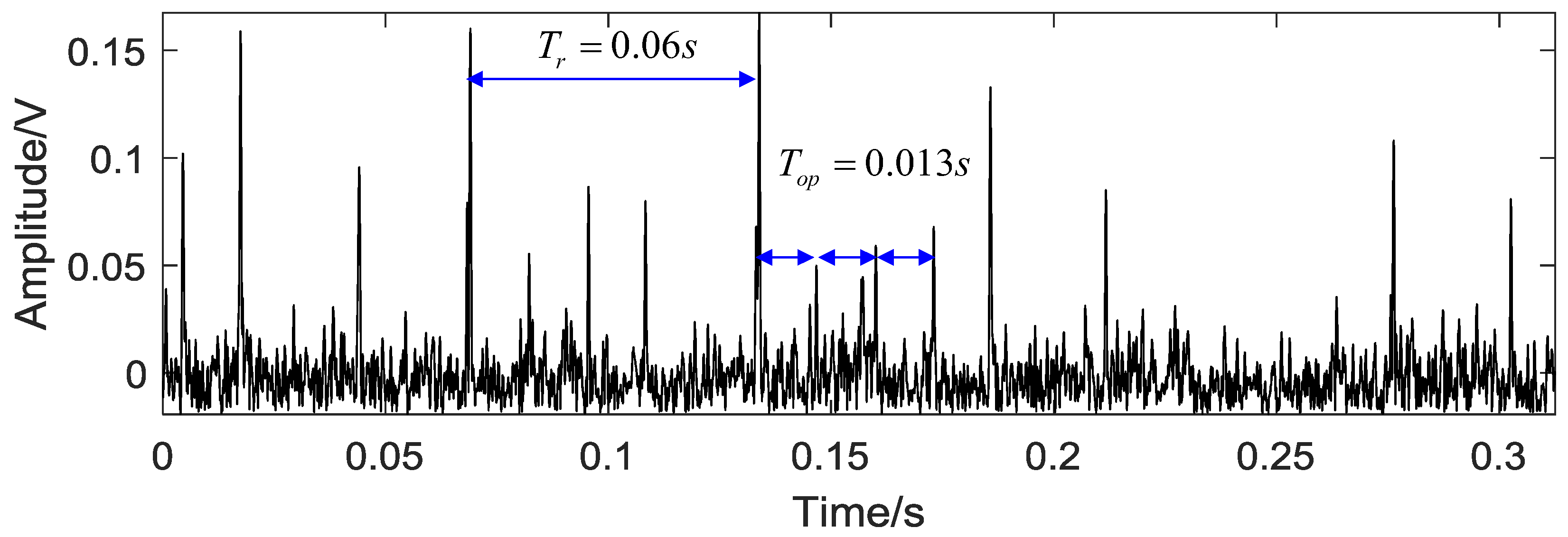
5.3. Case 2: Bearing Rolling Element Fault
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar]
- He, W.P.; Ding, Y.; Zi, Y.Y.; Selesnick, I.W. Sparsity-based algorithm for detecting faults in rotating machines. Mech. Syst. Signal Process. 2016, 72–73, 46–64. [Google Scholar]
- Dong, G.; Chen, J.; Zhao, F. A frequency-shifted bispectrum for rolling element bearing diagnosis. J. Sound Vib. 2015, 339, 396–418. [Google Scholar]
- Žvokelj, M.; Zupan, S.; Prebil, I. Non-linear multivariate and multiscale monitoring and signal denoising strategy using Kernel Principal Component Analysis combined with Ensemble Empirical Mode Decomposition method. Mech. Syst. Signal Process. 2011, 25, 2631–2653. [Google Scholar]
- Guo, W.; Tse, P.W. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals. J. Sound Vib. 2013, 332, 423–441. [Google Scholar]
- Wang, H.; Gao, J.; Jiang, Z.; Zhang, J. Rotating Machinery Fault Diagnosis Based on EEMD Time-Frequency Energy and SOM Neural Network. Arab. J. Sci. Eng. 2014, 39, 5207–5217. [Google Scholar]
- Wang, J.; He, Q. Wavelet Packet Envelope Manifold for Fault Diagnosis of Rolling Element Bearings. IEEE Trans. Instrum. Meas. 2016, 65, 2515–2526. [Google Scholar]
- Rauber, T.W.; de Assis Boldt, F.; Varejao, F.M. Heterogeneous Feature Models and Feature Selection Applied to Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 637–646. [Google Scholar]
- Pincus, S.M. Approximate Entropy as a Measure of System Complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [PubMed]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery Health Prognosis for Electric Vehicles Using Sample Entropy and Sparse Bayesian Predictive Modeling. IEEE Trans. Ind. Electron. 2016, 63, 2645–2656. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 21906. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef] [Green Version]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Li, Y.B.; Xu, M.Q.; Wei, Y.; Huang, W.H. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abasolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Bio.-Med. Eng. 2017, 64, 2872–2879. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Proc. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Zhu, W.; Yang, J. Applying Improved Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG. Appl. Sci. 2017, 7, 92. [Google Scholar] [CrossRef]
- Guido, R.C. A tutorial review on entropy-based handcrafted feature extraction for information fusion. Inf. Fusion 2018, 41, 161–175. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Fernandez, A.; Escudero, J. Dispersion entropy for the analysis of resting-state MEG regularity in Alzheimer’s disease. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 6417–6420. [Google Scholar]
- Zhang, H.; Liu, X. Analysis of Parameter Selection for Permutation Entropy in Logistic Chaotic Series. In Proceedings of the 2018 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Xiamen, China, 25–26 January 2018; pp. 398–402. [Google Scholar]
- Ding, X.; He, Q.; Luo, N. A fusion feature and its improvement based on locality preserving projections for rolling element bearing fault classification. J. Sound Vib. 2015, 335, 367–383. [Google Scholar] [CrossRef]
- Ji, Z.; Pang, Y.W.; He, Y.Q.; Zhang, H.F. Semi-supervised LPP algorithms for learning-to-rank-based visual search reranking. Inf. Sci. 2015, 302, 83–93. [Google Scholar] [CrossRef]
- Cong, F.Y.; Zhong, W.; Tong, S.G.; Tang, N.; Chen, J. Research of singular value decomposition based on slip matrix for rolling bearing fault diagnosis. J. Sound Vib. 2015, 344, 447–463. [Google Scholar] [CrossRef]
- Cong, F.; Chen, J.; Dong, G.; Zhao, F. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2013, 34, 218–230. [Google Scholar] [CrossRef]
- Aggarwal, A.; Kumar, M.; Rawat, T.K.; Upadhyay, D.K. Optimal Design of 2D FIR Filters with Quadrantally Symmetric Properties Using Fractional Derivative Constraints. Circ. Syst. Signal Process. 2016, 35, 2213–2257. [Google Scholar] [CrossRef]
- Koshita, S.; Onizawa, N.; Abe, M.; Hanyu, T.; Kawamata, M. Realization of FIR Digital Filters Based on Stochastic/Binary Hybrid Computation. In Proceedings of the 2016 IEEE 46th International Symposium on Multiple-Valued Logic (ISMVL), Sapporo, Japan, 18–20 May 2016; pp. 223–228. [Google Scholar]
- Liu, Y.; Parhi, K.K. Architectures for Recursive Digital Filters Using Stochastic Computing. IEEE Trans. Signal Process. 2016, 64, 3705–3718. [Google Scholar] [CrossRef]
- Zhang, S.B.; Lu, S.L.; He, Q.B.; Kong, F.R. Time-varying singular value decomposition for periodic transient identification in bearing fault diagnosis. J. Sound Vib. 2016, 379, 213–231. [Google Scholar] [CrossRef]










| Type | Pitch Diameter/D (mm) | Ball Diameter/d (mm) | Number of Roller (Z) | Contact Angle/ |
|---|---|---|---|---|
| 32,207 | 53.31 | 9.52 | 17 | 14.04 |
| 30,304 | 36.35 | 8.26 | 13 | 11.3 |
| Type | |||||
|---|---|---|---|---|---|
| value | 6 | 2 | 6 | 1 | 128 |
| Raw Signal | Proposed Method | EEMD | WP | Fast Kurtogram | |
|---|---|---|---|---|---|
| SNR ()/dB | −24.1 | −15.9 | −21.3 | −22.5 | −17.4 |
| Kurtosis | 3.54 | 14.1 | 4.7 | 4.1 | 4.8 |
| Raw Signal | Proposed Method | EEMD | WP | Fast Kurtogram | |
|---|---|---|---|---|---|
| SNR()/dB | −25.7 | −15.4 | −22.6 | −19.6 | −17.7 |
| Kurtosis | 3.1 | 4.5 | 3.3 | 4.1 | 3.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Tong, S.; Cong, F.; Xu, J. Research of Feature Extraction Method Based on Sparse Reconstruction and Multiscale Dispersion Entropy. Appl. Sci. 2018, 8, 888. https://doi.org/10.3390/app8060888
Zhang Y, Tong S, Cong F, Xu J. Research of Feature Extraction Method Based on Sparse Reconstruction and Multiscale Dispersion Entropy. Applied Sciences. 2018; 8(6):888. https://doi.org/10.3390/app8060888
Chicago/Turabian StyleZhang, Yidong, Shuiguang Tong, Feiyun Cong, and Jian Xu. 2018. "Research of Feature Extraction Method Based on Sparse Reconstruction and Multiscale Dispersion Entropy" Applied Sciences 8, no. 6: 888. https://doi.org/10.3390/app8060888





