A Mechanical Musculo-Skeletal System for a Human-Shaped Robot Arm
Abstract
:1. Introduction
2. Actuator with Non-Linear Elasticity System
2.1. Structure and Design of l-ANLES


2.2. Structure and Design of r-ANLES
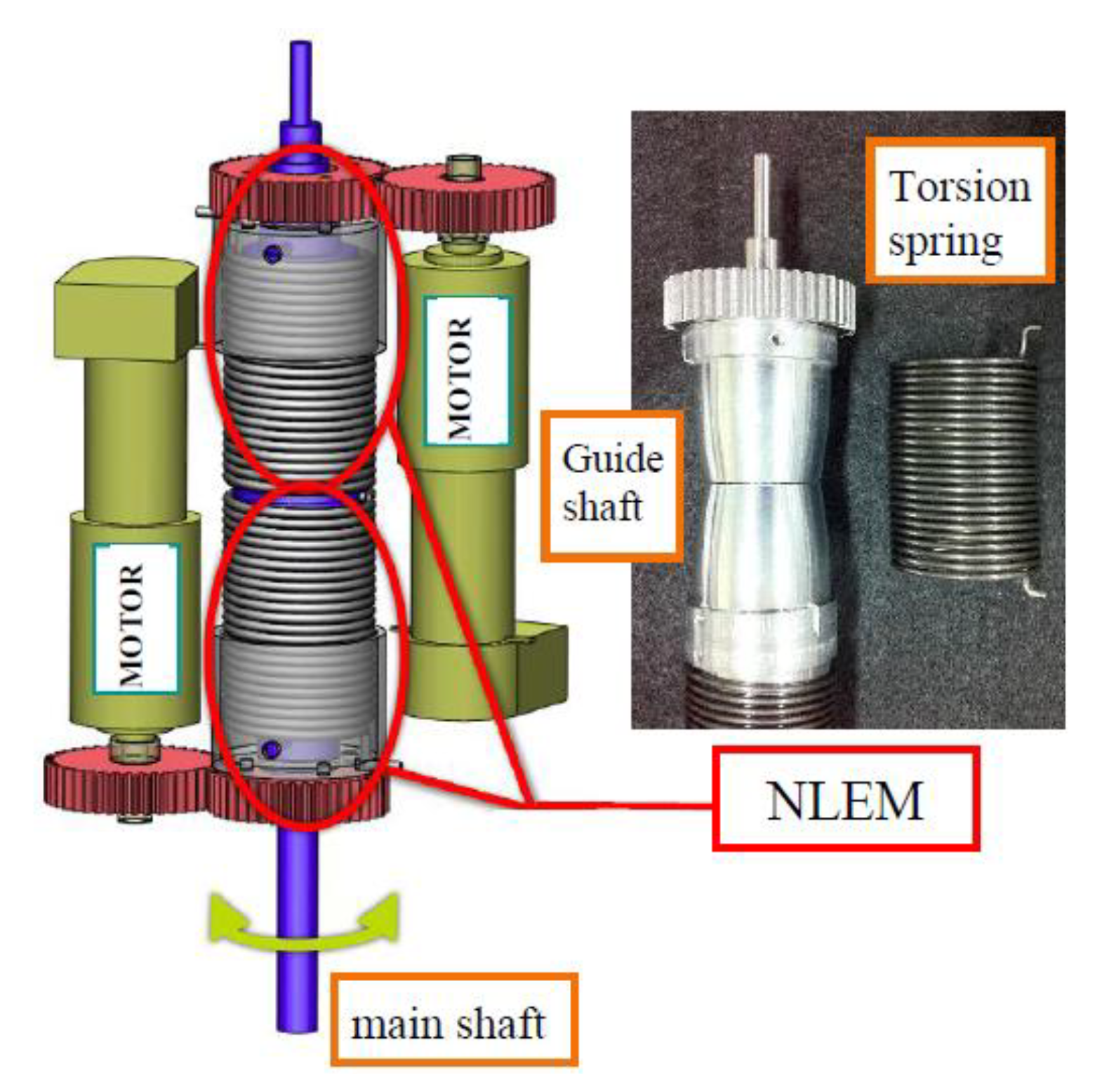
2.3. Design of Non-Linear Elasticity


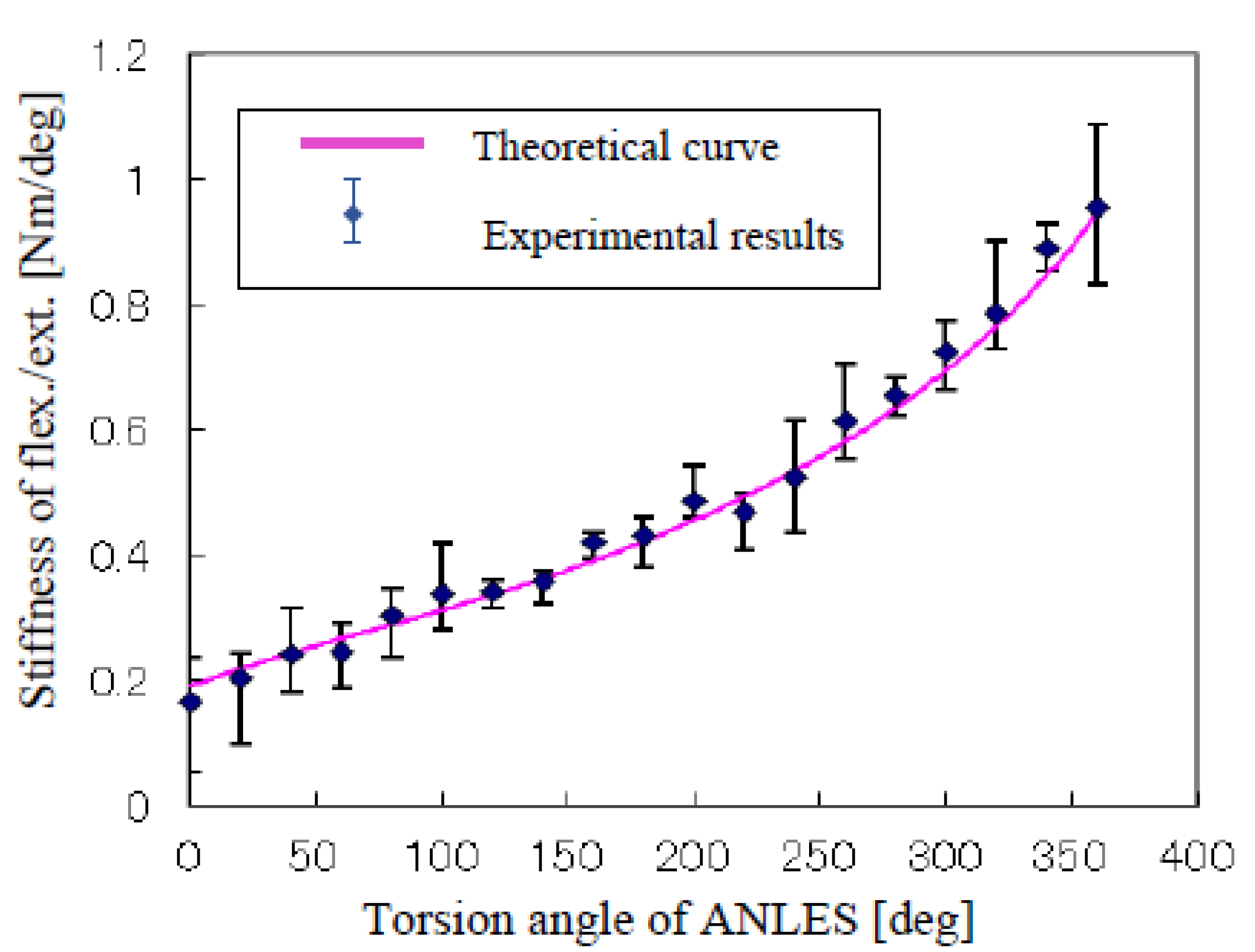
2.4. Stiffness of Rotary Joint
A. The case of l-ANLES

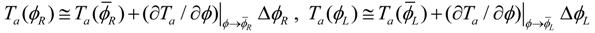
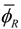 and
and 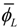 are torsion angles of the l-ANLESes provided by the individual motors and ∆ϕR = ϕR −
are torsion angles of the l-ANLESes provided by the individual motors and ∆ϕR = ϕR − 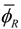 , ∆ϕL = ϕL −
, ∆ϕL = ϕL − 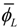
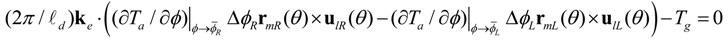
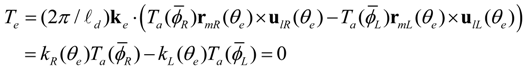
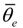 , kR(
, kR( 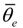 ) and kL(
) and kL( 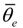 ) become constants. Therefore,
) become constants. Therefore,
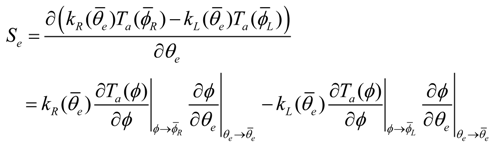
 to always have opposite signs in a counteractive configuration, as shown in Figure 6, we can calculate the absolute value of Se as,
to always have opposite signs in a counteractive configuration, as shown in Figure 6, we can calculate the absolute value of Se as,
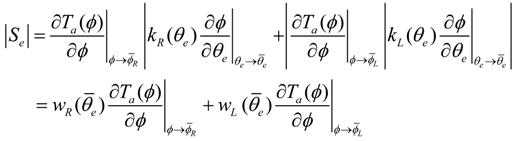
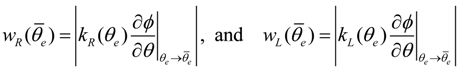 are positive constant values under a constant joint angle
are positive constant values under a constant joint angle 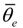 Equation (9) suggests that the joint stiffness can be adjusted by setting
Equation (9) suggests that the joint stiffness can be adjusted by setting 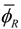 and
and 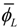 under holding Equation (6), and that the non-linearity of Ta(ϕ) is indispensable for the joint stiffness to be varied, because if Ta(ϕ) is linear with respect to ϕ, ∂Ta(ϕ)/∂ϕ takes a constant value, which means the stiffness Se is also constant regardless of ϕ.
under holding Equation (6), and that the non-linearity of Ta(ϕ) is indispensable for the joint stiffness to be varied, because if Ta(ϕ) is linear with respect to ϕ, ∂Ta(ϕ)/∂ϕ takes a constant value, which means the stiffness Se is also constant regardless of ϕ. 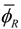 and
and 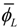 will be subject to gravitational effects as described above, which might narrow the adjustable range of stiffness. A weight compensator introduced in the upper arm, described in the following section, will alleviate this problem.
will be subject to gravitational effects as described above, which might narrow the adjustable range of stiffness. A weight compensator introduced in the upper arm, described in the following section, will alleviate this problem.B. The case of r-ANLES
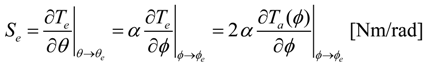

3. Two-DOF Upper Arm
| axis | Flexion/Extension | Lateral/Medial Rotation | ||
|---|---|---|---|---|
| Actuator ( Motor ) | Maxon RE25 × 2 Blushless DC 20 W Stall torque 250 mNm | Faulhaber 3257 × 2 Blushless DC 80 W Stall torque 540 mNm | ||
| Reduction gear ratio | 132 | 134 | ||
| Sensor (Rotary Encoder) | Maxon HEDS 5540 × 2 | Faulhaber IE2-16 × 2 | ||
| spring | modulus of longitudinal elasticity | 1.86 × 105 [N/mm2] | ||
| Wire diameter | 1.9 mm | 4.0 mm | ||
| Coil diameter | 32.7 mm | 36 mm | ||
| Number of coiling | 24 | 15 | ||
| pitch | 2.0 mm | 4.2 mm | ||
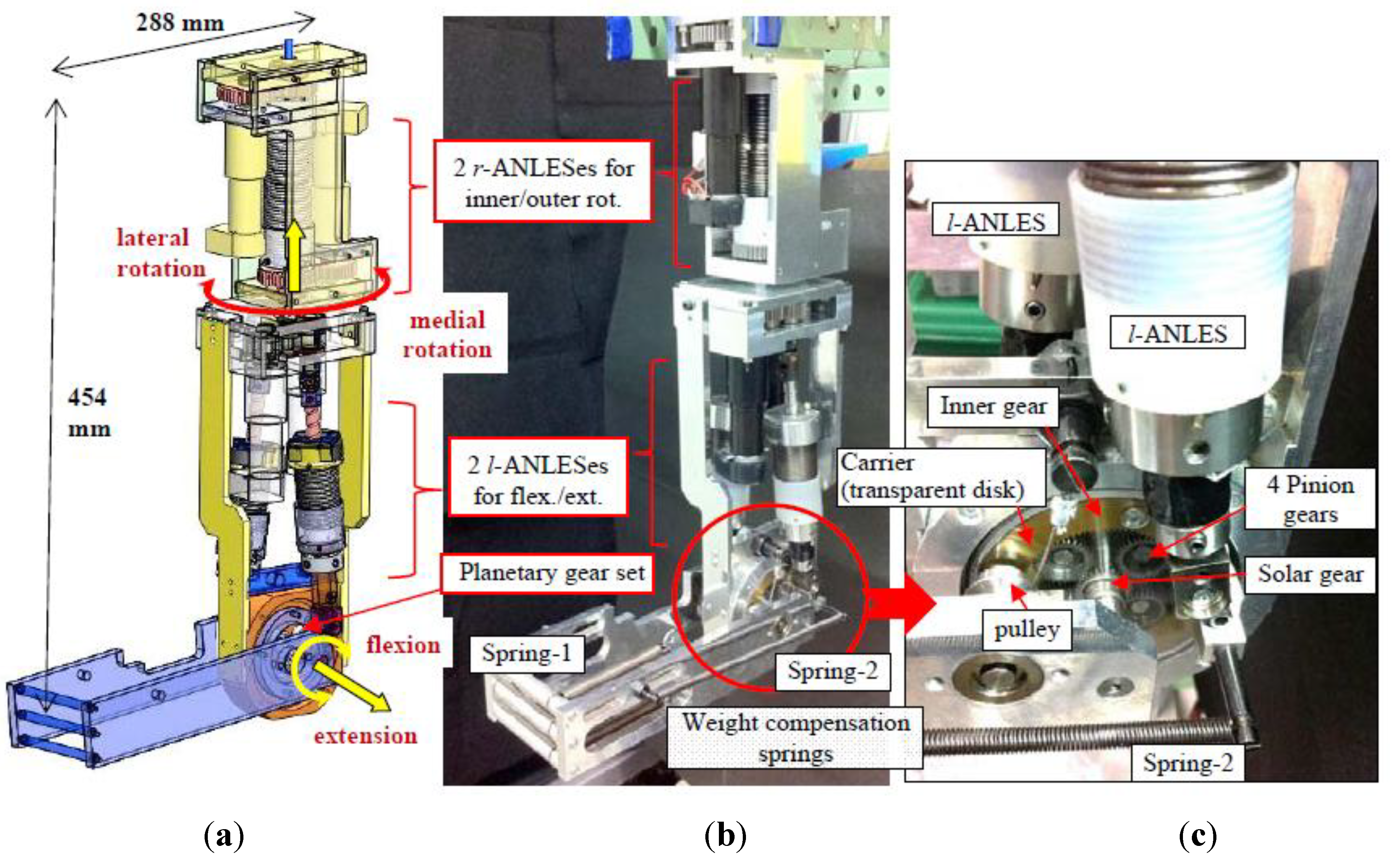
3.1. Elbow Joint
3.2. Lateral/Medial Rotation of the Upper Arm
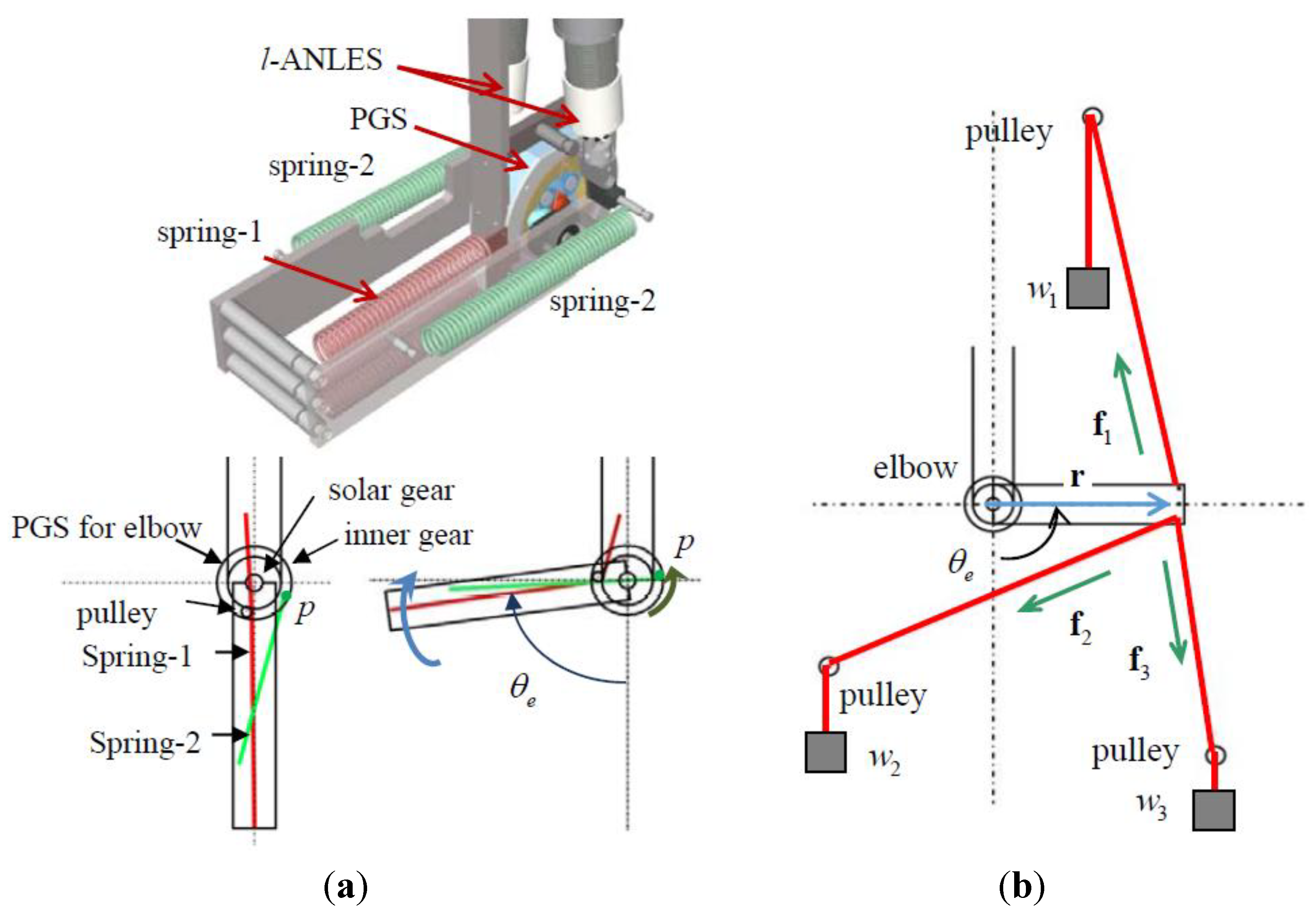
3.3 Weight Compensator
- (1)
- The weights w1, w2 and w3 are adjusted so that the elbow joint takes a specified joint angle θe that is measured by the optical encoder attached to the rotary axis of the elbow joint.
- (2)
- Then, the torque loaded around the elbow joint is measured bywhere, r = [rx ry]T is a vector from the elbow joint to the distal end of the forearm, and fi = [fix fiy]T, (i = 1,2,3) is force vectors generated by the weights.τe = rx(f1y + f2y +f3y) − ry(f1x + f2x + f3x)
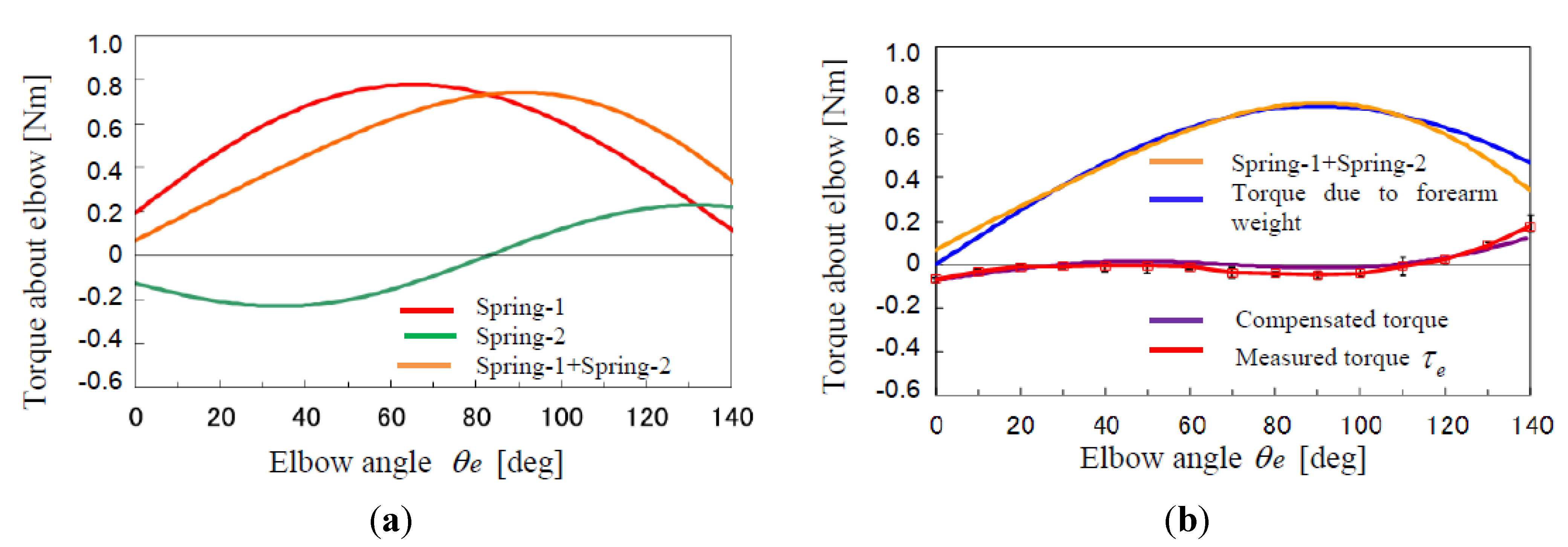
3.4. Stiffness Control of the Flexion/Extension Axis and the Lateral/Medial Rotation Axis
- (1)
- The non-linear elasticity of the ANLES obeys the one shown in Figure 5.
- (2)
- Two motors of the l-ANLESes are rotated so that the elbow angle reaches 90° and two motors of the r-ANLESes are rotated so that the lateral/medial rotation angle reaches 0 deg. The motors of the l-ANLESes and r-ANLESes are controlled by a normal PID controller.
- (3)
- In the above state, the torsion angles of both l-ANLESes and r-ANLESes are almost zero because the pre-torsion of ANLESes to sustain the forearm weight is not needed due to the weight compensator.
- (4)
- The motors of the l-ANLESes or the r-ANLESes are rotated by the same angle to give the torsion springs of the l-ANLESes or the r-ANLESes the same amount of torsion angle in order to increase the stiffness of the elbow or the lateral/medial joint.
- (5)
- A weight W was loaded at the forearm tip downward in the case of the elbow joint, or horizontally in the case of the lateral/medial rotation axis. The weight was adjusted to attain a 5-degree rotation of the joint that is measured by the optical encoder and displayed on the computer screen in each setting of the torsion angle of ANLESes. Then, the stiffness is obtained as: (Nm/rad) with the forearm length l.

4. Conclusions
- (1)
- The magnitude and the adjustable range of joint stiffness can be precisely designed by designing the shape of the guide-shaft.
- (2)
- No particular kind of non-linear elastic elements are necessary to construct the ANLES.
Acknowledgments
Conflicts of Interest
Appendix A
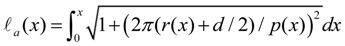
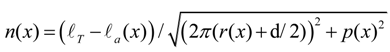
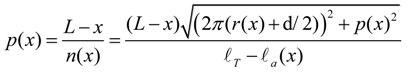
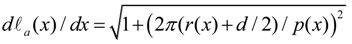
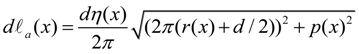
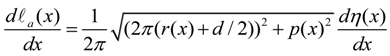
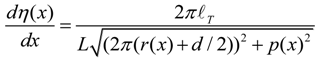
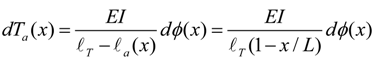
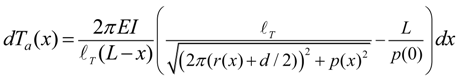
References
- Shadmehe, R.; Arbib, M.A. A mathematical analysis of the force-stiffness characteristics of muscles in control of a single joint system. Biol. Cybern. 1992, 66, 463–477. [Google Scholar] [CrossRef]
- Matthews, P.B.C. The dependence of tension upon extension in the stretch reflex of the soleus muscle of the decerebrated cat. J. Physiol. 1959, 147, 521–546. [Google Scholar]
- Fel’dman, A.G. Functional tuning of the neurons system with control of movement or maintenance of a steady posture. Biofizika 1966, 11, 498–508. [Google Scholar]
- Hoffer, J.A.; Andrearsen, S. Regulation of soleus muscle stiffness in premammiliary cats. J. Neurophysiol. 1981, 45, 267–285. [Google Scholar]
- Dolan, J.M.; Friedman, M.B.; Nagurka, M.L. Dynamic and Loaded Impedance of Human Arm Posture. IEEE Trans. Syst. Man Cybern. 1993, 23, 698–709. [Google Scholar] [CrossRef]
- Mussa-Ivaldi, N.H.; Bizzi, E. Neural, Mechanical, and Geometrical Factors Subserving Arm Posture in Humans. J. Neurosci. 1985, 5, 2732–2743. [Google Scholar]
- Jocobsen, S.C.; Wood, J.E.; Knutti, D.F.; Biggers, K.B. The UTAH/M.I.T. Dexterous Hand: Work in Progress. Int. J. Rob. Res. 1984, 3, 21–51. [Google Scholar] [CrossRef]
- Jacobsen, S.C.; Ko, H.; Inversen, E.K.; Davis, C.C. Antagonistic Control of a Tendon Driven Manipulator. In Proceedings of the 1989 IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989.
- Laurin-Kovitz, K.F.; Colgate, J.E.; Carnes, S.D.R. Design of Components for Programmable Passive Impedance. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991.
- Yi, B.J.; Freeman, R.A. Geometric Characteristics of Antagonistic Stiffness In Redundantly Actuated Mechanisms. In Proceedings of the 1993 IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993.
- Kobayasi, H.; Hyoudou, K.; Ogane, D. On Tendon-Driven Robotics Mechanisms with Redundant Tendons. Int. J. Rob. Res. 1998, 17, 561–571. [Google Scholar] [CrossRef]
- Lee, Y.T.; Choi, H.R.; Chung, W.K.; Youm, Y. Stiffness Control of a Coupled Tendon-Driven Robot Hand. IEEE Contr. Syst. Mag. 1994, 14, 10–19. [Google Scholar]
- Yi, B.J.; Freeman, R.A. Synthesis of Actively Adjustable Springs by Antagonistic Redundant Actuation. J. Dyn. Syst. Meas. Contr. 1992, 114, 454–461. [Google Scholar] [CrossRef]
- Chen, S.F.; Kao, I. Conservative Congruence Transformation for Joint and Cartesian Stiffness Matrices of Robotic Hands and Fingers. Int. J. Rob. Res. 2000, 19, 835–847. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P.M. Modeling and Control of McKibben Artificial Muscle Robot Actuators. IEEE Contr. Syst. Mag. 2000, 20, 15–28. [Google Scholar] [CrossRef]
- Tondu, B.; Ippolito, S.; Guiochet, J.; Daidie, A. A Seven-degrees-of-Freedom Robot-arm Driven by Pneumatic Artificial Muscles for Humanoid Robots. Int. J. Robot. Res. 2005, 24, 257–274. [Google Scholar] [CrossRef]
- Verrelst, B.; Van Ham, R.; Vanderborght, B.; Daerden, F.; Lefeber, D.; Vermeulen, J. The Pneumatic Biped “Lucy” Actuated with Pleated Pneumatic Artificial Muscles. Autonom. Rob. 2005, 18, 201–213. [Google Scholar] [CrossRef]
- Koganezawa, K.; Watanabe, Y.; Shimizu, N. Antagonistic Muscle-Like Actuator and Its Application to Multi-DOF Forearm Prosthesis. Adv. Rob. 1999, 12, 771–789. [Google Scholar] [CrossRef]
- Migliore, S.A.; Brown, E.A.; DeWeerth, S.P. Biologically Inspired Joint Stiffness Control. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 4508–4517.
- Tonietii, G.; Schiavi, R.; Bicchi, A. Design and Control of a Variable Stiffness Actuator for Safe and Fast Physical Human/Robot Interaction. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 526–531.
- Schiavi, R.; Grioli, G.; Sen, S.; Bicchi, A. VSA-II: A Novel Prototype of Variable Stiffness Actuator for Safe and Performing Robots Interacting with Humans. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2171–2176.
- Wolf, S.; Hirzinger, G. A New Variable Stiffness Design: Matching Requirements of the Next Robot Generation. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May, 2008; pp. 1741–1746.
- Haddadin, S.; Albu-Schaffer, A.; Hirzinger, G. The Role of the Robot Mass and Velocity in Physical Human-Robot Interaction-Part 2: Constrained Blunt Impacts. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA2008), Pasadena, CA, USA, 19–23 May 2008; p. 1339.
- Ham, R.; Sugar, T.G.; Vanderborght, B.; Hollander, K.W.; Lefeber, D. Compliant Actuator Design. IEEE Rob. Autom. Mag. 2009, 16, 81–94. [Google Scholar] [CrossRef]
- Ham, V.; Vanderborght, B.; Van Damme, M.; Verrelst, B.; Lefeber, D. MACCEPA, the Mechanically Adjustable Compliance and Controllable Equilibrium Position Actuator: Design and Implementation in a Biped Robot. Rob. Autonom. Syst. 2007, 55, 761–768. [Google Scholar] [CrossRef]
- Schiavi, R.; Grioli, G.; Sen, S.; Bicchi, A. VSA-II: A Novel Prototype of Variable Stiffness Actuator for Safe and Performing Robots Interacting with Humans. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2171–2176.
- Wolf, S.; Hirzinger, G. A New Variable Stiffness Design: Matching Requirements of the Next Robot Generation. Proceedings of the 2008 IEEE International Conference on Robotics and Automation 1741–1746.
- Byeong-Sang, K.; Song, J. Hybrid Dual Actuator Unit: A Design of a Variable Stiffness Actuator Based on an Adjustable Moment Arm Mechanism. Proceedings of the 2010 IEEE International Conference on Robotics and Automation 1655–1660.
- Vanderborght, B.; Albu-Schaeffer, A.; Bicchi, A.; Caldwell, D.; Tsagarakis, N.; Van Damme, M.; Lefeber, D.; Van Ham, R.; Burdet, E.; Carloni, R.; et al. Variable Impedance Actuators: A Review. Rob. Autonom. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Morita, T.; Sugano, S. Design and Development of a New Robot Joint Using a Mechanical Impedance Adjuster. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 2469–2475.
- Van Ham, R.; Van Damme, M.; Verrelst, B.; Vanderbought, B.; Lefeber, D. MACCEPA, The Mechanically Adjustable Compliance and Controllable Equilibrium Position Actuator: A 3DOF Joint with Two Independent Compliances. Int. Appl. Mech. 2007, 43, 467–474. [Google Scholar] [CrossRef]
- Koganezawa, K. Mechanical Stiffness Control for Antagonistically Driven Joints. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems (IROS 2005), Edmonton, Canada, 2–6 August 2005; pp. 2512–2519.
- Koganezawa, K.; Yamashita, H. Stiffness Control of Multi-DOF Joint. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2009), St.Louis, USA, 11–15 October 2009; pp. 363–370.
- Koganezawa, K.; Takami, G.; Watanabe, M. Antagonistic Control of Multi-DOF Joint. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2012), Vilamoura, Portugal, 7–12, October 2012; pp. 2895–2900.
- Watkins, J. Structure and Function of the Musculoskeletal System; Human Kinetics: Champaign, IL, USA, 1999; p. 186. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Koganezawa, K. A Mechanical Musculo-Skeletal System for a Human-Shaped Robot Arm. Actuators 2014, 3, 124-141. https://doi.org/10.3390/act3020124
Koganezawa K. A Mechanical Musculo-Skeletal System for a Human-Shaped Robot Arm. Actuators. 2014; 3(2):124-141. https://doi.org/10.3390/act3020124
Chicago/Turabian StyleKoganezawa, Koichi. 2014. "A Mechanical Musculo-Skeletal System for a Human-Shaped Robot Arm" Actuators 3, no. 2: 124-141. https://doi.org/10.3390/act3020124





