Reliability Analysis and Optimization Method of a Mechanical System Based on the Response Surface Method and Sensitivity Analysis Method
Abstract
:1. Introduction
2. Basic Theories
2.1. Reliability State Function
2.2. First-Order Second-Moment (FOSM) Method
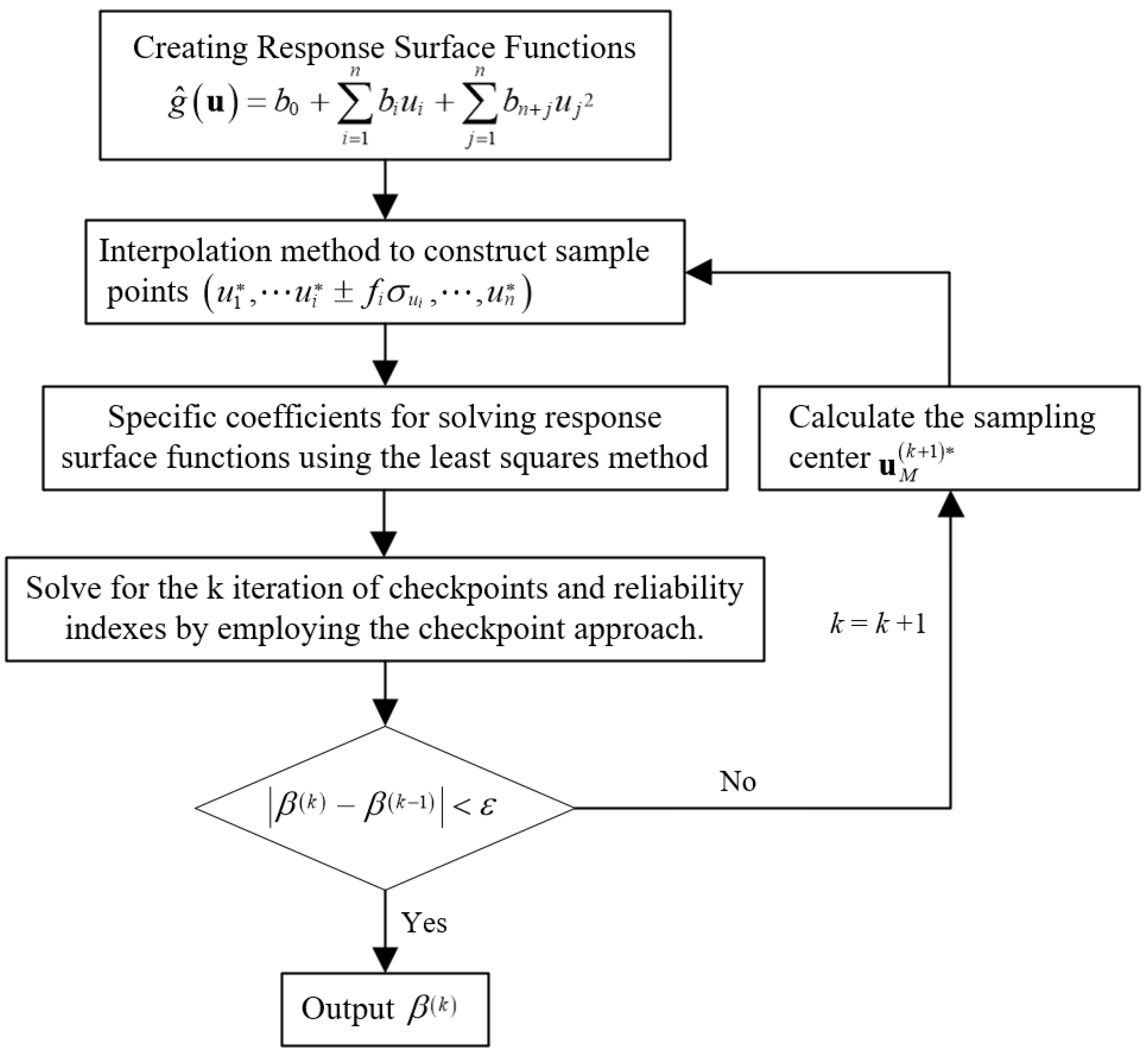
2.3. Response Surface Method (RSM)
2.4. Sensitivity Analysis of Errors
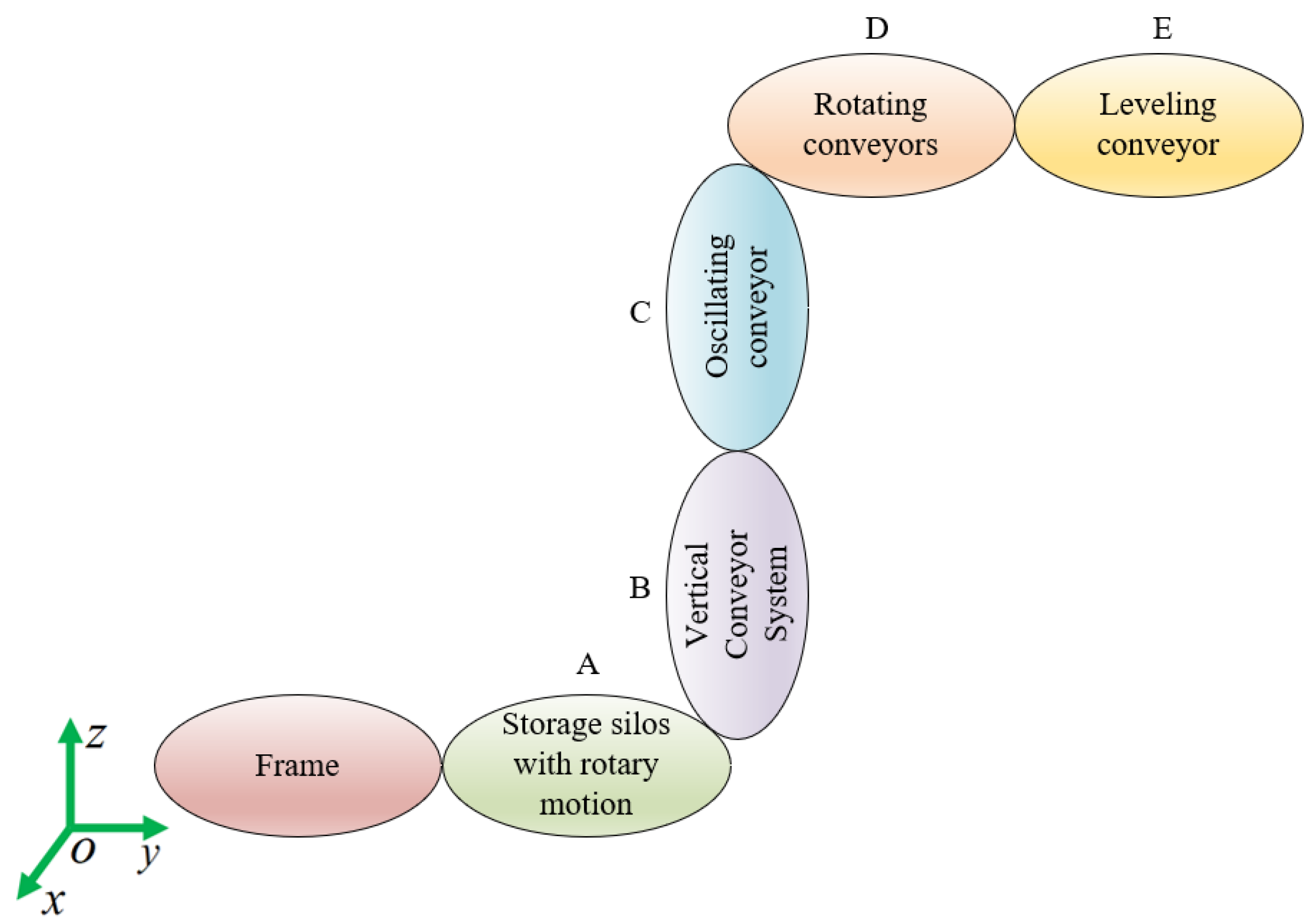
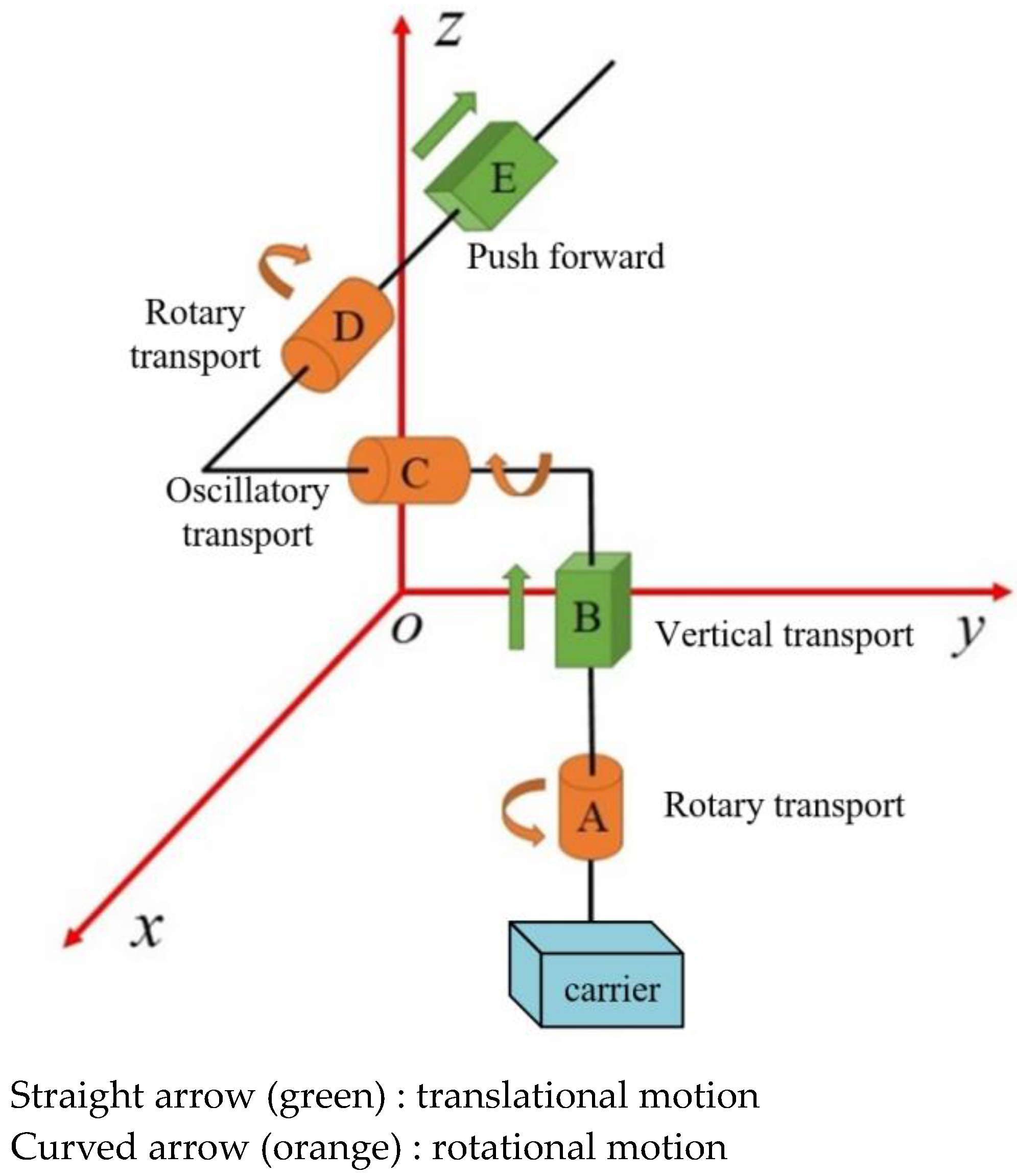
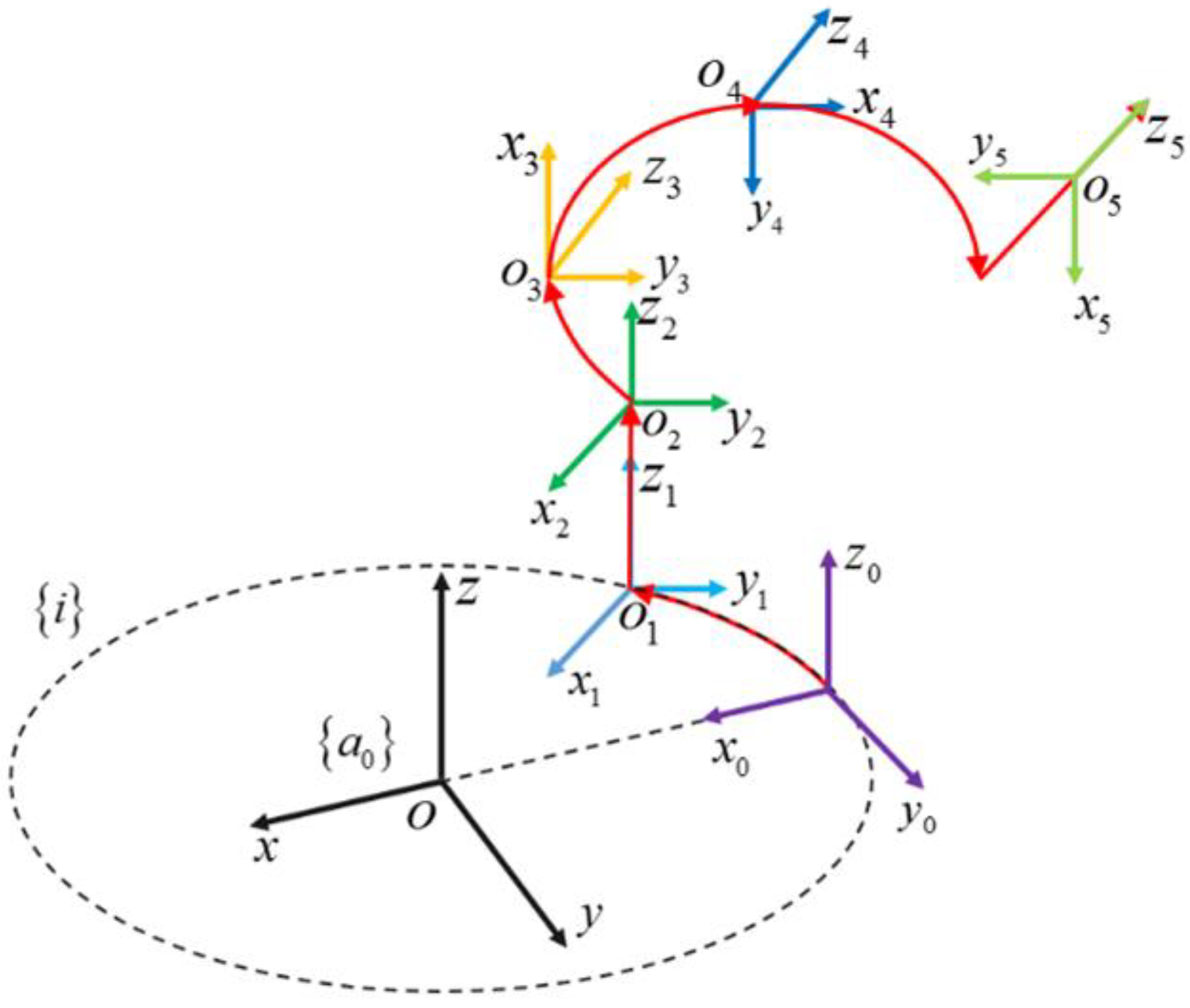
3. Random Errors of Transport System
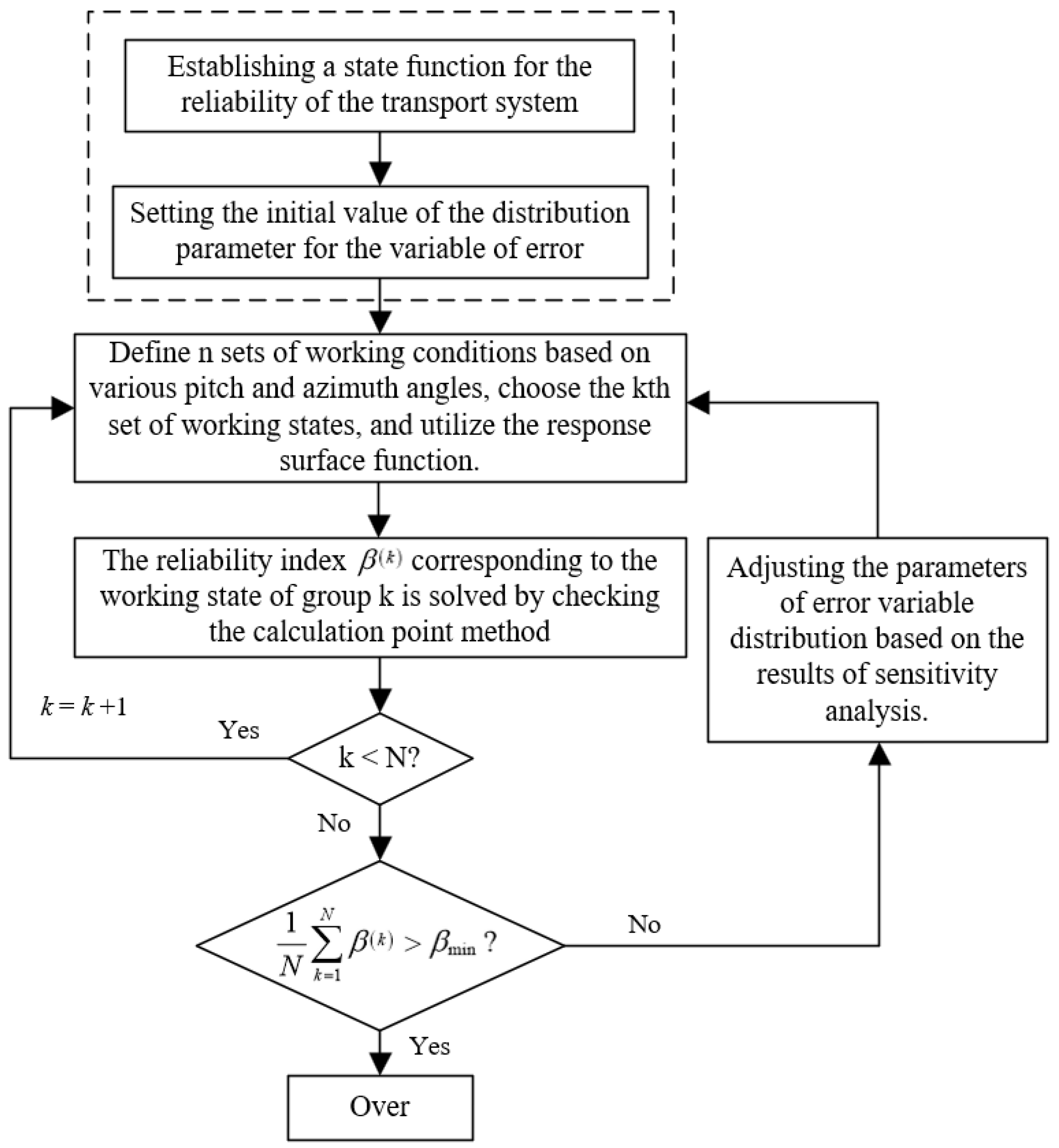
4. Reliability Analysis and Optimization of Transport Systems
4.1. Reliability Assessment of Transport Systems under Shock Effects
4.2. Reliability Optimization of a Transport System Based on Sensitivity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- An, X.; Gosling, P.D.; Zhou, X. Analytical Structural Reliability Analysis of a Suspended Cable. Struct. Saf. 2016, 58, 20–30. [Google Scholar] [CrossRef]
- Lee, I.; Noh, Y.; Yoo, D. A Novel Second-Order Reliability Method (SORM) Using Noncentral or Generalized Chi-Squared Distributions. J. Mech. Des. 2012, 134, 100912. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, J.; Peng, W.; Yang, L. Hierarchical Response Surface Modeling and Reliability Analysis of Complex Mechanical System Based on Composite Function. Acta Armamentarii 2018, 39, 590. [Google Scholar] [CrossRef]
- Tang, J. Mechanical System Reliability Analysis Using a Combination of Graph Theory and Boolean Function. Reliab. Eng. Syst. Saf. 2001, 72, 21–30. [Google Scholar] [CrossRef]
- Li, X.-Y.; Li, X.; Feng, J.; Li, C.; Xiong, X.; Huang, H.-Z. Reliability Analysis and Optimization of Multi-Phased Spaceflight with Backup Missions and Mixed Redundancy Strategy. Reliab. Eng. Syst. Saf. 2023, 237, 109373. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An Active Learning Reliability Method Combining Kriging and Monte Carlo Simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M.; Relun, N. A Combined Importance Sampling and Kriging Reliability Method for Small Failure Probabilities with Time-Demanding Numerical Models. Reliab. Eng. Syst. Saf. 2013, 111, 232–240. [Google Scholar] [CrossRef]
- Depina, I.; Le, T.M.H.; Fenton, G.; Eiksund, G. Reliability Analysis with Metamodel Line Sampling. Struct. Saf. 2016, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, B.; Yang, W. Modular Approach to Kinematic Reliability Analysis of Industrial Robots. Reliab. Eng. Syst. Saf. 2023, 229, 108841. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Qian, L.; Chen, G.; Zhou, S. Time-Dependent Kinematic Reliability Analysis of Gear Mechanism Based on Sequential Decoupling Strategy and Saddle-Point Approximation. Reliab. Eng. Syst. Saf. 2022, 220, 108292. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, S.; Wu, J.; Wang, F.; Han, X. Kinematic Trajectory Accuracy Reliability Analysis for Industrial Robots Considering Intercorrelations among Multi-Point Positioning Errors. Reliab. Eng. Syst. Saf. 2023, 229, 108808. [Google Scholar] [CrossRef]
- Huang, P.; Huang, H.-Z.; Li, Y.-F.; Li, H. Positioning Accuracy Reliability Analysis of Industrial Robots Based on Differential Kinematics and Saddlepoint Approximation. Mech. Mach. Theory 2021, 162, 104367. [Google Scholar] [CrossRef]
- Zhuang, X. Time-Dependent Kinematic Reliability of a Dual-Axis Driving Mechanism for Satellite Antenna Considering Non-Uniform Planar Revolute Joint Clearance. Acta Astronaut. 2022, 197, 91–106. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Yu, D.; Hong, J.; Chen, F. An Enhanced Method of Resizing Support Links for a Planar Closed-Loop Overconstrained Deployable Structure Considering Kinematic Reliability and Surface Accuracy. Aerosp. Sci. Technol. 2020, 104, 105988. [Google Scholar] [CrossRef]
- Weng, Y.-Y.; Zhang, X.-Y.; Lu, Z.-H.; Zhao, Y.-G. A Conditional Extreme Value Distribution Method for Dynamic Reliability Analysis of Stochastic Structures. Struct. Saf. 2024, 106, 102398. [Google Scholar] [CrossRef]
- Lampart, M.; Zapoměl, J. Chaos Identification of a Colliding Constrained Body on a Moving Belt. Nonlinear Dynam. 2021, 104, 2723–2732. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A Comprehensive Survey of the Analytical, Numerical and Experimental Methodologies for Dynamics of Multibody Mechanical Systems with Clearance or Imperfect Joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Villecco, F. On the Evaluation of Errors in the Virtual Design of Mechanical Systems. Machines 2018, 6, 36. [Google Scholar] [CrossRef]
- Sun, Y.-Z.; Fan, W.-X. Computer simulation of the working process of chain thrust mechanism. China Mech. Eng. 1998, 9, 18–20. [Google Scholar]
- Liu, X.-L. Hybrid Reliability Analysis Method Based on Probabilistic and Non-Probabilistic Convex Model; Hunan University: Changsha, China, 2012. [Google Scholar]
- Zhang, Y.-M. Connotation and Development of Mechanical Reliability-based Design. J. Mech. Eng. 2010, 46, 167–188. [Google Scholar] [CrossRef]
- Dong, C. Modern Structural System Reliability Theory and Its Application; Science Press: Beijing, China, 2001. [Google Scholar]
- Khuri, A.I.; Mukhopadhyay, S. Response Surface Methodology. WIREs Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, Y.; Zhao, X.; Zhang, Y. Application of Response Surface Method Based on New Strategy in Structural Reliability Analysis. Structures 2023, 57, 105202. [Google Scholar] [CrossRef]
- Chen, L.-T. Study on the Computational Methods of the Structural Acoustic Sensitivity. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2013. Available online: https://kns.cnki.net/kcms2/article/abstract?v=0kbmF0AymBCizK60RwSW-vUwvDvb8KUvGP_RBQRb7o3A4Q6HqrM9TKbzIU6SsQa1iaNkmJcVcRz0BpeYsM7KL35T6n4WclY9VFGPtKfNcm_fZC1EUu3EX1BXdeNq5hS7&uniplatform=NZKPT&language=CHS (accessed on 8 December 2023).
- Wei, P.-F. Research on the Reliability and Sensitivity Analysis of Structural Systems. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2015. Available online: https://kns.cnki.net/kcms2/article/abstract?v=0kbmF0AymBDiz1rW-HjAC52AOASCQN15fmdC2g5LYhNkH-X5DKVtVcXi7UfV-UX_-oIx1hZt_zZdJFeCrW7PKHYxhJJhuR1gAJJVnfpEOAYUjhi2P1IHcFQ8cfTv0faHANZ4r5_LShk=&uniplatform=NZKPT&language=CHS (accessed on 8 December 2023).
- Yang, Z. Reliability-Based Sensitivity and Reliability-Based Robust Design for Mechanical Components with Non-Normal Random Variable. Ph.D. Thesis, Northeastern University, Shenyang, China, 2010. Available online: https://kns.cnki.net/kcms2/article/abstract?v=0kbmF0AymBCEL0fGXS5eqj89K-L8Iua1kc9GCF1LESNzr3BXfXvqAR233U1uFysW98mFB_mXTDJLrRGH8wgJoFfNWIlSPVNEKEYf-ld5A5p8v76_dxcCaI95sbp63gEG&uniplatform=NZKPT&language=CHS (accessed on 8 December 2023).
- Zhou, J.-Y.; Zhu, D.-W.; Wang, Z.-L. Reliability–based Design Optimization Strategy for Structures by Universal Generating Functions. China Mech. Eng. 2021, 32, 1442–1448. [Google Scholar]
- Li, H.-C.; Sun, Z.-L.; Wang, H. Analysis of Structural Reliability Sensitivity Based on Dimensionality Reduction and Visualization Technique. Acta Armamentarii 2014, 35, 1876–1882. [Google Scholar]




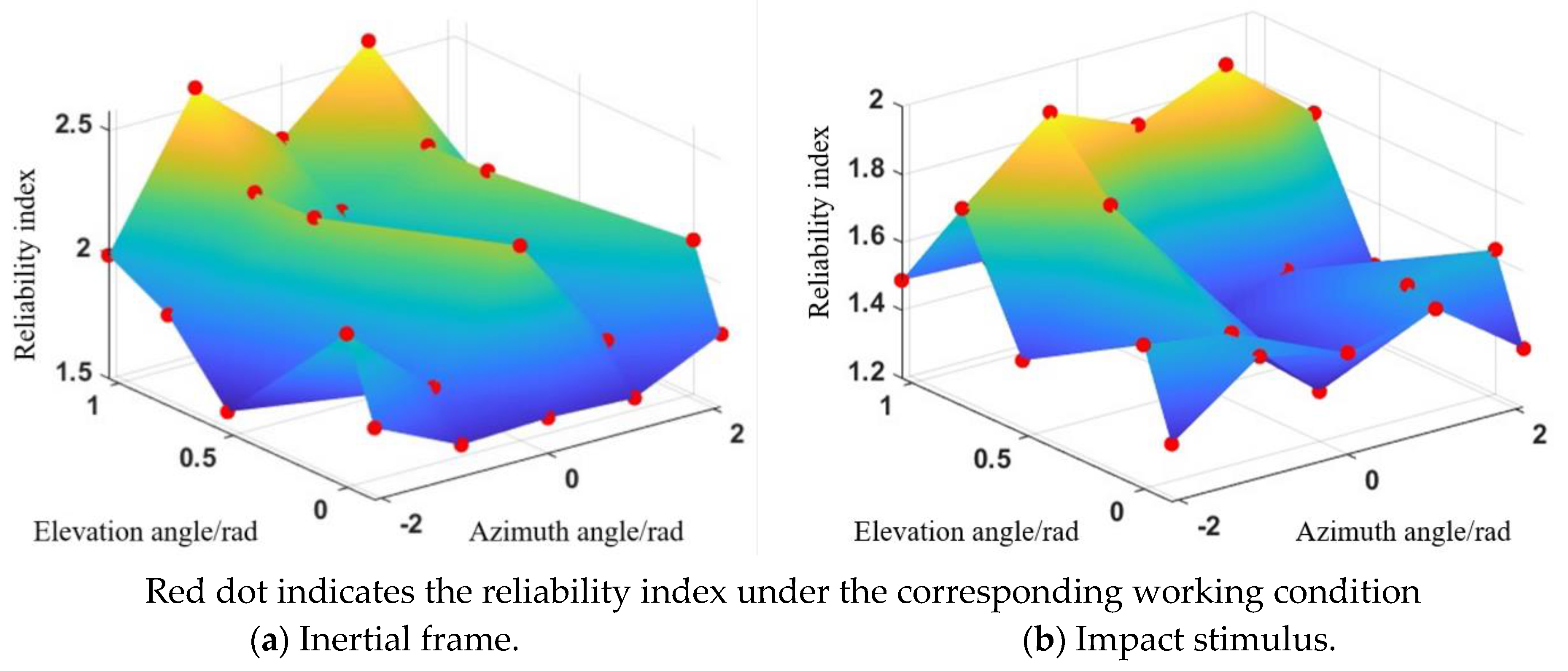

| No. | Error | Error Item | No. | Error | Error Item |
|---|---|---|---|---|---|
| 1 | Azimuth angle error | 7 | Rotational error around y-axis | ||
| 2 | Rotational error around x-axis | 8 | Rotary error around y-axis | ||
| 3 | Displacement error in y-direction | 9 | Slewing error around z-axis | ||
| 5 | Rotational error around x-axis | 10 | Displacement error in z-direction | ||
| 6 | Travel Error of vertical conveyor system | 11 | Up-swing angle error of oscillating conveyor | ||
| 4 | Storage silos with rotary motion rotation error | 12 | Angle error of rotating conveyors rotating |
| No. | Symbol of Mean Square Deviation | Numerical Value | No. | Symbol of Mean Square Deviation | Numerical Value |
|---|---|---|---|---|---|
| 1 | 0.75 mrad | 7 | 1.5 mm | ||
| 2 | 0.05 mrad | 8 | 0.15 mrad | ||
| 3 | 0.5 mm | 9 | 0.15 mrad | ||
| 4 | 3.5 mrad | 10 | 0.25 mm | ||
| 5 | 0.25 mrad | 11 | 2.5 mrad | ||
| 6 | 0.25 mrad | 12 | 1.5 mrad |
| No. | Azimuth Angle/rad | Elevation Angle/rad | Inertial Frame | Impact Stimulus | ||
|---|---|---|---|---|---|---|
| β | R | β | R | |||
| 1 | −2.0944 | −0.1222 | 1.7923 | 96.35% | 1.3716 | 91.49% |
| 2 | −2.0944 | 0 | 2.1205 | 98.30% | 1.6254 | 94.80% |
| 3 | −2.0944 | 0.5236 | 1.5854 | 94.36% | 1.4156 | 92.15% |
| 4 | −2.0944 | 0.7854 | 1.8649 | 96.89% | 1.7815 | 96.26% |
| 5 | −2.0944 | 1.0472 | 1.9955 | 97.70% | 1.4874 | 93.15% |
| 6 | −1.0472 | −0.1222 | 1.6290 | 94.83% | 1.5594 | 94.05% |
| 7 | −1.0472 | 0 | 1.8101 | 96.49% | 1.5904 | 94.41% |
| 8 | −1.0472 | 0.5236 | 2.2733 | 98.85% | 1.8031 | 96.43% |
| 9 | −1.0472 | 0.7854 | 2.2643 | 98.82% | 1.9943 | 97.69% |
| 10 | −1.0472 | 1.0472 | 2.5762 | 99.50% | 1.4770 | 93.02% |
| 11 | 0 | −0.1222 | 1.6437 | 94.98% | 1.4992 | 93.31% |
| 12 | 0 | 0 | 2.2865 | 98.89% | 1.3476 | 91.11% |
| 13 | 0 | 0.5236 | 1.8808 | 97.01% | 1.3820 | 91.65% |
| 14 | 0 | 0.7854 | 2.0945 | 98.19% | 1.8872 | 97.04% |
| 15 | 0 | 1.0472 | 2.2766 | 98.86% | 1.5993 | 94.51% |
| 16 | 1.0472 | −0.1222 | 1.6290 | 94.83% | 1.5594 | 94.05% |
| 17 | 1.0472 | 0 | 1.8101 | 96.49% | 1.5904 | 94.41% |
| 18 | 1.0472 | 0.5236 | 2.2733 | 98.85% | 1.4696 | 92.92% |
| 19 | 1.0472 | 0.7854 | 2.2643 | 98.82% | 1.9943 | 97.69% |
| 20 | 1.0472 | 1.0472 | 2.5762 | 99.50% | 1.4770 | 93.02% |
| 21 | 2.0944 | −0.1222 | 1.7923 | 96.35% | 1.3716 | 91.49% |
| 22 | 2.0944 | 0 | 2.1205 | 98.30% | 1.6254 | 94.80% |
| 23 | 2.0944 | 0.5236 | 1.5854 | 94.36% | 1.4156 | 92.15% |
| 24 | 2.0944 | 0.7854 | 1.8649 | 96.89% | 1.7815 | 96.26% |
| 25 | 2.0944 | 1.0472 | 1.9955 | 97.70% | 1.4874 | 93.15% |
| Min | — | — | 1.5854 | 94.36% | 1.3476 | 91.11% |
| Average | — | — | 2.0017 | 97.73% | 1.5837 | 94.34% |
| No. | Error Symbol | Sensitivity/% | No. | Error Symbol | Sensitivity/% |
|---|---|---|---|---|---|
| 1 | 0.1360 | 7 | 0.1884 | ||
| 2 | 0.0042 | 8 | 0.0166 | ||
| 3 | 0.1331 | 9 | 0.0972 | ||
| 4 | 0.0522 | 10 | 0.1296 | ||
| 5 | 0.0497 | 11 | 0.0995 | ||
| 6 | 0.0508 | 12 | 0.0427 |
| Name | Adjusted Parameters | Before Adjustment | After Adjustment | ||
|---|---|---|---|---|---|
| First optimization | 5.23 mm | 3.66 mm | 1.6839 | 95.39% | |
| Second optimization | 6.75 mrad | 4.73 mrad | 1.7708 | 96.17% | |
| Third optimization | 1.5 mm | 1.0 mm | 1.8132 | 96.51% | |
| Fourth optimization | 0.75 mrad | 0.50 mrad | 1.8494 | 96.78% | |
| Fifth optimization | 0.5 mm | 0.3 mm | 1.8735 | 96.95% | |
| Sixth optimization | 0.25 mm | 0.17 mm | 1.8912 | 97.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Yue, P.; Zhao, Y.; Sun, S. Reliability Analysis and Optimization Method of a Mechanical System Based on the Response Surface Method and Sensitivity Analysis Method. Actuators 2023, 12, 465. https://doi.org/10.3390/act12120465
Zhao L, Yue P, Zhao Y, Sun S. Reliability Analysis and Optimization Method of a Mechanical System Based on the Response Surface Method and Sensitivity Analysis Method. Actuators. 2023; 12(12):465. https://doi.org/10.3390/act12120465
Chicago/Turabian StyleZhao, Lei, Pengfei Yue, Yang Zhao, and Shiyan Sun. 2023. "Reliability Analysis and Optimization Method of a Mechanical System Based on the Response Surface Method and Sensitivity Analysis Method" Actuators 12, no. 12: 465. https://doi.org/10.3390/act12120465





