Output-Feedback Position Tracking Servo System with Feedback Gain Learning Mechanism via Order-Reduction Speed-Error-Stabilization Approach

Abstract

This paper presents a novel trajectory-tracking technique for servo systems treating only the position measurement as the output subject to practical concerns: system parameter and load uncertainties. There are two main contributions: (a) the use of observers without system parameter information for estimating the position reference derivative and speed and acceleration errors and (b) an order reduction exponential speed error stabilizer via active damping injection to enable the application of a feedback-gain-learning position-tracking action. A hardware configuration using a QUBE-servo2 and myRIO-1900 experimentally validates the closed-loop improvement under various scenarios.

1. Introduction

Servo systems play a pivotal role in determining the performance level of mechatronics system applications, including home appliances, personal mobility, factory machines, and so on. Increasing attention regarding the group motion control technology indicates the need for high technical specifications for these applications due to their safety and reliability specifications [1,2,3,4,5,6]. Recent synchronization techniques can be considered as a possible solution to this grouping control problem in industrial applications [7,8].

First, high-level closed-loop servo performance (speed and position control) must be secured to implement novel synchronization techniques with promising properties under various operating conditions. There are several types of motors, such as DC, brushless DC (BLDC), induction, and permanent magnet synchronous motors (PMSMs) available for the mechanical part of a servo system. Conventional (but simple) and advanced control techniques can be applied to implement closed-loop servo systems. The multi-loop proportional-integral (PI) controller, consisting of current (inner), speed (middle), and position (outer) loops, has normally been used to implement a closed-loop servo system whose feedback gain can be determined through trial-and-error and frequency-domain analysis tools (Bode and Nyquist plots) [9,10]. However, the tuning result is only feasible for a given operating point, and an additional gain scheduling technique must be used to widen the feasible operating region [11]. The feedback linearization-based multi-loop approach solves this problem by adding system-parameter-dependent compensation terms in the feed-forward loop, and their PI gains allow closed-loop dynamics governed by a first-order low-pass filter (LPF) using passive damping in an open-loop system [12]. The parameter dependence on the feed-forward terms and PI gains can be handled by adopting additional online parameter estimators as in [13,14,15]. Adaptive controllers have been recently suggested as a possible advanced solution to the speed tracking problem subject to parameter and load uncertainties, incorporating numerous parameter estimators [16,17,18]. Interestingly, an online self-tuner continuously updates the feedback gain according to an analytic rule to ensure closed-loop stability, but the optimality of the steady-state gain remains questionable [17]. A parameter-dependent observer that estimates both the state and disturbances was incorporated into a robust controller to enhance the disturbance attenuation performance of a closed-loop system [19]. In a separate study, a robust speed controller included a nonlinear disturbance observer (DOB) to estimate the desired feed-forward terms in order to secure improved closed-loop robustness and accuracy, which also alleviates the level of system-parameter dependence [20]. This type of DOB was adopted for a sliding-mode controller, including the discontinuous feedback loop, to reduce the chattering level during steady-state operation [21]. Alternatively, predictive controllers were used to pursue closed-loop optimality by predicting the state using system parameter and load information, incorporating a numerical optimization process online [22,23,24]. As another approach to the online self-tuning technique [17], an additional stabilizer for the self-tuner was included and used as a damping injection term in a proportional-type energy-shaping controller [25,26], which, however, limits the application area regarding speed regulation. There were several output-feedback controllers, including the extended state observer (ESO) involving the system parameter dependence (at least partially) and repetitive offline optimization process for an optimal observer gain [27,28,29].

This study attempts to solve the output-feedback position-tracking problem considering the challenges arising from previous results, corresponding to the exact servo system parameter information requirements (at least partially, for the controller and observers) and limiting the robustness associated with the integral actions and DOBs. The features (contributions) of the proposed tracking technique are summarized as follows:

• an extended state observer (for the position reference derivative and controlled errors involving speed and its acceleration) equipped with a specially structured tuning factor yielding the first-order exponential convergent estimation error behavior; and
• the combination of an active damping injection pole-zero cancellation PI controller and nonlinear DOB for the first-order exponential convergent speed error stabilizer without dependence on the exact servo system parameter values.

The resultant feedback system does not suffer from any magnitude or phase distortions between the reference and actual servo system position. The experimental setup using a QUBE-servo2 and myRIO-1900 indicates the feasibility of the proposed solution by experimentally showing the improvements in closed-loop performance.

2. Servo System Dynamics

This section introduces simple servo system dynamics by a DC power source (a DC motor and a brushless DC motor) to clarify the main idea behind this study. The input voltage $v_s\left(t\right)$ (in V) applied to the stator initiates the stator current $i_s\left(t\right)$ (in A) and rotor position $\theta \left(t\right)$ (in rad) and speed $\omega \left(t\right)$ (in rad/s), which forms a linear time-invariant system subject to the mismatched disturbance $T_L\left(t\right)$ (the load torque in Nm) as follows:

$$\begin{array}{ccc}\hfill \frac{d\theta \left(t\right)}{dt}& =& \omega \left(t\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill J_m\frac{d\omega \left(t\right)}{dt}& =& -B_m\omega \left(t\right)+T_e\left(t\right)-T_L\left(t\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill L_s\frac{d{i}_s\left(t\right)}{dt}& =& -R_s{i}_s\left(t\right)-{\varphi }_s\left(t\right)+v_s\left(t\right),\forall t\ge 0,\hfill \end{array}$$

(3)

with the output torque $T_e\left(t\right)=k_T{i}_s\left(t\right)$ (in Nm), the back electromotive force (EMF) ${\varphi }_s\left(t\right)=k_e\omega \left(t\right)$ (in V) for some coefficients $k_T>0$ and $k_e>0$ ($k_T=k_e$ for permanent magnet-type systems), and the system parameters of $J_m$ (rotor inertia in kgm${}^2$), $B_m$ (rotor friction in Nm/rad/s), $L_s$ (stator inductance in mH), and $R_s$ (stator resistance in $\Omega$).

The system parameters can experience dramatic variations depending on the operating conditions; thus, this study decomposes the original system parameters into their nominal values (provided by the manufacturer) and perturbation terms to address this practical challenging point (for instance, $J_m=J_{m,0}+\Delta J_m$ for the rotor inertia case). This yields another expression for the system representation (2) and (3) by combining them after applying an additional time derivative to the speed dynamics (2):

$$\begin{array}{c}\hfill c_{\omega ,0}\frac{d^2\omega \left(t\right)}{d{t}^2}=v_s\left(t\right)+{\overline{d}}_{\omega }\left(t\right),\forall t\ge 0,\end{array}$$

(4)

which has a known coefficient $c_{\omega ,0}=\frac{J_{m,0}{L}_{s,0}}{k_{T,0}}$ (its true version $c_{\omega }=\frac{J_m{L}_s}{k_T}$ and variation $\Delta c_{\omega }=c_{\omega }-c_{\omega ,0}$) and an unknown time-varying lumped disturbance ${\overline{d}}_{\omega }\left(t\right)=-\Delta c_{\omega }\frac{d^2\omega \left(t\right)}{d{t}^2}-B_m\frac{d\omega \left(t\right)}{dt}-R_s{i}_s\left(t\right)-{\varphi }_s\left(t\right)-\frac{d{T}_L\left(t\right)}{dt}$. This representation resolves the two major problems associated with the plant-model mismatches caused by parameter and load variations.

The following section derives an advanced observer-based output-feedback position-tracking control law using the position and speed dynamics (1) and (4), considering the stator voltage $v_s\left(t\right)$ and the position $\theta \left(t\right)$ as the control input (design variable) and the system output, respectively.

3. Position-Tracking Control Law

3.1. Control Objective

Consider the first-order time-varying system for an error ${\tilde{\theta }}^{*}\left(t\right):={\theta }_{ref}\left(t\right)-{\theta }^{*}\left(t\right)$ with a position reference trajectory ${\theta }_{ref}\left(t\right)$, given by

$$\begin{array}{c}\hfill {\dot{\tilde{\theta }}}^{*}\left(t\right)=-{\widehat{\omega }}_{pc}\left(t\right){\tilde{\theta }}^{*}\left(t\right),\forall t\ge 0,\end{array}$$

(5)

with its base system defined by ${\tilde{\theta }}_{base}^{*}:={\tilde{\theta }}^{*}{|}_{{\widehat{\omega }}_{pc}\left(t\right)={\widehat{\omega }}_{pc}\left(0\right)}$ for some ${\widehat{\omega }}_{pc}\left(0\right)={\omega }_{pc}>0$ that satisfies

$$\begin{array}{c}\hfill {\dot{\tilde{\theta }}}_{base}^{*}\left(t\right)=-{\omega }_{pc}{\tilde{\theta }}_{base}^{*}\left(t\right),\forall t\ge 0.\end{array}$$

(6)

Note that the notation $\dot{f}\left(t\right)$ is used to abbreviate $\dot{f}\left(t\right)=\frac{df\left(t\right)}{dt}$ for convenience. This study chooses the time-varying system (5) as the desired closed-loop performance to achieve a superior convergence rate from its base system (6) by applying the boosting property ${\widehat{\omega }}_{pc}\left(t\right)\ge {\omega }_{pc}$, $\forall t\ge 0$, as proved by Lemma 1 in Section 4. To attain this goal, the exponential convergence given by

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\theta \left(t\right)={\theta }^{*}\left(t\right)\end{array}$$

(7)

is taken into account as the control objective of this study.

Remark 1.

The base system (6) can be written in low-pass filter (LPF) for slowly time-varying reference signals ${\dot{\theta }}_{ref}\left(t\right)\approx 0$ as

$$\begin{array}{c}\hfill {\dot{\theta }}_{base}^{*}\left(t\right)={\omega }_{pc}({\theta }_{ref}\left(t\right)-{\theta }_{base}^{*}\left(t\right)),\forall t\ge 0,\end{array}$$

(8)

with its Laplace transform:

$$\begin{array}{c}\hfill \frac{{\Theta }_{base}^{*}\left(s\right)}{{\Theta }_{ref}\left(s\right)}=\frac{{\omega }_{pc}}{s+{\omega }_{pc}},\forall s\in \mathbb{C},\end{array}$$

subject to the cut-off frequency ${\omega }_{pc}=2\pi f_{pc}$ in rad/s (or, equivalently, as $f_{pc}=\frac{{\omega }_{pc}}{2\pi }$ in Hz). Therefore, the design parameter ${\widehat{\omega }}_{pc}\left(0\right)={\omega }_{pc}$ can be determined as the cut-off frequency of the LPF (8) for the mapping ${\theta }_{ref}\left(t\right)\mapsto {\theta }_{base}^{*}\left(t\right)$.

3.2. Position Control with Feedback-Gain-Learning Algorithm

The position dynamics (1) gives an equivalent form by introducing the additional design variable ${\omega }_{ref}\left(t\right)$ as

$$\begin{array}{c}\hfill \dot{\theta }\left(t\right)=\omega \left(t\right)={\omega }_{ref}\left(t\right)-\tilde{\omega }\left(t\right),\forall t\ge 0,\end{array}$$

where $\tilde{\omega }\left(t\right):={\omega }_{ref}-\omega \left(t\right)$, $\forall t\ge 0$. This yields the open-loop position-error dynamics for the actual position error $\tilde{\theta }:={\theta }_{ref}\left(t\right)-\theta \left(t\right)$ such that

$$\begin{array}{c}\hfill \dot{\tilde{\theta }}\left(t\right)=-{\omega }_{ref}\left(t\right)+\tilde{\omega }\left(t\right)+{\theta }_{ref,v}\left(t\right),\forall t\ge 0,\end{array}$$

(9)

where ${\theta }_{ref,v}\left(t\right):={\dot{\theta }}_{ref}\left(t\right)$, which is treated as an unknown time-varying signal.

Remark 2.

In the case of a multi-servo system synchronization problem, the position reference ${\theta }_{ref}\left(t\right)$ can be given as a neighboring-stage servo system output, which can be solved by the proposed controller while ensuring the exponential convergence (7) so that ${lim}_{t\to \infty }\theta \left(t\right)={\theta }_{ref}\left(t\right)$. Considering a two multi-servo system example (where ${\theta }_1\left(t\right)$ and ${\theta }_2\left(t\right)$ denote the first and second system, respectively), it holds that $\tilde{\theta }\left(t\right)={\theta }_1\left(t\right)-{\theta }_2\left(t\right)$, ${\omega }_{ref}\left(t\right)={\omega }_{2,ref}\left(t\right)$, $\tilde{\omega }\left(t\right)={\omega }_{2,ref}\left(t\right)-{\omega }_2\left(t\right)$, and ${\theta }_{ref,v}\left(t\right)={\dot{\theta }}_1\left(t\right)$.

3.2.1. Position Reference Derivative Observer

Consider the relationship ${\dot{\theta }}_{ref}\left(t\right)={\theta }_{ref,v}\left(t\right)$ and its decomposition ${\theta }_{ref,v}\left(t\right)={\theta }_{ref,v,0}+\Delta {\theta }_{ref,v}\left(t\right)$ with respect to the DC (${\theta }_{ref,v,0}$) and AC ($\Delta {\theta }_{ref,v}$) components (e.g., ${\dot{\theta }}_{ref,v,0}=0$ and $\Delta {\dot{\theta }}_{ref,v}\left(t\right)\ne 0$). Then, it holds that

$$\begin{array}{c}\hfill {\dot{\theta }}_{ref}\left(t\right)={\theta }_{ref,v}\left(t\right),{\dot{\theta }}_{ref,v}\left(t\right)=f_{{\theta }_{ref}}\left(t\right),\forall t\ge 0,\end{array}$$

(10)

where $f_{{\theta }_{ref}}\left(t\right):=\Delta {\dot{\theta }}_{ref,v}\left(t\right)$ and $|f_{{\theta }_{ref}}\left(t\right)|\le {\overline{f}}_{{\theta }_{ref}}$, $\forall t\ge 0$, whose estimation can be accomplished by the proposed observer with its output error $e_{{\theta }_{ref}}\left(t\right):={\theta }_{ref}\left(t\right)-{\widehat{\theta }}_{ref}\left(t\right)$ such that

$$\begin{array}{ccc}\hfill {\dot{\widehat{\theta }}}_{ref}\left(t\right)& =& l_{{\theta }_{ref},1}{e}_{{\theta }_{ref}}\left(t\right)+{\widehat{\theta }}_{ref,v}\left(t\right),\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\dot{\widehat{\theta }}}_{ref,v}\left(t\right)& =& l_{{\theta }_{ref},2}{e}_{{\theta }_{ref}}\left(t\right),\forall t\ge 0,\hfill \end{array}$$

(12)

with observer gains $l_{{\theta }_{ref},i}>0$, $i=1,2$, and state ${\widehat{\theta }}_{ref,v}\left(t\right)$ representing the estimate for ${\theta }_{ref,v}\left(t\right)$. The proposed observer consisting of (11) and (12) forms the same structure as the conventional extended state observer (ESO), except for the gain structure design

$$\begin{array}{c}\hfill l_{{\theta }_{ref,1}}=2{\omega }_{obs,{\theta }_{ref}},l_{{\theta }_{ref,2}}={\omega }_{obs,{\theta }_{ref}}^2,\end{array}$$

for a given ${\omega }_{obs,{\theta }_{ref}}>0$, which reduces the observer gain-tuning complexity, ensuring the first-order estimation error ($e_{{\theta }_{ref,v}}\left(t\right):={\theta }_{ref,v}\left(t\right)-{\widehat{\theta }}_{ref,v}\left(t\right)$) convergence behavior. For details, see Section 4.

3.2.2. Position-Tracking Control

This subsection proposes a position-tracking control law for updating the design variable ${\omega }_{ref}\left(t\right)$ as

$$\begin{array}{c}\hfill {\omega }_{ref}\left(t\right)={\widehat{\omega }}_{pc}\left(t\right)\tilde{\theta }\left(t\right)+{\widehat{\theta }}_{ref,v}\left(t\right),\forall t\ge 0,\end{array}$$

(13)

with the position-reference-derivative estimate ${\widehat{\theta }}_{ref,v}\left(t\right)$ obtained from the observer (11) and (12) and the feedback gain learning mechanism for ${\widehat{\omega }}_{pc}\left(t\right)$ such that

$$\begin{array}{c}\hfill {\dot{\widehat{\omega }}}_{pc}\left(t\right)={\gamma }_{pc}({\tilde{\theta }}^2\left(t\right)+{\rho }_{pc}{\tilde{\omega }}_{pc}\left(t\right)),{\widehat{\omega }}_{pc}\left(0\right)={\omega }_{pc},\end{array}$$

(14)

$\forall t\ge 0$, driven by the nonlinear excitation term ${\tilde{\theta }}^2\left(t\right)$ and error ${\tilde{\omega }}_{pc}\left(t\right):={\omega }_{pc}-{\widehat{\omega }}_{pc}\left(t\right)$, according to the learning and restoration rates ${\gamma }_{pc}>0$ and ${\rho }_{pc}>0$. The nonlinearity in the feedback gain learning algorithm (14) makes it nontrivial for closed-loop stability analysis tasks. For more details, see Section 4.

3.3. Observer-Based Speed Error Stabilizer

3.3.1. Speed and Acceleration Error Observers

The proposed solution requires feedback involving the first and second derivatives (speed and acceleration) of the servo system position to stabilize the speed error dynamics and avoid the need for stator current measurements. It is difficult to extract the correct speed and acceleration trajectory by applying direct time differentiation to the position measurement owing to its high-frequency noise component. To overcome this system-parameter dependence problem, consider the relationship $\dot{\omega }\left(t\right)=a\left(t\right)$ (acceleration), definition $\tilde{a}\left(t\right):=a_{ref}\left(t\right)-a\left(t\right)$ with $a_{ref}\left(t\right):={\dot{\omega }}_{ref}\left(t\right)$, and decomposition $\tilde{a}\left(t\right)={\tilde{a}}_0+\Delta \tilde{a}\left(t\right)$ with respect to the DC (${\tilde{a}}_0$) and AC ($\Delta \tilde{a}\left(t\right)$) components (e.g., ${\dot{\tilde{a}}}_0=0$ and $\Delta \dot{\tilde{a}}\left(t\right)\ne 0$). Then, it holds that

$$\begin{array}{c}\hfill \dot{\tilde{\omega }}\left(t\right)=\tilde{a}\left(t\right),\dot{\tilde{a}}\left(t\right)=f_a\left(t\right),\forall t\ge 0,\end{array}$$

(15)

where $f_a\left(t\right):=\Delta \dot{\tilde{a}}\left(t\right)$ and $|f_a\left(t\right)|\le {\overline{f}}_a$, $\forall t\ge 0$, whose estimation can be obtained by the proposed observer with the output $y_{\tilde{\theta }}\left(t\right):={\int }_0^t{\omega }_{ref}\left(\tau \right)d\tau -\theta \left(\tau \right)d\tau$ (so that ${\dot{y}}_{\tilde{\theta }}\left(t\right)=\tilde{\omega }\left(t\right)$ and ${\ddot{y}}_{\tilde{\theta }}\left(t\right)=\tilde{a}\left(t\right)$) with error $e_{\tilde{\theta }}\left(t\right):=y_{\tilde{\theta }}\left(t\right)-{\widehat{y}}_{\tilde{\theta }}\left(t\right)$:

$$\begin{array}{ccc}\hfill {\dot{\widehat{y}}}_{\tilde{\theta }}\left(t\right)& =& l_{\tilde{\theta },1}{e}_{\tilde{\theta }}\left(t\right)+{\widehat{x}}_{\tilde{\omega }}\left(t\right),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\dot{\widehat{x}}}_{\tilde{\omega }}\left(t\right)& =& l_{\tilde{\theta },2}{e}_{\tilde{\theta }}\left(t\right)+{\widehat{x}}_{\tilde{a}}\left(t\right),\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\dot{\widehat{x}}}_{\tilde{a}}\left(t\right)& =& l_{\tilde{\theta },3}{e}_{\tilde{\theta }}\left(t\right),\forall t\ge 0,\hfill \end{array}$$

(18)

with observer gains $l_{\tilde{\theta },i}>0$, $i=1,2,3$, and states ${\widehat{x}}_{\tilde{\omega }}\left(t\right)$ and ${\widehat{x}}_{\tilde{a}}\left(t\right)$ representing the estimates for $\tilde{\omega }\left(t\right)$ and $\tilde{a}\left(t\right)$, respectively. The proposed observer consisting of (16)–(18) forms the same structure as the conventional ESO, except for the gain structure design:

$$\begin{array}{c}\hfill l_{\tilde{\theta },1}=3{\omega }_{obs,\tilde{\theta }},l_{\tilde{\theta },2}=3{\omega }_{obs,\tilde{\theta }}^2,l_{\tilde{\theta },3}={\omega }_{obs,\tilde{\theta }}^3,\end{array}$$

for a given ${\omega }_{obs,\tilde{\theta }}>0$, which reduces the observer gain tuning complexity and ensures the first-order estimation error ($e_{\tilde{\omega }}:=\tilde{\omega }-{\widehat{x}}_{\tilde{\omega }}$, $e_{\tilde{a}}:=\tilde{a}-{\widehat{x}}_{\tilde{a}}$) convergence behavior. For details, see Section 4.

3.3.2. Speed Error Stabilizer

The open-loop second-order speed dynamics (4) provide another expression regarding the error $\tilde{\omega }\left(t\right)={\omega }_{ref}\left(t\right)-\omega \left(t\right)$:

$$\begin{array}{c}\hfill c_{\omega ,0}\ddot{\tilde{\omega }}\left(t\right)=-v_s\left(t\right)+d_{\omega }\left(t\right),\forall t\ge 0,\end{array}$$

(19)

with the newly defined disturbance $d_{\omega }\left(t\right):=c_{\omega ,0}{\ddot{\omega }}_{ref}\left(t\right)-{\overline{d}}_{\omega }\left(t\right)$, whose servo system parameter information-free solution is proposed as

$$\begin{array}{c}\hfill v_s\left(t\right)=(k_{d,\omega }+c_{\omega ,0}{\lambda }_{\omega }){\widehat{x}}_{\tilde{a}}\left(t\right)+k_{d,\omega }{\lambda }_{\omega }{\widehat{x}}_{\tilde{\omega }}\left(t\right)+{\widehat{d}}_{\omega }\left(t\right),\end{array}$$

(20)

$\forall t\ge 0$, with two tuning gains, $k_{d,\omega }>0$ and ${\lambda }_{\omega }>0$. Meanwhile, the observer-based nonlinear DOB estimates the disturbance $d_{\omega }\left(t\right)$ by updating ${\widehat{d}}_{\omega }\left(t\right)$ according to the following rule:

$$\begin{array}{ccc}\hfill {\dot{z}}_{d_{\omega }}\left(t\right)& =& -l_{d_{\omega }}{z}_{d_{\omega }}\left(t\right)-l_{d_{\omega }}^2{c}_{\omega ,0}{\widehat{x}}_{\tilde{a}}\left(t\right)+l_{d_{\omega }}{v}_s\left(t\right),\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill {\widehat{d}}_{\omega }\left(t\right)& =& z_{d_{\omega }}\left(t\right)+l_{d_{\omega }}{c}_{\omega ,0}{\widehat{x}}_{\tilde{a}}\left(t\right),\hfill \end{array}$$

(22)

with gain $l_{d_{\omega }}>0$. The proposed control law (20) exponentially stabilizes the speed error by reducing the second-order open-loop dynamics to first-order dynamics owing to the specially structured gains invoking the pole-zero cancellation. For details, see Section 4. Figure 1 shows the proposed output-feedback system structure.

4. Closed Loop Analysis

This section derives the beneficial closed-loop properties by analyzing the position control loop (Section 4.1), the speed error stabilization loop (Section 4.2), and the entire output-feedback system (Section 4.3).

4.1. Position Control Loop

This loop consists of three components: the feedback gain learning mechanism (14), the position reference derivative observers (11) and (12), and the control action (13). First, Lemma 1 presents the property of the gain learning mechanism (14) boosting the feedback gain such that ${\widehat{\omega }}_{pc}\left(t\right)\ge {\omega }_{pc}$, $\forall t\ge 0$.

Lemma 1.

The feedback-gain learning mechanism (14) guarantees the attainment of the initial condition ${\widehat{\omega }}_{pc}\left(0\right)={\omega }_{pc}$ as the minimum value for ${\widehat{\omega }}_{pc}\left(t\right)$, e.g.,

$$\begin{array}{c}\hfill {\widehat{\omega }}_{pc}\left(t\right)\ge {\omega }_{pc},\forall t\ge 0.\end{array}$$

(23)

Proof. 

Integrating the feedback gain learning mechanism (14) gives us

$$\begin{array}{c}\hfill {\widehat{\omega }}_{pc}=e^{-{\gamma }_{pc}{\rho }_{pc}t}{\omega }_{pc}+{\int }_0^t{e}^{-{\gamma }_{pc}{\rho }_{pc}(t-\tau )}({\gamma }_{pc}{\rho }_{pc}{\omega }_{pc}+{\gamma }_{pc}{\tilde{\theta }}^2)d\tau ,\end{array}$$

which indicates the existence of a lower bound of ${\widehat{\omega }}_{pc}$ owing to the positive sign of ${\gamma }_{pc}{\rho }_{pc}{\omega }_{pc}+{\gamma }_{pc}{\tilde{\theta }}^2$. This completes the proof. □

Lemma 2 describes the output-error-convergence behavior driven by the position-reference-derivative observer (11) and (12), which plays a vital role in demonstrating the convergence property of its estimation error.

Lemma 2.

The position reference derivative observer (11) and (12) ensures the exponential convergence:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{e}_{{\theta }_{ref}}\left(t\right)=e_{{\theta }_{ref}}^{*}\left(t\right),\end{array}$$

(24)

subject to the gain setting $\frac{2{\overline{f}}_{{\theta }_{ref}}}{{\omega }_{obs,{\theta }_{ref}}}\approx 0$, where the desired trajectory $e_{{\theta }_{ref}}^{*}\left(t\right)$ represents the solution to the first-order convergent system:

$$\begin{array}{c}\hfill {\dot{e}}_{{\theta }_{ref}}^{*}\left(t\right)=-{\omega }_{obs,{\theta }_{ref}}{e}_{{\theta }_{ref}}^{*}\left(t\right),\forall t\ge 0.\end{array}$$

Proof. 

The output error $e_{{\theta }_{ref}}$ gives second-order dynamics by combining (10), (11), and (12) such that

$$\begin{array}{c}\hfill {\ddot{e}}_{{\theta }_{ref}}=-2{\omega }_{obs,{\theta }_{ref}}{\dot{e}}_{{\theta }_{ref}}-{\omega }_{obs,{\theta }_{ref}}^2{e}_{{\theta }_{ref}}+f_{{\theta }_{ref}},\end{array}$$

with its equivalent expression obtained from the Laplace transform:

$$\begin{array}{c}\hfill (s+{\omega }_{obs,{\theta }_{ref}})E_{{\theta }_{ref}}\left(s\right)=X_{{\theta }_{ref}}\left(s\right),\forall s\in \mathbb{C},\end{array}$$

where $X_{{\theta }_{ref}}\left(s\right)=\frac{1}{s+{\omega }_{obs,{\theta }_{ref}}}{F}_{{\theta }_{ref}}\left(s\right)$, which defines the performance error dynamics for ${ϵ}_{{\theta }_{ref}}:=e_{{\theta }_{ref}}^{*}-e_{{\theta }_{ref}}$ as

$$\begin{array}{c}\hfill {\dot{ϵ}}_{{\theta }_{ref}}=-{\omega }_{obs,{\theta }_{ref}}{ϵ}_{{\theta }_{ref}}-x_{{\theta }_{ref}},{\dot{x}}_{{\theta }_{ref}}=-{\omega }_{obs,{\theta }_{ref}}{x}_{{\theta }_{ref}}+f_{{\theta }_{ref}},\forall t\ge 0.\end{array}$$

These error dynamics yield the time derivative of the positive definite function $V_{obs,pos}:=\frac{1}{2}{ϵ}_{{\theta }_{ref}}^2+\frac{k_{{\theta }_{ref}}}{2}{x}_{{\theta }_{ref}}^2$ with $k_{{\theta }_{ref}}>0$ as

$$\begin{array}{ccc}\hfill {\dot{V}}_{obs,pos}& =& {ϵ}_{{\theta }_{ref}}(-{\omega }_{obs,{\theta }_{ref}}{ϵ}_{{\theta }_{ref}}-x_{{\theta }_{ref}})-\frac{k_{{\theta }_{ref}}{\omega }_{obs,{\theta }_{ref}}}{2}{x}_{{\theta }_{ref}}^2-k_{{\theta }_{ref}}(\frac{{\omega }_{obs,{\theta }_{ref}}}{2}{x}_{{\theta }_{ref}}^2-f_{{\theta }_{ref}}{x}_{{\theta }_{ref}})\hfill \\ & \le & -\frac{{\omega }_{obs,{\theta }_{ref}}}{2}{ϵ}_{{\theta }_{ref}}^2-(\frac{k_{{\theta }_{ref}}{\omega }_{obs,{\theta }_{ref}}}{2}-\frac{1}{2{\omega }_{obs,{\theta }_{ref}}})x_{{\theta }_{ref}}^2,\forall t\ge 0,\forall \left|x_{{\theta }_{ref}}\right|\ge \frac{2{\overline{f}}_{{\theta }_{ref}}}{{\omega }_{obs,{\theta }_{ref}}},\hfill \end{array}$$

where Young’s inequality ($xy\le \frac{ϵ}{2}{x}^2+\frac{1}{2ϵ}{y}^2$, $\forall ϵ>0$) verifies the inequality above, which shows that (defining $k_{{\theta }_{ref}}:=\frac{2}{{\omega }_{obs,{\theta }_{ref}}}(\frac{1}{2{\omega }_{obs,{\theta }_{ref}}}+\frac{1}{2})$)

$$\begin{array}{ccc}\hfill {\dot{V}}_{obs,pos}& \le & -\frac{{\omega }_{obs,{\theta }_{ref}}}{2}{ϵ}_{{\theta }_{ref}}^2-\frac{1}{2}{x}_{{\theta }_{ref}}^2\hfill \\ & \le & -{\alpha }_{obs,pos}{V}_{obs,pos},\forall t\ge 0,\forall \left|x_{{\theta }_{ref}}\right|\ge \frac{2{\overline{f}}_{{\theta }_{ref}}}{{\omega }_{obs,{\theta }_{ref}}},\hfill \end{array}$$

(25)

with ${\alpha }_{obs,pos}:=min\{\frac{1}{{\omega }_{obs,{\theta }_{ref}}},\frac{1}{k_{{\theta }_{ref}}}\}$. This completes the proof. □

Remark 3.

The result of Lemma 2 (exponential convergence (24)) makes it reasonable to assume that

$$\begin{array}{c}\hfill {\dot{e}}_{{\theta }_{ref}}=-{\omega }_{obs,{\theta }_{ref}}{e}_{{\theta }_{ref}},\forall t\ge 0,\end{array}$$

(26)

which leads to the following chain of implications (using (11)):

$$\begin{array}{ccc}\hfill {\ddot{e}}_{{\theta }_{ref}}=-{\omega }_{obs,{\theta }_{ref}}{\dot{e}}_{{\theta }_{ref}}& \iff & ({\dot{\theta }}_{ref,v}-{\ddot{\widehat{\theta }}}_{ref})=-{\omega }_{obs,{\theta }_{ref}}({\theta }_{ref,v}-{\dot{\widehat{\theta }}}_{ref})\hfill \\ & \iff & ({\dot{\theta }}_{ref,v}-(l_{{\theta }_{ref}}{\dot{e}}_{{\theta }_{ref}}+{\dot{\widehat{\theta }}}_{ref,v}))=-{\omega }_{obs,{\theta }_{ref}}({\theta }_{ref,v}-(l_{{\theta }_{ref}}{e}_{{\theta }_{ref}}+{\widehat{\theta }}_{ref,v}))\hfill \\ & \iff & {\dot{e}}_{{\theta }_{ref,v}}-l_{{\theta }_{ref}}{\dot{e}}_{{\theta }_{ref}}=-{\omega }_{obs,{\theta }_{ref}}{e}_{{\theta }_{ref},v}+{\omega }_{obs,{\theta }_{ref}}{l}_{{\theta }_{ref}}{e}_{{\theta }_{ref}},\forall t\ge 0.\hfill \end{array}$$

Applying (26), this allows us to conclude that

$$\begin{array}{c}\hfill {\dot{e}}_{{\theta }_{ref,v}}=-{\omega }_{obs,{\theta }_{ref}}{e}_{{\theta }_{ref,v}},\forall t\ge 0,\end{array}$$

(27)

which plays a vital role in demonstrating the beneficial position control loop property in Lemma 3.

Lemma 3.

The proposed position-tracking control loop shown in Figure 1 guarantees the ${\mathcal{L}}_2$-stability for the input-output mapping $\tilde{\omega }\left(t\right)\mapsto \tilde{\theta }\left(t\right)$.

Proof. 

The substitution of the proposed position-tracking control (13) into the open-loop dynamics (9) results in

$$\begin{array}{c}\hfill \dot{\tilde{\theta }}=-{\widehat{\omega }}_{pc}\tilde{\theta }+e_{{\theta }_{ref},v}+\tilde{\omega }=-{\omega }_{pc}\tilde{\theta }+{\tilde{\omega }}_{pc}\tilde{\theta }+e_{{\theta }_{ref},v}+\tilde{\omega },\forall t\ge 0,\end{array}$$

(28)

which turns the positive definite function $V_{pc}:=\frac{1}{2}{\tilde{\theta }}^2+\frac{1}{2{\gamma }_{pc}}{\tilde{\omega }}_{pc}^2+\frac{k_{{\theta }_{ref},v}}{2}{e}_{{\theta }_{ref},v}^2$ with $k_{{\theta }_{ref},v}>0$ (using (14) and (27)) into

$$\begin{array}{ccc}\hfill {\dot{V}}_{pc}& =& \tilde{\theta }(-{\omega }_{pc}\tilde{\theta }+{\tilde{\omega }}_{pc}\tilde{\theta }+e_{{\theta }_{ref},v}+\tilde{\omega })-{\tilde{\omega }}_{pc}({\tilde{\theta }}^2+{\rho }_{pc}{\tilde{\omega }}_{pc})-k_{{\theta }_{ref},v}{\omega }_{obs,{\theta }_{ref}}{e}_{{\theta }_{ref},v}^2\hfill \\ & \le & -\frac{{\omega }_{pc}}{2}{\tilde{\theta }}^2+\tilde{\omega }\tilde{\theta }-{\rho }_{pc}{\tilde{\omega }}_{pc}^2-(k_{{\theta }_{ref},v}{\omega }_{obs,{\theta }_{ref}}-\frac{1}{2{\omega }_{pc}})e_{{\theta }_{ref},v}^2,\forall t\ge 0,\hfill \end{array}$$

with the application of Young’s inequality. The coefficient $k_{{\theta }_{ref,v}}:=\frac{1}{{\omega }_{obs,{\theta }_{ref}}}(\frac{1}{{\omega }_{pc}}+\frac{1}{2})$ rearranges the upper bound of ${\dot{V}}_{pc}$ as

$$\begin{array}{ccc}\hfill {\dot{V}}_{pc}& \le & -\frac{{\omega }_{pc}}{2}{\tilde{\theta }}^2-{\rho }_{pc}{\tilde{\omega }}_{pc}^2-\frac{1}{2}{e}_{{\theta }_{ref},v}^2+\tilde{\omega }\tilde{\theta }\hfill \\ & \le & -{\alpha }_{pc}{V}_{pc}+\tilde{\omega }\tilde{\theta },\forall t\ge 0,\hfill \end{array}$$

(29)

with ${\alpha }_{pc}:=min\{{\omega }_{pc},2{\rho }_{pc}{\gamma }_{pc},\frac{1}{k_{{\theta }_{ref},v}}\}$, which shows the strict passivity for the mapping $\tilde{\omega }\mapsto \tilde{\theta }$, indicating the ${\mathcal{L}}_2$ stability [30]. This completes the proof. □

The inequality (29) supporting the result of Lemma 3 is the main purpose of this subsection, and it is used to prove the entire set of output-feedback system properties using Theorems 1 and 2 in Section 4.3.

4.2. Speed Error Stabilization Loop

This loop consists of three components: the speed and acceleration error observer (16)–(18), the DOB (21) and (22), and the control action (20). First, Lemma 2 provides the output error convergence behavior driven by the speed and acceleration error observer (16)–(18), which plays a vital role in showing the estimation error’s convergence property.

Lemma 4.

The speed and acceleration error observer (16)–(18) ensures the exponential convergence

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{e}_{\tilde{\theta }}\left(t\right)=e_{\tilde{\theta }}^{*}\left(t\right),\end{array}$$

subject to the gain setting $\frac{2{\overline{f}}_a}{{\omega }_{obs,\tilde{\theta }}}\approx 0$, where the desired trajectory $e_{\tilde{\theta }}^{*}\left(t\right)$ represents the solution to the first-order convergent system:

$$\begin{array}{c}\hfill {\dot{e}}_{\tilde{\theta }}^{*}\left(t\right)=-{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{\theta }}^{*}\left(t\right),\forall t\ge 0.\end{array}$$

Proof. 

The output error $e_{\tilde{\theta }}$ inherits third-order dynamics through the combination of (15)–(18) such that

$$\begin{array}{c}\hfill {\stackrel{⃛}{e}}_{\tilde{\theta }}=-3{\omega }_{obs,\tilde{\theta }}{\ddot{e}}_{\tilde{\theta }}-3{\omega }_{obs,\tilde{\theta }}^2{\dot{e}}_{\tilde{\theta }}-{\omega }_{obs,\tilde{\theta }}^3{e}_{\tilde{\theta }}+f_a,\end{array}$$

with the equivalent expression obtained from the Laplace transform:

$$\begin{array}{c}\hfill (s+{\omega }_{obs,\tilde{\theta }})E_{\tilde{\theta }}\left(s\right)=X_{1,\tilde{\theta }}\left(s\right),\forall s\in \mathbb{C},\end{array}$$

where $X_{1,\tilde{\theta }}\left(s\right)=\frac{1}{s+{\omega }_{obs,\tilde{\theta }}}{X}_{2,\tilde{\theta }}\left(s\right)$ and $X_{2,\tilde{\theta }}\left(s\right)=\frac{1}{s+{\omega }_{obs,\tilde{\theta }}}{F}_a\left(s\right)$, which defines the performance error dynamics for ${ϵ}_{\tilde{\theta }}:=e_{\tilde{\theta }}^{*}-e_{\tilde{\theta }}$ as

$$\begin{array}{c}\hfill {\dot{ϵ}}_{\tilde{\theta }}=-{\omega }_{obs,\tilde{\theta }}{ϵ}_{\tilde{\theta }}-x_{1,\tilde{\theta }},{\dot{x}}_{1,\tilde{\theta }}=-{\omega }_{obs,\tilde{\theta }}{x}_{1,\tilde{\theta }}+x_{2,\tilde{\theta }},{\dot{x}}_{2,\tilde{\theta }}=-{\omega }_{obs,\tilde{\theta }}{x}_{2,\tilde{\theta }}+f_a,\forall t\ge 0.\end{array}$$

These error dynamics yield the time derivative of the positive definite function $V_{obs,spd}:=\frac{1}{2}{ϵ}_{\tilde{\theta }}^2+\frac{k_{x_1}}{2}{x}_{1,\tilde{\theta }}^2+\frac{k_{x_2}}{2}{x}_{2,\tilde{\theta }}^2$ with $k_{x_1}>0$ and $k_{x_2}>0$ as

$$\begin{array}{ccc}\hfill {\dot{V}}_{obs,spd}& =& {ϵ}_{\tilde{\theta }}(-{\omega }_{obs,\tilde{\theta }}{ϵ}_{\tilde{\theta }}-x_{1,\tilde{\theta }})+k_{x_1}{x}_{1,\tilde{\theta }}(-{\omega }_{obs,\tilde{\theta }}{x}_{1,\tilde{\theta }}+x_{2,\tilde{\theta }})+k_{x_2}{x}_{2,\tilde{\theta }}(-{\omega }_{obs,\tilde{\theta }}{x}_{2,\tilde{\theta }}+f_a)\hfill \\ & \le & -\frac{{\omega }_{obs,\tilde{\theta }}}{2}{ϵ}_{\tilde{\theta }}^2-(k_{x,1}{\omega }_{obs,\tilde{\theta }}-\frac{1}{2{\omega }_{obs,\tilde{\theta }}}-\frac{1}{2})x_{1,\tilde{\theta }}^2-(\frac{k_{x,2}{\omega }_{obs,\tilde{\theta }}}{2}-\frac{k_{x_1}^2}{2})x_{2,\tilde{\theta }}^2\hfill \\ & & -k_{x,2}(\frac{{\omega }_{obs,\tilde{\theta }}}{2}{x}_{2,\tilde{\theta }}^2-f_a{x}_{2,\tilde{\theta }}),\forall t\ge 0,\hfill \end{array}$$

with the application of the Young’s inequality. The coefficients $k_{x_1}:=\frac{1}{{\omega }_{obs,\tilde{\theta }}}(\frac{1}{2{\omega }_{obs,\tilde{\theta }}}+1)$ and $k_{x_2}:=\frac{2}{{\omega }_{obs,\tilde{\theta }}}(\frac{k_{x,1}^2}{2}+\frac{1}{2})$ rearrange the upper bound of ${\dot{V}}_{obs,spd}$ as

$$\begin{array}{ccc}\hfill {\dot{V}}_{obs,spd}& \le & -\frac{{\omega }_{obs,\tilde{\theta }}}{2}{ϵ}_{\tilde{\theta }}^2-\frac{1}{2}{x}_{1,\tilde{\theta }}^2-\frac{1}{2}{x}_{2,\tilde{\theta }}^2,\hfill \\ & \le & -{\alpha }_{obs,spd}{V}_{obs,spd},\forall t\ge 0,\forall \left|x_{2,\tilde{\theta }}\right|\ge \frac{2{\overline{f}}_a}{{\omega }_{obs,\tilde{\theta }}},\hfill \end{array}$$

(30)

with ${\alpha }_{obs,spd}:=min\{{\omega }_{obs,\tilde{\theta }},\frac{1}{k_{x_1}},\frac{1}{k_{x_2}}\}$, which completes the proof. □

Remark 4.

The result of Lemma 2 makes it reasonable to assume that

$$\begin{array}{c}\hfill {\dot{e}}_{\tilde{\theta }}=-{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{\theta }},\forall t\ge 0,\end{array}$$

(31)

which leads to the following chain of implications (using (11)):

$$\begin{array}{ccc}\hfill {\ddot{e}}_{\tilde{\theta }}=-{\omega }_{obs,\tilde{\theta }}{\dot{e}}_{\tilde{\theta }}& \iff & (\dot{\tilde{\omega }}-{\ddot{\widehat{y}}}_{\tilde{\theta }})=-{\omega }_{obs,\tilde{\theta }}(\tilde{\omega }-{\dot{\widehat{y}}}_{\tilde{\theta }})\hfill \\ & \iff & (\dot{\tilde{\omega }}-(l_{\tilde{\theta },1}{\dot{e}}_{\tilde{\theta }}+{\dot{\widehat{x}}}_{\tilde{\omega }}))=-{\omega }_{obs,\tilde{\theta }}(\tilde{\omega }-(l_{\tilde{\theta },1}{e}_{\tilde{\theta }}+{\widehat{x}}_{\tilde{\omega }}))\hfill \\ & \iff & {\dot{e}}_{\tilde{\omega }}-l_{\tilde{\theta },1}{\dot{e}}_{\tilde{\theta }}=-{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{\omega }}+{\omega }_{obs,\tilde{\omega }}{l}_{\tilde{\theta },1}{e}_{\tilde{\theta }},\forall t\ge 0.\hfill \end{array}$$

From (31), this indicates that ${\dot{e}}_{\tilde{\omega }}=-{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{\omega }}$, $\forall t\ge 0$, which, together with (17) and following the same reasoning process above, yields ${\dot{e}}_{\tilde{a}}=-{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{a}}$, $\forall t\ge 0$. Thus, the corresponding vector form for $e_{\tilde{\omega }}:={\left[\begin{array}{cc}{e}_{\tilde{\omega }}& e_{\tilde{a}}\end{array}\right]}^T$ is obtained as

$$\begin{array}{c}\hfill {\dot{e}}_{\tilde{\omega }}=-{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{\omega }},\forall t\ge 0,\end{array}$$

(32)

which plays a vital role in showing the beneficial closed-loop properties described by Theorems 1 and 2 in Section 4.3.

Lemma 5 presents the motion of the disturbance estimate ${\widehat{d}}_{\omega }\left(t\right)$ governed by the observer-based nonlinear DOB (21) and (22).

Lemma 5.

The observer-based nonlinear DOB (21) and (22) drives the disturbance estimate ${\widehat{d}}_{\omega }$ to satisfy

$$\begin{array}{c}\hfill {\dot{\widehat{d}}}_{\omega }\left(t\right)=l_{d_{\omega }}(d_{\omega }\left(t\right)-{\widehat{d}}_{\omega }\left(t\right))+c_{d_{\omega }}^T{e}_{\tilde{\omega }}\left(t\right),\forall t\ge 0,\end{array}$$

(33)

for some constant vector $c_{d_{\omega }}\in {\mathbb{R}}^2$.

Proof. 

The time derivative of the output (22) is obtained along the dynamics (21) as

$$\begin{array}{ccc}\hfill {\dot{\widehat{d}}}_{\omega }& =& {\dot{z}}_{d_{\omega }}+l_{d_{\omega }}{c}_{\omega ,0}{\dot{\widehat{x}}}_{\tilde{a}}\hfill \\ & =& -l_{d_{\omega }}({\widehat{d}}_{\omega }-l_{d_{\omega }}{c}_{\omega ,0}{\widehat{x}}_{\tilde{a}})-l_{d_{\omega }}^2{c}_{\omega ,0}{\widehat{x}}_{\tilde{a}}+l_{d_{\omega }}{v}_s+l_{d_{\omega }}{c}_{\omega ,0}\ddot{\tilde{\omega }}-l_{d_{\omega }}{c}_{\omega ,0}{\dot{e}}_{\tilde{a}}\hfill \\ & =& l_{d_{\omega }}(c_{\omega ,0}\ddot{\tilde{\omega }}+v_s-{\widehat{d}}_{\omega })-l_{d_{\omega }}{c}_{\omega ,0}{\omega }_{obs,\tilde{\theta }}{e}_{\tilde{a}}\hfill \\ & =& l_{d_{\omega }}(d_{\omega }-{\widehat{d}}_{\omega })-l_{d_{\omega }}{c}_{\omega ,0}{\omega }_{obs,\tilde{\theta }}{e}_2^T{e}_{\tilde{\omega }},\hfill \end{array}$$

where the result of Remark 4 verifies the third equality above, which completes the proof. □

The definition of the disturbance estimation error $e_{d_{\omega }}:=d_{\omega }-{\widehat{d}}_{\omega }$, together with (33), gives

$$\begin{array}{c}\hfill {\dot{e}}_{d_{\omega }}\left(t\right)=-l_{d_{\omega }}{e}_{d_{\omega }}\left(t\right)-c_{d_{\omega }}^T{e}_{\tilde{\omega }}\left(t\right)+f_{d_{\omega }}\left(t\right),\forall t\ge 0,\end{array}$$

(34)

with $f_{d_{\omega }}:={\dot{d}}_{\omega }$ and $|f_{d_{\omega }}|\le {\overline{f}}_{d_{\omega }}$, $\forall t\ge 0$, which is used in the proofs for Theorems 1 and 2 in Section 4.3. Lemma 6 provides the closed-loop speed error behavior governed by the control action (20) causing the order reduction because of the pole-zero cancellation nature.

Lemma 6.

The proposed speed error stabilization loop shown in Figure 1 guarantees the perturbed first-order speed error dynamics

$$\begin{array}{c}\hfill \dot{\tilde{\omega }}\left(t\right)=-{\lambda }_{\omega }\tilde{\omega }\left(t\right)+a_{\tilde{\omega },1}{x}_e\left(t\right),\end{array}$$

(35)

with the filtered signal $x_e\left(t\right)$ such that

$$\begin{array}{c}\hfill {\dot{x}}_e\left(t\right)=-a_{\tilde{\omega },2}{x}_e\left(t\right)+(e_{d_{\omega }}\left(t\right)+c_{\tilde{\omega }}^T{e}_{\tilde{\omega }}\left(t\right)),\forall t\ge 0,\end{array}$$

(36)

for some constant $a_{\tilde{\omega },i}>0$, $i=1,2$ and constant vector $c_{\tilde{\omega }}\in {\mathbb{R}}^2$.

Proof. 

The substitution of the proposed speed error stabilizer (20) into the open-loop dynamics (19) results in

$$\begin{array}{ccc}\hfill c_{\omega ,0}\ddot{\tilde{\omega }}& =& -(k_{d,\omega }+c_{\omega ,0}{\lambda }_{\omega })\dot{\tilde{\omega }}-k_{d,\omega }{\lambda }_{\omega }\tilde{\omega }+e_{d_{\omega }}+c_{\tilde{\omega }}^T{e}_{\tilde{\omega }}\hfill \\ & =& -k_{d,\omega }\dot{\tilde{\omega }}+c_{\omega ,0}{\lambda }_{\omega }(\dot{r}-\dot{\tilde{\omega }})+k_{d,\omega }{\lambda }_{\omega }(r-\tilde{\omega })+e_{d_{\omega }}+c_{\tilde{\omega }}^T{e}_{\tilde{\omega }},\forall t\ge 0,\hfill \end{array}$$

where $r:=0$ (such that $\dot{r}=0$) and $c_{\tilde{\omega }}:={\left[\begin{array}{cc}{k}_{d,\omega }{\lambda }_{\omega }& (k_{d,\omega }+c_{\omega ,0}{\lambda }_{\omega })\end{array}\right]}^T$, whose equivalent form is obtained by taking the Laplace transform of both sides:

$$\begin{array}{c}\hfill (c_{\omega ,0}{s}^2+(k_{d,\omega }+c_{\omega ,0}{\lambda }_{\omega })s+k_{d,\omega }{\lambda }_{\omega })\tilde{\Omega }\left(s\right)={\lambda }_{\omega }(c_{\omega ,0}s+k_{d,\omega })R\left(s\right)+E_{d_{\omega }}\left(s\right)+c_{\tilde{\omega }}^T{E}_{\tilde{\omega }}\left(s\right),\end{array}$$

$\forall s\in \mathbb{C}$. This causes the order reduction through the factorization $(c_{\omega ,0}{s}^2+(k_{d,\omega }+c_{\omega ,0}{\lambda }_{\omega })s+k_{d,\omega }{\lambda }_{\omega })=(c_{\omega ,0}s+k_{d,\omega })(s+{\lambda }_{\omega })$ such that

$$\begin{array}{c}\hfill (s+{\lambda }_{\omega })\tilde{\Omega }\left(s\right)={\lambda }_{\omega }R\left(s\right)+\frac{1}{c_{\omega ,0}}{X}_e\left(s\right),\forall s\in \mathbb{C},\end{array}$$

with $X_e\left(s\right):=\frac{1}{s+\frac{k_{d,\omega }}{c_{\omega ,0}}}(E_{d_{\omega }}\left(s\right)+c_{\tilde{\omega }}^T{E}_{\tilde{\omega }}\left(s\right))$, which completes the proof by taking the inverse Laplace transform. □

The closed-loop speed error dynamics (35) and (36) as the main results of this subsection help to prove the useful closed-loop properties described by Theorems 1 and 2 in Section 4.3.

4.3. Entire System Properties

This subsection provides the main analysis results using the subsystem properties given by Lemmas 1–6. Theorem 1 proves the boundedness property of the position error controlled by the proposed output-feedback system shown in Figure 1.

Theorem 1.

The proposed output-feedback system shown in Figure 1 guarantees the boundedness property

$$\begin{array}{c}\hfill |\tilde{\theta }\left(t\right)|\le c_1{e}^{-c_{2}t},\forall t\ge 0,\forall \left|e_{d_{\omega }}\right|\ge \frac{2{\overline{f}}_{d_{\omega }}}{l_{d_{\omega }}}\end{array}$$

(37)

for some constant $c_i>0$, $i=1,2$.

Proof. 

Considering (35) and (36), it follows from ${\mathbf{x}}_{sc}:={\left[\begin{array}{cc}\tilde{\omega }& x_e\end{array}\right]}^T$ that

$$\begin{array}{c}\hfill {\dot{\mathbf{x}}}_{sc}={\mathbf{A}}_{sc}{\mathbf{x}}_{sc}+e_2(e_{d_{\omega }}+c_{\tilde{\omega }}^T{e}_{\tilde{\omega }}),\forall t\ge 0,\end{array}$$

(38)

where ${\mathbf{A}}_{sc}:=\left[\begin{array}{cc}-{\lambda }_{\omega }& a_{\tilde{\omega },1}\\ 0& -a_{\tilde{\omega },2}\end{array}\right]$ and $e_2:=\left[\begin{array}{c}0\\ 1\end{array}\right]$. The stability of ${\mathbf{A}}_{sc}$ ensures the existence of the unique solution ${\mathbf{P}}_{sc}>\mathbf{0}$ to the matrix equation ${\mathbf{A}}_{sc}^T{\mathbf{P}}_{sc}+{\mathbf{P}}_{sc}{\mathbf{A}}_{sc}=-\mathbf{I}$, which defines the positive definite function as

$$\begin{array}{c}\hfill V:=V_{pc}+\frac{k_{sc}}{2}{\mathbf{x}}_{sc}^T{\mathbf{P}}_{sc}{\mathbf{x}}_{sc}+\frac{k_{d_{\omega }}}{2}{e}_{d_{\omega }}^2+\frac{k_{\tilde{\omega }}}{2}{\parallel e_{\tilde{\omega }}\parallel }^2,k_{sc}>0,k_{d_{\omega }}>0,k_{\tilde{\omega }}>0\forall t\ge 0,\end{array}$$

whose time derivative is obtained using (29), (32), (34), and (38):

$$\begin{array}{ccc}\hfill \dot{V}& =& {\dot{V}}_{pc}+k_{sc}{\mathbf{x}}_{sc}^T{\mathbf{P}}_{sc}({\mathbf{A}}_{sc}{\mathbf{x}}_{sc}+e_2(e_{d_{\omega }}+c_{\tilde{\omega }}^T{e}_{\tilde{\omega }}))+k_{d_{\omega }}{e}_{d_{\omega }}(-l_{d_{\omega }}{e}_{d_{\omega }}-c_{d_{\omega }}^T{e}_{\tilde{\omega }}+f_{d_{\omega }})\hfill \\ & & -k_{\tilde{\omega }}{\omega }_{obs,\tilde{\theta }}{\parallel e_{\tilde{\omega }}\parallel }^2\hfill \\ & \le & -\frac{{\alpha }_{pc}}{2}{V}_{pc}-(k_{sc}-\frac{1}{2{\alpha }_{pc}}-1){\parallel {\mathbf{x}}_{sc}\parallel }^2-(\frac{k_{d_{\omega }}{l}_{d_{\omega }}}{2}-\frac{k_{sc}^2{\parallel {\mathbf{P}}_{sc}\parallel }^2}{2}-\frac{1}{2})e_{d_{\omega }}^2\hfill \\ & & -(k_{\tilde{\omega }}{\omega }_{obs,\tilde{\theta }}-\frac{k_{sc}^2\parallel {\mathbf{P}}_{sc}{\parallel }^2{\parallel c_{\tilde{\omega }}\parallel }^2}{2}-\frac{k_{d_{\omega }}^2{\parallel c_{d_{\omega }}\parallel }^2}{2}){\parallel e_{\tilde{\omega }}\parallel }^2-k_{d_{\omega }}(\frac{l_{d_{\omega }}}{2}{e}_{d_{\omega }}^2-f_{d_{\omega }}{e}_{d_{\omega }}),\forall t\ge 0.\hfill \end{array}$$

The coefficients $k_{sc}:=\frac{1}{2{\alpha }_{pc}}+\frac{3}{2}$, $k_{d_{\omega }}:=\frac{2}{l_{d_{\omega }}}(\frac{k_{sc}^2{\parallel {\mathbf{P}}_{sc}\parallel }^2}{2}+1)$, and $k_{\tilde{\omega }}:=\frac{1}{{\omega }_{obs,\tilde{\theta }}}(\frac{k_{sc}^2\parallel {\mathbf{P}}_{sc}{\parallel }^2{\parallel c_{\tilde{\omega }}\parallel }^2}{2}+\frac{k_{d_{\omega }}^2{\parallel c_{d_{\omega }}\parallel }^2}{2}+\frac{1}{2})$ rearrange the upper bound of $\dot{V}$ as

$$\begin{array}{ccc}\hfill \dot{V}& \le & -\frac{{\alpha }_{pc}}{2}{V}_{pc}-\frac{1}{2}\parallel {\mathbf{x}}_{sc}{\parallel }^2-\frac{1}{2}{e}_{d_{\omega }}^2-\frac{1}{2}{\parallel e_{\tilde{\omega }}\parallel }^2\hfill \\ & \le & -\alpha V,\forall t\ge 0,\forall |e_{d_{\omega }}|\ge \frac{2{\overline{f}}_{d_{\omega }}}{l_{d_{\omega }}},\hfill \end{array}$$

(39)

with $\alpha :=min\{\frac{{\alpha }_{pc}}{2},\frac{1}{k_{sc}{\lambda }_{max}\left({\mathbf{P}}_{sc}\right)},\frac{1}{k_{d_{\omega }}},\frac{1}{k_{\tilde{\omega }}}\}$. This completes the proof by using the comparison principle in [30]. □

Theorem 1 roughly derives the exponential position convergence

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\theta \left(t\right)={\theta }_{ref}\left(t\right),\end{array}$$

with a large DOB gain $l_{d_{\omega }}$ such that $\frac{2{\overline{f}}_{d_{\omega }}}{l_{d_{\omega }}}\approx 0$ by showing that $\dot{V}\le -\alpha V$, $\forall t\ge 0$, from inequality (39), which is assumed when proving the main result in Theorem 2.

Theorem 2.

The proposed output-feedback system shown in Figure 1 accomplishes the control objective (7) (e.g., the exponential convergence ${lim}_{t\to \infty }\tilde{\theta }\left(t\right)={\tilde{\theta }}^{*}\left(t\right)$).

Proof. 

Defining the performance error as ${ϵ}^{*}:={\tilde{\theta }}^{*}-\tilde{\theta }$ means that

$$\begin{array}{ccc}\hfill {\dot{ϵ}}^{*}& =& {\dot{\tilde{\theta }}}^{*}-\dot{\tilde{\theta }}=-{\widehat{\omega }}_{pc}{\tilde{\theta }}^{*}+{\widehat{\omega }}_{pc}\tilde{\theta }-e_{{\theta }_{ref,v}}-\tilde{\omega }\hfill \\ & =& -{\widehat{\omega }}_{pc}{ϵ}^{*}-e_{{\theta }_{ref,v}}-\tilde{\omega },\forall t\ge 0,\hfill \end{array}$$

which turns the composite-type positive definite function

$$\begin{array}{c}\hfill V^{*}:=\frac{1}{2}{\left({ϵ}^{*}\right)}^2+\kappa V,\kappa >0,\forall t\ge 0,\end{array}$$

into (using feedback gain boosting property ${\widehat{\omega }}_{pc}\ge {\omega }_{pc}$ shown in Lemma 1)

$$\begin{array}{ccc}\hfill {\dot{V}}^{*}& =& {ϵ}^{*}(-{\widehat{\omega }}_{pc}{ϵ}^{*}-e_{{\theta }_{ref,v}}-\tilde{\omega })+\kappa \dot{V}\hfill \\ & \le & -\frac{{\omega }_{pc}}{3}{\left({ϵ}^{*}\right)}^2-(\kappa \alpha -\frac{3}{2{\omega }_{pc}{k}_{sc}{\lambda }_{min}\left({\mathbf{P}}_{sc}\right)}-\frac{3}{2{\omega }_{pc}{k}_{{\theta }_{ref},v}})V,\forall t\ge 0,\hfill \end{array}$$

with the application of Young’s inequality. The coefficient $\kappa :=\frac{1}{\alpha }(\frac{3}{2{\omega }_{pc}{k}_{sc}{\lambda }_{min}\left({\mathbf{P}}_{sc}\right)}+\frac{3}{2{\omega }_{pc}{k}_{{\theta }_{ref},v}}+1)$ rearranges the upper bound of ${\dot{V}}^{*}$ as

$$\begin{array}{c}\hfill {\dot{V}}^{*}\le -\frac{{\omega }_{pc}}{3}{\left({ϵ}^{*}\right)}^2-V\le -{\alpha }^{*}{V}^{*},\forall t\ge 0,\end{array}$$

where ${\alpha }^{*}:=min\{\frac{2{\omega }_{pc}}{3},\frac{1}{\kappa }\}$, which completes the proof. □

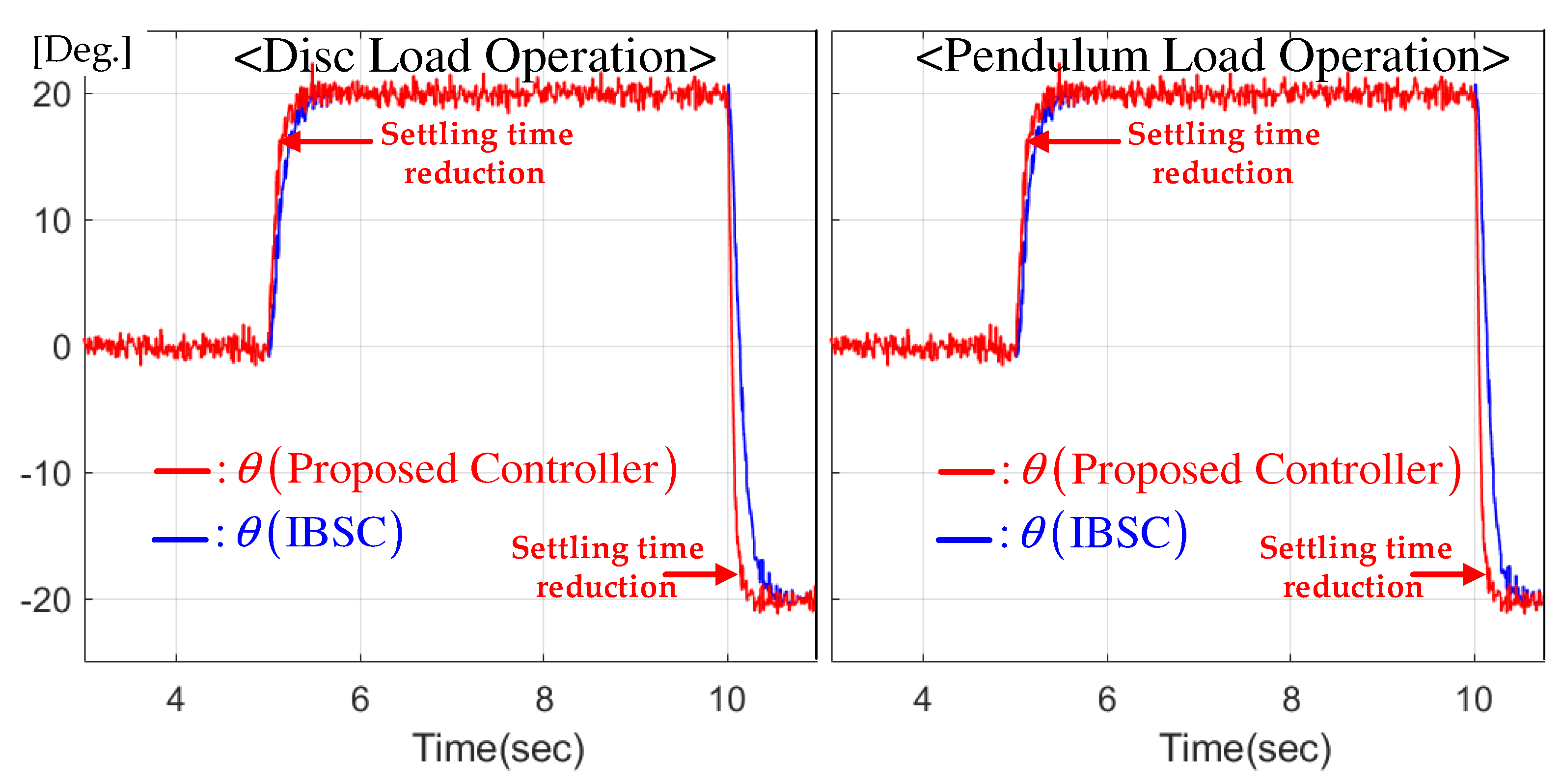
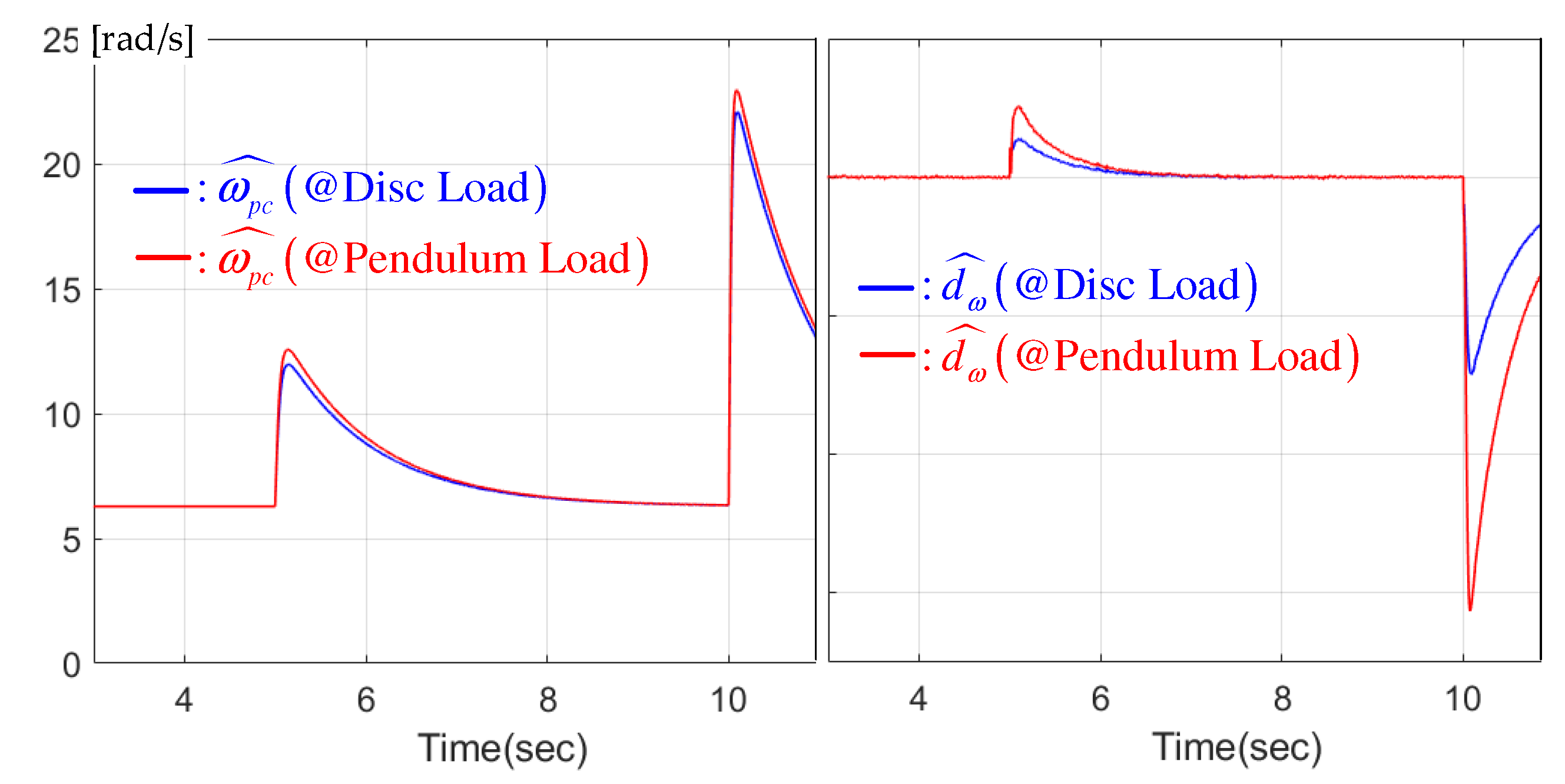
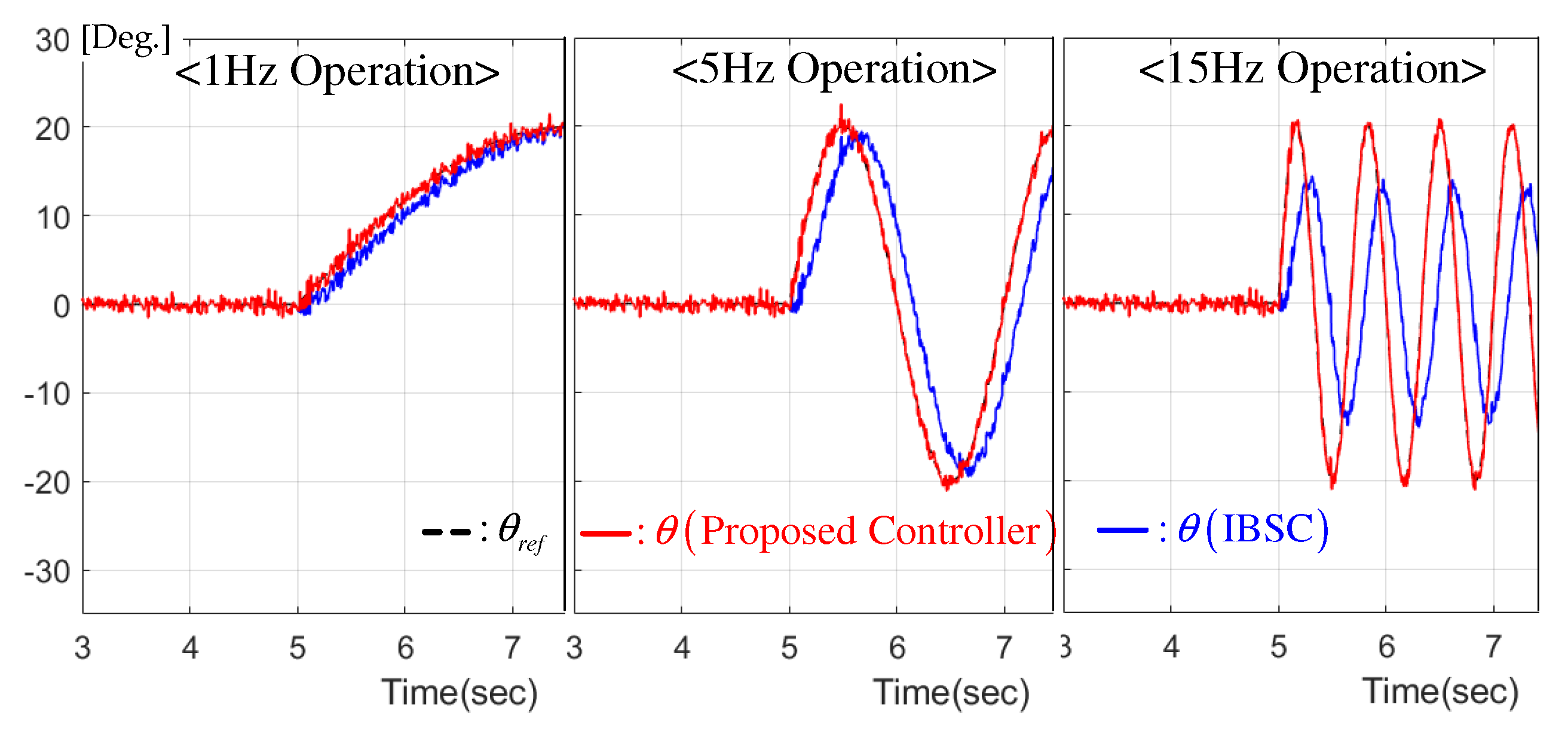
5. Experimental Results

This section provides experimental comparison data as actual evidence that demonstrates the effectiveness of the proposed technique. Data were obtained from the experimental platform in Figure 2 comprising the QUBE-servo2 (servo system), myRIO-1900 (processor), and LabVIEW software. The nominal servo system parameters were set as $J_{m,0}=0.7J_m$, $B_{m,0}=1.1B_m$, $R_{a,0}=0.8R_a$, $L_{a,0}=1.2L_a$, and $k_{T,0}=k_{e,0}=1.3k_T$, based on manufacturer values $J_m$, $B_m$, $R_a$, $L_a$, $k_T$, and $k_e$ (see the datasheet provided by Quanser). The MathScript in LabVIEW software implemented the control and estimation algorithms under control and sampling periods of $0.1$ ms.

The tuning result of the proposed controller is given by: (position reference derivative observer) ${\omega }_{obs,{\theta }_{ref}}=1200$, (position-tracking control) $f_{pc}=1$ Hz (${\omega }_{pc}=2\pi f_{pc}=6.28$ rad/s), ${\gamma }_{pc}=1000$, ${\rho }_{pc}=1000/{\gamma }_{pc}$, (speed and acceleration error observers) ${\omega }_{\tilde{\theta }}=1800$, (speed error stabilizer) $k_{d,\omega }=0.01$, ${\lambda }_{\omega }=600$, and (DOB) $l_{d_{\omega }}=300$.

An integral back-stepping controller (IBSC) including the active-damping injection term was used for the comparison study, which is given by (position loop) ${\omega }_{ref}\left(t\right)={\omega }_{pc}\tilde{\theta }\left(t\right)$, (speed loop) $i_{s,ref}\left(t\right)=\frac{1}{k_{T,0}}(-k_{d,sc}\omega \left(t\right)+J_0{\omega }_{sc}\tilde{\omega }\left(t\right)+k_{d,sc}{\omega }_{sc}{\int }_0^t\tilde{\omega }\left(\tau \right)d\tau )$, $\tilde{\omega }\left(t\right)={\omega }_{ref}\left(t\right)-\omega \left(t\right)$, (current loop) $v_s\left(t\right)=-k_{d,cc}{i}_s\left(t\right)+L_0{\omega }_{cc}{\tilde{i}}_s\left(t\right)+k_{d,cc}{\omega }_{cc}{\int }_0^t{\tilde{i}}_s\left(\tau \right)d\tau +k_{T,0}\omega \left(t\right)$, and ${\tilde{i}}_s\left(t\right):=i_{s,ref}\left(t\right)-i_s\left(t\right)$, with its tuning results: (active damping) $k_{d,sc}=0.02$, $k_{d,cc}=1$, (speed and current cut-off frequencies) ${\omega }_{sc}=2\pi 5$ rad/s, ${\omega }_{cc}=2\pi 100$ rad/s.

The positioning performances of these two controllers were evaluated under the tracking and regulation tasks for two different loads—disc and pendulum loads—to clarify the closed-loop robustness improvement against load variations.

5.1. Reference Trajectory Tracking Performance

This subsection highlights the performance improvement by investigating the position tracking behavior for two different cases: a piece-wise constant reference (in stair form) and sinusoidal references.

5.1.1. Case I: Stair Reference

This experiment sets the position reference to zero initially and increases and decreases it to 20 and $-20$ sequentially. Figure 3 indicates the position tracking behaviors using the proposed and IBSC techniques and shows that the proposed controller shortens the transient periods without any over-/undershoots with the cooperation of the feedback-gain learning mechanism that ensures the boosting property proven in Lemma 1.

The left panel of Figure 4 presents the actual position feedback gain responses from the feedback-gain learning mechanism (14). The right panel of Figure 4 shows the observer-based nonlinear DOB responses. Figure 5 indicates the rapid state estimation error removal performance from the speed and acceleration error observers, leading to the closed-loop performance improvement shown in Figure 3.

5.1.2. Case II: Sinusoidal Reference

This experiment considered three different sinusoidal position references increasing in frequency 1, 5, and 15 Hz under the pendulum load condition. As indicated in Figure 6, a significant performance improvement was observed owing to the perfect trajectory tracking nature of the proposed technique without any distortion between the reference and the actual servo system position. The exponential convergence property proven in Theorem 2 provides this meaningful advantage in cooperation with the novel subsystems shown in Figure 1.

5.2. Constant Reference Regulation Performance

This experiment fixed the position reference to zero while a load torque ($T_L=0.002$ Nm, requiring a stator current $i_s\approx 1.23$ A, as shown in Figure 8) was suddenly applied to the closed-loop system. Figure 7 presents a considerable regulation performance improvement using the proposed controller, eliminating the transient periods despite the abrupt change in load condition. The corresponding dynamic current responses are shown in Figure 8, which shows that there were no significant differences from the current responses driven by the proposed and IBSC technique, but in improvement in the position regulation performance was observed, as shown in Figure 7, due to the novel subsystems for the position loop.

6. Conclusions

This study proposes an advanced solution to the position-tracking problem for servo systems, incorporating intelligence and improved robustness in the feedback loop. The systematic controller design process not only results in beneficial closed-loop properties by analyzing the closed-loop dynamics, but also provides a significant tracking performance improvement for time-varying reference trajectories without any phase delay or magnitude distortions based on the experimental study results. This result will be extended to multi-servo system synchronization applications, considering the interactions between local agents as disturbances, in a future study.