Description of Hot Compressive Stress-Strain Curves Using Transfer Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Steel Fabrication and Sample Preparation
2.2. Modeling Using Transfer Functions and Model Accuracy Estimation Method
3. Results
3.1. Comparison of Measured and Model-Calculated Stress-Strain Curves
3.2. Polynomial Transfer Function Coefficients
3.3. Implemantation of Transfer Functions in other Simulation and Industrial Environents
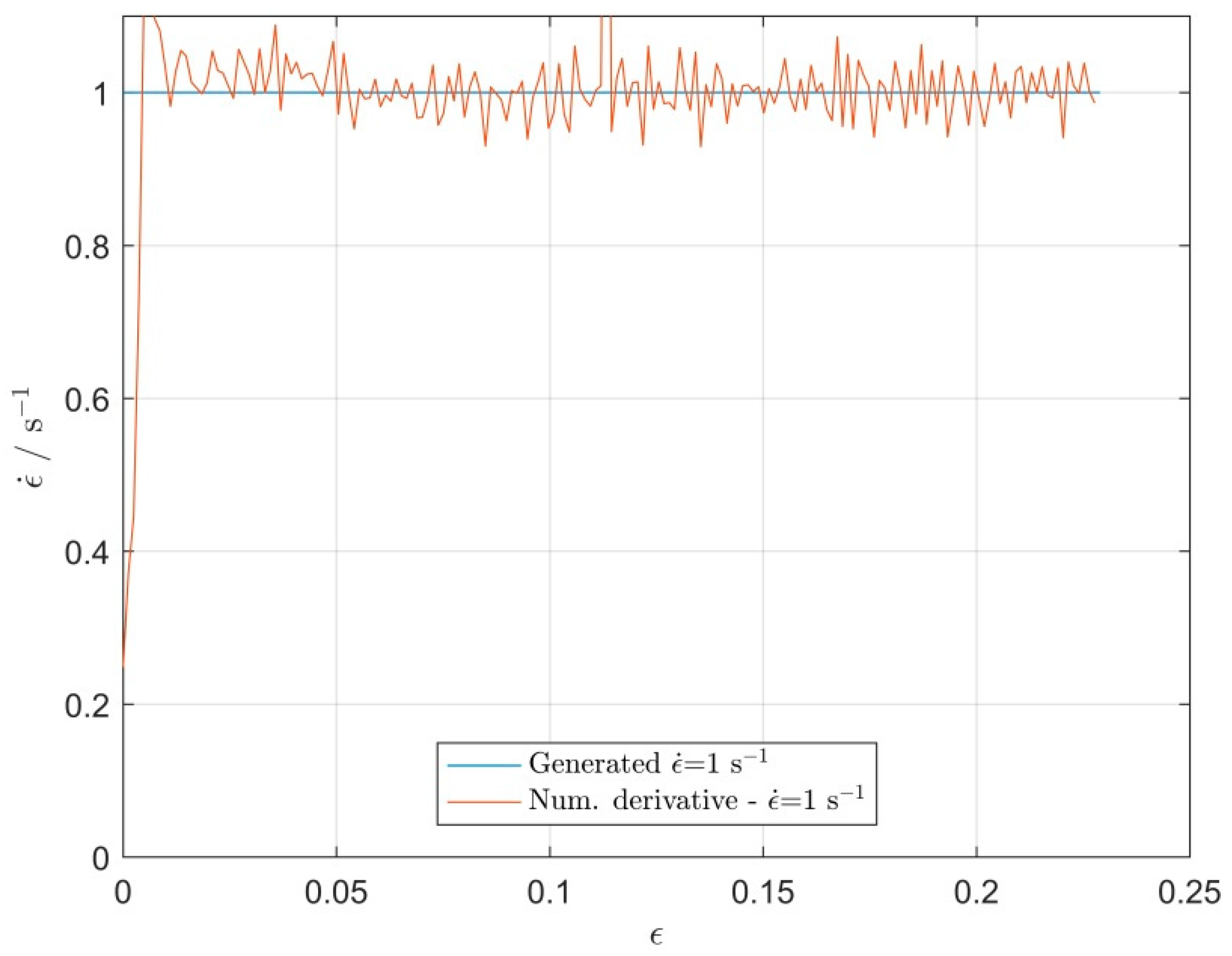
3.4. Some Aspects of Strain Rate Input Signal
3.5. Stress Prediction for Non-Constant Strain Rates
3.6. Zero Pole Analyses of Obtained Transfer Functions
4. Discussion
5. Conclusions
- Continuous type TF can accurately describe hot-deformation stress-strain relationship, but the individual model has to be used for specific temperature and strain-rate conditions.
- A disadvantage of the proposed TF model is a higher number of model parameters.
- Choices of strain or strain rate for input signal leads to comparable accuracy of obtained models. Selection of strain rate however leads to more dense roots of TF polynomials.
- Similar effect on roots of TF polynomials is obtained by substitution of time with strain in Laplacian transformation.
- Second or third order TF polynomials seem to offer appropriate dynamics for stress strain relationship description, but later offer better accuracy.
- Once TF polynomials are determined, one can easily predict strain response on any ‘reasonable’ strain-rate signal or measurement.
- Transfer Functions models are nowadays supported by most PLCs, PACs and other numerical computational environments and therefore description of stress-strain relationship by TF is supported down to the industrial level. If not by TF, one can transform TF to the preferable model form.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, D.-H.; Liu, Y.-M.; Sun, J.; Zhao, D.-W. A novel analytical approach to predict rolling force in hot strip finish rolling based on cosine velocity field and equal area criterion. Int. J. Adv. Manuf. Technol. 2016, 54, 843–850. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile deformation. Trans. AIME 1945, 12, 268–290. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates, and High Temperatures; ScienceOpen, Inc.: Burlington, MA, USA, 1983; pp. 541–547. [Google Scholar]
- Mirzadeh, H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions. Mech. Mater. 2015, 85, 66–79. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson–Cook, modified Johnson–Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, C.; Zhang, L.; Shen, W.; Xu, Q. A comparative study of constitutive models for flow stress behavior of medium carbon Cr–Ni–Mo alloyed steel at elevated temperature. J. Mater. Res. 2017, 32, 3875–3884. [Google Scholar] [CrossRef]
- Yang, L.-C.; Pan, Y.-T.; Chen, I.-G.; Lin, D.-Y.; Yang, L.-C.; Pan, Y.-T.; Chen, I.-G.; Lin, D.-Y. Constitutive Relationship Modeling and Characterization of Flow Behavior under Hot Working for Fe–Cr–Ni–W–Cu–Co Super-Austenitic Stainless Steel. Metals 2015, 5, 1717–1731. [Google Scholar] [CrossRef]
- Jorge Junior, A.M.; Balancin, O. Prediction of steel flow stresses under hot working conditions. Mater. Res. 2005, 8, 309–315. [Google Scholar] [CrossRef]
- Kugler, G.; Turk, R. Modeling the dynamic recrystallization under multi-stage hot deformation. Acta Mater. 2004, 52, 4659–4668. [Google Scholar] [CrossRef]
- Orend, J.; Hagemann, F.; Klose, F.B.; Maas, B.; Palkowski, H. A new unified approach for modeling recrystallization during hot rolling of steel. Mater. Sci. Eng. A 2015, 647, 191–200. [Google Scholar] [CrossRef]
- Lin, Y.C.; Liu, G. A new mathematical model for predicting flow stress of typical high-strength alloy steel at elevated high temperature. Comput. Mater. Sci. 2010, 48, 54–58. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Shen, W.; Liu, C.; Xia, Y.; Li, R. Study on constitutive modeling and processing maps for hot deformation of medium carbon Cr–Ni–Mo alloyed steel. Mater. Des. 2016, 90, 804–814. [Google Scholar] [CrossRef]
- Zheng, L.; Lee, T.L.; Liu, N.; Li, Z.; Zhang, G.; Mi, J.; Grant, P.S. Numerical and physical simulation of rapid microstructural evolution of gas atomised Ni superalloy powders. Mater. Des. 2017, 117, 157–167. [Google Scholar] [CrossRef]
- Vode, F.; Burja, J.; Tehovnik, F.; Arh, B. Lumped paramter model with inner state variables for modelling hot deformability of steels. Metalurgija 2017, 56, 111–114. [Google Scholar]
- Zhang, L.; Gong, D.; Li, Y.; Wang, X.; Ren, X.; Wang, E.; Zhang, L.; Gong, D.; Li, Y.; Wang, X.; et al. Effect of Quenching Conditions on the Microstructure and Mechanical Properties of 51CrV4 Spring Steel. Metals 2018, 8, 1056. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, F.; Lai, C.; Li, H.; Zhang, Q.; Luo, D. High Temperature Hot Deformation Behavior and Constitutive Model Construction of High Quality 51CrV4 Spring Steel. In Chinese Materials Conference; Springer: Singapore, 2018; pp. 191–199. [Google Scholar]
- Gavin, H.P. Linear Time-Invariant Dynamical Systems; Duke University: Durham, NC, USA, 2018. [Google Scholar]
- MATLAB, + Simulink2018a; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Eaton, J.W.; Bateman, D.; Hauberg, S. GNU Octave, version 4.2.2; Network Theory: London, UK, 2017. [Google Scholar]
- Akbari, Z.; Mirzadeh, H.; Cabrera, J.-M. A simple constitutive model for predicting flow stress of medium carbon microalloyed steel during hot deformation. Mater. Des. 2015, 77, 126–131. [Google Scholar] [CrossRef]
- Wu, H.-Y.; Yang, J.-C.; Zhu, F.-J.; Wu, C.-T. Hot compressive flow stress modeling of homogenized AZ61 Mg alloy using strain-dependent constitutive equations. Mater. Sci. Eng. A 2013, 574, 17–24. [Google Scholar] [CrossRef]
- Mirzadeh, H. Physically based constitutive description of OFHC copper at hot working conditions. Met. Mater. 2016, 53, 105–111. [Google Scholar] [CrossRef]
- Won Lee, H.; Im, Y.-T. Numerical modeling of dynamic recrystallization during nonisothermal hot compression by cellular automata and finite element analysis. Int. J. Mech. Sci. 2010, 52, 1277–1289. [Google Scholar] [CrossRef]
- Mazur, P.; Chmiel, M.; Czerwinski, R. Central processing unit of IEC 61131-3-based PLC. IFAC-PapersOnLine 2016, 49, 454–459. [Google Scholar] [CrossRef]
- Clarket, D.W.; Mohtadit, C.; Tuffs, P.S. Generalized Predictive Control Algorithm* Part, I. The Basic; Elsevier: New York, NY, USA, 1987; Volume 23. [Google Scholar]
- Abed, F.; Abdul-Latif, A.; Yehia, A.; Abed, F.; Abdul-Latif, A.; Yehia, A. Experimental Study on the Mechanical Behavior of EN08 Steel at Different Temperatures and Strain Rates. Metals 2018, 8, 736. [Google Scholar] [CrossRef]
- Enginsoy, H.; Bayraktar, E.; Kurşun, A.; Enginsoy, H.M.; Bayraktar, E.; Kurşun, A. A Comprehensive Study on the Deformation Behavior of Hadfield Steel Sheets Subjected to the Drop Weight Test: Experimental Study and Finite Element Modeling. Metals 2018, 8, 734. [Google Scholar] [CrossRef]
- Leith, D.J.; Leithead, W.E. Survey of gain-scheduling analysis and design. Int. J. Control 2000, 73, 1001–1025. [Google Scholar] [CrossRef]
- Michael, S.; Triantafyllou, F.S.H. Maneuring and Control of Marine Vehicles; Massachusetts Institute of Technology: Cambridge, MA, USA, 2003. [Google Scholar]
- Suttner, S.; Merklein, M. A new approach for the determination of the linear elastic modulus from uniaxial tensile tests of sheet metals. J. Mater. Process. Technol. 2017, 241, 64–72. [Google Scholar] [CrossRef]
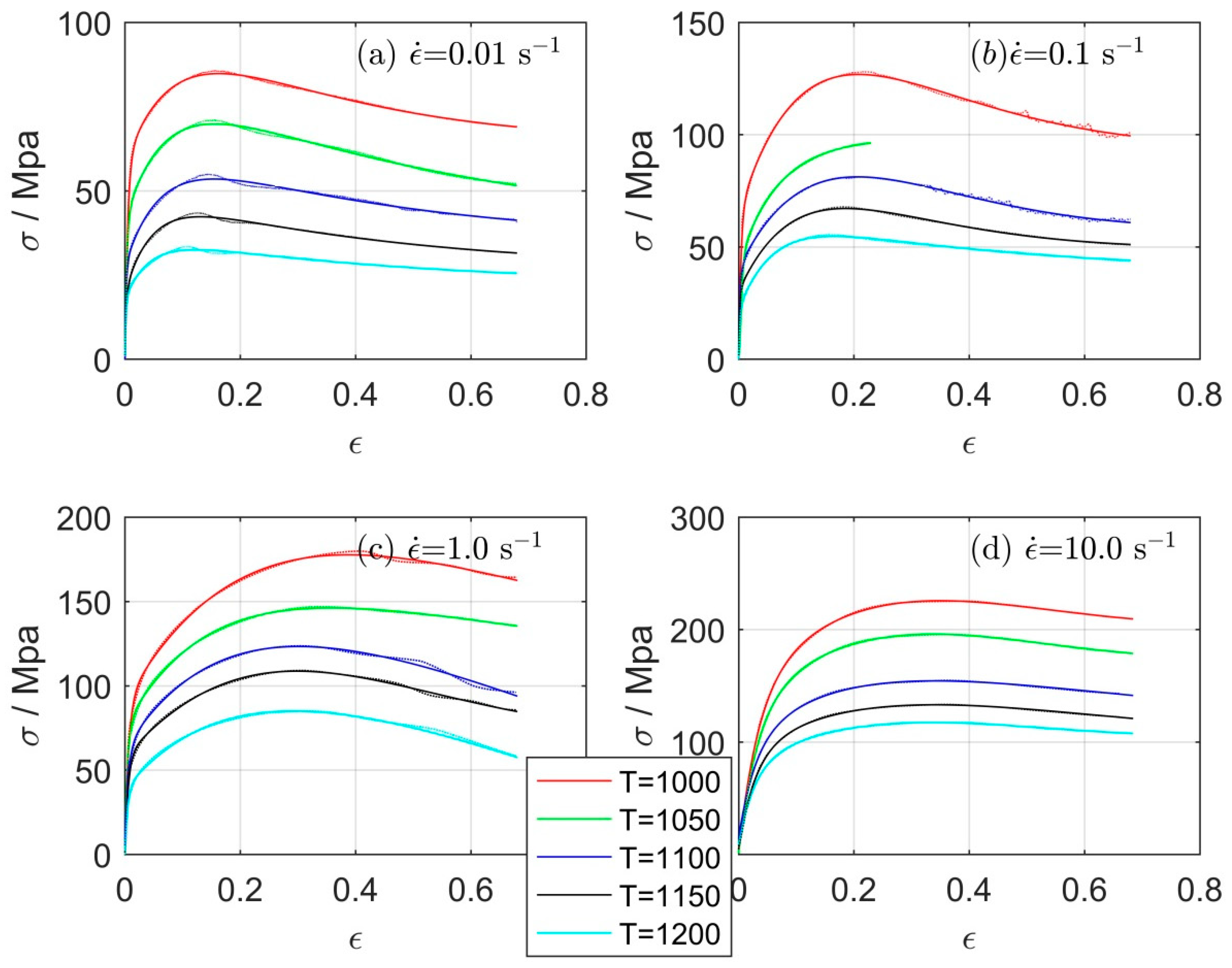

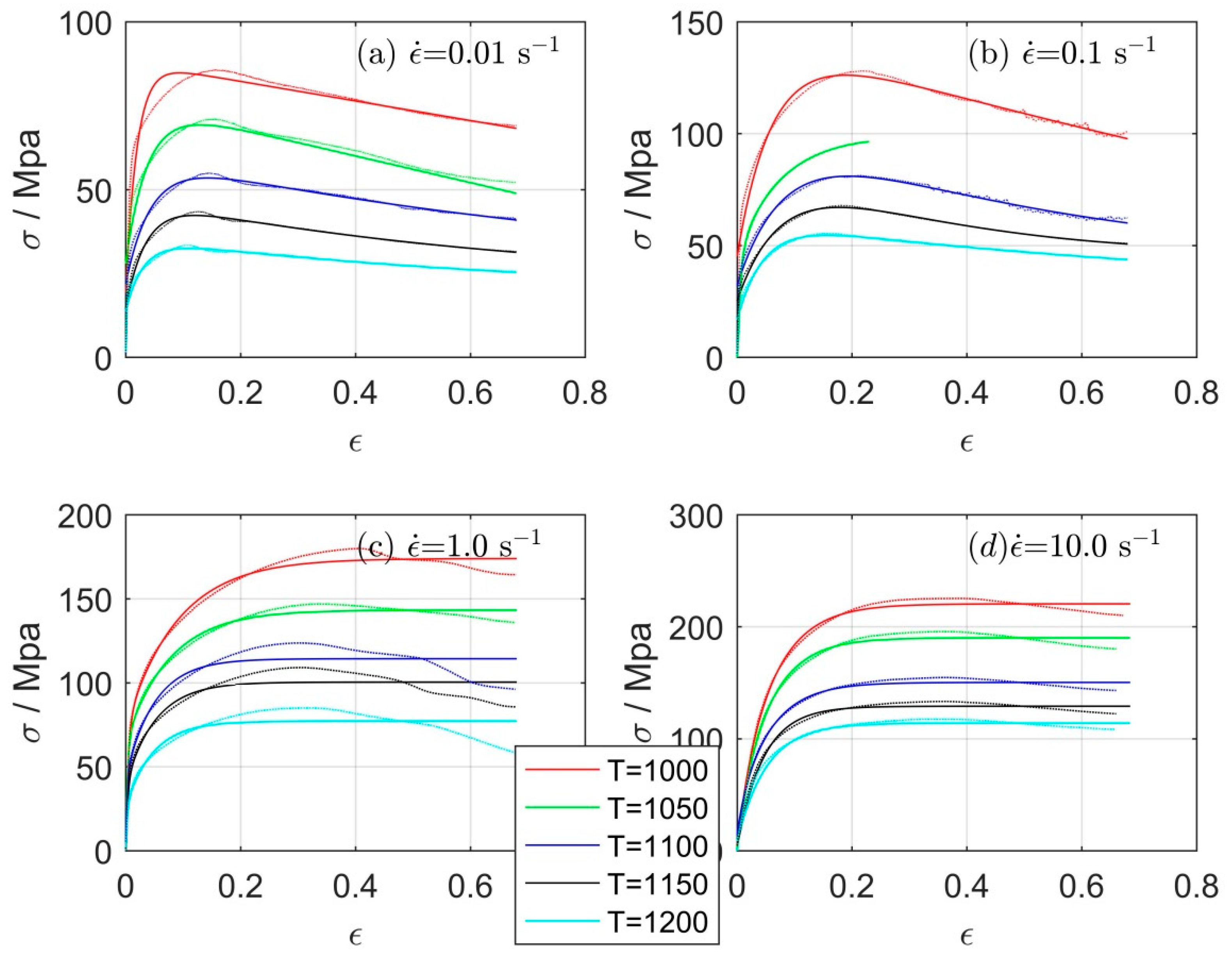
| C | Si | Mn | Cr | V |
|---|---|---|---|---|
| 0.50 | 0.30 | 0.95 | 1.00 | 0.15 |
| AARE/% | T = 1000 °C | T = 1050 °C | T = 1100 °C | T = 1150 °C | T = 1200 °C |
|---|---|---|---|---|---|
| = 0.01 s−1 | 0.82 | 0.93 | 1.05 | 0.64 | 0.69 |
| = 0.1 s−1 | 1.28 | 1.00 | 1.04 | 0.70 | 0.83 |
| = 1 s−1 | 1.02 | 0.59 | 1.10 | 1.55 | 1.37 |
| = 10 s−1 | 1.58 | 1.58 | 0.22 | 0.41 | 0.25 |
| a3 | a2 | a1 | a0 | b2 | b1 | b0 | |
|---|---|---|---|---|---|---|---|
| 1000//0.01 | −7.376 × 102 | 1.338 × 106 | 3.081 × 107 | 5.711 × 107 | 2.403 × 102 | 3.439 × 103 | 8.941 × 103 |
| 1000//0.1 | −1.066 × 102 | 1.211 × 105 | 5.752 × 106 | 3.390 × 107 | 2.637 × 102 | 5.241 × 103 | 4.145 × 104 |
| 1000//1 | −5.758 × 10−1 | 1.461 × 104 | 1.684 × 105 | 1.111 × 105 | 1.611 × 102 | 8.182 × 102 | 1.136 × 103 |
| 1000//10 | 1.589 × 10−1 | 4.730 × 102 | 4.427 × 103 | 2.160 × 104 | 3.500 × 101 | 2.295 × 102 | 1.048 × 103 |
| 1050//0.01 | −4.028 × 102 | 1.394 × 106 | 4.114 × 107 | 3.211 × 107 | 3.436 × 102 | 5.428 × 103 | 8.683 × 103 |
| 1050//0.1 | −6.808 × 101 | 8.533 × 104 | 1.570 × 106 | 1.409 × 107 | 1.758 × 102 | 1.603 × 103 | 1.915 × 104 |
| 1050//1 | 2.854 | 1.672 × 104 | 2.472 × 105 | 1.950 × 104 | 2.193 × 102 | 1.520 × 103 | 7.147 × 102 |
| 1050//10 | 8.608 × 10− | 4.429 × 102 | 3.892 × 103 | 1.921 × 104 | 3.657 × 101 | 2.264 × 102 | 1.091 × 103 |
| 1100//0.01 | −2.596 × 10−2 | 1.429 × 106 | 5.329 × 107 | 6.296 × 107 | 5.179 × 102 | 9.334 × 103 | 1.830 × 104 |
| 1100//0.1 | −4.620 × 101 | 1.585 × 105 | 3.688 × 106 | 9.175 × 106 | 3.933 × 102 | 4.126 × 103 | 1.574 × 104 |
| 1100//1 | 9.209 | 1.091 × 104 | 1.447 × 105 | −1.203 × 105 | 1.709 × 102 | 8.852 × 102 | 3.621 × 10−14 |
| 1100//10 | 1.403 | 3.963 × 102 | 4.189 × 103 | 3.550 × 103 | 4.268 × 101 | 2.556 × 102 | 3.353 × 102 |
| 1150//0.01 | 9.378 × 101 | 8.453 × 105 | 4.222 × 107 | 5.073 × 107 | 4.217 × 102 | 9.412 × 103 | 1.923 × 104 |
| 1150//0.1 | −4.426 × 101 | 1.606 × 105 | 5.077 × 106 | 1.299 × 107 | 5.316 × 102 | 7.034 × 103 | 2.646 × 104 |
| 1150//1 | −2.684 | 1.081 × 104 | 1.265 × 105 | 3.472 × 105 | 1.861 × 102 | 9.997 × 102 | 4.460 × 103 |
| 1150//10 | 4.321 × 10−1 | 3.464 × 102 | 3.132 × 103 | 4.888 × 103 | 4.140 × 101 | 2.256 × 102 | 4.773 × 102 |
| 1200//0.01 | 8.630 × 101 | 1.008 × 106 | 4.872 × 107 | 5.894 × 107 | 5.719 × 102 | 1.432 × 104 | 2.712 × 104 |
| 1200//0.1 | −1.980 × 101 | 1.036 × 105 | 5.033 × 106 | 7.441 × 106 | 4.679 × 102 | 8.789 × 103 | 1.913 × 104 |
| 1200//1 | −1.317 | 8.841 × 103 | 1.317 × 105 | −1.375 × 105 | 2.231 × 102 | 1.085 × 103 | 1.745 × 10−14 |
| 1200//10 | 8.736 × 10−1 | 3.175 × 102 | 2.830 × 103 | 1.370 × 104 | 4.218 × 101 | 2.669 × 102 | 1.293 × 103 |
| AARE/% | T = 1000 °C | T = 1050 °C | T = 1100 °C | T = 1150 °C | T = 1200 °C |
|---|---|---|---|---|---|
| = 0.01 s−1 | 3.25 | 4.10 | 2.54 | 1.61 | 1.55 |
| = 0.1 s−1 | 5.16 | 2.32 | 3.95 | 2.39 | 2.11 |
| = 1 s−1 | 2.82 | 2.19 | 5.96 | 7.13 | 7.55 |
| = 10 s−1 | 2.78 | 3.10 | 1.96 | 3.30 | 7.17 |
| a2 | a1 | a0 | b1 | b0 | |
|---|---|---|---|---|---|
| 1000/0.01 | 1.914 × 103 | 4.468 × 105 | −1.490 × 105 | 5.107 × 101 | 6.652 × 10−10 |
| 1000/0.1 | 2.621 × 102 | 3.010 × 104 | 1.524 × 105 | 2.740 × 101 | 1.887 × 102 |
| 1000/1 | −4.969 | 1.819 × 104 | 4.483 × 105 | 2.431 × 102 | 2.577 × 103 |
| 1000/10 | 2.504 × 10−1 | 4.836 × 102 | 2.183 × 104 | 7.601 × 101 | 9.907 × 102 |
| 1050/0.01 | 2.791 × 103 | 1.998 × 105 | −1.068 × 105 | 2.685 × 101 | 8.790 × 10−15 |
| 1050/0.1 | 3.202 × 102 | 1.369 × 104 | 8.552 × 104 | 1.382 × 101 | 1.193 × 102 |
| 1050/1 | 1.270 × 10−1 | 2.029 × 104 | 5.492 × 105 | 3.077 × 102 | 3.834 × 103 |
| 1050/10 | 1.422 × 10−1 | 4.562 × 102 | 2.304 × 104 | 8.508 × 101 | 1.213 × 103 |
| 1100/0.01 | 2.187 × 103 | 1.353 × 105 | 5.250 × 104 | 2.381 × 101 | 2.367 × 101 |
| 1100/0.1 | 3.216 × 102 | 1.253 × 104 | 1.033 × 104 | 1.400 × 101 | 2.412 × 101 |
| 1100/1 | 1.520 | 1.741 × 104 | 8.068 × 105 | 3.791 × 102 | 7.059 × 103 |
| 1100/10 | 1.382 | 5.424 × 102 | 2.676 × 104 | 1.171 × 102 | 1.781 × 103 |
| 1150/0.01 | 1.459 × 103 | 1.323 × 105 | 8.470 × 104 | 2.963 × 101 | 3.988 × 101 |
| 1150/0.1 | 2.515 × 102 | 1.150 × 104 | 1.901 × 104 | 1.593 × 101 | 4.216 × 101 |
| 1150/1 | −4.192 | 1.393 × 104 | 5.976 × 105 | 3.307 × 102 | 5.954 × 103 |
| 1150/10 | 2.924 × 10−1 | 2.871 × 102 | 3.799 × 103 | 3.541 × 101 | 2.945 × 102 |
| 1200/0.01 | 1.377 × 103 | 1.151 × 105 | 7.191 × 104 | 3.400 × 101 | 4.051 × 101 |
| 1200/0.1 | 1.674 × 102 | 1.320 × 104 | 9.008 × 103 | 2.299 × 101 | 2.873 × 101 |
| 1200/1 | 3.462 × 10−1 | 1.049 × 104 | 5.737 × 105 | 3.761 × 102 | 7.447 × 103 |
| 1200/10 | −1.229 | 8.061 × 102 | 1.636 × 105 | 7.588 × 102 | 1.437 × 104 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vode, F.; Malej, S.; Arh, B.; Tehovnik, F.; Podgornik, B. Description of Hot Compressive Stress-Strain Curves Using Transfer Functions. Metals 2019, 9, 290. https://doi.org/10.3390/met9030290
Vode F, Malej S, Arh B, Tehovnik F, Podgornik B. Description of Hot Compressive Stress-Strain Curves Using Transfer Functions. Metals. 2019; 9(3):290. https://doi.org/10.3390/met9030290
Chicago/Turabian StyleVode, Franci, Simon Malej, Boštjan Arh, Franc Tehovnik, and Bojan Podgornik. 2019. "Description of Hot Compressive Stress-Strain Curves Using Transfer Functions" Metals 9, no. 3: 290. https://doi.org/10.3390/met9030290
APA StyleVode, F., Malej, S., Arh, B., Tehovnik, F., & Podgornik, B. (2019). Description of Hot Compressive Stress-Strain Curves Using Transfer Functions. Metals, 9(3), 290. https://doi.org/10.3390/met9030290





