Evaluation of Energy-Based Model Generated Strain Signals for Carbon Steel Spring Fatigue Life Assessment
Abstract
:1. Introduction
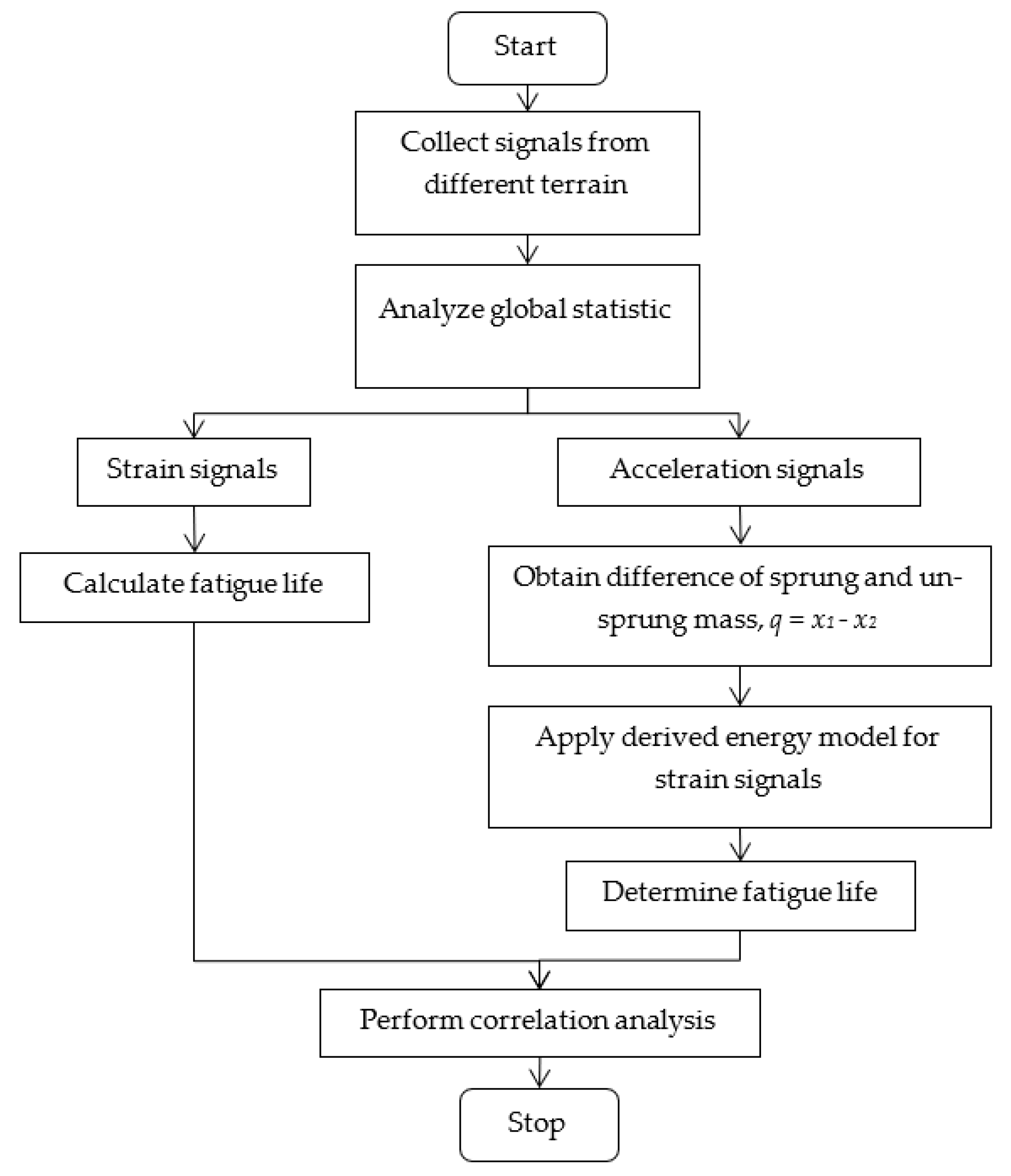
2. Methodology
2.1. Proposed Model
2.2. Fatigue Life Assessment
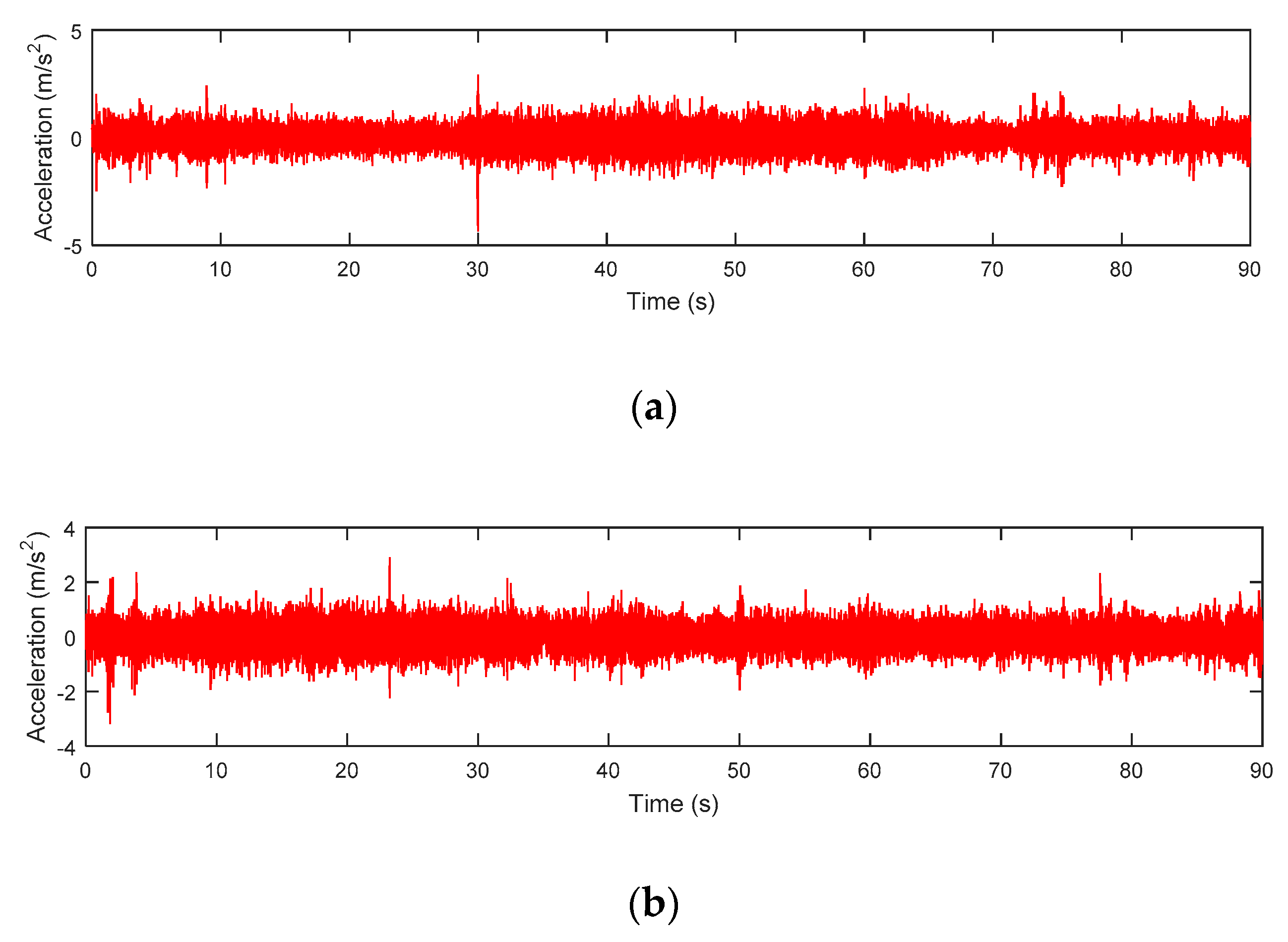
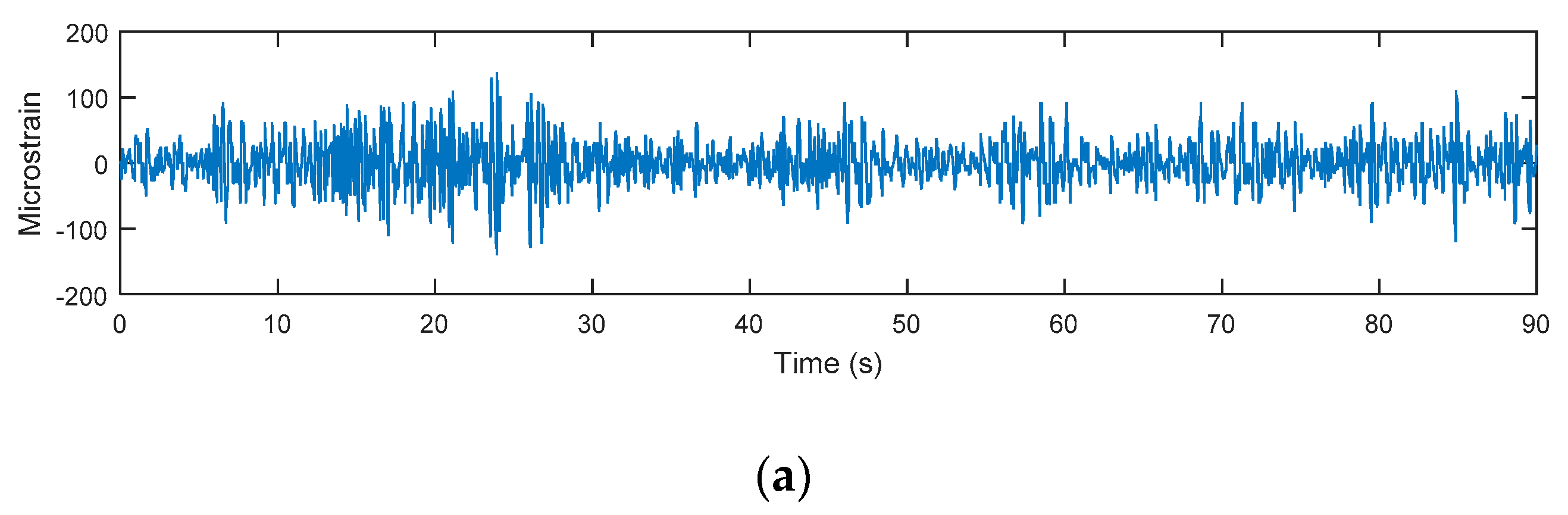
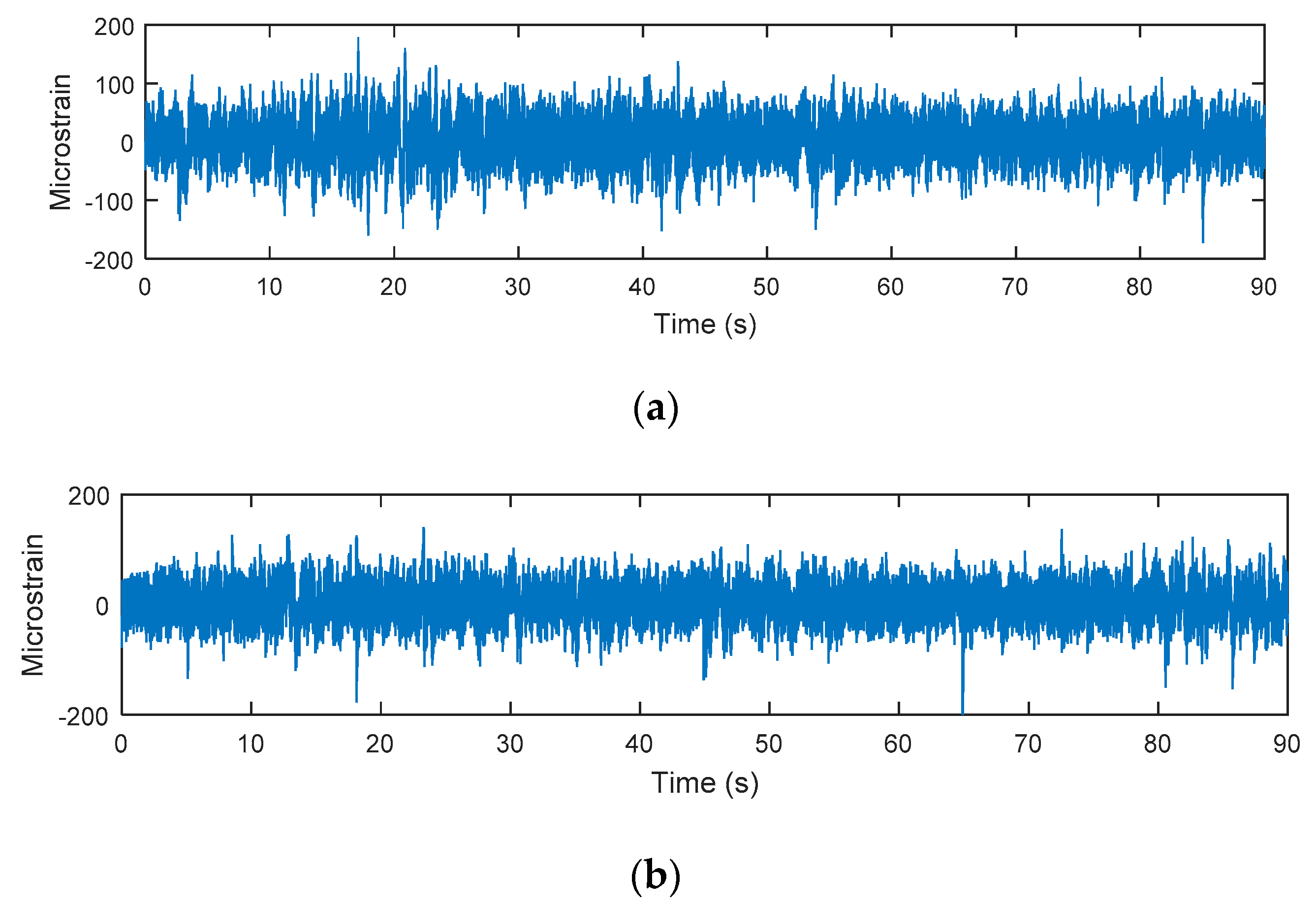
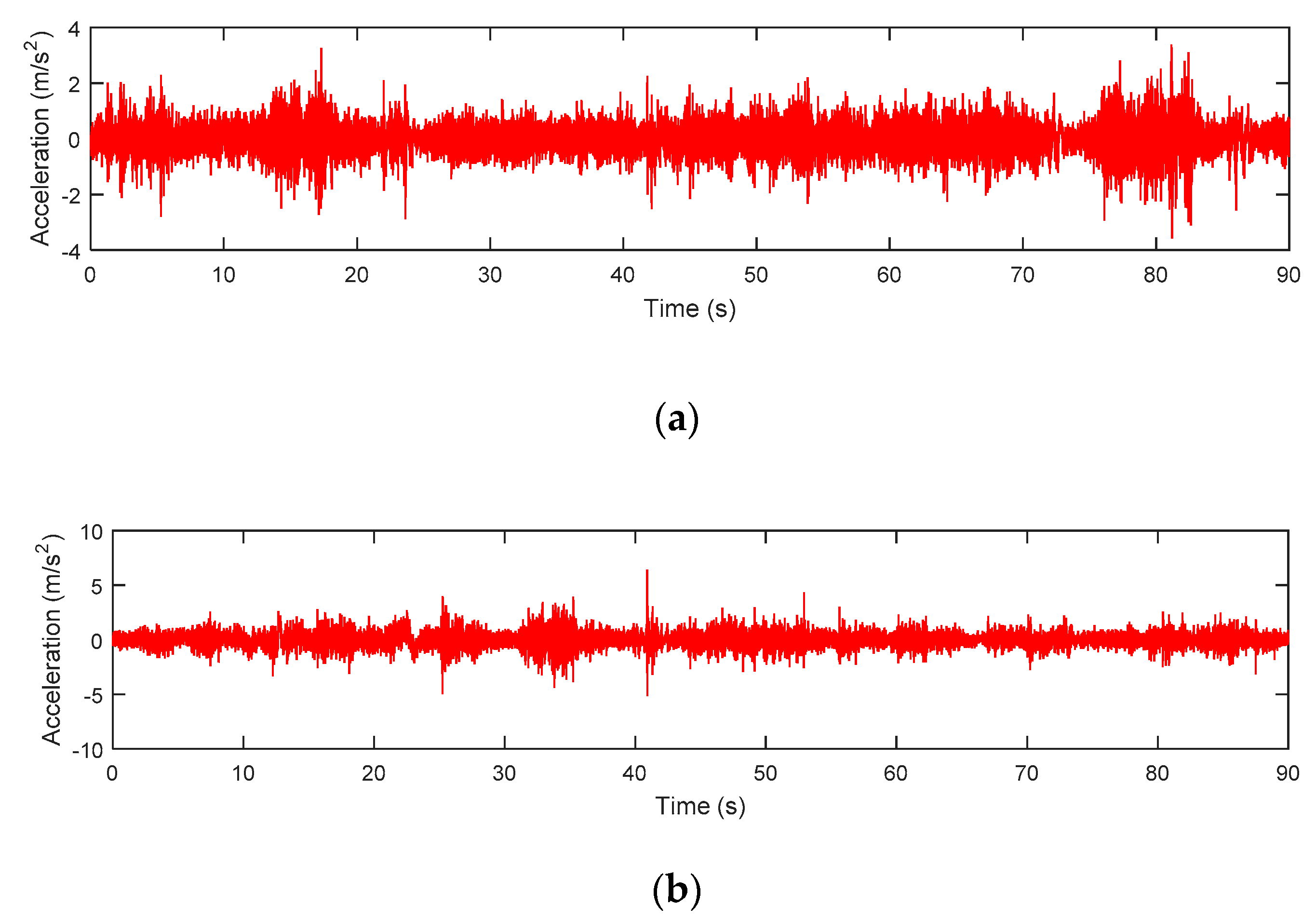
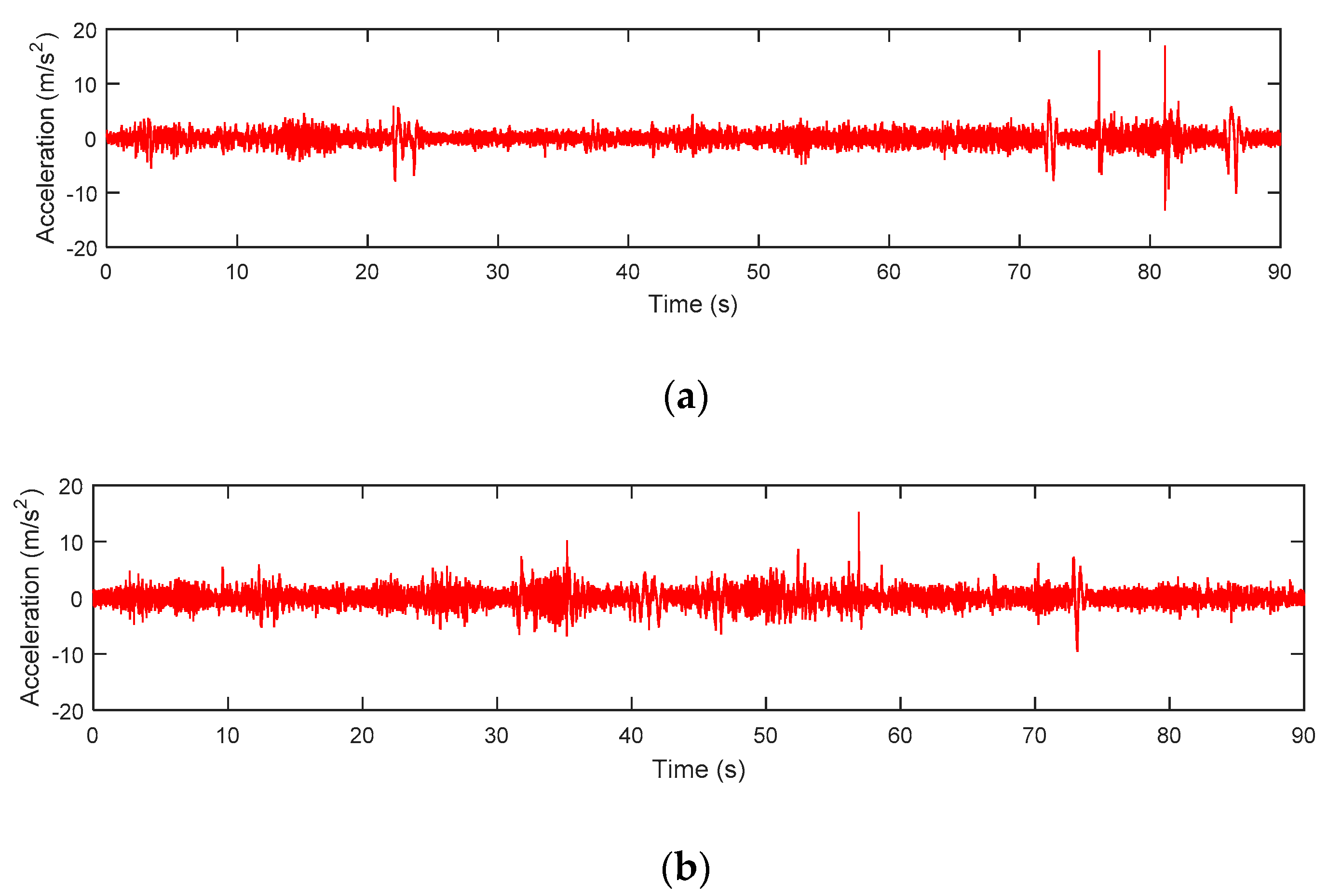
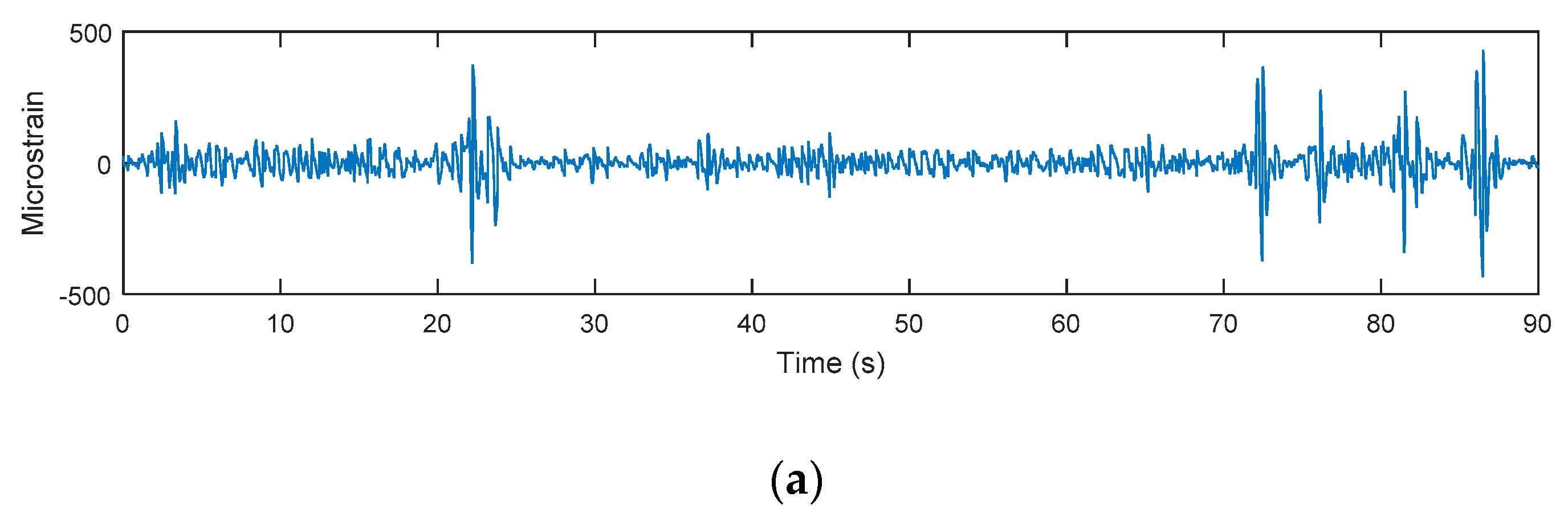
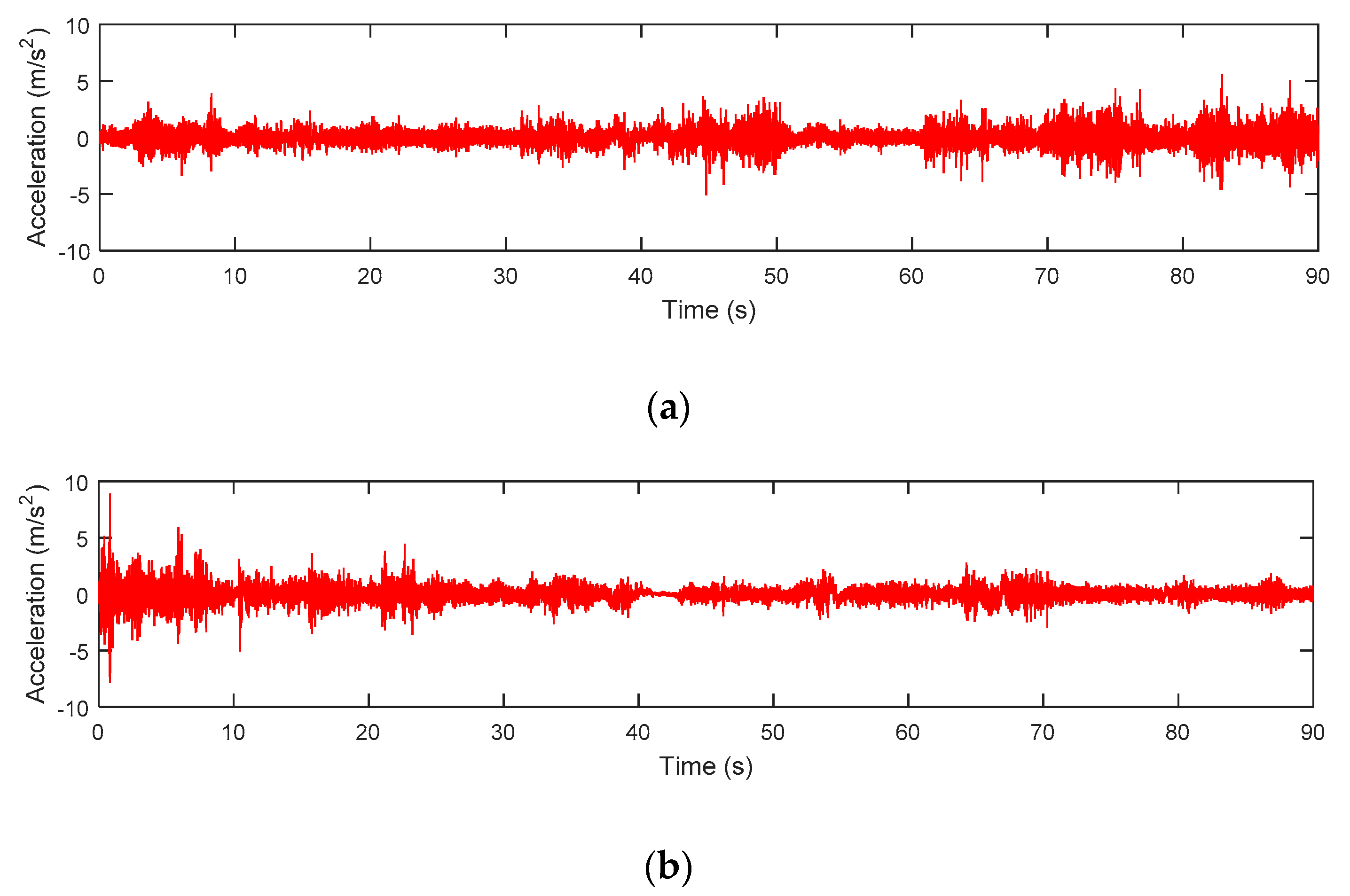
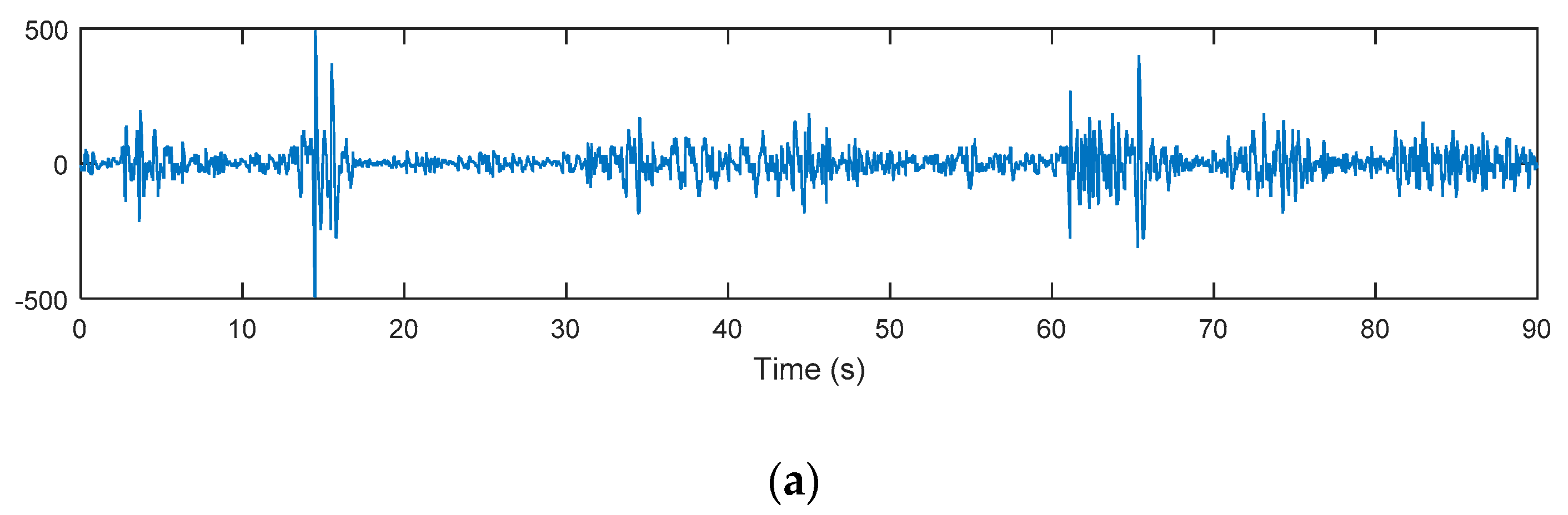
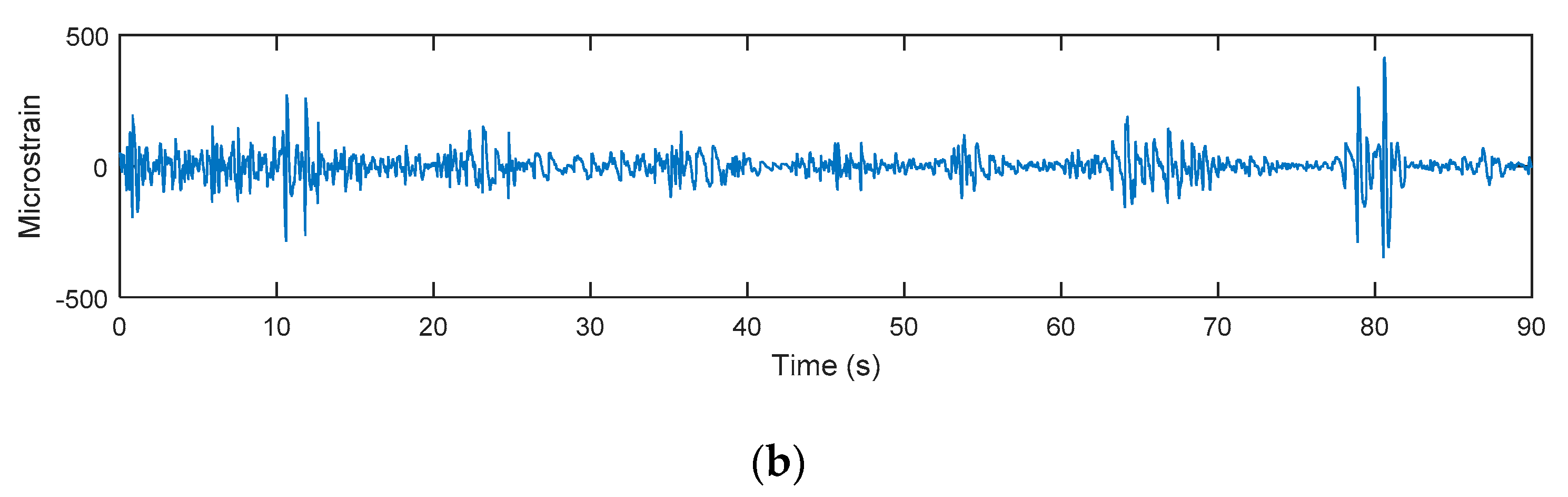
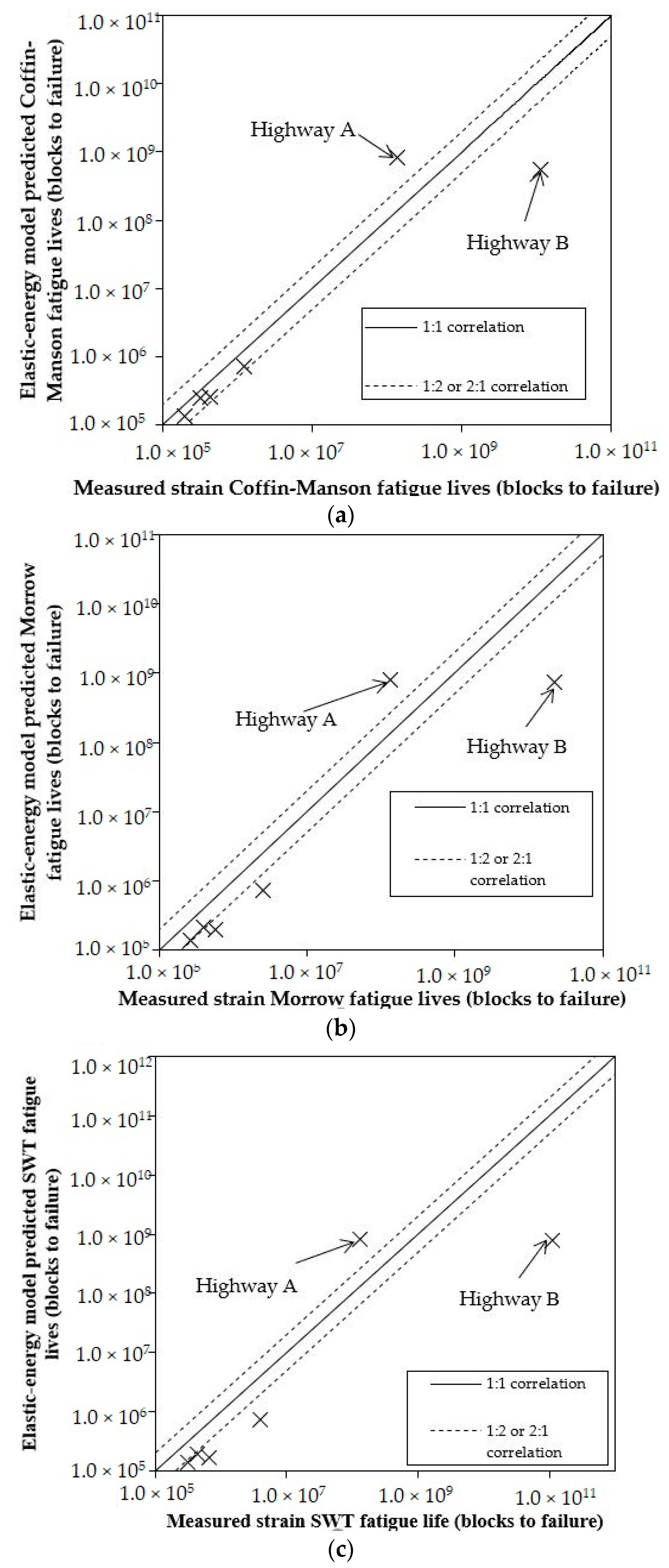
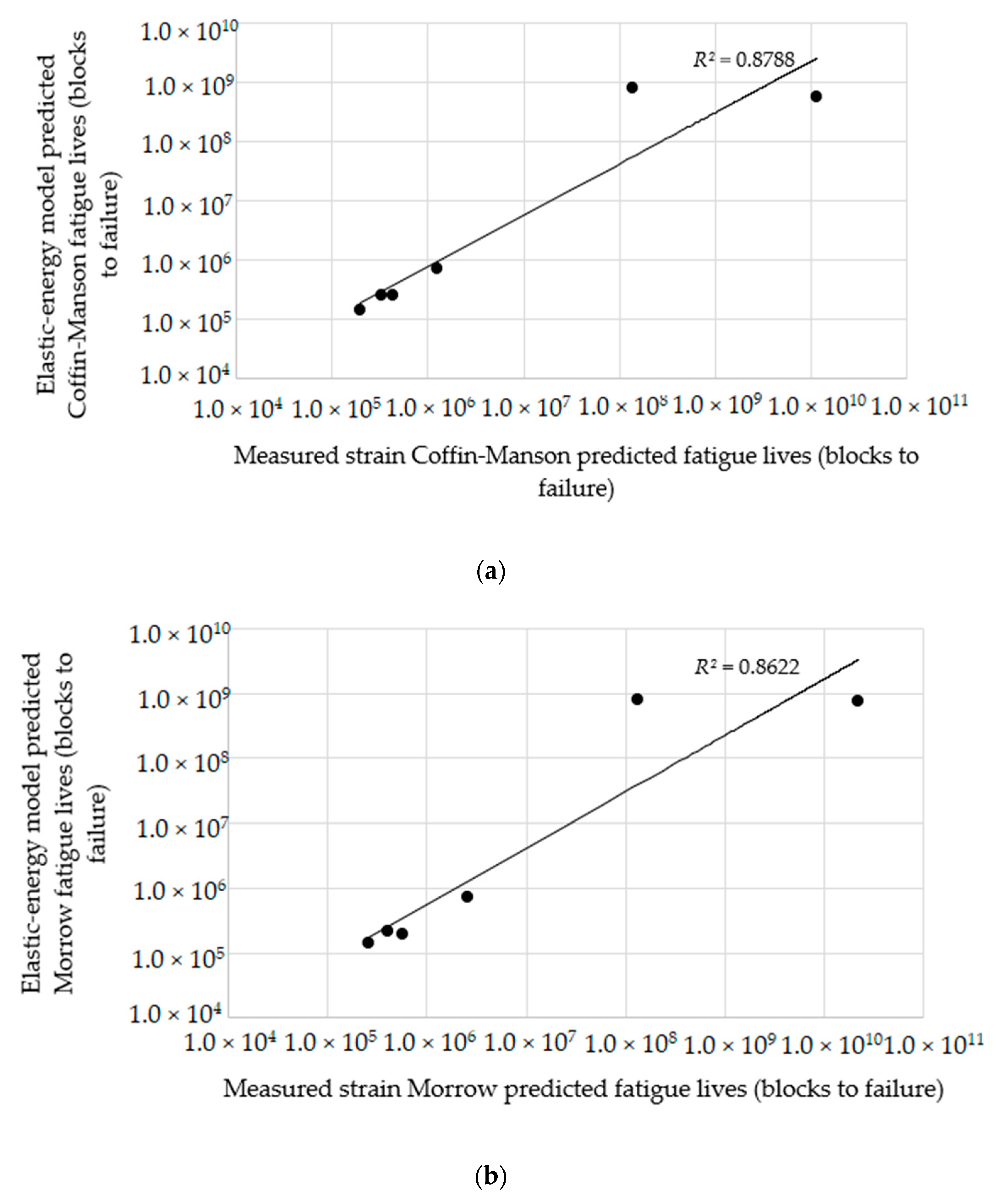
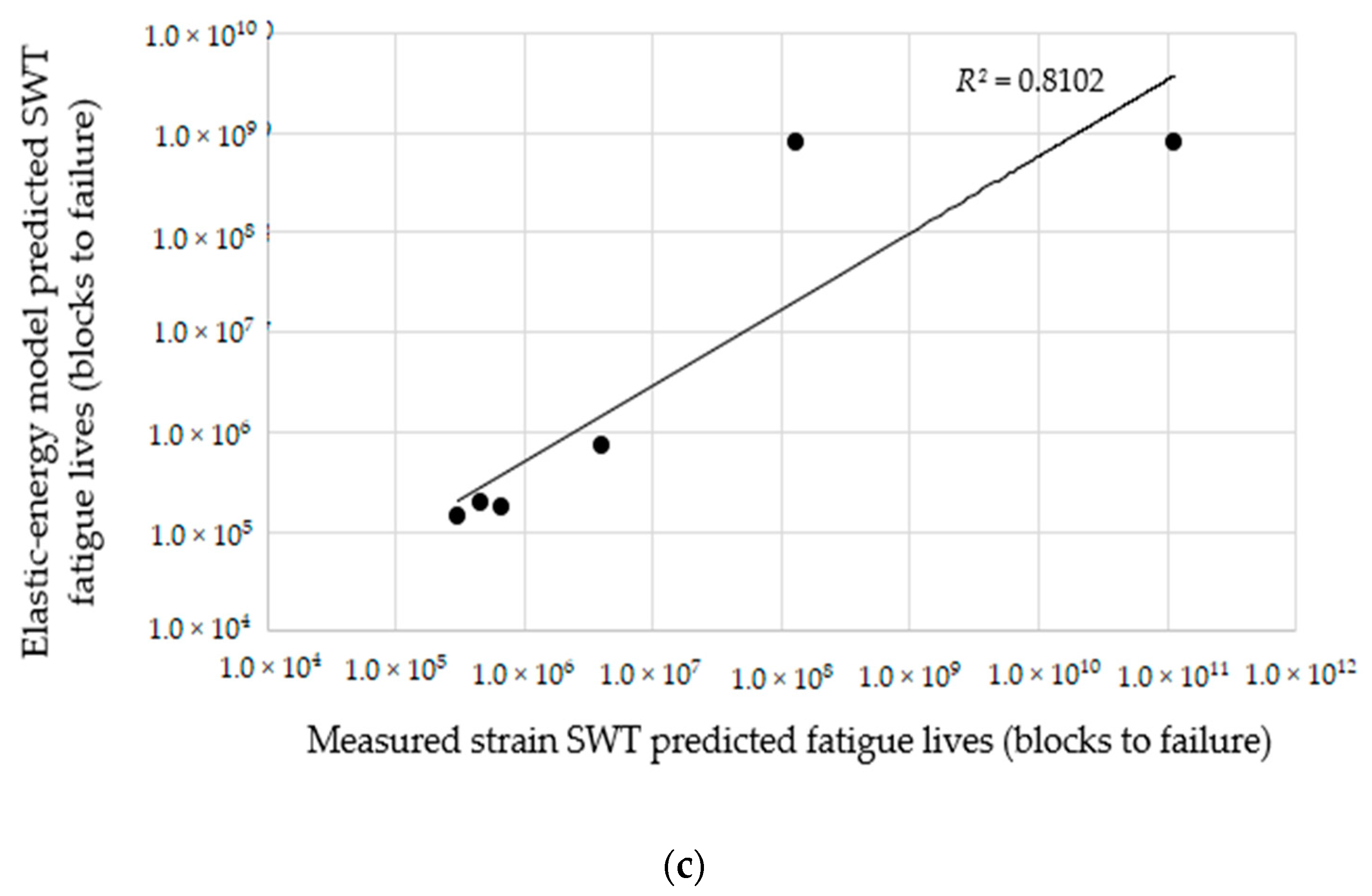
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferreira, C.; Ventura, P.; Morais, R.; Valente, A.L.G.; Neves, C.; Reis, M.C. Sensing methodologies to determine automotive damper condition under vehicle normal operation. Sens. Actuators A Phys. 2009, 156, 237–244. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Z.; Peng, W. Coordinated control of AFS and DYC for vehicle handling and stability based on optimal guaranteed cost theory. Veh. Syst. Dyn. 2009, 47, 57–79. [Google Scholar] [CrossRef]
- Kong, Y.S.; Omar, M.Z.; Chua, L.B.; Abdullah, S. Ride quality assessment of bus suspension system through modal frequency response approach. Adv. Mech. Eng. 2014, 6, 269721. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Generation of artificial road profile for automobile spring durability analysis. Jurnal Kejuruteraan 2018, 30, 123–128. [Google Scholar]
- Bridgelall, R.; Huang, Y.; Zhang, Z.; Deng, F. Precision enhancement of pavement roughness localization with connected vehicles. Meas. Sci. Technol. 2016, 27, 025012. [Google Scholar] [CrossRef] [Green Version]
- Tamboli, J.A.; Joshi, S.G. Optimum design of a passive suspension system of a vehicle subjected to actual random road excitations. J. Sound Vib. 1999, 219, 193–205. [Google Scholar] [CrossRef]
- Xu, K.; Wu, Y.; Wu, C.Q. Development of vibration loading profiles for accelerated durability tests of ground vehicles. In Proceedings of the 4th Annual Dynamic Systems and Control Conference, Arlington, VA, USA, 31 October–2 November 2011. [Google Scholar]
- Shafiullah, A.K.M.; Wu, Q. Generation and validation of loading profiles for highly accelerated durability tests of ground vehicle components. Eng. Fail. Anal. 2013, 33, 1–16. [Google Scholar] [CrossRef]
- Halfpenny, A.; Kihm, F. Mission profiling and test synthesis based on fatigue damage spectrum. In Proceedings of the FT342 Ninth International Fatigue Congress, Atlanta, GA, USA, 14–19 May 2006. [Google Scholar]
- Fauriat, W.; Mattrand, C.; Gayton, N.; Beakou, A.; Cembrzynski, T. Estimation of road profile variability from measured vehicle responses. Veh. Syst. Dyn. 2016, 54, 585–605. [Google Scholar] [CrossRef]
- Bogsjo, K.; Podgorski, K.; Rchlik, I. Models for road surface roughness. Veh. Syst. Dyn. 2012, 50, 725–747. [Google Scholar] [CrossRef]
- Lepine, J.; Rouillard, V.; Sek, M. Evaluation of machine learning algorithms for detection of road induced shocks buried in vehicle vibration signals. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2018. [Google Scholar] [CrossRef]
- Patil, K.S.; Jagtap, V.; Jadhav, S.; Bhosale, A.; Kedar, B. Performance evaluation of active suspension for passenger cars using Matlab. IOSR J. Mech. Civ. Eng. 2013, 2, 6–14. [Google Scholar]
- Fayyad, S.M. Constructing control system for active suspension system. Contemp. Eng. Sci. 2012, 5, 189–200. [Google Scholar]
- Marzbanrad, J.; Mohammadi, M.; Mostaani, M. Optimization of a passive vehicle suspension system for ride comfort enhancement with different speeds based on design of experiment (DOE) method. J. Mech. Eng. Res. 2013, 5, 50–59. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Vibration fatigue analysis of carbon steel coil spring under various road excitations. Metals 2018, 8, 617. [Google Scholar] [CrossRef]
- Abdullah, S.; Giacomin, J.A.; Yates, J.R. A mission synthesis algorithm for fatigue damage analysis. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2004, 218, 243–258. [Google Scholar] [CrossRef]
- Feng, L.; Lin, G.; Zhang, W.; Pang, H.; Wang, T. Design and optimization of a self-decoupled six-axis wheel force transducer for a heavy truck. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2015, 229, 1585–1610. [Google Scholar] [CrossRef]
- Qaji, A.J.; Silva, C.W.; Khan, A.; Khan, M.T. Performance analysis of a semiactive suspension system with particle swarm optimization and fuzzy logic control. Sci. World J. 2014, 2014, 174102. [Google Scholar]
- Kamalakannan, K.; ElayaPerumal, A.; Mangalaraman, S.; Arunachalam, K. Performance analysis and behaviour characteristic of CVD (semi active) in quarter car model. Jordan J. Mech. Ind. Eng. 2011, 5, 261–265. [Google Scholar]
- Mastinu, G.; Gobbi, M.; Miano, C. Optimal Design of Complex Mechanical Systems: With Applications to Vehicle Engineering; Springer: Berlin, Germany, 2006. [Google Scholar]
- Gonzales, M.A.C.; Barrios, D.B.; de Lima, N.B.; Goncalves, E. Importance of considering a material micro-failure criterion in the numerical modelling of the shot peening process applied to parabolic leaf spring. Lat. Am. J. Solids Struct. 2010, 7, 21–40. [Google Scholar]
- Bennett, K.C.; Regueiro, R.A.; Borja, R.I. Finite strain elastoplasticity considering the Eshelby stress for materials undergoing plastic volume change. J. Plast. 2016, 77, 214–245. [Google Scholar] [CrossRef] [Green Version]
- Graham Kelly, S. Mechanical Vibrations: Theory and Application; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Zhao, H.; Bi, S. Stiffness and stress characteristics of the generalized cross-spring pivot. Mech. Mach. Theory 2010, 45, 378–391. [Google Scholar] [CrossRef]
- Keller, S.G.; Gordon, A.P. Equivalent stress and strain distribution in compression springs subjected to bending. J. Strain Anal. Eng. Des. 2011, 46, 405–415. [Google Scholar] [CrossRef]
- Dragoni, E.; Bagaria, W.J. Numerical and experimental validation of a theoretical model for biomaterial helical springs. J. Strain Anal. Eng. Des. 2011, 48, 166–176. [Google Scholar] [CrossRef]
- Dragoni, E.; Bagaria, W.J. Mechanical design of bimaterial helical springs with circular cross-section. J. Strain Anal. Eng. Des. 2011, 46, 304–314. [Google Scholar] [CrossRef]
- Ilic, S. Methodology of Evaluation of In-Service Load Applied to the Output Shaft of Automatic Transmission. Ph.D. Thesis, The University of New South Wales, Sydney, Australia, 2006. [Google Scholar]
- Haiba, M.; Barton, D.C.; Brooks, P.C.; Levesley, M.C. The development of an optimisation algorithm based on fatigue life. Int. J. Fatigue 2003, 25, 299–310. [Google Scholar] [CrossRef]
- Jiang, R.; Murthy, D.N.P. A study of Weibull shape parameter: Properties and significance. Reliab. Eng. Syst. Saf. 2011, 96, 1619–1626. [Google Scholar] [CrossRef]
- Curiel, F.F.; Ambriz, R.R.; García, M.A.; Ramírez, M.C.; García, S. Smith Watson and Topper model in the determination of the fatigue life of an automotive steel. In Proceedings of the 17th International Conference on New Trends in Fatigue and Fracture, Lisbon, Portugal, 17–20 July 2018. [Google Scholar]
- Peng, Z.; Huang, H.Z.; Zhou, J.; Li, Y.F. A new cumulative fatigue damage rule based on dynamic residual S-N curve and material memory concept. Metals 2018, 8, 456. [Google Scholar] [CrossRef]
- Fernández-Canteli, A.; Blasón, S.; Correia, J.A.F.O.; de Jesus, A.M.P. A probabilistic interpretation of the Miner number for fatigue life prediction. Frattura ed Integrità Strutturale 2014, 30, 327–339. [Google Scholar] [CrossRef]
- Kuttler, K.L.; Shillor, M. Dynamic bilateral contact with discontinuous friction coefficient. Nonlinear Anal. Theory Methods Appl. 2001, 45, 309–327. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M.; Bruckmann, T. The need to generate a force time history towards life assessment of a coil spring. J. Mech. Eng. 2017, 4, 11–26. [Google Scholar]
- Valsange, P.S. Design of helical coil compression spring: A review. Int. J. Eng. Res. Appl. 2012, 2, 513–522. [Google Scholar]
- Shirahatti, A.; Prasad, P.S.S.; Panzade, P.; Kulkarni, M.M. Optimal design of passenger car suspension ride and road holding. J. Braz. Soc. Mech. Sci. Eng. 2008, 30, 66–76. [Google Scholar] [CrossRef]
- International Organization for Standardization. Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data; ISO 8608; International Organization for Standardization: Geneva, Switzerland, 1995; p. 30. [Google Scholar]
- International Organization for Standardization. Reporting Vehicle Road Surface Irregularities; Technical Report ISO/TC108/SC2/WG4 N57; International Organization for Standardization: Geneva, Switzerland, 1982. [Google Scholar]
- Bogsjo, K.; Rychlik, I. Vehicle fatigue damage caused by road irregularities. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 391–402. [Google Scholar] [CrossRef]
- Chaika, M.; Gorsich, D.; Sun, T.C. Some statistical tests in the study of terrain modelling. Int. J. Veh. Des. 2004, 36, 132. [Google Scholar] [CrossRef]
- Kong, Y.S.; Omar, M.Z.; Abdullah, S.; Chua, L.B. Fatigue life prediction of parabolic leaf spring under various road conditions. Eng. Fail. Anal. 2014, 46, 92–103. [Google Scholar] [CrossRef]
- Al Emran Hasan, M.M.; Ektesabi, M.; Kapoor, A. Fuzzy Logic Controller in an Electric Vehicle with Dynamically Changing Centre of Gravity. In Proceedings of the IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; pp. 1–6. [Google Scholar]
- Chen, X. Analysis of Crosswind Fatigue of Wind-Excited Structures with Nonlinear Aerodynamic Damping. Eng. Struct. 2014, 74, 145–156. [Google Scholar] [CrossRef]
- Runciman, A.; Xu, D.; Pelton, A.R.; Ritchie, R.O. An equivalent strain/Coffin-Manson approach to multiaxial fatigue and life prediction in superelastic Nitinol medical devices. Biomaterials 2011, 32, 4987–4993. [Google Scholar] [CrossRef]
- Sivák, P.; Ostertagová, E. Evaluation of fatigue tests by means of mathematical statistics. Procedia Eng. 2012, 48, 636–642. [Google Scholar] [CrossRef]
- Kim, J.; Lei, L.P.; Kang, B.S. Preform design in hydroforming of automobile lower arm by FEM. J. Mater. Process. Technol. 2003, 138, 58–62. [Google Scholar] [CrossRef]
- Bartolozzi, R.; Frendo, F. Stiffness and strength aspects in the design of automotive coil springs for Mcpherson front suspensions: A case study. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2011, 225, 1377–1391. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Development of multiple linear regression-based models for fatigue life evaluation of automotive coil springs. Mech. Syst. Signal Process. 2019, 118, 675–695. [Google Scholar] [CrossRef]











| Mechanical Properties | Value |
|---|---|
| Ultimate tensile strength, Su (MPa) | 1584 |
| Elastic modulus | 207 |
| Fatigue strength coefficient | 2063 |
| Fatigue strength exponent | −0.08 |
| Fatigue ductility coefficient | 9.56 |
| Fatigue ductility exponent | −1.05 |
| Road Class | Elastic-energy Model | Measured | ||
|---|---|---|---|---|
| r.m.s | Kurtosis | r.m.s | Kurtosis | |
| Highway A | 29.42 | 4.02 | 35.16 | 3.32 |
| Highway B | 25.64 | 3.81 | 32.37 | 3.45 |
| Rural A | 56.06 | 18.27 | 53.86 | 12.68 |
| Rural B | 49.83 | 14.64 | 46.71 | 9.49 |
| Campus A | 57.19 | 11.35 | 52.20 | 7.75 |
| Campus B | 55.17 | 15.16 | 54.91 | 8.98 |
| Roads | Strain Fatigue Durability Life (Blocks to Failure) | Energy Model Converted Fatigue Life (Blocks to Failure) |
|---|---|---|
| Highway A | 1.37 × 108 | 8.13 × 108 |
| Highway B | 1.13 × 1010 | 5.46 × 108 |
| Rural A | 1.98 × 105 | 1.37 × 105 |
| Rural B | 3.26 × 105 | 2.50 × 105 |
| Campus A | 4.28 × 105 | 2.56 × 105 |
| Campus B | 1.25 × 106 | 7.25 × 105 |
| Roads | Strain Fatigue Durability Life (Blocks to Failure) | Energy Model Converted Fatigue Life (Blocks to Failure) |
|---|---|---|
| Highway A | 1.32 × 108 | 7.91 × 108 |
| Highway B | 2.20 × 1010 | 7.42 × 108 |
| Rural A | 2.59 × 105 | 1.39 × 105 |
| Rural B | 3.99 × 105 | 2.15 × 105 |
| Campus A | 5.60 × 105 | 1.94 × 105 |
| Campus B | 2.55 × 106 | 7.23 × 105 |
| Roads | Strain Fatigue Durability Life (Blocks to Failure) | Energy Model Converted Fatigue Life (Blocks to Failure) |
|---|---|---|
| Highway A | 1.32 × 108 | 8.15 × 108 |
| Highway B | 1.12 × 1011 | 8.01 × 108 |
| Rural A | 3.05 × 105 | 1.39 × 105 |
| Rural B | 4.55 × 105 | 1.99 × 105 |
| Campus A | 6.58 × 105 | 1.74 × 105 |
| Campus B | 3.99 × 106 | 7.19 × 105 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Mohamed Haris, S. Evaluation of Energy-Based Model Generated Strain Signals for Carbon Steel Spring Fatigue Life Assessment. Metals 2019, 9, 213. https://doi.org/10.3390/met9020213
Kong YS, Abdullah S, Schramm D, Omar MZ, Mohamed Haris S. Evaluation of Energy-Based Model Generated Strain Signals for Carbon Steel Spring Fatigue Life Assessment. Metals. 2019; 9(2):213. https://doi.org/10.3390/met9020213
Chicago/Turabian StyleKong, Yat Sheng, Shahrum Abdullah, Dieter Schramm, Mohd Zaidi Omar, and Sallehuddin Mohamed Haris. 2019. "Evaluation of Energy-Based Model Generated Strain Signals for Carbon Steel Spring Fatigue Life Assessment" Metals 9, no. 2: 213. https://doi.org/10.3390/met9020213





