Stochastic Material Point Method for Analysis in Non-Linear Dynamics of Metals
Abstract
:1. Introduction
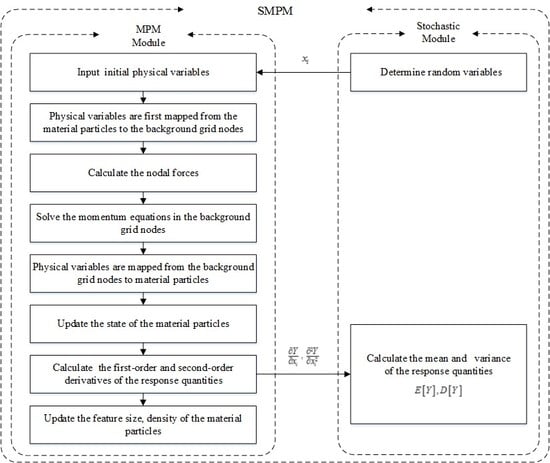
2. Stochastic Material Point Method
3. Material Property Equations
3.1. Equation of State
3.2. Constitutive Equation
3.3. Von Mises Elastic-Plastic Material Model
- Calculate the trial deviatoric stress tensor and the trial Von Mises flow stress .
- If the condition holds, the equivalent plastic strain increment can be calculated by Equation (20). Otherwise, the materials have no plastic deformation.
- Update equivalent plastic strain by .
- Update flow stress by Equation (19), get .
- Calculate the coefficient m with the new flow stress by Equation (16) and update the deviatoric stress which satisfies the condition in the yield surface with the radial return mapping.
4. Random Method
4.1. The Basic Random Variables and Random Response
4.2. The First-Order and Second-Order Derivatives of the Response Quantities
5. Results and Discussion
5.1. Example 1: The Uncertain Parameters are the State Equation Parameters
5.2. Example 2: The Uncertain Parameters are the Constitutive Equation Parameters
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lu, M.K.; Zhang, J.Y.; Zhang, H.W.; Zheng, Y.G.; Chen, Z. Time-discontinuous material point method for transient problems. Comput. Method Appl. Mech. 2018, 328, 663–685. [Google Scholar] [CrossRef]
- Beuth, L.; Wieckowski, Z.; Vermeer, P.A. Solution of quasi-static large-strain problems by the material point method. Int. J. Numer. Anal. Met. 2011, 35, 1451–1465. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. An introduction to SPH. Comput. Phys. Commun. 1988, 48, 89–96. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzot, G.; Villon, P. Generalizing the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Lu, Y.; Belytschko, T.; Gu, L. A new implementation of the element free Galerkin method. Comput. Method Appl. Mech. 1994, 113, 397–414. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Method Appl. Mech. 1996, 139, 289–314. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Liu, W.-K.; Li, S.; Belytschko, T. Moving least-square reproducing kernel methods (I) methodology and convergence. Comput. Method Appl. Mech. 1997, 143, 113–154. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Meth. Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Ren, H.L.; Zhuang, X.Y.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Method Appl. Mech. 2017, 318, 762–782. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.L.; Zhuang, X.Y.; Cai, Y.C.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Meth. Eng. 2016, 108, 1451–1476. [Google Scholar] [CrossRef] [Green Version]
- Sulsky, D.; Zhou, S.-J.; Schreyer, H.L.J.C.M.I.A.M. Application of a particle-in-cell method to solid mechanics. J. Comput. Phys. Commun. 1995, 87, 236–252. [Google Scholar] [CrossRef]
- Sulsky, D.; Schreyer, H.L. Axisymmetric form of the material point method with applications to upsetting and Taylor impact problems. Comput. Method Appl. Mech. 1996, 139, 409–429. [Google Scholar] [CrossRef]
- Sanchez, J.; Schreyer, H.; Sulsky, D.; Wallstedt, P. Solving quasi-static equations with the material-point method. Int. J. Numer. Meth. Eng. 2015, 103, 60–78. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. A three-dimensional large deformation meshfree method for arbitrary evolving cracks. Comput. Method Appl. Mech. 2007, 196, 2777–2799. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Zi, G.; Bordas, S.; Nguyen-Xuan, H. A simple and robust three-dimensional cracking-particle method without enrichment. Comput. Method Appl. Mech. 2010, 199, 2437–2455. [Google Scholar] [CrossRef]
- Andersen, S.; Andersen, L. Analysis of spatial interpolation in the material-point method. Comput. Struct. 2010, 88, 506–518. [Google Scholar] [CrossRef]
- Ching, H.; Batra, R. Determination of crack tip fields in linear elastostatics by the meshless local Petrov-Galerkin (MLPG) method. Cmes Comput. Model. Eng. 2001, 2, 273–289. [Google Scholar]
- Mason, M.; Chen, K.; Hu, P.G. Material point method of modelling and simulation of reacting flow of oxygen. Int. J. Comput. Fluid Dyn. 2014, 28, 420–427. [Google Scholar] [CrossRef]
- Ma, J.; Wang, D.; Randolph, M.F. A new contact algorithm in the material point method for geotechnical simulations. Int. J. Numer. Anal. Met. 2014, 38, 1197–1210. [Google Scholar] [CrossRef]
- Yang, P.F.; Liu, Y.; Zhang, X.; Zhou, X.; Zhao, Y.L. Simulation of Fragmentation with Material Point Method Based on Gurson Model and Random Failure. Cmes Comp. Model. Eng. 2012, 85, 207–237. [Google Scholar]
- Charlton, T.J.; Coombs, W.M.; Augarde, C.E. iGIMP: An implicit generalised interpolation material point method for large deformations. Comput. Struct. 2017, 190, 108–125. [Google Scholar] [CrossRef] [Green Version]
- Rastkar, S.; Zahedi, M.; Korolev, I.; Agarwal, A. A meshfree approach for homogenization of mechanical properties of heterogeneous materials. Eng. Anal. Bound. Elem. 2017, 75, 79–88. [Google Scholar] [CrossRef]
- Farahani, B.V.; Pires, F.M.A.; Moreira, P.M.G.P.; Belinha, J. A meshless method in the non-local constitutive damage models. Procedia Struct. Int. 2016, 1, 226–233. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.D.; Ma, J.X.; Shi, Y.Q.; Xu, C.L.; Lu, S.Z. A mesoscopic numerical analysis for combustion reaction of multi-component PBX explosives. Acta Mech. 2018, 229, 2267–2286. [Google Scholar] [CrossRef]
- Nairn, J.A.; Guilkey, J.E. Axisymmetric form of the generalized interpolation material point method. Int. J. Numer. Meth. Eng. 2015, 101, 127–147. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Qiu, X.M. Comparison study of MPM and SPH in modeling hypervelocity impact problems. Int. J. Impact Eng. 2009, 36, 272–282. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z. A multi-mesh MPM for simulating the meshing process of spur gears. Comput. Struct. 2003, 81, 1991–2002. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, Z.; Montgomery-Smith, S. Improved Material Point Method for Simulating the Zona Failure Response in Piezo-Assisted Intracytoplasmic Sperm Injection. Cmes Comp. Model. Eng. 2011, 73, 45–75. [Google Scholar]
- Ma, X.; Zhang, D.Z.; Giguere, P.T.; Liu, C. Axisymmetric computation of Taylor cylinder impacts of ductile and brittle materials using original and dual domain material point methods. Int. J. Impact Eng. 2013, 54, 96–104. [Google Scholar] [CrossRef]
- Lian, Y.P.; Zhang, X.; Liu, Y. Coupling of finite element method with material point method by local multi-mesh contact method. Comput. Method Appl. Mech. 2011, 200, 3482–3494. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, Z.; Sewell, T.D.; Gan, Y. Multiscale simulation of the responses of discrete nanostructures to extreme loading conditions based on the material point method. Comput. Method Appl. Mech. 2015, 297, 219–238. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Shi, X.H.; Xu, D.H.; Wang, S. Destroy probability of ship defensive structure subjected to underwater contact explosions. Adv. Mater. Res.-Switz. 2008, 44–46, 297–301. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Zhuang, X.; Nguyen-Thoi, T.; Rabczuk, T. A software framework for probabilistic sensitivity analysis for computationally expensive models. Adv. Eng. Softw. 2016, 100, 19–31. [Google Scholar] [CrossRef]
- Mie, G. Zur kinetischen Theorie der einatomigen Körper. Ann. Der Phys. 1903, 316, 657–697. [Google Scholar] [CrossRef]
- Grüneisen, E. Theorie des festen Zustandes einatomiger Elemente. Ann. Der Phys. 2010, 344, 257–306. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Bahri, A.; Guermazi, N.; Elleuch, K.; Urgen, M. On the erosive wear of 304 L stainless steel caused by olive seed particles impact: Modeling and experiments. Tribol. Int. 2016, 102, 608–619. [Google Scholar] [CrossRef]
- Wang, X.M.; Shi, J. Validation of Johnson-Cook plasticity and damage model using impact experiment. Int. J. Impact Eng. 2013, 60, 67–75. [Google Scholar] [CrossRef]
- Sorić, J.; Zahlten, W.J.T. Elastic-plastic analysis of internally pressurized torispherical shells. Thin-Walled Struct. 1995, 22, 217–239. [Google Scholar] [CrossRef]
- Kaminski, M. The Stochastic Perturbation Method for Computational Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Adomian, G.; Malakian, K. Inversion of stochastic partial differential operators—The linear case. J. Math. Anal. Appl. 1980, 77, 505–512. [Google Scholar] [CrossRef] [Green Version]
- Hamdia, K.M.; Silani, M.; Zhuang, X.; He, P.; Rabczuk, T. Stochastic analysis of the fracture toughness of polymeric nanoparticle composites using polynomial chaos expansions. Int. J. Fract. 2017, 206, 215–227. [Google Scholar] [CrossRef]
- Valdebenito, M.A.; Labarca, A.A.; Jensen, H.A. On the application of intervening variables for stochastic finite element analysis. Comput. Struct. 2013, 126, 164–176. [Google Scholar] [CrossRef]
- Kaminski, M.; Swita, P. Structural stability and reliability of the underground steel tanks with the Stochastic Finite Element Method. Arch. Civ. Mech. Eng. 2015, 15, 593–602. [Google Scholar] [CrossRef]
- Engen, M.; Hendriks, M.A.N.; Kohler, J.; Overli, J.A.; Aldstedt, E. A quantification of the modelling uncertainty of non-linear finite element analyses of large concrete structures. Struct. Saf. 2017, 64, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Beacher, G.B.; Ingra, T.S.; Engineering, G. Stochastic FEM in settlement predictions. J. Geotech. 1981, 107, 449–463. [Google Scholar]
- Kaminski, M. Generalized perturbation-based stochastic finite element method in elastostatics. Comput. Struct. 2007, 85, 586–594. [Google Scholar] [CrossRef]
- Kaminski, M. On generalized stochastic perturbation-based finite element method. Commun. Numer. Meth. Eng. 2006, 22, 23–31. [Google Scholar] [CrossRef]
- Kaminski, M. Probabilistic entropy in homogenization of the periodic fiber-reinforced composites with random elastic parameters. Int. J. Numer. Meth. Eng. 2012, 90, 939–954. [Google Scholar] [CrossRef]
- Guo, B.C.; Wang, B.X. Control charts for the coefficient of variation. Stat. Pap. 2018, 59, 933–955. [Google Scholar] [CrossRef]
- Yang, X.M. Numerical Simulation for Explosion and Phenomena; University of Science and Technology of China Press: Hefei, China, 2010. [Google Scholar]
- Long, X.Y.; Jiang, C.; Han, X.; Gao, W. Stochastic response analysis of the scaled boundary finite element method and application to probabilistic fracture mechanics. Comput. Struct. 2015, 153, 185–200. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D.J.S.B. Stochastic Finite Elements: A Spectral Approach. In Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991; Volume 224. [Google Scholar]
- Greene, M.S.; Liu, Y.; Chen, W.; Liu, W.K. Computational uncertainty analysis in multiresolution materials via stochastic constitutive theory. Comput. Method Appl. Mech. 2011, 200, 309–325. [Google Scholar] [CrossRef]
- Stefanou, G. The stochastic finite element method: Past, present and future. Comput. Method Appl. Mech. 2009, 198, 1031–1051. [Google Scholar] [CrossRef] [Green Version]
- Au, S.K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilist Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef] [Green Version]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lemaire, M. Structural Reliability; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]














| Location | E | F |
|---|---|---|
| Coordinates | (4.0 cm, 0.0 cm) | (6.0 cm, 0.0 cm) |
| Parameters | Determined Value | Mean | Standard Deviation | |
|---|---|---|---|---|
| C.V = 0.01 | C.V = 0.15 | |||
| S1 | 1.49 | 1.49 | 0.0149 | 0.2235 |
| S2 | 0.0 | 0.0 | 0.0 | 0.0 |
| S3 | 0.0 | 0.0 | 0.0 | 0.0 |
| γ0 | 2.17 | 2.17 | 0.0217 | 0.3255 |
| a | 0.46 | 0.46 | 4.6 × 10−3 | 0.069 |
| Method | Grid Numbers | Particle Numbers | Computing Time |
|---|---|---|---|
| Monte Carlo | 160,000 | 160,000 | 1,297,762 s |
| SMPM | 160,000 | 160,000 | 138 s |
| Location | H | I | G | K |
|---|---|---|---|---|
| Coordinates | (4.5 cm, 0.0 cm) | (4.5 cm, 3.0 cm) | (5.0 cm, 0.0 cm) | (5.5 cm, 0.0 cm) |
| Parameters | Determined Value | Mean | Standard Deviation | |
|---|---|---|---|---|
| C.V = 0.1 | C.V = 0.15 | |||
| A (MPa) | 792 | 792 | 79.2 | 118.8 |
| B (MPa) | 510 | 510 | 51.0 | 76.5 |
| 0.014 | 0.014 | 0.0014 | 2.1 × 10−3 | |
| 0.26 | 0.26 | 0.026 | 0.039 | |
| 1.03 | 1.03 | 0.103 | 0.1545 | |
| Location | C.V | Mean | Variance | ||||
|---|---|---|---|---|---|---|---|
| Monte Carlo (×10−2) | SMPM (×10−2) | Relative Errors (%) | Monte Carlo (×10−6) | SMPM (×10−6) | Relative Errors (%) | ||
| H | 0.1 | 0.91345878 | 0.91237754 | 0.12 | 0.61061724 | 0.61631472 | 0.93 |
| 0.15 | 0.91512557 | 0.91353660 | 0.17 | 1.37753594 | 1.38670813 | 0.67 | |
| I | 0.1 | 0.94050252 | 0.93940429 | 0.12 | 0.62727196 | 0.62988312 | 0.42 |
| 0.15 | 0.94204592 | 0.94042639 | 0.17 | 1.41455632 | 1.41723704 | 0.19 | |
| G | 0.1 | 0.95229046 | 0.95117980 | 0.12 | 0.63159823 | 0.63391311 | 0.37 |
| 0.15 | 0.95376624 | 0.95212650 | 0.17 | 1.42320844 | 1.42630451 | 0.22 | |
| K | 0.1 | 0.92692249 | 0.92582361 | 0.12 | 0.61809317 | 0.62174278 | 0.59 |
| 0.15 | 0.92852135 | 0.92690313 | 0.17 | 1.39413861 | 1.39892126 | 0.34 | |
| Location | C.V | Mean | Variance | ||||
|---|---|---|---|---|---|---|---|
| Monte Carlo (×10−2) | SMPM (×10−2) | Relative Errors (%) | Monte Carlo (×10−6) | SMPM (×10−6) | Relative Errors (%) | ||
| H | 0.1 | −0.6301295 | −0.6293716 | 0.12 | 0.29225172 | 0.29327005 | 0.35 |
| 0.15 | −0.6312935 | −0.6301712 | 0.18 | 0.65820611 | 0.65985761 | 0.25 | |
| I | 0.1 | −0.3286691 | −0.3283024 | 0.11 | 0.07606357 | 0.07693130 | 1.14 |
| 0.15 | −0.3291897 | −0.3286596 | 0.16 | 0.17150211 | 0.17309543 | 0.93 | |
| G | 0.1 | −0.6628665 | −0.6620950 | 0.12 | 0.30607402 | 0.30714616 | 0.35 |
| 0.15 | −0.6638928 | −0.6627540 | 0.17 | 0.68912090 | 0.69107885 | 0.28 | |
| K | 0.1 | −0.6529968 | −0.6522325 | 0.12 | 0.30601019 | 0.30857383 | 0.84 |
| 0.15 | −0.6541126 | −0.6529930 | 0.17 | 0.69014858 | 0.69429113 | 0.60 | |
| Location | C.V | Mean | Variance | ||||
|---|---|---|---|---|---|---|---|
| Monte Carlo (×10−2) | SMPM (×10−2) | Relative Errors (%) | Monte Carlo (×10−6) | SMPM (×10−6) | Relative Errors (%) | ||
| H | 0.1 | 0.39198667 | 0.39154413 | 0.11 | 0.11069985 | 0.11350495 | 2.53 |
| 0.15 | 0.39267753 | 0.39204154 | 0.16 | 0.24985084 | 0.25538614 | 2.22 | |
| I | 0.1 | 0.12396910 | 0.12390616 | 0.05 | 0.01075824 | 0.01095824 | 1.86 |
| 0.15 | 0.12408433 | 0.12404097 | 0.03 | 0.02422766 | 0.02465603 | 1.77 | |
| G | 0.1 | 0.40287346 | 0.40240417 | 0.12 | 0.11283936 | 0.11345652 | 0.55 |
| 0.15 | 0.40299641 | 0.40367725 | 0.17 | 0.25450105 | 0.25527716 | 0.30 | |
| K | 0.1 | 0.37985846 | 0.37939486 | 0.12 | 0.10439505 | 0.10440881 | 0.38 |
| 0.15 | 0.38052868 | 0.37983724 | 0.18 | 0.23554921 | 0.23491981 | 0.27 | |
| Method | Grid Numbers | Particle Numbers | Computing Time |
|---|---|---|---|
| Monte Carlo | 84,864 | 160,000 | 874,579 s |
| SMPM | 84,864 | 160,000 | 93 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Shi, Y.; Ma, J.; Xu, C.; Lu, S.; Xu, X. Stochastic Material Point Method for Analysis in Non-Linear Dynamics of Metals. Metals 2019, 9, 107. https://doi.org/10.3390/met9010107
Chen W, Shi Y, Ma J, Xu C, Lu S, Xu X. Stochastic Material Point Method for Analysis in Non-Linear Dynamics of Metals. Metals. 2019; 9(1):107. https://doi.org/10.3390/met9010107
Chicago/Turabian StyleChen, Weidong, Yaqin Shi, Jingxin Ma, Chunlong Xu, Shengzhuo Lu, and Xing Xu. 2019. "Stochastic Material Point Method for Analysis in Non-Linear Dynamics of Metals" Metals 9, no. 1: 107. https://doi.org/10.3390/met9010107