Numerical Investigation of Preload Process of Bolted Joint with Superelastic Shape Memory Alloy
Abstract
:1. Introduction
2. Constitutive Modeling for NiTi SMA under Cyclic Loading
2.1. Constitutive Equation and Internal Variables
- (i)
- Transformation to martensite phase:If and :
- (ii)
- Transformation to austenite phase:If and :where, and are the starting and finishing stresses of martensite transformation, and are the slope for the relation between critical transformation stress and temperature, and are the starting and finishing temperatures of austenite transformation, and are starting and finishing temperature of martensite transformation, is the volume fraction of martensite transformation at the end of transformation to martensite phase, and is the residual volume fraction of martensite transformation at the end of transformation to austenite phase. The parameters and are expressed as:
2.2. Evolution Law of Parameters Governed by Accumulated Martensite Volume Fraction
- (i)
- Evolution equation for residual martensite volume fraction:where is the maximum irreversible residual martensite volume fraction produced in the cyclic tension-unloading test with a peak stress equal to the finish stress of phase transformation from austenite to martensite, i.e., at the end of the stress plateau. is the maximum irreversible residual martensite strain corresponding to the maximum load of stable cycle phase transformation. is the uniaxial maximum phase transformation strain. The material parameter b is to govern the saturation rate of residual martensite volume fraction . The revised function is introduced in the evolution law associated with the loading stress level to determine the correlation between that level and the residual martensite fraction, and is written as:where , , is the value of at the endpoint of the forward transformation. The material parameter n is to describe the nonlinear relationship between the residual martensite volume fraction and the loading stress level. It can be found according to Equation (16a) that, in the forward phase, the value of increases with the increase of the loading stress level in the interval of , and reaches its maximum at the endpoint of forward transformation.
- (ii)
- Evolution law of transformation stress
3. FE Modeling for One-Dimensional Bar Element of SMA Ratcheting Behavior
3.1. Numerical Integration Algorithm
3.2. Solving for Incremental Stiffness Matrix
| Algorithm 1: Iteration procedure |
| Begin Step 1 Initialize variables, assumed at the beginning Step 2 Given and , calculate , , and if , goto Step 5 else if and goto Step 3 else goto Step 5 endif Step 3 Calculate if obtaining , and calculating , , , goto Step 4 endif Step 4 Calculate stiffness matrix and force increment , goto Step 5 Step 5 Calculate , and if , goto Step8 elseif and goto Step 6 else goto Step 8 endif Step 6 Calculate if obtaining , and calculating , , endif Step 7 Calculate stiffness matrix and force increment , goto Step 8 Step 8 Updating status variables End |
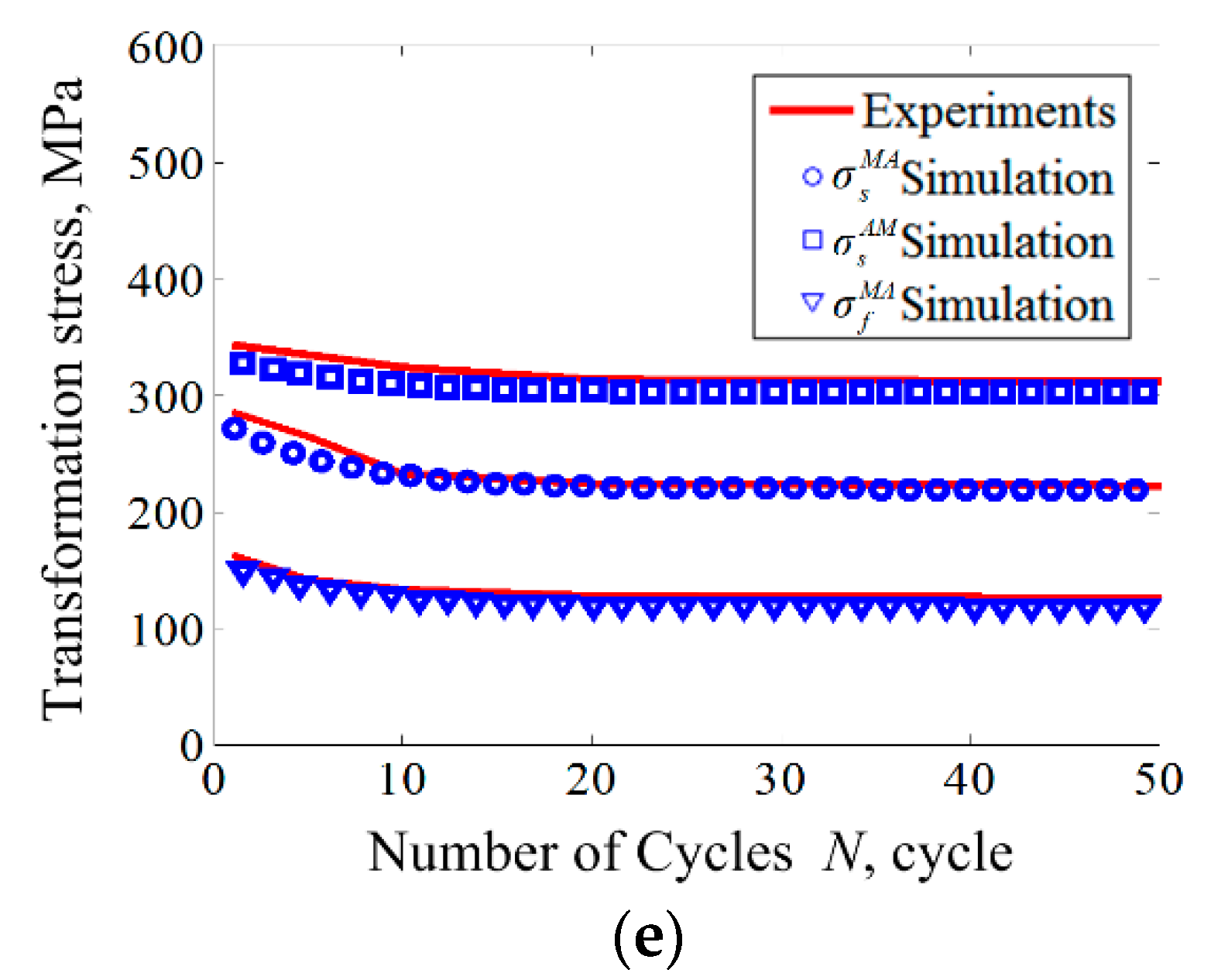
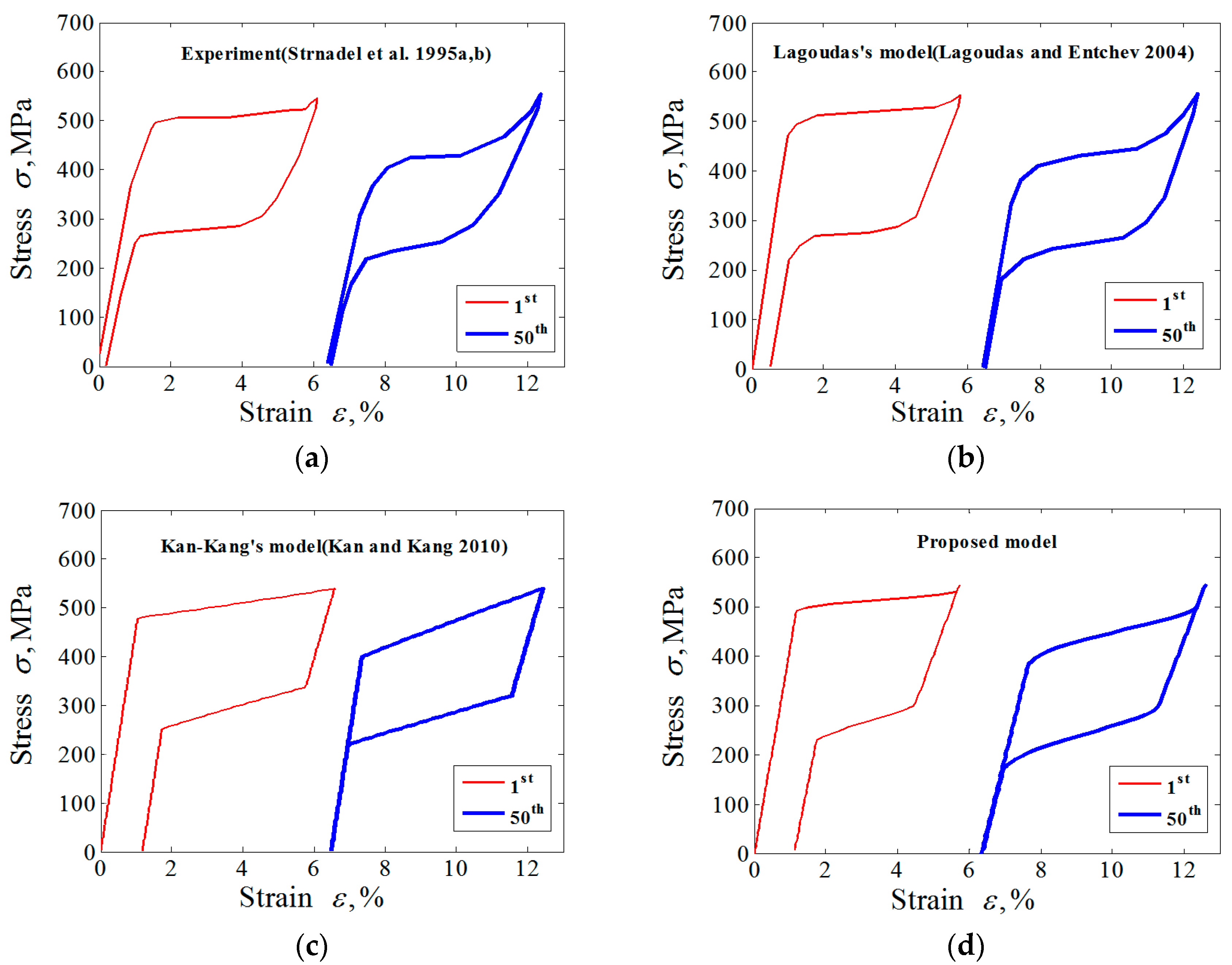
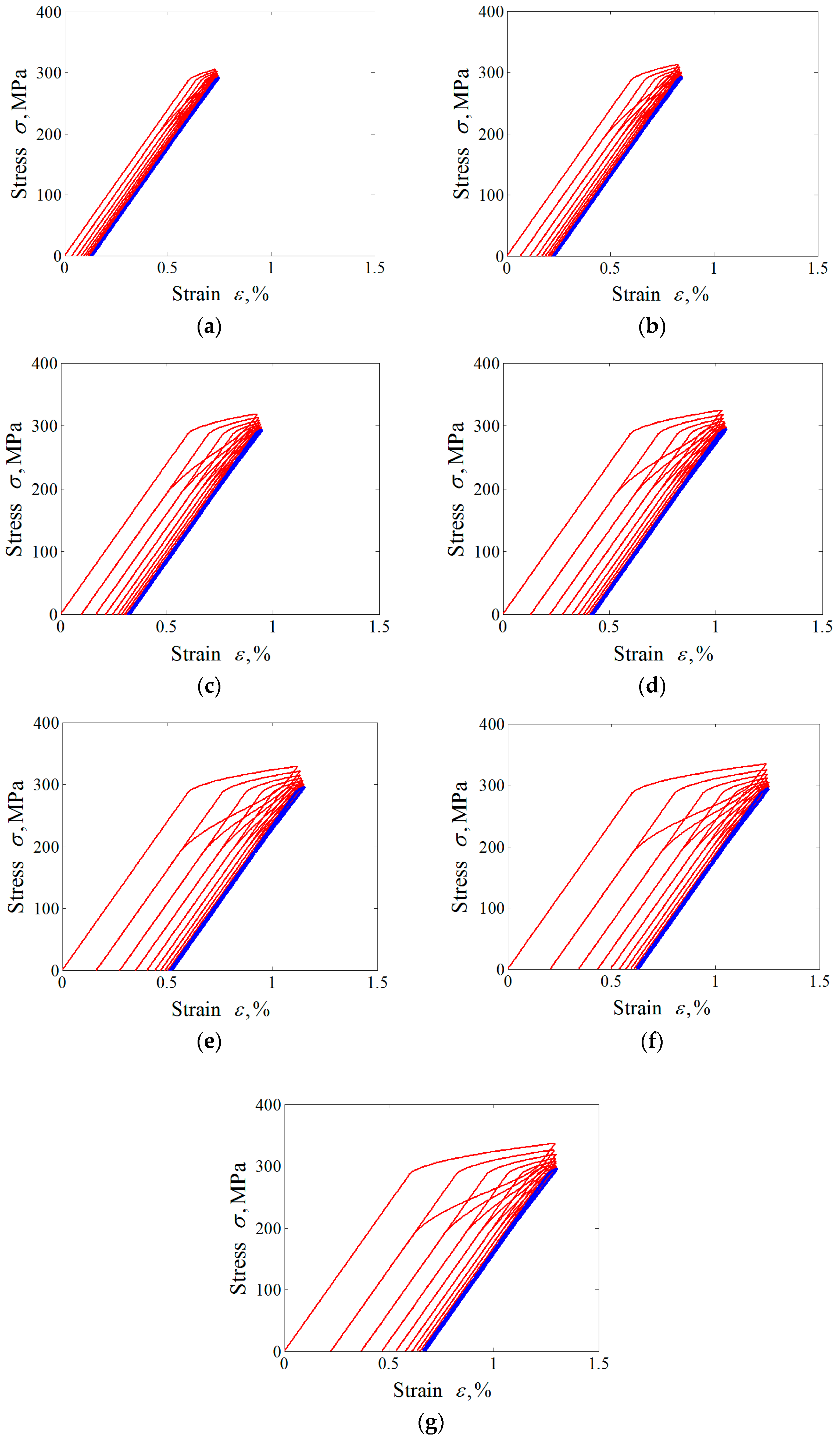
4. Numerical Simulation and Model Verification
5. Numerical Examples for the Analyses of Preload Force of SMA Bolted Joint
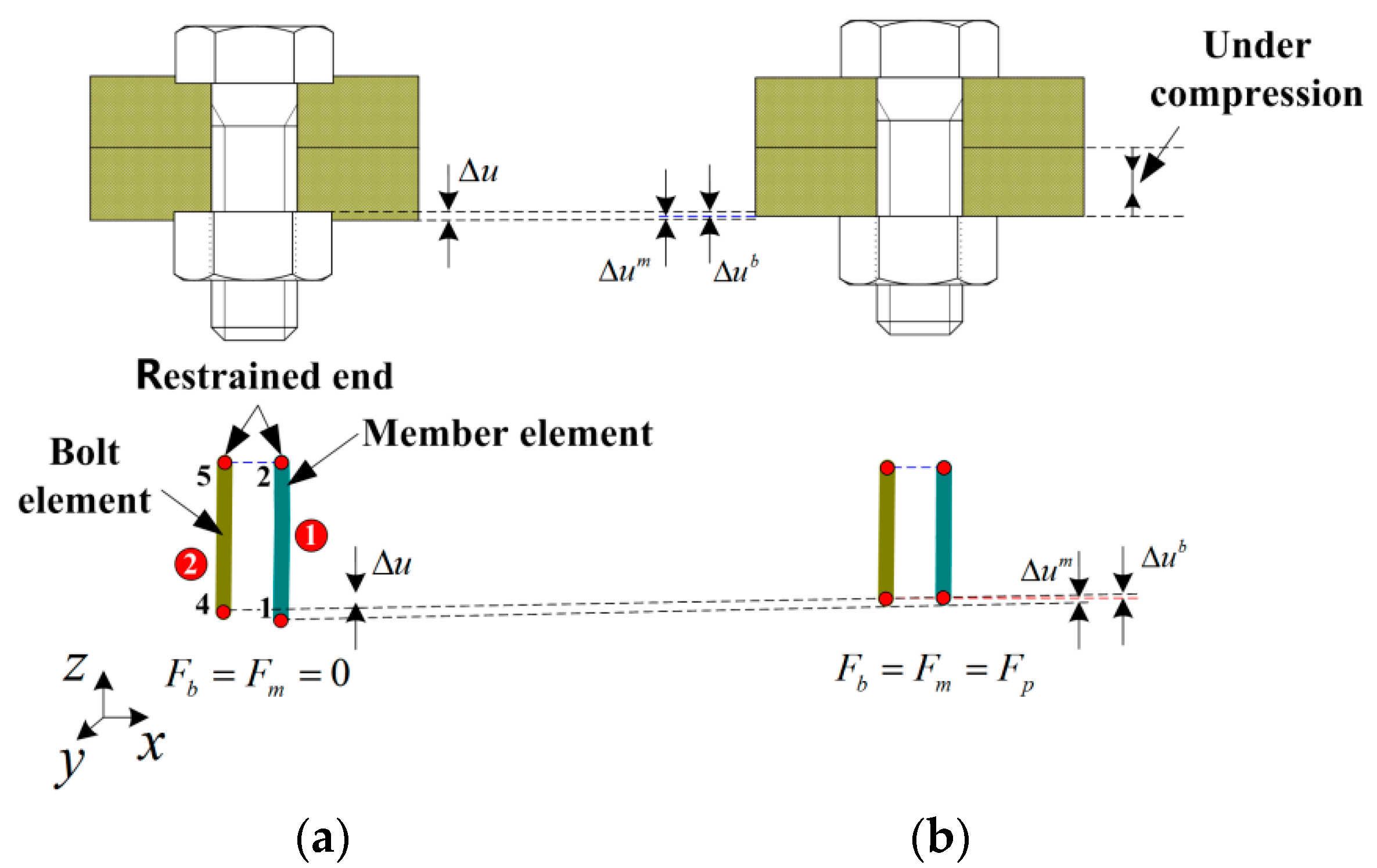
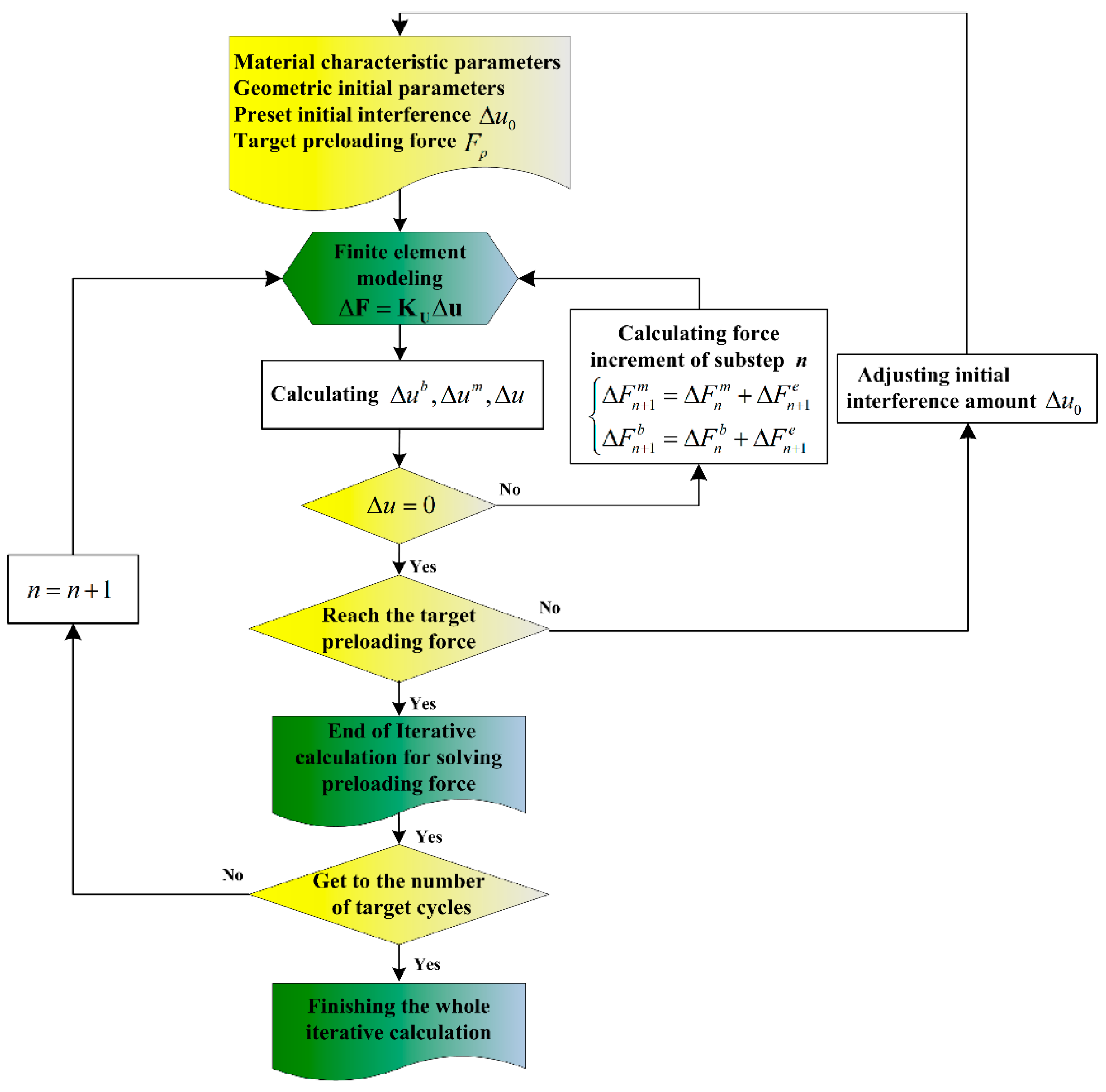
5.1. FE Modeling for the Preload Process of SMA Bolted Joint
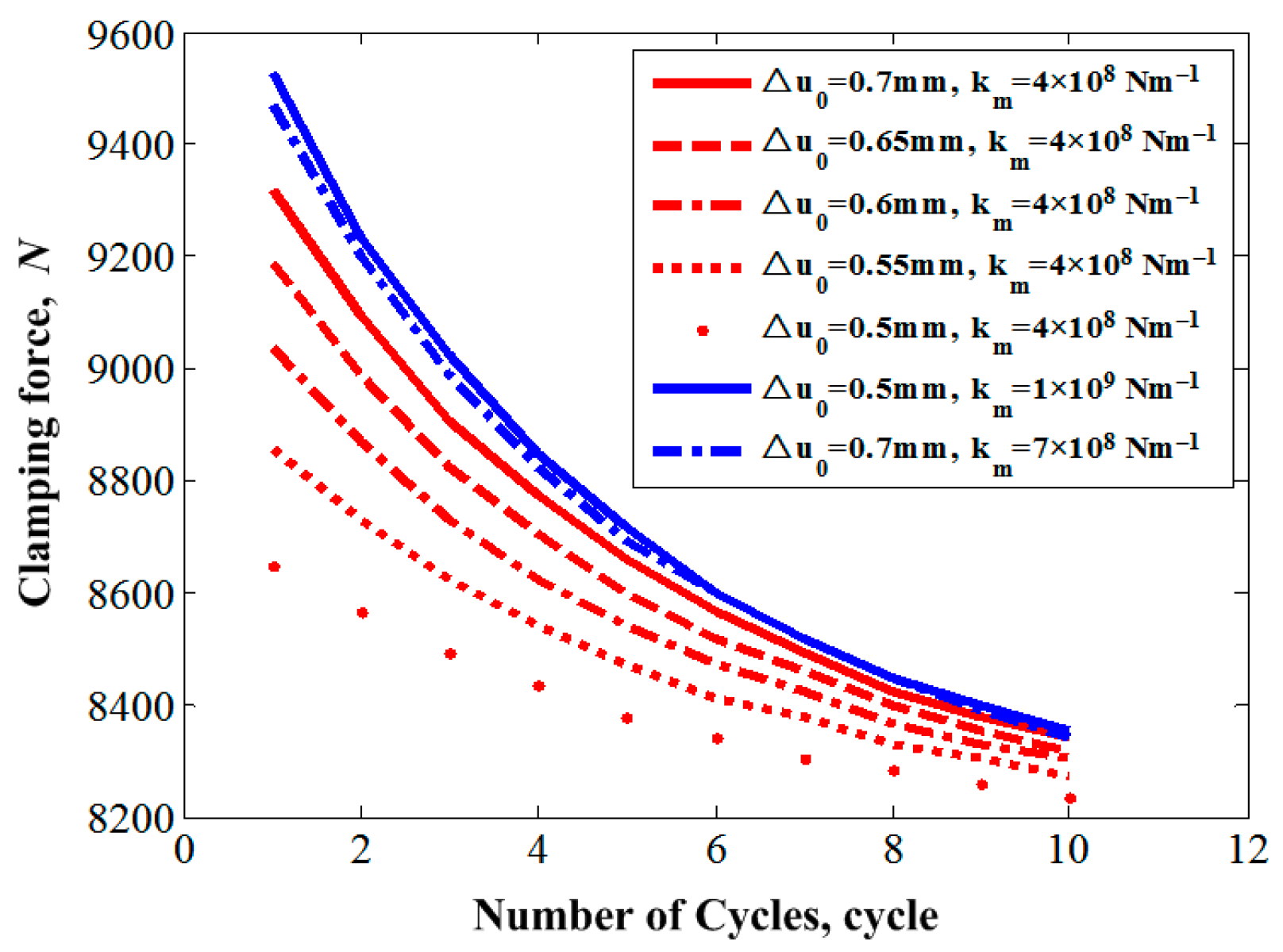
5.2. Simulations and Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Humbeeck, J.V. Non-medical applications of shape memory alloys. Mater. Sci. Eng. A 1999, 273–275, 134–148. [Google Scholar] [CrossRef]
- Duerig, T.; Pelton, A.; Stöckel, D. An overview of nitinol medical applications. Mater. Sci. Eng. A 1999, 273–275, 149–160. [Google Scholar] [CrossRef]
- Morgan, N.B. Medical shape memory alloy applications: The market and its products. Mater. Sci. Eng. A 2004, 378, 16–23. [Google Scholar] [CrossRef]
- Elahinia, M.H.; Hashemi, M.; Tabesh, M.; Bhaduri, S.B. Manufacturing and processing of NiTi implants: A review. Prog. Mater. Sci. 2012, 57, 911–946. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Cheraghi Bidsorkhi, H. MEMS applications of NiTi based shape memory alloys: A review. Micro Nanosyst. 2016, 8, 79–91. [Google Scholar] [CrossRef]
- Elahinia, M.H. Shape Memory Alloy Actuators: Design, Fabrication, and Experimental Evaluation, 1st ed.; Wiley: New York, NY, USA, 2016. [Google Scholar]
- Miyazaki, S.; Otsuka, K.; Suzuki, Y. Transformation pseudoelasticity and deformation behavior in a Ti–50.6 at % Ni alloy. Scr. Metall. 1981, 15, 87–292. [Google Scholar]
- Miyazaki, S.; Imai, T.; Lgo, Y. Effect of cyclic deformation on the pseudoelasticity characteristics of TiNi alloy. Metall. Trans. A 1986, 17, 115–120. [Google Scholar] [CrossRef]
- Strnadel, B.; Ohashi, S.; Ohtsuka, H.; Ishihara, T.; Miyazaki, S. Cyclic stress–strain characteristics of Ti–Ni and Ti-Ni-Cu shape memory alloys. Mater. Sci. Eng. A 1995, 202, 148–156. [Google Scholar] [CrossRef]
- Strnadel, B.; Ohashi, S.; Ohtsuka, H.; Miyazaki, S.; Ishihara, T. Effect of mechanical cycling on the pseudoelasticity characteristics of Ti–Ni and Ti–Ni–Cu alloys. Mater. Sci. Eng. A 1995, 203, 187–196. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G. Superelastic and cyclic response of NiTi SMA at various strain rates and temperatures. Mech. Mater. 2006, 38, 463–474. [Google Scholar] [CrossRef]
- Lagoudas, D.C.; Bo, Z. Thermomechanical modeling of polycrystalline SMAs under cyclic loading, Part II: Material characterization and experimental results for a stable transformation cycle. Int. J. Eng. Sci. 1999, 37, 1141–1173. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Anderson, R.; Karaman, I.; Gall, K.; Chumlyakov, Y. Cyclic deformation behavior of single crystal NiTi. Mater. Sci. Eng. A 2001, 314, 67–74. [Google Scholar] [CrossRef]
- Gall, K.; Maier, H.J. Cyclic deformation mechanisms in precipitated NiTi shape memory alloys. Acta Mater. 2002, 50, 4643–4657. [Google Scholar] [CrossRef]
- Wang, X.; Xu, B.; Yue, Z. Phase transformation behavior of pseudoelasticNiTi shape memory alloys under large strain. J. Alloys Compd. 2008, 463, 417–422. [Google Scholar] [CrossRef]
- Song, D.; Kang, G.; Kan, Q.; Yu, C.; Zhang, C. Non-proportional multiaxial transformation ratchetting of superelastic NiTi shape memory alloy: Experimental observations. Mech. Mater. 2014, 70, 94–105. [Google Scholar] [CrossRef]
- Grabe, C.; Bruhns, O.T. On the viscous and strain rate dependent behavior of polycrystalline NiTi. Int. J. Solids Struct. 2008, 45, 1876–1895. [Google Scholar] [CrossRef]
- Maletta, C.; Sgambitterra, E.; Furgiuele, F.; Casati, R.; Tuissi, A. Fatigue properties of a pseudoelastic NiTi alloy: Strain ratcheting and hysteresis under cyclic tensile loading. Int. J. Fatigue 2014, 66, 78–85. [Google Scholar] [CrossRef]
- Maletta, C.; Sgambitterra, E.; Furgiuele, F.; Casati, R.; Tuissi, A. Fatigue of pseudoelastic NiTi within the stress-induced transformation regime: A modified Coffin-Manson approach. Smart Mater. Struct. 2012, 21, 112001. [Google Scholar] [CrossRef]
- Song, D.; Kang, G.; Kan, Q.; Yu, C.; Zhang, C. Effects of peak stress and stress amplitude on multiaxial transformation ratchetting and fatigue life of superelastic NiTi SMA micro-tubes: Experiments and life-prediction model. Int. J. Fatigue 2017, 96, 252–260. [Google Scholar] [CrossRef]
- Morin, C.; Moumni, Z.; Zaki, W. A constitutive model for shape memory alloys accounting for thermomechanical coupling. Int. J. Plast. 2011, 27, 748–767. [Google Scholar] [CrossRef]
- He, Y.J.; Sun, Q.P. On non-monotonic rate dependence of stress hysteresis of superelastic shape memory alloy bars. Int. J. Solids Struct. 2011, 48, 1688–1695. [Google Scholar] [CrossRef]
- He, Y.J.; Sun, Q.P. Rate–dependent domain spacing in a stretched NiTi strip. Int. J. Solids Struct. 2010, 47, 2775–2783. [Google Scholar] [CrossRef]
- He, Y.J.; Sun, Q.P. Frequency-dependent temperature evolution in NiTi shape memory alloy under cyclic loading. Smart Mater. Struct. 2010, 19, 115014. [Google Scholar] [CrossRef]
- He, Y.; Yin, H.; Zhou, R.; Sun, Q. Ambient effect on damping peak of NiTi shape memory alloy. Mater. Lett. 2010, 64, 483–1486. [Google Scholar] [CrossRef]
- Yin, H.; He, Y.; Sun, Q. Effect of deformation frequency on temperature and stress oscillations in cyclic phase transition of NiTi shape memory alloy. J. Mech. Phys. Solids 2014, 67, 100–128. [Google Scholar] [CrossRef]
- Kan, Q.H.; Yu, C.; Kang, G.; Li, J.; Yan, W. Experimental observations on rate-dependent cyclic deformation of superelastic NiTi shape memory alloy. Mech. Mater. 2016, 97, 48–58. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Boyd, J.G.; Lagoudas, D.C. A thermodynamical constitutive model for shape memory materials. Part I: The monolithic shape memory alloy. Int. J. Plast. 1996, 12, 805–842. [Google Scholar] [CrossRef]
- Auricchio, F.; Lubliner, J. A uniaxial model for shape–memory alloys. Int. J. Solids Struct. 1997, 34, 3601–3618. [Google Scholar] [CrossRef]
- Zaki, W.; Moumni, Z. A three-dimensional model of the thermomechanical behavior of shape memory alloys. J. Mech. Phys. Solids 2007, 55, 2455–2490. [Google Scholar] [CrossRef]
- Ortiz, M.; Simo, J.C. An analysis of a new class of integration algorithms for elastoplastic constitutive relations. Int. J. Numer. Methods Eng. 1986, 23, 353–366. [Google Scholar] [CrossRef]
- Simo, J.C.; Ortiz, M. A unified approach to finite deformation elastoplastic analysis based on the use of hyperelastic constitutive equations. Comput. Methods Appl. Mech. Eng. 1985, 49, 221–245. [Google Scholar] [CrossRef]
- Lagoudas, D.C.; Entchev, P.B. Modelling of transformation-induced plasticity and its effect on the behavior of porous shape memory alloys. Part I: Constitutive model for fully dense SMAs. Mech. Mater. 2004, 36, 865–892. [Google Scholar] [CrossRef]
- Kan, Q.; Kang, G. Constitutive model for uniaxial transformation ratchetting of superelastic NiTi shape memory alloy at room temperature. Int. J. Plast. 2010, 26, 441–465. [Google Scholar] [CrossRef]
- Kan, Q.H.; Kang, G.Z.; Guo, S.J. Finite element implementation of a superelastic constitutive model for transformation ratchetting of NiTi alloy. Int. J. Comput. Methods 2012, 9, 1240022. [Google Scholar] [CrossRef]
- Kang, G.Z.; Kan, Q.H.; Qian, L.M.; Liu, Y.J. Ratcheting deformation of superelastic and shape memory NiTi Alloys. Mech. Mater. 2009, 41, 139–153. [Google Scholar] [CrossRef]
- Jiang, X.; Zhu, Y.; Hong, J.; Chen, X.; Zhang, Y. Investigation into the loosening mechanism of bolt in curvic coupling subjected to transverse loading. Eng. Fail. Anal. 2013, 32, 360–373. [Google Scholar] [CrossRef]
- Jiang, X.J.; Zhu, Y.S.; Hong, J.; Zhu, L.B. Development and Validation of an Analytical Model for Stiffness Analysis of Curvic Coupling in Tightening. J. Aerosp. Eng. 2013, 6, 509–522. [Google Scholar] [CrossRef]
- Jiang, X.J.; Zhu, Y.S.; Hong, J.; Zhu, L.B. Stiffness Analysis of curvic coupling in tightening by considering the different bolt structures. J. Aerosp. Eng. 2016, 29, 04015076. [Google Scholar] [CrossRef]
- Motosh, N. Determination of joint stiffness in bolted connections. J. Eng. Ind. 1976, 983, 858–861. [Google Scholar] [CrossRef]
- Nassar, S.A.; Abboud, A. An improved stiffness model for bolted joints. J. Mech. Des. 2009, 131, 1–10. [Google Scholar] [CrossRef]
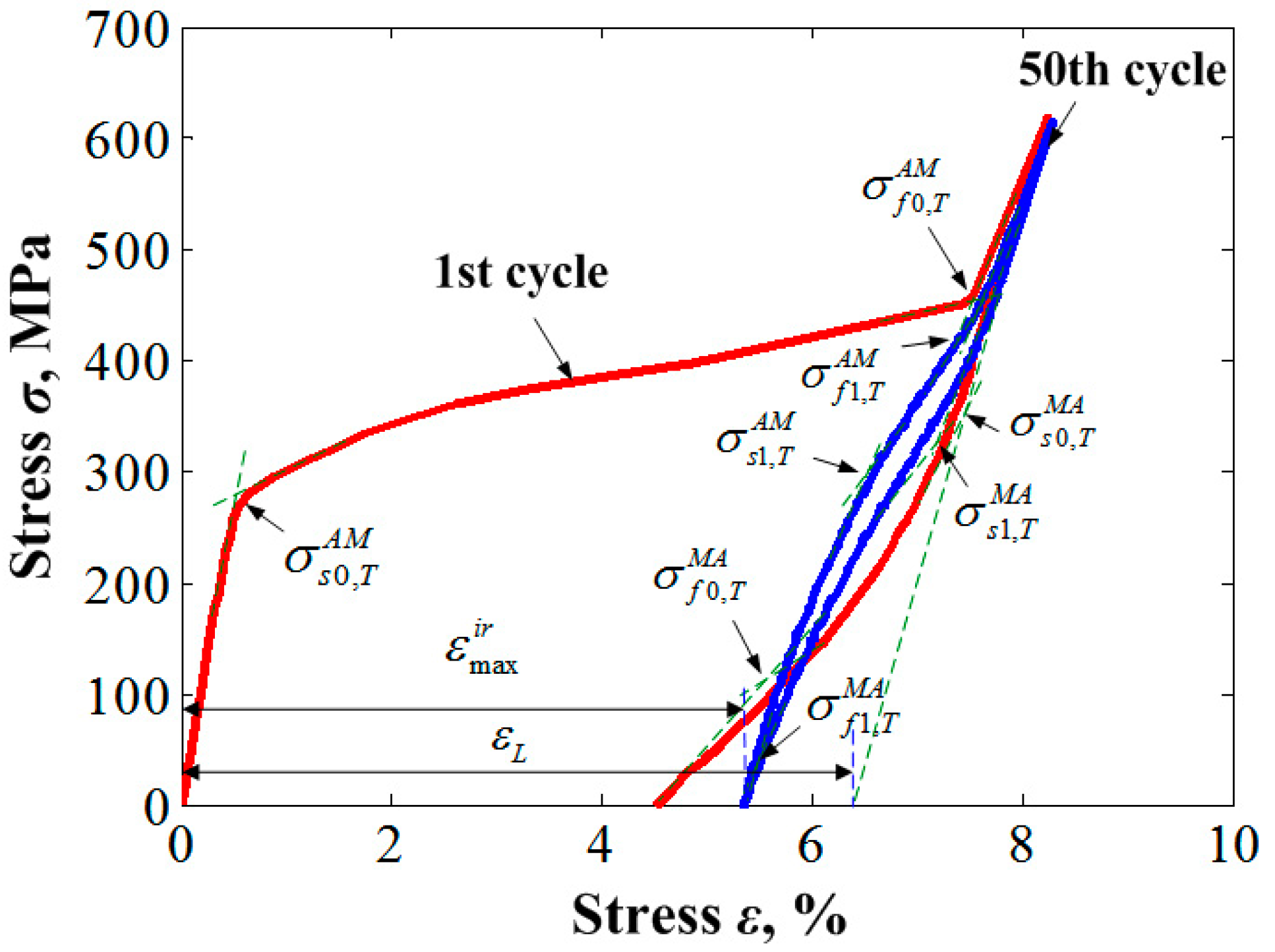
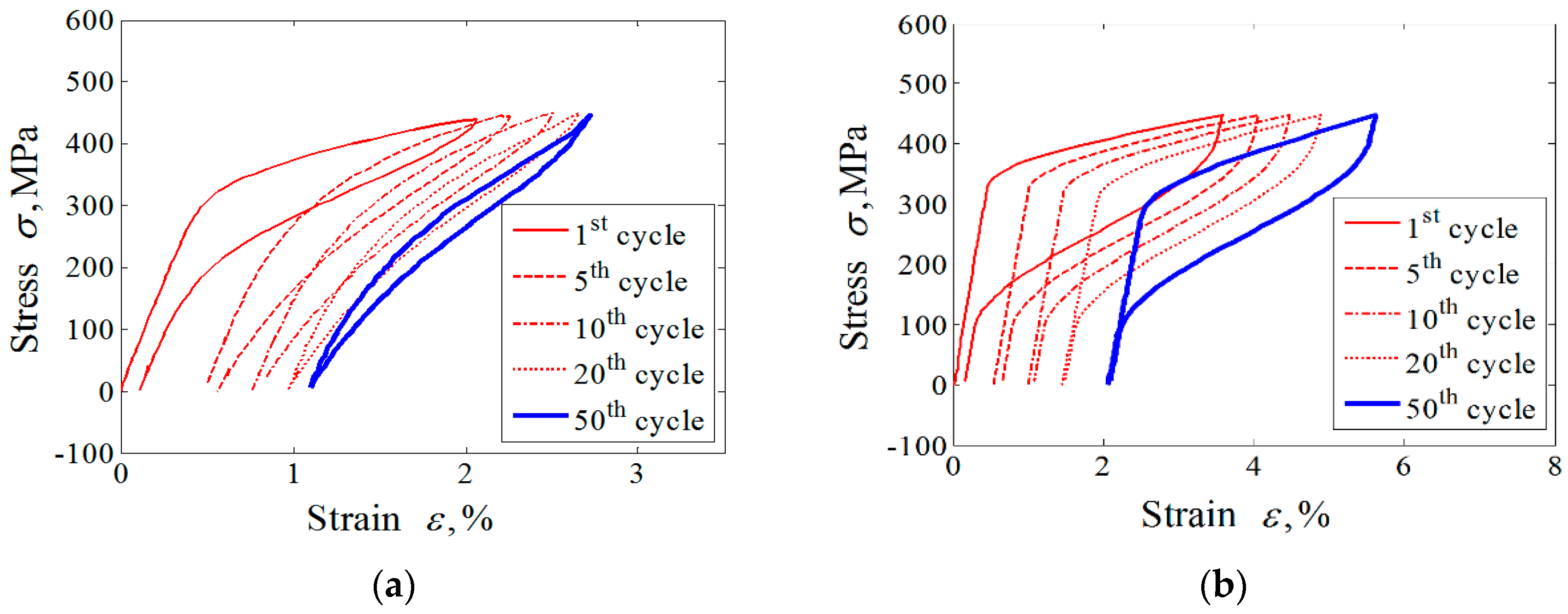
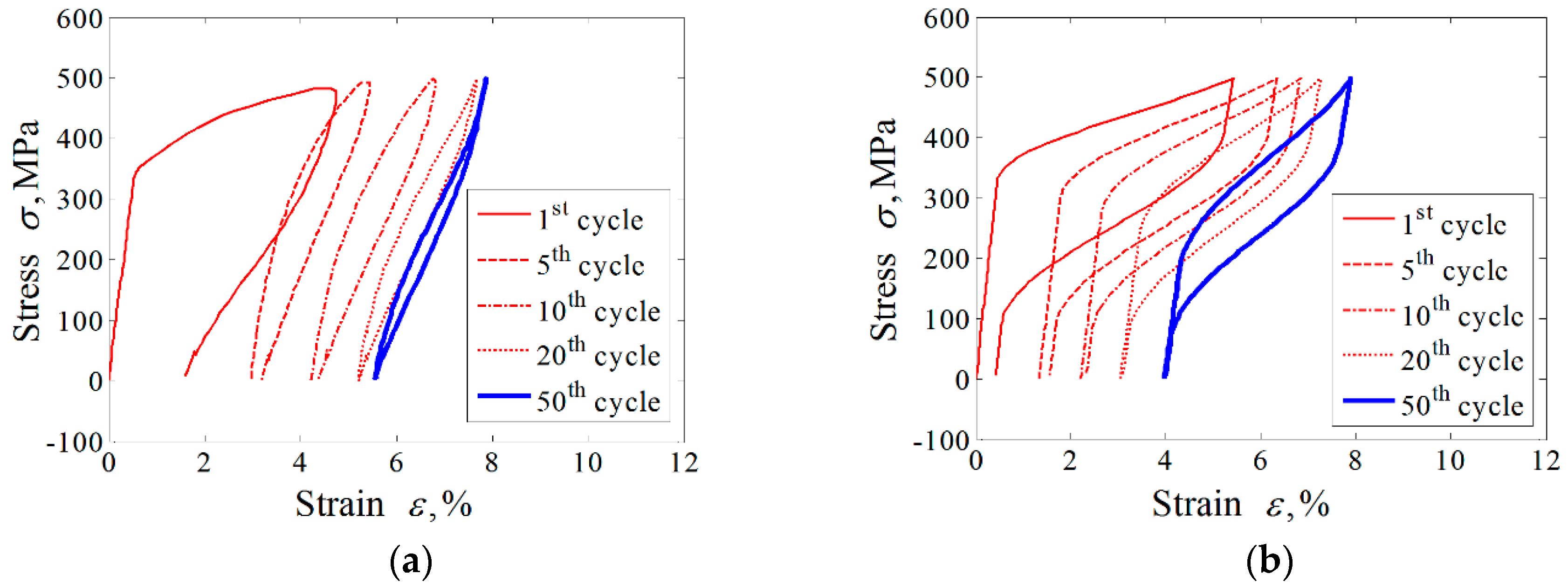

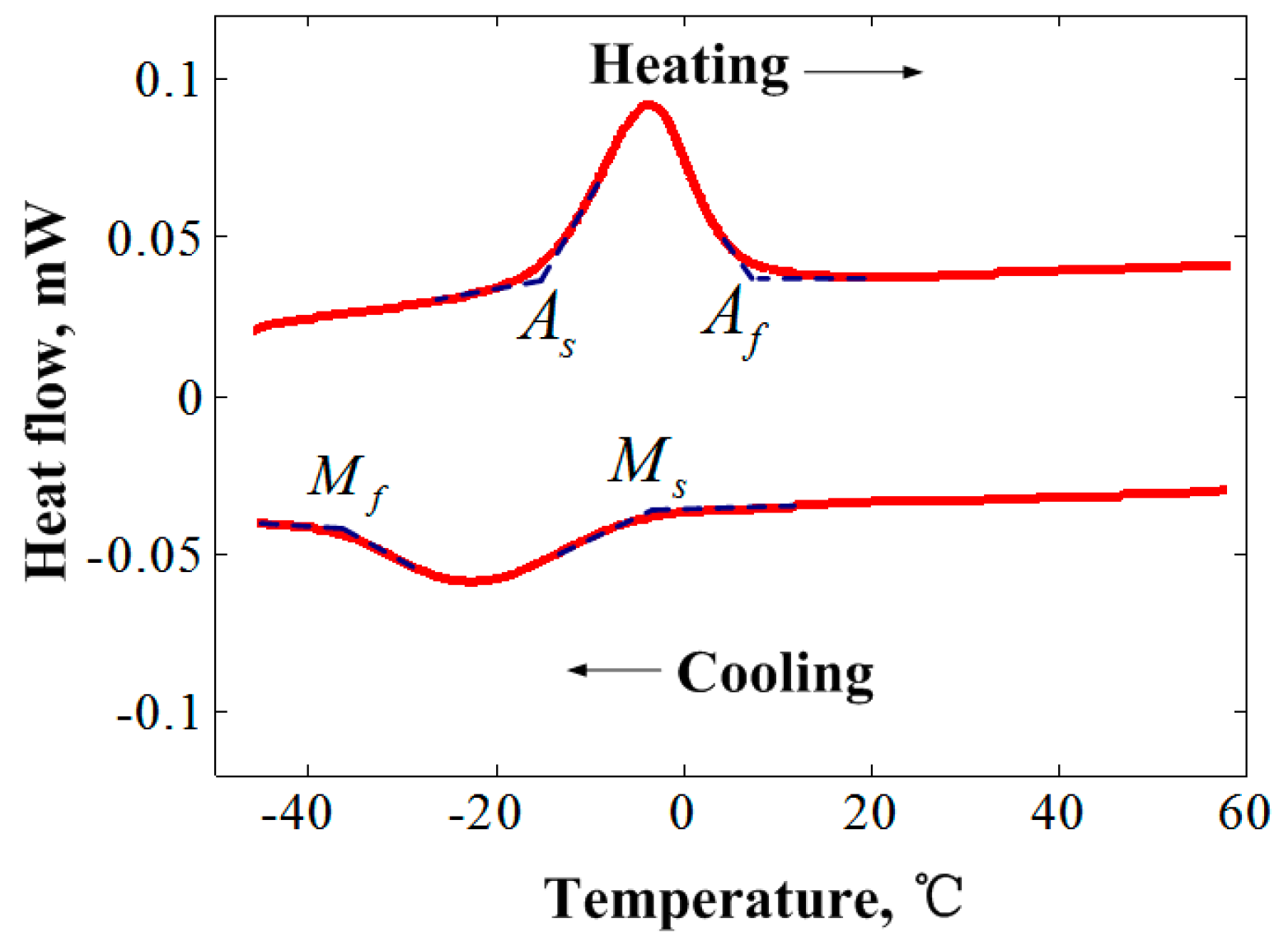



| Material Parameters |
|---|
| = 48 GPa; = 35 GPa; = 0.3; =0.3; = 0.063; = 295 K; = 285 MPa; = 458 MPa; = 345 MPa; = 164 MPa; = 225 MPa; = 458 MPa; = 310 MPa; = 125 MPa; = 0.05; = 0.05; = 0.05; = 0.05; = 3; = 0.84; = 0.5. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Wang, Y.; Pan, F.; Jing, Z.; Huang, J.; Li, B. Numerical Investigation of Preload Process of Bolted Joint with Superelastic Shape Memory Alloy. Metals 2018, 8, 730. https://doi.org/10.3390/met8090730
Jiang X, Wang Y, Pan F, Jing Z, Huang J, Li B. Numerical Investigation of Preload Process of Bolted Joint with Superelastic Shape Memory Alloy. Metals. 2018; 8(9):730. https://doi.org/10.3390/met8090730
Chicago/Turabian StyleJiang, Xiangjun, Yongkun Wang, Fengqun Pan, Ze Jing, Jin Huang, and Baotong Li. 2018. "Numerical Investigation of Preload Process of Bolted Joint with Superelastic Shape Memory Alloy" Metals 8, no. 9: 730. https://doi.org/10.3390/met8090730





