Mesomechanical Modeling and Numerical Simulation of the Diffraction Elastic Constants for Ti6Al4V Polycrystalline Alloy
Abstract
:1. Introduction
2. Two-Phase Model
2.1. Effective Elastic Properties of the Two-Phase Material
2.2. Macroscopic Stress-Strain of the Two-Phase Material
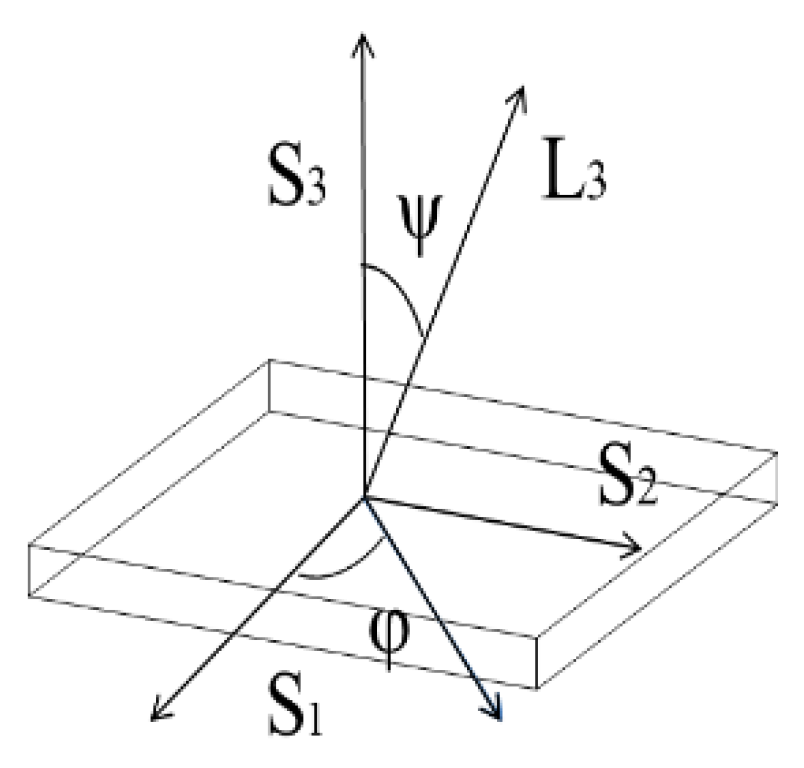
2.3. Microscopic Stress-Strain of the Two-Phase Material
3. Calculation Results and Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Geraci, G.; Aliabadi, M.H. Micromechanical modelling of cohesive thermoelastic cracking in orthotropic polycrystalline materials. Comput. Method. Appl. Mech. Eng. 2018, 339, 567–590. [Google Scholar] [CrossRef]
- Luo, G.Q.; Shi, L.P.; Zhong, Y.S.; Yang, L.; Ma, X.L.; Li, M.W.; He, X.D. Compressive damage of three-dimensional random fibrous ceramic materials: a meso-mechanics modeling and experimental study. Ceram. Int. 2018, 44, 15690–15699. [Google Scholar] [CrossRef]
- Benedetti, I.; Aliabadi, M.H. Multiscale modeling of polycrystalline materials: A boundary element approach to material degradation and fracture. Comput. Method. Appl. Mech. Eng. 2015, 289, 429–453. [Google Scholar] [CrossRef] [Green Version]
- Zou, F.; Rao, J.; Aliabadi, M.H. Highly accurate online characterisation of cracks in plate-like structures. NDT E Int. 2018, 94, 1–12. [Google Scholar] [CrossRef]
- Chen, D.; Torquato, S. Designing disordered hyperuniform two-phase material with novel physical properties. Acta Mater. 2018, 142, 152–161. [Google Scholar] [CrossRef]
- Xu, W.; Jia, M.; Zhu, Z.; Liu, M.; Lei, D.; Gou, X. n-Phase micromechanical framework for the conductivity and elastic modulus of particulate composites: Design to microencapsulated phase change materials (MPCMs)-cementitious composites. Mater. Des. 2018, 145, 108–115. [Google Scholar] [CrossRef]
- Donachie, M.J. Titanium: A Technical Guide, 2nd ed.; ASM International Materials Park: Novelty, OH, USA, 2000; p. 9. ISBN 0-87170-686-5. [Google Scholar]
- Wang, Z.B.; Sun, J.F.; Chen, W.Y.; Liu, L.B.; Wang, R.Q. Machining distortion of Titanium alloys aero engine case based on the energy principles. Metals 2018, 8, 464. [Google Scholar] [CrossRef]
- Zhou, X.W.; Chen, Y.H.; Huang, Y.D.; Mao, Y.Q.; Yu, Y.Y. Effects of niobium addition on the microstructure and mechanical properties of laser-welded joints of NiTiNb and Ti6Al4V alloys. J. Alloys Compd. 2018, 735, 2616–2624. [Google Scholar] [CrossRef]
- Langen, D.; Maier, H.J.; Hassel, T. The effect of SiC addition on microstructure and mechanical properties of gas tungsten arc-welded Ti-6Al-4V alloy. J. Mater. Eng. Perform. 2018, 27, 253–260. [Google Scholar] [CrossRef]
- Zhang, Q.; Liang, Z.L.; Cao, M.; Liu, Z.F.; Zhang, A.F.; Lu, B.H. Microstructure and mechanical properties of Ti6Al4V alloy prepared by selective laser melting combined with precision forging. T. Nonferr. Metal. Soc. 2017, 27, 1036–1042. [Google Scholar] [CrossRef]
- Hemery, S.; Nait-Ali, A.; Gueguen, M.; Villechaise, P. Mechanical study of crystalline orientation distribution in Ti-6Al-4V: An assessment of micro-texture induced load partitioning. Mater. Des. 2018, 137, 22–32. [Google Scholar] [CrossRef]
- Bhattiprolu, V.S.; Johnson, K.W.; Ozdemir, O.C.; Crawford, G.A. Influence of feedstock powder and cold spray processing parameters on microstructure and mechanical properties of Ti-6Al-4V cold spray depositions. Surf. Coat. Technol. 2018, 335, 1–12. [Google Scholar] [CrossRef]
- Collings, E.W. Materials Properties Handbook: Titanium Alloys; ASM International Materials Park: Novelty, OH, USA, 1993; pp. 50, 95. ISBN 978-0-87170-481-8. [Google Scholar]
- Nie, B.H.; Zhao, Z.H.; Chen, D.C.; Liu, S.; Liu, M.S.; Zhang, J.L.; Liang, F.M. Effect of basketweave microstructure on very high cycle fatigue behavior of TC21 Titanium alloy. Metals 2018, 8, 401. [Google Scholar] [CrossRef]
- Moussaoui, K.; Segonds, S.; Rubio, W.; Mousseigne, M. Studying the measurement by X-ray diffraction of residual stresses in Ti6Al4V titanium alloy. Mater. Sci. Eng. A 2016, 667, 340–348. [Google Scholar] [CrossRef]
- Lundbäck, A.; Pederson, R.; Colliander, M.H.; Brice, C.; Steuwer, A.; Heralic, A.; Buslaps, T.; Lindgren, L.E. Modeling and experimental measurement with synchrotron radiation of residual stresses in laser metal deposited Ti-6Al-4V. In Proceedings of the 13th World Conference on Titanium, Hoboken, NJ, USA, 16–20 August 2015; pp. 1279–1282. [Google Scholar]
- He, B.B. Two-Dimensional X-ray Diffraction; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009; p. 249. ISBN 978-0-470-22722-0. [Google Scholar]
- Wern, H.; Johannes, R.; Walz, H. Dependence of the X-ray elastic constants on the diffraction plane. Phys. Status Solidi R. 2015, 206, 545–557. [Google Scholar] [CrossRef]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. Berl. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Kröner, E. Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls. Zeitschrift Für Physik 1958, 151, 504–518. [Google Scholar] [CrossRef]
- Liu, M.; Ling, Z. The elastic constants of polycrystalline materials with cubic system structural single crystals, (in Chinese). Acta Phys. Sin. 2009, 58, 4096–4102. [Google Scholar]
- Wit, R.D. Diffraction elastic constants of a cubic polycrystal. J. Appl. Crystallogr. 1997, 30, 510–511. [Google Scholar] [CrossRef] [Green Version]
- Welzel, U.; Mittemeijer, E.J. Diffraction stress analysis of macro scopically elastically anisotropic specimens: On the concepts of diffraction elastic constants and stress factors. J. Appl. Phys. 2003, 93, 9001–9011. [Google Scholar] [CrossRef]
- Lundberg, M.; Saarimäki, J.; Moverare, J.J.; Peng, R.L. Effective X-ray elastic constant of cast iron. J. Mater. Sci. 2018, 53, 2766–2773. [Google Scholar] [CrossRef]
- Blaschke, D.N. Averaging of elastic constants for polycrystals. J. Mater. Sci. 2017, 122, 145110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Q.; Manke, D.R.; Sharifzadeh, S.; Alejandro, L.B.; Ashwin, R.; Kristie, J.K. The elastic constants of rubrene determined by Brillouin scattering and density functional theory. Appl. Phys. Lett. 2017, 110, 071903. [Google Scholar] [CrossRef] [Green Version]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Du, S.Y.; Wang, B. Composites Meso-Mechanics; Science Press: Beijing, China, 1998; p. 5. ISBN 7-03-006182-9. (In Chinese) [Google Scholar]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int. J. Solids. Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Ju, J.W.; Chen, T.M. Micromechanics and effective moduli of elastic composites containing randomly dispersed ellipsoidal inhomogeneities. Acta Mech. 1994, 103, 103–121. [Google Scholar] [CrossRef]
- Ju, J.W.; Chen, T.M. Effective elastic moduli of two-phase composites containing randomly dispersed spherical inhomogeneities. Acta Mech. 1994, 103, 123–144. [Google Scholar] [CrossRef]
- Sen, A.K.; Torquato, S. Effective conductivity of anisotropic two-phase composite media. Phys. Rev. B 1989, 39, 4504–4515. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids, 2nd ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 1987; p. 15. ISBN 90-247-3343-X. [Google Scholar]
- Hill, R. Eigenmodal deformations in elastic/plastic continua. J. Mech. Phys. Solids 1967, 15, 371–386. [Google Scholar] [CrossRef]
- Fréour, S.; Gloaguen, D.; François, M.; Guillen, R. Modelling and simulation of multi phase effects on X-ray elasticity constants. Phys. Status Solidi B 2003, 239, 297–309. [Google Scholar] [CrossRef]
- Hill, R. Continuum micro-mechanics of elastoplastic polycrystal. J. Mech. Phys. Solids 1965, 13, 89–101. [Google Scholar] [CrossRef]
- Budiansky, B. On the elastic moduli of some heterogeneous materials. J. Mech. Phys. Solids 1965, 13, 223–227. [Google Scholar] [CrossRef]
- Eshelby, J.D. Elastic inclusion and inhomogeneities. Prog. Solid. Mech. 1961, 2, 89–140. [Google Scholar]
- Petry, W.; Heiming, A.; Trampenau, J.; Alba, M.; Herzig, C. Phonon dispersion of the bcc phase of group-IV metals. I. bcc titanium. Phys. Rev. B 1991, 43, 10933–10947. [Google Scholar] [CrossRef]
- Stapleton, A.M.; Raghunathan, S.L.; Bantounas, I.; Stone, H.J.; Lindley, T.C.; Dye, D. Evolution of lattice strain in Ti-6Al-4V during tensile loading at room temperature. Acta Mater. 2008, 56, 6186–6196. [Google Scholar] [CrossRef]
- Ling, Z.; Liu, M. The New Exploration of Elastic Constants; Science Press: Beijing, China, 2011; p. 104. ISBN 978-7-03-031227-3. (In Chinese) [Google Scholar]
- Lee, Y.T.; Welsch, G. Young’s modulus and damping of Ti-6Al-4V alloy as a function of heat treatment and oxygen concentration. Mat. Sci. Eng. A 1990, 128, 77–89. [Google Scholar] [CrossRef]
| Al | V | Fe | C | O | N | H | Ti |
|---|---|---|---|---|---|---|---|
| 6.1 | 4.0 | 0.06 | 0.02 | 0.06 | <0.01 | 0.002 | Balance |
| Phase | C11 | C12 | C13 | C33 | C44 |
|---|---|---|---|---|---|
| α-Ti | 168 | 95 | 69 | 191 | 48 |
| β-Ti | 134 | 110 | 110 | 110 | 55 |
| Materials | Bulk Modulus K/GPa | Shear Modulus G/GPa | Elastic Modulus E/GPa | Poisson’s Ratio ν |
|---|---|---|---|---|
| α-Ti | 110.3 | 45.2 | 119.3 | 0.3197 |
| β-Ti | 118 | 30.2 | 83.5 | 0.3821 |
| Ti6Al4V | 114.1 a | 37a | 100.2a | 0.3537 a |
| 96.3 b | 42b | 110b | 0.330 b |
| Peak | {1010} | {1011} | {1012} | {1120} | {1013} | {2021} | |
|---|---|---|---|---|---|---|---|
| /GPa | 96 | 93 | 106 | 96 | 106 | 100 | 78 |
| /GPa | 105.5 | 106.5 | 110.8 | 105.5 | 115.3 | 105.6 | 80.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Liu, L.; Zhu, C.; Chen, K. Mesomechanical Modeling and Numerical Simulation of the Diffraction Elastic Constants for Ti6Al4V Polycrystalline Alloy. Metals 2018, 8, 822. https://doi.org/10.3390/met8100822
Chen Q, Liu L, Zhu C, Chen K. Mesomechanical Modeling and Numerical Simulation of the Diffraction Elastic Constants for Ti6Al4V Polycrystalline Alloy. Metals. 2018; 8(10):822. https://doi.org/10.3390/met8100822
Chicago/Turabian StyleChen, Qiang, Li Liu, Changjun Zhu, and Kanghua Chen. 2018. "Mesomechanical Modeling and Numerical Simulation of the Diffraction Elastic Constants for Ti6Al4V Polycrystalline Alloy" Metals 8, no. 10: 822. https://doi.org/10.3390/met8100822




