Electrical Resistivity Measurement of Carbon Anodes Using the Van der Pauw Method
Abstract
:1. Introduction
2. Experimental
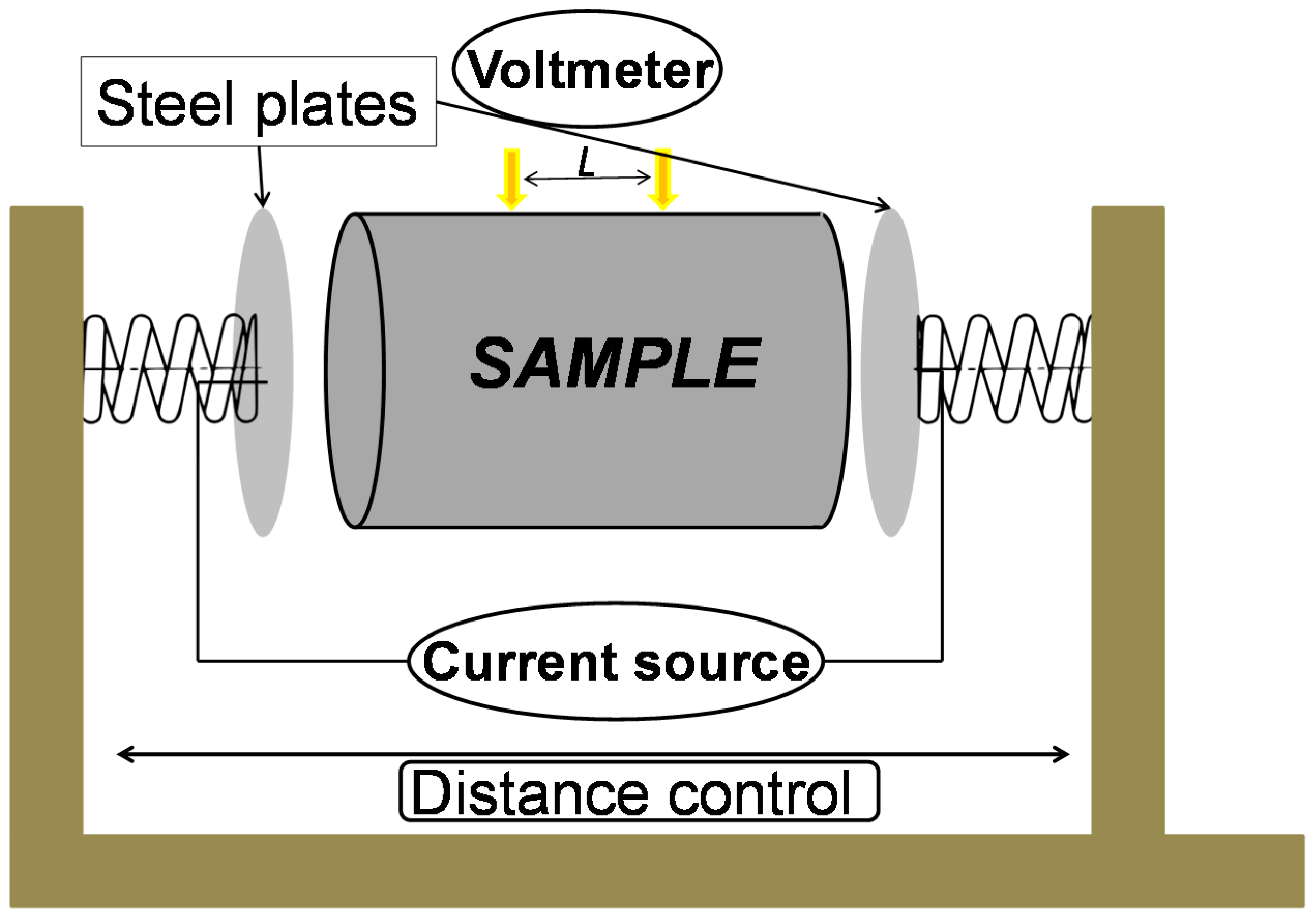
2.1. Standard Method
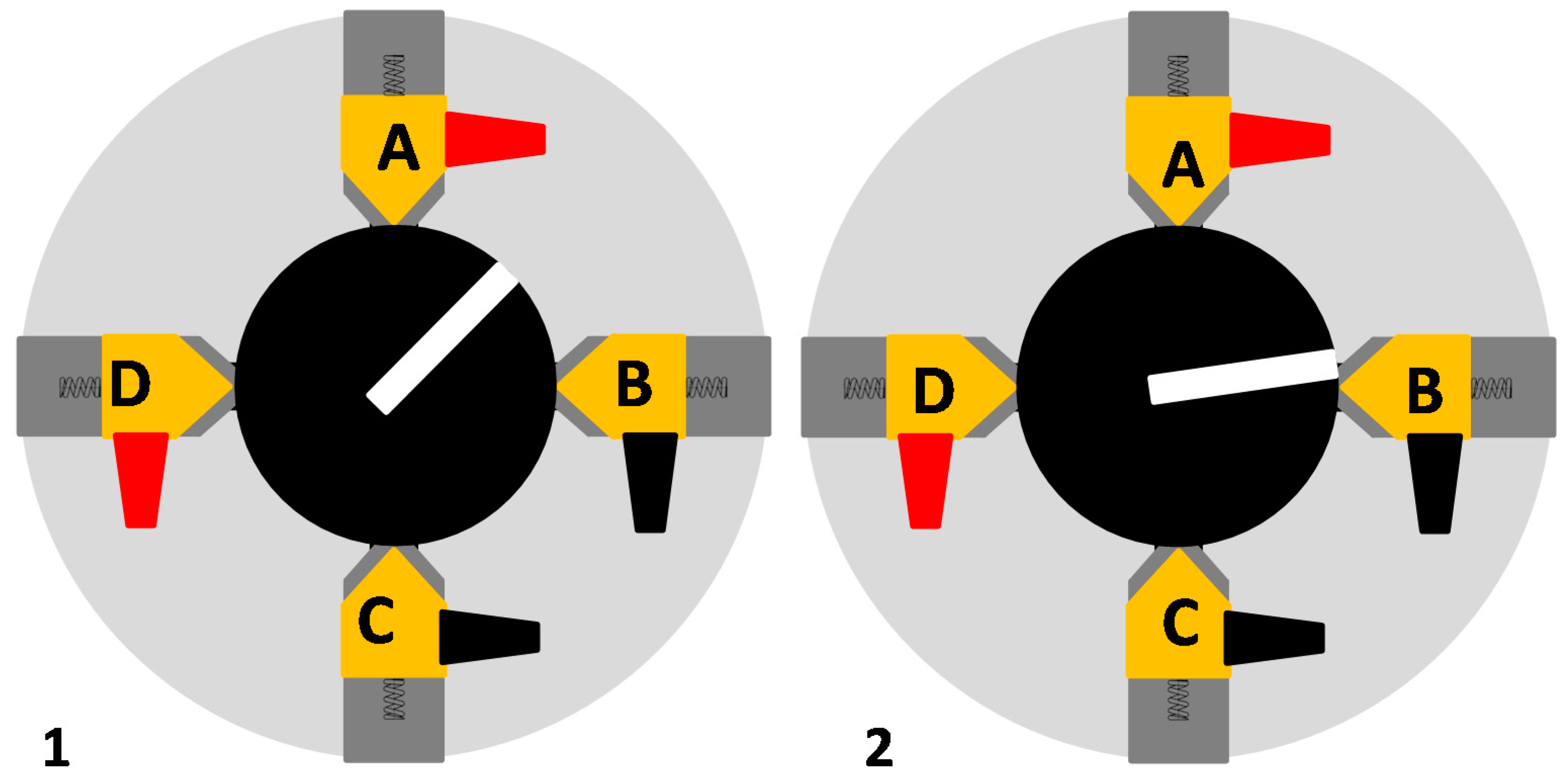
2.2. Van der Pauw Method
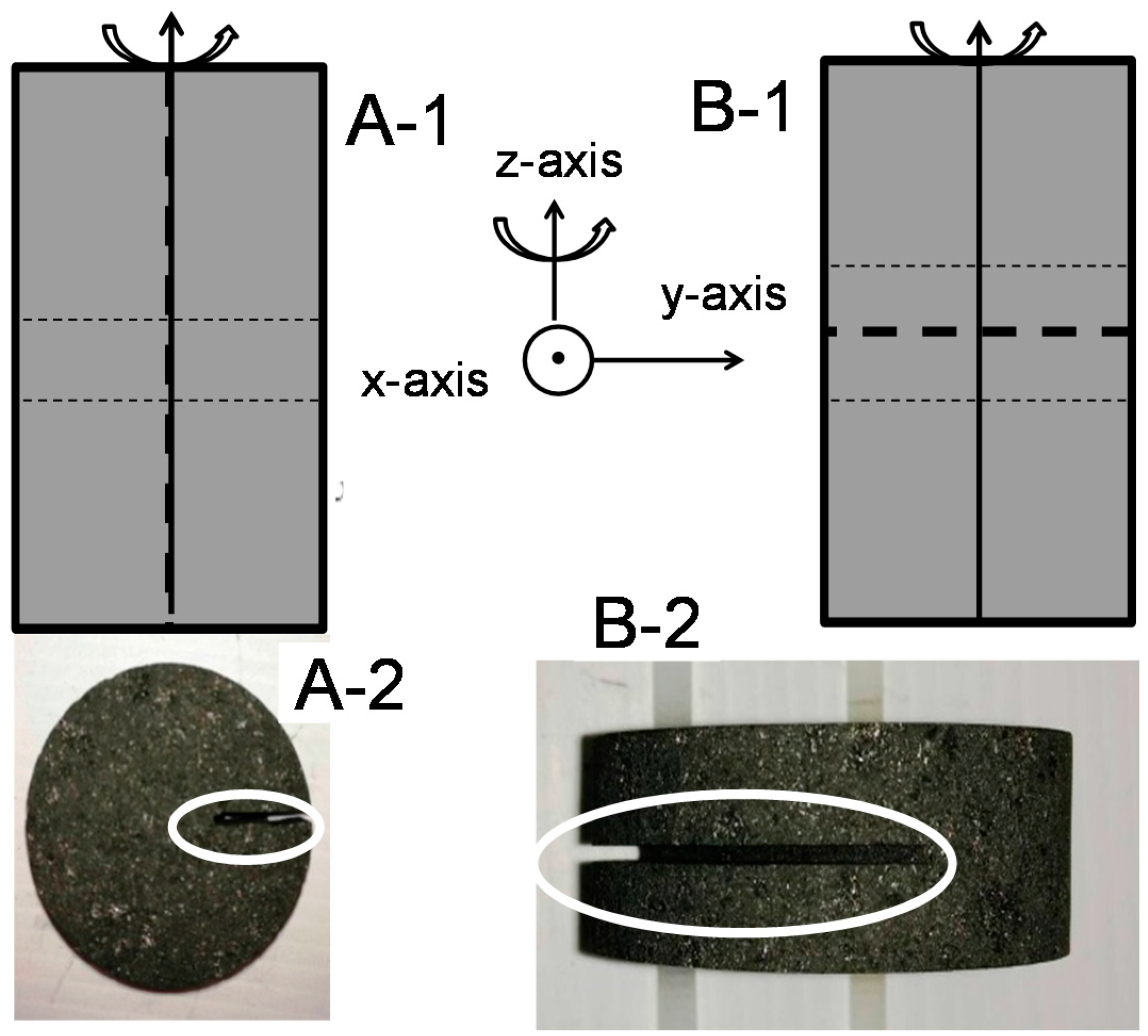
2.3. Samples Preparation
3. Results
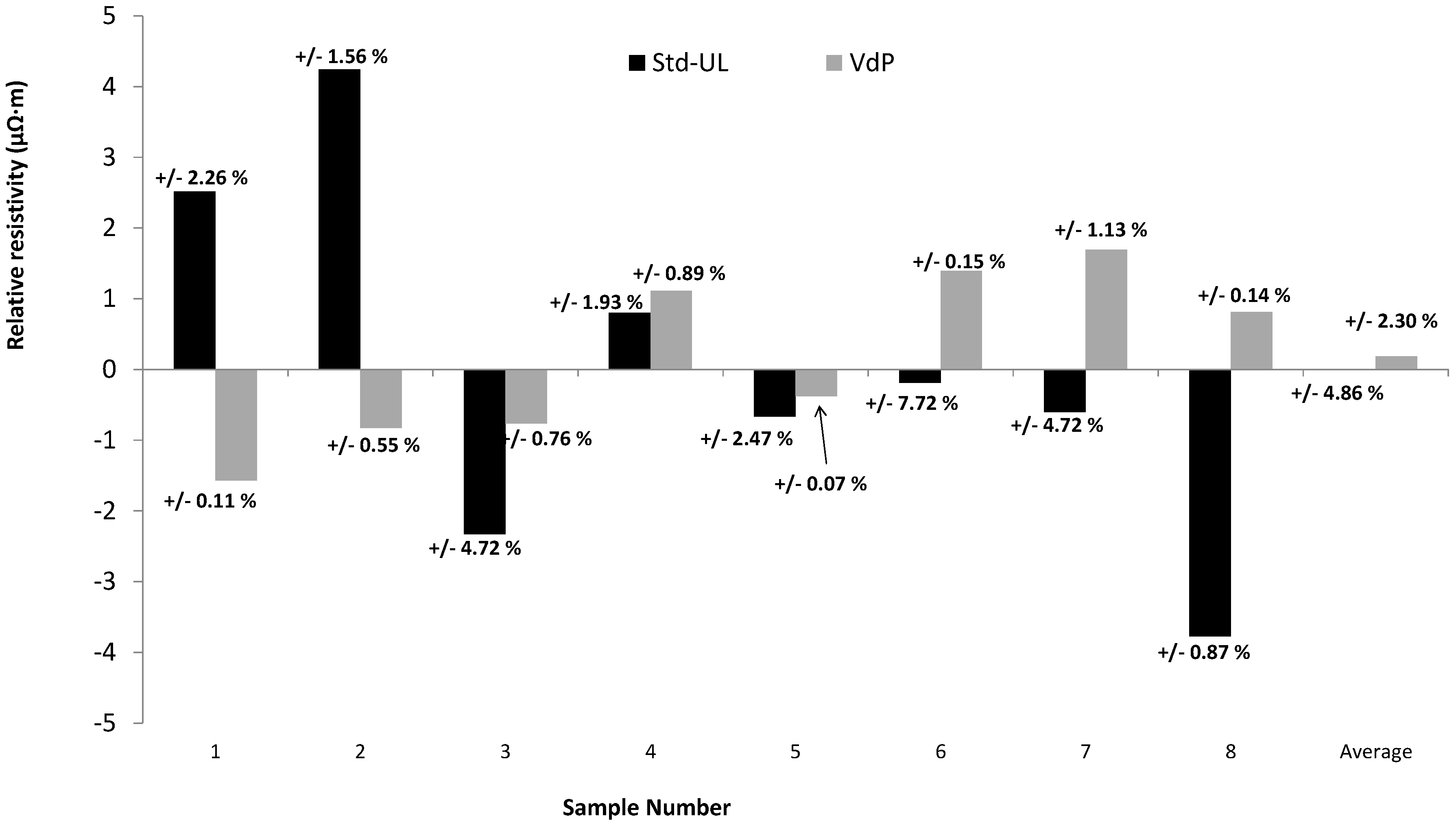
3.1. Comparison of Standard and Van de Pauw Methods
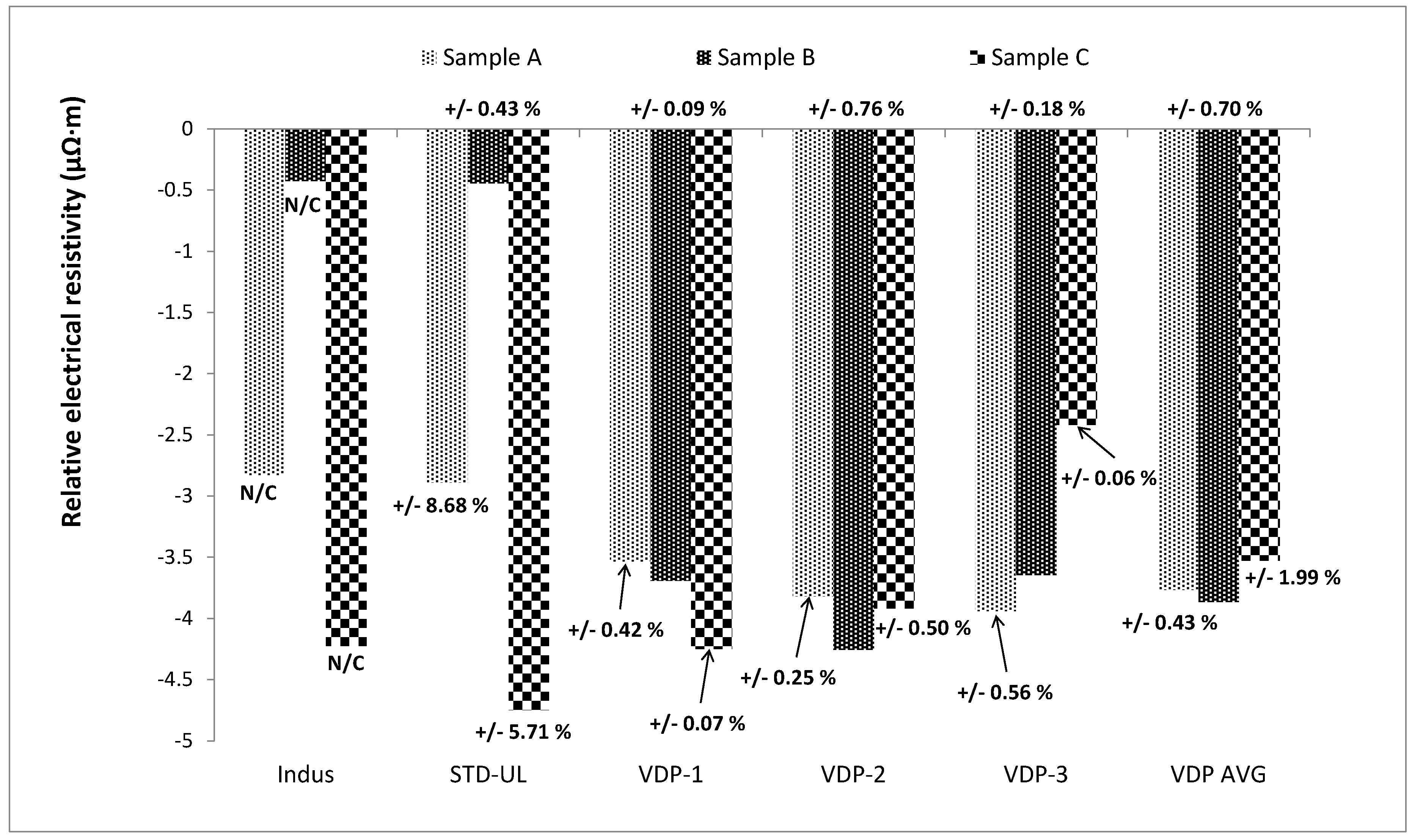
3.2. Validation of Van der Pauw Method for Intact Samples
3.3. Validation of Van der Pauw Method for Broken Samples
3.4. Validation of Van der Pauw Method for Intentionally-Generated Cracked Samples
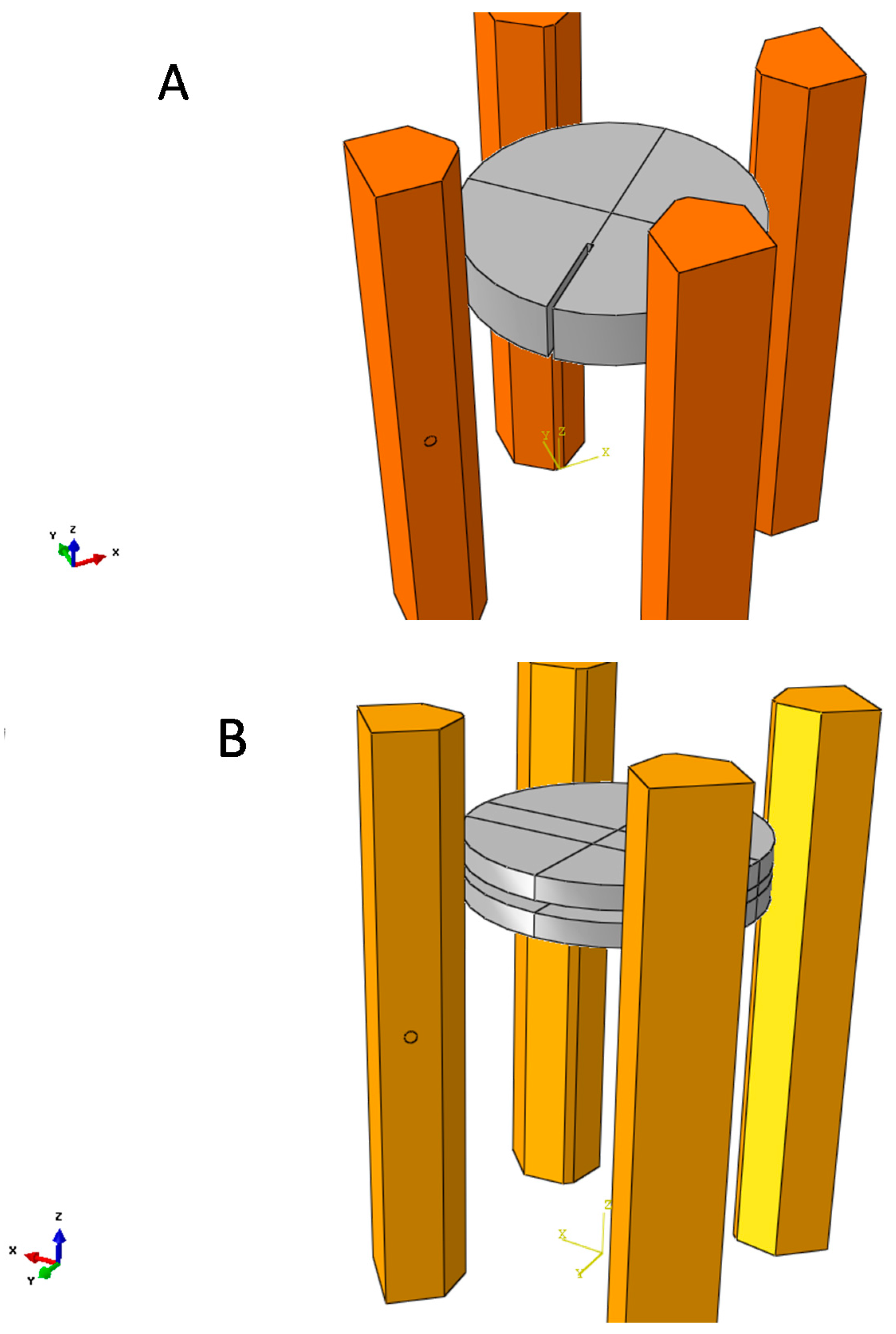
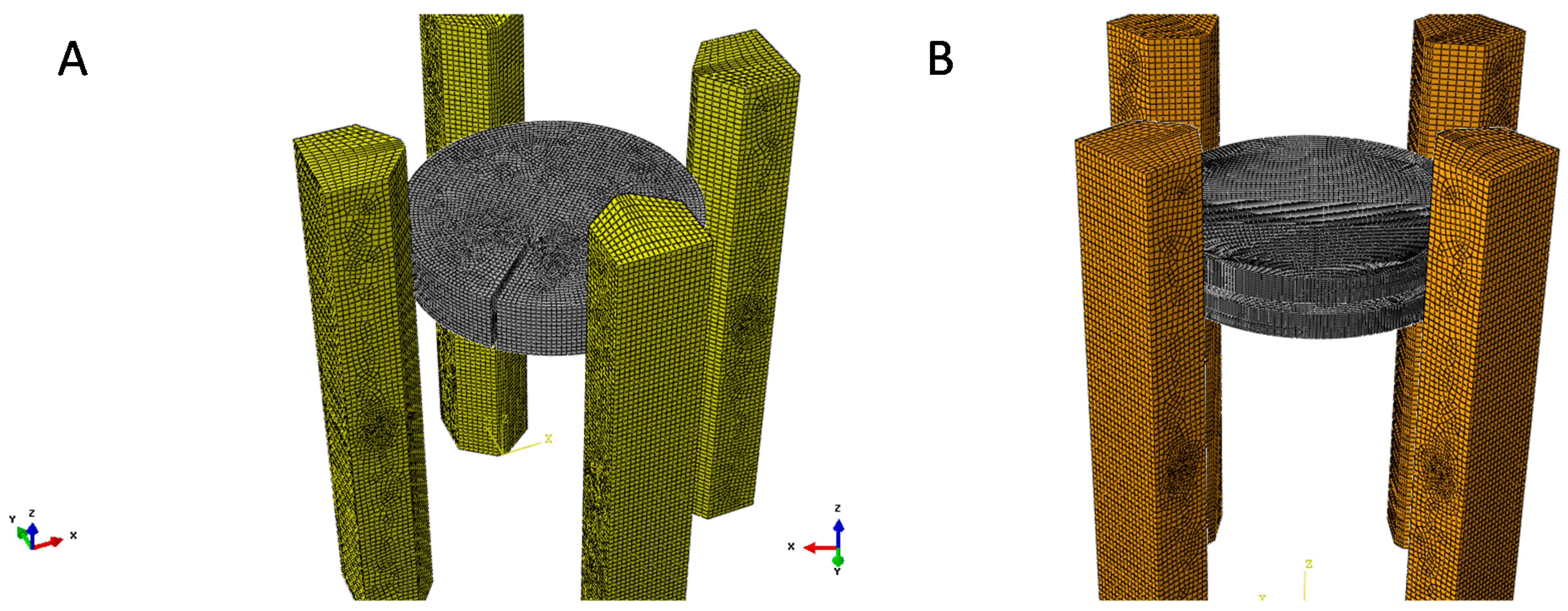
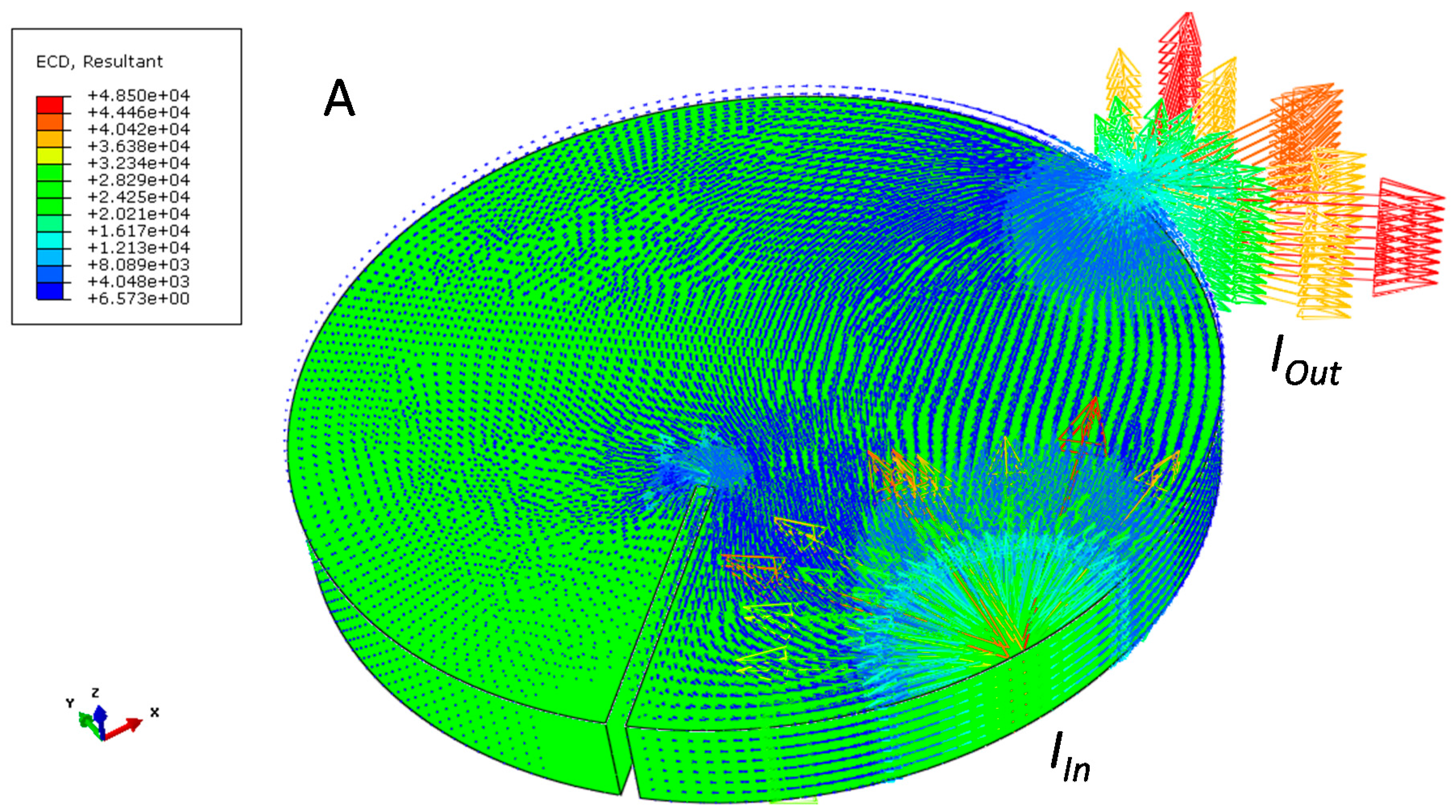
4. Finite Element Modelling of VdP Method
5. Detection of Defects Using VdP Method
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hall, C.M. Process of Reducing Aluminium from jts Fluoride Salts by Electrolysis. U.S. Patent 400,664, 2 April 1889. [Google Scholar]
- Héroult, P.L.T. Pour un Procede Electrolytique Pour la Preparation de L’aluminium: An Electrolytic Process for the Preparation of Aluminium bu Paul LT Heroult. French Patent 175,711, 1 September 1886. [Google Scholar]
- Chevarin, F.; Lemieux, L.; Ziegler, D.; Fafard, M.; Alamdari, H. Air and CO2 reactivity of carbon anodes and its constituents: An attempt to understand Dusting phenomenon. Light Met. 2015, 1147–1152. [Google Scholar] [CrossRef]
- Sadler, B.A.; Algie, S.H. Sub-Surface Carboxy Reactivity Testing of Anode Carbon; TMS: San Diego, CA, USA, 1991. [Google Scholar]
- Thibodeau, S.; Chaouki, H.; Alamdari, H.; Ziegler, D.; Fafard, M. Hight temperature compression test to determine the anode paste mechanical properties. Light Met. 2014, 1129–1134. [Google Scholar] [CrossRef]
- Clery, P. Green paste density as an indicator of mixing efficiency. In Proceedings of the TMS Annual Meeting, San Antonio, TX, USA, 15–19 February 1998; pp. 625–626. [Google Scholar]
- Picard, D.; Lauzon-Gauthier, J.; Duchesne, C.; Alamdari, H.; Fafard, M.; Ziegler, D. Automated crack detection method applied to CT images of backed carbon anode. Light Met. 2014, 1275–1280. [Google Scholar] [CrossRef]
- Picard, D.; Alamdari, H.; Ziegler, D.; St-Arnaud, P.-O.; Fafard, M. Characterization of a full-scale prebaked anode using X-ray computerized tomography. Light Met. 2011, 973–978. [Google Scholar] [CrossRef]
- Azari, K.; Alamdari, H.; Aryanpour, G.; Picard, D.; Fafard, M.; Adams, A. Mixing variables for prebaked anodes used in aluminium production. Powder Technol. 2013, 235, 341–348. [Google Scholar] [CrossRef]
- Picard, D.; Alamdari, H.; Ziegler, D.; Dumas, B.; Fafard, M. Characterization of pre-baked anode samples using X-ray computed tomography and porosity estimation. Light Met. 2012, 1283–1288. [Google Scholar] [CrossRef]
- Van der Pauw, L.J. A method of measuring specific resistivity and Hall effect of discs of arbitrary shape. Philips Res. Rep. 1958, 13, 1–9. [Google Scholar]
- Van der Pauw, L.J. A method of measuring the resistivity and Hall coefficient on lamellae of arbitrary shape. Philips Tech. Rev. 1958, 20, 220–224. [Google Scholar]
- Koon, D.W. Effect of contact size and placement, and of resistive inhomogeneities on van der Pauw measurements. Rev. Sci. Instrum. 1989, 60, 271–274. [Google Scholar] [CrossRef]
- De Vries, D.K.; Wieck, A.D. Potential distribution in the van der Pauw technique. Am. J. Phys. 1995, 63, 1074–1078. [Google Scholar] [CrossRef]
- Rietveld, G.; Koijmans, C.V.; Henderson, L.C.A.; Hall, M.J.; Harmon, S.; Warnecke, P.; Schumacher, B. DC Conductivity Measurements in the Van Der Pauw Geometry. IEEE Trans. Instrum. Meas. 2003, 52, 449–453. [Google Scholar] [CrossRef]
- Kasl, C.; Hoch, M.J.R. Effect of sample thickness on the van der Pauw technique for resistivity measurements. Rev. Sci. Instrum. 2005, 76, 033907. [Google Scholar] [CrossRef]
- Abaqus Analysis User’s Guide; Version 6; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- Mannweiler, U.; Keller, F. The design of a new anode technology for the aluminium industry. J. Miner. Met. Mater. Soc. 1994, 48, 15–21. [Google Scholar] [CrossRef]



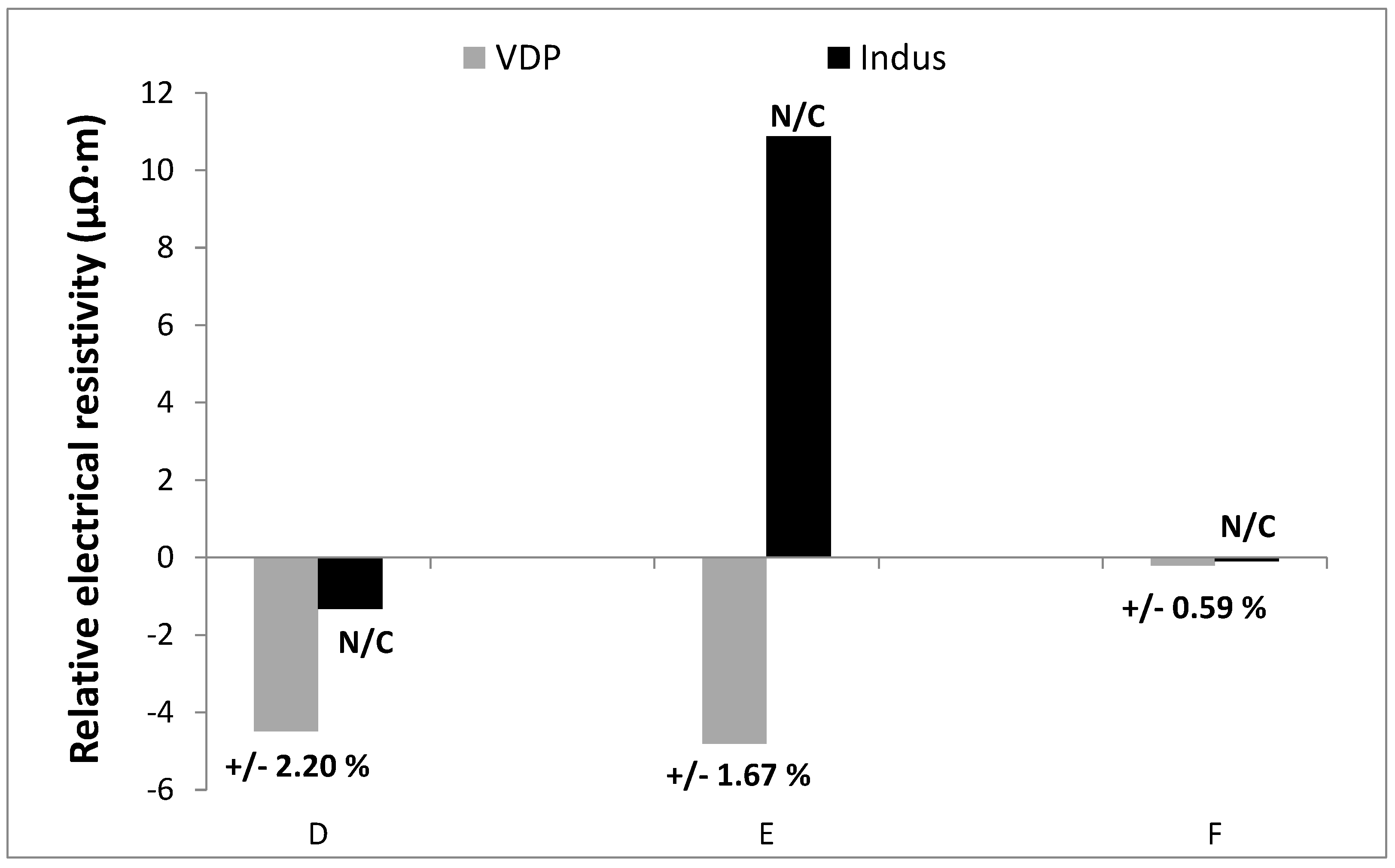
| Sample and Configuration | Relative Electrical Resistivity (μΩ∙m) |
|---|---|
| Measurements Using Standard Method | |
| Sample without defect | −2.4 ± 12% |
| Radial Crack | +5 ± 12% |
| void: 1.7% | |
| Transversal crack | +12.9 ± 21% |
| void: 0.18% | |
| Measurements using Van der Pauw method | |
| Sample without defect | +2.5 ± 0.4% |
| Radial Crack | +3.2 ± 2.5% |
| Crack placed between two probes | |
| Radial Crack | +3.3 ± 2% |
| Crack placed near the probe | |
| Transverse crack | +4.5 ± 8% |
| Crack Type and Position | Original Conductivity (S/m) | Electrical Conductivity Estimated Using FEM and VdP Methods (S/m) | Error |
|---|---|---|---|
| 2-mm wide crack, parallel to the axis of revolution, equal distance to sensors | 20,000 | 20,316 | +1.58% |
| 2-mm wide crack, parallel to the axis of revolution, close to one sensor | 20,000 | 20,260 | +1.30% |
| 0.1-mm thin crack, parallel to the axis of revolution, close to one sensor | 20,000 | 20,253 | +1.37% |
| Crack Type and Position | Original Conductivity (S/m) | Electrical Conductivity Estimated Using FEM and VdP Methods (S/m) | Error |
|---|---|---|---|
| 2-mm wide crack, normal to the axis of revolution | 20,000 | 19,362 | 3.19% |
| 0.1-mm thin crack, normal to the axis of revolution | 20,000 | 20,215 | +1.07% |
| Crack Type and Position | Original Conductivity (S/m) | Electrical Resistance Measured Using Finite Element Method | Difference |
|---|---|---|---|
| 2-mm wide crack, parallel to the axis of revolution, equal distance to sensors | 20,000 | R1 = 0.7 mΩ | 59.8% |
| R2 = 1.74 mΩ | |||
| 2-mm wide crack, parallel to the axis of revolution, close to one sensor | 20,000 | R1 = 0.52 mΩ | 73.9% |
| R2 = 1.99 mΩ | |||
| 0.1-mm thin crack, parallel to the axis of revolution, close to one sensor | 20,000 | R1 = 0.553 mΩ | 71.5% |
| R2 = 1.91 mΩ |
| Crack Type and Position | Original Conductivity (S/m) | Electrical Resistance Measured Using Finite Element Method | Difference |
|---|---|---|---|
| 2 mm wide crack, normal to the axis of revolution | 20,000 | R1 = 1.1 mΩ | 6.8% |
| R2 = 1.18 mΩ | |||
| 0.1 mm thin crack, normal to the axis of revolution | 20,000 | R1 = 1.086 mΩ | 0.99% |
| R2 = 1.0969 mΩ |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouget, G.; Chaouki, H.; Picard, D.; Ziegler, D.; Alamdari, H. Electrical Resistivity Measurement of Carbon Anodes Using the Van der Pauw Method. Metals 2017, 7, 369. https://doi.org/10.3390/met7090369
Rouget G, Chaouki H, Picard D, Ziegler D, Alamdari H. Electrical Resistivity Measurement of Carbon Anodes Using the Van der Pauw Method. Metals. 2017; 7(9):369. https://doi.org/10.3390/met7090369
Chicago/Turabian StyleRouget, Geoffroy, Hicham Chaouki, Donald Picard, Donald Ziegler, and Houshang Alamdari. 2017. "Electrical Resistivity Measurement of Carbon Anodes Using the Van der Pauw Method" Metals 7, no. 9: 369. https://doi.org/10.3390/met7090369




