A Hybrid Multi-Scale Model of Crystal Plasticity for Handling Stress Concentrations
Abstract
:1. Introduction
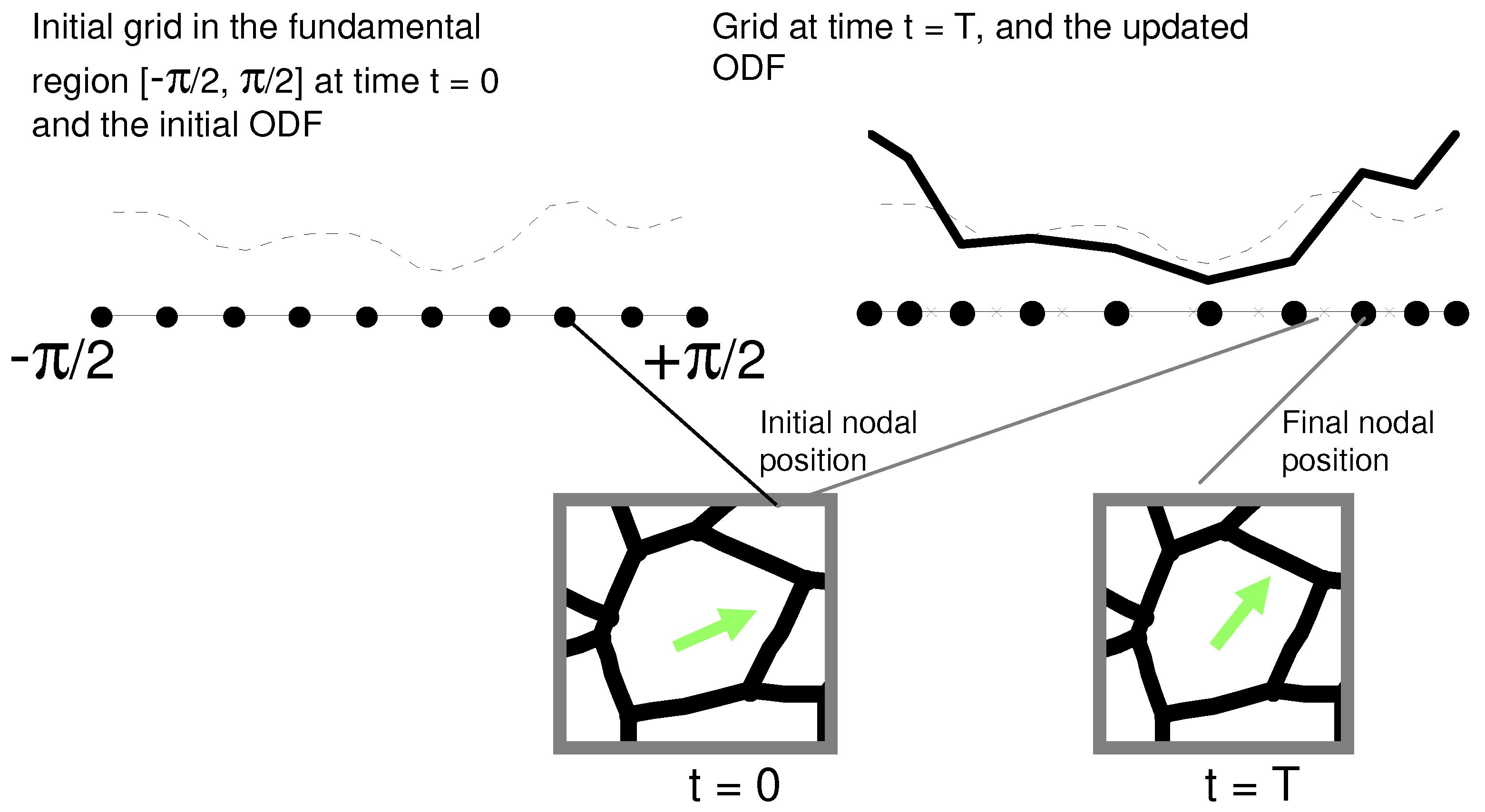
2. Representation of the ODF
2.1. Probability Update in Finite Element Spaces
2.2. ODF for Planar Polycrystals
2.3. Constitutive Modeling
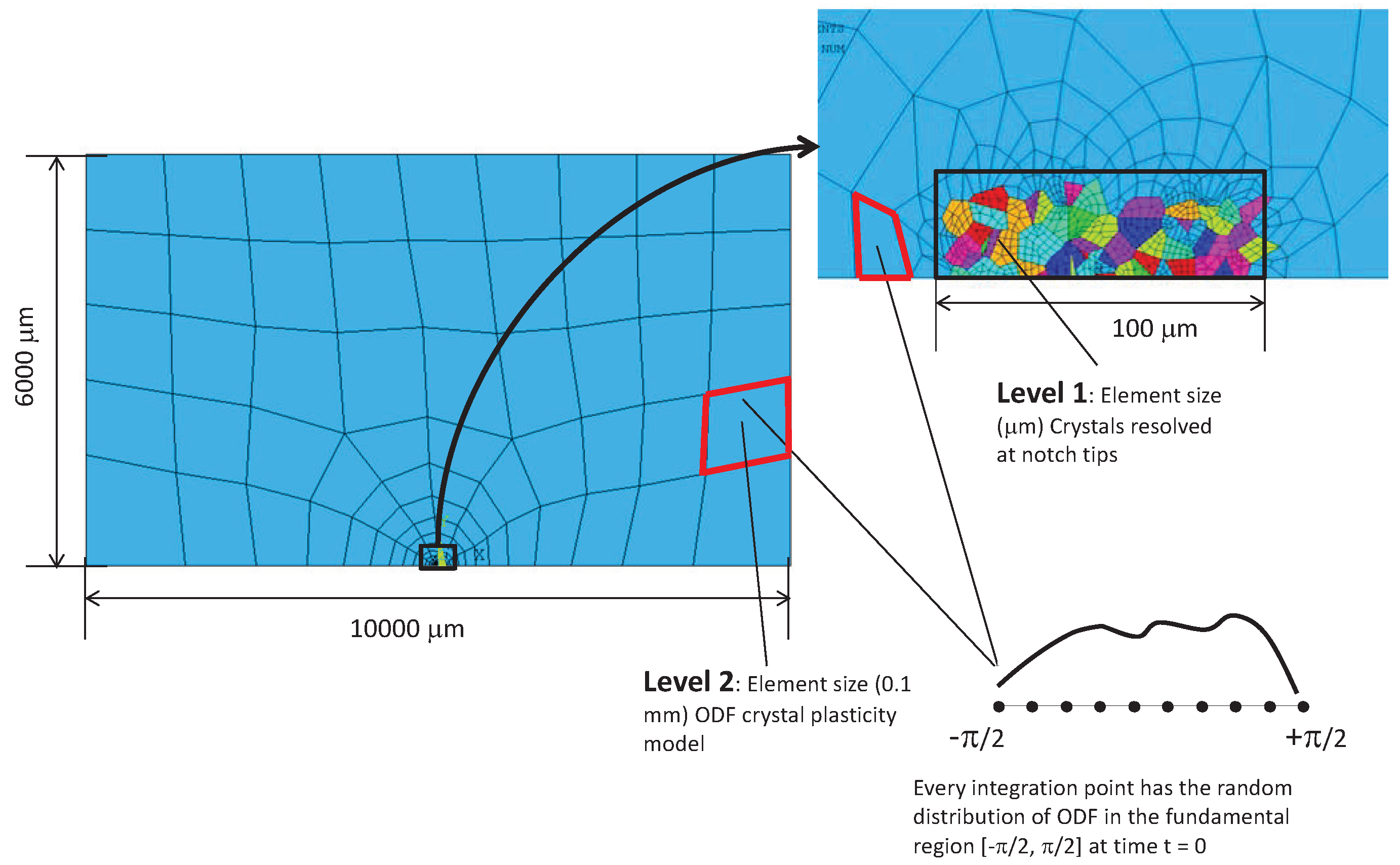
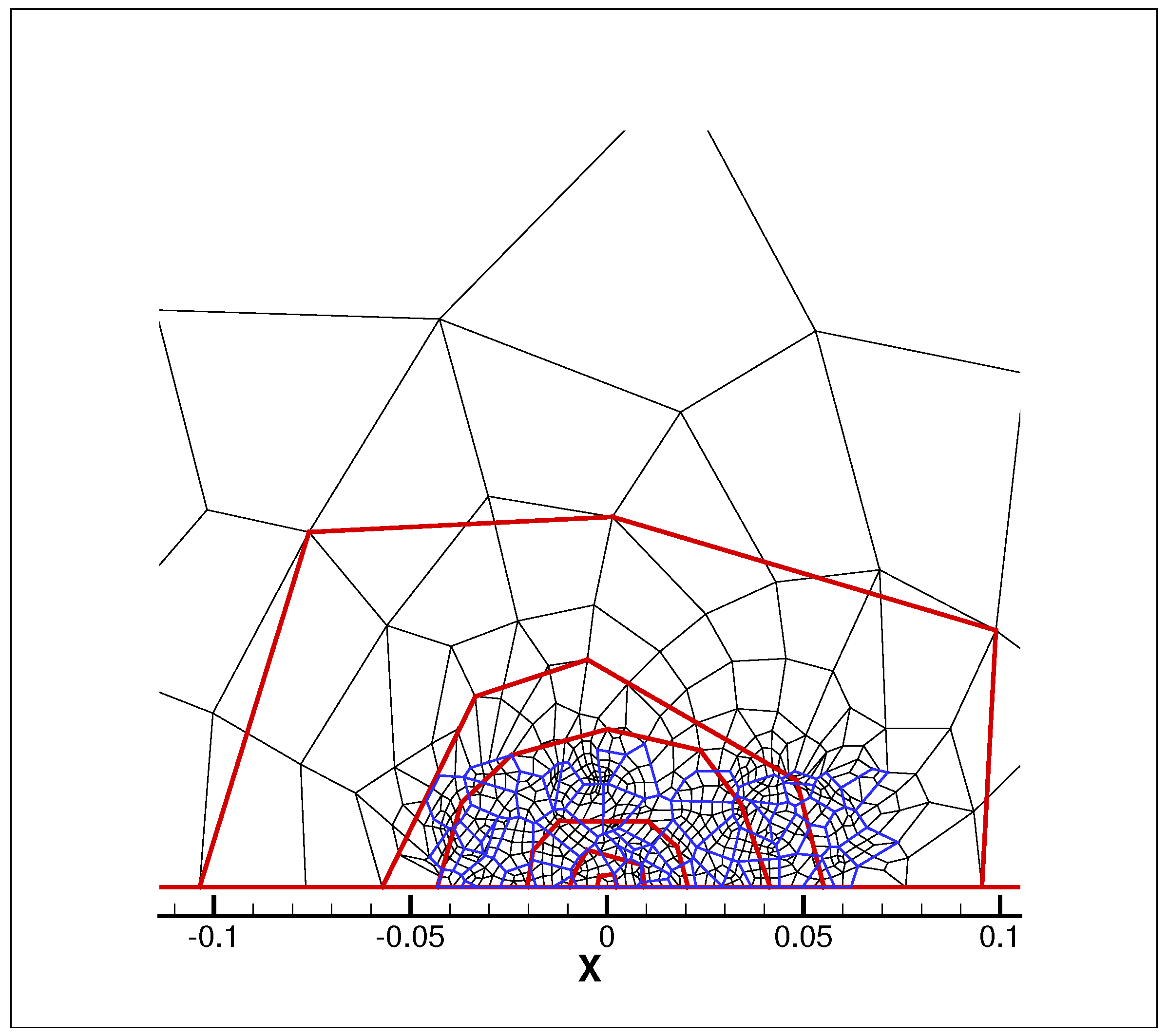
3. Finite Element Algorithm
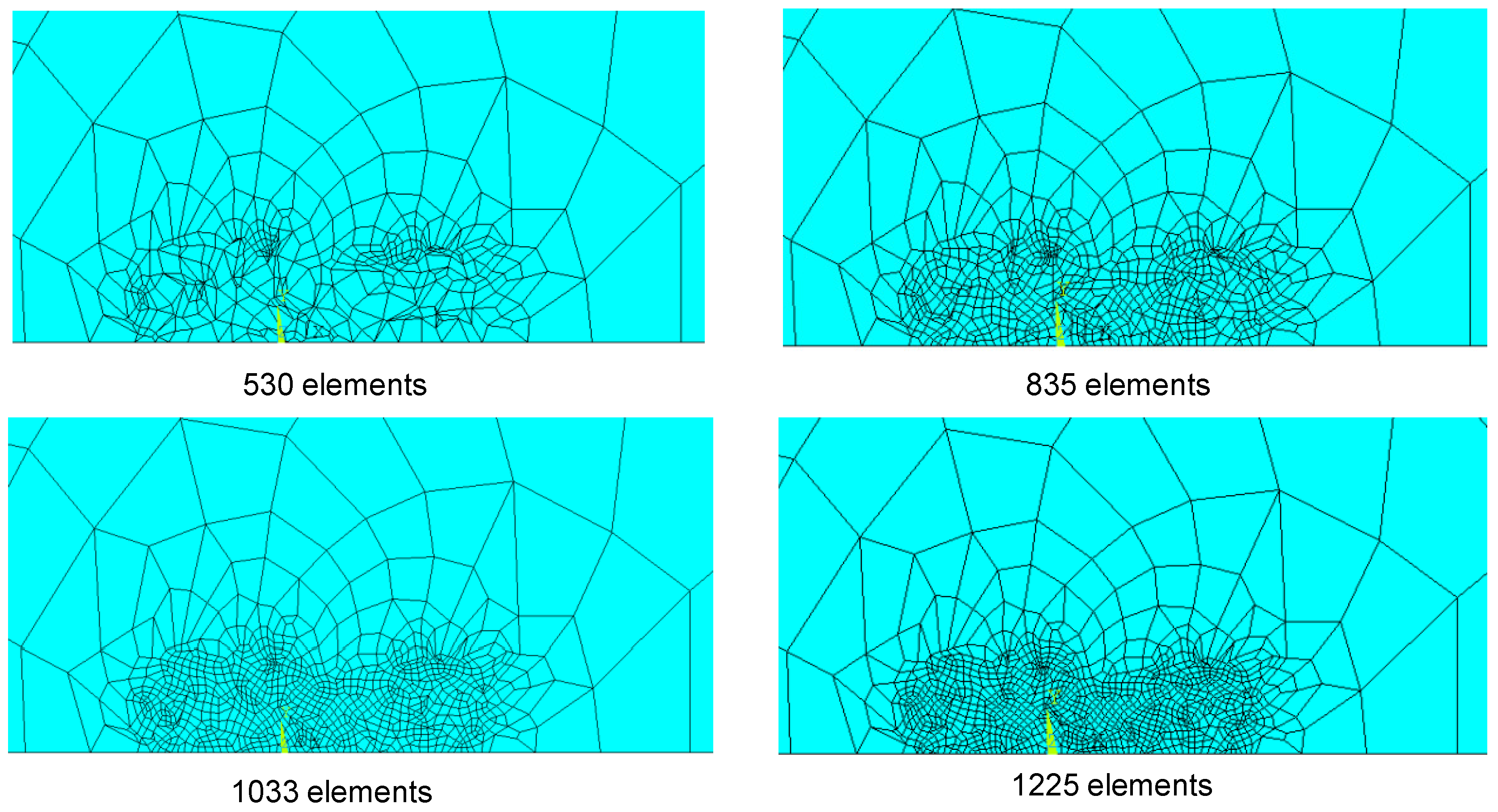
4. Numerical Results
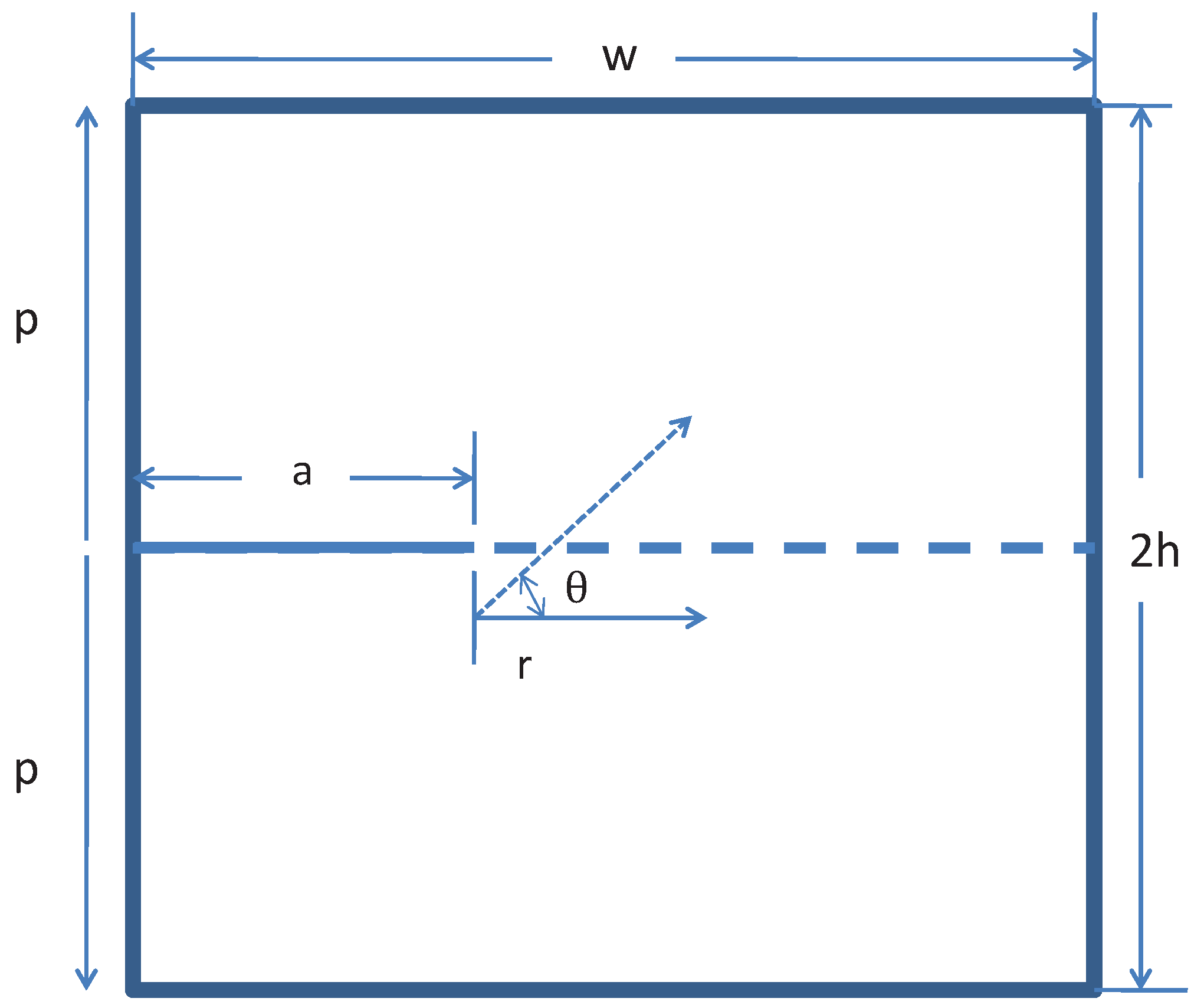
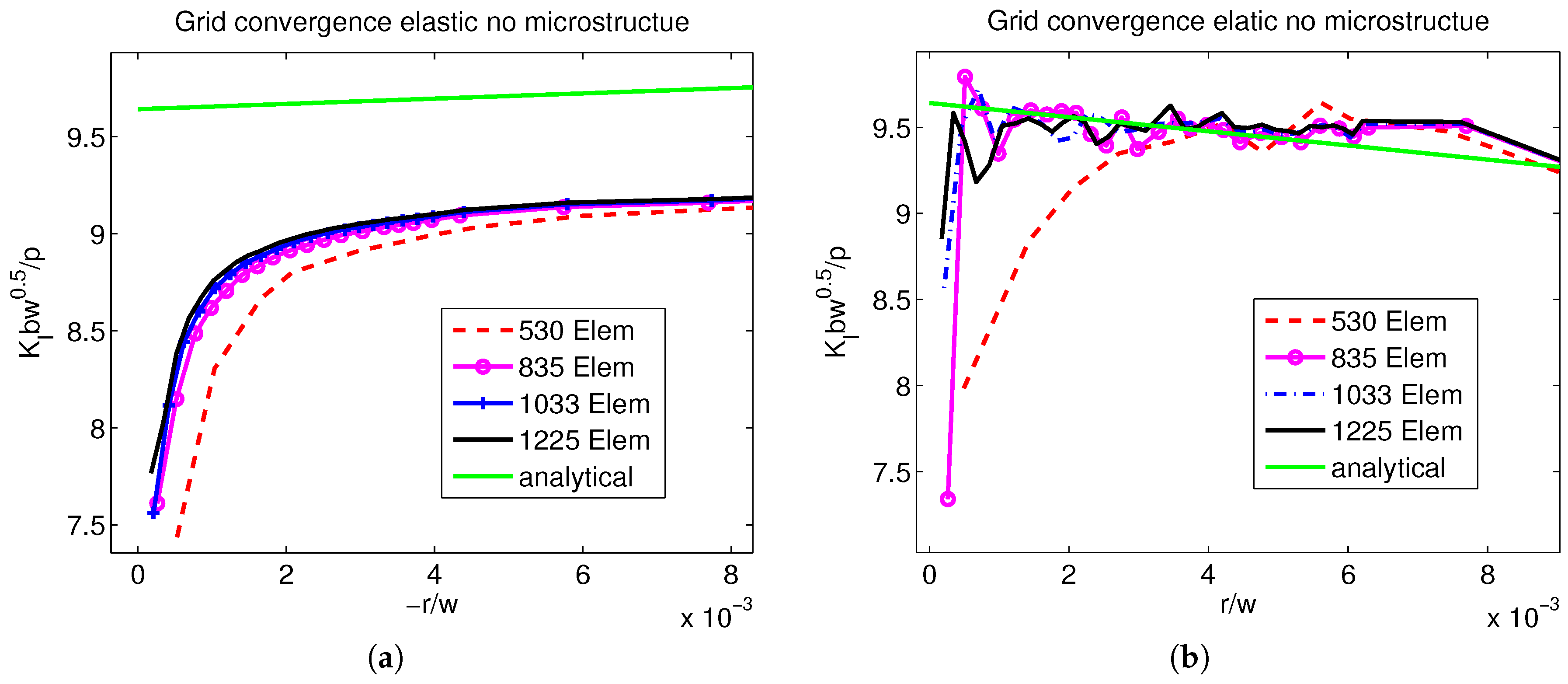
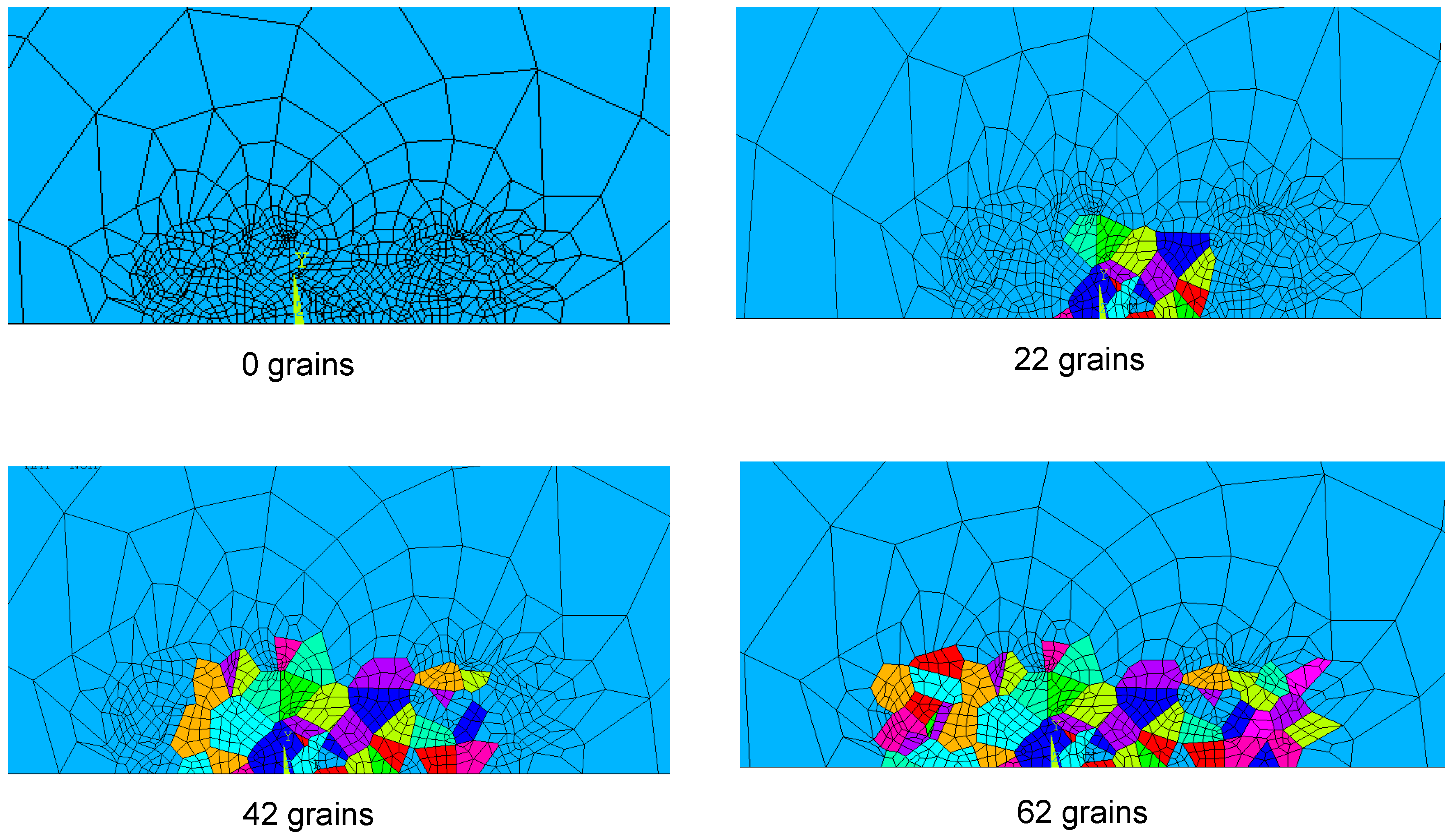
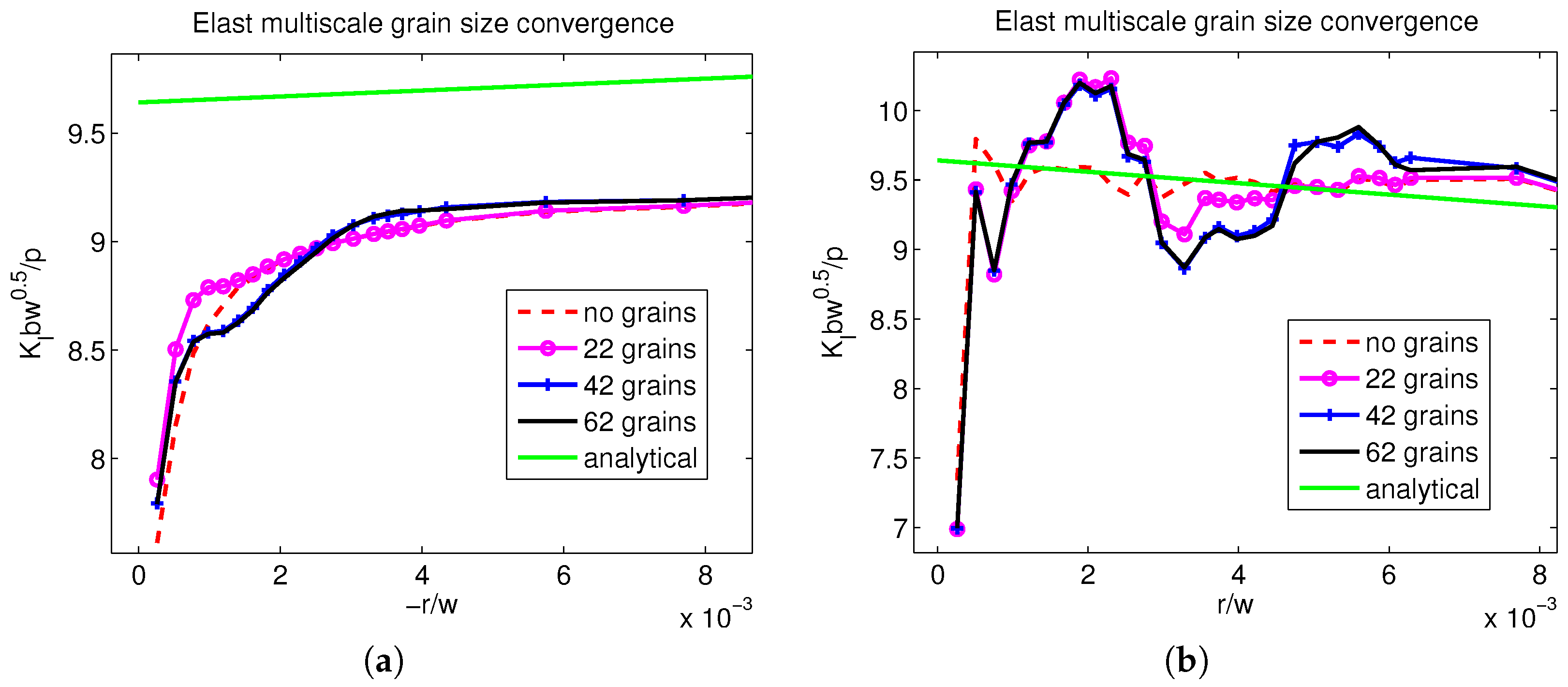
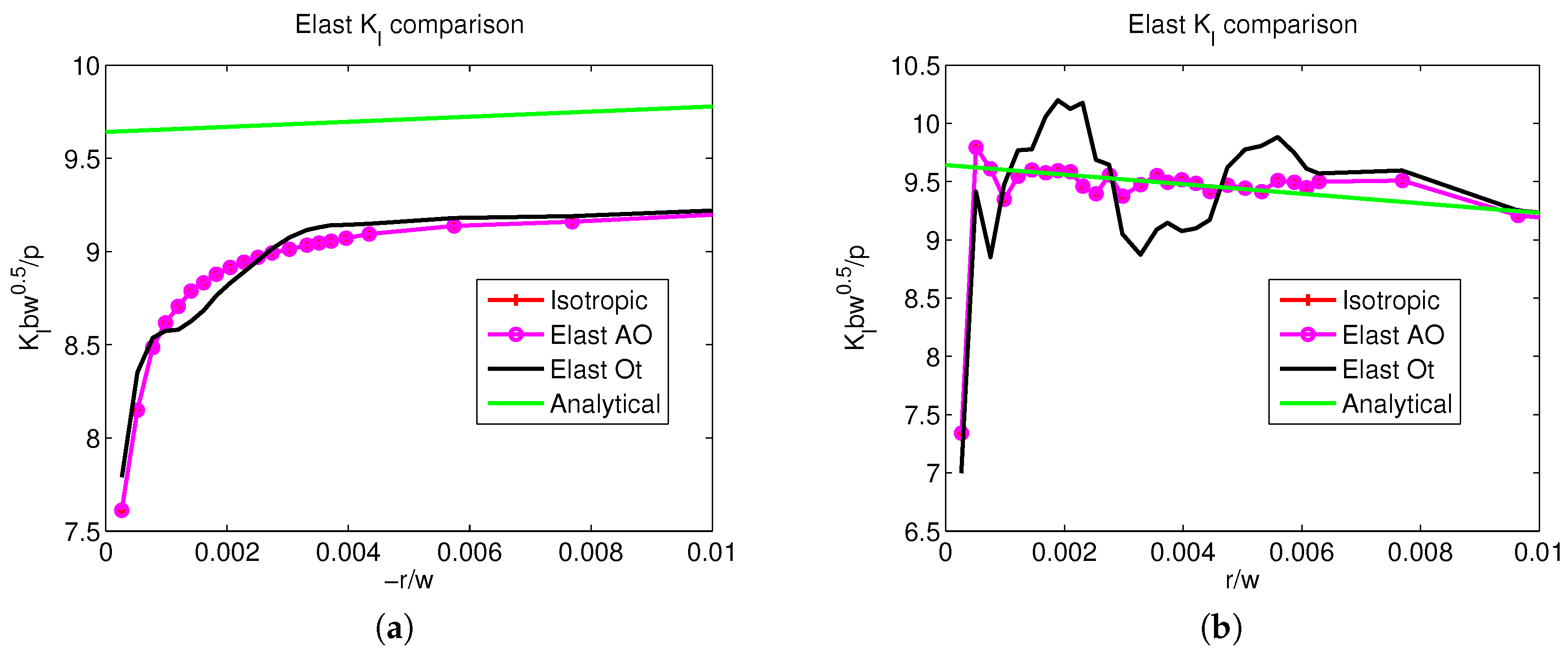
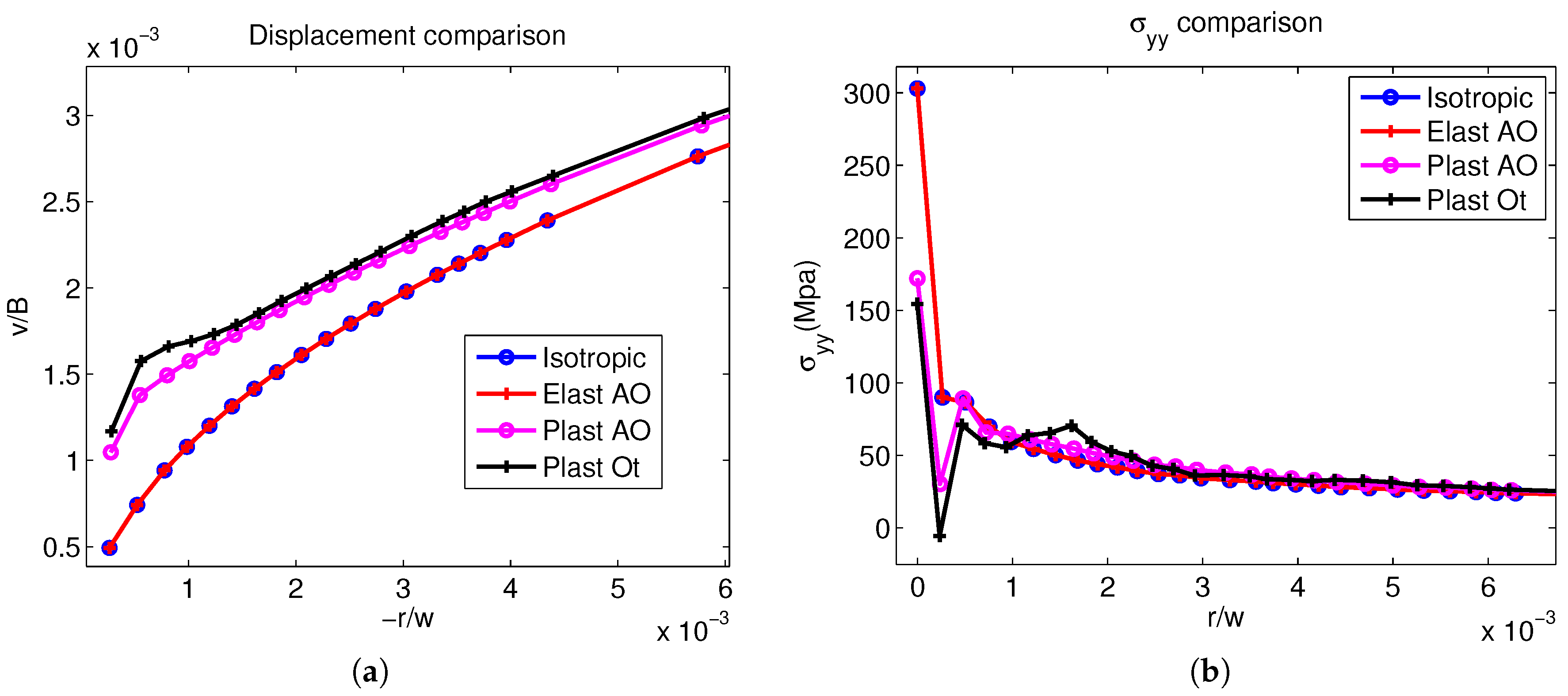
4.1. Linear Elastic Simulations
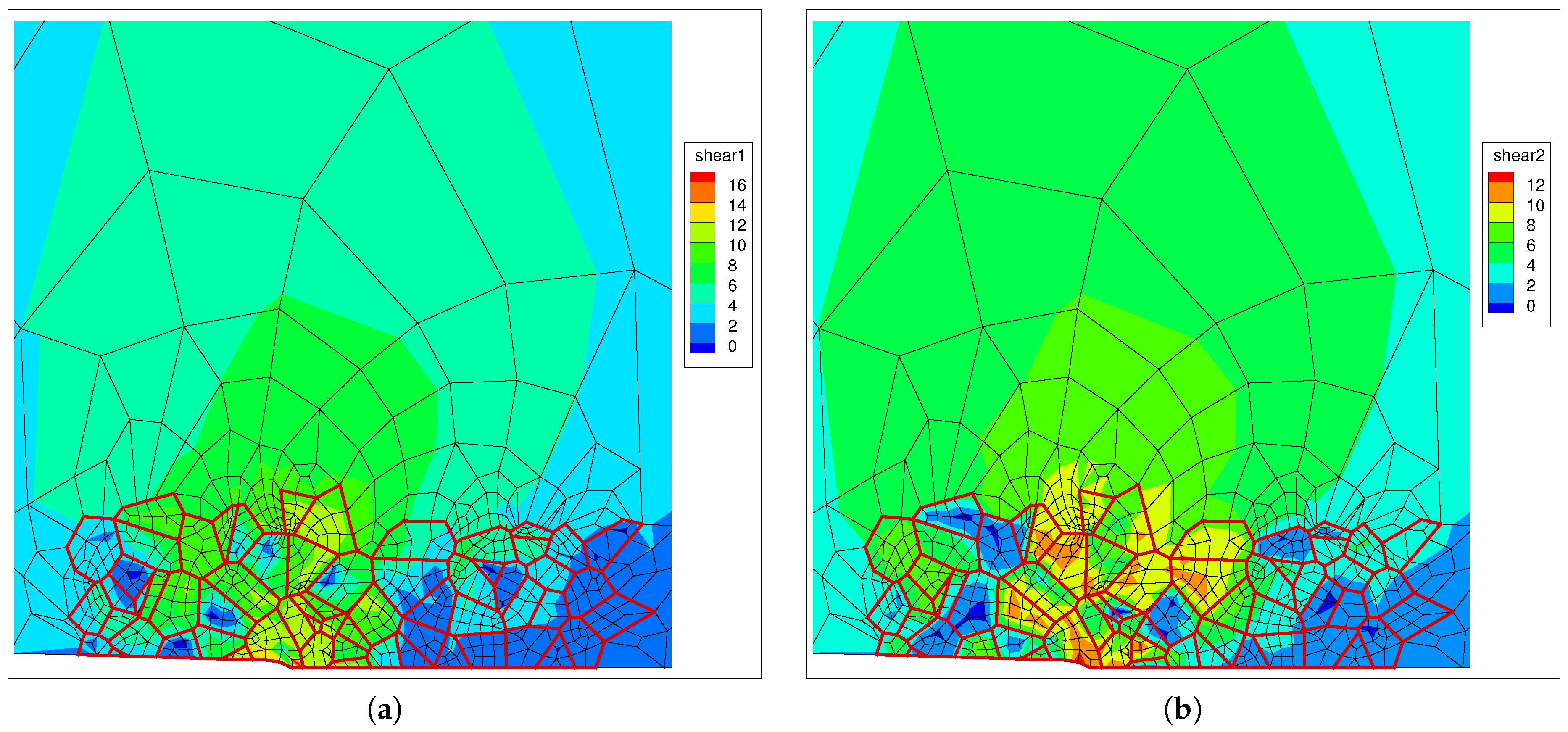
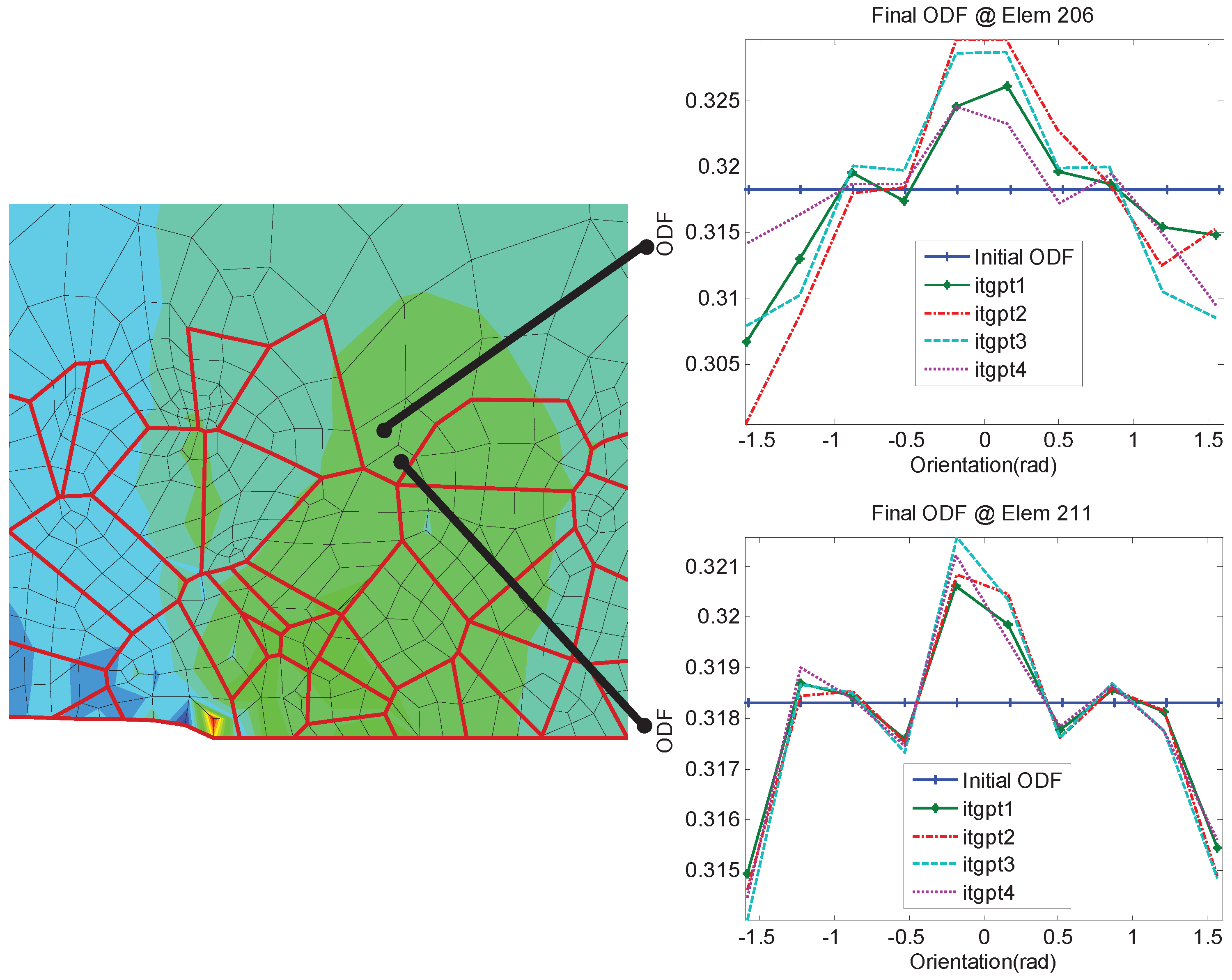
4.2. Elasto-Plastic Simulations
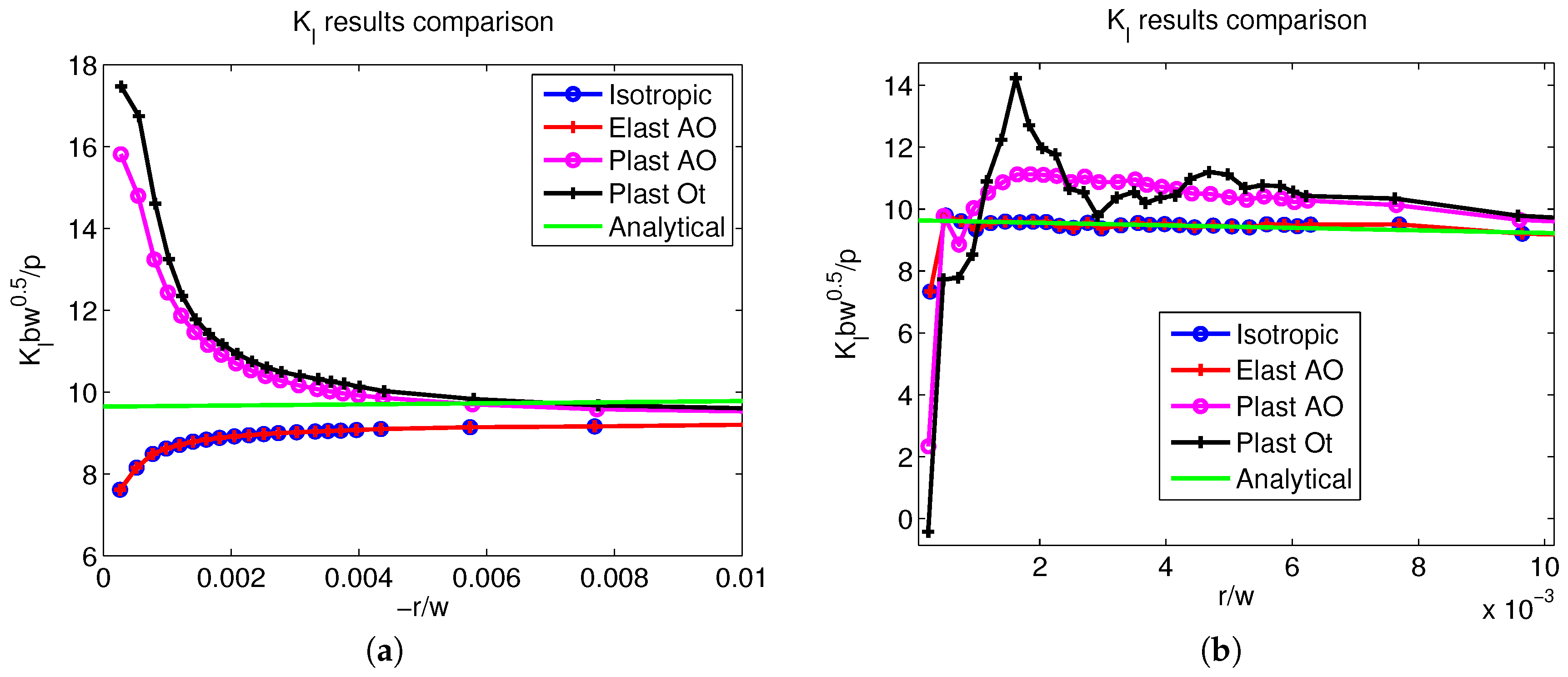
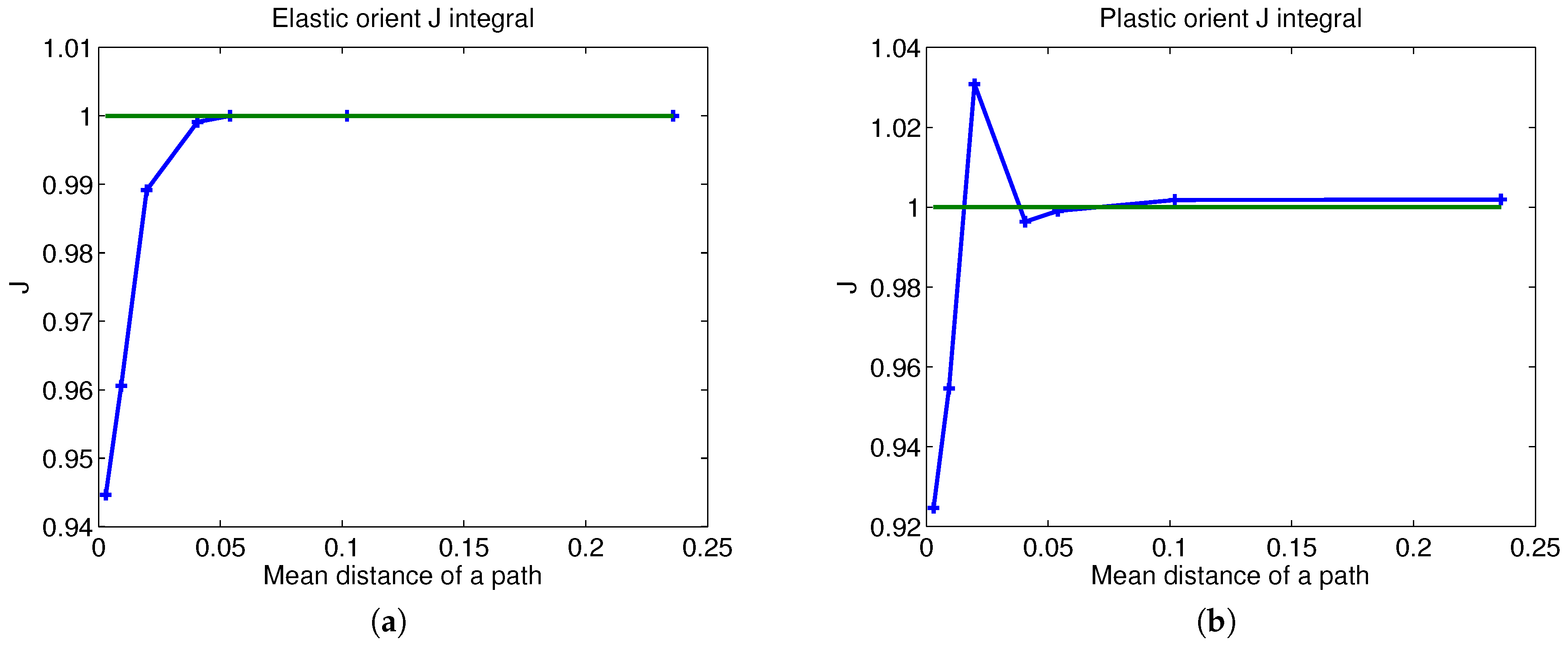
4.3. J Integral Calculation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Allison, J.; Backman, D.; Christodoulou, L. Integrated Computational Materials Engineering: A New Paradigm for the Global Materials Profession. J. Miner. Met. Mater. Soc. 2006, 58, 25–27. [Google Scholar] [CrossRef]
- Sundararaghavan, V.; Zabaras, N. Design of microstructure-sensitive properties in elasto-viscoplastic polycrystals using multi-scale homogenization. Int. J. Plast. 2006, 22, 1799–1824. [Google Scholar] [CrossRef]
- Sundararaghavan, V.; Zabaras, N. A multi-length scale continuum sensitivity analysis for the control of texture-dependent properties in deformation processing. Int. J. Plast. 2008, 24, 1581–1605. [Google Scholar] [CrossRef]
- Miller, R.; Tadmor, E.B.; Phillips, R.; Ortiz, M. Quasicontinuum simulation of fracture at the atomic scale. Model. Simul. Mater. Sci. Eng. 1998, 6, 607–638. [Google Scholar] [CrossRef]
- Dunne, F.P.E.; Wilkinson, A.J.; Allen, R. Experimental and computational studies of low cycle fatigue crack nucleation in a polycrystal. Int. J. Plast. 2007, 23, 273–295. [Google Scholar] [CrossRef]
- Clement, A. Prediction of deformation texture using a physical principle of conservation. Mater. Sci. Eng. 1982, 55, 203–210. [Google Scholar] [CrossRef]
- Sundararaghavan, V.; Kumar, A. Probabilistic modeling of microstructure evolution using finite element representation of statistical correlation functions. Int. J. Plast. 2012, 30–31, 62–80. [Google Scholar] [CrossRef]
- Kumar, A.; Dawson, P.R. The simulation of texture evolution using finite elements over orientation space. I. Development. Comput. Methods Appl. Mech. Eng. 1996, 130, 227–246. [Google Scholar] [CrossRef]
- Kumar, A.; Dawson, P.R. The simulation of texture evolution using finite elements over orientation space. II. Application to planar crystals. Comput. Methods Appl. Mech. Eng. 1996, 130, 247–261. [Google Scholar] [CrossRef]
- Chan, S.K.; Tuba, I.S.; Wilson, W.K. On the finite element method in linear fracture mechanics. Eng. Fract. Mech. 1970, 2, 1–17. [Google Scholar] [CrossRef]
- Anand, L.; Kothari, M. A computational procedure for rate-independent crystal plasticity. J. Mech. Phys. Solids 1966, 44, 525–558. [Google Scholar] [CrossRef]
- Sun, S.; Sundararaghavan, V. A probabilistic crystal plasticity model for modeling grain shape effects based on slip geometry. Acta Mater. 2012, 60, 5233–5244. [Google Scholar] [CrossRef]
- Gross, B.; Srawley, J.E.; Brown, W.F. Stress-Intensity Factors for a Single-Edge-Notch Tension Specimen by Boundary Collocation of a Stress Function; NASA Technical Report (No. NASA-TN-D-2395); National Aeronautics and Space Administration: Washington, DC, USA, 1964. [Google Scholar]
- McMeeking, R.M. Finite deformation analysis of crack-tip opening in elastic-plastic materials and implications for fracture. J. Mech. Phys. Solids 1977, 25, 357–381. [Google Scholar] [CrossRef]
- Rice, J.R. The role of large crack tip geometry changes in plane strain fracture. In Inelastic Behavior of Solids; Kanninen, M.F., Ed.; McGraw-Hill: New York, NY, USA, 1970; pp. 641–672. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Ramazani, A.; Sundararaghavan, V. A Hybrid Multi-Scale Model of Crystal Plasticity for Handling Stress Concentrations. Metals 2017, 7, 345. https://doi.org/10.3390/met7090345
Sun S, Ramazani A, Sundararaghavan V. A Hybrid Multi-Scale Model of Crystal Plasticity for Handling Stress Concentrations. Metals. 2017; 7(9):345. https://doi.org/10.3390/met7090345
Chicago/Turabian StyleSun, Shang, Ali Ramazani, and Veera Sundararaghavan. 2017. "A Hybrid Multi-Scale Model of Crystal Plasticity for Handling Stress Concentrations" Metals 7, no. 9: 345. https://doi.org/10.3390/met7090345




