1. Introduction
Pyro-metallurgical purification of ultra-pure aluminum relies almost entirely on methods that uses the principle of fractional crystallization. This principle is based on the ratio between the solubility of the impurities in the solid and molten phase of a metal, described by the distribution coefficient (
k), as shown in Equation (1) below.
where
CS is the concentration of impurity in the solid and
CL is the concentration of impurity in the liquid.
The distribution coefficient (
k) is one of the most important indicators in fractional crystallization methods and defines the purification degree that can be theoretically achieved in a system. For example, at equilibrium and not considering the influence of additional impurity elements, the distribution coefficient can be calculated from a binary phase diagram at a constant temperature [
1,
2,
3]. This coefficient is only valid by assumption of a complete diffusion of the expelled solid in the liquid. Therefore, a more realistic approach can be evaluated by taking the growth rate of the solid, the diffusion of the impurity into the melt and the thickness of the diffusion boundary layer into account. This optimized approach leads to the so called effective distribution coefficient (
keff), shown in Equation (2) and described in detail by Burton, Prim and Slichter (known as BPS model) [
3,
4,
5]. As it is seen in Equation (2), the diffusion layer thickness and the growth velocity of the crystallized material are the most important factors in this model, both able to be controlled in the best form through a mixing of the melt as well as cooling effect of the crystallizer. These two aspects are exactly the process parameters in a cooled finger technique and allow the consideration of this model into the interpretation of the experimental results of this study.
where
δ is the thickness of the diffusion boundary layer,
k0 is the ratio
Cs/
C0,
D is the impurity diffusivity in the melt and
V is the solid growth rate.
When a maximum mixing of the segregated solute into the melt occurs, the value of
keff becomes very close to that of
k, showing the optimum purification. In reality and while crystallizing, the rejected impurities enrich the melt ahead of the crystallization front, so that this region contains a higher amount of solute. A representation of this effect can be seen in
Figure 1.
The region, whose thickness is represented as
δ, is the so called diffusion boundary layer. In this area, the impurities are concentrated from the solid/liquid interface up to the distance where the solute concentration is approximately the same as that of the bulk. Within this film layer, impurity transport is assumed to occur only by diffusion, while ahead of this layer the transport is done mainly by convection, which can be increased by mixing mechanisms such as rotation or applying a magnetic field in the melt [
8,
9,
10].
Applying a mechanical agitation e.g., using an immersed rotor, leads to the reduction of the temperature gradient between the crystallization front and the melt besides the crucible wall, keeping the heat flow from the melt to the interface as small as possible. This rotation will also promote a mass flow in the melt, resulting not only in a lower thermal gradient but also in a stable boundary layer in front of the solid-liquid interface, allowing a uniform segregation of impurities [
11].
According to the BPS model (Equation (2)), for small values of growth rate, the thickness of the diffusion boundary layer (
δ) has a dependence on the rotation rate as well as viscosity of the liquid phase. Equation (3) describes this dependence as an upgrading of the BPS model. In this equation the increase of the angular velocity by increasing the rotation rate of the “cooled finger” will negatively influence the thickness of the diffusion boundary layer, which in turn will contribute to a lower effective distribution coefficient [
5].
where
ω is the angular velocity of the crystallized material,
v is the kinematic viscosity of the liquid, and
D is the diffusion coefficient of the solute.
With some exceptions, most impurities in aluminum have their
k values lower than unity, facilitating their removal by fractional crystallization. Some impurities however, have
k-values much bigger than one, such as Ti, V, Cr, and Zr, which are known as peritetic impurities.
Table 1 contains the distribution coefficients of most relevant impurities in aluminum according to different authors as well as some values obtained by own calculations using the FactSage
TM thermodynamic software (version 6.4, GTT-Technologies, Aachen, Germany) using the light metals database (FT Lite-FACT light metal alloy solutions (2013)). These calculations were conducted by extracting the solidus and liquidus curves from FactSage
TM for every binary system (up to 1 wt % concentration of element X in a Al-X system) and exporting them to excel, where each curve was fitted into a 6th-degree-polynomial equation as a function of temperature. This prevented inconsistencies, when extreme lower amounts of impurities are present or when the liquidus and solidus lines are too close to each other. The values of
CS and
CL at every specific temperature were then extracted from each liquidus-as well as solidus equation and then the thermodynamical distribution coefficient value (
k) was obtained (Equation (1)). Such calculations were made for the whole interval of concentrations. The values correlated well with the ones found in literature and the source of errors are mostly limited to the possibility of errors from the FactSage
TM database.
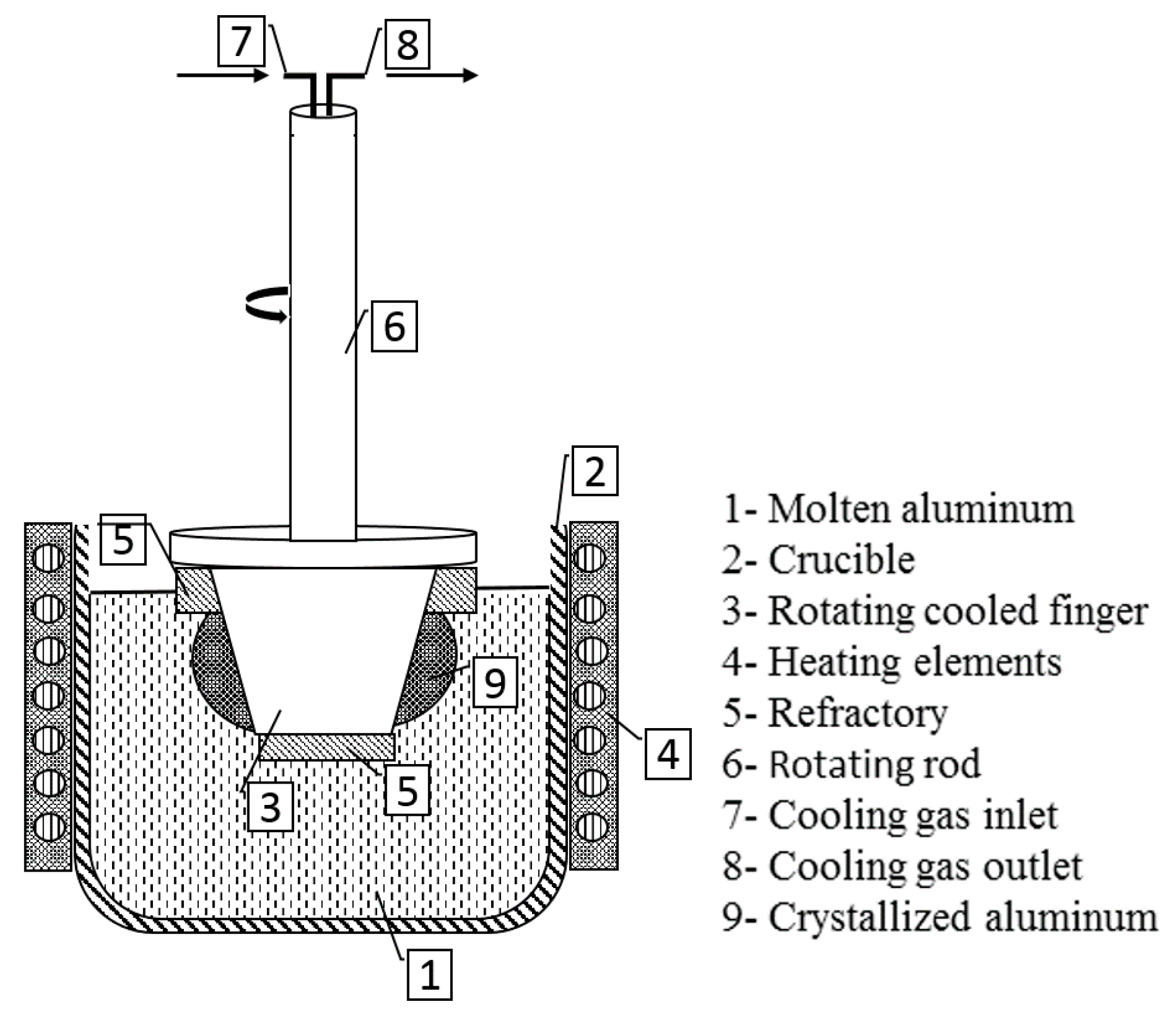
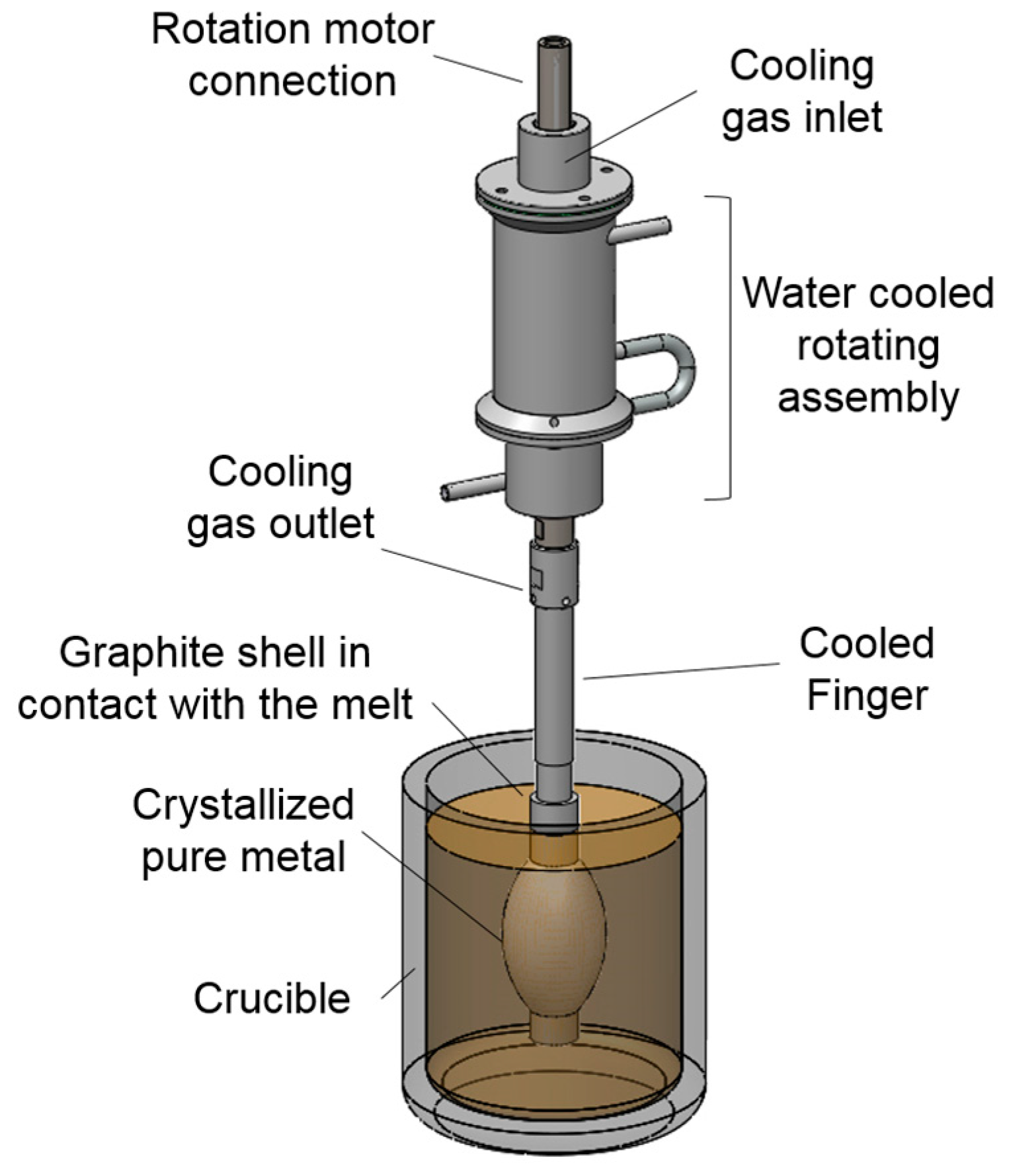
The innovative methodology of a rotational immersing cooled finger consists of an internally cooled tube that rotates inside a molten bath, as seen in
Figure 2. Since this patent filing in 1982, there were neither any scientific investigations found on this method, nor was there any fundamental research published.
Based on the same physical principle of well stablished methods like zone melting, vertical gradient freeze, pechiney crystallizer, etc. this method relies on the fractional crystallization principle, where a growth front is formed and moves radially towards the crucible wall. The rotational mechanism promotes a homogeneous mixing of the melt and a stable boundary layer, which assures an optimal segregation of impurities. The growth rate can be adjusted by combination of the cooling degree and the rotation rate to the targeted purification/productivity rate according to the requirements for subsequent processes.
This process was initially designed as a batch process, though it has big potential to be developed as a semi-continuous methodology. Around 60–70% of molten metal always remains in the crucible after removing the rotor with crystallized metal, it is then possible to be recharged, with further crude aluminum, while it is still molten to repeat the crystallization process.
4. Conclusions and Outlook
The cooled finger method is proved to be a potential fractional crystallization to achieve purification on aluminum and therefore suggested to be used as an alternative to the common Zone melting or vertical gradient freeze for other metallic systems like Ge, Si, etc. [
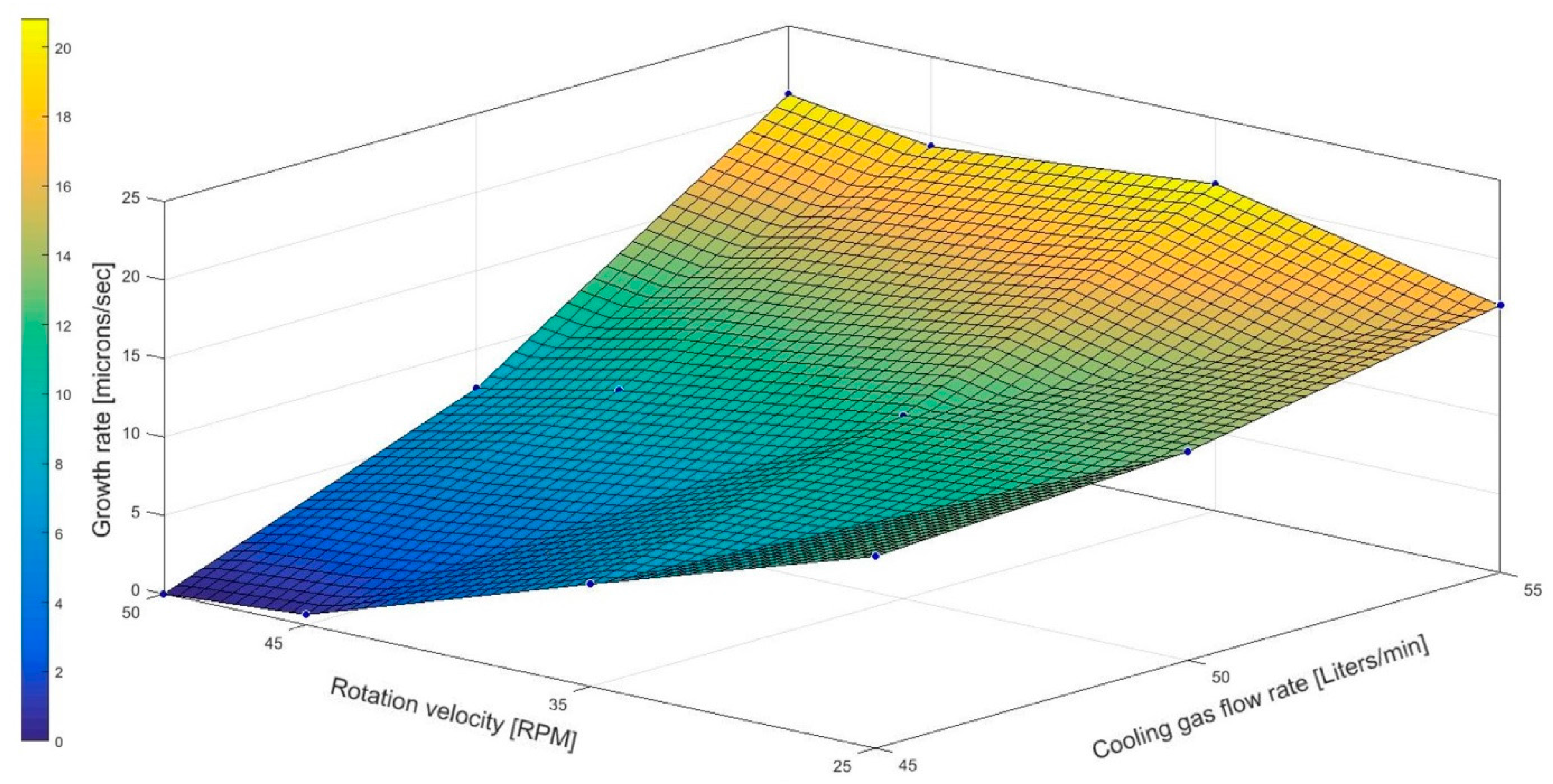
19]. Up to this date, this publication was the first oriented research that correlates the general theory of fractional crystallization to the cooled finger method in order to investigate and to stablish a first process window to purify aluminum via cooled finger. The results from the conducted experimental investigations proved the expectation from the theory on fractional crystallization and showed a dependency of the growth rate on the cooling gas flow—as well as rotation rates. The latter has a clear influence on the of purification efficiency.
The cooling at the solid/liquid growth interface together with the heat transfer from this interface to the solid phase enables an ever growing of the crystallized aluminum. Therefore it can be concluded that the growth rate is not only driven by the kinetics but also significantly by the heat transfer. The influences of other parameters like rotation and temperature gradient should be taken into account, since they have a significant impact on the achieved growth rate.
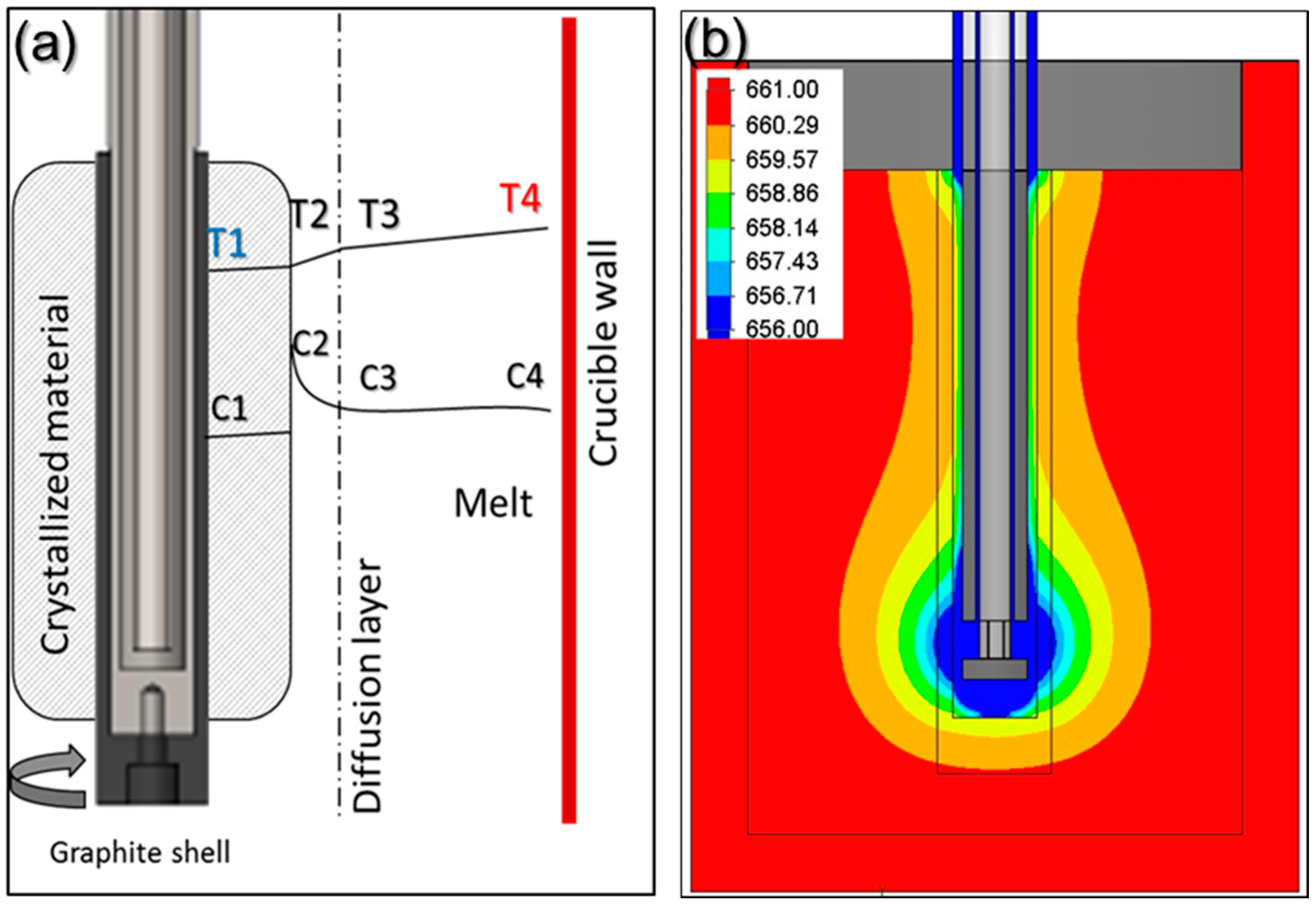
With the help of the software Solidworks
® (version 2017, Dassault Systèmes, Waltham, MA, USA), a basic simulation was performed (see
Figure 10b) representing the temperature profile in the melt and in the crystallized material. The results showed that the variation in the temperature gradient between the melt adjacent to crucible wall (T4) and the solidification front (T2) is in the order of 0.9 °C (comparing
Figure 10a,b). When rotation is applied during the experiments, it promotes a forced convection that assists on the reduction of this thermal gradient. This reduction will also decrease the average growth rate, as seen on
Table 3. Additionally, based on the theory of fractional crystallization (Equation (2)) and the experimental results shown in
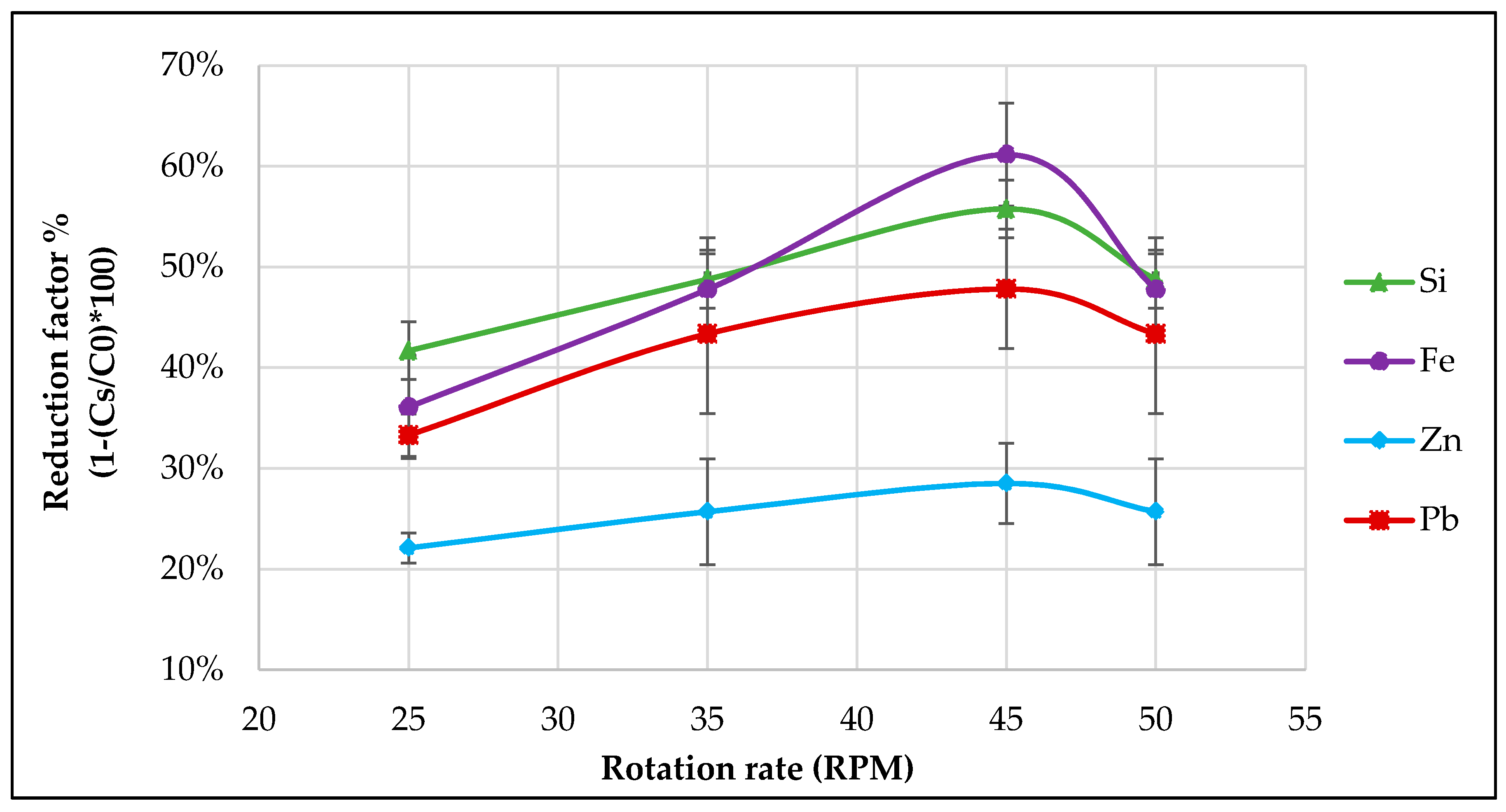
Figure 6, it is assumed that the applied rotation contributed in the decrease of the diffusion layer thickness, favoring a more efficient rejection of the solute into the melt.
With increasing the crystallized material diameter, the growth rate decreases due to the less efficient cooling of the solid formed, the proximity of the solid/liquid interface to the crucible wall and therefore smaller temperature gradient. Though, this fact wasn’t investigated in this paper due to the impossibility of an accurate measurement of the growth rate during the process. One alternative is to perform a “striation” trial, where for certain periods of time a disturbance on the growth front is generated by e.g., drop of temperature or addition of extra impurities [
20,
21]. A microscopy analysis later will reveal the intervals in distance of these disturbances and the growth rate across the whole crystallized material can be calculated. Despite the fact that smaller growth rates lead to a better purification efficiency, drastic reduction in growth rate can lead to higher process time and therefore an optimum thermal gradient and declining the solute build-up in the boundary layer by promoting an efficient mixing in the melt should be maintained. Also, the application of the most optimum combination of rotation- and cooling rate in the cooled finger method will allow a more efficient end-purification. This promotes a stable boundary layer, which together with a proper temperature gradient, allows a uniform growth as well as a controlled segregation of impurities. Higher rotation rates proved beneficial for the purification but at very high levels it rather causes a drop in purification, most likely due to back melting effect caused by high turbulence flow on the growth front.
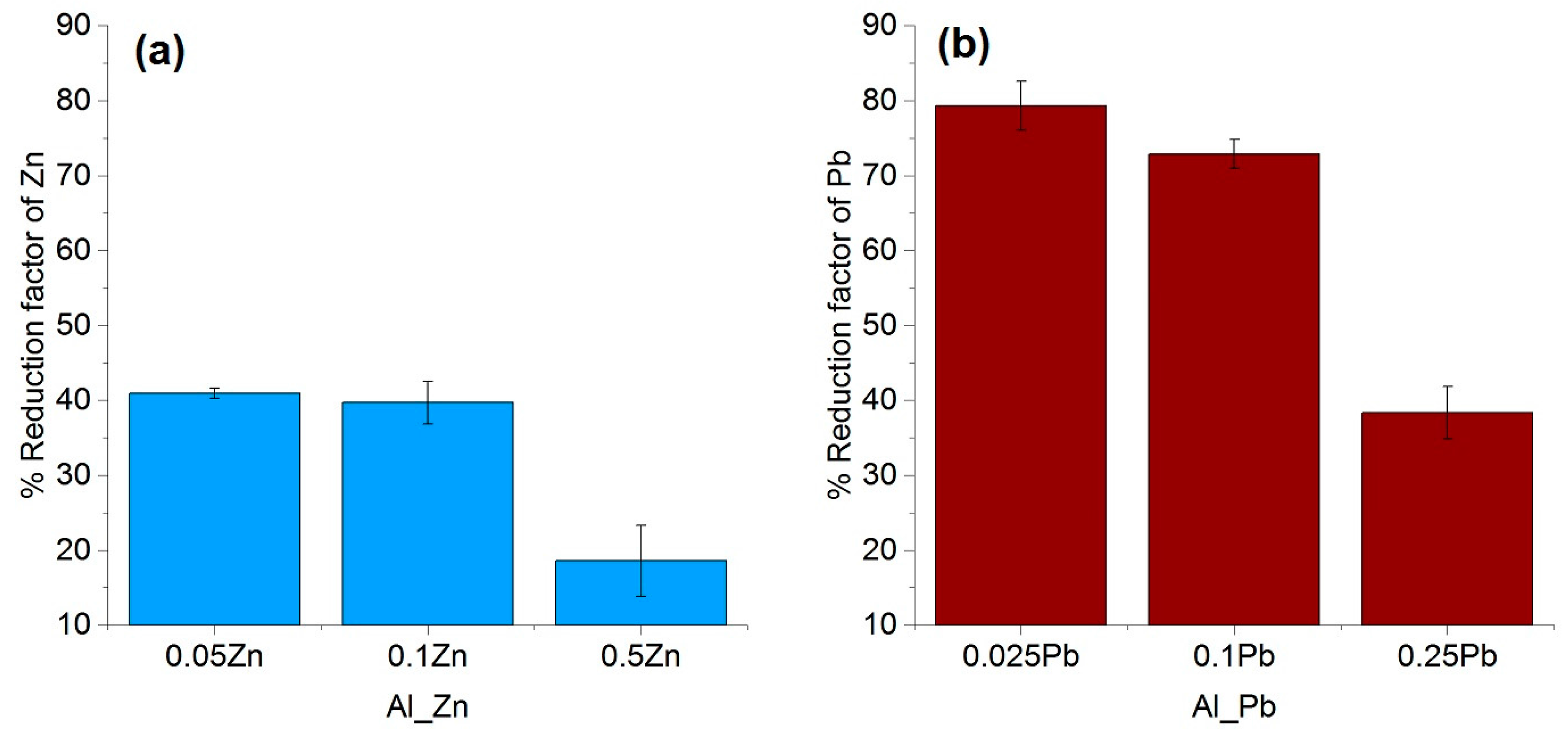
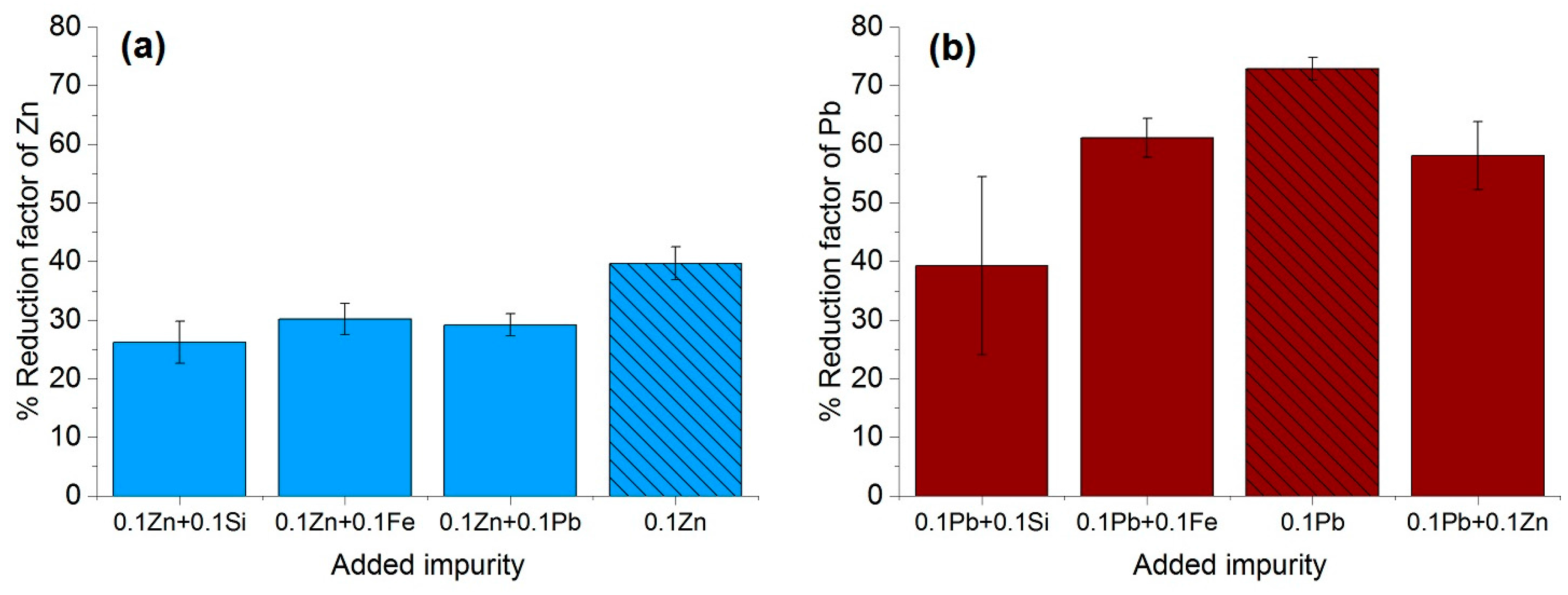
The purification factor obtained from the experiments showed a strong dependence on the process parameters, the initial chemical composition and the concentration of the impurities as well as the interaction between the impurity elements. The reduction factors of Pb and Zn revealed to be negatively affected by the other accompanying elements such as Fe and Si. Disturbances in the growth front are more likely to occur in multicomponent systems than in binary ones. A reduction in the growth rate of the process in order to keep the growth front stable will result in a higher reduction factor of impurities. This effect can be induced by an optimization in the rotation rate, therefore reducing the diffusion layer thickness. In addition, lower amounts of impurity (e.g., 0.025–0.05 wt %), results a much higher reduction factor, however, extreme lower initial concentration of the impurities were not yet studied in this proof of principle investigation.
The advantages of the cooled finger method in comparison with zone melting are the higher production rate and more efficient segregation of impurities. The crystallized material in the cooled finger process grows radially and generates a much bigger volume, while the growth in zone melting is in one direction along the length of a metallic bar and produces smaller masses. This fact in combination with the potential of cooled finger process to be scaled up to at least hundreds of Kilograms leads to significantly higher production rate in comparison to zone refining. Another advantage of cooled finger is its controllable mixing next to the growth front, leading to a decrease the diffusion layer thickness as described in page 2 (Equation (2)). The mixing behavior in cooled finger methodology is a mechanical aspect and independent from the heating behavior of the system. In contrast and in spite of applying induction heating in zone refining and hence inducing a turbulence at the growth front as well, the same fine controlling cannot be managed, because by changing the induction power not only the diffusion layer but also the zone length would be changed. All these aspects make the cooled finger technique a promising alternative to the currently common methods.