Reduction of Induced Central Damage in Cold Extrusion of Dual-Phase Steel DP800 Using Double-Pass Dies
Abstract
:1. Introduction
2. Materials and Methods
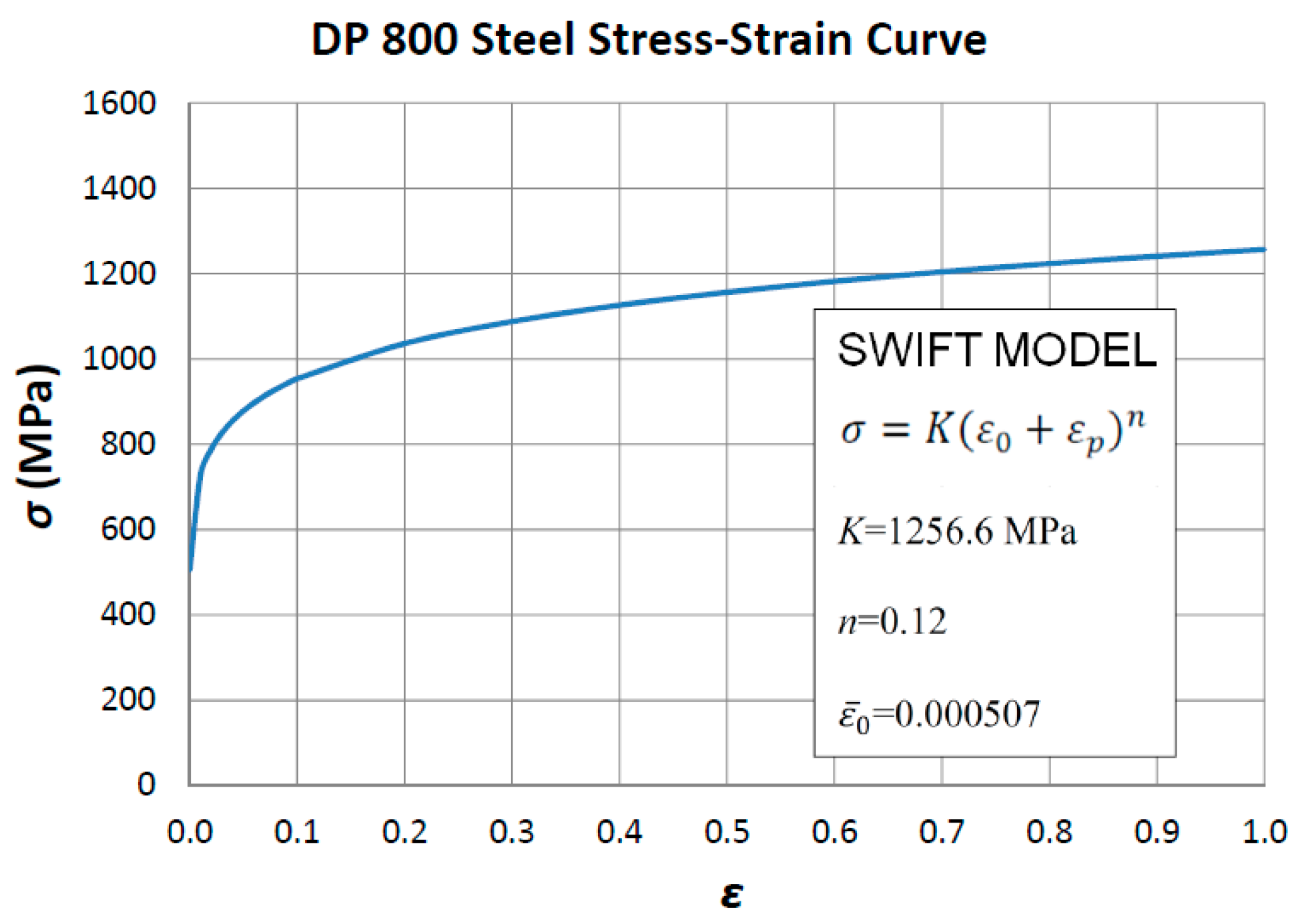
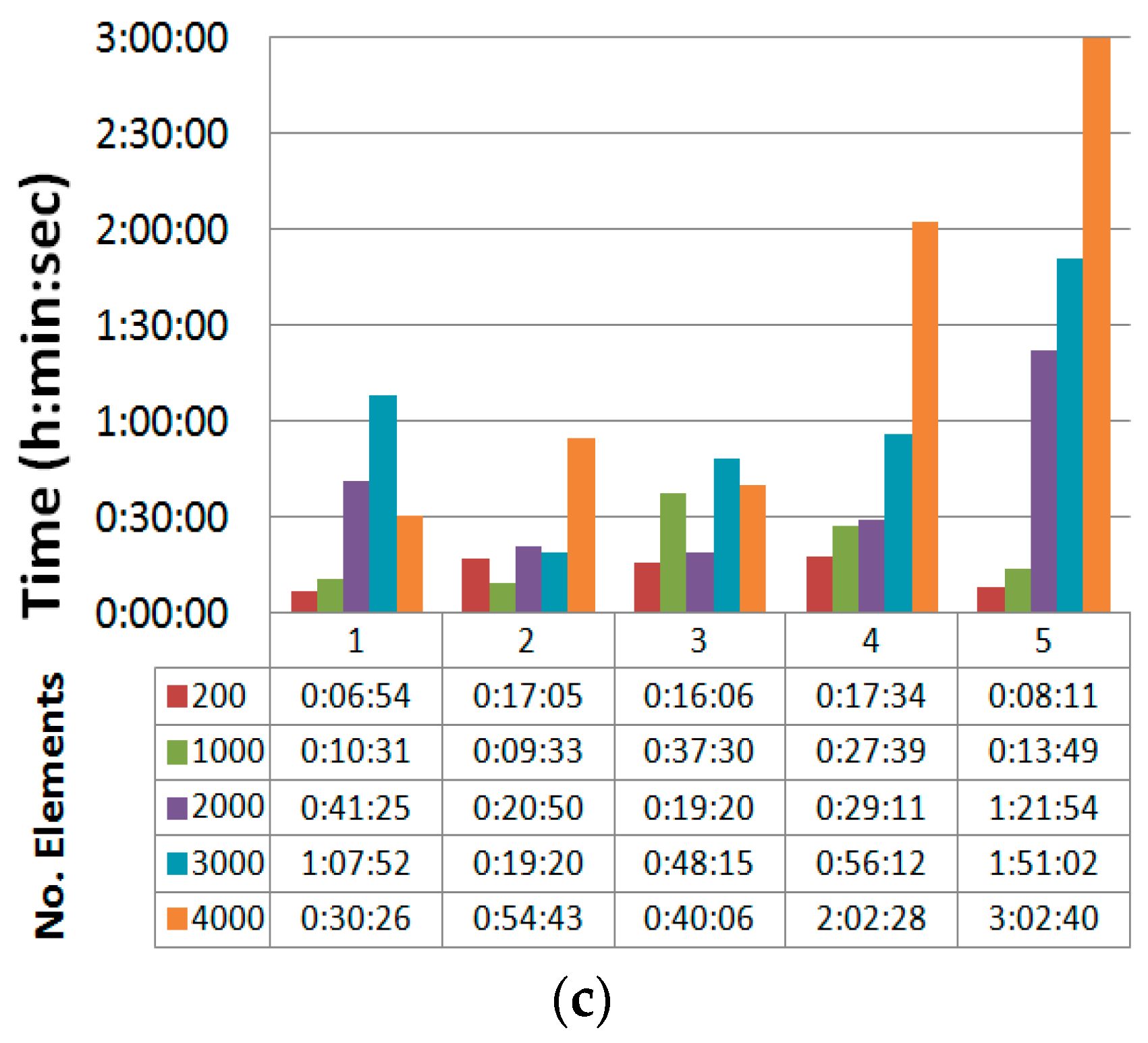
2.1. Finite Element Modelling with DEFORM F2™
- Object description: all data associated with an object, including geometry, mesh, temperature, material, etc.
- Material data: data describing the behavior of the material under the conditions which will experience during deformation.
- Inter object conditions: describes how the objects interact with each other, including contact and friction conditions between objects.
- Simulation controls: definition of parameters such as discrete time steps to model the process.
- n: number of steps;
- x: total movement of the primary die;
- V: ram velocity;
- ∆t: time increment per step.
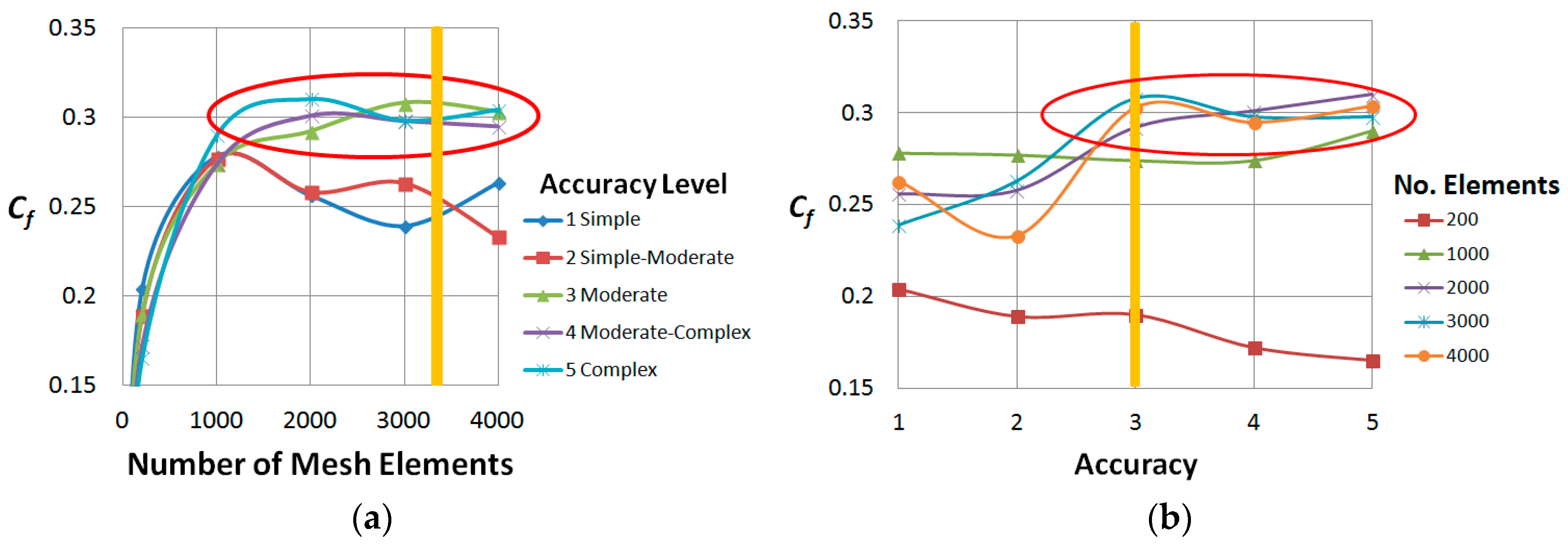
2.2. Finite Element Model Validation
3. Results and Discussion
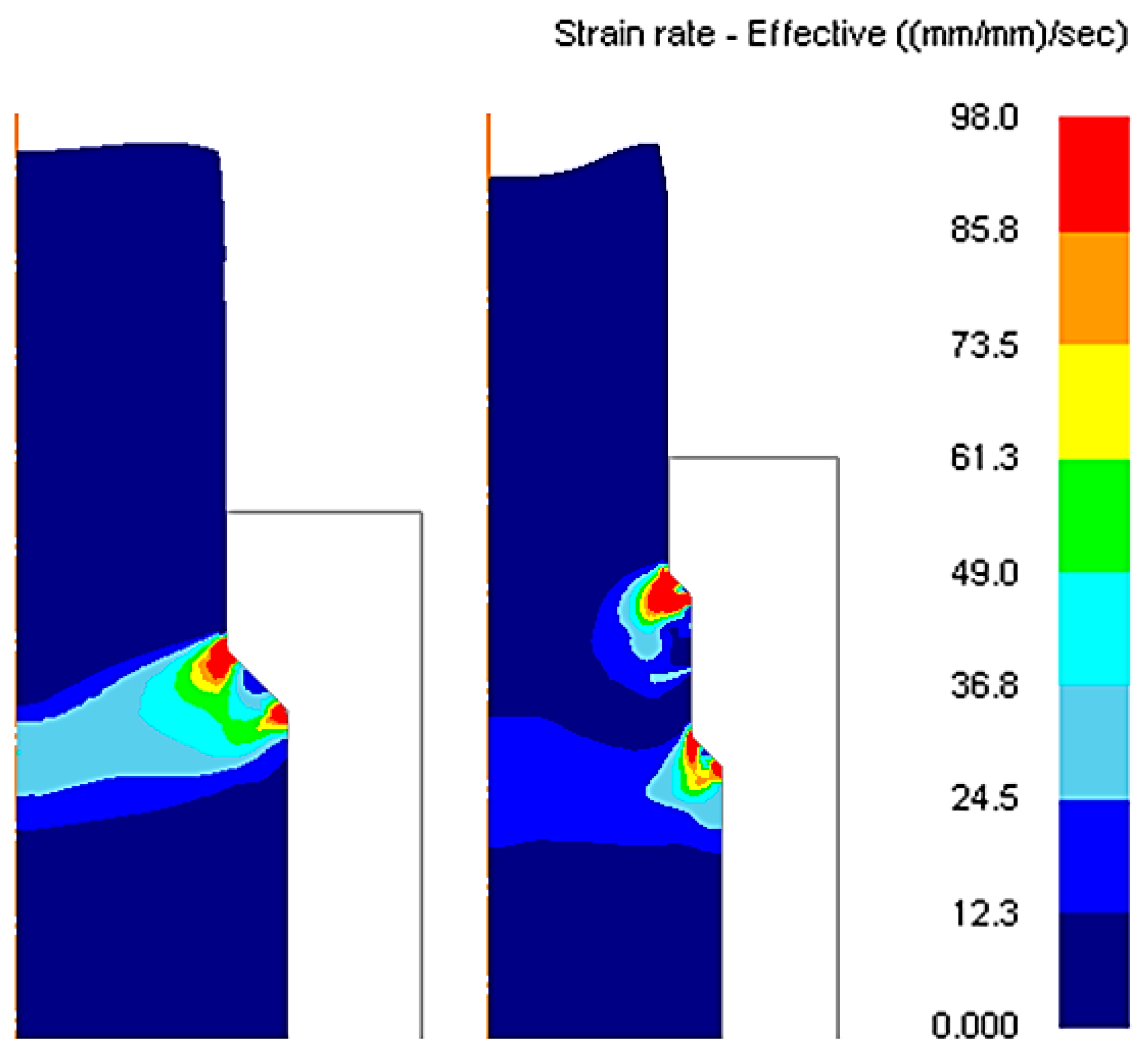
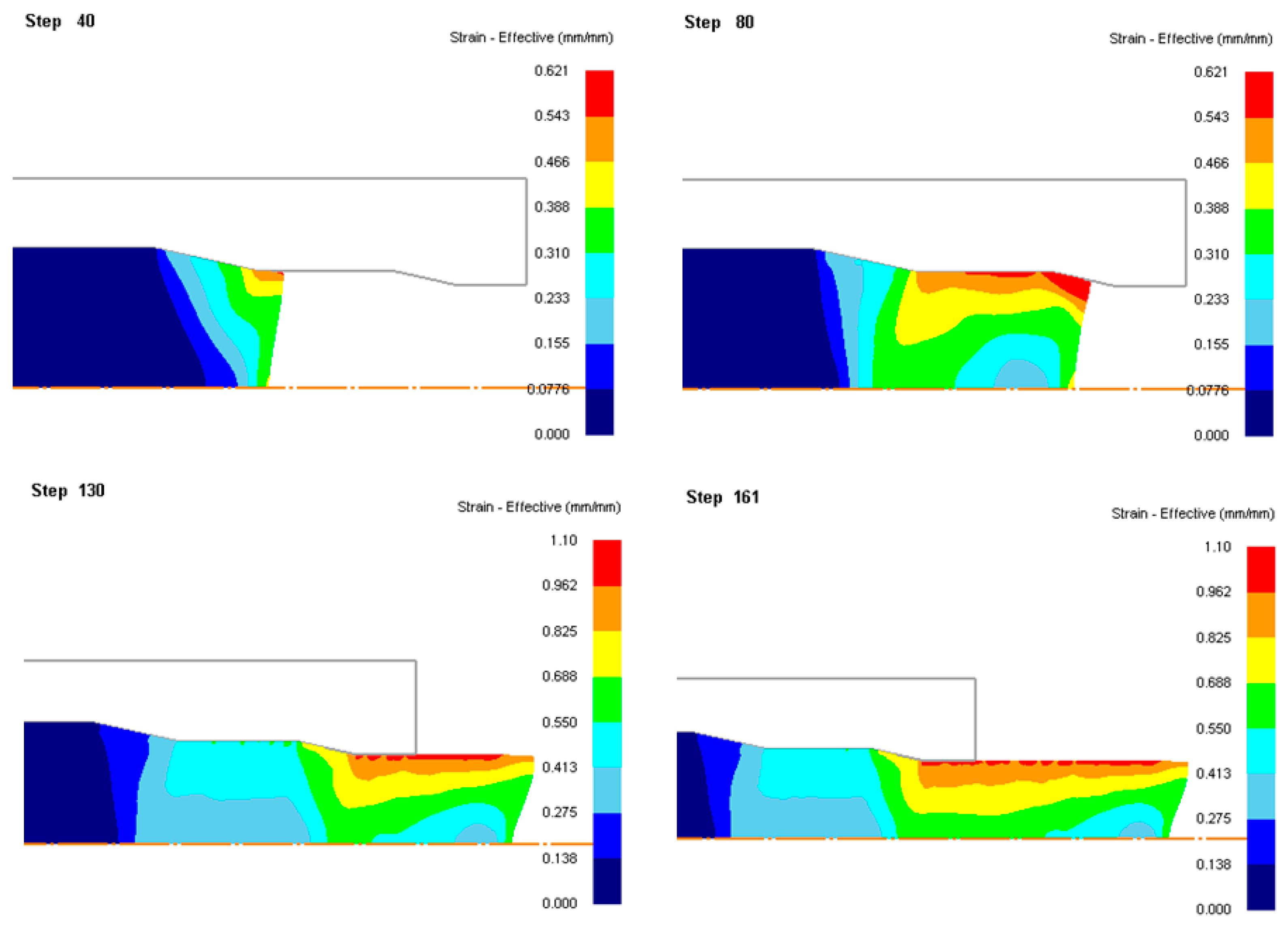
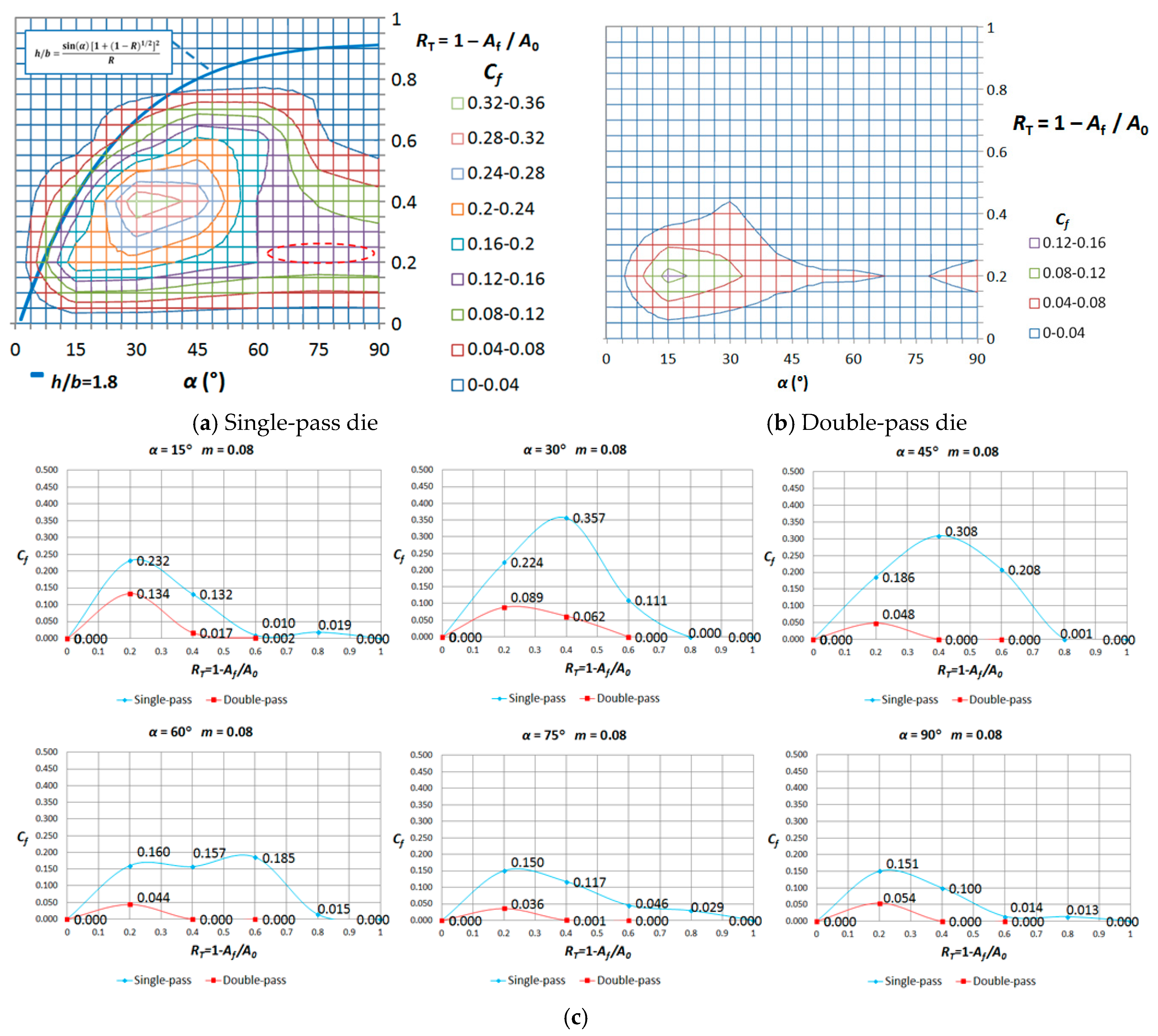
3.1. Single-Pass Dies
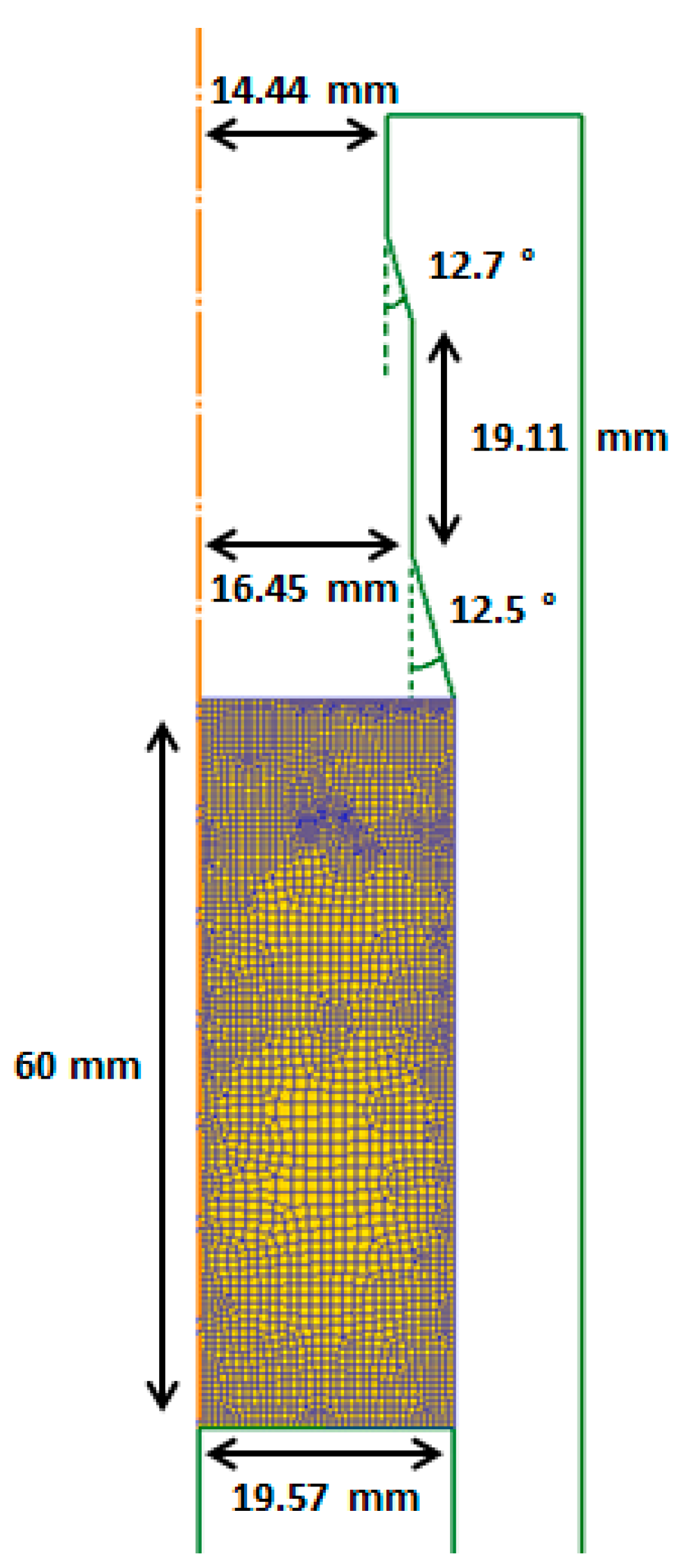
3.2. Double-Pass Dies
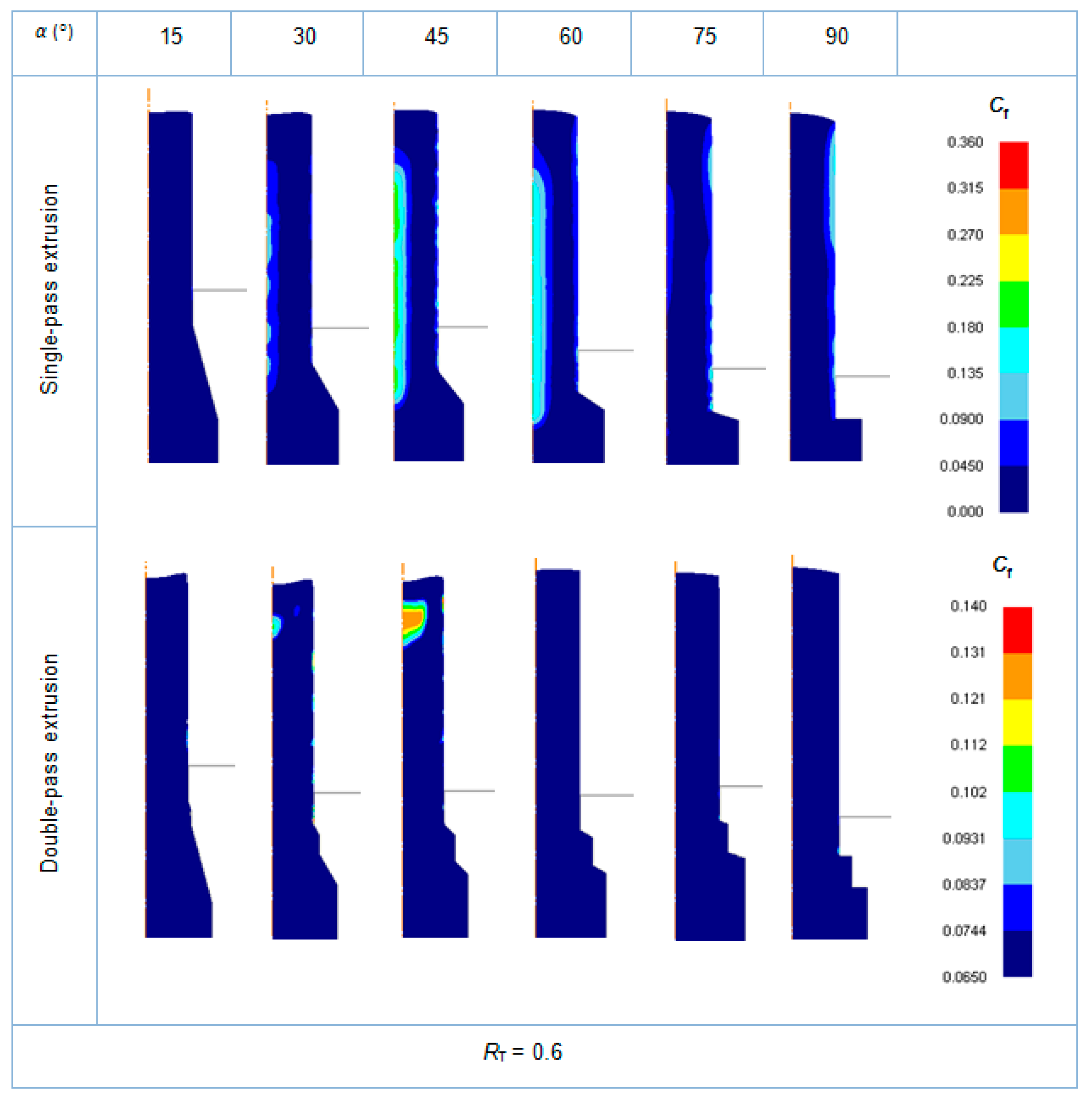
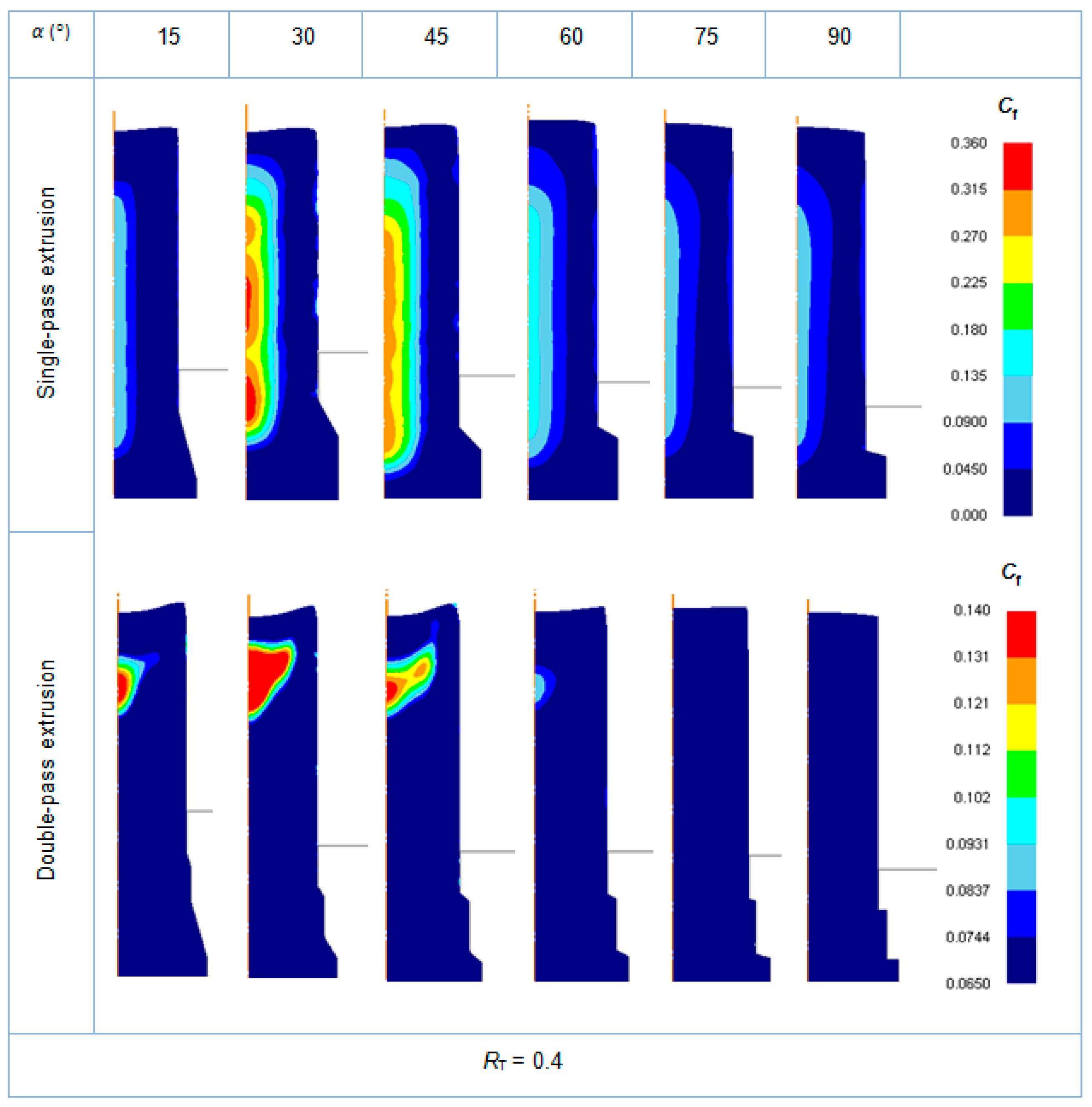
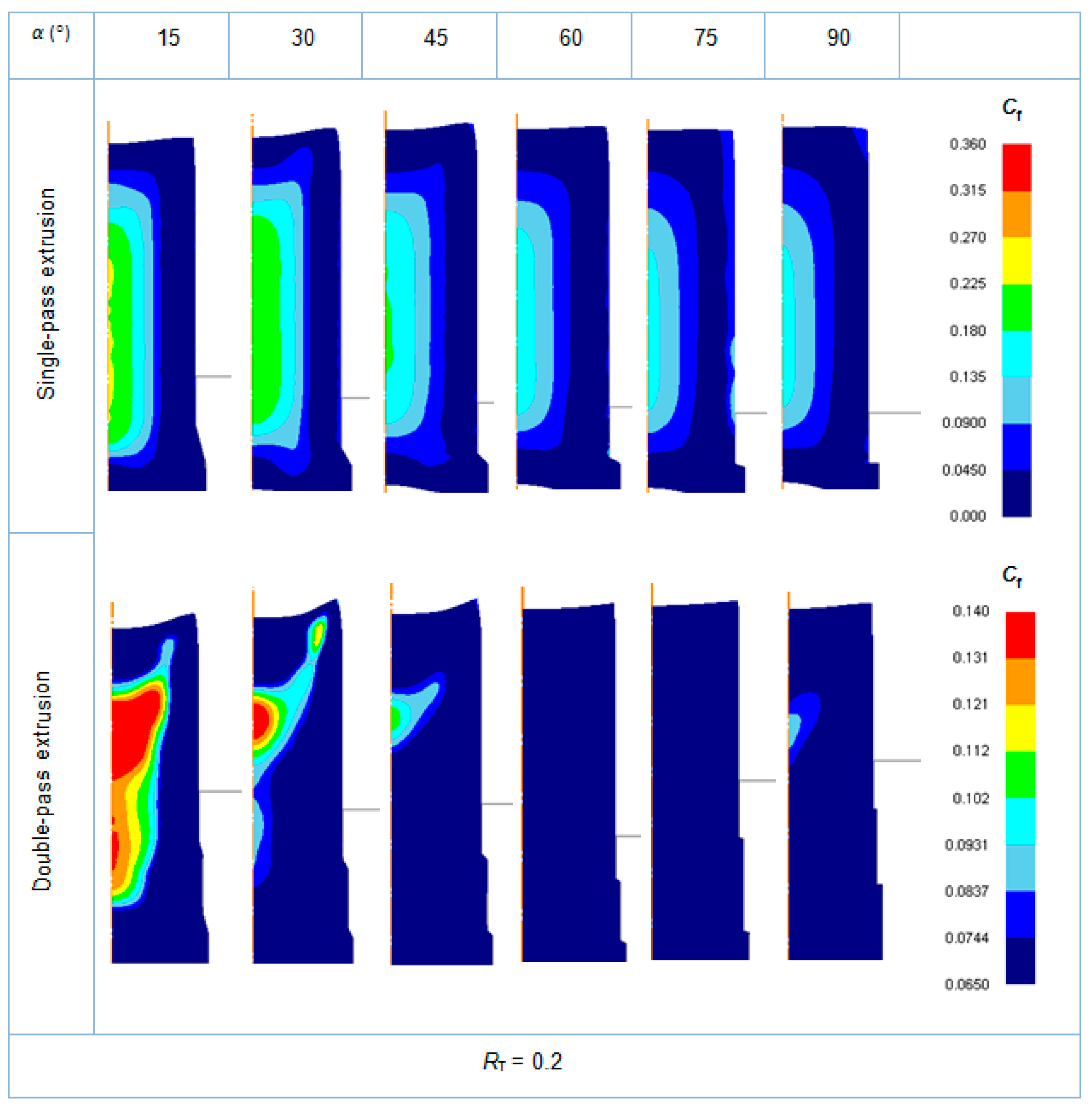
3.3. Single-Pass Dies vs. Double-Pass Dies
4. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bhargava, M.; Tewari, A.; Mishra, S.K. Forming limit diagram of advanced high strength steels (AHSS) based on strain-path diagram. Mater. Des. 2015, 85, 149–155. [Google Scholar] [CrossRef]
- Del Pozo, D.; López de Lacalle, L.N.; López, J.M.; Hernández, A. Prediction of press/die deformation for an accurate manufacturing of drawing dies. Int. J. Adv. Manuf. Technol. 2008, 37, 649–656. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A.; Muñoa, J.; Sánchez, J.A. The cam as the centre of gravity of the five-axis high speed milling of complex parts. Int. J. Prod. Res. 2005, 43, 1983–1999. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A.; Sánchez, J.A. Improving the high-speed finishing of forming tools for advanced high-strength steels (ahss). Int. J. Adv. Manuf. Technol. 2005, 29, 49–63. [Google Scholar] [CrossRef]
- Nasser, A.; Yadav, A.; Pathak, P.; Altan, T. Determination of the flow stress of five ahss sheet materials (DP 600, DP 780, DP 780-CR, DP 780-HY and TRIP 780) using the uniaxial tensile and the biaxial viscous pressure bulge (VPB) tests. J. Mater. Process. Technol. 2010, 210, 429–436. [Google Scholar] [CrossRef]
- Moeini, G.; Ramazani, A.; Myslicki, S.; Sundararaghavan, V.; Könke, C. Low cycle fatigue behaviour of DP steels: Micromechanical modelling vs. validation. Metals 2017, 7, 265. [Google Scholar] [CrossRef]
- Nam, W.J.; Bae, C.M. Microstructural evolution and its relation to mechanical properties in a drawn dual-phase steel. J. Mater. Sci. 1999, 34, 5661–5668. [Google Scholar] [CrossRef]
- Ramazani, A.; Kazemiabnavi, S.; Larson, R. Quantification of ferrite-martensite interface in dual phase steels: A first-principles study. Acta Mater. 2016, 116, 231–237. [Google Scholar] [CrossRef]
- Ramazani, A.; Mukherjee, K.; Schwedt, A.; Goravanchi, P.; Prahl, U.; Bleck, W. Quantification of the effect of transformation-induced geometrically necessary dislocations on the flow-curve modelling of dual-phase steels. Int. J. Plast. 2013, 43, 128–152. [Google Scholar] [CrossRef]
- Evin, E.; Tomáš, M. The influence of laser welding on the mechanical properties of dual phase and trip steels. Metals 2017, 7, 239. [Google Scholar] [CrossRef]
- Gutiérrez-Regueras, J.M.; Camacho, A.M. Investigations on the influence of blank thickness (t) and length/wide punch ratio (LD) in rectangular deep drawing of dual-phase steels. Comput. Mater. Sci. 2014, 91, 134–145. [Google Scholar] [CrossRef]
- García-Domínguez, A.; Claver, J.; Camacho, A.M.; Sebastián, M.A. Comparative analysis of extrusion processes by finite element analysis. Procedia Eng. 2015, 100, 74–83. [Google Scholar] [CrossRef]
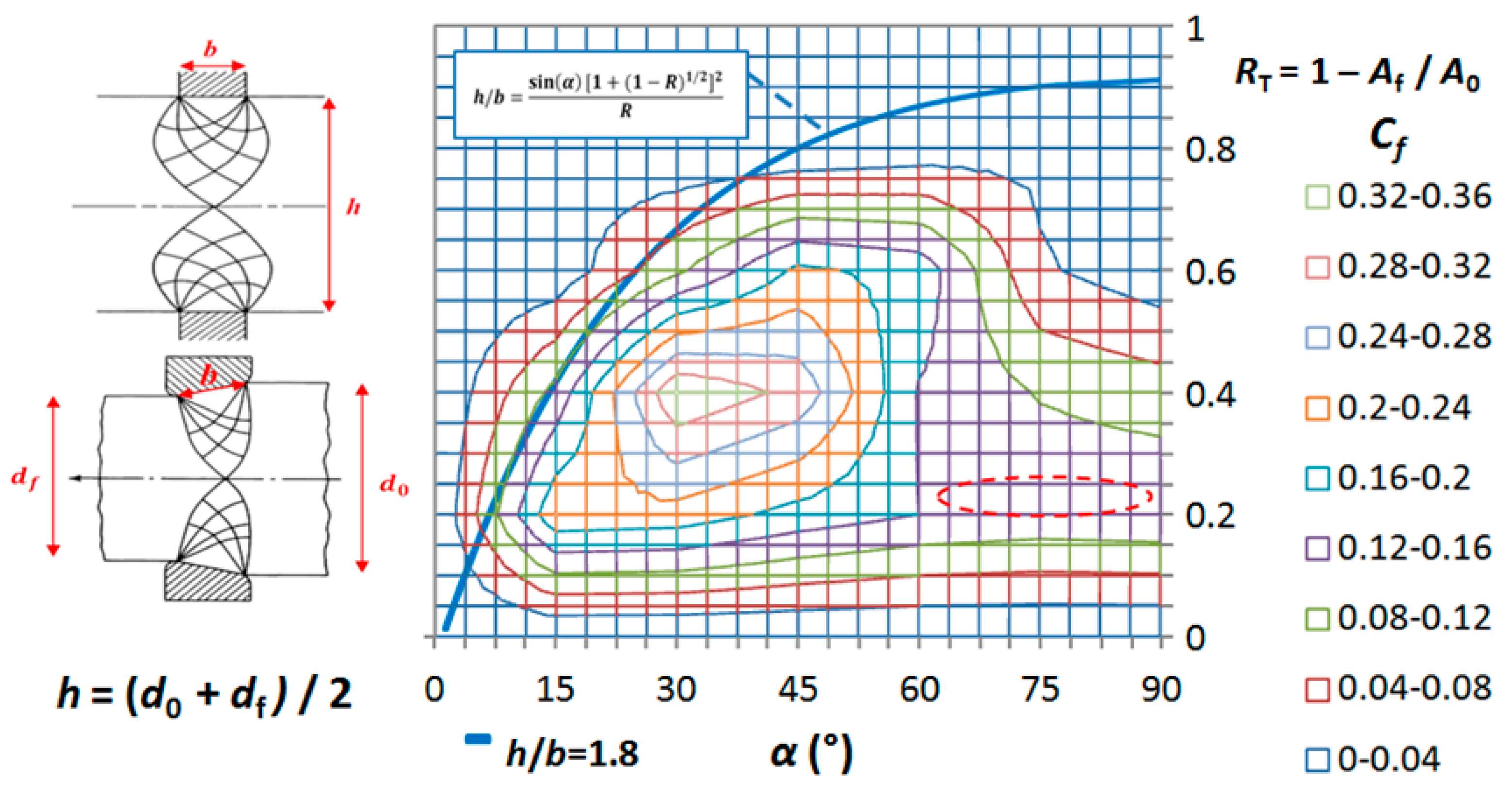
- Parghazeh, A.; Haghighat, H. Prediction of central bursting defects in rod extrusión process with upper bound analysis method. Trans. Nonferrous Met. Soc. China 2016, 26, 2892–2899. [Google Scholar] [CrossRef]
- Camacho, A.M.; Gonzalez, C.; Rubio, E.M.; Sebastian, M.A. Influence of geometrical conditions on central burst appearance in axisymmetrical drawing processes. J. Mater. Process. Technol. 2006, 177, 304–306. [Google Scholar] [CrossRef]
- Oh, S.-I.; Walters, J.; Wu, W.-T. Finite element method applications in bulk forming. In ASM Handbook. Metals Process Simulation; Furrer, D.U., Semiatin, S.L., Eds.; ASM International: Materials Park, OH, USA, 2010; Volume 22B, pp. 267–289. ISBN 978-1-61503-005-7. [Google Scholar]
- Pathak, N.; Butcher, C.; Worswick, M.J.; Bellhouse, E.; Gao, J. Damage evolution in complex-phase and dual-phase steels during edge stretching. Materials 2017, 10, 346. [Google Scholar] [CrossRef] [PubMed]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.R.F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in-situ deformation experiments and crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Darabi, A.C.; Chamani, H.R.; Kadkhodapour, J. 3D micromechanical modeling of failure and damage evolution in dual phase steel based on a real 2D microstructure. Acta Mech. Solida Sin. 2016, 29, 95–110. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Khalifa, N.B.; Hering, O.; Meya, R.; Myslicki, S.; Walther, F. Forming-induced damage and its effects on product properties. CIRP Ann. Manuf. Technol. 2017, 66, 281–284. [Google Scholar] [CrossRef]
- Dieter, G.E.; Kuhn, H.A.; Semiatin, S.L. Handbook of Workability and Process Design; ASM International: Materials Park, OH, USA, 2003; ISBN 978-0-87170-778-9. [Google Scholar]
- Reddy, N.V.; Dixit, P.M.; Lal, G.K. Ductile fracture criteria and its prediction in axisymmetric drawing. Int. J. Mach. Tool Manuf. 2000, 40, 95–111. [Google Scholar] [CrossRef]
- Reddy, N.V.; Dixit, P.M.; Lal, G.K. Central bursting and optimal die profile for axisymmetric extrusion. J. Manuf. Sci. Eng.-Trans. ASME 1996, 118, 579–584. [Google Scholar] [CrossRef]
- Soyarslan, C. Modelling Damage for Elastoplasticity. Ph.D. Thesis, Middle East Technical University, Çankaya Ankara, Turkey, 2008. [Google Scholar]
- Wagener, H.W.; Haats, J. Crack prevention and increase of workability of brittle materials by cold extrusion. Stud. Appl. Mech. 1995, 43, 373–386. [Google Scholar]
- Scientific Forming Technologies Corporation. DEFORM-F2 v11.0 User’s Manual; Scientific Forming Technologies Corporation: Columbus, OH, USA, 2014. [Google Scholar]
- Kalpakjian, S.; Schmid, S.R. Manufacturing Engineering and Technology, 7th ed.; Pearson: Mexico, 2014; ISBN 978-0133128741. [Google Scholar]
- Cockcroft, M.; Latham, D. Ductility and the workability of metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Gariety, M.; Ngaile, G. Cold and Hot Forging. Fundamentals and Applications; ASM International: Materials Park, OH, USA, 2005. [Google Scholar]
- Avitzur, B. Analysis of central bursting defects in extrusion and wire drawing. J. Eng. Ind. 1968, 90, 79–91. [Google Scholar] [CrossRef]
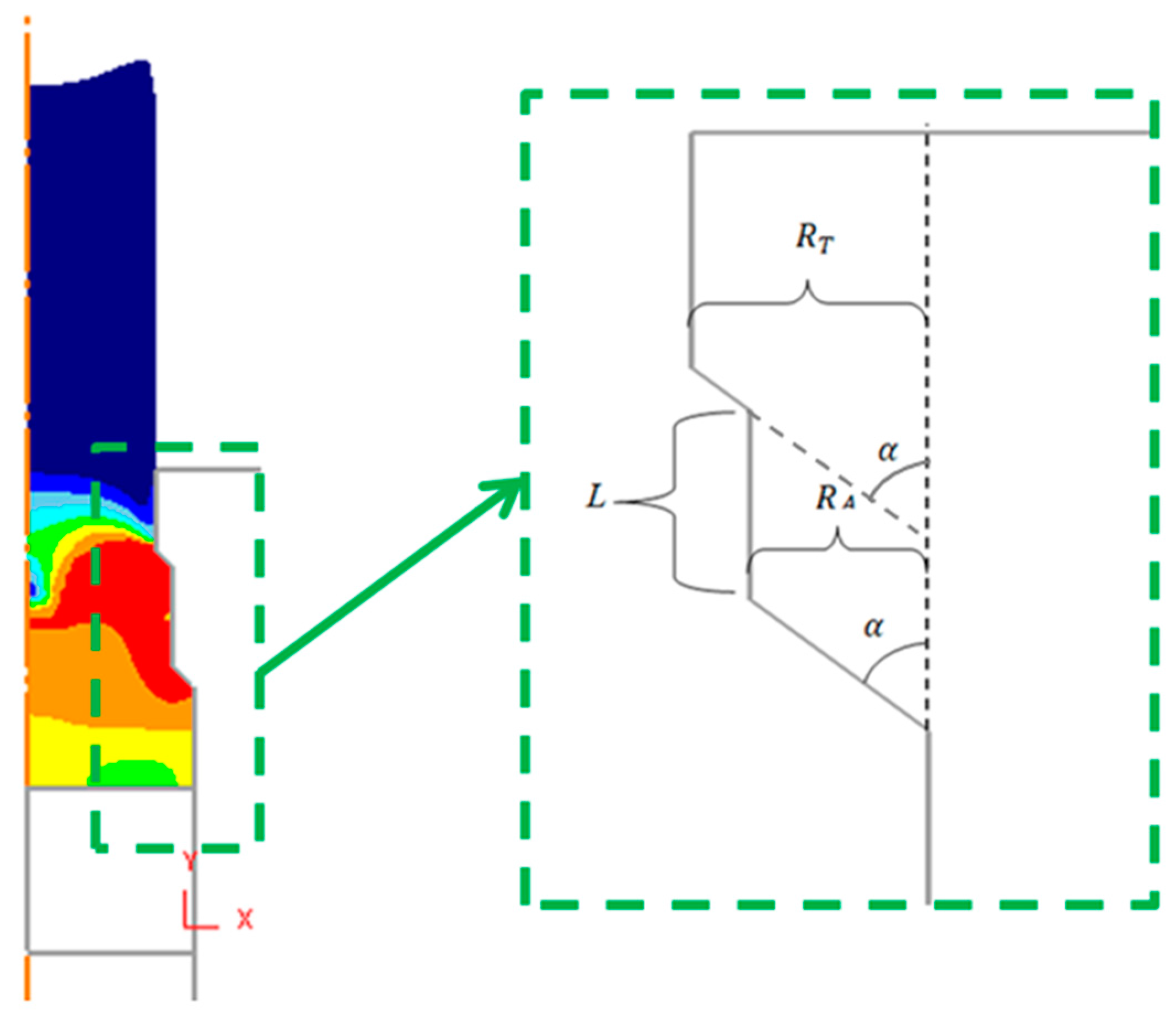


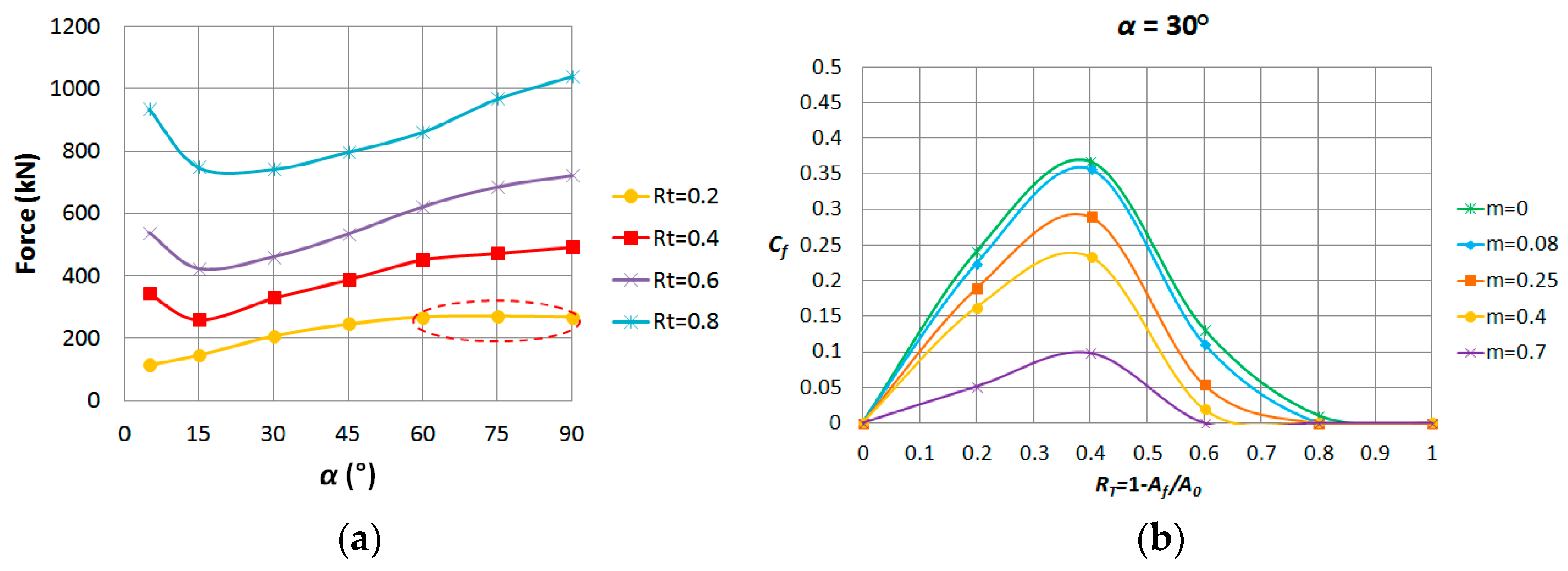
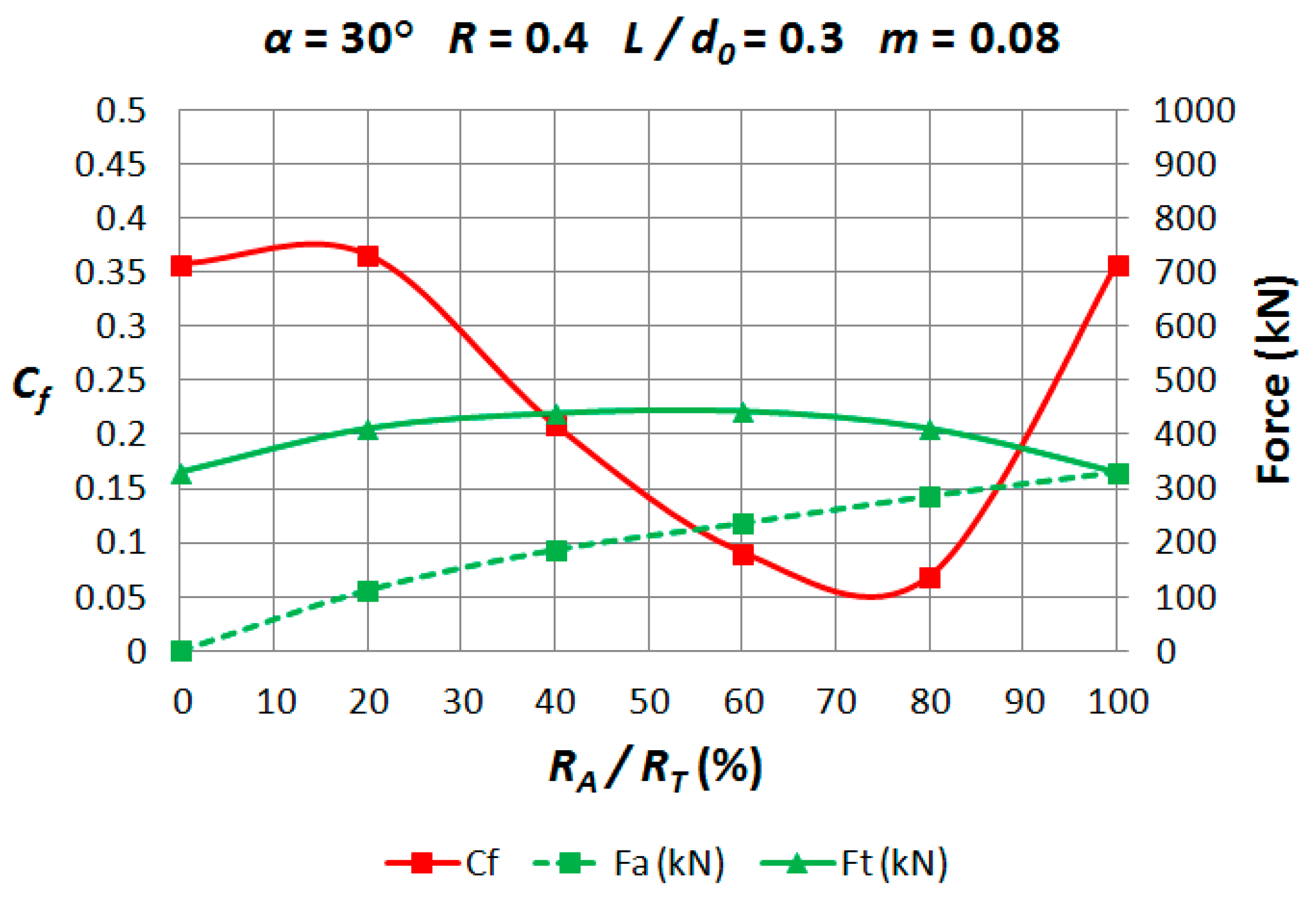
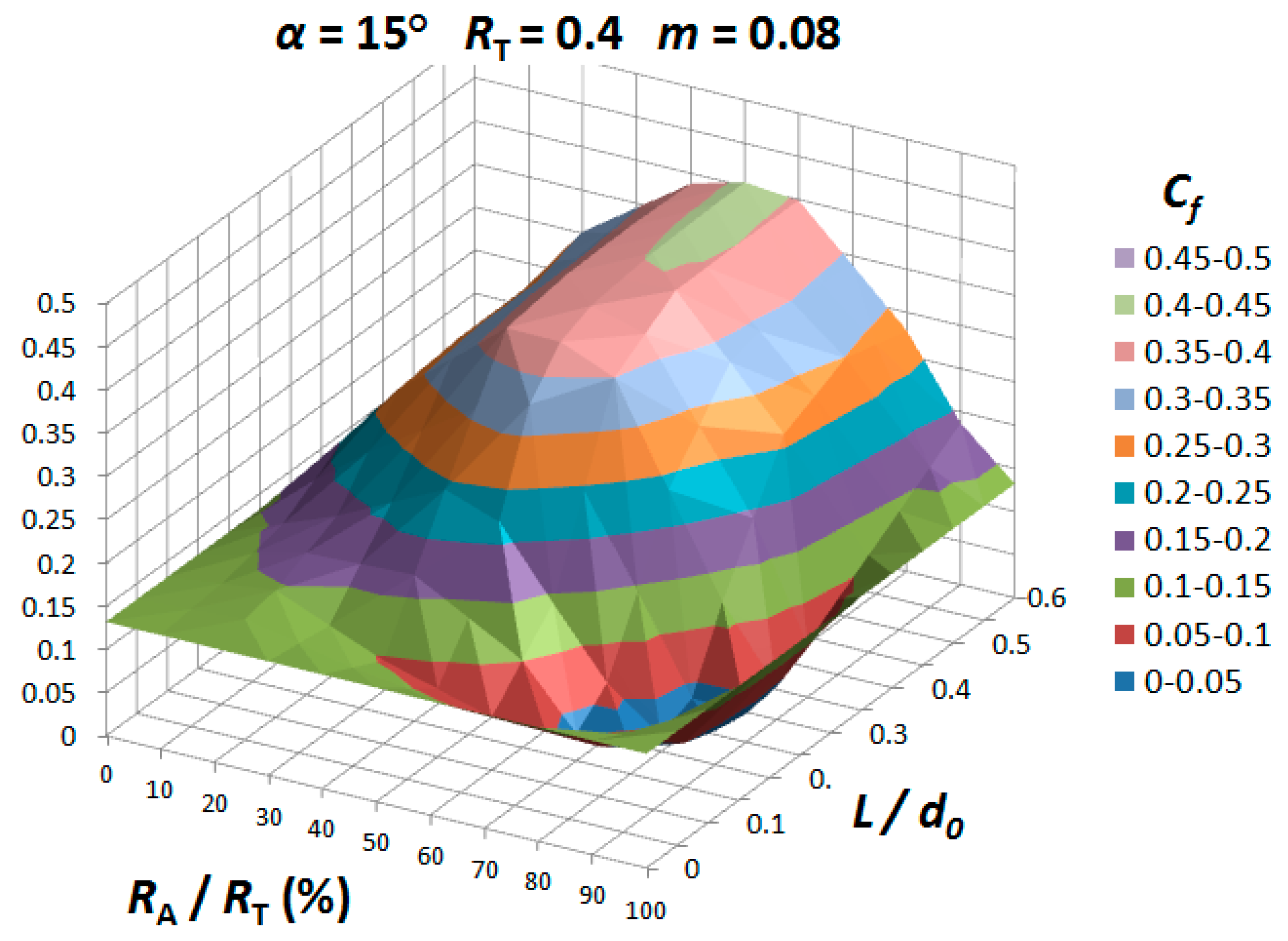
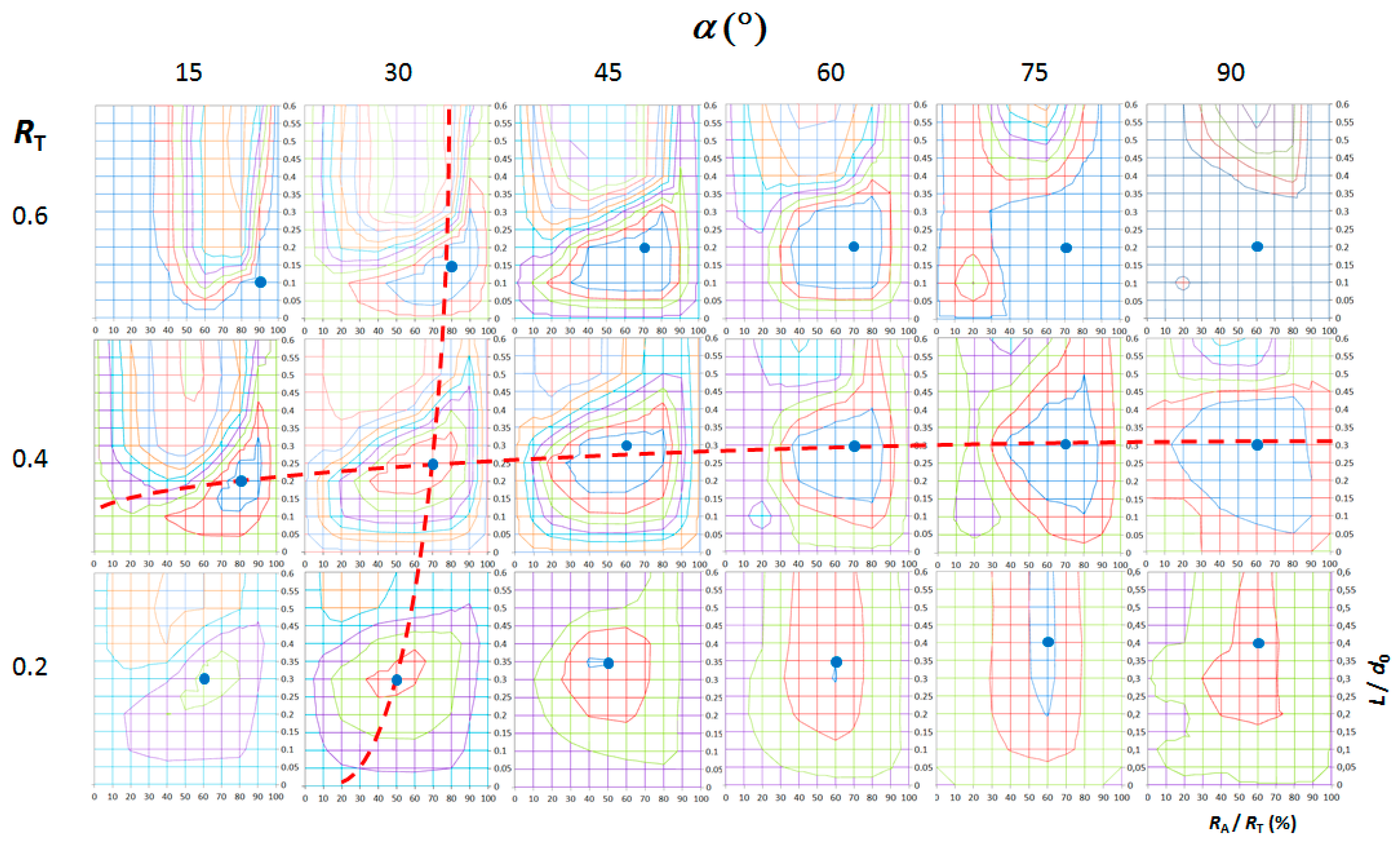
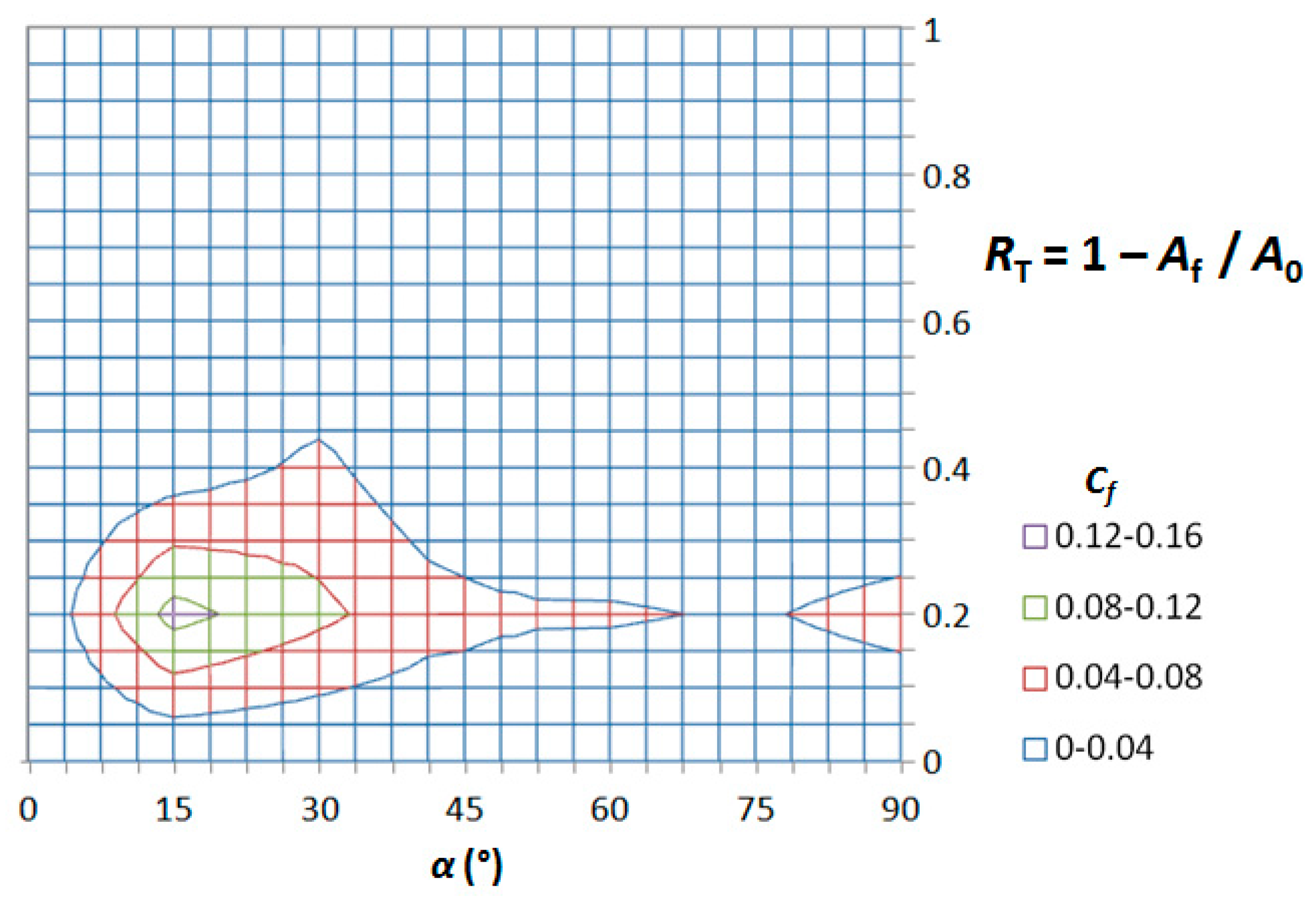
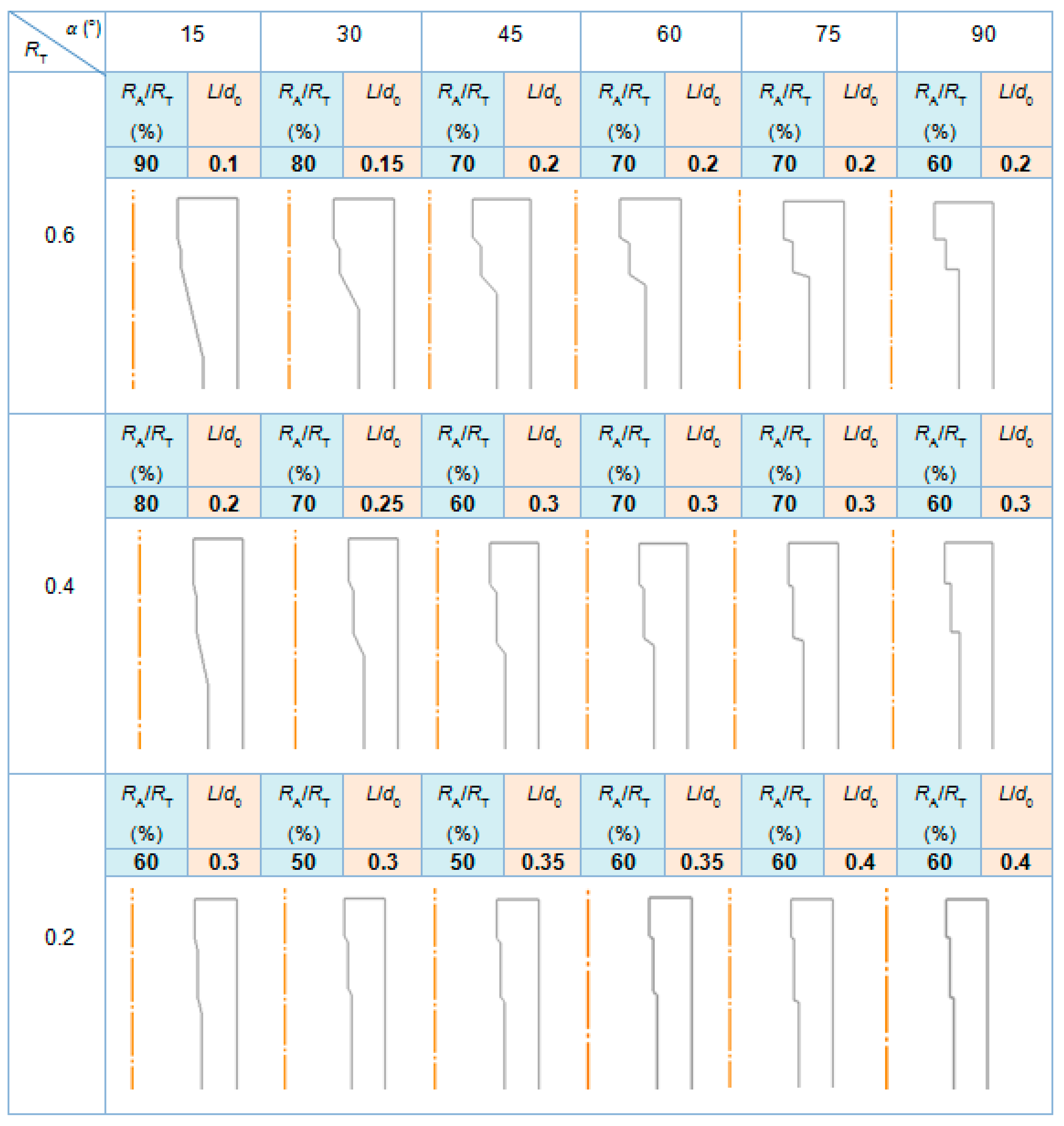
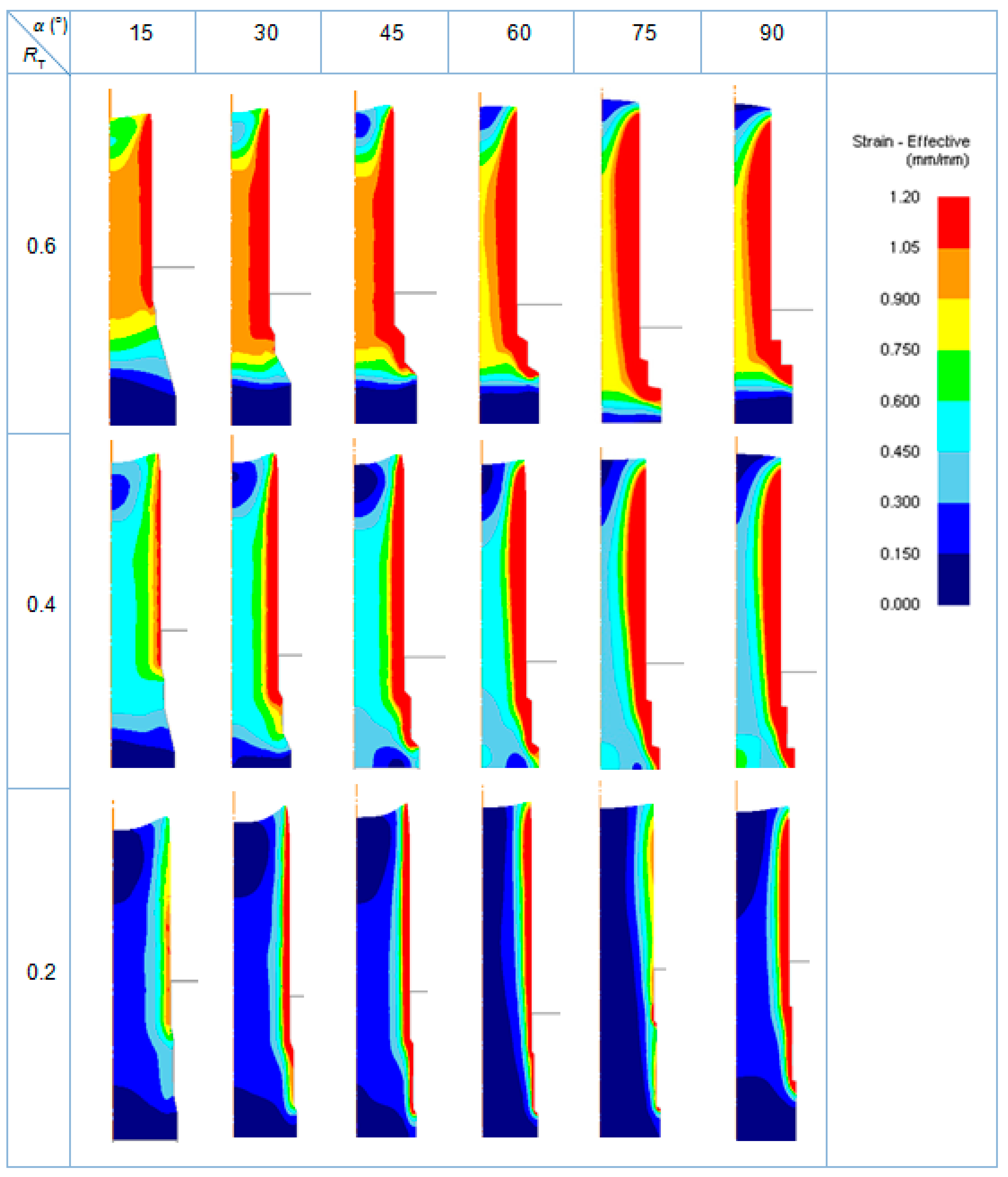
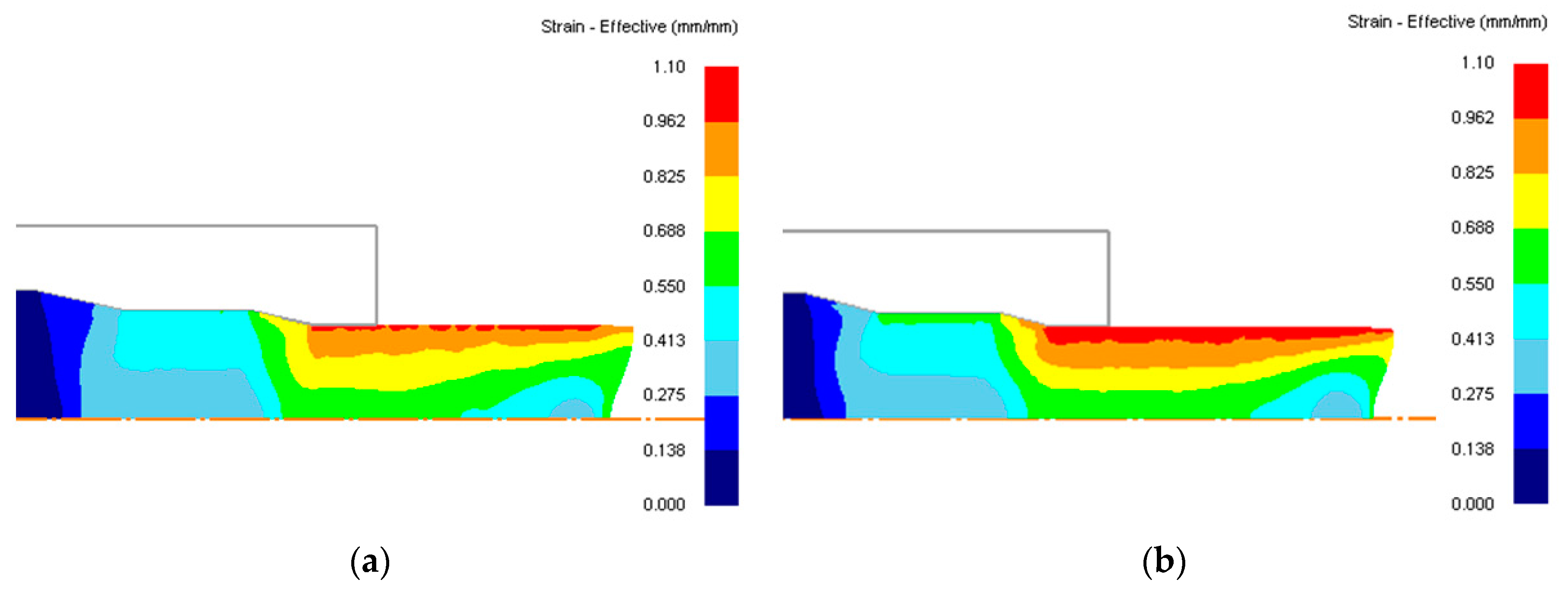
| α (°) | |||||
|---|---|---|---|---|---|
| 15 | 30 | 45 | 60 | 75 | 90 |
| RT | |||
|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 |
| RA/RT | |||||
|---|---|---|---|---|---|
| 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
| L/d0 | ||||||
|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amigo, F.J.; Camacho, A.M. Reduction of Induced Central Damage in Cold Extrusion of Dual-Phase Steel DP800 Using Double-Pass Dies. Metals 2017, 7, 335. https://doi.org/10.3390/met7090335
Amigo FJ, Camacho AM. Reduction of Induced Central Damage in Cold Extrusion of Dual-Phase Steel DP800 Using Double-Pass Dies. Metals. 2017; 7(9):335. https://doi.org/10.3390/met7090335
Chicago/Turabian StyleAmigo, Francisco Javier, and Ana María Camacho. 2017. "Reduction of Induced Central Damage in Cold Extrusion of Dual-Phase Steel DP800 Using Double-Pass Dies" Metals 7, no. 9: 335. https://doi.org/10.3390/met7090335






