Numerical Simulation of Ti/Al Bimetal Composite Fabricated by Explosive Welding
Abstract
:1. Introduction
2. Explosive Welding Model
2.1. Geometric Model of Explosive Welding
2.2. Equation of State (EOS) and Constitutive Model
2.3. Algorithm Selection
3. Simulation Results
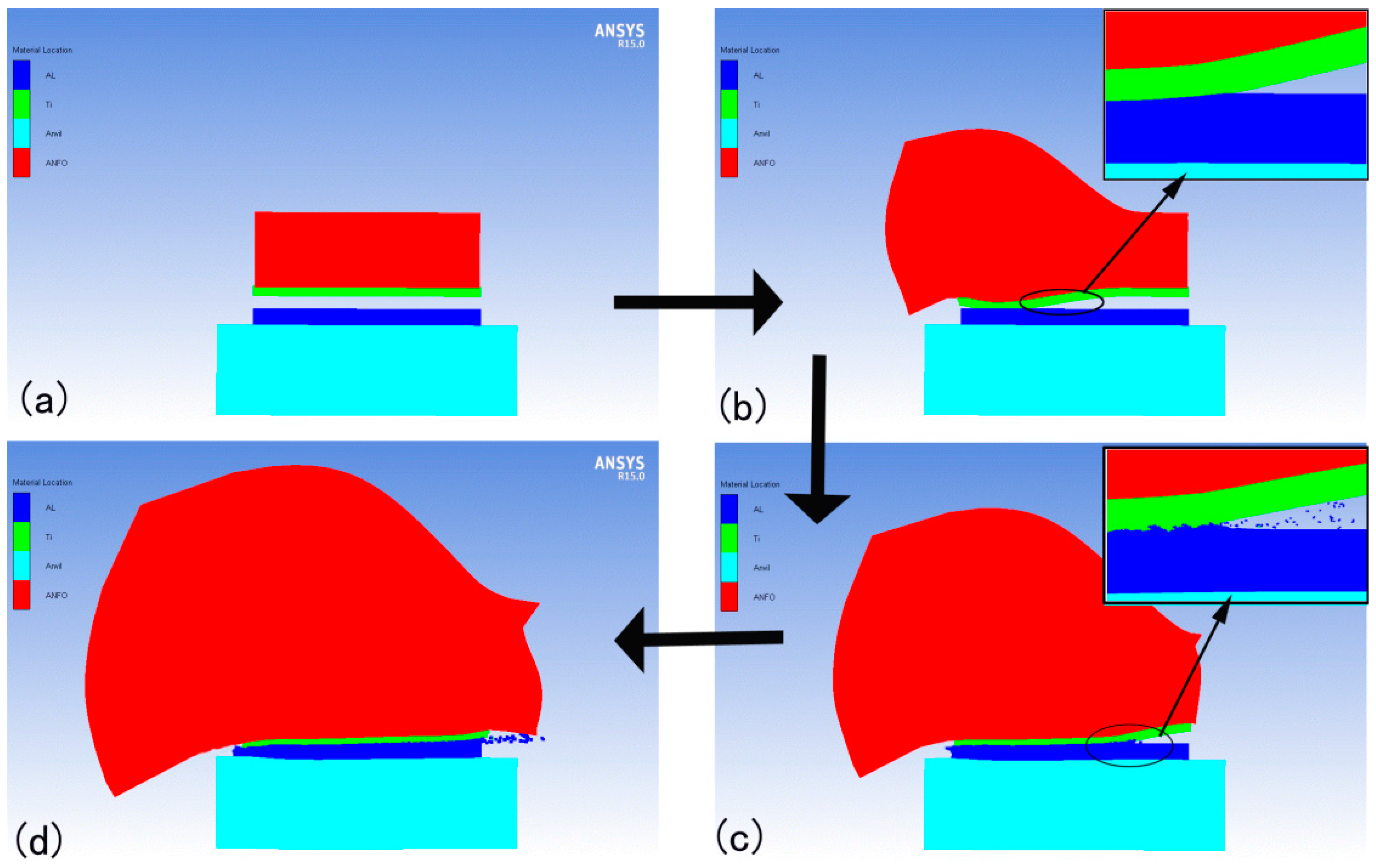
3.1. Kinematic Characteristics of EXW and Jet Formation
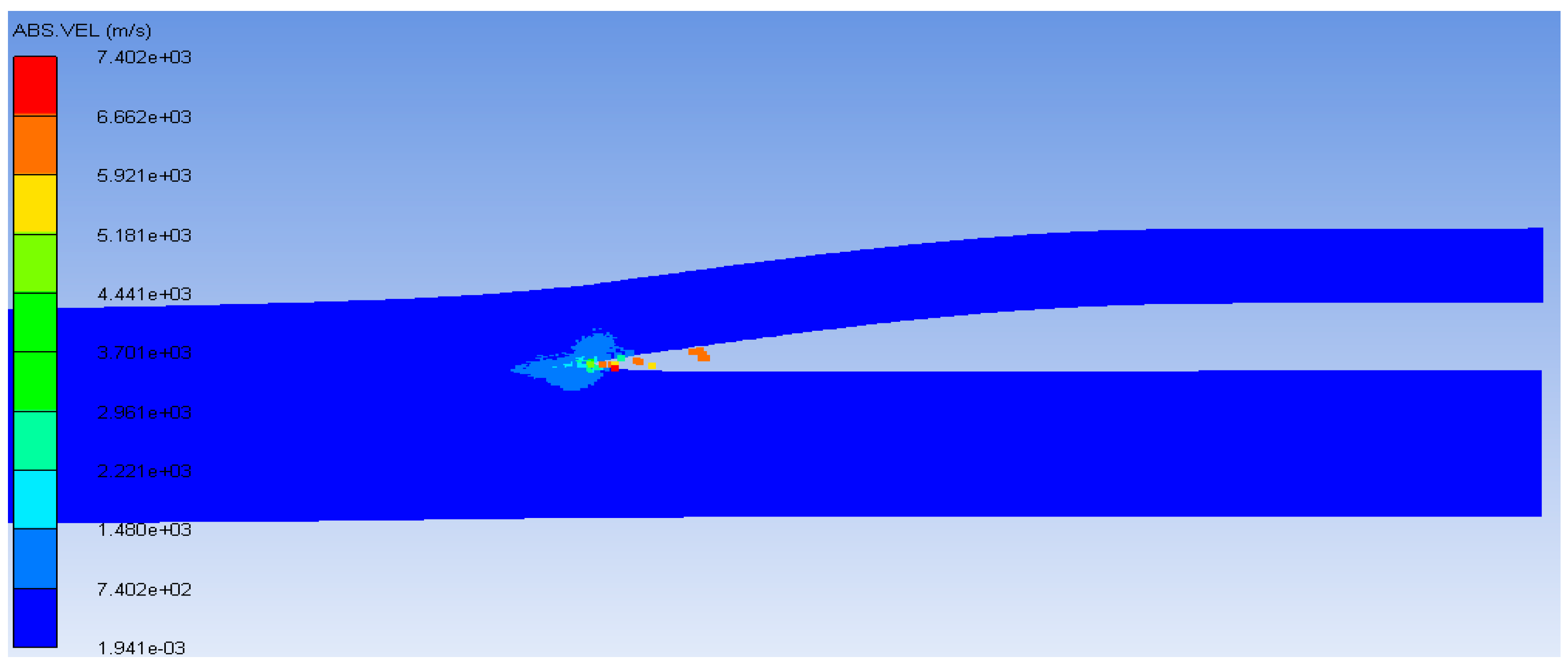
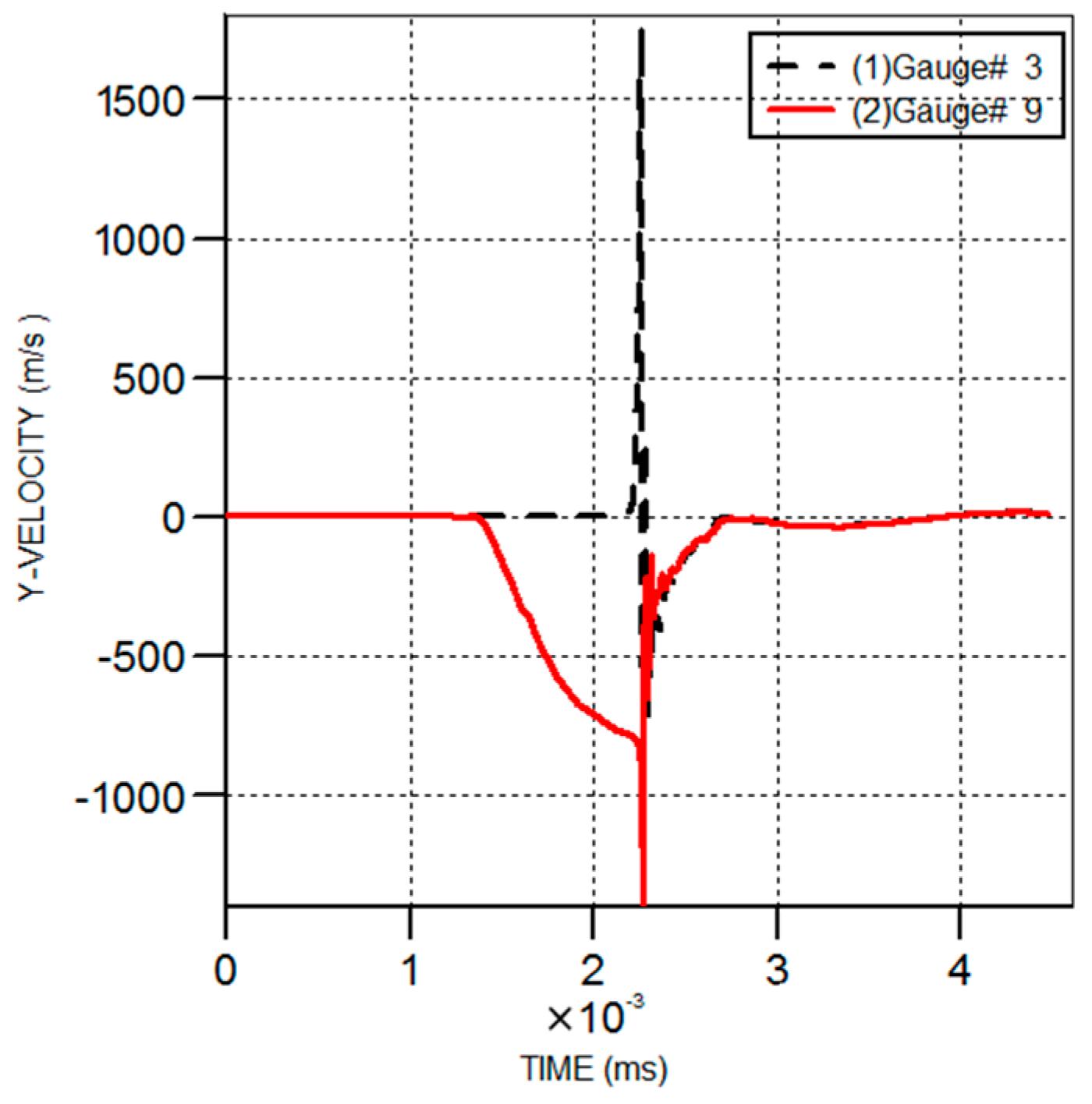
3.2. Velocity Distribution
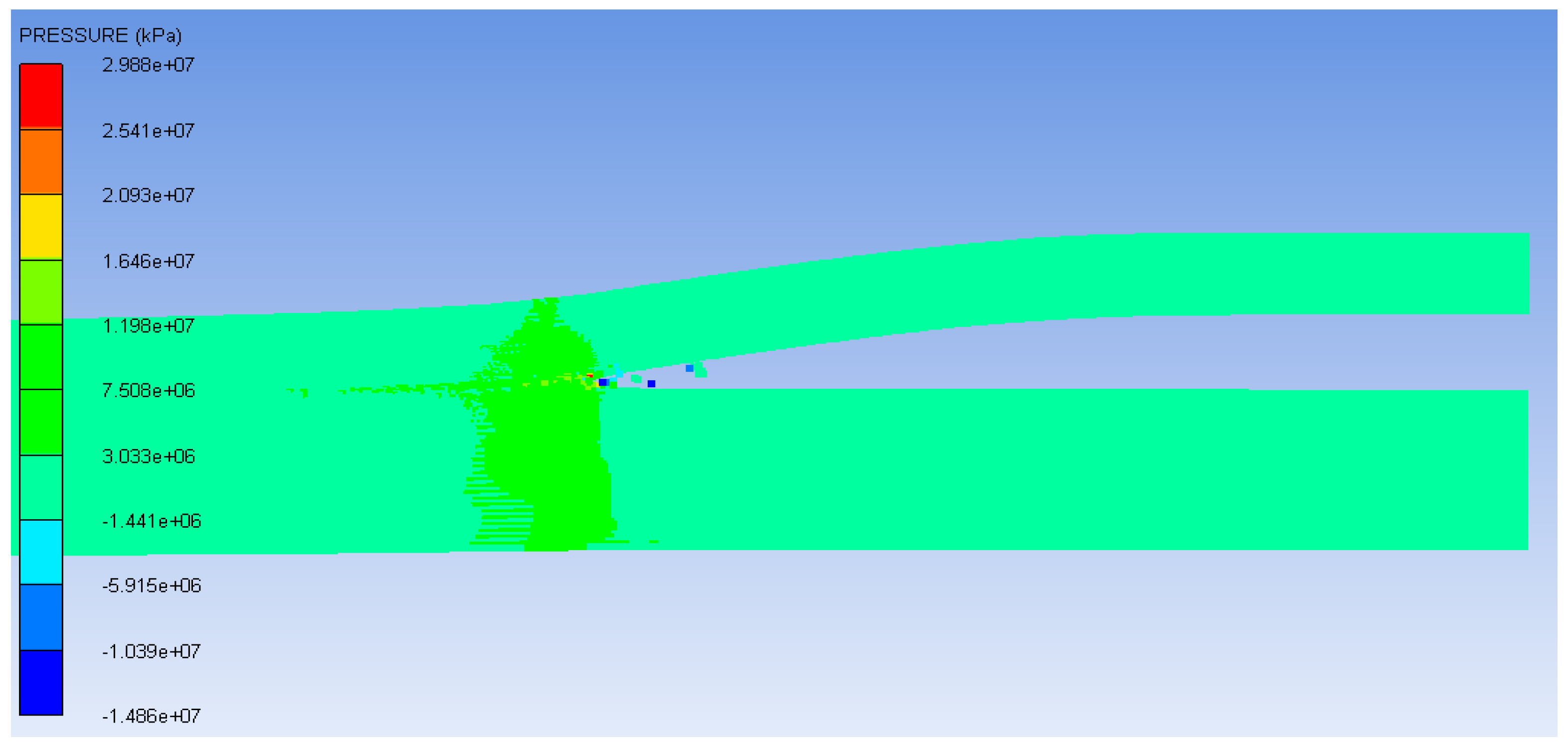
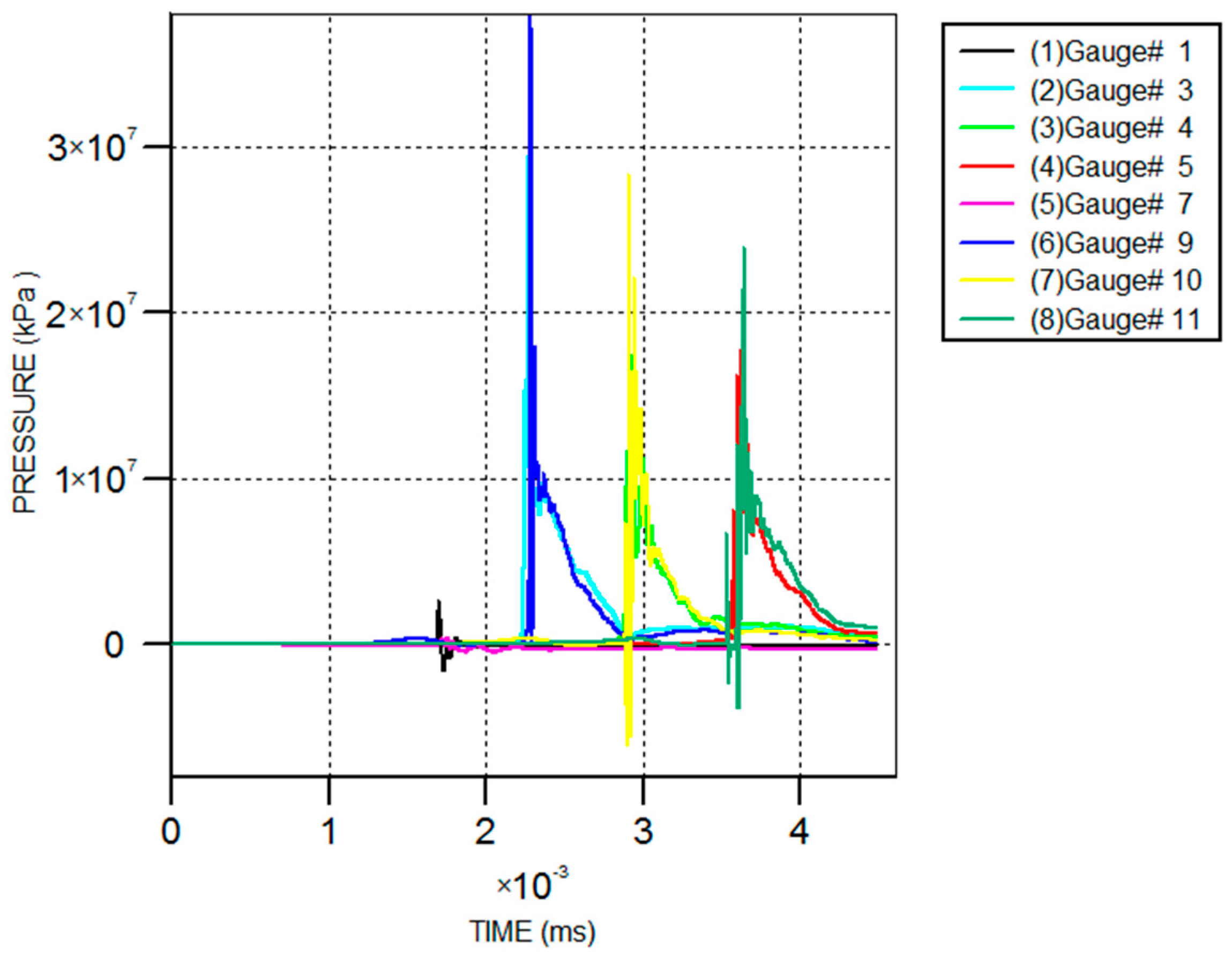
3.3. Pressure Distribution
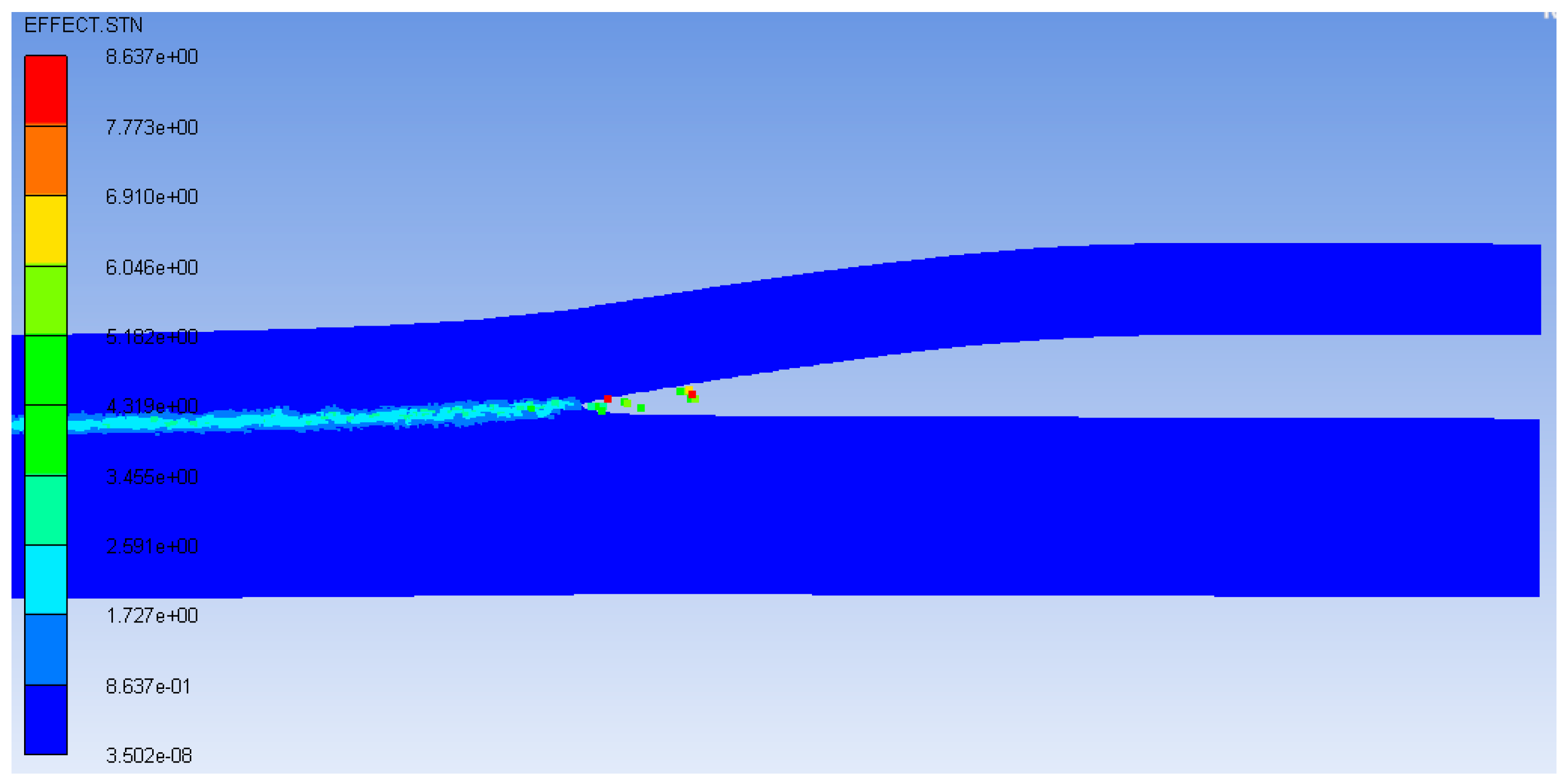
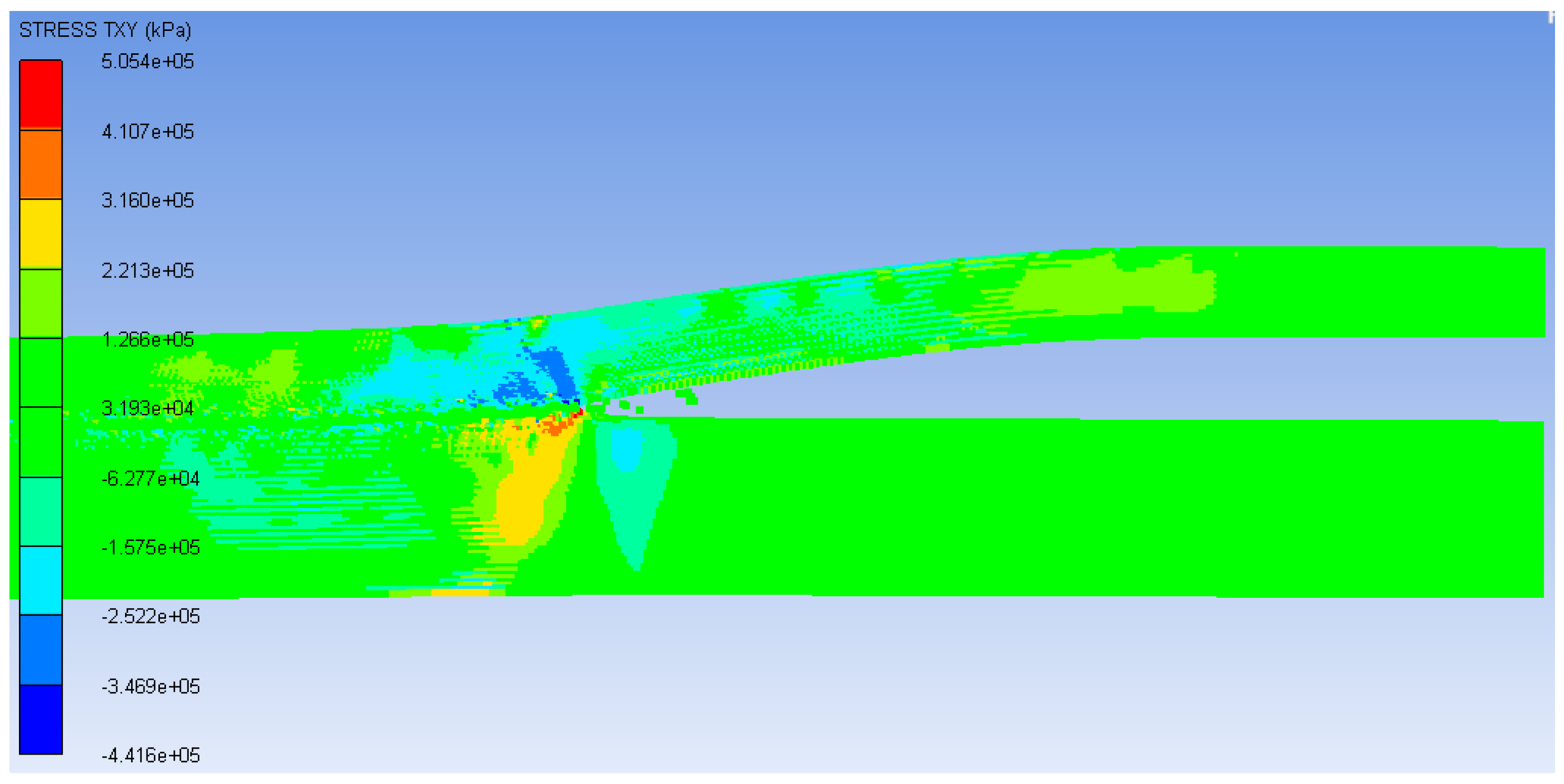
3.4. Plastic Strain and Shear Stress Distribution
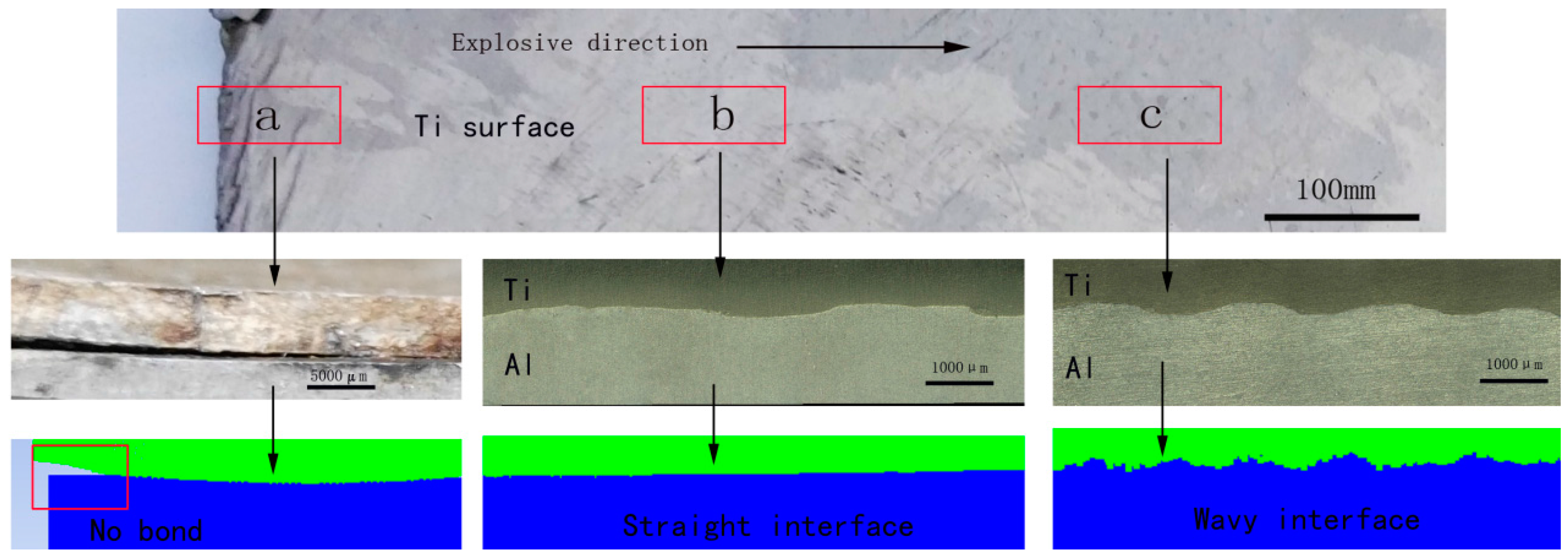
3.5. Interface Morphology of Composite Plate
4. Conclusions
- The typical physics of explosive welding process can be reproduced using the present model, such as the expansion of the explosives, flyer plate bending, oblique impact of metal plates, and jetting, which are not possible to capture in experiments. The jet phenomenon which originated mostly from the aluminum plate was observed in the collision region.
- After detonation, the flyer plate is accelerated gradually and collides with the base plate. The jet velocity is the highest and can reach 7402 m/s near the collision zone.
- The pressure at the detonation point is too small to achieve bonding between the two plates, which is the reason for the boundary effect of explosive welding. The pressure could reach an order of magnitude of 107 kPa when the detonation energy tends to be stable.
- There emerges an obvious narrow region of plastic strain near the collision zone. The shear stress between the two plates has opposite signs.
- The interface morphology changes from straight to wave along the propagation of the detonation wave in the simulation, which is consistent with the actual interface morphology of the Ti/Al bimetal composite acquired in the experiment.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Findik, F. Recent developments in explosive welding. Mater. Des. 2011, 32, 1081–1093. [Google Scholar] [CrossRef]
- Loureiro, A.; Mendes, R.; Ribeiro, J.B.; Leal, R.M.; Galvao, I. Effect of explosive mixture on quality of explosive welds of copper to aluminium. Mater. Des. 2016, 95, 256–267. [Google Scholar] [CrossRef]
- Fronczek, D.M.; Wojewoda-Budka, J.; Chulist, R.; Sypien, A.; Korneva, A.; Szulc, Z.; Schell, N.; Zieba, P. Structural properties of Ti/Al clads manufactured by explosive welding and annealing. Mater. Des. 2016, 91, 80–89. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z. Microstructural characteristics and mechanical properties of 2205/AZ31B laminates fabricated by explosive welding. Metals 2017, 7, 125. [Google Scholar] [CrossRef]
- Mousavi, A.; Al-Hassani, S.T.S. Numerical and experimental studies of the mechanism of the wavy interface formations in explosive/impact welding. J. Mech. Phys. Solids 2005, 53, 2501–2528. [Google Scholar]
- Nassiri, A.; Kinsey, B. Numerical studies on high-velocity impact welding: Smoothed particle hydrodynamics (SPH) and arbitrary Lagrangian-Eulerian (ALE). J. Manuf. Process. 2016, 24, 376–381. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Y.; Liu, H.; Shen, Z.; Hu, Y.; Gao, Y.; Guo, C. Numerical study of the mechanism of explosive/impact welding using smoothed particle hydrodynamics method. Mater. Des. 2012, 35, 210–219. [Google Scholar] [CrossRef]
- Nassiri, A.; Chini, G.; Vivek, A.; Daehn, G.; Kinsey, B. Arbitrary Lagrangian-Eulerian finite element simulation and experimental investigation of wavy interfacial morphology during high velocity impact welding. Mater. Des. 2015, 88, 345–358. [Google Scholar] [CrossRef]
- Aizawa, Y.; Nishiwaki, J.; Harada, Y.; Muraishi, S.; Kumai, S. Experimental and numerical analysis of the formation behavior of intermediate layers at explosive welded Al/Fe joint interfaces. J. Manuf. Process. 2016, 24, 100–106. [Google Scholar] [CrossRef]
- Abe, A. Numerical study of the mechanism of wavy interface generation in explosive welding. JSME Int. J. Ser. B Fluid. Therm. Eng. 1997, 40, 395–401. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, W.; Cao, X.; Zhang, T.; Xie, R.; Liu, R. Numerical study on the interfacial behavior of Mg/Al plate in explosive/impact welding. Sci. Eng. Compos. Mater. 2017, 24. [Google Scholar] [CrossRef]
- Grignon, F.; Benson, D.; Vecchio, K.S.; Meyers, M.A. Explosive welding of aluminum to aluminum: Analysis, computations and experiments. Int. J. Impact Eng. 2004, 30, 1333–1351. [Google Scholar] [CrossRef]
- Carrino, L.; Paradiso, V.; Franchitti, S.; Squillace, A.; Russo, S. Superplastic forming/diffusion bonding of a titanium alloy for the realization of an aircraft structural component in multi-sheets configuration. Key Eng. Mater. 2012, 504–506, 717–722. [Google Scholar] [CrossRef]
- Li, X.J.; Mo, F.; Wang, X.H.; Liu, X.W. Numerical study on mechanism of explosive welding. Sci. Technol. Weld. Join. 2012, 17, 36–41. [Google Scholar] [CrossRef]
- Fan, M.; Domblesky, J.; Jin, K.; Qin, L.; Cui, S.; Guo, X.; Kim, N.; Tao, J. Effect of original layer thicknesses on the interface bonding and mechanical properties of Ti/Al laminate composites. Mater. Des. 2016, 99, 535–542. [Google Scholar] [CrossRef]
- Xia, H.B.; Wang, S.G.; Ben, H.F. Microstructure and mechanical properties of Ti/Al explosive cladding. Mater. Des. 2014, 56, 1014–1019. [Google Scholar] [CrossRef]
- Bataev, I.A.; Bataev, A.A.; Mali, V.I.; Pavliukova, D.V. Structural and mechanical properties of metallic-intermetallic laminate composites produced by explosive welding and annealing. Mater. Des. 2012, 35, 225–234. [Google Scholar] [CrossRef]
- Lee, E.; Finger, M.; Collins, W. JWL Equation of State Coefficients for High Explosives; Lawrance Livermore National Laboratory: Livermore, CA, USA, 1973. [Google Scholar]
- Liu, R.; Wang, W.; Zhang, T.; Yuan, X. Numerical study of Ti/Al/Mg three-layer plates on the interface behavior in explosive welding. Sci. Eng. Compos. Mater. 2016, 24. [Google Scholar] [CrossRef]
- AUTODYN, version 6.1; Century Dynamics Incorporated: Concord, CA, USA, 2007.
- Corbett, B.M. Numerical simulations of target hole diameters for hypervelocity impacts into elevated and room temperature bumpers. Int. J. Impact Eng. 2006, 33, 431–440. [Google Scholar] [CrossRef]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef]
- Zhou, C.E.; Liu, G.R.; Lou, K.Y. Three-dimensional penetration simulation using smoothed particle hydrodynamics. Int. J. Comput. Method 2007, 4, 671–691. [Google Scholar] [CrossRef]
- Liu, M.B.; Zhang, Z.L.; Feng, D.L. A density-adaptive SPH method with kernel gradient correction for modeling explosive welding. Comput. Mech. 2017, 1–17. [Google Scholar] [CrossRef]
- Nassiri, A. Investigation of Wavy Interfacial Morphology in Magnetic Pulsed Welding: Mathematical Modeling, Numerical Simulations and Experimental Tests. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, July 2015. [Google Scholar]
- Mousavi, A.; Burley, S.J.; Al-Hassani, S.T.S. Simulation of explosive welding using the Williamsburg equation of state to model low detonation velocity explosives. Int. J. Impact Eng. 2005, 31, 719–734. [Google Scholar] [CrossRef]
- Hayhurst, C.J.; Clegg, R.A. Cylindrically symmetric SPH simulations of hypervelocity impacts on thin plates. Int. J. Impact Eng. 1997, 20, 337–348. [Google Scholar] [CrossRef]
- Yan, Y.B.; Zhang, Z.W.; Shen, W.; Wang, J.H.; Zhang, L.K.; Chin, B.A. Microstructure and properties of magnesium AZ31B–aluminum 7075 explosively welded composite plate. Mater. Sci. Eng. A 2010, 527, 2241–2245. [Google Scholar] [CrossRef]
- Kahraman, N.; Gulenc, B.; Findik, F. Corrosion and mechanical-microstructural aspects of dissimilar joints of Ti-6Al-4V and Al plates. Int. J. Impact Eng. 2007, 34, 1423–1432. [Google Scholar] [CrossRef]
- Sui, G.F.; Li, J.S.; Sun, F.; Ma, B.; Li, H. 3D finite element simulation of explosive welding of three-layer plates. Sci. China Phys. Mech. Astron. 2011, 54, 890–896. [Google Scholar] [CrossRef]
- Akbari-Mousavi, S.A.A.; Barrett, L.M.; Al-Hassani, S.T.S. Explosive welding of metal plates. J. Mater. Process. Technol. 2008, 202, 224–239. [Google Scholar] [CrossRef]
- Mastanaiah, P.; Reddy, G.M.; Prasad, K.S.; Murthy, C.V.S. An investigation on microstructures and mechanical properties of explosive cladded C103 niobium alloy over C263 niobium alloy. J. Mater. Process. Technol. 2014, 214, 2316–2324. [Google Scholar] [CrossRef]
- Zheng, Y. Explosive Welding and Metallic Composite and Their Engineering Application; Central South University Press: Changsha, China, 2002. [Google Scholar]

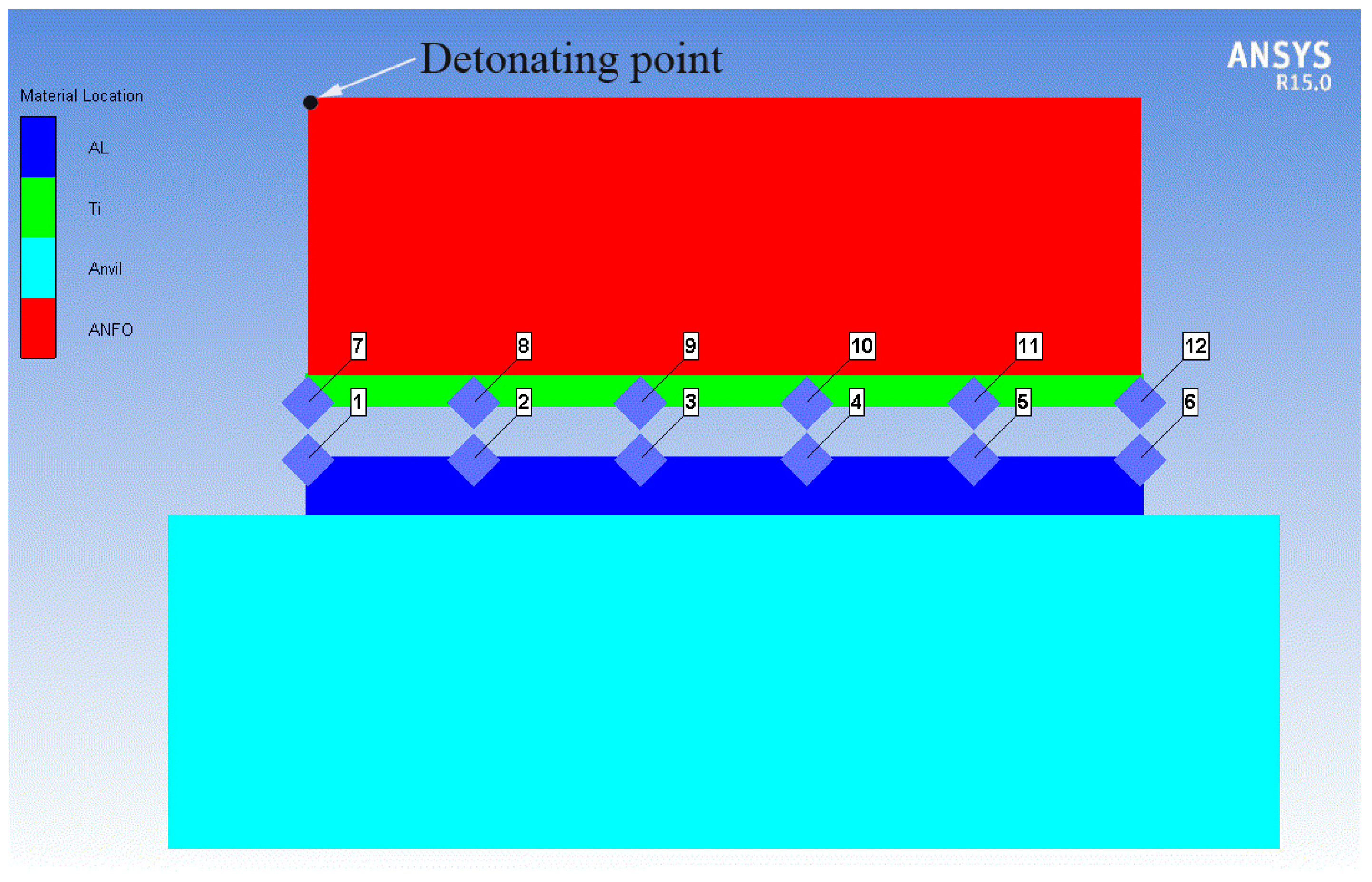
| Material | Geometry (Length × Height) (mm) |
|---|---|
| Explosive—ANFO | 20 × 5 |
| Flyer plate—TA1 | 20 × 2 |
| Base plate—Al 1060 | 20 × 3 |
| Anvil—Steel 1006 | 20 × 8 |
| V/(m·s−1) | ρ/(kg·m−3) | E0/GJ | A/GJ | B/GJ | R1 | R2 | ω |
|---|---|---|---|---|---|---|---|
| 2500 | 790 | 2.48 | 491 | 0.89 | 3.9 | 1.18 | 0.33 |
| Materials | ρ/(kg·m−3) | C | m | n | Tmelt/°C | Rτ/GPa | Y0/GPa |
|---|---|---|---|---|---|---|---|
| TA1 | 4520 | 0.03 | 0.8 | 0.32 | 1660 | 55 | 0.16 |
| Al 1060 | 2770 | 0.01 | 1 | 0.41 | 660 | 27 | 0.04 |
| Steel 1006 | 7896 | 0.22 | 1 | 0.36 | 1811 | 81.8 | 0.35 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, C.; Yu, H.; Zhao, F.; Wu, Z. Numerical Simulation of Ti/Al Bimetal Composite Fabricated by Explosive Welding. Metals 2017, 7, 407. https://doi.org/10.3390/met7100407
Li Y, Liu C, Yu H, Zhao F, Wu Z. Numerical Simulation of Ti/Al Bimetal Composite Fabricated by Explosive Welding. Metals. 2017; 7(10):407. https://doi.org/10.3390/met7100407
Chicago/Turabian StyleLi, Yan, Cuirong Liu, Haibo Yu, Fei Zhao, and Zhisheng Wu. 2017. "Numerical Simulation of Ti/Al Bimetal Composite Fabricated by Explosive Welding" Metals 7, no. 10: 407. https://doi.org/10.3390/met7100407




