Thermodynamic Database for Mg Alloys—Progress in Multicomponent Modeling
Abstract
:1. Introduction

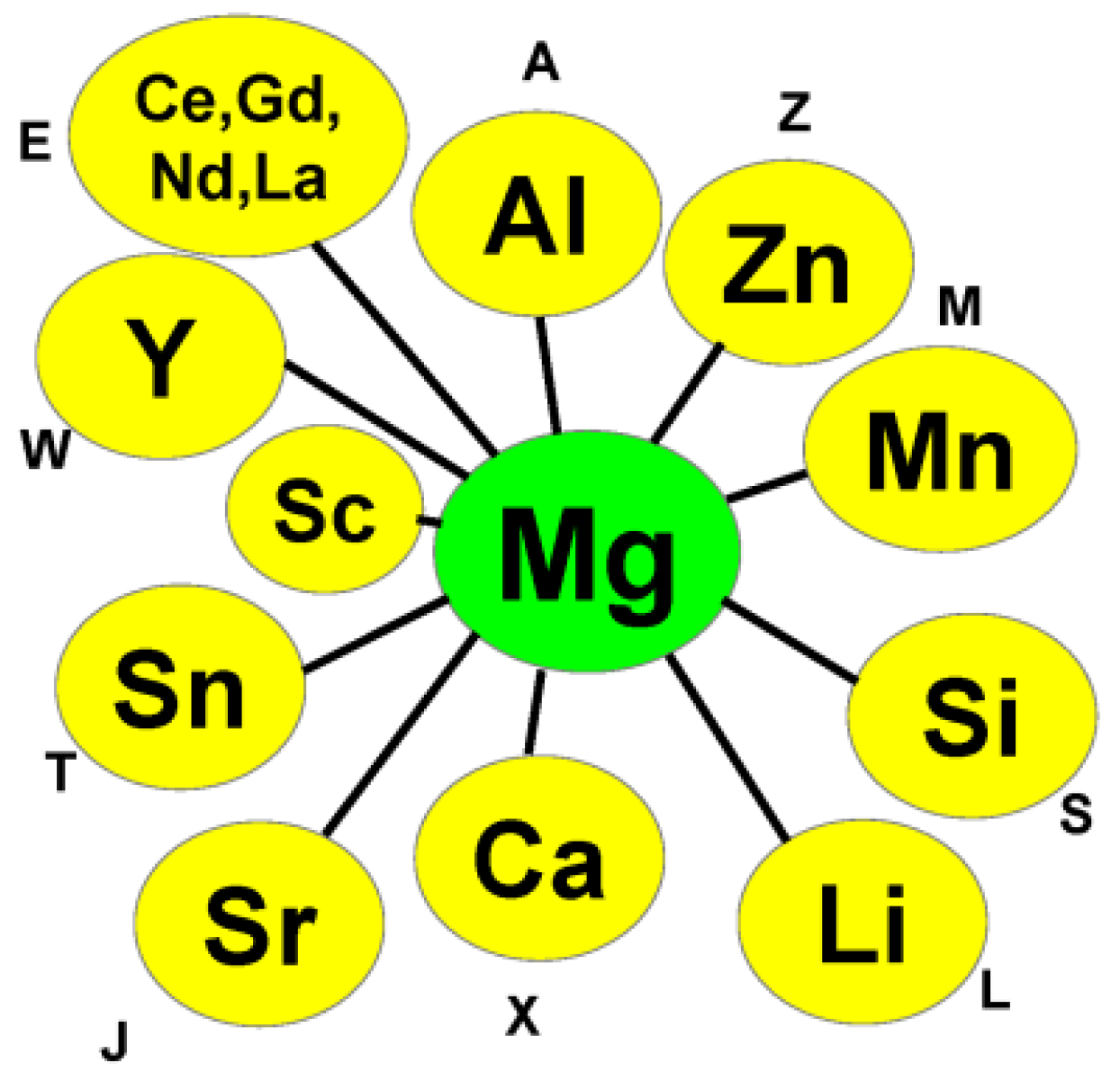
2. Investigated Binary Alloy Systems
| Al | Ca | Ce | Cu | Fe | Gd | La | Li | Mg | Mn | Nd | Ni | Sc | Si | Sn | Sr | Y | Zn | Zr | |
| Ag | |||||||||||||||||||
| Al | |||||||||||||||||||
| Ca | |||||||||||||||||||
| Ce | |||||||||||||||||||
| Cu | |||||||||||||||||||
| Fe | |||||||||||||||||||
| Gd | |||||||||||||||||||
| La | |||||||||||||||||||
| Li | |||||||||||||||||||
| Mg | |||||||||||||||||||
| Mn | |||||||||||||||||||
| Nd | |||||||||||||||||||
| Ni | |||||||||||||||||||
| Sc | |||||||||||||||||||
| Si | Modeling status | ||||||||||||||||||
| Sn | A | Complete binary modeling, Reliable description | |||||||||||||||||
| Sr | B | Complete binary modeling, Less reliable description | |||||||||||||||||
| Y | C | No binary modeling, extrapolation of terminal solution phases only | |||||||||||||||||
| Zn | |||||||||||||||||||
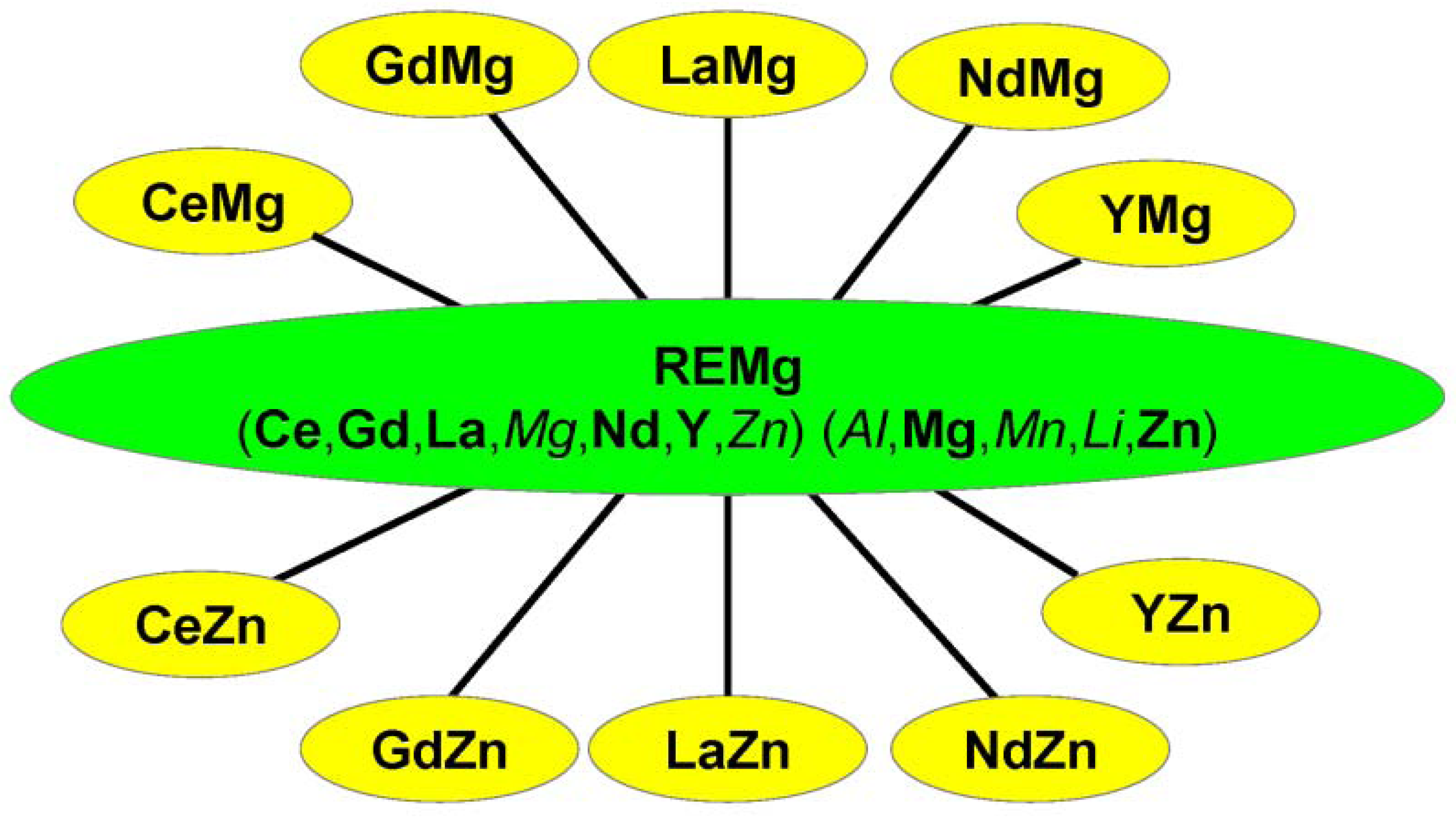
3. Investigated Ternary and Multicomponent Alloy Systems
| System | Modeling status | Ternary intermetallic solid solution phases | Ternary stoichiometric phases | Year of study | Ref. |
|---|---|---|---|---|---|
| Mg-Ag-Al | B | Ag(Al,Mg)3, Ag(Al,Mg)4 | Al4GdMg | 1997 | [16] |
| Mg-Ag-Cu | B | none | - | 1997 | [16] |
| Mg-Al-Ca | A | C14-Ca(Mg,Al)2 C15-Ca(Al,Mg)2 *C36-Ca(Al,Mg)2 Ca8(Al,Mg)3 | - | 2009 | [17,18] |
| Mg-Al-Ce | A | Ce(Mg,Al); Ce(Mg,Al)12; Ce(Mg,Al)2 | Al13CeMg6 | 2002 | [19] |
| Mg-Al-Cu | A | *C14-Cu(Mg,Al)2; C15-Cu(Al,Mg)2; *C36-Cu(Al,Mg)2 | Al7Cu3Mg6 Al3CuMg V-Al5Cu6Mg2 | 1998 | [20] |
| Mg-Al-Gd | A | - | Al4GdMg | 2001 | [21] |
| Mg-Al-Li | A | γMg17(Al,Li)12; Li(Al,Mg) | Al53Li33Mg14 | 2001 | [22] |
| Mg-Al-Mn | A | - | Al18Mg3Mn2 | 2007 | [23,24] |
| Mg-Al-Sc | A | Sc(Al,Mg); Sc(Al,Mg)2; Sc(Al,Mg)3 | - | 1999 | [25] |
| Mg-Al-Si | A | *C36-(Al,Mg,Si)(Al,Mg,Si)2 | - | 2001 | [22] |
| Mg-Al-Sr | A | Sr(Mg,Al)2; Sr6(Mg,Al)23; Sr9(Mg,Al)38; Sr2(Mg,Al)17; Sr(Al,Mg)2; Sr(Al,Mg)4 | Al38Mg58Sr4 | 2007 | [26] |
| Mg-Al-Sn | A | none | - | 2007 | [27] |
| Mg-Al-Zn | A | βMg2(Al,Zn)3; γMg17(Al,Zn)12; (Mg,Al)Zn; (Mg,Al)2Zn3; C14-(Mg,Al) Zn2; (Mg,Al)2Zn11; *θ-AlMgZn; *τ-AlMgZn | - | 2006 | [28] |
| Mg-Ca-Ce | A | Ce5(Mg,Ca)41 | - | 2007 | [29] |
| Mg-Ca-Li | A | C14-Ca(Mg,Li)2 | - | 2002 | [30] |
| Mg-Ca-Si | A | *Ca(Ca,Mg)Si | Ca7Mg6Si14 | 2003 | [31] |
| Mg-Ca-Sn | A | (Ca,Mg)CaSn | - | 2011 | [32] |
| Mg-Ca-Sr | A | C14-(Ca,Sr)Mg2 | - | 2009 | [33] |
| Mg-Ca-Zn | A | C14-Ca(Mg,Zn)2 | Ca2Mg6Zn3 | 2004 | [34] |
| Mg-Ce-La | A | (Ce,La)Mg; (Ce,La)Mg3;(Ce,La)5Mg41; (Ce,La)Mg12; (Ce,La)2Mg17 | - | 2012 | [35] |
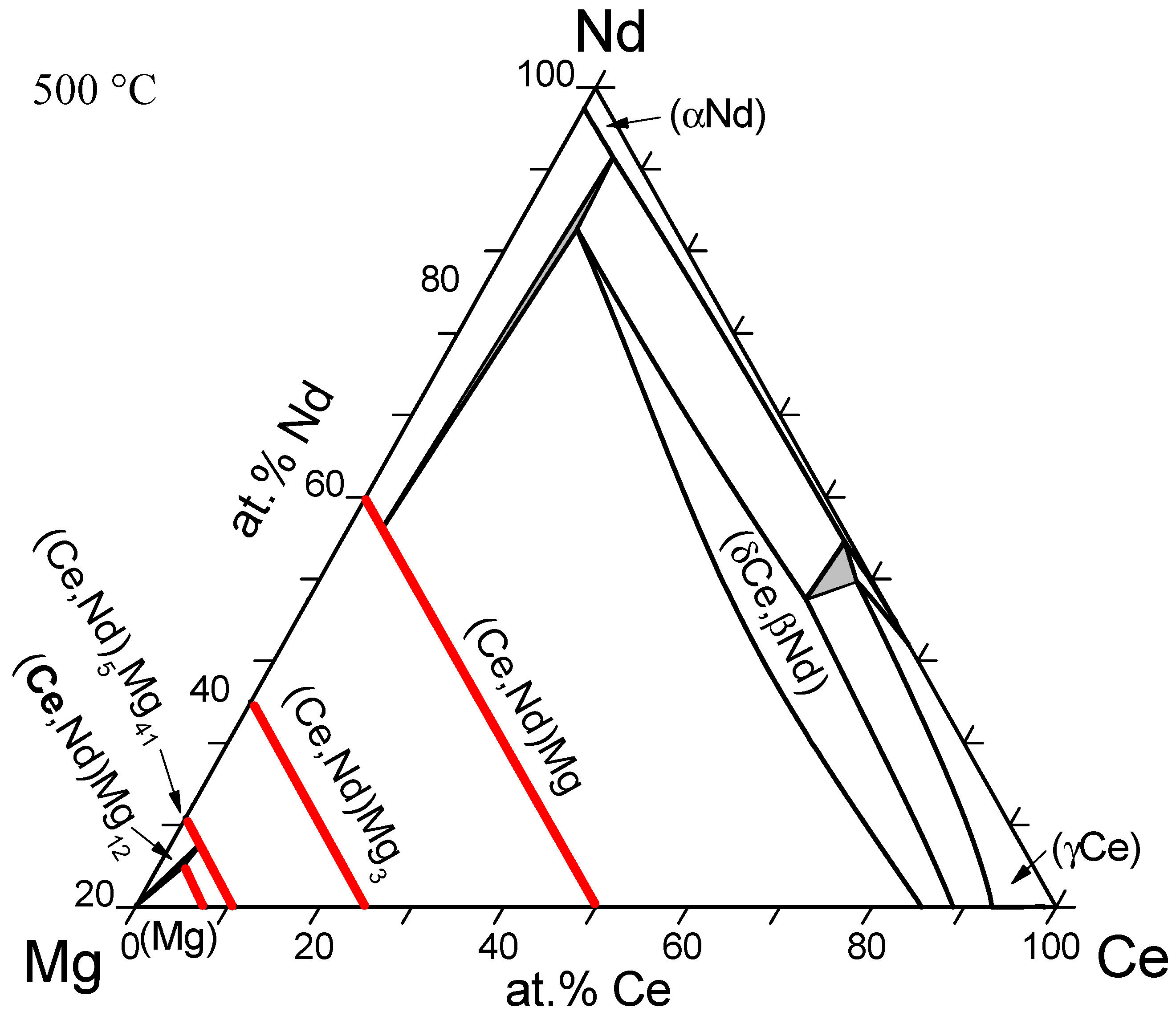
| Mg-Ce-Nd | A | (Ce,Nd)Mg; (Ce,Nd)Mg3; (Ce,Nd)5Mg41; (Ce,Nd)Mg12 | - | 2011 | [36] |
| Mg-Ce-Sn | A | MgCeSn | 2012 | [37] | |
| Mg-Ce-Y | B | (Ce,Y)Mg; (Ce,Y)Mg2; (Ce,Y)Mg3; (Ce,Y)5Mg41; (Ce,Y)Mg12; (Y,Ce)Mg2; (Y,Ce)5Mg24;*(Ce,Y)Mg5 | - | 2010 | [38] |
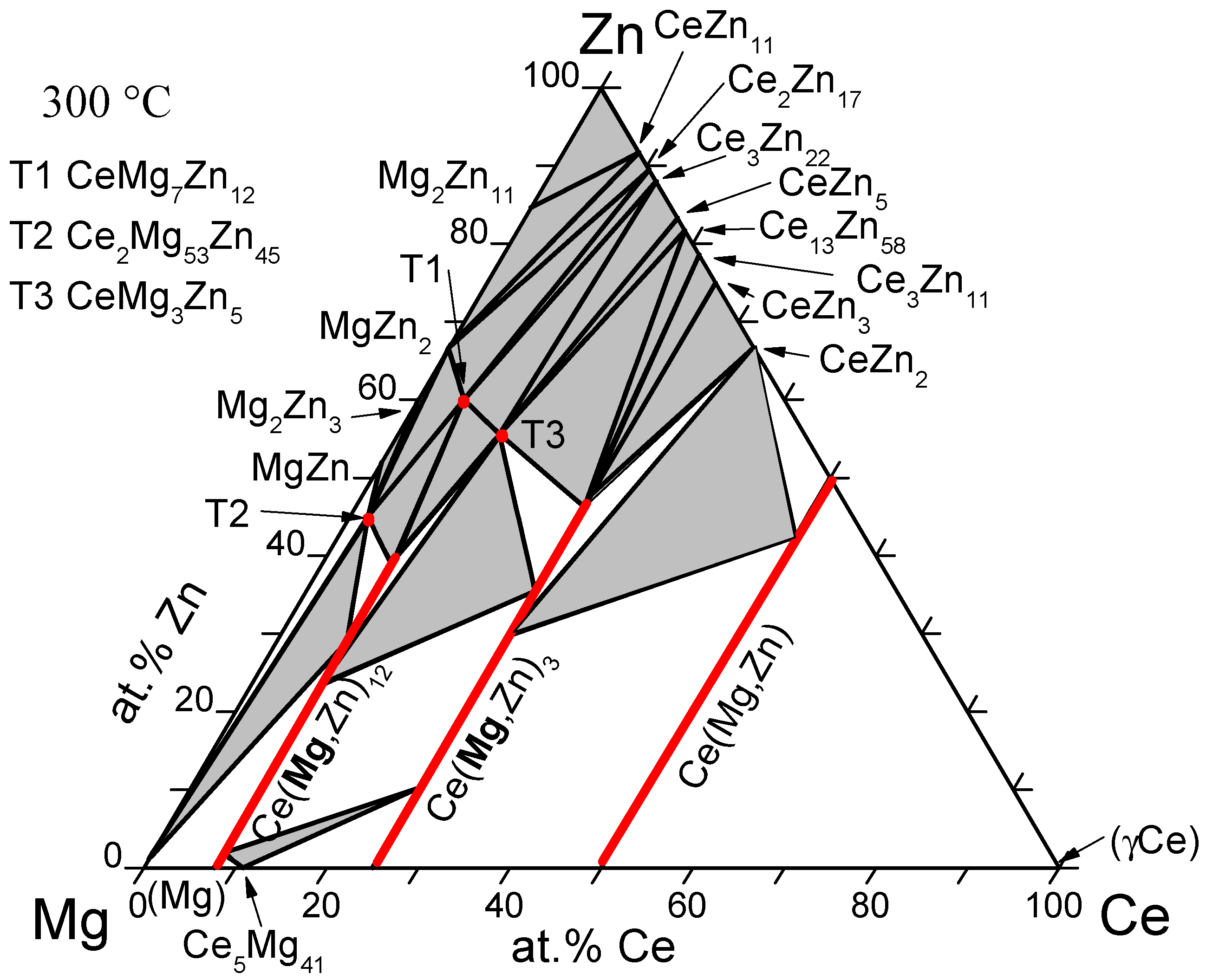
| Mg-Ce-Zn | A | (Ce,Zn)Mg; (Ce,Zn)Mg3; (Ce,Zn)Mg12 | CeMg7Zn12; Ce2Mg53Zn45CeMg3Zn5 | 2010 | [39] |
| Mg-Cu-Li | A | Cu(Mg,Li)2; Cu2(Mg,Li) | Cu8Li2Mg15 | 2000 | [40] |
| Mg-Cu-Si | A | C15- Cu(Mg,Si)2 | Cu16Mg6Si7_sigma Cu3Mg2Si_tau | 1998 | [41] |
| Mg-Cu-Y | A | none | - | 1997 | [41] |
| Mg-Cu-Zn | A | C14- Mg(Cu,Zn)2; C15- Mg(Cu,Zn)2; *C36- Mg(Cu,Zn)2 Mg(Cu,Zn) | - | 1998 | [42] |
| Mg-Gd-Li | A | (Gd,Li)Mg; (Gd,Li)Mg2; (Gd,Li)Mg3; (Gd,Li)Mg5 | - | 2001 | [43] |
| Mg-Gd-Y | B | (Gd,Y)Mg; (Gd,Y)Mg2 (Gd,Y)Mg3; (Gd,Y)Mg5 (Y,Gd)Mg2; (Y,Gd)5Mg24 | - | 2010 | [38] |
| Mg-Gd-Zn | A | (Gd,Zn)Mg; (Gd,Zn)Mg2 (Gd,Zn)Mg3; (Gd,Zn)Mg5 | 14H-GdMg12Zn I-Gd6Mg38Zn56 | 2012 | [44] |
| Mg-Fe-Si | B | Fe(Mg,Si) | - | 2007 | [45] |
| Mg-La-Nd | A | (La,Nd)Mg; (La,Nd)Mg3 (La,Nd)5Mg41; (La,Nd)Mg12 (La,Nd)2Mg17 | - | 2012 | [35] |
| Mg-La-Si | A | (La,Mg)5Si4; (La,Mg)3Si2 *(La,Mg)0.6Si0.4 | La2Mg4Si4 La25Mg25Si50 La2Mg77Si La32Mg66Si | 2010 | [46] |
| Mg-La-Zn | B | La(Mg,Zn) ; La(Mg,Zn)3 La2(Mg,Zn)17 | I-LaMgZn | 2010 | [47] |
| Mg-Li-Si | A | (Mg,Li)2Si | Li12Mg3Si4 Li2MgSi Li8MgSi6 | 2004 | [48] |
| Mg-Mn-Sc | B | none | - | 1999 | [49] |
| Mg-Mn-Zn | B | none | - | 2006 | [50] |
| Mg-Nd-Y | B | (Y,Nd)Mg; (Y,Nd)Mg3 (Y,Nd)5Mg41; (Y,Nd)Mg2 (Y,Nd)5Mg24; *(Y,Nd)Mg5 | - | 2008 | [51] |
| Mg-Nd-Zn | B | Nd(Mg,Zn) ;Nd(Mg,Zn)3 *Nd8 (Mg,Zn)92 | Mg35Nd5Zn60 Mg30Nd15Zn55 | 2011 | [52] |
| Mg-Si-Sn | A | Mg2(Sn,Si) | - | 2011 | [32] |
| Mg-Y-Zn | A | Y(Mg,Zn) ;Y(Mg,Zn)5 *I-YMg3(Mg,Zn)6*Z-Y7Mg28(Mg,Zn)65*W-Y25Mg25(Mg,Zn)50 | 14H-YMg12Zn 18R-YMg10Zn | 2012 | [53] |
| System | Modeling status | Ternary intermetallic solid solution phases | Ternary stoichiometric phases | Year of study | Ref. |
|---|---|---|---|---|---|
| Ag-Al-Cu | B | none | 2004 | [54] | |
| Al-C-Si | B | (Al,Si)4C3 | Al4SiC4 Al8SiC7 | [55] | |
| Al-Ca-Fe | B | none | - | 1994 | [56] |
| Al-Ca-Sr | A | C15-(Ca,Sr)Mg2 Al4(Ca,Sr) Al4(Ca,Sr)Al2(Ca,Sr) Al7(Ca,Sr)8 | - | 2009 | [33] |
| Al-Ce-Nd | B | (Ce,Nd)3Al11 (Ce,Nd)Al3 (Ce,Nd)Al (Ce,Nd)Al2 (Ce,Nd)3Al (Ce,Nd)3Al | - | 2003 | [57] |
| Al-Ce-Si | A | Ce(Al,Si)2 | AlCeSi2 Al1.6CeSi0.4 | 2004 | [58] |
| Al-Cu-Gd | B | Gd(Al,Cu)2 Gd(Al,Cu)5 Gd(Al,Cu)2 | AlCu17Gd2 AlCuGd Al2.1Cu0.9Gd Al3.2Cu7.8Gd Al4.4Cu6.6Gd Al8.9Cu2.1Gd3 Al8Cu4Gd | 2009 | [59] |
| Al-Cu-Li | B | - | Al2CuLi Al55Cu11Li33 Al57Cu11Li32 Al60Cu32Li8 | 1994 | [41] |
| Al-Cu-Mn | B | none | - | 2003 | [60] |
| Al-Cu-Si | B | none | - | 1997 | [41] |
| Al-Cu-Sn | A | none | - | 2008 | [61] |
| Al-Cu-Zn | B | (Al,Cu)5Cu4Zn | - | - | [41] |
| Al-Fe-Mn | B | none | - | 1997 | [41] |
| Al-Fe-Si | B | - | Al35Fe37Si28 Al40Fe25Si35 Al49Fe16Si35 Al54Fe26Si20 Al60Fe15Si25 Al64Fe20Si16 Al66Fe19Si15 | 1999 | [62] |
| Al-Li-Si | A | - | LiAlSi Li5.3Al0.7Si2 Li8Al3Si5 | 2001 | [63] [64] |
| Al-Mn-Si | B | *Al18Mn4(Al,Si) *Al19Mn6(Al,Si) | Al2MnSi3 | 1998 | [41] |
| Al-Si-Zn | B | none | - | 1998 | [41] |
| Al-Sn-Zn | B | none | - | 1991 | [41] |
| Ca-Fe-Si | B | none | - | 1994 | [56] |
| Ca-Li-Si | B | - | Ca2Li5Si3 Ca2LiSi Ca2LiSi3 CaLi2Si CaLiSi2 | 2003 | Unpublished |
| Ca-Sr-Zn | B | (Ca,Sr)Zn2 (Ca,Sr)Zn5 (Ca,Sr)Zn13 | - | 2003 | [65] |
| Cu-Fe-Si | B | none | - | 2002 | [66] |
| Cu-La-Ni | B | La(Cu,Ni) La(Cu,Ni)2 La(Cu,Ni)5 La(Cu,Ni) | - | 2012 | [67] |
| Cu-Sn-Zn | B | none | - | 1998 | [68] |
| Fe-Mn-Si | B | (Fe,Mn)Si (Fe,Mn)5Si3 (Fe,Mn)3Si | - | 1993 | [69] |
| Mn-Y-Zr | B | none | - | 1997 | [70] |
- (i) Those extending from binary intermetallic phases with limited, though significant, solubility of the third component of the majority component are marked in a bold font. For example, the phase denoted as Ag(Al,Mg)3 extends from the binary AgMg3 into the ternary Mg-Ag-Al systems but not throughout since there is no stable AgAl3 phase.
- (ii) Complete solid solubility exists, such as in the Mg-Ca-Li system between the C14-type phases CaMg2 and CaLi2. Thus, none of the two mutually substituting components Mg and Li is denoted as majority species in the C14-Ca(Mg,Li)2 phase.
- (iii) Truly ternary phases, marked by an asterisk (*), are stable over a significant solid solution range in the ternary system only, which does not extend to a binary edge system. All the phases compiled in the column “Ternary stoichiometric phases” are, of course, also truly ternary phases.
| System | Modeling status | Higher intermetallic solid solution phases | Higher stoichiometric phases | Year of study | Ref. |
|---|---|---|---|---|---|
| Mg-Al-Ca-Sr | A | C14-(Ca,Sr)(Mg,Al)2 | - | 2009 | [71] |
| Mg-Al-Ca-Mn-Sr | A | C14-(Ca,Sr)(Mg,Al)2 | - | 2009 | [71] |
| Mg-Al-Cu-Si | B | none | Al5Cu2Mg8Si6 | 2012 | [72] |
| Mg-Al-Li-Si | A | none | - | 2001 | [22] |
| Mg-Al-Mn-Zn | A | none | - | 2006 | [73] |
| Mg-Ca-Ce-Sn | A | (Ca,Mg)(Ca,Ce)Sn | - | 2012 | [37] |
| Mg-Ca-Si-Sn | A | (Ca,Mg)Ca(Sn,Si) | - | 2011 | [32] |
| Mg-Ce-Gd-Y | B | none | - | 2010 | [38] |
| Mg-Ce-Mn-Sc | B | none | - | 2001 | [74] |
| Mg-Gd-Mn-Sc | B | none | - | 2001 | [74] |
| Mg-Mn-Sc-Y | B | none | - | 2001 | [74] |
4. Crystal Structure Guided Modeling of Multicomponent Intermetallic Solution Phases



- • (Ce,La)Si2 (tI12-ThSi2 structure type)
- • (Ce,La)Si (oP8-FeB structure type)
- • (Ce,La)5Si4 (Zr5Si4 structure type)
- • (Ce,La)3Si2 (tP10-U3Si2 structure type)
- • (Ce,La)5Si3-HT (tI32-Cr5B3 structure type)



5. Conclusions
Conflict of Interest
References
- Luo, A.A.; Fu, P.; Peng, L.; Kang, X.; Li, Z.; Zhu, T. Solidification microstructure and mechanical properties of cast magnesium-aluminum-tin alloys. Met. Mater. Trans. 2012, 43A, 360–368. [Google Scholar]
- Luo, A.A.; Powell, B.R.; Sachdev, A.K. Computational phase equilibria and experimental investigation of magnesium-aluminum-calcium alloys. Intermetallics 2012, 24, 22–29. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, A.A.; Chang, A. The solidification microstructure and precipitation investigation of magnesium-rich alloys containing Zn and Ce. In Magnesium Technology 2011; Sillekens, W.H., Agnew, S.R., Neelameggham, N.R., Mathaudhu, S.N., Eds.; The Minerals, Metals Materials Society: Warrendale, PA, USA, 2011; pp. 267–270. [Google Scholar]
- Hänzi, A.C.; Dalla Torre, F.H.; Zhao, L.; Gunde, P.; Schmid-Fetzer, R.; Kuehlein, M.; Löffler, J.F.; Uggowitzer, P.J. Design strategy for microalloyed ultra-ductile magnesium alloys. Phil. Mag. Lett. 2009, 89, 377–390. [Google Scholar] [CrossRef]
- Kaufman, L.; Bernstein, H. Computer Calculations of Phase Diagrams; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Lukas, H.L.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Pisch, A.; Schmid-Fetzer, R. Development of a thermodynamic Mg-alloy database by experiments and modeling. In Magnesium Alloys and Their Applications; Mordike, B.L., Kainer, K.U., Eds.; Wiley-VCH Verlag GmbH: Frankfurt, Germany, 1998; pp. 139–144. [Google Scholar]
- Schmid-Fetzer, R.; Gröbner, J. Focused development of magnesium alloys using the calphad approach. Adv. Eng. Mater. 2001, 3, 947–961. [Google Scholar] [CrossRef]
- Schmid-Fetzer, R.; Janz, A.; Gröbner, J.; Ohno, M. Aspects of quality assurance in a thermodynamic Mg alloy database. Adv. Eng. Mater. 2005, 7, 1142–1149. [Google Scholar] [CrossRef]
- Gröbner, J.; Janz, A.; Kozlov, A.; Mirkovic, D.; Schmid-Fetzer, R. Phase diagrams of advanced magnesium alloys containing Al, Ca, Sn, Sr and Mn. JOM 2008, 12, 32–38. [Google Scholar]
- Gröbner, J.; Schmid-Fetzer, R. Key issues in thermodynamic Mg alloy database. Metall. Mater. 2012. submitted for publication. [Google Scholar]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Bale, C.W.; Bélisle, E.; Chartrand, P.; Decterov, S.A.; Eriksson, G.; Hack, K.; Jung, I.-H.; Kang, Y.-B.; Melançon, J.; Pelton, A.D.; et al. FactSage thermochemical software and databases-Recent developments. Calphad 2009, 33, 295–311. [Google Scholar] [CrossRef]
- Cao, W.; Chen, S.; Zhang, F.; Wu, K.; Yang, Y.; Chang, Y.; Schmid-Fetzer, R.; Oates, W.A. PANDAT software with PanEngine, PanOptimizer and PanPrecipitation for multi-component phase diagram calculation and materials property simulation. Calphad 2009, 33, 328–342. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Lim, M.S.; Tibballs, J.E.; Rossiter, P.L. An assessment of thermodynamic equilibria in the Ag-Al-Cu-Mg quaternary system in relation to precipitation reactions. Z. Metallkd. 1997, 88, 236–245. [Google Scholar]
- Gröbner, J.; Kevorkov, D.; Chumak, I.; Schmid-Fetzer, R. Experimental investigation and thermodynamic calculation of ternary Al-Ca-Mg phase equilibria. Z. Metallkde. 2003, 94, 976–982. [Google Scholar]
- Janz, A.; Gröbner, J.; Cao, H.; Zhu, J.; Chang, Y.A.; Schmid-Fetzer, R. Thermodynamic modeling of the Mg-Al-Ca system. Acta Mater. 2009, 57, 682–694. [Google Scholar] [CrossRef]
- Gröbner, J.; Kevorkov, D.; Schmid-Fetzer, R. Thermodynamic modeling of Al-Ce-Mg equilibria coupled with key experiments. Intermetallics 2002, 10, 415–422. [Google Scholar] [CrossRef]
- Buhler, T.; Fries, S.G.; Spencer, P.J.; Lukas, H.L. A thermodynamic assessment of the Al-Cu-Mg ternary system. J. Phase Equilbria 1998, 19, 317–329. [Google Scholar] [CrossRef]
- Gröbner, J.; Kevorkov, D.; Schmid-Fetzer, R. Thermodynamic calculation of Al-Gd and Al-Gd-Mg phase equilibria checked by key experiments. Z. Metallkde. 2001, 92, 22–27. [Google Scholar]
- Kevorkov, D. Thermodynamics and Phase Equilibria of the Mg-Al-Li-Si System. Ph.D dissertaion, Technische Universität Clausthal, Clausthal-Zellerfeld, Germany, 2001. [Google Scholar]
- Du, Y.; Wang, J.; Zhao, J.; Schuster, J.C.; Weitzer, F.; Schmid-Fetzer, R.; Ohno, M.; Xu, H.; Liu, Z.K.; Shang, S.; et al. Reassessment of the Al-Mn system and a thermodynamic description of the Al-Mg-Mn system. Int. J. Mater. Res. 2007, 98, 855–871. [Google Scholar]
- Ohno, M.; Schmid-Fetzer, R. Thermodynamic assessment of Mg-Al-Mn phase equilibria, focusing on Mg-rich alloys. Z. Metallkde. 2005, 96, 857–869. [Google Scholar]
- Gröbner, J.; Schmid-Fetzer, R.; Pisch, A.; Cacciamani, G.; Riani, P.; Parodi, N.; Borzone, G.; Saccone, A.; Ferro, R. Experimental investigations and thermodynamic calculation in the Al-Mg-Sc system. Z. Metallkde. 1999, 90, 872–880. [Google Scholar]
- Janz, A.; Gröbner, J.; Mirkovic, D.; Medraj, M.; Zhu, J.; Chang, Y.A.; Schmid-Fetzer, R. Experimental study and thermodynamic calculation of Al-Mg-Sr phase equilibria. Intermetallics 2007, 15, 506–519. [Google Scholar] [CrossRef]
- Doernberg, E.; Kozlov, A.; Schmid-Fetzer, R. Experimental investigation and thermodynamic calculation of Mg-Al-Sn phase equilibria and solidification microstructures. J. Phase Equilbria Diffus. 2007, 28, 523–535. [Google Scholar] [CrossRef]
- Ohno, M.; Mirkovic, D.; Schmid-Fetzer, R. Phase equilibria and solidification of Mg-rich Mg-Al-Zn alloys. Mater. Sci. Eng. A 2006, 421, 328–337. [Google Scholar] [CrossRef]
- Hampl, M.; Gröbner, J.; Schmid-Fetzer, R. Experimental study of phase equilibria and solidification microstructures of Mg-Ca-Ce alloys combined with thermodynamic modelling. J. Mater. Sci. 2007, 42, 10023–10031. [Google Scholar] [CrossRef]
- Gröbner, J.; Schmid-Fetzer, R.; Pisch, A.; Colinet, C.; Pavlyuk, V.V.; Dmytriv, G.S.; Kevorkov, D.G.; Bodak, O.I. Phase equilibria, calorimetric study and thermodynamic modeling of Mg-Li-Ca alloys. Thermochim. Acta 2002, 389, 85–94. [Google Scholar] [CrossRef]
- Gröbner, J.; Chumak, I.; Schmid-Fetzer, R. Experimental study of ternary Ca-Mg-Si phase equilibria and thermodynamic assessment of Ca-Si and Ca-Mg-Si systems. Intermetallics 2003, 11, 1065–1074. [Google Scholar] [CrossRef]
- Kozlov, A.; Gröbner, J.; Schmid-Fetzer, R. Phase formation in Mg-Sn-Si and Mg-Sn-Si-Ca alloys. J. Alloys Comp. 2011, 509, 3326–3337. [Google Scholar] [CrossRef]
- Janz, A.; Schmid-Fetzer, R. Thermodynamics and constitution of Mg-Al-Ca-Sr-Mn alloys: Part I. Experimental investigation and thermodynamic modeling of subsystems Mg-Ca-Sr and Al-Ca-Sr. J. Phase Equilbria Diffus. 2009, 30, 146–156. [Google Scholar] [CrossRef]
- Brubaker, C.O.; Liu, Z.K. A computational thermodynamic model of the Ca-Mg-Zn system. J. Alloys Comp. 2004, 370, 114–122. [Google Scholar] [CrossRef]
- Gröbner, J.; Hampl, M.; Schmid-Fetzer, R.; Easton, M.A.; Zhu, S.; Gibson, M.A.; Nie, J.F. Phase analysis of Mg-La-Nd and Mg-Ce-La alloys. Intermetallics 2012, 28, 92–101. [Google Scholar] [CrossRef]
- Gröbner, J.; Kozlov, A.; Schmid-Fetzer, R.; Easton, M.A.; Zhu, S.; Gibson, M.A.; Nie, J.F. Thermodynamic analysis of as-cast and heat-treated microstructures of Mg-Ce-Nd alloys. Acta Mater. 2011, 59, 613–622. [Google Scholar] [CrossRef]
- Kozlov, A.; Gröbner, J.; Schmid-Fetzer, R. Phase formation in Mg-Sn alloys modified by Ca and Ce. J. Phase Equilbria Diffus. 2012. submitted for publication. [Google Scholar]
- Gröbner, J.; Schmid-Fetzer, R. Thermodynamic modeling of the Mg-Ce-Gd-Y system. Scripta Mater. 2010, 63, 674–679. [Google Scholar] [CrossRef]
- Chiu, C.N.; Gröbner, J.; Kozlov, A.; Schmid-Fetzer, R. Experimental study and thermodynamic assessment of ternary Mg-Zn-Ce phase relations focused on Mg-rich alloys. Intermetallics 2010, 18, 399–405. [Google Scholar] [CrossRef]
- Braga, M.H.; Malheiros, L.F.; Haemaelaeinen, M. The Cu-Li-Mg system at room temperature. Thermochim. Acta 2000, 344, 47–54. [Google Scholar] [CrossRef]
- Ansara, I.; Dinsdale, A.T.; Rand, M.H. COST507-Definition of Thermochemical and Thermophysical Properties to Provide a Database for the Development of New Light Alloys,Volume 2: Thermochemical Database for Light Metal Alloys; Office for Official Publications of the European Communities: Luxembourg, Luxembourg, 1998. [Google Scholar]
- Liang, P.; Seifert, H.J.; Lukas, H.L.; Ghosh, G.; Effenberg, G.; Aldinger, F. Thermodynamic modelling of the Cu-Mg-Zn ternary system. Calphad 1998, 22, 527–544. [Google Scholar] [CrossRef]
- Kevorkov, D.G.; Gröbner, J.; Schmid-Fetzer, R.; Pavlyuk, V.V.; Dmytriv, G.S.; Bodak, O.I. The ternary Gd-Li-Mg system: Phase diagram study and computational evaluation. J. Phase Equilbria 2001, 22, 34–42. [Google Scholar] [CrossRef]
- Gröbner, J.; Kozlov, A.; Fang, X.; Geng, J.; Nie, J.F.; Schmid-Fetzer, R. Phase equilibria and transformations in ternary Mg-rich Mg-Gd-Zn alloys including the thermodynamic optimization of the binary Gd-Zn. J. Alloys Comp. 2012. submitted for publication. [Google Scholar]
- Du, Y.; Zhao, J.R.; Zhang, C.; Chen, H.L.; Zhang, L.J. Thermodynamic modeling of the Fe-Mg-Si system. J. Min. Metall. 2007, 43B, 39–56. [Google Scholar]
- Zhou, S.; Liu, L.; Yuan, X.; Zheng, F.; Jin, Z. Thermodynamic assessment of La-Si and Mg-La-Si systems. J. Alloys Comp. 2010, 490, 253–259. [Google Scholar] [CrossRef]
- Qi, H.Y.; Huang, G.X.; Liu, R.D.; Zhang, K.; Liu, L.B.; Jin, Z.P. Thermodynamic optimization of La-Zn and La-Mg-Zn systems. J. Alloys Comp. 2010, 497, 336–343. [Google Scholar] [CrossRef]
- Kevorkov, D.; Schmid-Fetzer, R.; Zhang, F. Phase eguilibria and thermodynamics of the Mg-Si-Li system and remodeling of the Mg-Si system. J. Phase Equilbria Diffus. 2004, 25, 140–151. [Google Scholar]
- Von Buch, F.; Lietzau, J.; Mordike, B.L.; Pisch, A.; Schmid-Fetzer, R. Development of Mg-Sc-Mn alloys. Mater. Sci. Eng. A 1999, 263, 1–7. [Google Scholar] [CrossRef]
- Ohno, M.; Schmid-Fetzer, R. Mg-rich phase equilibria of Mg-Mn-Zn alloys analyzed by computational thermochemistry. Int. J. Mater. Res. 2006, 97, 526–532. [Google Scholar]
- Guo, C.P.; Du, Z.M.; Li, C.R. Thermodynamic description of the Ce-Mg-Y and Mg-Nd-Y systems. Int. J. Mater. Res. 2008, 99, 650–668. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, A.A.; Peng, L.M.; Stone, D.S.; Chang, Y.A. Thermodynamic modeling and experimental investigation of the magnesium-neodymium-zinc alloys. Intermetallics 2011, 19, 1720–1726. [Google Scholar] [CrossRef]
- Gröbner, J.; Kozlov, A.; Fang, X.; Geng, J.; Nie, J.F.; Schmid-Fetzer, R. Phase equilibria and transformations in ternary Mg-rich Mg-Y-Zn alloys. Acta Mater. in press.
- Witusiewicz, V.T.; Hecht, U.; Fries, S.G.; Rex, S. The Ag-Al-Cu system II. A thermodynamic evaluation of the ternary system. J. Alloys Comp. 2004, 387, 217–227. [Google Scholar]
- Gröbner, J.; Lukas, H.L.; Aldinger, F. Thermodynamic calculation of the Al-Si-C ternary system. Calphad 1996, 20, 247–254. [Google Scholar] [CrossRef]
- Anglezio, J.C.; Servant, C.; Ansara, I. Contribution to the experimental and thermodynamic assessment of the Al-Ca-Fe-Si system-I. Al-Ca-Fe, Al-Ca-Si, Al-Fe-Si and Ca-Fe-Si systems. Calphad 1994, 18, 273–309. [Google Scholar] [CrossRef]
- Cacciamani, G.; Cardinale, A.M.; Borzone, G.; Ferro, R. Thermodynamic modelling and optimization of the Al-Ce-Nd system. Calphad 2003, 27, 227–233. [Google Scholar] [CrossRef]
- Gröbner, J.; Mirkovic, D.; Schmid-Fetzer, R. Thermodynamic aspects of the constitution, grain refining and solidification enthalpies of Al-Ce-Si alloys. Metall. Mater. Trans A 2004, 35, 3349–3362. [Google Scholar] [CrossRef]
- Zhang, L.G.; Dong, H.Q.; Huang, G.X.; Shan, J.; Liu, L.B.; Jin, Z.P. Thermodynamic assessment of the Al-Cu-Gd system. Calphad 2009, 33, 664–672. [Google Scholar] [CrossRef]
- Miettinen, J. Thermodynamic description of the Cu-Al-Mn system in the copper-rich corner. Calphad 2003, 27, 103–114. [Google Scholar] [CrossRef]
- Mirković, D.; Gröbner, J.; Schmid-Fetzer, R. Liquid demixing and microstructure formation in ternary Al-Sn-Cu alloys. Mat. Sci. Eng. A 2008, 487, 456–467. [Google Scholar] [CrossRef]
- Liu, Z.K.; Chang, Y.A. Thermodynamic assessment of the Al-Fe-Si system. Metall. Mater. Trans A 1999, 30A, 1081–1095. [Google Scholar]
- Gröbner, J.; Kevorkov, D.; Schmid-Fetzer, R. The Al-Li-Si system, Part 2: Experimental study and thermodynamic calculation of the polythermal equilibria. J. Solid State Chem. 2001, 156, 506–511. [Google Scholar] [CrossRef]
- Kevorkov, D.; Gröbner, J.; Schmid-Fetzer, R. The Al-Li-Si system, Part 1: A new structure type Li8Al3Si5 and the ternary solid state phase equilibria. J. Solid State Chem. 2001, 156, 500–505. [Google Scholar] [CrossRef]
- Zhong, Y.; Ozturk, K.; Liu, Z.K. Thermodynamic modeling of the Ca-Sr-Zn ternary system. J. Phase Equilbria 2003, 24, 340–346. [Google Scholar] [CrossRef]
- Wang, C.P.; Ohnuma, I.; Kainuma, R.; Ishida, K. Phase equilibria in Fe-Cu-X (X: Co, Cr, Si, V) ternary systems. J. Phase Equilbria 2002, 23, 236–245. [Google Scholar] [CrossRef]
- An, X.; Li, Q.; Zhang, J.; Chen, S.; Yang, Y. Phase equilibria of the La-Ni-Cu ternary system at 673 K: Thermodynamic modeling and experimental validation. Calphad 2012, 36, 8–15. [Google Scholar] [CrossRef]
- Jantzen, T.; Spencer, P.J. Thermodynamic assessment of the Cu-Pb-Zn and Cu-Sn-Zn systems. Calphad 1998, 22, 417–434. [Google Scholar] [CrossRef]
- Forsberg, A.; Agren, J. Thermodynamic evaluation of the Fe-Mn-Si system and the γ/ε martensitic transformation. J. Phase Equilbria 1993, 14, 354–363. [Google Scholar] [CrossRef]
- Flandorfer, H.; Gröbner, J.; Stamou, A.; Hasiotis, N.; Saccone, A.; Rogl, P.; Wouters, R.; Seifert, H.J.; Macciò, D.; Ferro, R.; et al. Experimental investigations and thermodynamic calculations in the ternary system Mn-Y-Zr. Z. Metallkd. 1997, 88, 529–538. [Google Scholar]
- Janz, A.; Gröbner, J.; Schmid-Fetzer, R. Thermodynamics and constitution of Mg-Al-Ca-Sr-Mn alloys: Part II. Procedure for multicomponent key sample selection and application to the Mg-Al-Ca-Sr and Mg-Al-Ca-Sr-Mn systems. J. Phase Equilbria Diffus. 2009, 30, 157–175. [Google Scholar] [CrossRef]
- Löffler, A.; Gröbner, J.; Hampl, M.; Engelhardt, H.; Schmid-Fetzer, R.; Rettenmayr, M. Solidifying incongruently melting intermetallic phases as bulk single phases using the example of Al2Cu and Q-phase in the Al-Mg-Cu-Si system. J. Alloys Comp. 2012, 515, 123–127. [Google Scholar] [CrossRef]
- Ohno, M.; Mirkovic, D.; Schmid-Fetzer, R. Liquidus and solidus temperatures of Mg-rich Mg-Al-Mn-Zn alloys. Acta Mater. 2006, 54, 3883–3891. [Google Scholar] [CrossRef]
- Gröbner, J.; Schmid-Fetzer, R. Selection of promising quaternary candidates from Mg-Mn-(Sc, Gd, Y, Zr) for development of creep-resistant magnesium alloys. J. Alloys Comp. 2001, 320, 296–301. [Google Scholar] [CrossRef]
- Bulanova, M.V.; Zheltov, P.N.; Meleshevich, K.A. Lanthanum-cerium-silicon system. J. Alloys Comp. 2002, 347, 149–155. [Google Scholar] [CrossRef]
- Sinha, V.K.; Wallace, W.E. Hydrogen sorption by the hyperstoichiometric cerium-nickel-copper (Ce1 + x Ni2.5Cu2.5) alloys. J. Phys. Chem. 1984, 88, 105–107. [Google Scholar] [CrossRef]
- Kharchenko, O.I.; Kondratiuk, L.M.; Rak, M.M. Ternary systems (Y,Ce)-Ni-Cu. Vestn. L’vov. Univ. Khim. 1986, 27, pp. 50–52. Available online: http://www.nbuv.gov.ua/portal/Chem_Biol/Vlnu_kh/index.html (accessed on 9 September 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schmid-Fetzer, R.; Gröbner, J. Thermodynamic Database for Mg Alloys—Progress in Multicomponent Modeling. Metals 2012, 2, 377-398. https://doi.org/10.3390/met2030377
Schmid-Fetzer R, Gröbner J. Thermodynamic Database for Mg Alloys—Progress in Multicomponent Modeling. Metals. 2012; 2(3):377-398. https://doi.org/10.3390/met2030377
Chicago/Turabian StyleSchmid-Fetzer, Rainer, and Joachim Gröbner. 2012. "Thermodynamic Database for Mg Alloys—Progress in Multicomponent Modeling" Metals 2, no. 3: 377-398. https://doi.org/10.3390/met2030377




