Influence of Layer-Thickness Proportions and Their Strength and Elastic Properties on Stress Redistribution during Three-Point Bending of TiB/Ti-Based Two-Layer Ceramics Composites
Abstract
:1. Introduction
2. Objects and Methods of Research
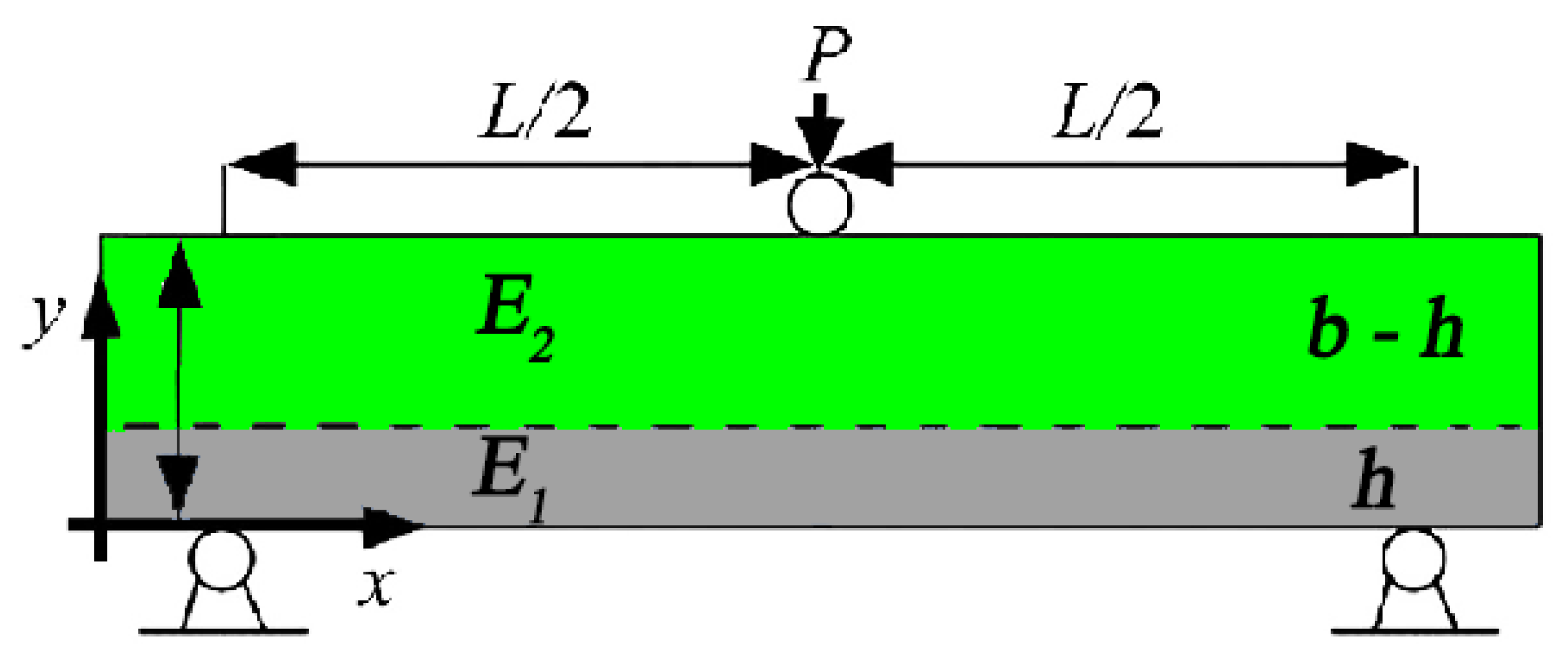
2.1. Statement of the Problem
- To determine the region of bilayer parameters in which brittle failure will begin in the upper layer earlier than in the lower layer;
- To determine the strength of the beam materials based on the ultimate load and bilayer parameters.
| Variable, Parameter | Definition |
| , beam width; | |
| , beam thickness; | |
| , beam cross-section; | |
| , bottom-layer thickness; | |
| , top-layer thickness; | |
| , supports distance; | |
| x, y, z | , Cartesian coordinates; |
| , neutral axis coordinate; | |
| , neutral axis curvature | |
| P | Load; |
| , Young’s modulus; | |
| , bottom-layer Young’s modulus; | |
| , top-layer Young’s modulus; | |
| , bilayer parameter for Young’s modulus ratio; | |
| , bilayer parameter for bottom-layer-thickness ratio; | |
| , bilayer parameter for layers’ flexural strength ratio; | |
| , normal component of the stress tensor in the beam cross-section; | |
| , diffusion interlayer zone thickness; | |
| , dimensionless coordinate along beam axis; | |
| , dimensionless coordinate orthogonal beam axis along y; | |
| , dimensionless coordinate orthogonal beam axis along z; | |
| , dimensionless neutral axis coordinate; | |
| , dimensionless diffusion interlayer zone thickness; | |
| , dimensionless supports distance; | |
| , dimensionless load; | |
| , , , | , component of the stress tensor in coordinates; |
| , neutral axis curvature in the beam center; | |
| , maximum stress deflection angle of the x-axis; | |
| , elastic limit for bottom-layer material; | |
| , | , elastic zone dimensionless x,y coordinates for bottom layer; |
| , tangential modulus; | |
| , tangential and Young’s modulus ratio for bottom layer. |
2.2. Subjects of Research
2.3. Research Methods
3. Results and Discussion
3.1. Model Development
3.1.1. The Elastic Case: Finding Stresses
3.1.2. Fracture Criterion of the Layer
3.1.3. Consideration of Elastic–Plastic Properties of the Lower Layer
3.2. Experimental Results
3.2.1. The Bending Strength of Each Material Is Known
- We choose the material of each layer in the composite and determine (or take from the reference literature) their elastic moduli, i.e., and , and obtain ;
- We determine (or take from reference literature) the bending strength of each material separately, i.e., and , and obtain ;
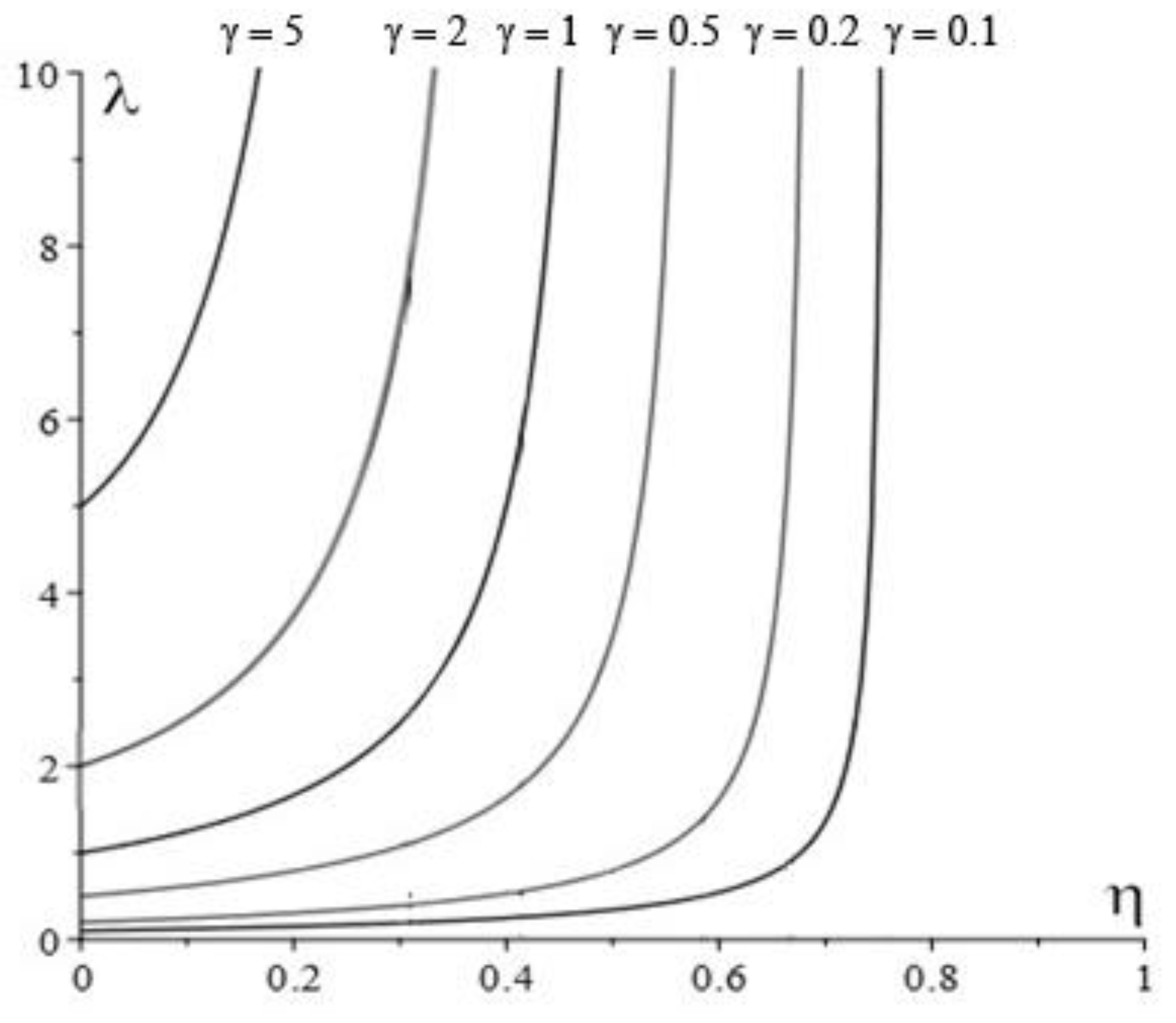
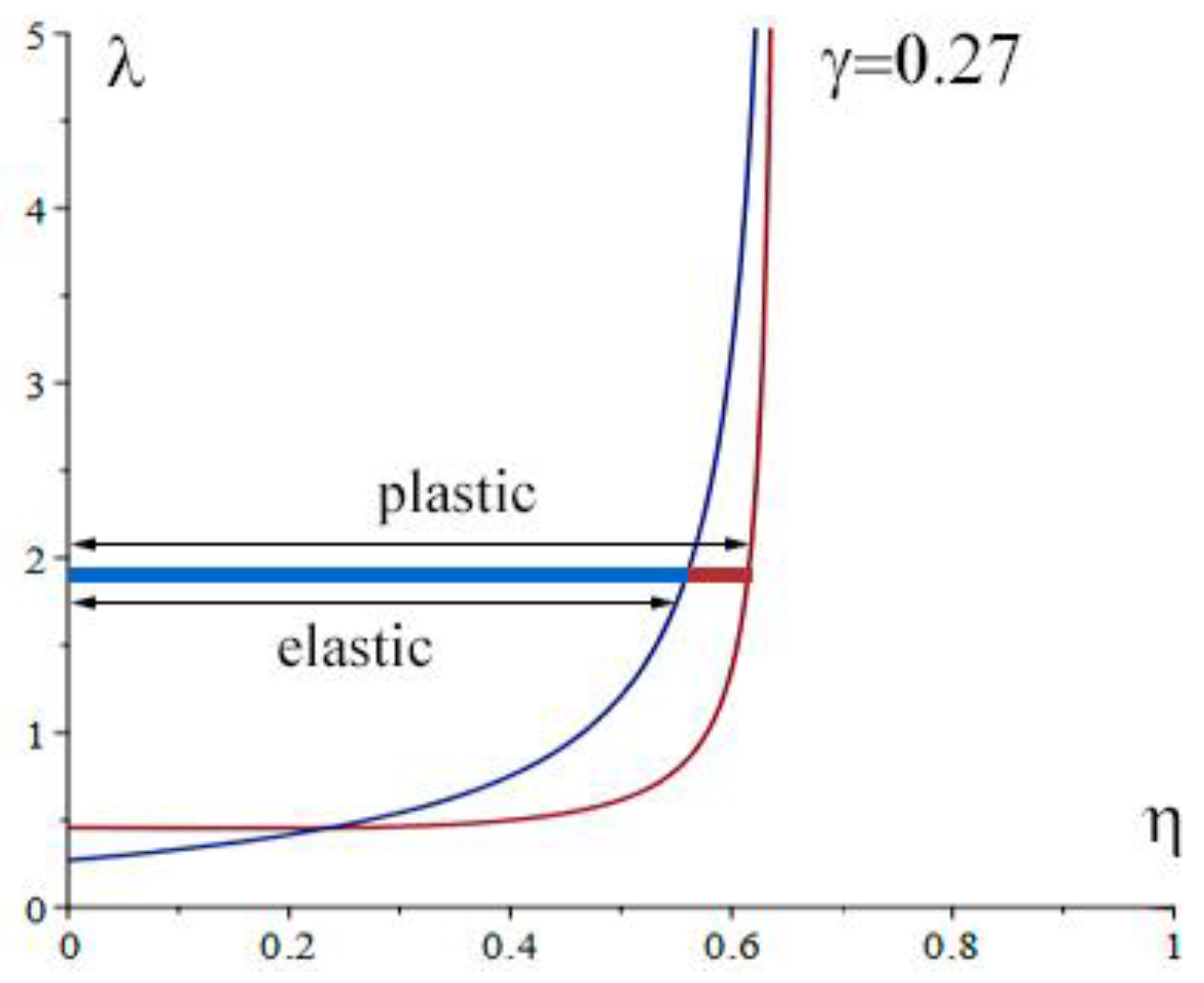
- Using inequalities (13), we determine the range , in which the failure occurs at the expense of the upper layer and at the expense of the lower layer.
3.2.2. The Bending Strength of the Layer Materials Is Not Known
- We choose the material of each layer, determine (or take from reference books) their elastic moduli and , and we obtain ;
- We measure the width a and the thickness b of the sample section, the thickness of the lower layer h, and the distance between the supports L;
- We perform a three-point loading experiment on the specimen from which we obtain the value of ultimate load ;
- We calculate the dimensionless parameters: , and cross-sectional area .
3.3. Maximum Load Setting
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, J.; Yang, F.; Zhang, C.; Chen, C.; Guo, Z. The “Pinning” Effect of in-Situ TiB Whiskers on the Hot Deformation Behavior and Dynamic Recrystallization of (10 Vol%) TiB/Ti–6Al–4V Compos. J. Mater. Res. Technol. 2023, 22, 1695–1707. [Google Scholar] [CrossRef]
- Li, S.; Han, Y.; Shi, Z.; Huang, G.; Zong, N.; Le, J.; Qiu, P.; Lu, W. Synergistic Strengthening Behavior and Microstructural Optimization of Hybrid Reinforced Titanium Matrix Composites during Thermomechanical Processing. Mater. Charact. 2020, 168, 110527. [Google Scholar] [CrossRef]
- Jeje, S.O.; Shongwe, M.B.; Rominiyi, A.L.; Olubambi, P.A. Spark Plasma Sintering of Titanium Matrix Composite—A Review. Int. J. Adv. Manuf. Technol. 2021, 117, 2529–2544. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, F.; Chen, C.; Shao, Y.; Lu, B.; Sui, Y.; Guo, Z. Mechanical Property and Microstructure of In-Situ TiB/Ti Composites via Vacuum Sintering and Hot Rolling. J. Alloys Compd. 2022, 911, 165042. [Google Scholar] [CrossRef]
- Liang, S.; Li, W.; Jiang, Y.; Cao, F.; Dong, G.; Xiao, P. Microstructures and Properties of Hybrid Copper Matrix Composites Reinforced by TiB Whiskers and TiB2 Particles. J. Alloys Compd. 2019, 797, 589–594. [Google Scholar] [CrossRef]
- Bagliuk, G.A.; Stasiuk, A.A.; Savvakin, D.G. Effect of Titanium Diboride Content on Basic Mechanical Properties of Composites Sintered from TiH2+ TiB2 Powder Mixtures. Powder Metall. Met. Ceram. 2020, 58, 642–650. [Google Scholar] [CrossRef]
- Tan, D.-W.; Chen, Z.-W.; Wei, W.-X.; Song, B.-C.; Guo, W.-M.; Lin, H.-T.; Wang, C.-Y. Wear Behavior and Mechanism of TiB2-Based Ceramic Inserts in High-Speed Cutting of Ti6Al4V Alloy. Ceram. Int. 2020, 46, 8135–8144. [Google Scholar] [CrossRef]
- Huang, K.; Chen, W.; Wu, M.; Wang, J.; Jiang, K.; Liu, J. Microstructure and Densification of the Ti6Al4V–70% TiB2 Metal-Ceramic by Coupled Multi-Physical Fields-Activated Sintering. J. Alloys Compd. 2020, 820, 153091. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Wang, Z.; Yue, X.; Ji, P.-J.; Shu, S.-L. Simultaneously Improved Strength and Toughness of In Situ Bi-Phased TiB2–Ti (C, N)–Ni Cermets by Mo Addition. J. Alloys Compd. 2020, 820, 153068. [Google Scholar] [CrossRef]
- Han, J.; Liu, Z.; Jia, Y.; Wang, T.; Zhao, L.; Guo, J.; Xiao, S.; Chen, Y. Effect of TiB2 Addition on Microstructure and Fluidity of Cast TiAl Alloy. Vacuum 2020, 174, 109210. [Google Scholar] [CrossRef]
- Ozerov, M.; Klimova, M.; Sokolovsky, V.; Stepanov, N.; Popov, A.; Boldin, M.; Zherebtsov, S. Evolution of Microstructure and Mechanical Properties of Ti/TiB Metal-Matrix Composite during Isothermal Multiaxial Forging. J. Alloys Compd. 2019, 770, 840–848. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, N.; Shi, C.; He, C.; Liu, E. Regulation of the Interface Binding and Mechanical Properties of TiB/Ti via Doping-Induced Chemical and Structural Effects. Comput. Mater. Sci. 2020, 174, 109506. [Google Scholar] [CrossRef]
- Lin, Y.; Lin, Z.; Chen, Q.; Lei, Y.; Fu, H. Laser In-Situ Synthesis of Titanium Matrix Composite Coating with TiB–Ti Network-like Structure Reinforcement. Trans. Nonferrous Met. Soc. China 2019, 29, 1665–1676. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, Y.; Pan, C.; Liang, L.; Wang, X. Microstructural Modeling and Strengthening Mechanism of TiB/Ti-6Al-4V Discontinuously-Reinforced Titanium Matrix Composite. Materials 2019, 12, 827. [Google Scholar] [CrossRef]
- Xueqiao, L.; Tounan, J.; Shejun, D.; Lei, C.; Yinghua, L.; Yongping, L. Formation Mechanism of the Tubular TiB In Situ Formed in TiB/Ti-6Al-4V Composite Coatings by Laser Cladding. Rare Met. Mater. Eng. 2018, 47, 915–919. [Google Scholar]
- Jianwei, M.; Guangfa, H.; Liqiang, W.; Yuanfei, H.; Weijie, L. Microstructural Evolutions of In-Situ TiB Whisker Reinforcement during Laser Welding TiB/Ti Composites. Rare Met. Mater. Eng. 2017, 46, 112–117. [Google Scholar]
- Selvakumar, M.; Ramkumar, T.; Mohanraj, M.; Chandramohan, P.; Narayanasamy, P. Experimental Investigations of Reciprocating Wear Behavior of Metal Matrix (Ti/TiB) Composites. Archiv. Civ. Mech. Eng. 2020, 20, 26. [Google Scholar] [CrossRef]
- Konstantinov, A.S.; Bazhin, P.M.; Stolin, A.M.; Kostitsyna, E.V.; Ignatov, A.S. Ti-B-Based Composite Materials: Properties, Basic Fabrication Methods, and Fields of Application. Compos. Part A. 2018, 108, 79–88. [Google Scholar] [CrossRef]
- Wang, S.; Huang, L.; Zhang, R.; An, Q.; Sun, F.; Meng, F.; Geng, L. Effects of Rolling Deformation on Microstructure Orientations and Tensile Properties of TiB/(TA15-Si) Composites. Mater. Charact. 2022, 194, 112425. [Google Scholar] [CrossRef]
- Hasan, M.; Zhao, J.; Jiang, Z. Micromanufacturing of Composite Materials: A Review. Int. J. Extrem. Manuf. 2019, 1, 012004. [Google Scholar] [CrossRef]
- Huang, M.; Xu, C.; Fan, G.; Maawad, E.; Gan, W.; Geng, L.; Lin, F.; Tang, G.; Wu, H.; Du, Y.; et al. Role of Layered Structure in Ductility Improvement of Layered Ti-Al Metal Composite. Acta Mater. 2018, 153, 235–249. [Google Scholar] [CrossRef]
- Bazhin, P.M.; Konstantinov, A.S.; Chizhikov, A.P.; Pazniak, A.I.; Kostitsyna, E.V.; Prokopets, A.D.; Stolin, A.M. Laminated Cermet Composite Materials: The Main Production Methods, Structural Features and Properties (Review). Ceram. Int. 2021, 47, 1513–1525. [Google Scholar] [CrossRef]
- Wan, H.; Leung, N.; Jargalsaikhan, U.; Ho, E.; Wang, C.; Liu, Q.; Peng, H.-X.; Su, B.; Sui, T. Fabrication and Characterisation of Alumina/Aluminium Composite Materials with a Nacre-like Micro-Layered Architecture. Mater. Des. 2022, 223, 111190. [Google Scholar] [CrossRef]
- Charkviani, R.V.; Pavlov, A.A.; Pavlova, S.A. Interlaminar Strength and Stiffness of Layered Composite Materials. Procedia Eng. 2017, 185, 168–172. [Google Scholar] [CrossRef]
- Cao, Z.H.; Sun, W.; Ma, Y.J.; Li, Q.; Fan, Z.; Cai, Y.P.; Zhang, Z.J.; Wang, H.; Zhang, X.; Meng, X.K. Strong and Plastic Metallic Composites with Nanolayered Architectures. Acta Mater. 2020, 195, 240–251. [Google Scholar] [CrossRef]
- Mo, T.; Chen, J.; Chen, Z.; He, W.; Liu, Q. Microstructure Evolution During Roll Bonding and Growth of Interfacial Intermetallic Compounds in Al/Ti/Al Laminated Metal Composites. JOM 2019, 71, 4769–4777. [Google Scholar] [CrossRef]
- Ma, M.; Huo, P.; Liu, W.C.; Wang, G.J.; Wang, D.M. Microstructure and Mechanical Properties of Al/Ti/Al Laminated Composites Prepared by Roll Bonding. Mater. Sci. Eng. 2015, 636, 301–310. [Google Scholar] [CrossRef]
- Nasakina, E.O.; Sudarchikova, M.A.; Demin, K.Y.; Gol’Dberg, M.A.; Baskakova, M.I.; Tsareva, A.M.; Ustinova, Y.N.; Leonova, Y.O.; Sevost’yanov, M.A. The Effect of the Titanium Surface Layer Thickness on the Characteristics of a Layered Composite Material. Proc. J. Phys. Conf. Ser. IOP Publ. 2019, 1281, 012057. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, Y.; Löfler, L.; Bartosik, M.; Nayak, G.K.; Renk, O.; Holec, D.; Mayrhofer, P.H.; Zhang, Z. Atomic Insights on Intermixing of Nanoscale Nitride Multilayer Triggered by Nanoindentation. Acta Mater. 2021, 214, 117004. [Google Scholar] [CrossRef]
- Prokopets, A.D.; Bazhin, P.M.; Konstantinov, A.S.; Chizhikov, A.P.; Antipov, M.S.; Avdeeva, V.V. Structural Features of Layered Composite Material TiB2/TiAl/Ti6Al4 Obtained by Unrestricted SHS-Compression. Mater. Lett. 2021, 300, 130165. [Google Scholar] [CrossRef]
- Song, K.; Xu, Y.; Zhao, N.; Zhong, L.; Shang, Z.; Shen, L.; Wang, J. Evaluation of Fracture Toughness of Tantalum Carbide Ceramic Layer: A Vickers Indentation Method. J. Mater. Eng. Perform. 2016, 25, 3057–3064. [Google Scholar] [CrossRef]
- Du, W.; Han, B.; Li, X.; Wu, H.; Miao, K.; Li, R.; Wu, H.; Liu, C.; Fang, W.; Fan, G. Fracture Mechanism of High Toughness Ti2AlNb/Ti6Al4V Layered Metal Composites. Mater. Lett. 2023, 348, 134717. [Google Scholar] [CrossRef]
- Wu, H.; Fan, G.; Jin, B.C.; Geng, L.; Cui, X.; Huang, M.; Li, X.; Nutt, S. Enhanced Fracture Toughness of TiBw/Ti3Al Composites with a Layered Reinforcement Distribution. Mater. Sci. Eng. 2016, 670, 233–239. [Google Scholar] [CrossRef]
- Ladeveze, P.; LeDantec, E. Damage Modelling of the Elementary Ply for Laminated Composites. Compos. Sci. Technol. 1992, 43, 257–267. [Google Scholar] [CrossRef]
- Polilov, A.N.; Sklemina, O.Y. Delamination of Composites and the Scale Effect of Glued Joint Strength. Polym. Sci. Ser. D 2023, 16, 104–110. [Google Scholar] [CrossRef]
- Williams, K.V.; Vaziri, R.; Poursartip, A. A Physically Based Continuum Damage Mechanics Model for Thin Laminated Composite Structures. Int. J. Solids Struct. 2003, 40, 2267–2300. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Morozov, E.V. Chapter 7—Laminated Composite Plates. In Advanced Mechanics of Composite Materials and Structures, 4th ed.; Vasiliev, V.V., Morozov, E.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 437–574. ISBN 978-0-08-102209-2. [Google Scholar] [CrossRef]
- McCartney, L.N. Physically Based Damage Models for Laminated Composites. Proc. Inst. Mech. Eng. 2003, 217, 163–199. [Google Scholar] [CrossRef]
- Öchsner, A. Classical Beam Theories of Structural Mechanics/eBook: Physics and Astronomy; Springer: New York City, NY, USA, 2021. [Google Scholar] [CrossRef]
- Bazhina, A.D.; Chizhikov, A.; Konstantinov, A.; Khomenko, N.; Bazhin, P.; Avdeeva, V.; Chernogorova, O.; Drozdova, E. Structure, Phase Composition and Mechanical Characteristics of Layered Composite Materials Based on TiB/XTi-Al/α-Ti (x = 1, 1.5, 3) Obtained by Combustion and High-Temperature Shear Deformation. Mater. Sci. Eng. 2022, 858, 144161. [Google Scholar] [CrossRef]
- Bazhin, P.; Konstantinov, A.; Chizhikov, A.; Prokopets, A.; Bolotskaia, A. Structure, Physical and Mechanical Properties of TiB-40 Wt.%Ti Composite Materials Obtained by Unrestricted SHS Compression. Mater. Today Commun. 2020, 25, 101484. [Google Scholar] [CrossRef]
- Ding, H.; Cui, X.; Gao, N.; Sun, Y.; Zhang, Y.; Huang, L.; Geng, L. Fabrication of (TiB/Ti)-TiAl composites with a controlled laminated architecture and enhanced mechanical properties. J. Mater. Sci. Technol. 2021, 62, 221–233. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhang, B.; Jin, Y.; Zhang, H.; Wang, Y.; Ye, J.; Liu, Q.; Hou, Z.; Zhang, Z.; Ye, F. Design and anti-penetration performance of TiB/Ti system functionally graded material armor fabricated by SPS combined with tape casting. Ceram. Int. 2020, 46, 28244–28249. [Google Scholar] [CrossRef]
- Lapshin, O.V.; Boldyreva, E.V.; Boldyrev, V.V. Role of Mixing and Milling in Mechanochemical Synthesis (Review). Russ. J. Inorg. Chem. 2021, 66, 433–453. [Google Scholar] [CrossRef]
- Tomilin, O.B.; Muryumin, E.E.; Fadin, M.V.; Shchipakin, S.Y. Preparation of Luminophore CaTiO3:Pr3+ by Self-Propagating High-Temperature Synthesis. Russ. J. Inorg. Chem. 2022, 67, 431–438. [Google Scholar] [CrossRef]
- Bazhin, P.M.; Chizhikov, A.P.; Konstantinov, A.S.; Prokopets, A.D.; Kostitsyna, E.V.; Bolotskaya, A.V.; Stolin, A.M.; Khomenko, N.Y. TiB/30 wt.% Ti layered composite material obtained by free SHS compression on a Ti6Al4V titanium alloy. IOP Conf. Ser. Mater. Sci. Eng. 2020, 848, 012009. [Google Scholar] [CrossRef]
- Bazhin, P.M.; Stolin, A.M.; Konstantinov, A.S.; Chizhikov, A.P.; Prokopets, A.D.; Alymov, M.I. Structural Features of Titanium Boride-Based Layered Composite Materials Produced by Free SHS Compression. Dokl. Chem. 2019, 488, 246–248. [Google Scholar] [CrossRef]
- Chizhikov, A.; Konstantinov, A.; Bazhin, P.; Stolin, A. Features of Molding and Structure of Composite Materials Based on TiB/Ti, Obtained by Free SHS Compression Method. Mater. Sci. Forum. 1009, 2020, 37–42. [Google Scholar] [CrossRef]
- Stolin, A.M.; Bazhin, P.M.; Konstantinov, A.S.; Alymov, M.I. Production of Large Compact Plates from Ceramic Powder Materials by Unconfined SHS Compaction. Dokl. Chem. 2018, 480, 136–138. [Google Scholar] [CrossRef]
- Bazhin, P.M.; Stolin, A.M.; Konstantinov, A.S.; Kostitsyna, E.V.; Ignatov, A.S. Ceramic Ti—B Composites Synthesized by Combustion Followed by High-Temperature Deformation. Materials 2016, 9, 1027. [Google Scholar] [CrossRef]



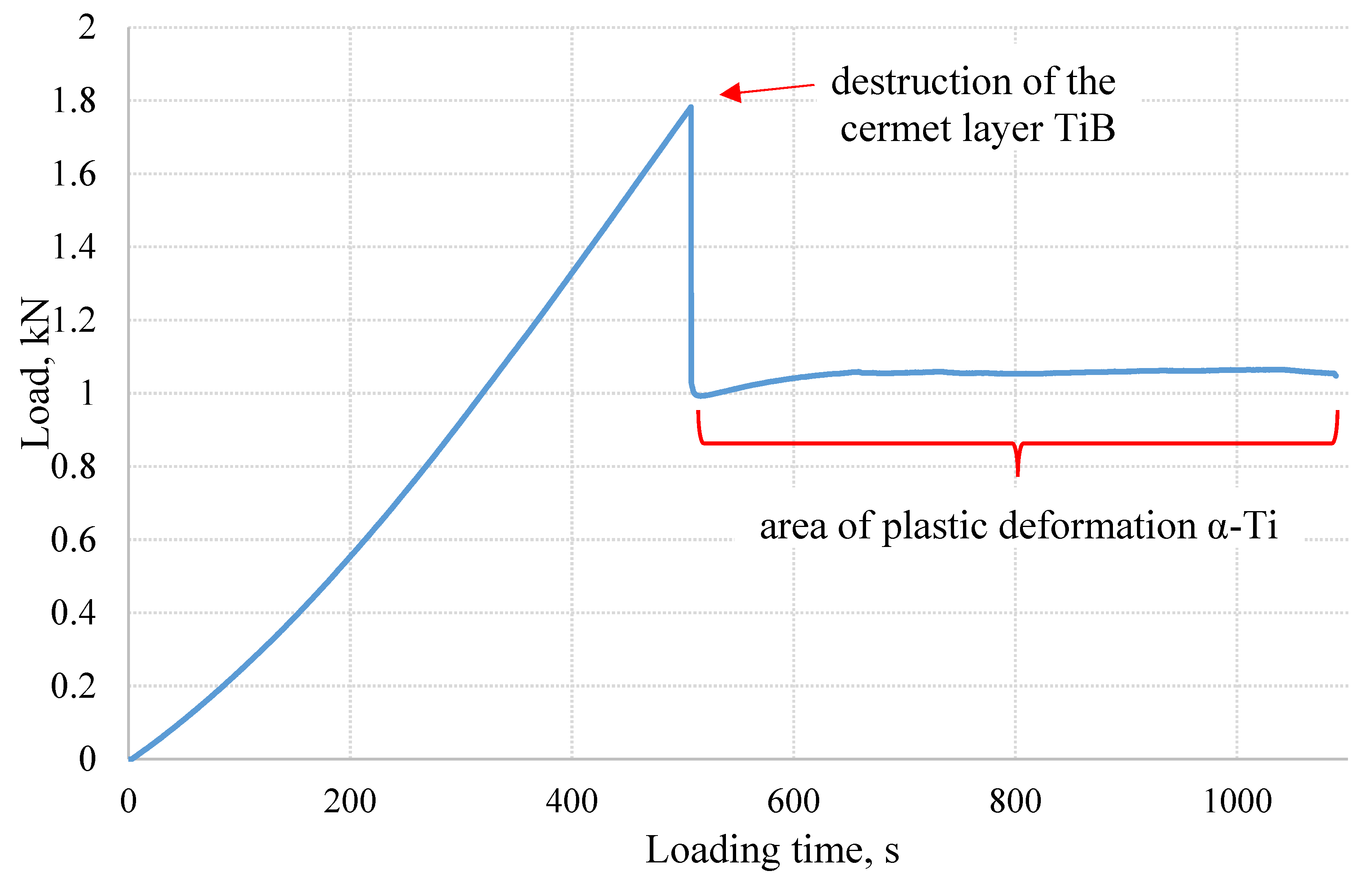

| Sample Number | Distance between Supports, L mm | Sample Width, a mm | Sample Thickness, b mm | Bottom-Layer Thickness h mm | Max. Force, P* N | Bending Strength Limit of the Top Layer TiB, MPa | Bending Strength Limit of the Bottom Layer TiB, MPa | GPa | GPa | |
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 42.7 | 3.95 | 7.1 | 1 | 0.140 | 1486.2 | 564 | 1100 | 407 | 110 |
| S2 | 1.1 | 0.155 | 1534.8 | |||||||
| S3 | 1.2 | 0.169 | 1782.4 | |||||||
| S4 | 3.5 | 0.493 | 2614.5 | |||||||
| S5 | 3.6 | 0.507 | 2651.8 | |||||||
| S6 | 0.98 | 0.138 | 1548.6 | |||||||
| S7 | 0.92 | 0.130 | 1821.8 | |||||||
| S8 | 0.85 | 0.120 | 1525.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khvostunkov, K.; Bazhin, P.; Ni, Q.-Q.; Bazhina, A.; Chizhikov, A.; Konstantinov, A. Influence of Layer-Thickness Proportions and Their Strength and Elastic Properties on Stress Redistribution during Three-Point Bending of TiB/Ti-Based Two-Layer Ceramics Composites. Metals 2023, 13, 1480. https://doi.org/10.3390/met13081480
Khvostunkov K, Bazhin P, Ni Q-Q, Bazhina A, Chizhikov A, Konstantinov A. Influence of Layer-Thickness Proportions and Their Strength and Elastic Properties on Stress Redistribution during Three-Point Bending of TiB/Ti-Based Two-Layer Ceramics Composites. Metals. 2023; 13(8):1480. https://doi.org/10.3390/met13081480
Chicago/Turabian StyleKhvostunkov, Kirill, Pavel Bazhin, Qing-Qing Ni, Arina Bazhina, Andrey Chizhikov, and Alexander Konstantinov. 2023. "Influence of Layer-Thickness Proportions and Their Strength and Elastic Properties on Stress Redistribution during Three-Point Bending of TiB/Ti-Based Two-Layer Ceramics Composites" Metals 13, no. 8: 1480. https://doi.org/10.3390/met13081480





