Mutual Interactions of Lamb Waves in Nonlinear Elastic Plates
Abstract
:1. Introduction
- (1)
- As the characteristics of the nonlinear modulation are practically important for its applications, the mutual interactions of Lamb waves in nonlinear elastic plates are studied in this study;
- (2)
- The Lamb wave mutual interaction theory can be utilized to guide nonlinear mode selection;
- (3)
- The fatigue damage in the metal plate can be detected by the Lamb wave mutual interaction.
2. Nonlinear Modulation Generation of Lamb Waves
2.1. Lamb Wave Propagation
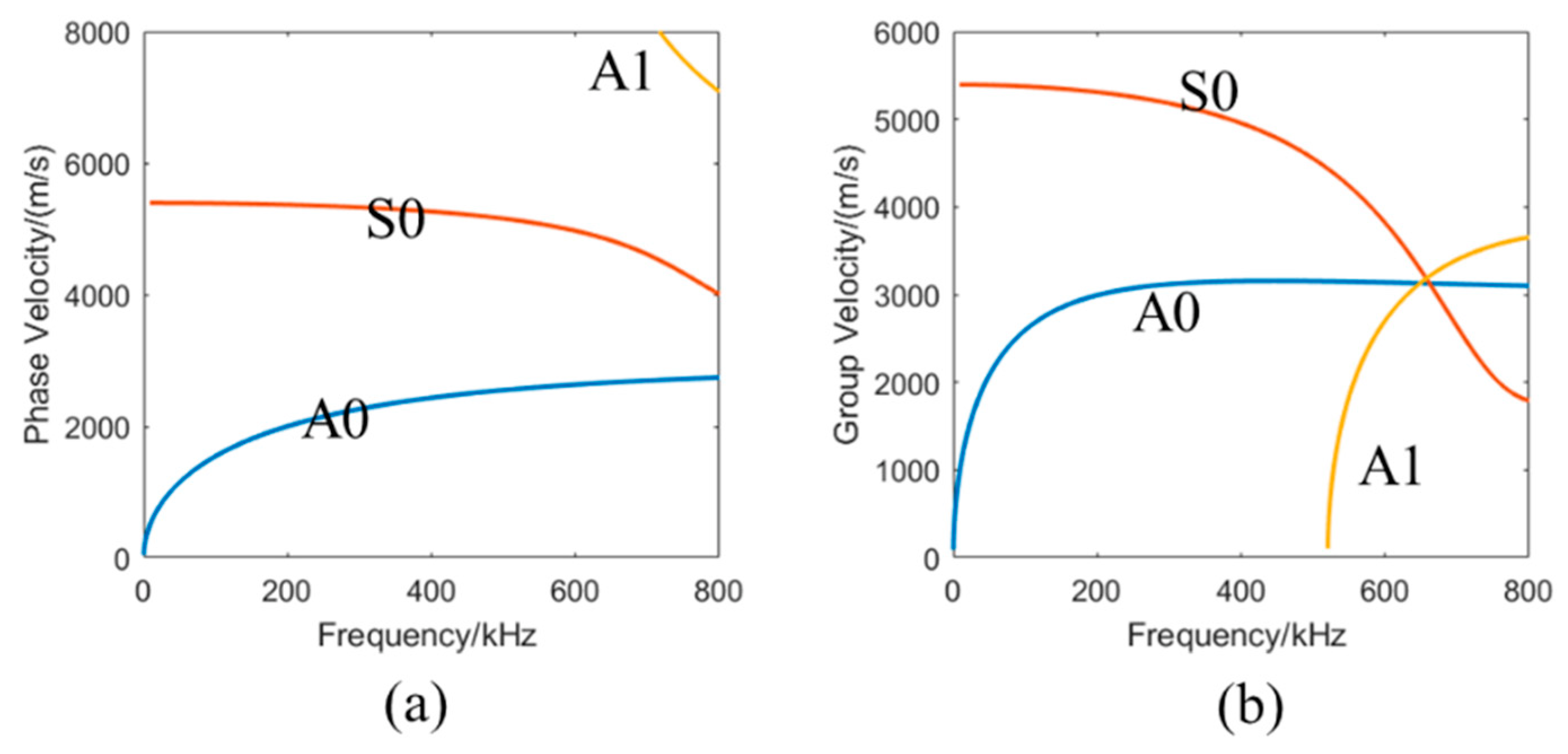
2.2. The Dispersion Property
2.3. Mutual Interaction
3. Nonzero Power Flux
- (1)
- Symmetric–symmetric or antisymmetric–antisymmetric mutual interactions.
- (2)
- Symmetric–antisymmetric mutual interaction.
4. Synchronism Condition
5. Experimental Research
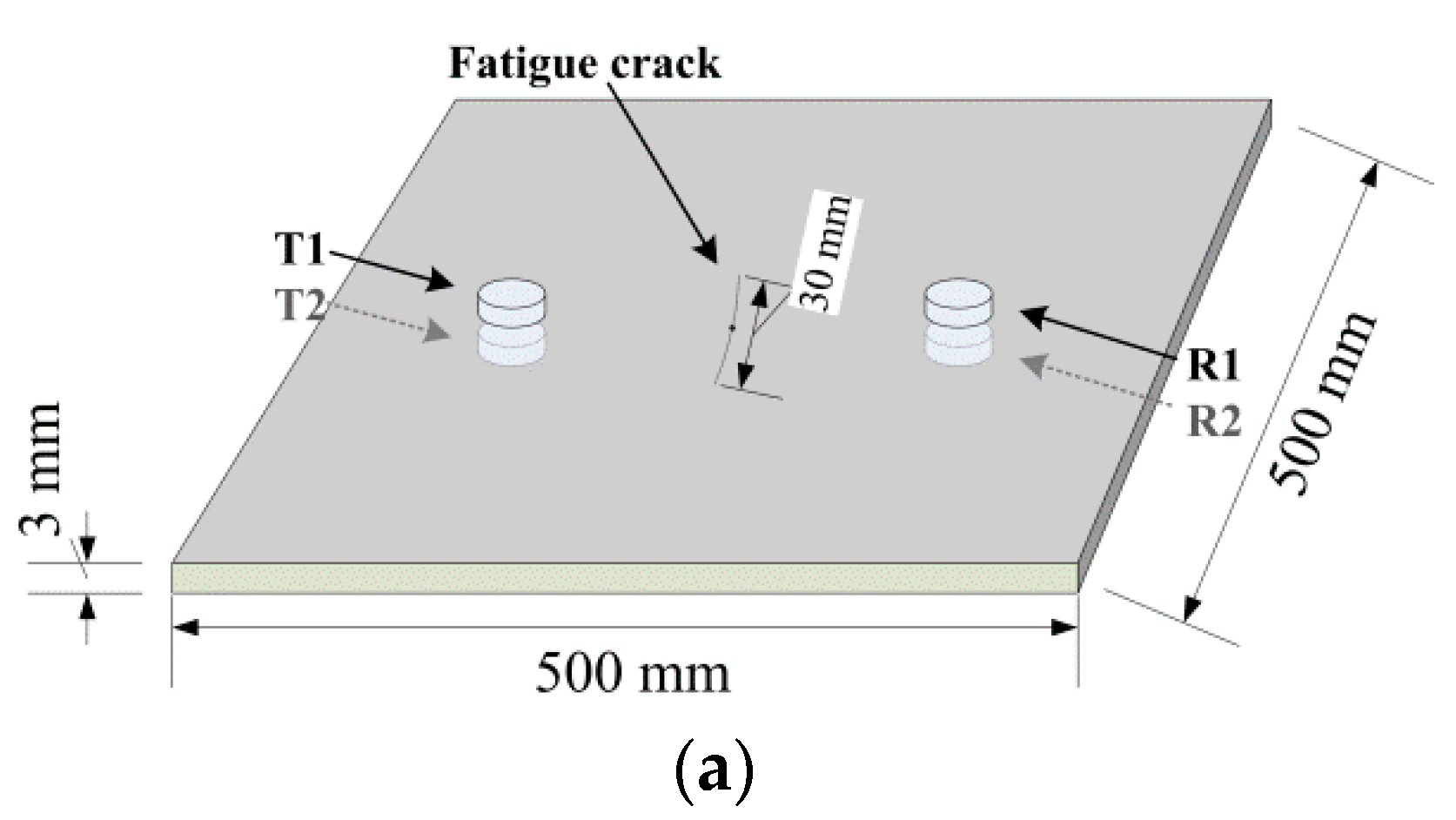
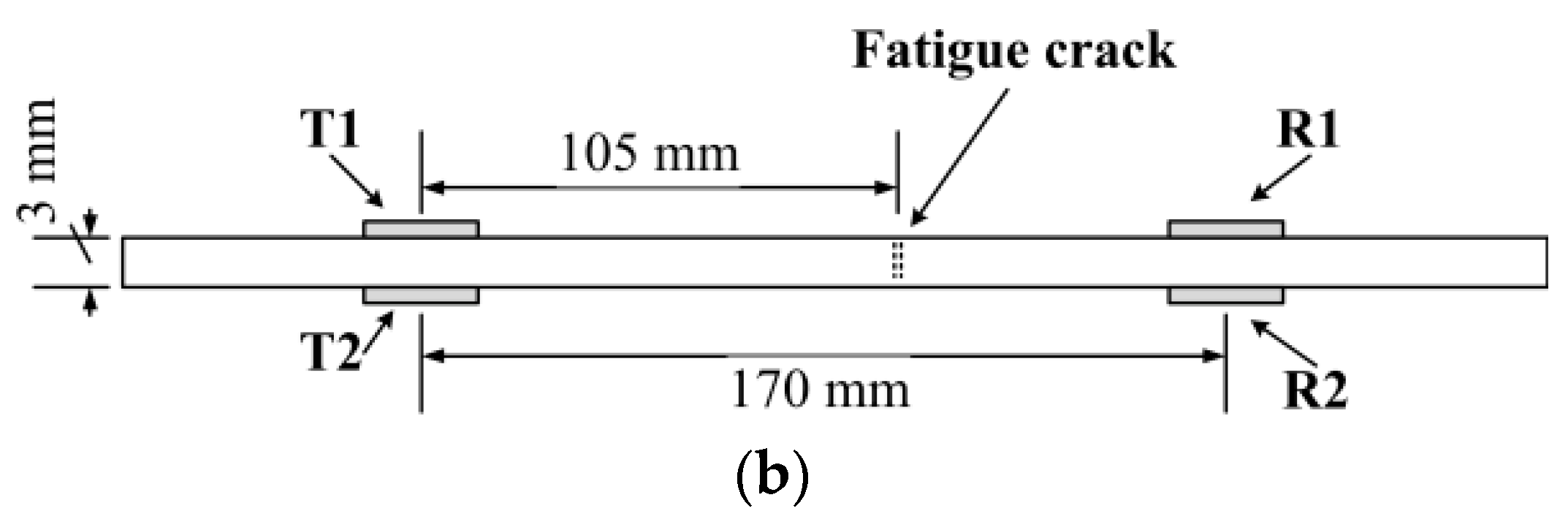
5.1. Experimental Setup
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Nonlinear Forcing Terms
References
- Li, W.; Xiao, J.; Deng, M. Micro-defect imaging with an improved resolution using nonlinear ultrasonic Lamb waves. J. Appl. Phys. 2022, 131, 185101. [Google Scholar] [CrossRef]
- Li, W.; Lan, Z.; Hu, N.; Deng, M. Modeling and simulation of backward combined harmonic generation induced by one-way mixing of longitudinal ultrasonic guided waves in a circular pipe. Ultrasonics 2021, 113, 106356. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Lan, Z.; Hu, N.; Deng, M. Theoretical and numerical investigations of the nonlinear acoustic response of feature guided waves in a welded joint. Wave Motion 2021, 101, 102696. [Google Scholar] [CrossRef]
- Krishna Chillara, V.; Lissenden, C.J. Interaction of guided wave modes in isotropic weakly nonlinear elastic plates: Higher harmonic generation. J. Appl. Phys. 2012, 111, 124909. [Google Scholar] [CrossRef]
- Zhao, J.; Chillara, V.K.; Ren, B.; Cho, H.; Qiu, J.; Lissenden, C.J. Second harmonic generation in composites: Theoretical and numerical analyses. J. Appl. Phys. 2016, 119, 064902. [Google Scholar] [CrossRef]
- Liu, Y.; Chillara, V.K.; Lissenden, C.J.; Rose, J.L. Third harmonic shear horizontal and Rayleigh Lamb waves in weakly nonlinear plates. J. Appl. Phys. 2013, 114, 195. [Google Scholar] [CrossRef]
- Duan, W.; Niu, X.; Gan, T.-H.; Kanfoud, J.; Chen, H.-P. A numerical study on the excitation of guided waves in rectangular plates using multiple point sources. Metals 2017, 7, 552. [Google Scholar] [CrossRef] [Green Version]
- Jankauskas, A.; Mazeika, L. Ultrasonic guided wave propagation through welded lap joints. Metals 2016, 6, 315. [Google Scholar] [CrossRef] [Green Version]
- Draudvilienė, L.; Meškuotienė, A. The methodology for the reliability evaluation of the signal processing methods used for the dispersion estimation of Lamb waves. IEEE Trans. Instrum. Meas. 2021, 71, 1–7. [Google Scholar] [CrossRef]
- Draudviliene, L.; Tumsys, O.; Mazeika, L.; Zukauskas, E. Estimation of the Lamb wave phase velocity dispersion curves using only two adjacent signals. Compos. Struct. 2021, 258, 113174. [Google Scholar] [CrossRef]
- Sohn, H.; Lim, H.J.; DeSimio, M.P.; Brown, K.; Derriso, M. Nonlinear ultrasonic wave modulation for online fatigue crack detection. J. Sound Vib. 2014, 333, 1473–1484. [Google Scholar] [CrossRef]
- Solodov, I.; Busse, G. Nonlinear air-coupled emission: The signature to reveal and image microdamage in solid materials. Appl. Phys. Lett. 2007, 91, 251910. [Google Scholar] [CrossRef]
- Jhang, K.-Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Liu, Y.; Khajeh, E.; Lissenden, C.J.; Rose, J.L. Interaction of torsional and longitudinal guided waves in weakly nonlinear circular cylinders. J. Acoust. Soc. Am. 2013, 133, 2541–2553. [Google Scholar] [CrossRef]
- Cho, H.; Hasanian, M.; Shan, S.; Lissenden, C.J. Nonlinear guided wave technique for localized damage detection in plates with surface-bonded sensors to receive Lamb waves generated by shear-horizontal wave mixing. NDT E Int. 2019, 102, 35–46. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J.; Xu, W. Nonlinear features of guided wave scattering from rivet hole nucleated fatigue cracks considering the rough contact surface condition. Smart Mater. Struct. 2018, 27, 105044. [Google Scholar] [CrossRef]
- Shan, S.; Hasanian, M.; Cho, H.; Lissenden, C.J.; Cheng, L. New nonlinear ultrasonic method for material characterization: Codirectional shear horizontal guided wave mixing in plate. Ultrasonics 2019, 96, 64–74. [Google Scholar] [CrossRef]
- Hong; Ming; Zhongqing; Mao; Zhu; Todd; Michael, D. Uncertainty quantification for acoustic nonlinearity parameter in Lamb wave-based prediction of barely visible impact damage in composites. Mech. Syst. Signal Process. 2017, 82, 448–460. [Google Scholar] [CrossRef] [Green Version]
- Pineda Allen, J.C.; Ng, C.T. Nonlinear guided-wave mixing for condition monitoring of bolted joints. Sensors 2021, 21, 5093. [Google Scholar] [CrossRef]
- Aseem, A.; Ng, C.T. Debonding detection in rebar-reinforced concrete structures using second harmonic generation of longitudinal guided wave. Ndt E Int. 2021, 122, 102496. [Google Scholar] [CrossRef]
- Liu, Y.; Chillara, V.K.; Lissenden, C.J. On selection of primary modes for generation of strong internally resonant second harmonics in plate. J. Sound Vib. 2013, 332, 4517–4528. [Google Scholar] [CrossRef]
- Jin Lim, H.; Sohn, H.; Liu, P. Binding conditions for nonlinear ultrasonic generation unifying wave propagation and vibration. Appl. Phys. Lett. 2014, 104, 214103. [Google Scholar] [CrossRef]
- Kim, Y.; Lim, H.J.; Sohn, H. Nonlinear ultrasonic modulation based failure warning for aluminum plates subject to fatigue loading. Int. J. Fatigue 2018, 114, 130–137. [Google Scholar] [CrossRef]
- Lim, H.J.; Sohn, H.; Kim, Y. Data-driven fatigue crack quantification and prognosis using nonlinear ultrasonic modulation. Mech. Syst. Signal Process. 2018, 109, 185–195. [Google Scholar] [CrossRef]
- Ding, X.; Xu, C.; Deng, M.; Zhao, Y.; Bi, X.; Hu, N. Experimental investigation of the surface corrosion damage in plates based on nonlinear Lamb wave methods. Ndt E Int. 2021, 121, 102466. [Google Scholar] [CrossRef]
- Cirtautas, D.; Samaitis, V.; Mažeika, L.; Raišutis, R.; Žukauskas, E. Selection of Higher Order Lamb Wave Mode for Assessment of Pipeline Corrosion. Metals 2022, 12, 503. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.; Zhu, B.; Cho, Y. Nonlinear Ultrasonic Guided Wave Method Using Semi-Analytical Finite Element (SAFE) Technique on a Damaged SWO-V Spring Coil. Metals 2021, 11, 752. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Dover Publications: New York, NY, USA, 1975. [Google Scholar]
- Matsuda, N.; Biwa, S. Phase and group velocity matching for cumulative harmonic generation in Lamb waves. J. Appl. Phys. 2011, 109, 094903. [Google Scholar] [CrossRef] [Green Version]
- Auld, B.A. Acoustic Fields and Waves in Solids, 2nd ed.; Krieger Publishing Company: Malabar, FL, USA, 1990. [Google Scholar]
- De Lima, W.; Hamilton, M. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. 2003, 265, 819–839. [Google Scholar] [CrossRef]
- Müller, M.F.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am. 2010, 127, 2141–2152. [Google Scholar] [CrossRef]



| Secondary Mode Type | v | ||
|---|---|---|---|
| Symmetric | {S 0 A} | ||
| Antisymmetric | {A 0 S} |
| Fundamental Wave Field | Secondary Modulation |
|---|---|
| Symmetric–symmetric | Symmetric |
| Antisymmetric–antisymmetric | |
| Symmetric–antisymmetric | Antisymmetric |
| No. | Waves | Primary Mode | Frequency | Synchronism | Theoretical Modulation |
|---|---|---|---|---|---|
| 1 | a | S0 | 195 kHz | Only for fb + fa | S0 mode at 468 kHz |
| b | S0 | 273 kHz | |||
| 2 | a | S0 | 210 kHz | Only for fb − fa | S0 mode at 246 kHz |
| b | S0 | 456 kHz | |||
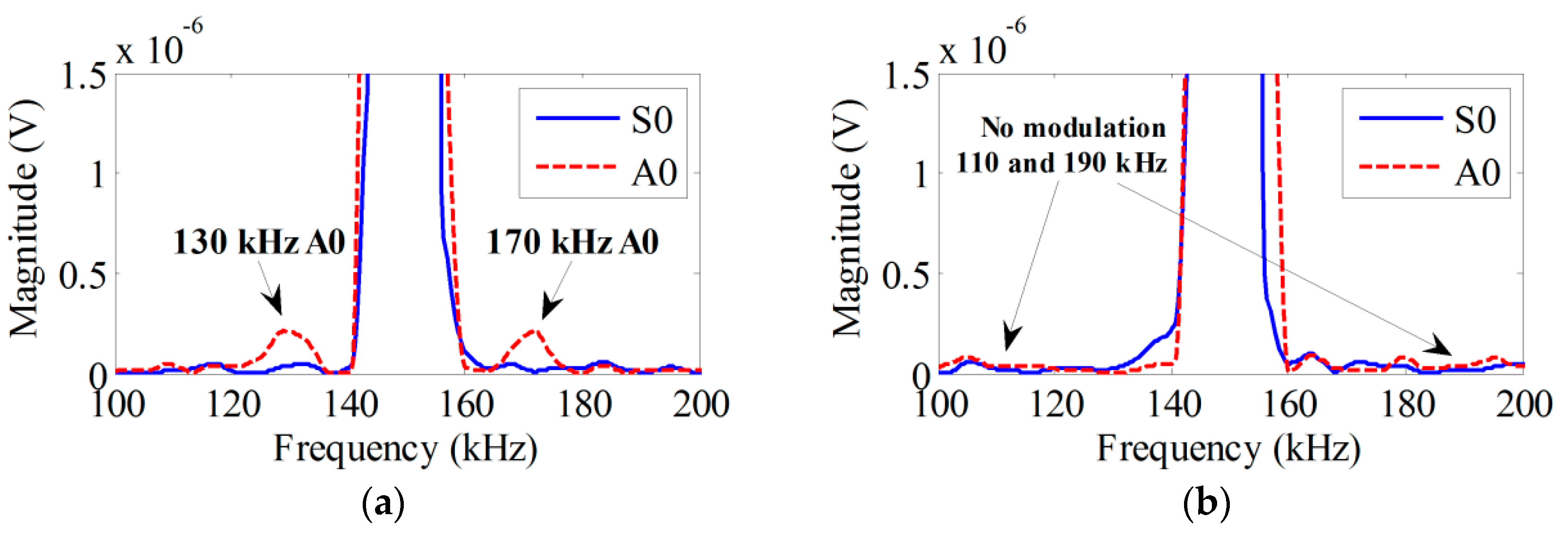
| 3 | a | A0 | 20 kHz | Both fb + fa and fb − fa | A0 mode at 170 kHz and 130 kHz |
| b | S0 | 150 kHz | |||
| 4 | a | A0 | 40 kHz | None | None |
| b | S0 | 150 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Zhang, G.; Hou, H.; Wang, L. Mutual Interactions of Lamb Waves in Nonlinear Elastic Plates. Metals 2022, 12, 2175. https://doi.org/10.3390/met12122175
Ma S, Zhang G, Hou H, Wang L. Mutual Interactions of Lamb Waves in Nonlinear Elastic Plates. Metals. 2022; 12(12):2175. https://doi.org/10.3390/met12122175
Chicago/Turabian StyleMa, Shuyi, Guixian Zhang, Hongfeng Hou, and Lidong Wang. 2022. "Mutual Interactions of Lamb Waves in Nonlinear Elastic Plates" Metals 12, no. 12: 2175. https://doi.org/10.3390/met12122175




