Effect of Hydrogen in Mixed Gases on the Mechanical Properties of Steels—Theoretical Background and Review of Test Results
Abstract
:1. Introduction
2. Fugacity of Hydrogen in Gas Mixtures
- P: total pressure,
- R: universal gas constant, 8.314 J/(mol K),
- T: absolute temperature, K,
- Vm: molar volume.
- xHH: molar fraction of H2,
- P: total pressure of the gas mixture,
- b: co-volume constant of the gas mixture.
- pHH, pGas: partial pressures of H2 and the other gas, respectively,
- bHH, bGas: co-volume constants of H2 and the other gas, respectively.
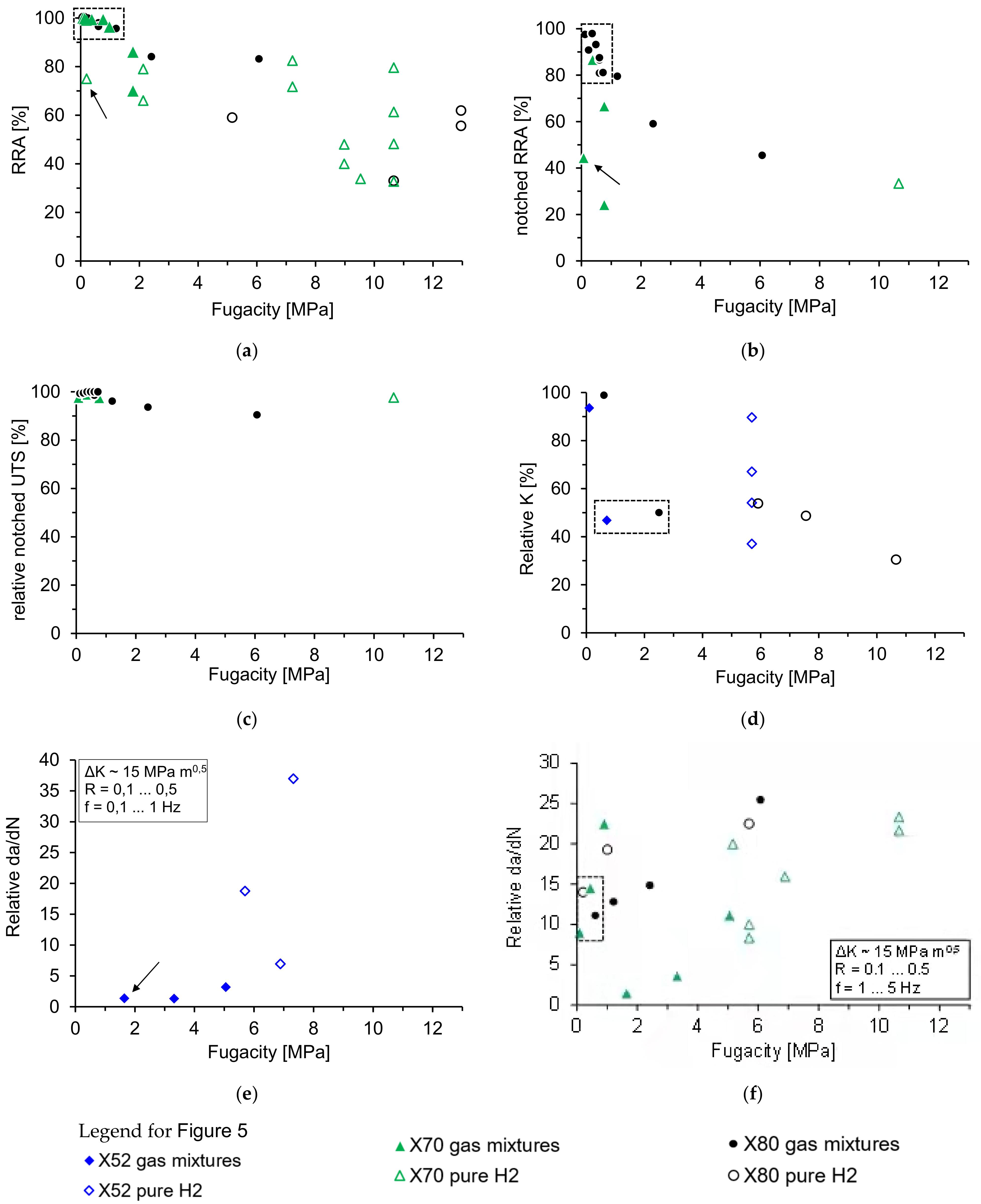
3. Compilation and Interpretation of Literature Results for Mechanical Properties as a Function of Hydrogen Fugacity
3.1. Tensile Tests
3.2. Fracture Toughness Tests
3.3. Fatigue Crack Growth Tests
3.4. General Comments
4. Conclusions
- For materials testing purposes requiring a defined atmosphere, testing in CH4-H2 mixtures is preferred compared to N2-H2 mixtures to simulate the effect of H2 additions to NG.
- The reviewed results imply no significant difference between tests in pure H2 gas and tests in gas mixtures at the same hydrogen fugacity. This needs to be verified experimentally.
- Among the test methods reviewed here, fatigue crack growth testing is the most sensitive method to measure hydrogen effects in pipeline steels even at a very low fugacity (less than 0.5 MPa). Fracture toughness testing appears less sensitive followed by tensile testing, especially with smooth specimens.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cerniauskas, S.; Junco, A.J.C.; Grube, T.; Robinius, M.; Stolten, D. Options of natural gas pipeline reassignment for hydrogen: Cost assessment for a Germany case study. Int. J. Hydrog. Energy 2020, 45, 12095–12107. [Google Scholar] [CrossRef] [Green Version]
- Michler, T.; Wackermann, K.; Schweizer, F. Review and Assessment of the Effect of Hydrogen Gas Pressure on the Embrittlement of Steels in Gaseous Hydrogen Environment. Metals 2021, 11, 637. [Google Scholar] [CrossRef]
- Marchi, C.S.; Somerday, B.P.; Larson, R.S.; Rice, S.F. Solubility of hydrogen and its isotopes in metals from mixed gases. J. Nucl. Mater. 2008, 372, 421–425. [Google Scholar] [CrossRef]
- Somerday, B.P.; Sofronis, P.; Nibur, K.A.; Marchi, C.S.; Kirchheim, R. Elucidating the variables affecting accelerated fatigue crack growth of steels in hydrogen gas with low oxygen concentrations. Acta Mater. 2013, 61, 6153–6170. [Google Scholar] [CrossRef]
- Michler, T.; Boitsov, I.E.; Malkov, I.L.; Yukhimchuk, A.A.; Naumann, J. Assessing the effect of low oxygen concentrations in gaseous hydrogen embrittlement of DIN 1.4301 and 1.1200 steels at high gas pressures. Corros. Sci. 2012, 65, 169–177. [Google Scholar] [CrossRef]
- Ez-Zaki, H.; Christien, F.; Bosch, C.; Briottet, L.; Bertin, M.; Levasseur, O.; Leriverain, A. Effect of hydrogen content in natural gas blend on the mechanical properties of a L485-MB low-alloyed steel. In Proceedings of the ASME 2020 Pressure Vessels & Piping Conference, Viral Conference, 19–24 July 2020; ASME Press: Minneapolis, MN, USA, 2020; p. PVP2020–21228. [Google Scholar] [CrossRef]
- Shang, J.; Zheng, J.; Hua, Z.; Li, Y.; Gu, C.; Cui, T.; Meng, B. Effects of stress concentration on the mechanical properties of X70 in high-pressure hydrogen-containing gas mixtures. Int. J. Hydrog. Energy 2020, 45, 28204–28215. [Google Scholar] [CrossRef]
- Baek, U.; Nahm, S.; Lee, H.; Lee, Y. Mechanical Properties of X70 Steel in Gaseous Hydrogen. In Proceedings of the International Hydrogen Conference (IHC 2012): Hydrogen-Materials Interactions, Moran, WY, USA, 9–12 September 2012; pp. 219–226. [Google Scholar] [CrossRef]
- Meng, B.; Gu, C.; Zhang, L.; Zhou, C.; Li, X.; Zhao, Y.; Zheng, J.; Chen, X.; Han, Y. Hydrogen effects on X80 pipeline steel in high-pressure natural gas/hydrogen mixtures. Int. J. Hydrog. Energy 2017, 42, 7404–7412. [Google Scholar] [CrossRef]
- Marchi, C.S.; Somerday, B.P.; Robinson, S.L. Permeability, solubility and diffusivity of hydrogen isotopes in stainless steels at high gas pressures. Int. J. Hydrog. Energy 2007, 32, 100–116. [Google Scholar] [CrossRef]
- Sugimoto, H.; Fukai, Y. Solubility of hydrogen in metals under high hydrogen pressures: Thermodynamical calculations. Acta Met. Mater. 1992, 40, 2327–2336. [Google Scholar] [CrossRef]
- Marchi, C.S.; Somerday, B.P. Thermodynamics of Gaseous Hydrogen and Hydrogen Transport in Metals. In Proceedings of the MRS Spring 2008 Meeting, Session HH: “The Hydrogen Economy”, San Francisco, CA, USA, 24–28 March 2008; pp. 1–12. [Google Scholar]
- Chenoweth, D.R. Gas-Transfer Analysis. Section H-Real Gas Results Via the Van der Waals Equation of State and Virial Expansion Extension of its Limiting Abel-Noble Form; U.S. Department of Energy, Office of Scientific and Technical Information: Washington, DC, USA, 1983; p. 87. [Google Scholar]
- Chenoweth, D.R.; Paolucci, S. Compressible flow of a two-phase fluid between finite vessels-II. Int. J. Multiph. Flow. 1992, 18, 669–689. [Google Scholar] [CrossRef]
- Michels, A.; Wouters, H.; de Boer, J. Isotherms of nitrogen between 0° and 150° and at pressures from 20 to 80 atm. Physica 1934, 1, 587–594. [Google Scholar] [CrossRef]
- Michels, A.; Lunbeck, R.J.; Wolkers, G.J. Thermodynamical properties of nitrogen as functions of density and temperature between −125° and +150 °C and densities up to 760 Amagat. Physica 1951, 17, 801–816. [Google Scholar] [CrossRef]
- Isotherms of hydrogen, of nitrogen, and of hydrogen-nitrogen mixtures, at 0° and 20 °C, up to a pressure of 200 atmospheres. Proc. R. Soc. Lond. Ser. A 1926, 111, 552–576. [CrossRef] [Green Version]
- Trappeniers, N.J.; Wassenaar, T.; Abels, J.C. Isotherms and thermodynamic properties of methane at temperatures between 0° and 150°C and at densities up to 570 amagat. Phys. A 1979, 98, 289–297. [Google Scholar] [CrossRef]
- Kvalnes, H.M.; Gaddy, V.L. The compressibility isotherms of methane at pressures to 1000 atmospheres and at temperatures from −70 to 200°. J. Am. Chem. Soc. 1931, 53, 394–399. [Google Scholar] [CrossRef]
- Schley, P.; Jaeschke, M.; Küchenmeister, C.; Vogel, E. Viscosity measurements and predictions for natural gas. Int. J. Thermophys. 2004, 25, 1623–1652. [Google Scholar] [CrossRef]
- Mihara, S.; Sagara, H.; Arai, Y.; Saito, S. The Compressibility Factors of Hydrogen Methane, Hydrogen Ethane and Hydrogen Propane Gaseous Mixtures. J. Chem. Eng. 1977, 10, 395–399. [Google Scholar] [CrossRef] [Green Version]
- Azizi, N.; Behbahani, R.; Isazadeh, M.A. An efficient correlation for calculating compressibility factor of natural gases. J. Nat. Gas Chem. 2010, 19, 642–645. [Google Scholar] [CrossRef]
- Čapla, L.; Buryan, P.; Jedelský, J.; Rottner, M.; Linek, J. Isothermal pVT measurements on gas hydrocarbon mixtures using a vibrating-tube apparatus. J. Chem. Thermodyn. 2002, 34, 657–667. [Google Scholar] [CrossRef]
- Zhou, J.; Patil, P.; Ejaz, S.; Atilhan, M.; Holste, J.C.; Hall, K.R. (p, Vm, T) and phase equilibrium measurements for a natural gas-like mixture using an automated isochoric apparatus. J. Chem. Thermodyn. 2006, 38, 1489–1494. [Google Scholar] [CrossRef]
- Langelandsvik, L.I.; Solvang, S.; Rousselet, M.; Metaxa, I.N.; Assael, M.J. Dynamic viscosity measurements of three natural gas mixtures-comparison against prediction models. Int. J. Thermophys. 2007, 28, 1120–1130. [Google Scholar] [CrossRef]
- Duncan, A.; Lam, P.-S.; Adams, T. Tensile testing of carbon steel in high pressure hydrogen. In Proceedings of the ASME 2007 Pressure Vessels and Piping Conference, San Antonio, TX, USA, 22–26 July 2007; p. PVP2007–PVP26736. [Google Scholar]
- Kussmaul, K.; Deimel, P.; Sattler, E. Tensile properties of the steel X70TM in high pressure hydrogen gas with admixtures of oxygen at different strain rates. In Proceedings of the 10th World Energy Conference Cocoa Hydrogen Energy Progress X, Boca Beach, FL, USA, 20–24 June 1994; pp. 285–293. [Google Scholar]
- Michler, T.; Naumann, J. Microstructural aspects upon hydrogen environment embrittlement of various bcc steels. Int. J. Hydrog. Energy 2010, 35, 821–832. [Google Scholar] [CrossRef]
- Bae, D.S.; Sung, C.E.; Bang, H.J.; Lee, S.P.; Lee, J.K.; Son, I.S.; Cho, Y.R.; Baek, U.B.; Nahm, S.H. Effect of highly pressurized hydrogen gas charging on the hydrogen embrittlement of API X70 steel. Met. Mater. Int. 2014, 20, 653–658. [Google Scholar] [CrossRef]
- Hejazi, D.; Calka, A.; Dunne, D.; Pereloma, E. Effect of gaseous hydrogen charging on the tensile properties of standard and medium Mn X70 pipeline steels. Mater. Sci. Technol. 2016, 32, 675–683. [Google Scholar] [CrossRef] [Green Version]
- Baek, U.B.; Lee, H.M.; Baek, S.W.; Nahm, S.H. Hydrogen Embrittlement for X-70 Pipeline Steel in High Pressure Hydrogen Gas. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; ASME Press: Boston, MA, USA, 2015; p. PVP2015–PVP45475. [Google Scholar] [CrossRef]
- Zhou, D.; Li, T.; Huang, D.; Wu, Y.; Huang, Z.; Xiao, W.; Wang, Q.; Wang, X. The experiment study to assess the impact of hydrogen blended natural gas on the tensile properties and damage mechanism of X80 pipeline steel. Int. J. Hydrog. Energy 2021, 46, 7402–7414. [Google Scholar] [CrossRef]
- Moro, I.; Briottet, L.; Lemoine, P.; Andrieu, E.; Blanc, C.; Odemer, G. Hydrogen embrittlement susceptibility of a high strength steel X80. Mater. Sci. Eng. A 2010, 527, 7252–7260. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Zhao, W.; Zhao, Y.; Ouyang, K.; Deng, Q.; Wang, Y.; Jiang, W. Effects of surface oxide films on hydrogen permeation and susceptibility to embrittlement of X80 steel under hydrogen atmosphere. Int. J. Hydrog. Energy 2018, 43, 3353–3365. [Google Scholar] [CrossRef]
- Batisse, R.; Cuni, A.; Wastiaux, S.; Briottet, L.; Lemoine, P.; de Dinechin, G.; Chagnot, C.; Castilan, F.; Klosek, V.; Langlois, P.; et al. Investigation of X80-steel grade for hydrogen gas transmission pipelines. In Proceedings of the 2008 International Gas Research Conference, Paris, France, 8–10 October 2008; Gas Technology Institute: Paris, France, 2008; pp. 1572–1588. [Google Scholar]
- Van Wortel, H.; Gomes, M.; Demofoni, G.; Capelle, J.; Alliat, J.; Chatzidouros, E. Final report “Preparing for the hydrogen economy by using the existing natural gas system as a catalyst (NATURALHY) WP3.2: Transmission pipelines, 2009” Funded by the EU within the 6th framework programme.
- Zhou, Z.; Zhang, K.; Hong, Y.; Zhu, H.; Zhang, W.; He, Y.; Zhou, C.; Zheng, J.; Zhang, L. The dependence of hydrogen embrittlement on hydrogen transport in selective laser melted 304L stainless steel. Int. J. Hydrog. Energy 2021, 46, 16153–16163. [Google Scholar] [CrossRef]
- Shi, H.; Xing, Y.; Wang, X. Influence law of hydrogen content in coal gas system on hydrogen embrittlement sensitivity of X80 pipeline steel. Corros. Prot. 2018, 39, 336–339. [Google Scholar]
- Shang, J.; Wang, J.Z.; Chen, W.F.; Wei, H.T.; Zheng, J.Y.; Hua, Z.L.; Zhang, L.; Gu, C.H. Different effects of pure hydrogen vs. hydrogen/natural gas mixture on fracture toughness degradation of two carbon steels. Mater. Lett. 2021, 296, 129924. [Google Scholar] [CrossRef]
- Marchi, C.S.; Somerday, B.P.; Nibur, K.A.; Stalheim, D.G.; Boggess, T.; Jansto, S. Fracture and fatigue of commercial grade API pipeline steels in gaseous hydroge. In Proceedings of the ASME 2010 Pressure Vessels and Piping Division Conference (PVP 2010), Washington, DC, USA, 18–22 July 2010; p. PVP2010–2PVP5825. [Google Scholar]
- Cialone, H.J.; Holbrook, J.H. Sensitivity of Steels to Degradation in Gaseous Hydrogen. In ASTM STP 962; Raymond, E.L., Ed.; ASTM International: Philadelphia, PA, USA, 1988; pp. 134–152. [Google Scholar]
- Ronevich, J.A.; Marchi, C.S. Materials compatibility concerns for hydrogen blended into natural gas. In Proceedings of the ASME 2021 Pressure Vessels and Piping Conference (PVP2021), Virtual Online Conference, 12–16 July 2021; ASME Press: New York, NY, USA, 2021; p. PVP2021–PVP62045. [Google Scholar]
- Stalheim, D.; Jansto, S.G.; Boggess, T.; Ningileri, S.; Bromley, D. Microstructure and mechanical property performance evaluation of commercial grade API pipeline steels in high pressure gaseous hydrogen. In Proceedings of the 2012 International Hydrogen Conference Hydrogen-Materials Interactions, Moran, WY, USA, 9–12 September 2012; Somerday, B.P., Sofronis, P., Eds.; ASME Press: Jackson Lake Lodge, WY, USA, 2012; pp. 209–218. [Google Scholar]
- An, T.; Zhang, S.; Feng, M.; Luo, B.; Zheng, S.; Chen, L.; Zhang, L. Synergistic action of hydrogen gas and weld defects on fracture toughness of X80 pipeline steel. Int. J. Fatigue 2019, 120, 23–32. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; An, T.; Zheng, S.; Yang, K.; Lv, L.; Xie, C.; Chen, L.; Zhang, L. Investigating the influence mechanism of hydrogen partial pressure on fracture toughness and fatigue life by in-situ hydrogen permeation. Int. J. Hydrog. Energy 2021, 46, 20621–20629. [Google Scholar] [CrossRef]
- Drexler, E.S.; Slifka, A.J.; Amaro, R.L.; Sowards, J.W.; Connolly, M.J.; Martin, M.L.; Lauria, D.S. Fatigue Testing of Pipeline Welds and Heat-Affected Zones in Pressurized Hydrogen Gas. J. Res. Natl. Inst. Stand. Technol. 2019, 124, 124008. [Google Scholar] [CrossRef]
- Drexler, E.S.; Slifka, A.J.; Amaro, R.L.; Barbosa, N.; Lauria, D.S.; Hayden, L.E.; Stalheim, D.G. Fatigue crack growth rates of API X70 pipeline steel in a pressurized hydrogen gas environment. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 517–525. [Google Scholar] [CrossRef]
- Slifka, A.J.; Drexler, E.S.; Stalheim, D.G.; Amaro, R.L.; Lauria, D.S.; Stevenson, A.E.; Hayden, L.E. The effect of microstructure on the hydrogen-assisted fatigue of pipeline steels. In Proceedings of the ASME 2013 Pressure Vessels and Piping Conference (PVP2013), Paris, France, 14–18 July 2013; ASME Press: Paris, France, 2013; p. PVP2013–PVP97217. [Google Scholar]
- Drexler, E.S.; Amaro, R.L.; Slifka, A.J.; Bradley, P.E.; Lauria, D.S. Operating Hydrogen Gas Transmission Pipelines at Pressures Above 21 MPa. J. Press. Vessel Technol. 2018, 140, 61702. [Google Scholar] [CrossRef]
- Baek, U.B.; Nahm, S.H.; Kim, W.S.; Ronevich, J.A.; Marchi, C.S. Compatibility and suitability of existing steel pipeline for transport of hydrogen-natural gas blends. In Proceedings of the International Conference on Hydrogen Safety, Hamburg, Germany, 11–13 September 2017. [Google Scholar]
- Slifka, A.J.; Drexler, E.S.; Nanninga, N.E.; Levy, Y.S.; McColskey, J.D.; Amaro, R.L.; Stevenson, A.E. Fatigue crack growth of two pipeline steels in a pressurized hydrogen environment. Corros. Sci. 2014, 78, 313–321. [Google Scholar] [CrossRef]
- Ronevich, J.A.; Somerday, B.P.; Feng, Z. Hydrogen accelerated fatigue crack growth of friction stir welded X52 steel pipe. Int. J. Hydrog. Energy 2017, 42, 4259–4268. [Google Scholar] [CrossRef] [Green Version]
- Chandra, A.; Thodla, R.; Prewitt, T.J.; Matthews, W.; Sosa, S. Fatigue Crack Growth Study of X70 Line Pipe Steel in Hydrogen Containing Natural Gas Blends. In Proceedings of the ASME 2021 Pressure Vessels and Piping Conference (PVP2021), Virtual Conference, 12–16 July 2021; ASME Press: New York, NY, USA, 2021; p. PVP2021–PVP61821. [Google Scholar]
- Engel, V.C.; Marewski, U.; Schnotz, G.; Silcher, H.; Steiner, M.; Zickler, S. Bruchmechanische Prüfungen von Werkstoffen für Gasleitungen zur Bewertung der Wasserstofftauglichkeit: Erste Ergebnisse (In German), 3R Fachzeitschrift Für Sichere Und Effiziente Rohrleitungssysteme. Pipelintechnik 2020, 10–11, 34–41. [Google Scholar]
- Lee, J.A. Rapid and low cost method to determine the plane strain fracture toughness (K1C) in hydrogen. In Proceedings of the 2012 International Hydrogen Conference Hydrogen-Materials Interactions, Moran, WY, USA, 9–12 September 2012; Sofronis, P., Ed.; ASME Press: Jackson Lake Lodge, WY, USA, 2012; pp. 461–470. [Google Scholar]
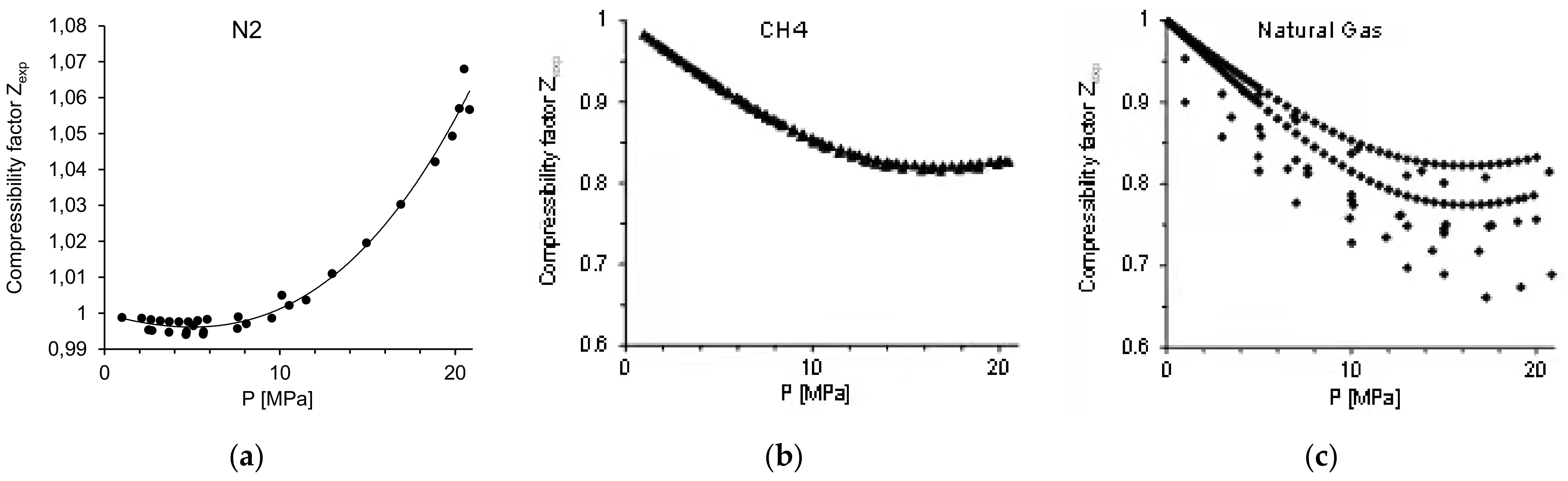

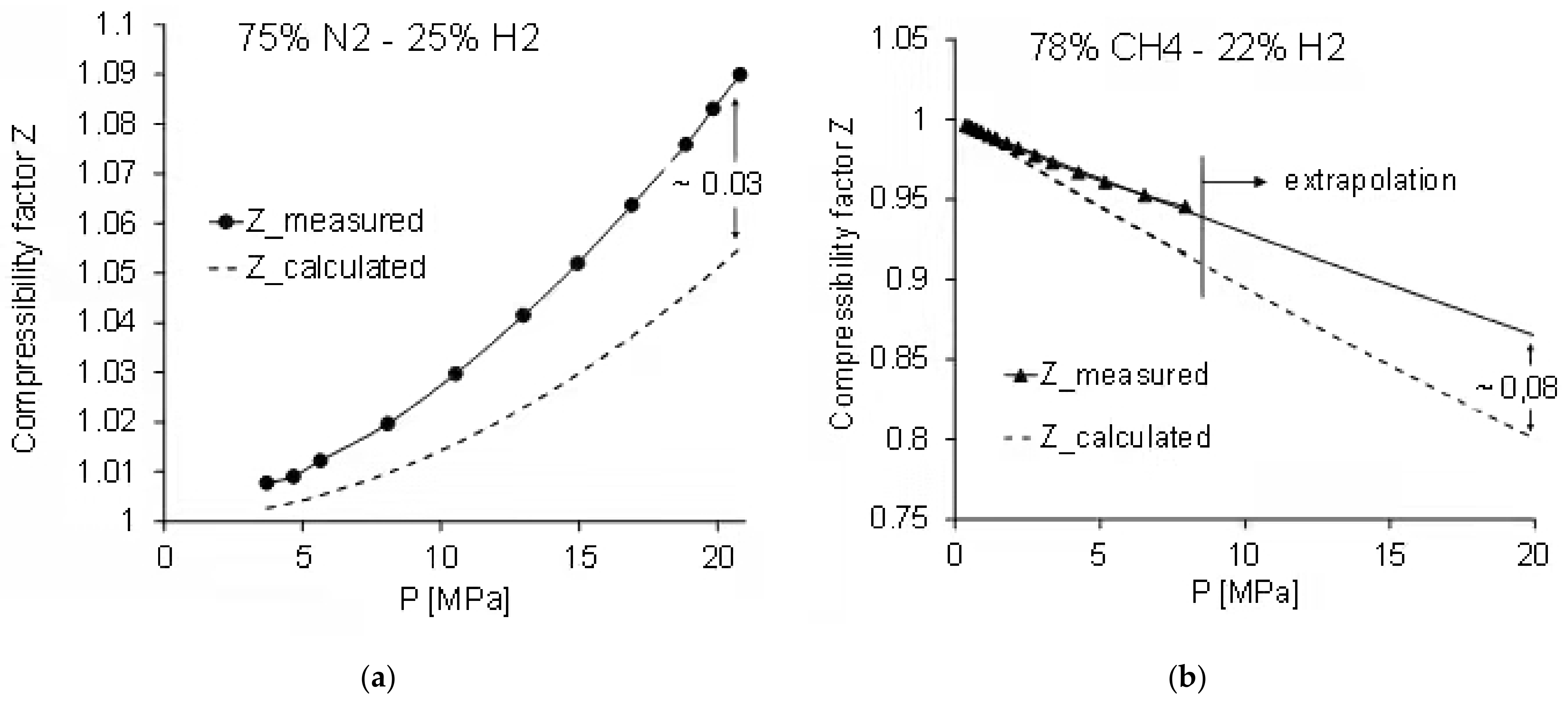
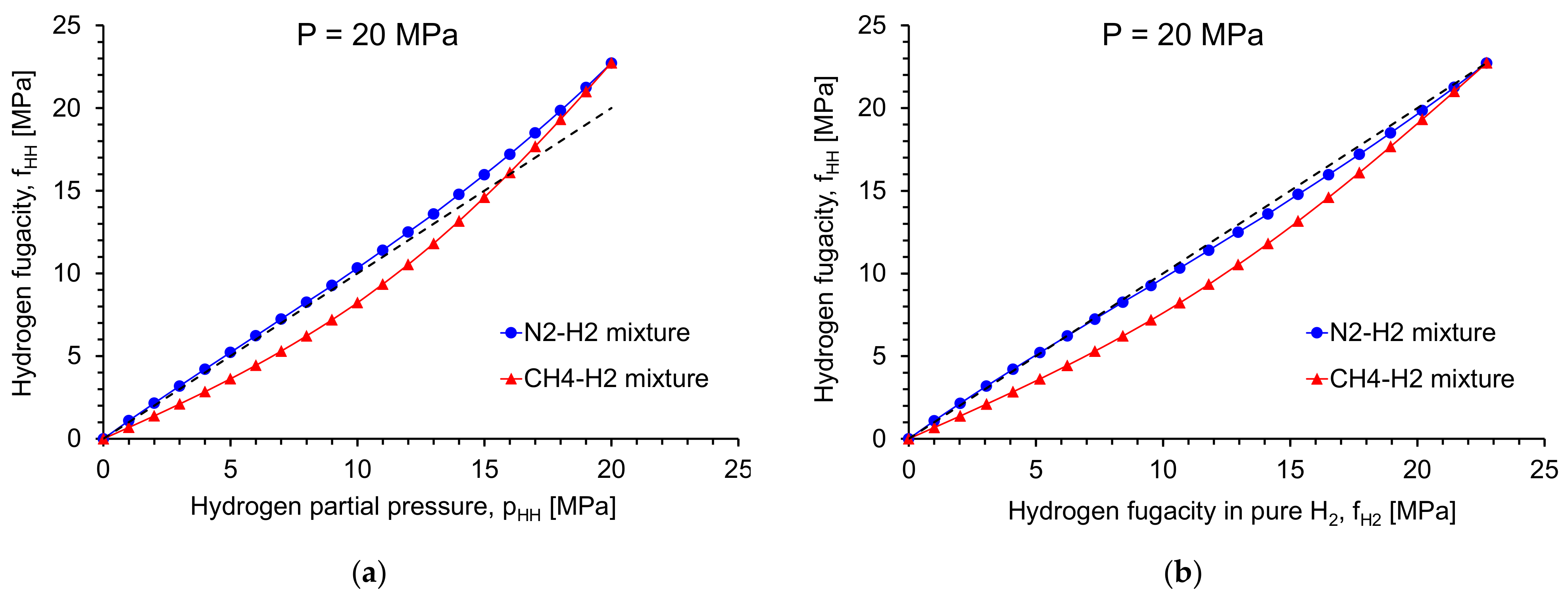
| Coefficient | N2 | CH4 |
|---|---|---|
| A, MPa−5 | 0 | −0.00000006 |
| B, MPa−4 | 0 | 0.00000200 |
| C, MPa−3 | 0.00000551 | −0.00000243 |
| D, MPa−2 | 0.00009256 | 0.00012034 |
| E, MPa−1 | −0.00133489 | −0.01709066 |
| F | 0.99979310 | 1.00027004 |
| R² | 0.98691955 | 0.99889577 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michler, T.; Elsässer, C.; Wackermann, K.; Schweizer, F. Effect of Hydrogen in Mixed Gases on the Mechanical Properties of Steels—Theoretical Background and Review of Test Results. Metals 2021, 11, 1847. https://doi.org/10.3390/met11111847
Michler T, Elsässer C, Wackermann K, Schweizer F. Effect of Hydrogen in Mixed Gases on the Mechanical Properties of Steels—Theoretical Background and Review of Test Results. Metals. 2021; 11(11):1847. https://doi.org/10.3390/met11111847
Chicago/Turabian StyleMichler, Thorsten, Christian Elsässer, Ken Wackermann, and Frank Schweizer. 2021. "Effect of Hydrogen in Mixed Gases on the Mechanical Properties of Steels—Theoretical Background and Review of Test Results" Metals 11, no. 11: 1847. https://doi.org/10.3390/met11111847






