Magnetic Field Generated during Electric Current-Assisted Sintering: From Health and Safety Issues to Lorentz Force Effects

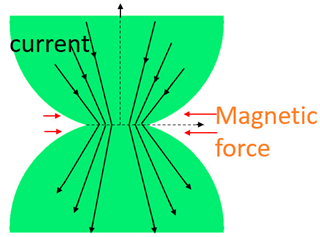
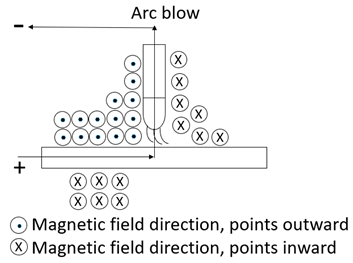
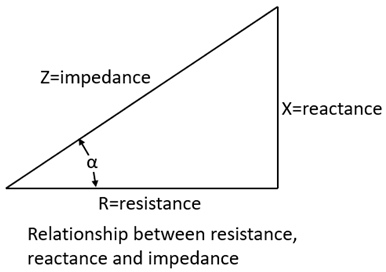
Abstract

In the past decade, a renewed interest on electromagnetic processing of materials has motivated several investigations on the interaction between matter, electric and magnetic fields. These effects are primarily reconducted to the Joule heating and very little attention has been dedicated to the magnetic field contributions. The magnetic field generated during electric current-assisted sintering has not been widely investigated. Magnetism could have significant effects on sintering as it generates significant magnetic forces, resulting in inductive electrical loads and preferential heating induced by overlapping magnetic fields (i.e., proximity effect). This work summarizes the magnetic field effects in electric current-assisted processing; it focuses on health and safety issues associated with large currents (up to 0.4 MA); using FEM simulations, it computes the self-generated magnetic field during spark plasma sintering (SPS) to consolidate materials with variable magnetic permeability; and it quantifies the Lorentz force acting at interparticle contact points. The results encourage one to pay more attention to magnetic field-related effects in order to engineer and exploit their potentials.

1. Magnetic Field Effects in Electromagnetic Processing of Materials (EPM)

In electromagnetic processing of materials (EPM) [1], research has been mostly focused on current and temperature effects, often neglecting the magnetic contribution. The purpose of this paper is to investigate the effects of self-generated magnetic fields by a current passing across the processed material. This work does not cover externally applied magnetic fields, as such a topic was extensively discussed by Guo et al. [2].

As early as 1886, Elihu Thompson developed the first resistance welding machine, which represented a major improvement in joining technology with a wide range of applications [3]. At that stage, it was already clear that ferromagnetic objects (both constituting the welding fixtures or the work piece) should be avoided. High current (exceeding several hundreds of Amperes) would generate a strong magnetization of these ferromagnetic materials, resulting in a decreased welding efficiency limiting the maximum output current [4]. Curiously, at that time, ferromagnetic materials in the vicinity of the welding equipment were intentionally employed to increase the resistive load on the generator.

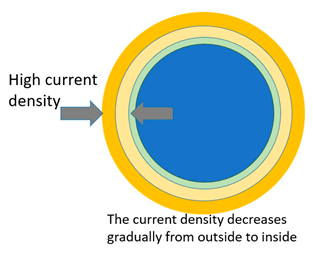
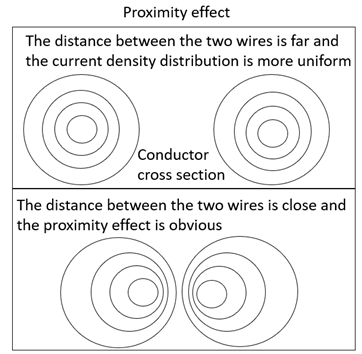
Electric current-assisted sintering (ECAS) techniques began their journey from the beginning of the last century. Compared with conventional sintering techniques, ECAS has the following advantages: low furnace temperature, short processing duration, direct Joule heating on the workpiece, and significantly improved material properties [2,5,6,7,8]. While magnetic field effects have been well-investigated in the case of welding, they still remain unexplored in sintering. The magnetic fields effects in ECAS, being secondary effects, are poorly discussed in the literature. Table 1 summarizes magnetic-related effects in EPM. It includes several electromagnetic phenomena, their applications, physical principle and their mathematical formulation. White and Fasenfest [9] proposed a method for evaluating the discrete Biot–Savart law. Wheeler et al. [10] investigated the skin effect as early as 1942, and he also proposed a mathematical formulation for different configurations and operating frequencies. Ahmad et al. [11] analyzed the skin effect in detail by proposing computer models. The proximity effect occurring at high frequency (>100 kHz) with applications in pipe welding was analyzed in Ref. [12]. Such an effect caused a current density increase in the vicinity of the strip edge zone. Zhao et al. [13] investigated the influence of the proximity effect on the welding process, including high-frequency welding of H-shaped steel and T-shaped steel. Thus far, no work has been published on the possible influence of the proximity effect on sintering. J. Trapp [14] quantified the pinch effect and its impact on the sintering of ideal spherical particles. Yurlova et al. [15] investigated the influence of the pinch effect on the sintering process, and their result suggests that magnetic forces would result in a modification of the sample shape, allowing an easy extraction out of the die. These effects became apparent under low-pressure conditions. The concept of the undesired “arc blow” effect induced by the magnetic field was analyzed by Tomoyuki et al. [16] in 2011. The experimental conditions needed for preventing arc blow were discussed by Yamaguchi et al. [17] and M. Vural [18]. Lockwood et al. [19] explained that under AC conditions, an electrical arc is more stable than in DC, and they correlated the influence of electromagnetic force with the porosity of the welded materials. With some analogies, Adamian and Shneerson [20] investigated the mechanisms of electric wire explosion where a strong radial compression induced by the magnetic field contributes to fragmentation of the particles.

Table 1. Magnetic field effects in electromagnetic processing of materials (EPM). The possible implications on sintering are listed in italics.

Effect Name	Principle and Mathematical Formulation	Typical Use, Implications on Sintering
Biot–Savart Law	This formulation resembles well the magnetic-induced effect in using DC currents. The Biot–Savart Law quantifies the magnetic field strength inside and outside the conductor. It refers to an infinitely long wire with radius r [9,22,23]. $$B=\frac{{\mu }_{0}I}{2\pi r_0}$$ μ0—The vacuum permeability, with value of 4π × 10−7 H/m. r0 is the radius of the conductor	It can be used to calculate the magnetic field strength in the vicinity of a conductor. It can accurately identify the health and safety exposure distance [9,22,23]. Health and safety hazard for the operators and magnetization of the electrically conductive sample under an electrical discharge.
Skin effect	It commonly occurs in high-frequency alternating current, resulting in preferential current flow within the skin depth. $$\mathsf{\Delta }=\sqrt{\frac{2}{\omega \mu \gamma }}$$ Δ—(m), the radial depth that the current can reach from the surface of the wire. Where $\omega , \mu$, and $\gamma$ are angular frenquency, permeability, and conductivity. According to Lenz’s law, the induced current is always in the opposite direction to the imposed current, which eventually leads to the current in the conductor tending to approach the surface of the conductor [10,11,12,24]. Eddy currents are loops of electrical current within a conductor resulting from a changing magnetic field [24,25].	Heat generation localized on the skin depth. This effect was commonly used in induction heating of a workpiece [10,11,13,24]. Preferential heating by skin effect. Possibility to counterbalance radiative heat losses.
AC resistance change in the vicinity of the Curie temperature	An alternating (i.e., time-variable) current flowing across a ferromagnetic conductor sees an increase in resistivity due to the skin effect. These effects disappear above the Curie temperature [26,27].	For ferromagnetic materials (i.e., Ni, Fe, Co), the Curie temperature should be considered during heating [26,27]. Precise calibration of the temperatures and rapid drop of electrical resistance at a temperature greater than the Curie point.
	This effect occurs under high-frequency current (100 kHz) and it was typically used to generate overheating by promoting an interaction between magnetic fields. Eddy currents result in preferential current distribution [11,13,24].	When using high-frequency alternating current for welding, the proximity effect should be considered [11,13]. Not investigated in sintering. It is expected to provide further overheating at interparticle contact points.
Pinch effect	Pinch effect refers to the compressive forces acting on the conductive media as a result of the magnetic forces. The conductive media can be in the form of a liquid, a solid, or a plasma. These effects are particularly strong in the presence of large currents as in the case of a capacitor discharge [14,15,28,29].	The pinch effect induces a shape change of the sample, easing its extraction out of the die [15]. Might not have strong implications in pressure-assisted sintering. Pinch-related pressure is several orders of magnitude lower than the sintering pressure (≈ MPa).
	This phenomenon was often encountered in the welding. The magnetic bias blow is caused by the unbalanced magnetic field around the electrical arc [17,18,19].	An AC current is less susceptible to arc blowing compared to DC [17,18,19]. Arcing is usually seen as an undesired effect in sintering.
Reactance dependence on duty cycle	Ferromagnetic materials significantly increase the reactance, reducing the welding or sintering current [19]. $$Z=R+jX$$ where Z, R, and X are impedance, resistance, and reactance, respectively, the unit is ohm, and j is the imaginary unit.	Ferromagnetic materials increase the reactance, and leads to an increase in impedance, ultimately resulting in a decrease in current [19]. Implications on the material selected as tooling.

Magnetic materials subjected to an alternating electrical discharge greatly increase their inductance, thereby reducing the welding current. The result is a direct consequence of Lenz’s law. This also explains the rationale for choosing different types of power supplies (AC/DC) for different materials. The magnetic field also generates undesired interference with the probing devices, thus affecting the readings of temperature, current, voltage. Zhang and Senkara [21] investigated how a spot welding high current affected these signals. In response to this problem, they adopted fiber-optic displacement sensors, which are insensitive to the high magnetic fields.

In summary, magnetic-related effects are complex and Table 1 suggests a simplification of these phenomena. This manuscript is divided into two parts. The first part provides some FEM simulations to quantify magnetic strength generated by a spark plasma sintering machine, both at the tooling level and the interparticle level for materials with different magnetic permeability (i.e., copper, iron, alumina, graphite). The second part of the paper provides some preliminary experimental evidence of the magnetic field effects on sintering.

2. The Combined Experimental/Computational Methodology

The primary purpose of this paper was to develop accurate simulations accounting for the magnetic field effects. The Multiphysics coupling was recreated using a built-in scheme using Comsol Multiphysics [30]. The electrothermal model was built according to the model proposed in Ref. [31]. It reproduced the spark plasma sintering (SPS) sample geometry, upper punch, lower punch, and SPS die, as shown in Figure 1.

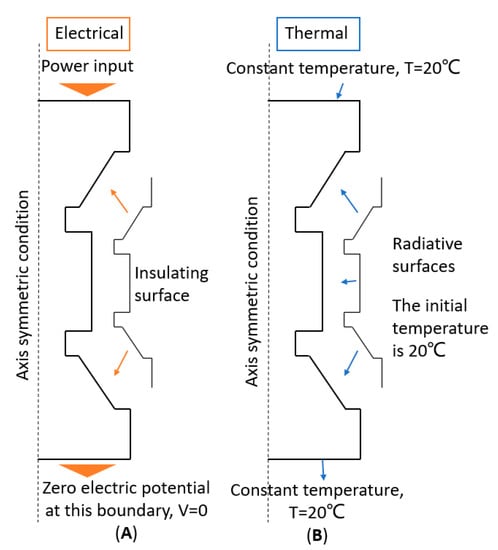
Figure 1. Assumed spark plasma sintering (SPS) model’s boundary conditions for (A) electric and (B) thermal fields.

The electrical and thermal boundary conditions are summarized in Figure 1. Axially symmetric boundary conditions were applied along the axial axis. An electrical power input was applied to the upper ram while the lower one was grounded. The lateral surfaces of graphite elements were assumed to be electrically insulated. The initial temperature of all components was 20 °C, and the upper and lower ends were water-cooled and maintained at the preset temperature of 20 °C. The SPS process was operated in vacuum (≤5 Pa), so convection heat transfer was ignored. The heat on the graphite surface was mainly transferred to the environment by radiation, and the surface emissivity of graphite elements was assumed to be equal to 0.8 [32].

FEM conditions are summarized as follows. Parameters and formula settings of electric field.

No initial electric potential at all components.

Electric insulation boundary: $n\times J=0$

Provide the power input at this boundary (current density/electric potential):

$$\begin{gathered} V=V_0 \\ -n\times J=J_n \end{gathered}$$

where $V_0$ and $J_n$ are the power supply formula in voltage and current, respectively.

The electric current equation at the domain where the current passes is:

$$\begin{gathered} \nabla \times J=Q_{j,v} \\ J=\sigma E+\frac{\partial \mathit{D}}{\partial \mathit{t}}+J_{\mathbf{e}} \\ E=-\nabla v \\ {J}_c=\sigma E \\ D={\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_{r}E \end{gathered}$$

where $\sigma$, ${\mathsf{\epsilon }}_0$ and ${\mathsf{\epsilon }}_r$ are the electric conductivity, vacuum dielectric constant, and relative permittivity.

$${\mathsf{\epsilon }}_0=8.8542\times {10}^{-12}\left[F/m\right]$$

Parameters and formula settings of magnetic field.

Initial magnetic vector potential at all components: $A=0$

Magnetic insulation boundary: $n\times A=0$

Coupling electric and magnetic fields:

$$\begin{gathered} \nabla \times H=J \\ B=\nabla \times A \\ E=-\frac{\partial \mathit{A}}{\partial \mathit{t}} \\ J=\sigma E+\sigma v\times B+J_e \\ B={\mu }_0{\mu }_{r}H \\ {J}_C=\sigma E \end{gathered}$$

where A, J, ${\mu }_0$ and ${\mu }_r$ are the magnetic vector potential, current density, permeability of vacuum, and relative permeability of the material.

3. Health Effects and Safe Distance for the Operators

During the electric current-assisted sintering process, large current can result in a strong magnetic field, which might exceed the safety exposure limits. To the best of our knowledge, such an issue has not been discussed in the literature. To meet the safety requirements, the resulting magnetic field should be kept under control. Exposure limits are inversely proportional to the frequency accordingly to the guidelines proposed by the International Commission on Non-Ionizing Radiation Protection in 2010 [33]. In DC, a well-accepted standard for the magnetic field exposure limit is 5 Gauss (0.0005 T), whereas for AC, the exposure frequencies differ from country to country.

Here, we simulated the magnetic field generated by reference SPS machines (FCT systems, Germany) operated in DC. The results are shown in Table 2 and Table 3, and as expected, the safety distance increases with the applied current (i.e., increasing the specimen dimension). The analysis in Table 2 also includes a conservative scenario where electromagnetic shielding (i.e., sintering chamber) is not employed. This assumption reflects the situation of unshielded or partially unshielded cables/conductors. The good match between simulated results and the Bio–Savart law confirms the accuracy of the simulations. The representative distribution of the magnetic field distribution is shown in Figure 2.

Table 2. Safety distance test under DC conditions, for different currents assuming an exposure limit of 5 Gauss.

Standard Commercialized SPS Types	Dimension Components [mm]	Max Pressing Force [kN]	Max Current [A]	Safety Distance without Shield (DC) [cm]	Biot–Savart Distance Calculation [cm] *
HP D 2.5	Ø 30	25	3000	118.9	120
HP D 10	Ø 50	100	5500	217.7	200
HP D 25	Ø 80	250	8000	314.7	320
HP D 60	Ø 120	600	16,000	629.8	640
HP D 125	Ø 150	1250	24,000	956.3	960
HP D 250	Ø 300	2500	48,000/24,000	1894/1949	1920/960

* Biot–Savart calculation assumes an infinitely long conductor.

Table 3. Electrical conductivity and relative magnetic permeability samples considered in the simulations 20 °C.

	Electrical Conductivity (S m)	Relative Permeability
Graphite	8.3 × 104	1
Iron	1.12 × 107	200,000
Alumina	1 × 10−12	1
Copper	5.714 × 107	1

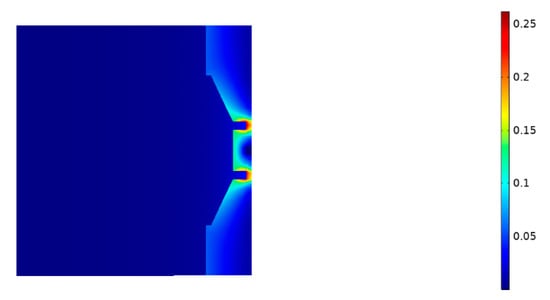
Figure 2. Simulation of magnetic field distribution (units in Tesla) using an alumina sample with 30 mm diameter, and assuming a current of 3000 A DC and no sintering chamber (i.e., shield). The safety distance to meet the 5 Gauss line is 119 cm.

A more realistic simulation is instead achieved by considering a 2 cm-thick stainless steel chamber (relative permeability is 1.06) [34]. The results are presented in Figure 3. The magnetic field strength on the outside of the stainless steel is greatly reduced compared to the magnetic field strength on the inside, which shows that the stainless-steel shell can effectively reduce the magnetic field strength, thereby protecting the safety of the operator.

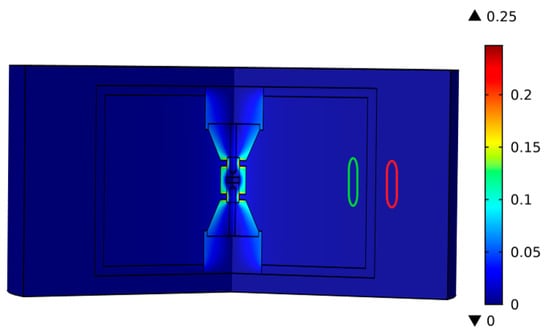
Figure 3. Magnetic field distribution when using a 30 mm sample of alumina and current of 3000 A, adding a 2 cm-thickness stainless-steel shell. The magnetic field strength at the position represented by the green circle within the chamber is 1.94 × 10⁻³ T, while the magnetic field outside the chamber (red circle) is 1.218 × 10⁻⁷ T. The chamber can effectively shield the magnetic field down to a safe level for the operator.

4. Magnetic Field Distribution during SPS of Different Materials: Electrical Conductivity and Magnetic Permeability Effects

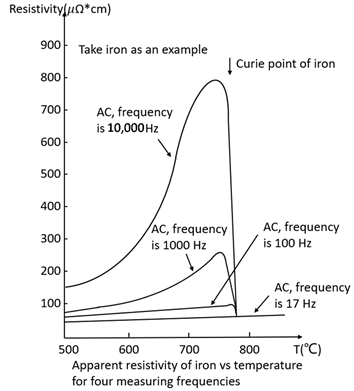
As discussed in the introduction, the ferromagnetic material below the Curie temperature is expected to become magnetized under the application of an electrical discharge. As a representative example, Sales et al. [26] investigated the changes in electrical resistance in the vicinity of the Curie temperature of ferromagnetic materials. These effects are summarized in Table 1 under the section “AC Resistance change in the vicinity of the Curie temperature.” Assuming a DC discharge, magnetization effects are expected to occur depending on the electrical conductivity and magnetic permeability, as shown in Table 3.

The SPS simulations were done assuming a DC voltage of 10 V DC that represents the upper operating limit of the equipment. The sample diameter of the sample was 30 mm with a height of the sample of 8 mm. The magnetic saturation of the 2.4 T effect for soft iron was accounted for in the simulations. The resulting magnetic field distribution is shown in Figure 4.

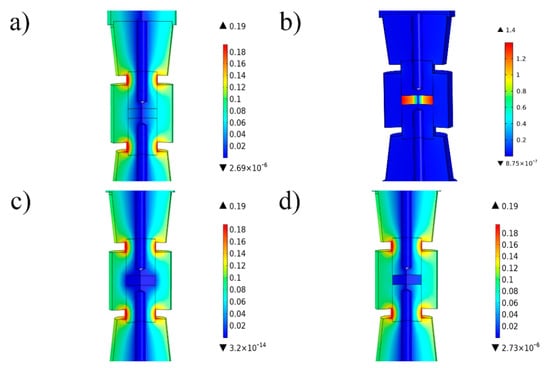
Figure 4. Comparison of magnetic field distribution for different materials assuming a voltage of 10 V; (a) the maximum recorded field strength within the graphite sample was 0.053 T, (b) that for iron was 1.4 T, and (c) that for alumina was as low as 9.1 × 10⁻¹⁰ T. Simulations in (d) were performed at a temperature exceeding the Curie point, reaching 0.014 T within the iron sample.

According to Figure 4, the magnetic field strength depends strongly on the materials properties. For graphite and alumina, the magnetic field distribution is relatively uniform. The peak value of magnetic strength is 0.19 T, and it radially increases. For iron, the magnetic field distribution is different, the peak value of magnetic strength is 1.4 T (much larger than 0.19 T), and the magnetic intensity of the sample is much higher than those of the surrounding components. The intensity of the magnetic field increases with the radius and reaches the maximum value at the edge of the sample. It needs to be pointed out that the properties of ferromagnetic materials changed drastically when the temperature exceeded the Curie point, due to the ferromagnetic to paramagnetic transition. In Figure 4d, the temperature of the iron sample exceeded the Curie point, and the peak value of the magnetic field strength reduced from 1.4 to 0.19 T.

In the literature, there are some examples of sintering under the application of an externally applied magnetic field. For example, Eikeland et al. [35] investigated the externally applied magnetic field prior to sintering, resulting in an improved degree of alignment of SrFe₁₂O₁₉. Using a different approach, Li et al. [36] applied an external magnetic field using a inductor coil on iron-based powders using a field strength up to 0.5 T AC 50 Hz. The results suggested an enhanced diffusion of the alloying elements resulting from the application of an external magnetic field. The implications of these magnetic fields are not well-investigated, and it is expected that any magnetic-related effect might have a radial dependence. Further work might be needed to understand and exploit these effects.

5. Magnetic Field Effects at Interparticle Contacts

In this section, magnetic field effects occurring at the interparticle contact point are investigated. The analysis accounts for the impact of electro-magneto-thermal effects on the sintering process. Magnetic effects are intensified by increasing the current. Selected ECAS [37] techniques are rationalized in Table 4 with respect to pressure, discharge time, voltage, current, and sintered material compositions.

Table 4. Representative sintering parameters for electric current-assisted sintering (ECAS) techniques based on high current density.

Inventor, Year, Reference	Pressure, Discharge Time, Voltage, Current Density	Sintered Material
Cremer, US1944	≈100 MPa, 10 ms, 5–20 V, ≈60 kAcm−2	Cu, Al, brass
Parker, US1968	10 MPa, 1 ms, >150 kAcm−2 2000 Jcm−3	Ti, Fe

The electro-magnetothermal effect is summarized in Figure 5 for a copper sphere with a diameter of 100 µm and current density of 60 kA/cm² (6 × 10⁸ A/m²) under a discharge time of 50 ms. The effect of the neck growth was investigated for contact areas of 154.94 and 754.77 μm².

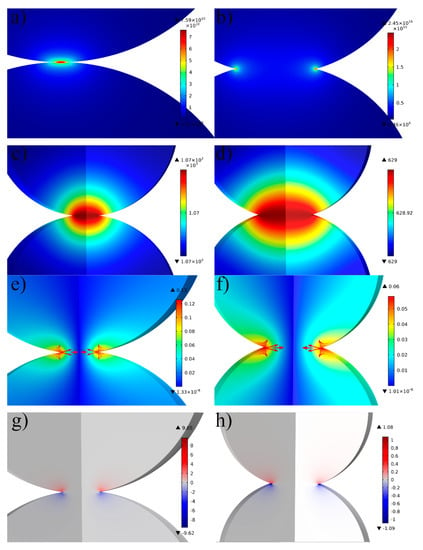
Figure 5. Comparison of electro, thermal, and magnetic effects for 100 µm copper sphere discharged under a current density of 60 kA/cm², with the first column for small contact area and second column for large contact area (154.94 and 754.77 μm², respectively). (a) Current density distribution graph for small contact (peak current density was 7.59 × 10¹⁰ A/m²) and (b) large contact area (peak current density was 2.45 × 10¹⁰ A/m²). The temperature distribution graph under (c) small and (d) large contact area. Magnetic field distribution with arrows indicating the Lorentz force for (e) small contact area (peak magnetic intensity reached 0.13 T) and for (f) large contact area (peak magnetic intensity reached 0.06 T). Z-axis component Lorentz force contribution for (g) small contact area (max of 9.65 N/mm³) and (h) for large contact area (max of 1.08 N/mm³).

The boundary conditions were similar to those for the SPS model under a significantly increased current density.

The analysis of current density distribution is presented in Figure 5a,b. The current flows from top to bottom following the curvature of the particles, and it was subjected to the neck constriction effect. Analysis of temperature distribution (Figure 5c,d) suggests an even temperature distribution because of the high thermal diffusivity of copper; in reality, a temperature increase at the interparticle contact point should be expected because of contact resistance effects (not accounted by the proposed model). The contact resistance has an inverse dependence on the pressure. Analysis of the magnetic field strength distribution (Figure 5e,f) confirms strong magnetic effects at the interparticle contact point. The analysis of the Lorentz force distribution is presented using the arrows in Figure 5e,f. The resulting Lorentz force includes a radial compressive component and Z-axis repulsive component, which tend to repel the particles from each other. The Z-component Lorentz force plays a significant role in the molten metal ejection, and its color mapping distribution is shown in Figure 5g,h. This phenomenon has some analogies with the repulsion generated in metal wire explosion. It is even more commonly seen in welding as described in Ref. [38] In welding, this effect can be reduced by controlling the welding force, preventing the formation of a molten phase.

The magnetic forces are expected to be more significant for when paramagnetic copper is replaced with iron (diameter of the particles was 100 μm). The current density at the maximum cross-section through the copper powder was set at 60 and 200 kA/cm² for iron. Figure 6 shows the contribution of the Z-axis for iron, where the Lorentz force reached the peak value of 321 N/mm³, far greater than the 9.65 N/mm³ for copper. This level of force is enough to affect the shape of the particle under such high current density.

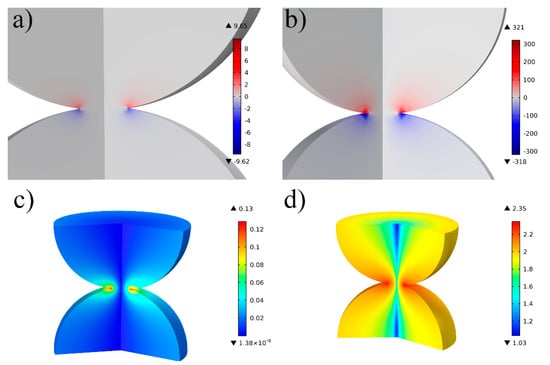
Figure 6. Lorentz force z-axis contribution (a,b) and magnetic field distribution (c,d) in the case of copper (60 kA/cm²) in the first column and iron in the second column (200 kA/cm²).

The proposed model requires some experimental validation. For example, Guyot et al. [39] investigated the microscopic particle surface morphology on electrical discharge copper spheres with a diameter of 50 μm. Their results evidence the formation of molten droplets on the spheres possibly because of the Lorentz Force. In order to validate such an hypothesis, we employed 5 mm copper spheres, as shown in Figure 7.

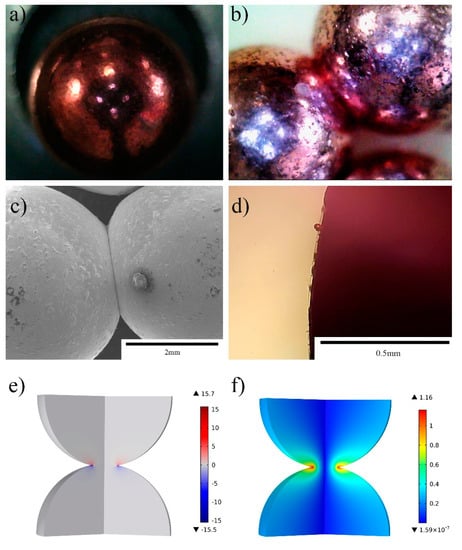
Figure 7. (a) Surface morphology of as-received 5 mm copper spheres. (b,c) Overall appearance with optical microscope and SEM after application of a current of 15 kA/cm² for 0.4 s. (d) Local appearance with optical microscope at a current 7.5 kA/cm² for 0.6 s. (e,f) The Lorentz force contribution Z-component and the magnetic field strength distribution were simulated using a current of 15 kA/cm² for 0.4 s, the Lorentz force peak value was 15.7 N/mm³, and the peak magnetic field strength was 1.16 T.

Figure 7a shows the surface of the copper ball before application of an electric current, and the surface was smooth. Figure 7b,c show the overall morphology of bonded particles after application of a 15 kA/cm² discharge for 0.4 s. The two copper balls were bonded together well at the contact position. Surprisingly, there are many protrusions on the surface of the copper ball that might originate by the molten material being ejected due to the Lorentz force. Figure 7d shows a similar observation when using a current of 7.5 kA/cm² for 0.6 s. Figure 7e,f map the Lorentz force and magnetic distribution, and the peak value was iron at 15.7 N/mm³, which is sufficient to promote molten metal ejection under a high current density [40].

The Joule heat generated by the high current softens or even partially melts the copper spheres at their interparticle contact. At the same time, the high current produces strong magnetic effects, and the liquid copper is ejected from the neck under the action of the repulsive Lorentz force, resulting in the formation of molten droplets, which reprecipitated on the spheres.

6. Conclusions

This article analyzed the possible role of magnetic fields on electric current-assisted processing. The first section surveyed these effects considering the Biot–Savart Law, skin effect, AC resistance change in the vicinity of the Curie temperature, proximity effect, pinch effect, and reactance dependence on duty cycle. By using finite element simulation, we could determine the safe distance (i.e., exclusion zone from the current conductor) for the operator. The second section simulates the magnetic field distribution at the tooling level (punch/die/sample assembly) during spark plasma sintering of the materials with variable electrical conductivity and different magnetic permeability. The same analysis was carried out at the interparticle level in the case of copper and iron spherical particles. The model was experimentally validated using 15 kA/cm² for 0.4 s, where the molten droplet ejection was correlated with the strong repulsive Lorentz force acting on the molten copper. The results suggest that magnetic-related effects cannot be neglected when using ferromagnetic materials, when using extremely large currents. Further investigation should be dedicated to pulsing and frequency-related effects and how to exploit magnetic-related effects.