Prediction of Leidenfrost Temperature in Spray Cooling for Continuous Casting and Heat Treatment Processes
Abstract
:1. Introduction
2. Laboratory Measurements
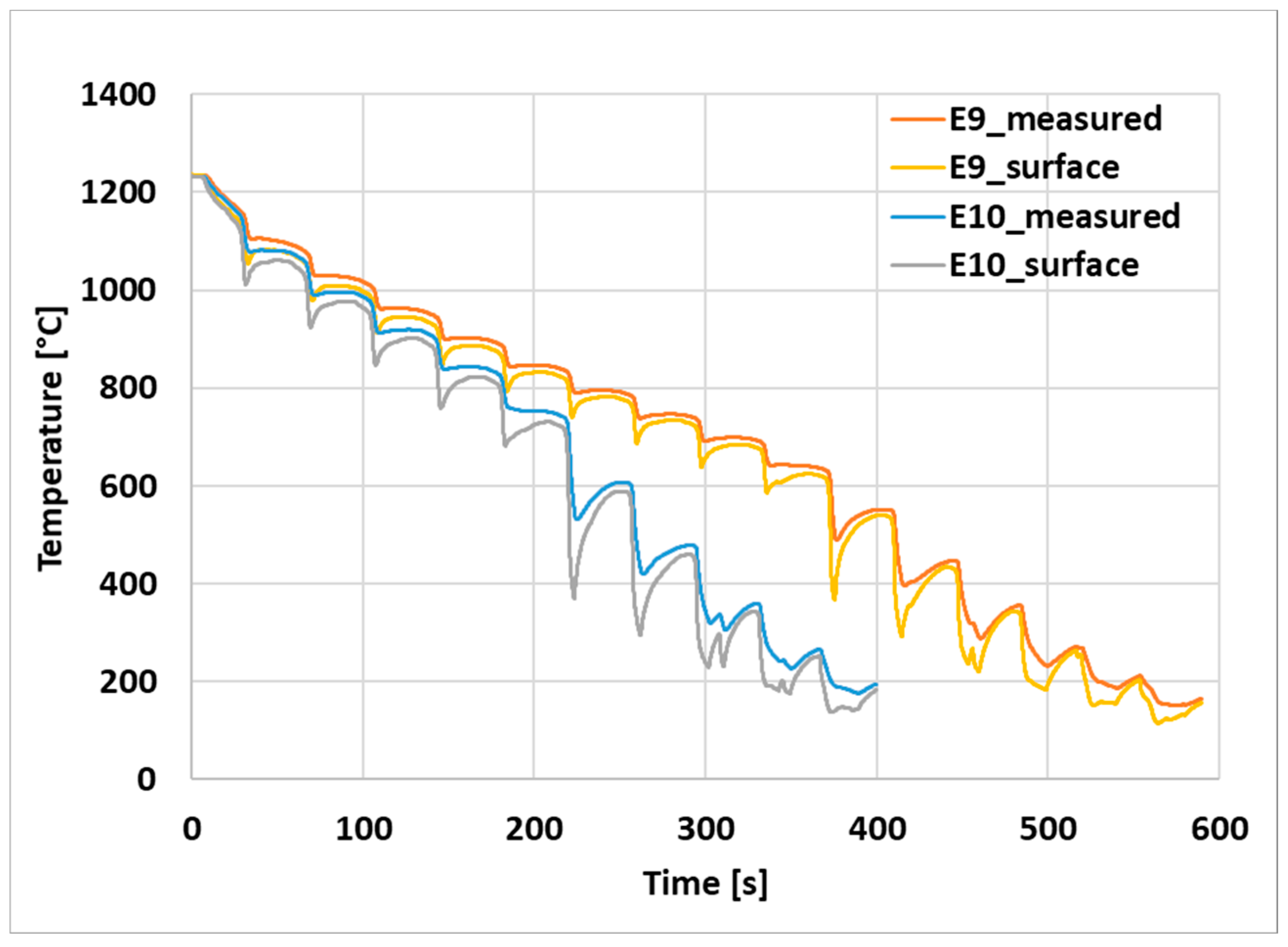
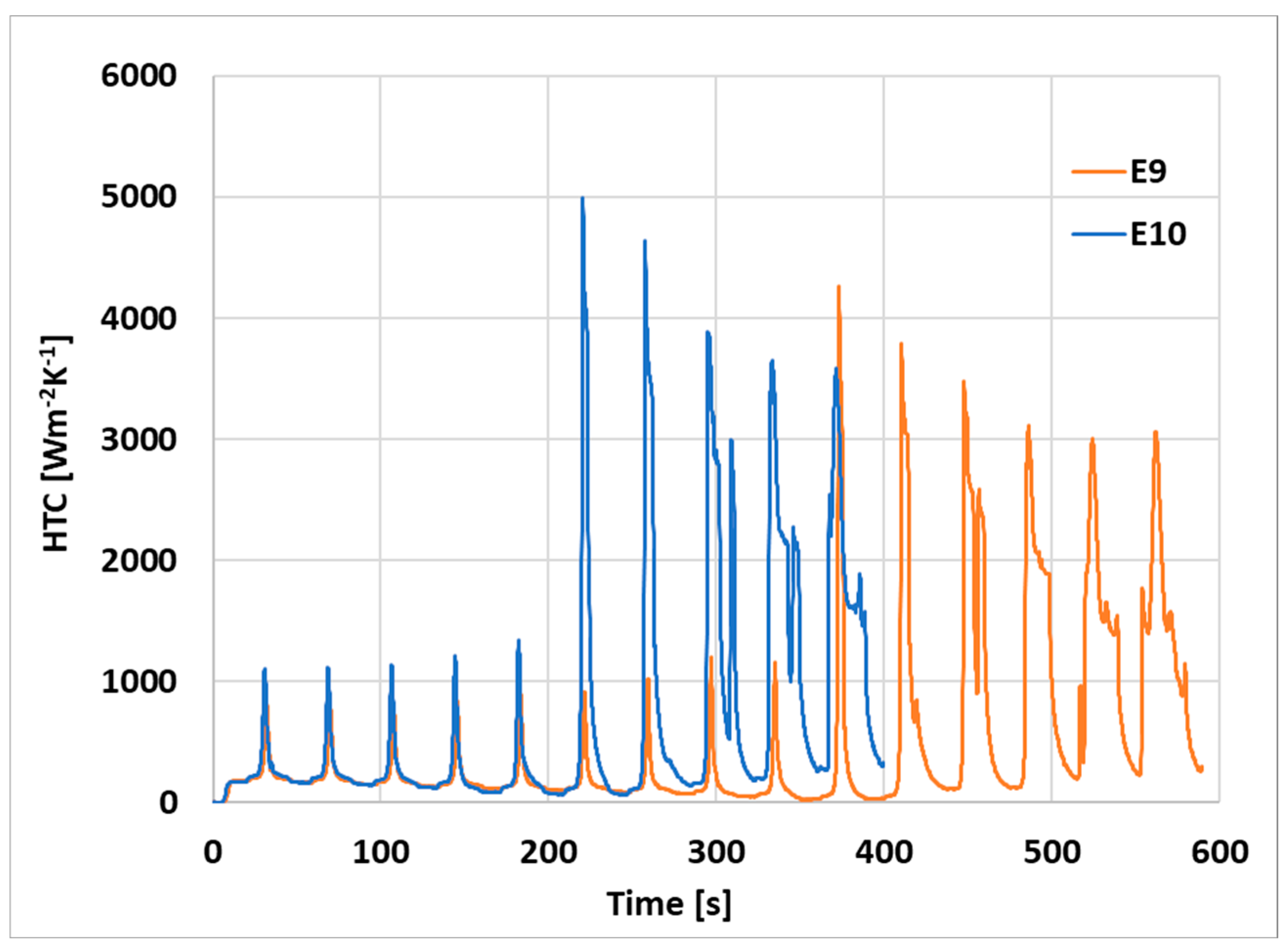
2.1. Plan of Experiments
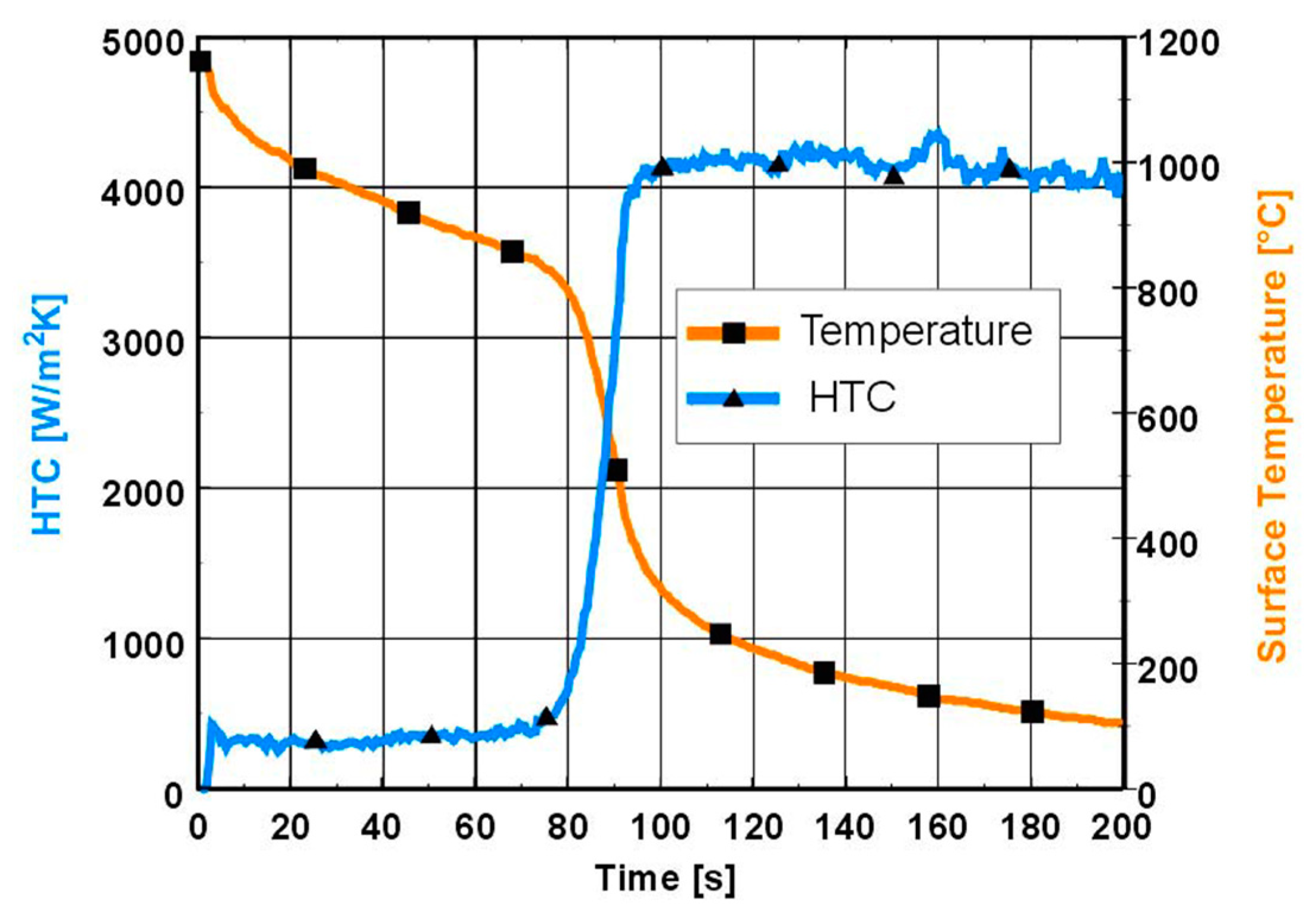
2.2. Heat Transfer Coefficient and Leidenfrost Temperature Measurement
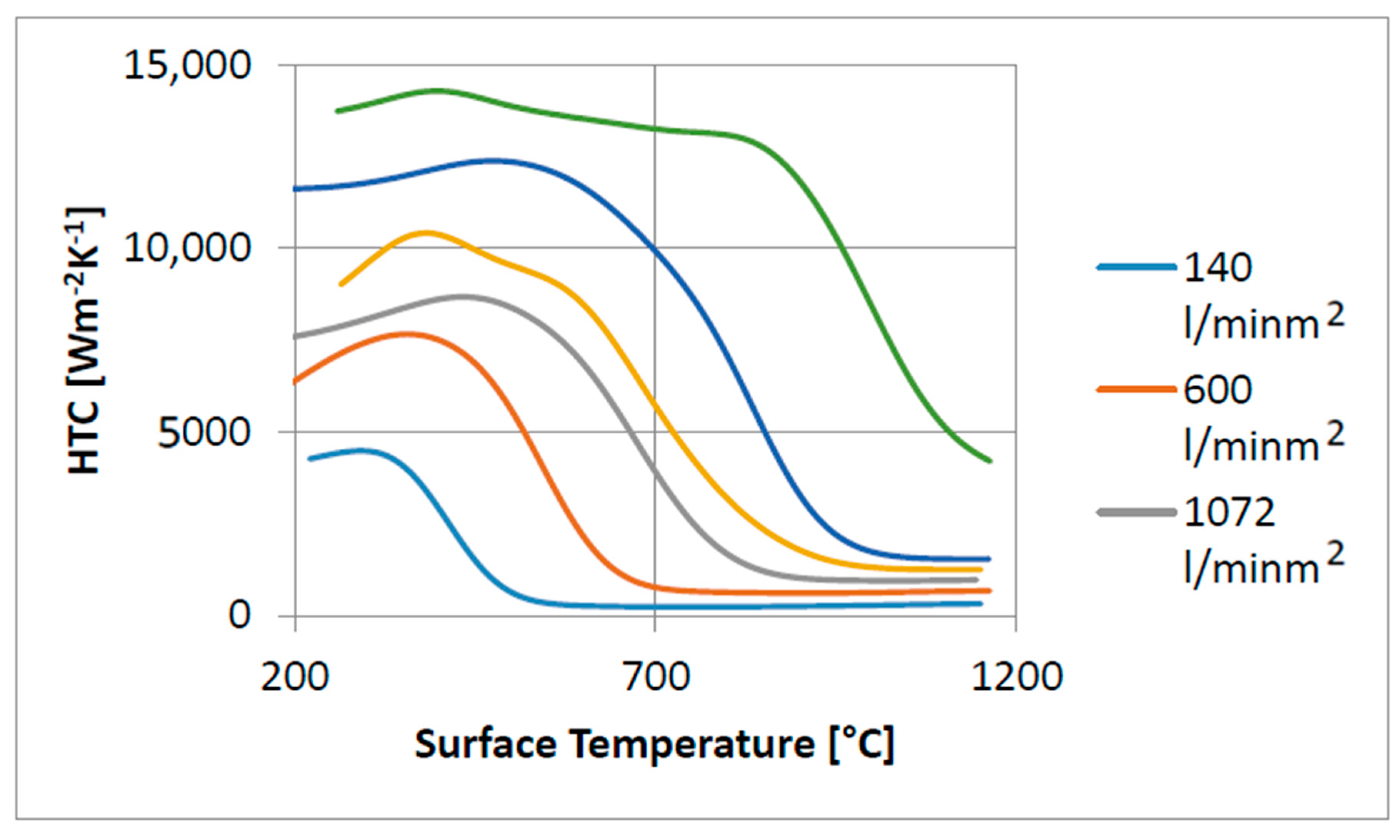
2.3. Water Impingement Density Measurement
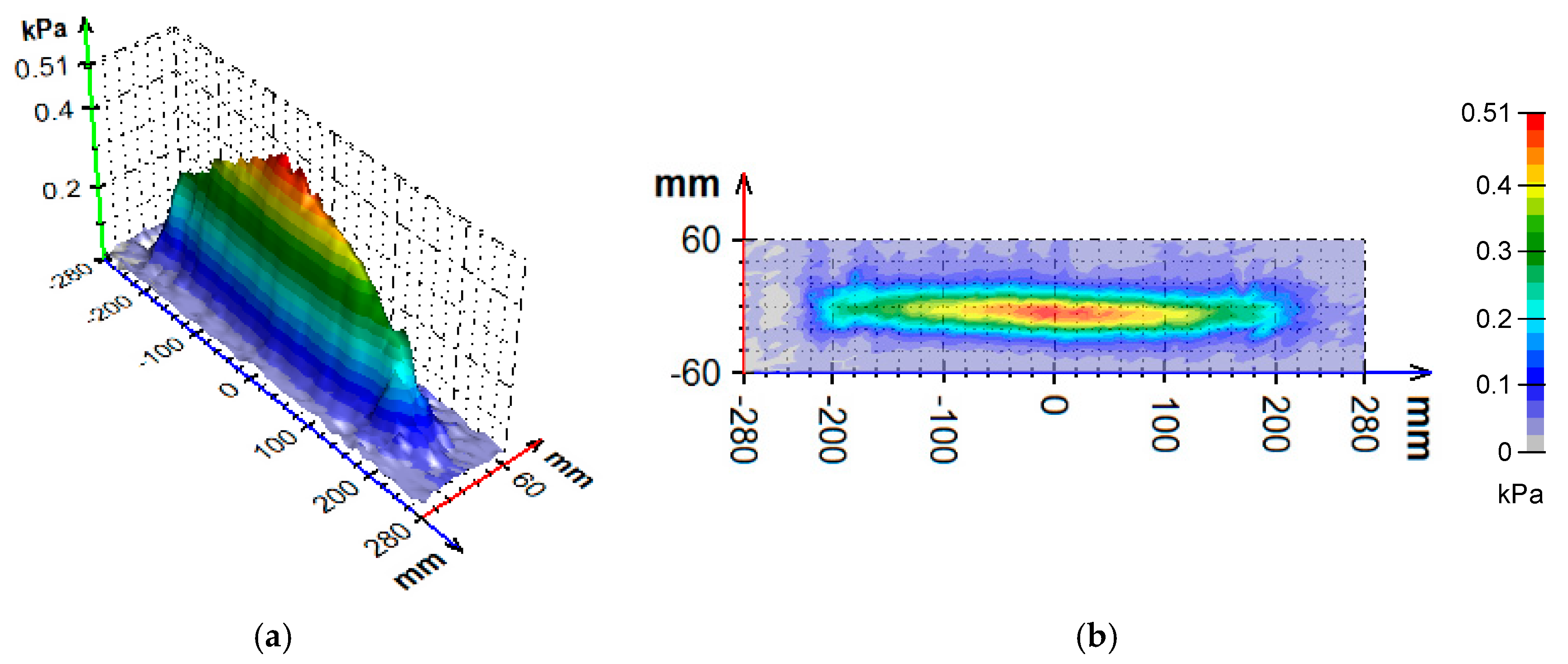
2.4. Impact Pressure Measurement
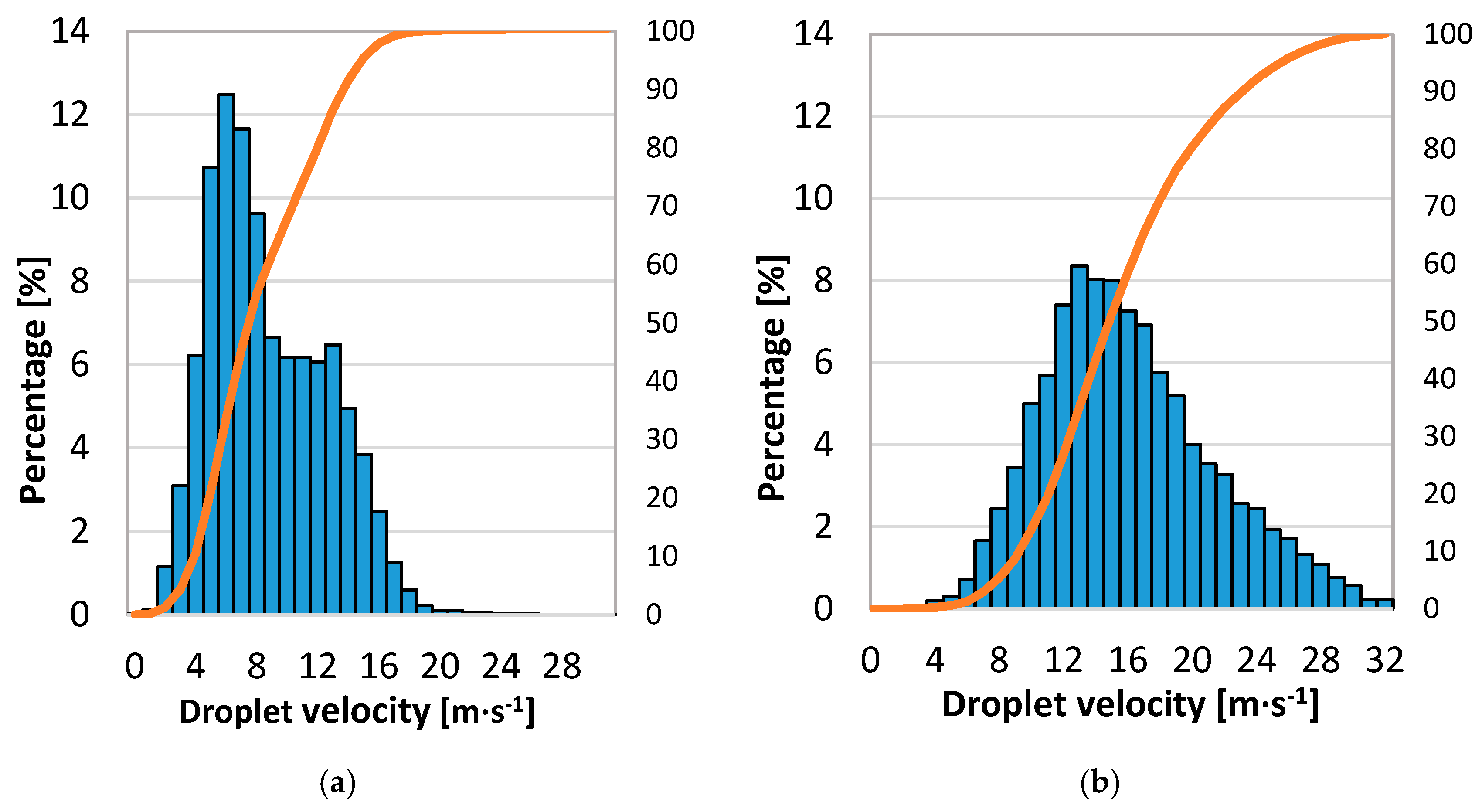
2.5. Droplet Size and Velocity
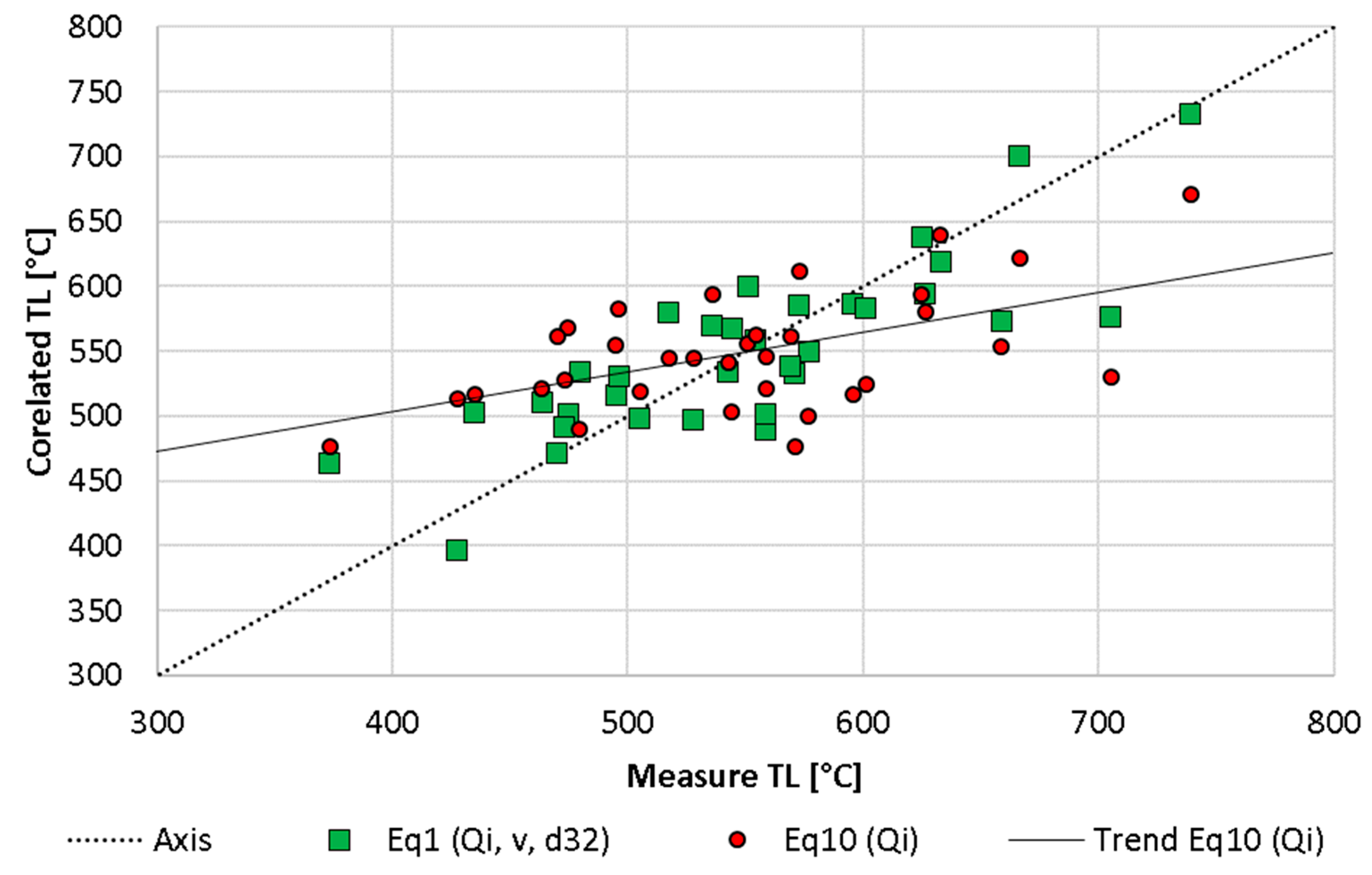
3. Correlations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, G.; Mudawar, I. Review of spray cooling—Part 2: High temperature boiling regimes and quenching applications. Int. J. Heat Mass Transf. 2017, 115, 1206–1222. [Google Scholar] [CrossRef]
- Yao, S.C.; Cox, T.L. A General Heat Transfer Correlation for Impacting Water Sprays on High-Temperature Surfaces. Exp. Heat Transf. 2002, 15, 207–219. [Google Scholar] [CrossRef]
- Al-Ahmadi, H.M.; Yao, S.C. Spray Cooling of High Temperature Metals Using High Mass Flux Industrial Nozzles. Exp. Heat Transf. 2008, 21, 38–54. [Google Scholar] [CrossRef]
- Raudensky, M.; Horsky, J. Secondary cooling in continuous casting and Leidenfrost temperature effects. Ironmak. Steelmak. 2005, 32, 159–164. [Google Scholar] [CrossRef]
- Bernardin, J.; Mudawar, I. A leidenfrost point model for impinging droplets and sprays. J. Heat Transf. Trans. ASME 2004, 126, 272–278. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, Z.; Zhao, Z.; Bi, C.; Guo, Y.; Huang, J. Laboratory Experimental Setup and Research on Heat Transfer Characteristics during Secondary Cooling in Continuous Casting. Metals 2019, 9, 61. [Google Scholar] [CrossRef] [Green Version]
- Gradeck, M.; Kouachi, A.; Lebouché, M.; Volle, F.; Maillet, D.; Borean, J.L. Boiling curves in relation to quenching of a high temperature moving surface with liquid jet impingement. Int. J. Heat Mass Transf. 2009, 52, 1094–1104. [Google Scholar] [CrossRef] [Green Version]
- Sinha, J. Effects of Surface Roughness, Oxidation Level, and Liquid Subcooling on the Minimum Film Boiling Temperature. Exp. Heat Transf. 2003, 16, 45–60. [Google Scholar] [CrossRef]
- Brožová, T.; Chabičovský, M.; Horský, J. Influence of the surface roughness on the cooling intensity during spray cooling. In Proceedings of the 25th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 25–27 May 2016; pp. 41–46. [Google Scholar]
- Chabičovský, M.; Resl, O.; Raudenský, M. Impact of oxide layer on spray cooling intensity and homogeneity during continuous casting of the steel. In Proceedings of the 27th International Conference on Metallurgy and Materials, Brno, Czech Republic, 23–25 May 2018; pp. 69–74. [Google Scholar]
- Chabičovský, M.; Hnízdil, M.; Tseng, A.A.; Raudenský, M. Effects of oxide layer on Leidenfrost temperature during spray cooling of steel at high temperatures. Int. J. Heat Mass Transf. 2015, 88, 236–246. [Google Scholar] [CrossRef]
- Raudensky, M.; Hnizdil, M.; Kotrbacek, P. Why oxides intensify spray cooling? In Proceedings of the the 30th International Steel Industry Conference, Paris, France, 28–29 December 2020; pp. 92–93. [Google Scholar]
- Fukuda, H.; Nakata, N.; Kijima, H.; Kuroki, T.; Fujibayashi, A.; Takata, Y.; Hidaka, S. Effects of Surface Conditions on Spray Cooling Characteristics. ISIJ Int. 2016, 56, 628–636. [Google Scholar] [CrossRef] [Green Version]
- Raudensky, M.; Hnizdil, M.; Hwang, J.Y.; Lee, S.H.; Kim, S.Y. Influence of the water temperature on the cooling intensity of mist nozzles in continuous casting. Mater. Tehnol. 2012, 46, 311–315. [Google Scholar]
- Yigit, C.; Sozbir, N.; Yao, S.C.; Guven, H.; Issa, R. Experimental measurements and computational modeling for the spray cooling of a steel plate near the leidenfrost temperature. Isi Bilimi Tek. Derg. J. Therm. Sci. Technol. 2011, 31, 27–36. [Google Scholar]
- Ondrouskova, J.; Pohanka, M.; Vervaet, B. Heat-flux computation from measured-temperature histories during hot rolling. Mater. Tehnol. 2013, 47, 85–87. [Google Scholar]
- Komínek, J.; Pohanka, M. Estimation of the number of forward time steps for the sequential Beck approach used for solving inverse heat-conduction problems. Mater. Tehnol. 2016, 50, 207–210. [Google Scholar] [CrossRef]
- Beck, J.V.; Woodbury, K.A. Inverse heat conduction problem: Sensitivity coefficient insights, filter coefficients, and intrinsic verification. Int. J. Heat Mass Transf. 2016, 97, 578–588. [Google Scholar] [CrossRef] [Green Version]


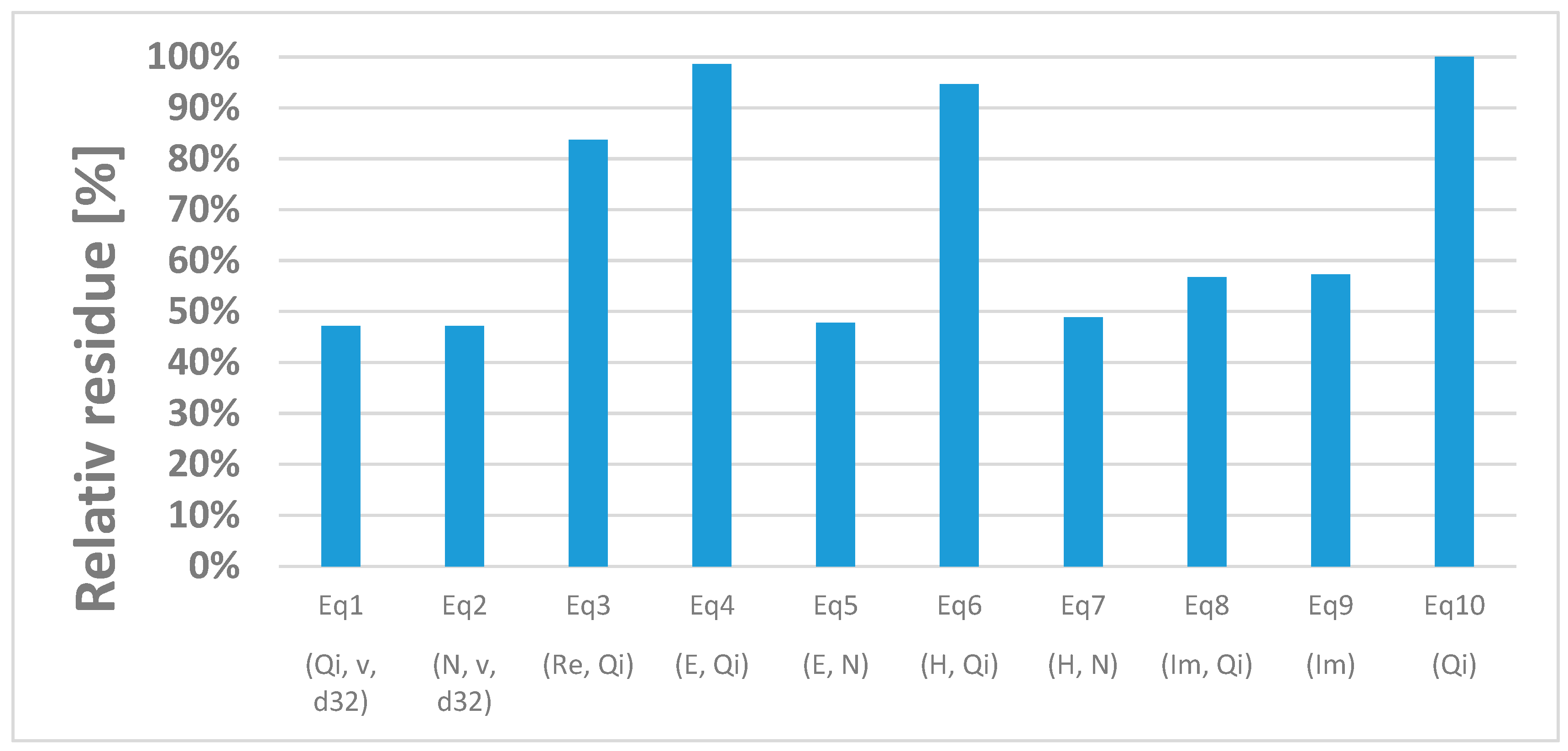
| Experiment | Nozzle Type | Standoff (mm) | Water Flowrate (l·min−1) |
|---|---|---|---|
| E1 | mist | 360 | 4 |
| E2 | mist | 200 | 7 |
| E3 | mist | 190 | 20 |
| E4 | mist | 145 | 9 |
| E5 | mist | 345 | 5 |
| E6 | mist | 200 | 10 |
| E7/E8 | mist | 250 | 6 |
| E9/E10 | mist | 250 | 11 |
| E11 | water | 250 | 6 |
| E12 | water | 250 | 11 |
| Correlation Number | Formula | Res2 |
|---|---|---|
| Equation (1) | 2096 | |
| Equation (2) | 2096 | |
| Equation (3) | 3724 | |
| Equation (4) | 4382 | |
| Equation (5) | 2126 | |
| Equation (6) | 4206 | |
| Equation (7) | 2175 | |
| Equation (8) | 2521 | |
| Equation (9) | 2546 | |
| Equation (10) | 4445 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hnizdil, M.; Kominek, J.; Lee, T.-W.; Raudensky, M.; Carnogurska, M.; Chabicovsky, M. Prediction of Leidenfrost Temperature in Spray Cooling for Continuous Casting and Heat Treatment Processes. Metals 2020, 10, 1551. https://doi.org/10.3390/met10111551
Hnizdil M, Kominek J, Lee T-W, Raudensky M, Carnogurska M, Chabicovsky M. Prediction of Leidenfrost Temperature in Spray Cooling for Continuous Casting and Heat Treatment Processes. Metals. 2020; 10(11):1551. https://doi.org/10.3390/met10111551
Chicago/Turabian StyleHnizdil, Milan, Jan Kominek, Tae-Woo Lee, Miroslav Raudensky, Maria Carnogurska, and Martin Chabicovsky. 2020. "Prediction of Leidenfrost Temperature in Spray Cooling for Continuous Casting and Heat Treatment Processes" Metals 10, no. 11: 1551. https://doi.org/10.3390/met10111551
APA StyleHnizdil, M., Kominek, J., Lee, T.-W., Raudensky, M., Carnogurska, M., & Chabicovsky, M. (2020). Prediction of Leidenfrost Temperature in Spray Cooling for Continuous Casting and Heat Treatment Processes. Metals, 10(11), 1551. https://doi.org/10.3390/met10111551





