Impact Response of Aluminum Foam Sandwiches for Light-Weight Ship Structures
Abstract
: The structures realized using sandwich technologies combine low weight with high energy absorbing capacity, so they are suitable for applications in the transport industry (automotive, aerospace, shipbuilding industry) where the “lightweight design” philosophy and the safety of vehicles are very important aspects. While sandwich structures with polymeric foams have been applied for many years, currently there is a considerable and growing interest in the use of sandwiches with aluminum foam core. The aim of this paper was the analysis of low-velocity impact response of AFS (aluminum foam sandwiches) panels and the investigation of their collapse modes. Low velocity impact tests were carried out by a drop test machine and a theoretical approach, based on the energy balance model, has been applied to investigate their impact behavior. The failure mode and the internal damage of the impacted AFS have also been investigated by a Computed Tomography (CT) system.1. Introduction
The “lightweight design” philosophy is essential in the transport industry (automotive, aerospace, shipbuilding industry); lightweight structures are commonly used to increase payload, to reach higher speed and to obtain a lower fuel consumption. Thus, new materials and technologies have been adopted and, in particular, the use of sandwich structures has steadily increased in the last years. In order to meet the ever growing request of lighter vehicles and ships, the transport industry is engaged in the design and construction of structures quite different from the traditional ones, and as a consequence, a lack of experiences concerning the strength of many structural details has become apparent. A wide use of sandwich structures requires that all differences respect to the traditional ones be adequately accounted for. Thus, there is a need for new research activities in order to provide the designers of sandwich structures with new reliable data.
Moreover, problems of collision and crashing are very important for high speed terrestrial and marine vehicles and sandwich structures have so far shown good capabilities in absorbing energy, so it is necessary to acquire a better knowledge concerning the impact behavior of structural details built up resorting to sandwich technologies.
Core deformation and failure are decisive factors for the energy absorption capability of sandwich structures. After fracture of the skin, the impacting object may damage and penetrate into the core. With aluminum honeycomb cores, damage consists of crushing or “buckling” of cell walls in a region surrounding the impact point, while, in foam cores, damage looks more like a crack for low-energy impacts [1].
While polymeric foams have been applied for many years, currently there is a significant and growing interest in metal foams for transport applications. Aluminum foam sandwiches (AFS) [2,3], obtained by combining metal face sheets with a lightweight metal foam core, have peculiar properties (low specific weight, efficient capacity of energy dissipation, high impact strength, acoustic and thermal insulation, high damping), that made them interesting for a number of practical applications, such as the realization of lightweight structures with high mechanical strength and good capacity of energy dissipation under impacts. Aluminum sandwich structures are suitable for applications in high speed marine and terrestrial vehicles, as they allow a speed increase with a good passenger comfort thanks to their specific weight and high damping capacity. The use of lightweight materials is an important issue for ships and, in comparison with cars, a high flexibility of materials processing is needed, because ship are not realized in large series with highly standardized components, so aluminum foams or panels have a lot of advantages for possible applications in ship construction [4]. Closed cell metal foams are being developed for lightweight ship components such as elevator platforms, water-tight doors, hatches and bulkheads as declared by the Fraunhofer USA Center for Manufacturing and Advanced Materials, Delaware, USA.
Aluminum foams represent an attractive and interesting material for the development of highly efficient energy absorbers thanks to their capacity to undergo large strain at almost constant stress [5]. Foams can absorb a large amount of mechanical energy when they are deformed due to their high porosity, while stresses are limited to the compressive strength of the material, so they can act as impact energy absorbers which limit accelerations in crash situations. Foamed organic material has low specific weight, but the energy amount convertible to strain energy is relatively low for the low strength of the polymeric foams. As metal foams can have much higher collapse strengths than polymer-based foams, they can find applications in areas not accessible to foams up to date.
Low velocity impact tests were carried out on a range of polymeric foam sandwiches by Hazizan et al. [6] and an energy balance model was applied to predict their low velocity impact response.
In a previous research paper of the authors [7], the structural response of aluminum foam sandwiches under static loading was compared with that of the PVC foam sandwiches.
The failure mode and the damaged structure of the impacted panels have been also investigated by a Computed Tomography (CT) system, which allows a three-dimensional reconstruction of the analyzed object [8]. This non-invasive technique have been used to quantitatively characterize the microstructure and the internal architecture of different typologies of closed cell aluminum alloy foam [9] and to obtain the data for Finite Element models of open-cell aluminum foam specimens [10].
Aim of the present research was the analysis of low-velocity impact response of AFS panels and the investigation of their collapse modes. Two types of AFS panels were analyzed; they differ for the foam quality and for the skin-core adhesion. Low velocity impact tests were carried out at different impact velocities by a drop test machine in order to investigate and compare the structural response of the two AFS types in terms of energy absorption capacity. The collapse mode and the internal damage of the impacted panels have been investigated using 3D Computed Tomography. A theoretical approach, based on the energy balance model, has been applied to investigate their impact behavior and the model parameters were obtained directly from the measurements carried out on the tomographic images of the impacted sandwiches.
This combined experimental and theoretical study has particular importance for applications that require lightweight structures with a high capacity of energy dissipation, such as the transport industry.
2. Materials and Methods
2.1. Materials
Two different commercial aluminum alloy foam sandwiches have been investigated (Figure 1): the first one (Schunk-Honsel Entwicklungsgemeinschaft) with faces obtained by extrusion (integral skins), the second one (Alulight® International GmbH) with faces bonded to the core by an epoxy adhesive.
The chemical composition, physical and geometrical properties of the investigated AFS panels are reported in Tables 1 and 2.
2.2. Methods
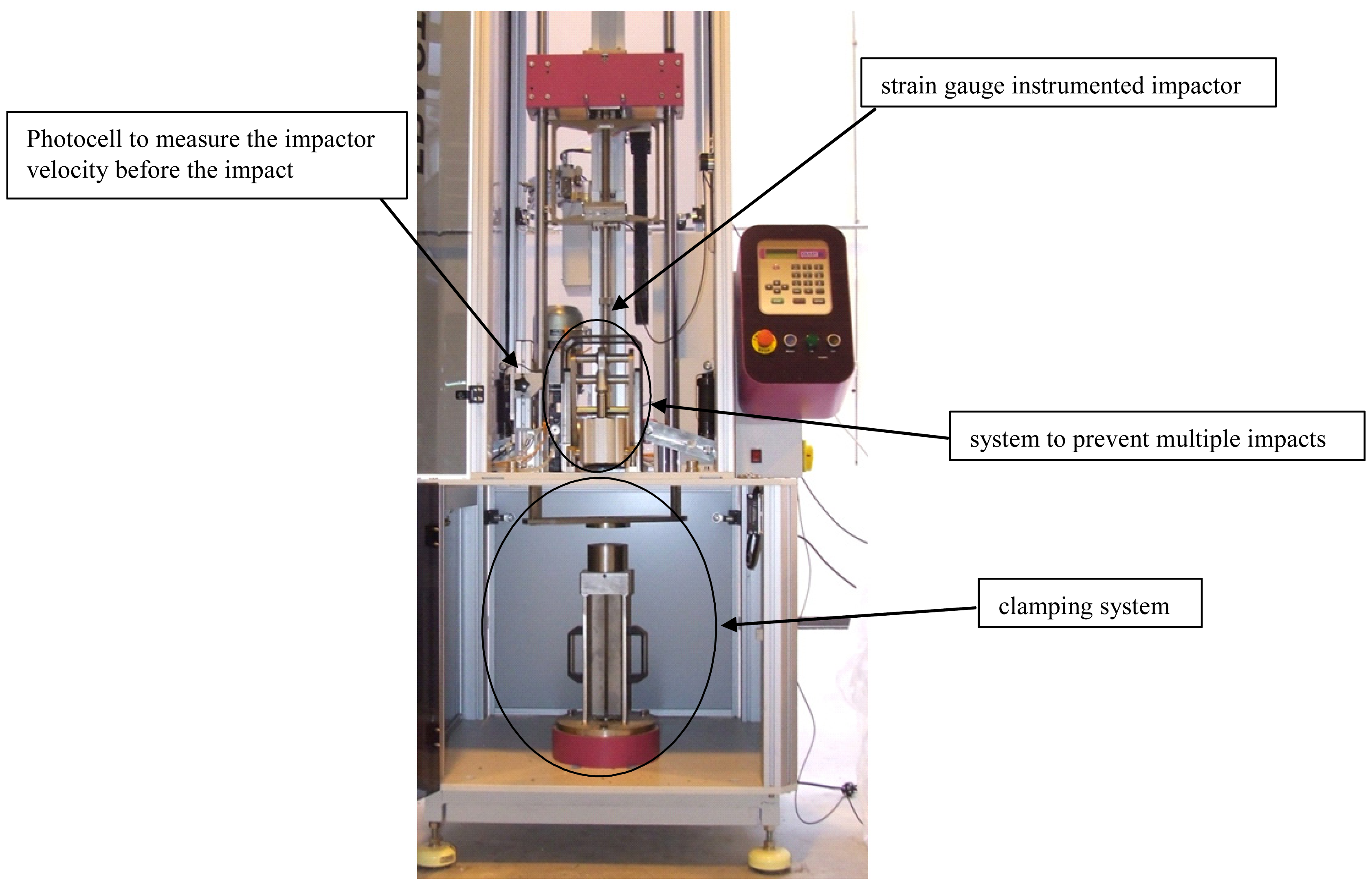
The low-velocity impact tests were carried out by means of the Ceast Fractovis Plus drop test machine (Figure 2), able to eliminate multiple impacts. The mass of the impactor and the drop height are variable, allowing for a wide range of impact energies.
The impacted damage of the aluminum foam core, undetectable by visual inspection, was analyzed by the 3D Computed Tomography System Y.CT Vario (Figure 3).
This unit is equipped with an X-ray source having maximum voltage and current of 225 kV and 7.1 mA, respectively, depending on the focal spot size that can be chosen among these values: 250 μm, 300 μm, 500 μm and 800 μm. The detector system is a flat panel with a resolution of 1920 × 1536 pixels. The scans, reported in this paper, were conducted with 250 μm focus and X-rays were set at a voltage of 210 kV and at a current of about 1.1 mA. A conical X-ray beam scanned the sample, which was rotated at increments of 0.0087 rad/s for each rotation step. This procedure was then repeated until a full rotation of 2π rad was achieved, and a total of 1440 projections were then obtained to be used in the 3D profile generation. The voxels have cubic shape with edge length in the range between 0.033 to 0.050 mm and the image size is 2048 × 2048 pixels. The integration time was chosen equal to 500 ms. It is important to underline that this NDT technique does not require the cutting and polishing of the samples to carry out the X-ray measurements. This allows significant savings in time and the investigation of the internal damage without perturbing the impacted specimen. The system, based on a variable focal-spot size technology, creates the cross-sectional images of three-dimensional objects using X-rays. A volumetric representation of the item to be inspected is obtained as a result of the CT. Both the material inner and outer structures and the geometric dimensions of the item to be inspected are recognizable.
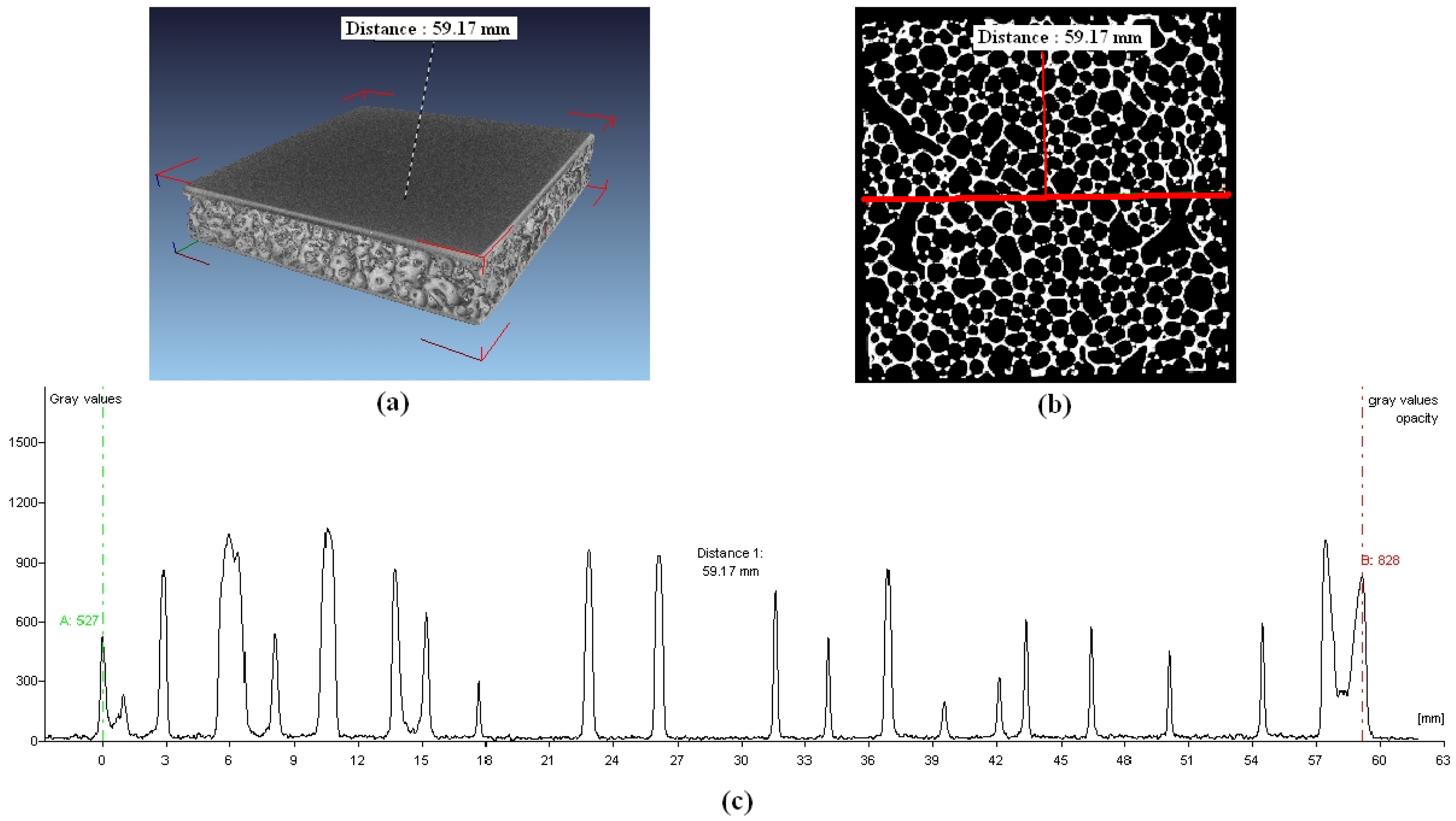
Figure 4 shows the 3D reconstruction of an AFS Schunk panel by means of the CT. This non-destructive technique allows the investigation of the foam porosity and the localization and quantification of the pores; the analysis, in terms of grey levels intensity, along the middle line, drawn on the sample middle section, is reported in Figure 4.
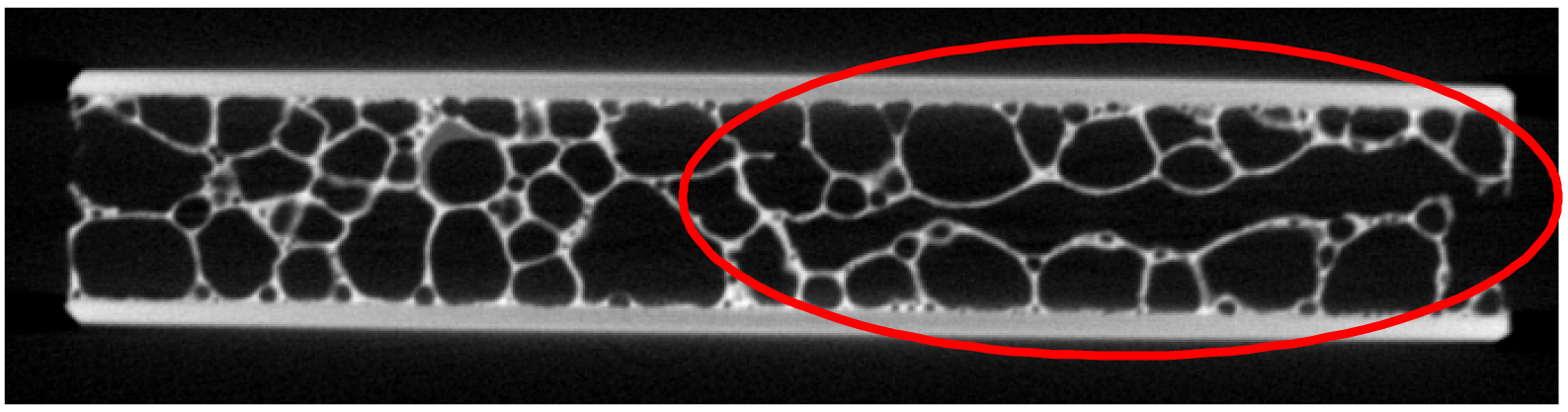
Because of the non-homogeneity of the AFS panels, it is strongly necessary to check the sample before carrying out the impact test. It was decided to discard the panels which showed the following defect types in their whole volume: a cell crossing the whole section along the thickness, a cell whose largest dimension is greater than 5 times the average cell size or greater than 15 mm, as the one shown in Figure 5. The percentage of discarded samples was lower than 10%.
3. Experimental Section
3.1. Low-Velocity Impact Tests
Dynamic impact tests were performed on specimens of the two AFS typologies (Schunk and Alulight) with an impactor mass of about 7 kg and different values of impact velocity ranging from 1.5 to 8 ms−1. The impact energy values range from 8 to 225 J. The impactor, having a hemispherical tip with diameter of 20 mm, is instrumented by means of strain gauge, which allows the measurement of a force value until 40 kN (Figure 6). The AFS specimens (60 × 60 × 11 mm, foam core thickness 9 mm and skin thickness 1 mm) were fully fixed by a rigid metallic plate with a diameter of 40 mm, as shown in Figure 7, without crushing the sample.
The impact force was measured using the strain gauge mounted in the impactor of the drop test machine and the variation of this signal with time was recorded by a dedicated computer and analysed by the software. The velocity during impact is calculated by the integration of the acceleration over time, obtained by the impact force divided by the mass of the dropweight, then the displacement signal is obtained by means of the integration of the displacement.
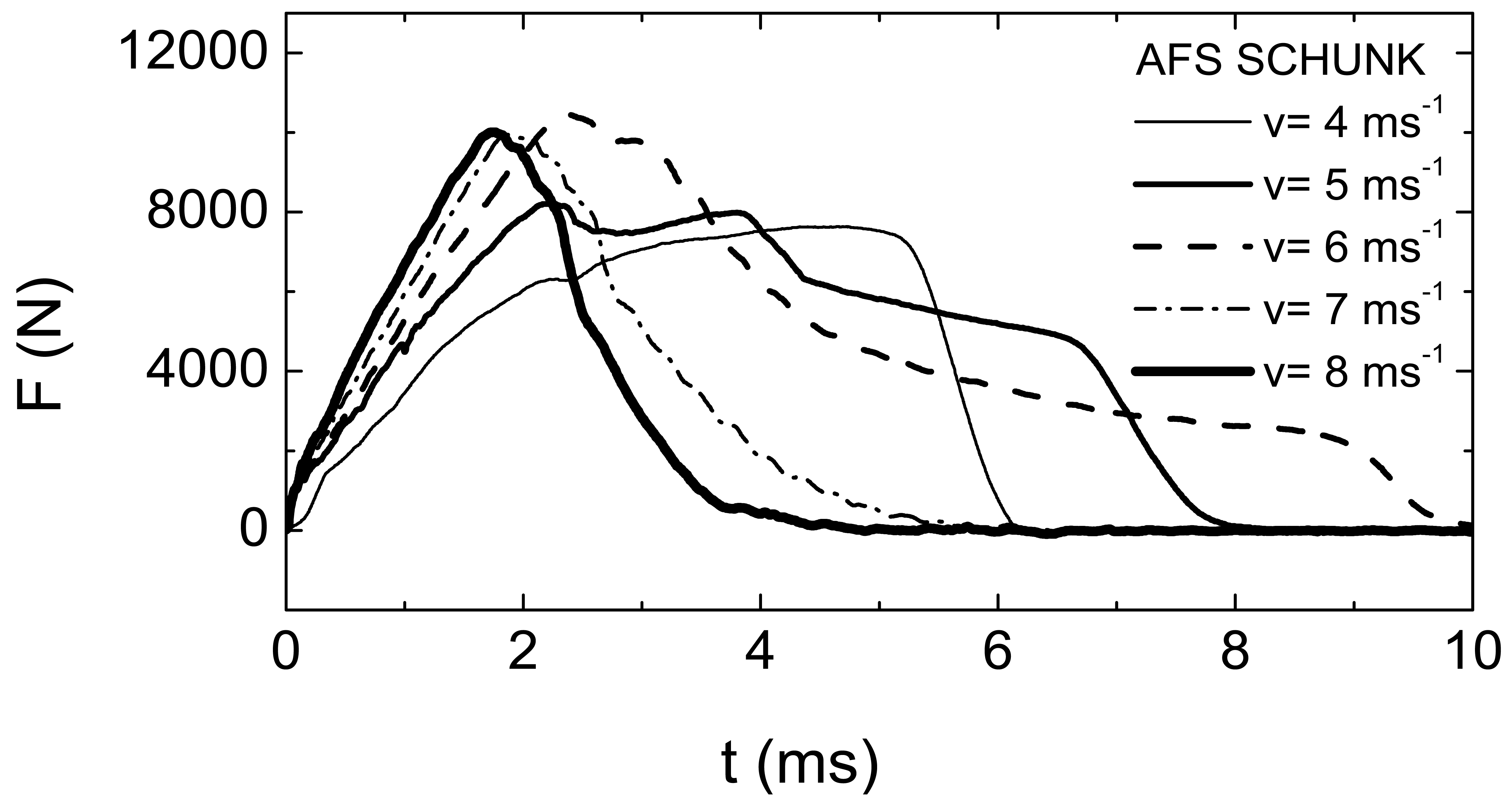
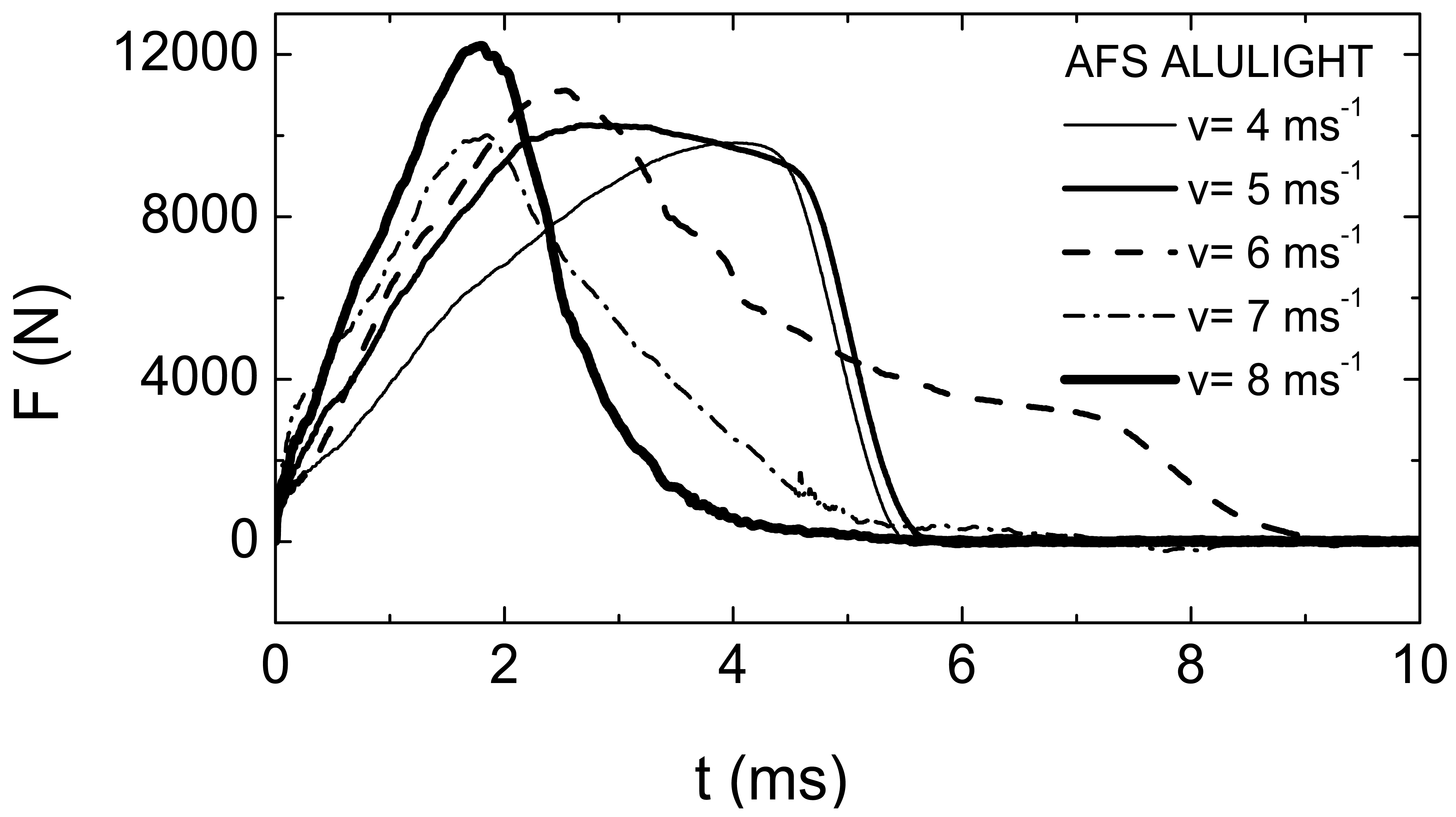
The measured load-time curves at different impact velocities (v = 4, 5, 6, 7, 8 ms−1), corresponding to AFS Schunk and Alulight specimens, are given in Figures 8 and 9.
The contact force peak—velocity curves, obtained by all the tests performed on the two AFS typologies, are shown in Figure 10.
The data scattering, observed in the tests, is due to the different porosity distributions of the aluminum foams, so it is important to check the foam quality by means of non-destructive techniques, such as the CT. Table 3 reports the results of all the experimental tests in terms of absorbed energy and contact force peak. The energy amount, required to produce the complete failure of the sandwiches, was evaluated equal to 142 J for AFS Alulight panels and 122 J for AFS Schunk panels. The experimental results confirm the better response of AFS Alulight under impact loading even if they have a worse skin-core adhesion respect to the AFS Schunk, taking into account that there is no an high difference of core density between the two AFS types. Thus, the dynamic response of these sandwiches is not influenced by the skin-core adhesion and depends on the quality and mechanical properties of the foam core as confirmed by Mahfuz et al. [11], who demonstrated that a significant portion of the initial impact energy is absorbed by the core material.
Figure 11 shows the AFS panels after the impact at different impact velocities (v = 4, 5 and 6 m/s), confirming that the out-of-plane displacements are greater for AFS Schunk panels.
Figure 12 shows the tomographic images just for AFS Alulight and Schunk panels after the impact at v = 4 m/s. These tomographic images allow a better understanding of their failure mode, which is characterized by the progressive crushing of the foam cells with a more uniform distribution of the impacted load.
The post-impact investigation of the specimens confirms the results of the tests conducted by Compston et al. [12]; the AFS specimens experienced extensive ductile fracture with large out-of-plane displacement compared to the predominantly elastic behavior of the polymeric sandwiches; as a consequence the impact damage can be often detectable by a simple visual inspection of the sandwich structures. Moreover, the AFS structures are relatively intact compared to the more catastrophic and localized fracture of the polymeric sandwiches, so they exhibit a better post-impact damage tolerance and mechanical properties [7,8,12]. Thus, the AFS panels are a better choice with respect to the sandwich panels to realize progressive energy absorbers.
3.2. Energy Balance Model
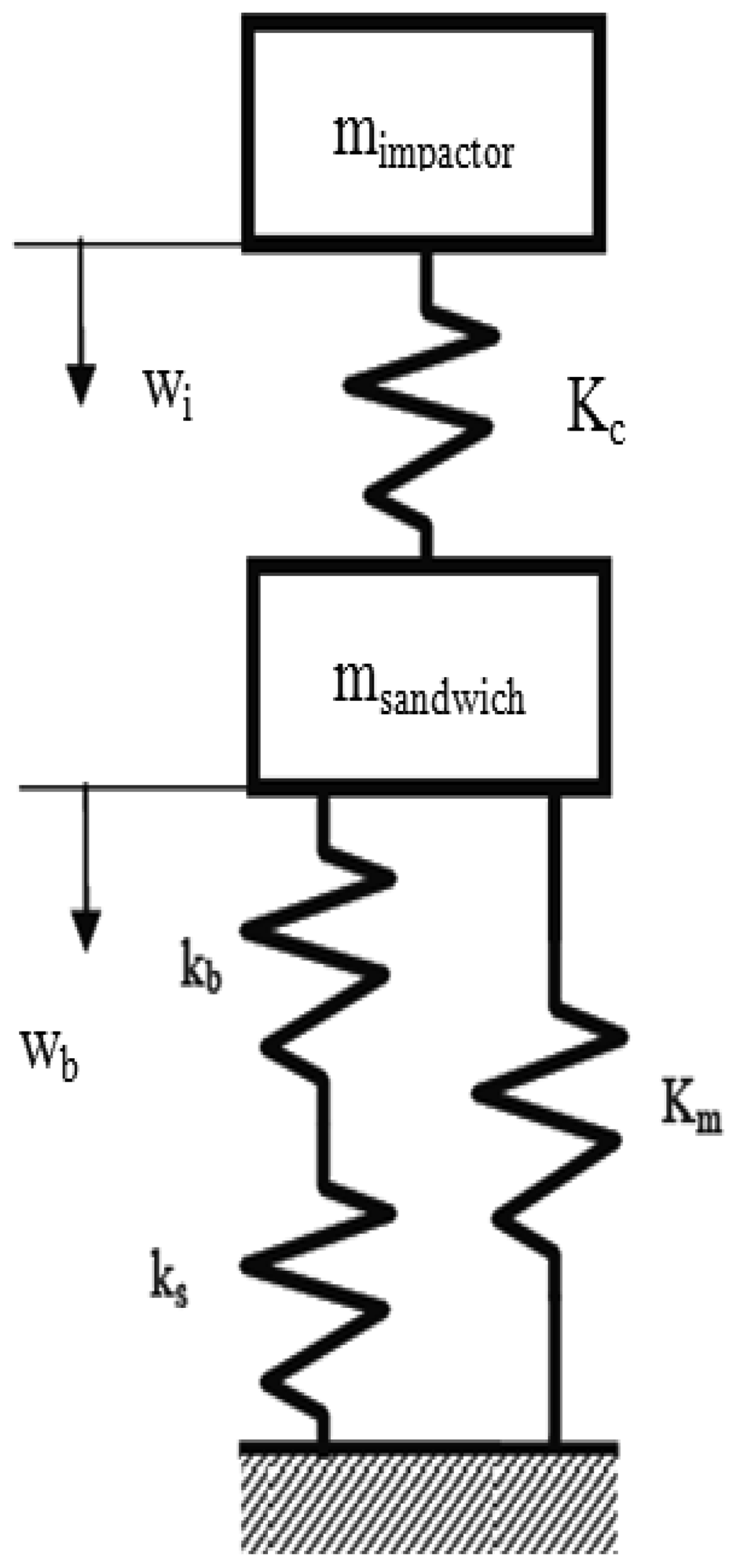
The impact response of the sandwich structures was modeled using a theoretical approach, based on the energy-balance model [1] in order to examine the relative effects of the bending, shear and indentation components of the deformation. The sandwich beam was modeled as a combination of two springs (Figure 13), according to the model proposed by Shivakumar et al. [13]: a linear spring Kbs to account for the global deflection wb and a nonlinear spring Ki to represent the local indentation effects.
The sandwich panel, clamped around its edges, experiences the local displacement α, due to the indentation of the top face and to the core crushing, and the global displacement wb due to the bending and the shear of the entire panel.
Although the impact event is a highly dynamic event, statistically determined contact laws can be used in the impact dynamics analysis of low-velocity impacts because strain rate and wave propagation effects are negligible with commonly used material systems [1]. It was assumed that the target responds quasi-statically during the impact event and that all the initial kinetic energy has been absorbed. This assumption is realistic in the investigated cases because the drop test machine (Figure 2) is able to eliminate multiple impacts, so there isn't any bouncing back of the impactor resulting from elastic deformation of the specimen. The energy needed to create damage can be neglected for impacts that produce only small amounts of damage, so the energy-balance equation (1) can be written as:
As the plate is thick, it can be assumed that the contribution of membrane forces can be neglected [14] as it is generally assumed in literature [1,6,14] for the energy balance model of the impact response of the sandwich panels.
The energy absorbed in bending and shear effects at maximum displacement (force) wmax (Fmax) is equal to:
Contact effects between the impactor and the sandwich structure can be calculated using the Meyer contact law, which relates the indentation depth α to the applied load F and is expressed by:
Finally, the energy balance for the sandwich structure can be obtained considering that the initial kinetic energy is equal to the energy absorption in bending, shear and contact effects:
This theoretical approach has been applied in the current study to investigate the impact response of AFS panels. This energy-balance model, once validated using data from tests carried out at some impact velocities, can be used to predict the maximum impact force for a given impact velocity or energy applying Equation (5).
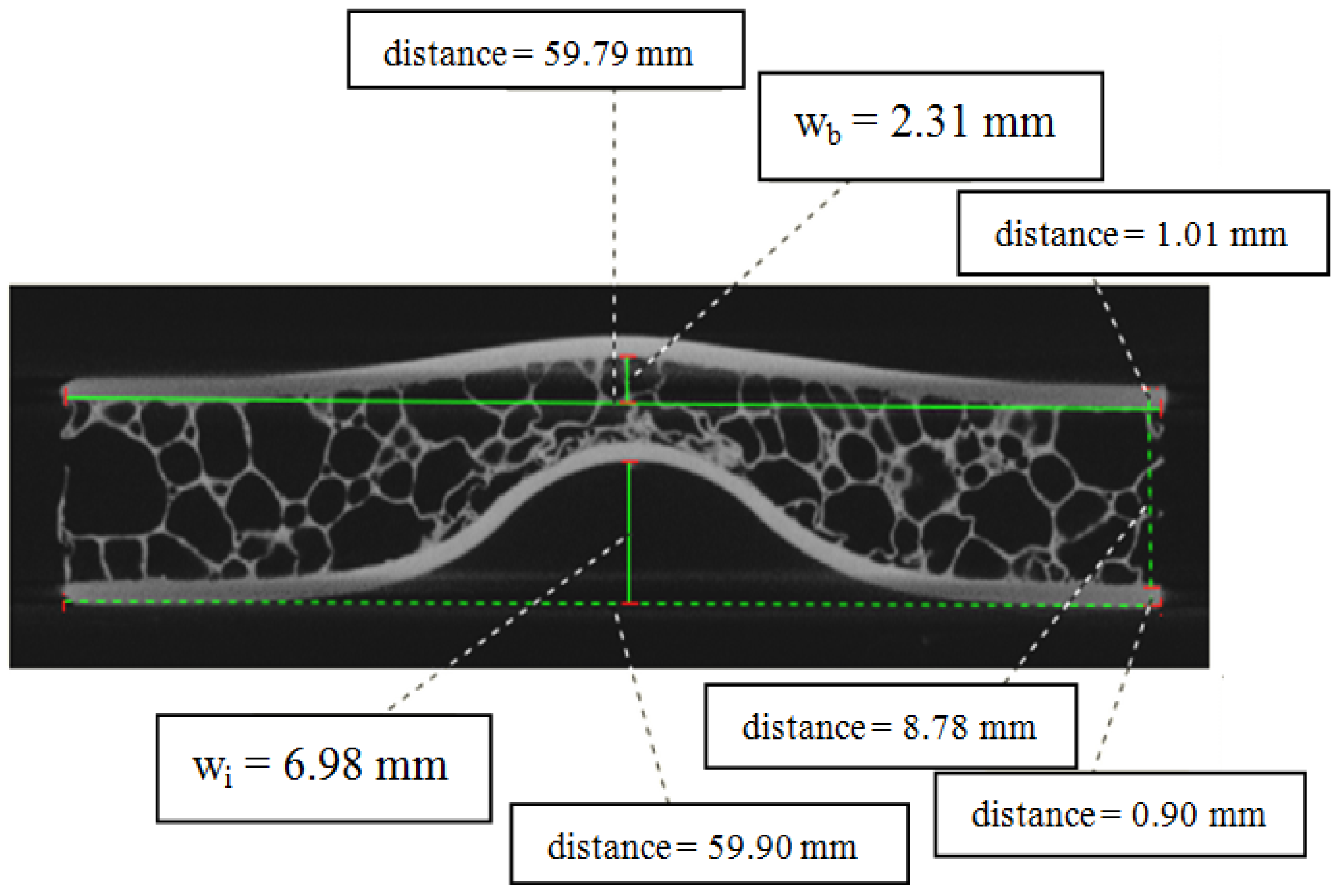
The parameters of the energy balance model are generally determined in literature from the results of static tests. In this scientific research the parameters were obtained directly from the measurements carried out on the CT images (Figure 14); the vertical displacement wb of the core at bottom face sheet interface and the impactor displacement wi were measured by analysing the CT images of midplanes of the panels impacted at velocities lower than 5 ms−1, that didn't produce the complete failure of the panels. The core compression displacement α is obtained by the subtraction between the impactor displacement wi and the vertical displacement wb of the core.
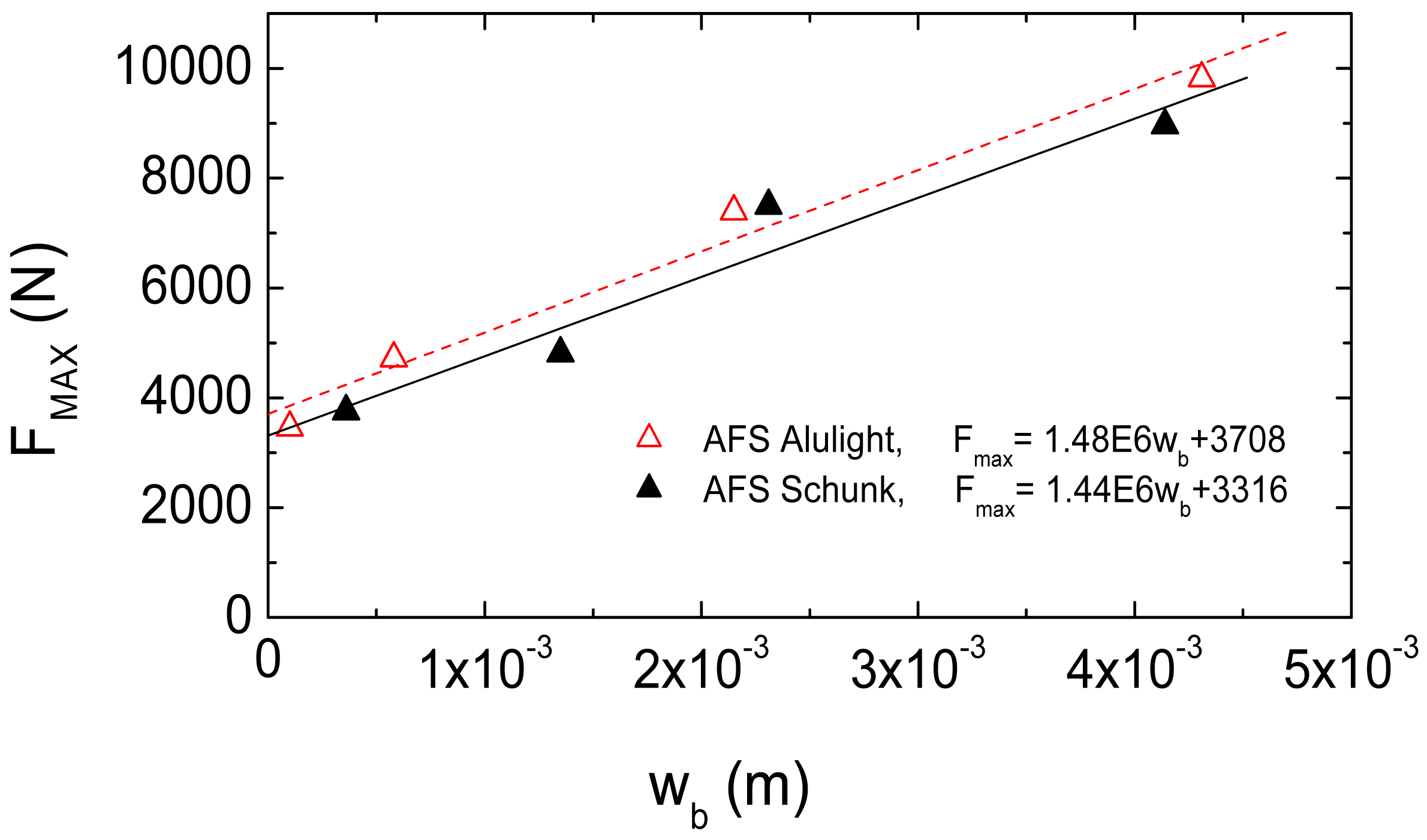
According to the spring-mass model, it can be assumed a linear relationship between the impact load and the corresponding global displacement wb of the sandwich panel and the Kbs stiffness is the slope of this linear function. Moreover, the Kbs stiffness does not change with the impact velocity, so the Kbs stiffness was assessed in the present research paper by the slope of the linear function interpolating the peak loads at different impact velocities, obtained by the impact tests, versus the corresponding bending and shear deflections of the midplane of the panel, that were measured using the CT. The values of the force contact loads Fmax, obtained by the experimental tests, were plotted versus the corresponding values of the deflection wb of the panel midplane and a linear regression was performed in order to obtain the values of the stiffness Kbs for each AFS typology, as shown in Figure 15.
The contribution of the energy dissipation due to bending and shear Ebs was evaluated applying Equation (2) and the contact energy Ec was obtained simply by subtracting these values of Ebs from the values of the total dissipated energy.
Considering the bilogarithmic expression of Equation (4), a linear equation is obtained:
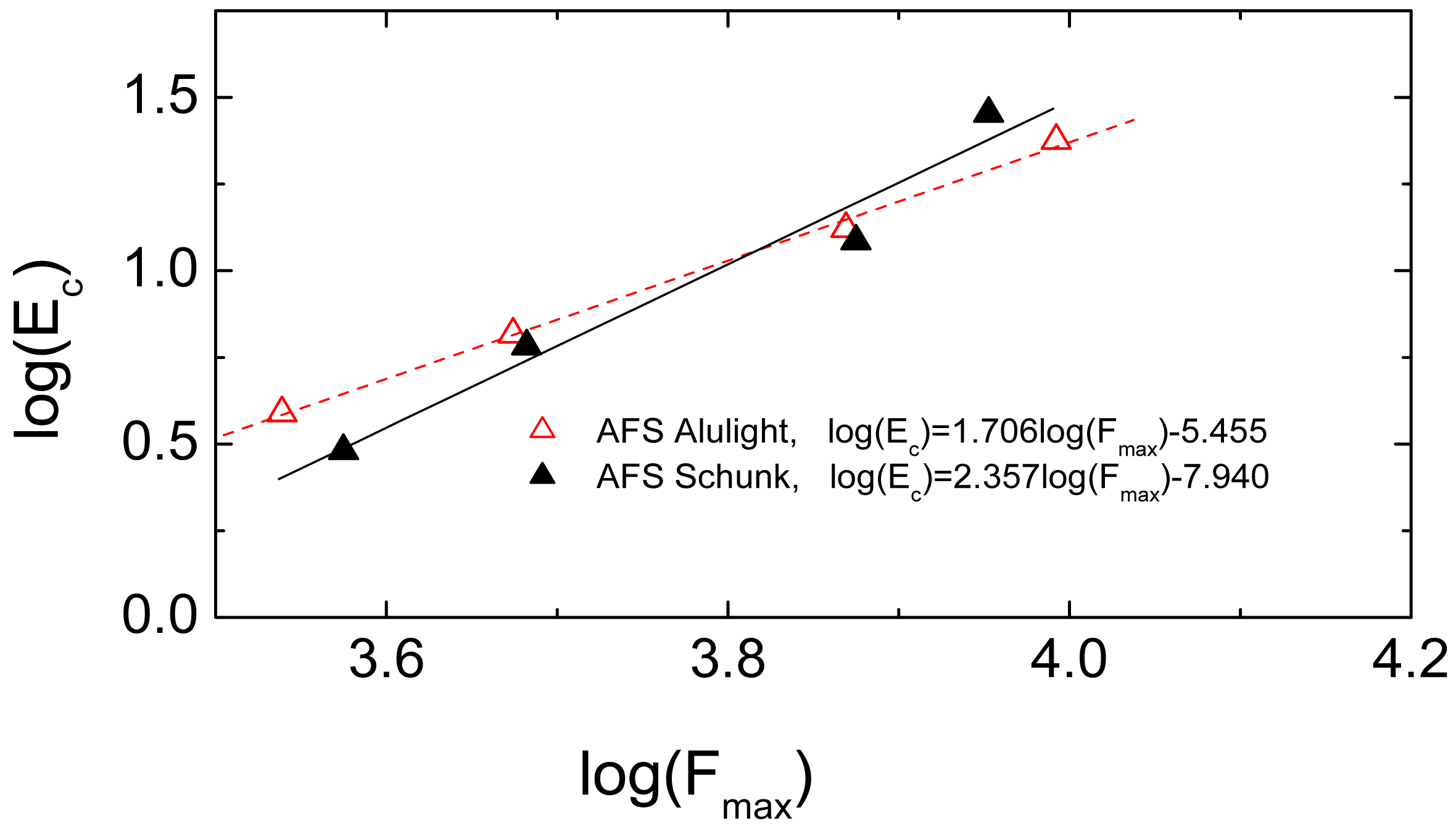
The values of the contact energy Ec were plotted versus the corresponding values of the peak load Fmax in a bilogarithmic scale and a linear regression was performed in order to assess the contact parameters (n, Ki) of equation (6), as shown in Figure 16; the value of n was obtained by the slope of the linear equation interpolating the data and the value of Ki by the constant term of the linear equation.
The obtained values of the Ki and n constants are: n = 1.42 and Ki = 1.51E7 Nm−1.42 for AFS Alulight, n = 0.74 and Ki = 4.70E5 Nm−0.74 for AFS Schunk.
4. Conclusions
The impact behavior of aluminum foam sandwiches have been investigated by experimental tests and analytical approach, based on the energy balance model. The model parameters were obtained from the measurements carried out on the CT images of the impacted panels and not from the results of static tests, as it is usually done in literature.
The failure mode and the damage have been investigated by Computed Tomography. The investigation of the aluminum foams by means of the 3D CT is very useful to check their quality in terms of porosity distribution, which influences the mechanical properties of the foams.
Low velocity impact tests on AFS structures have shown that the dynamic response of these sandwiches depends on the quality and mechanical properties of the foam core material.
The AFS structures are relatively intact compared to the more catastrophic and localized fracture of the polymeric sandwiches, so they are a better choice with respect to the polymeric sandwiches to realize progressive energy absorbers.
The obtained results have particular importance for applications that require lightweight structures with a high capacity of energy dissipation, such as the transport industry, where problems of collision and crash have increased in the last years. The use of these sandwich structures can lead to a weight reduction of the ships, providing an adequate structural strength under operating conditions.







| AFS-Alulight | AFS-Schunk | |
|---|---|---|
| Skin | Al 99.6%, O 0.4% | Al 98.97%, Mn 1.03% |
| Core | Al 82.3%, Si 17%, Ti 0.14%, O 0.56% | Al 92.83%, Si 7.03%, Ti 0.14% |
| Epoxy adhesive | C 72.12%, O 27.71%, Cl 0.17% |
| AFS-Alulight | AFS-Schunk | |||
|---|---|---|---|---|
| Skin | Core | Skin | Core | |
| material | Al (99.5%) | AlSi10 | AlMn1 | AlSi7 |
| density [kg/dm3] | 2.73 | 0.53 ± 0.06 | 2.73 | 0.45 ± 0.04 |
| thickness [mm] | 1 | 9 | 1 | 9 |
| total density of AFS panel [kg/dm3] | 0.95 ± 0.05 | 0.87 ± 0.04 | ||
| total thickness of AFS panel [mm] | 11 | 11 | ||
| AFS-Alulight | AFS-Schunk | |||
|---|---|---|---|---|
| v [m/s] | Fmax [N] | E [J] | Fmax [N] | E [J] |
| 1.5 | 3,458 | 8 | 3,757 | 8 |
| 2 | 4,722 | 14 | 4,810 | 14 |
| 3 | 7,398 | 31 | 7,499 | 31 |
| 4 | 9,822 | 56 | 8,967 | 56 |
| 4 | - | - | 7,567 | 56 |
| 4 | - | - | 7,640 | 56 |
| 5 | 10,257 | 88 | 8,214 | 88 |
| 6 | 11,112 | 127 | 10,460 | 127 |
| 6 | - | - | 9,132 | 127 |
| 7 | 10,010 | 139 | 9,948 | 130 |
| 8 | 11,010 | 144 | 8,769 | 119 |
| 8 | 9,542 | 134 | 8,740 | 117 |
| 8 | 10,150 | 137 | 10,010 | 134 |
| 8 | 12,213 | 158 | 7,253 | 110 |
References
- Abrate, S. Impact on Composite Structures; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth Heinmann: Burlington, VT, USA, 2000. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Banhart, J.; Schmoll, C.; Neumann, U. Light-weight aluminum foam structures for ships. Proceedings of the Conference on Materials in Oceanic Environment (Euromat '98), Lisbon, Portugal, 22–24 July 1998; Faria, L., Ed.; Federation of European Materials Societies (FEMS): Lisbon, Portugal, 1998; 1, pp. 55–63. [Google Scholar]
- Baumeister, J.; Banhart, J.; Weber, M. Aluminum foams for transport industry. Mater. Des. 1997, 18, 217–220. [Google Scholar]
- Hazizan, M.A.; Cantwell, W.J. The low velocity impact response of foam-based sandwich structures. Compos. Part B 2002, 33, 193–204. [Google Scholar]
- Crupi, V.; Epasto, G.; Guglielmino, E. Low velocity impact strength of sandwich materials. J. Sandw. Struct. Mater. 2011, 13, 409–426. [Google Scholar]
- Crupi, V.; Epasto, G.; Guglielmino, E. Computed tomography analysis of damage in composites subjected to impact loading. Fract. Struct. Integr. 2011, 17, 32–41. [Google Scholar]
- Olurin, O.B.; Arnold, M.; Körner, C.; Singer, R.F. The investigation of morphometric parameters of aluminum foams using micro-computed tomography. Mater. Sci. Eng. 2002, A328, 334–343. [Google Scholar]
- Wicklein, M.; Thoma, K. Numerical investigations of the elastic and plastic behaviour of an open-cell aluminum foam. Mater. Sci. Eng. 2005, A397, 391–399. [Google Scholar]
- Mahfuz, H.; Al Mamum, W.; Jeelani, S. Effect of core density and implanted delamination on the high strain rate response of foam core sandwich composites. Sandw. Constr. 1997, 5, 597–606. [Google Scholar]
- Compston, P.; Styles, M.; Kalyanasundaram, S. Low energy impact damage modes in aluminum foam and polymer foam sandwich structures. J. Sandw. Struct. Mater. 2006, 8, 365–379. [Google Scholar]
- Shivakumar, K.N.; Elber, W.; Illg, W. Prediction of impact force and duration during low-velocity impact on circular composite laminates. Trans. ASME J. Appl. Mech. 1985, 52, 674–680. [Google Scholar]
- Foo, C.C.; Seah, L.K.; Chai, G.B. Low-velocity impact failure of aluminum honeycomb sandwich panels. Compos. Struct. 2008, 85, 20–28. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Crupi, V.; Epasto, G.; Guglielmino, E. Impact Response of Aluminum Foam Sandwiches for Light-Weight Ship Structures. Metals 2011, 1, 98-112. https://doi.org/10.3390/met1010098
Crupi V, Epasto G, Guglielmino E. Impact Response of Aluminum Foam Sandwiches for Light-Weight Ship Structures. Metals. 2011; 1(1):98-112. https://doi.org/10.3390/met1010098
Chicago/Turabian StyleCrupi, Vincenzo, Gabriella Epasto, and Eugenio Guglielmino. 2011. "Impact Response of Aluminum Foam Sandwiches for Light-Weight Ship Structures" Metals 1, no. 1: 98-112. https://doi.org/10.3390/met1010098






