Visualization of Complex Processes in Cardiovascular System during Electrical Auricular Vagus Nerve Stimulation
Abstract
:1. Introduction
2. Preliminaries
3. Materials and Methods
3.1. Experimental Setup
3.2. The Description of the Algorithm
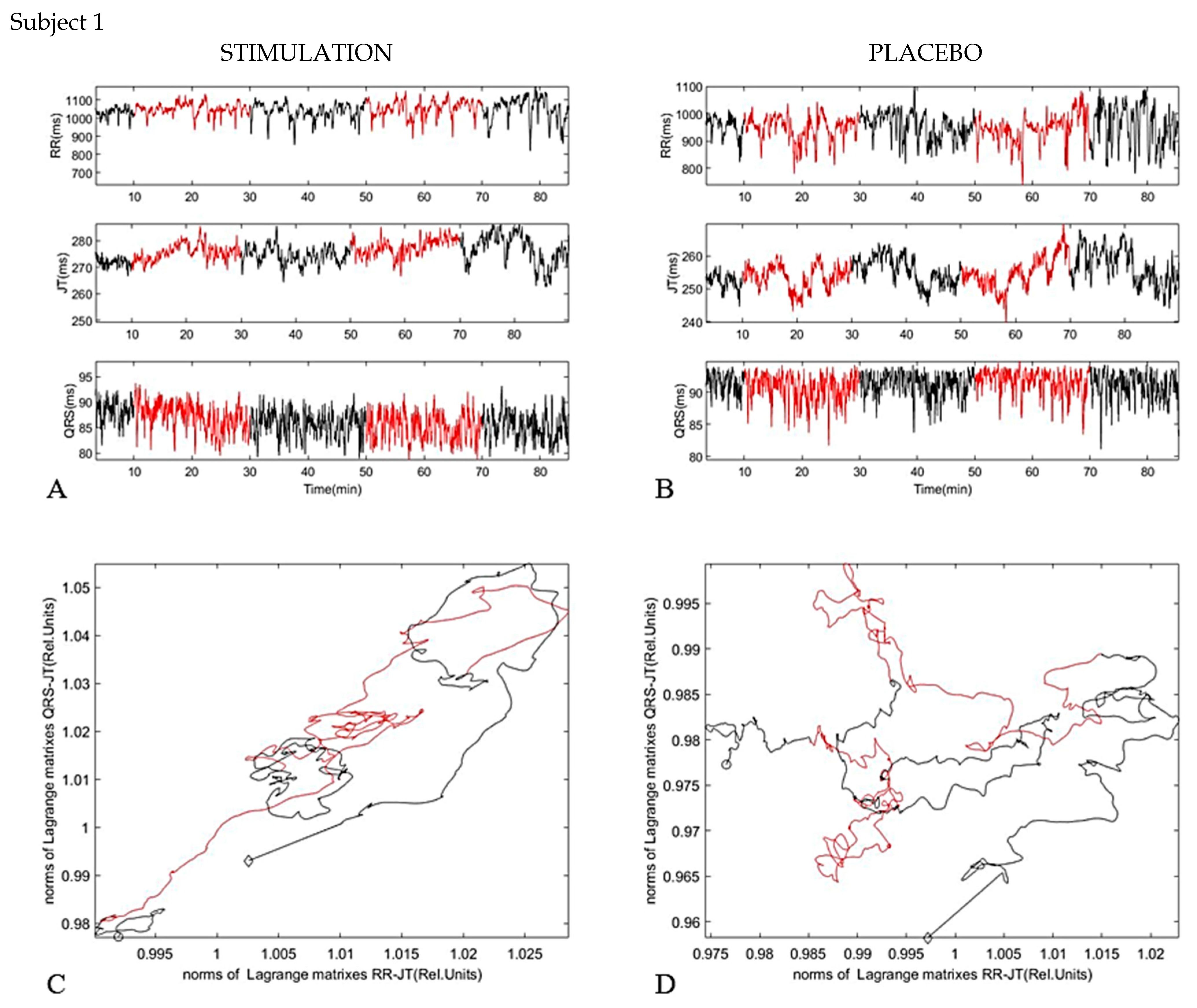
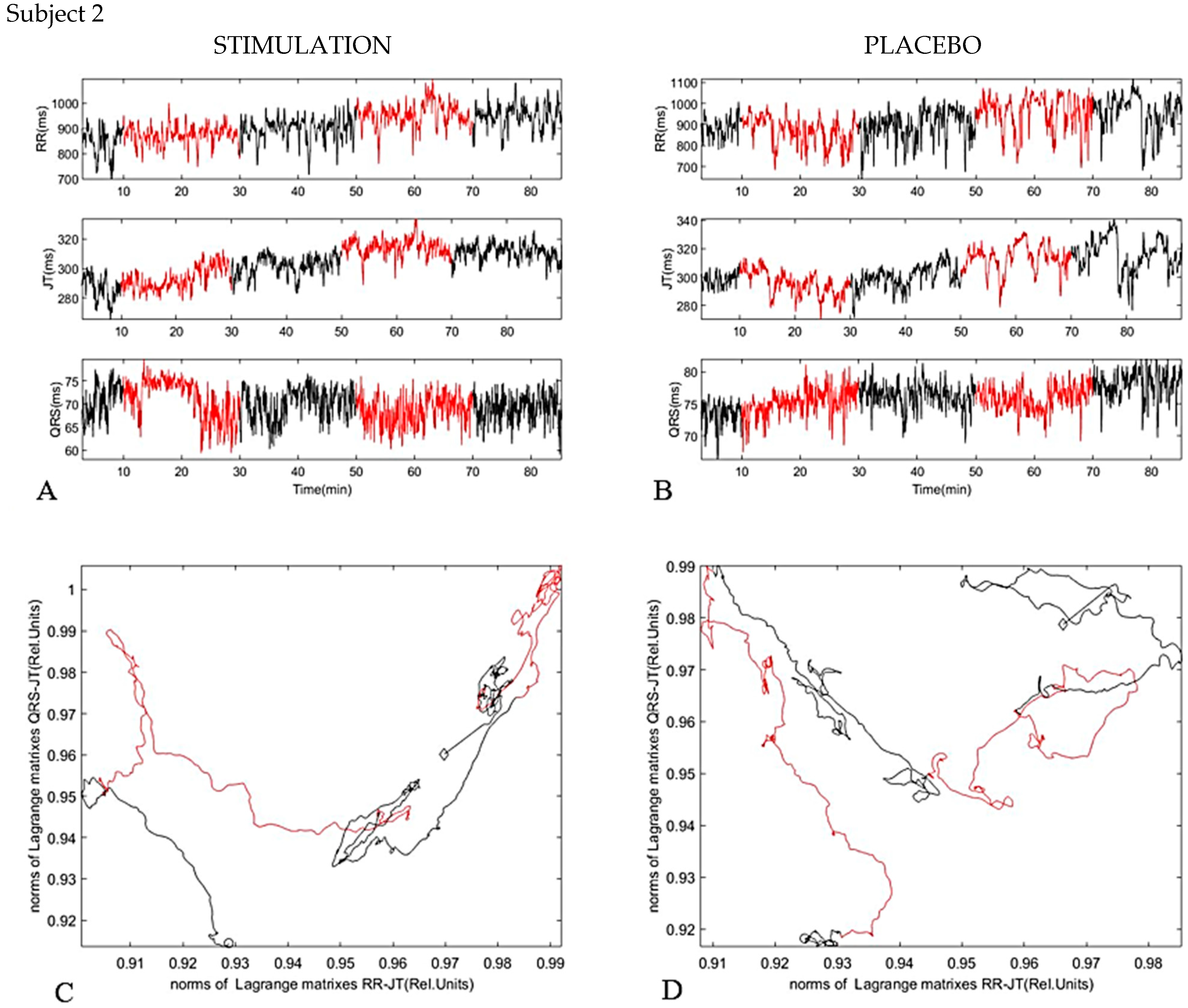
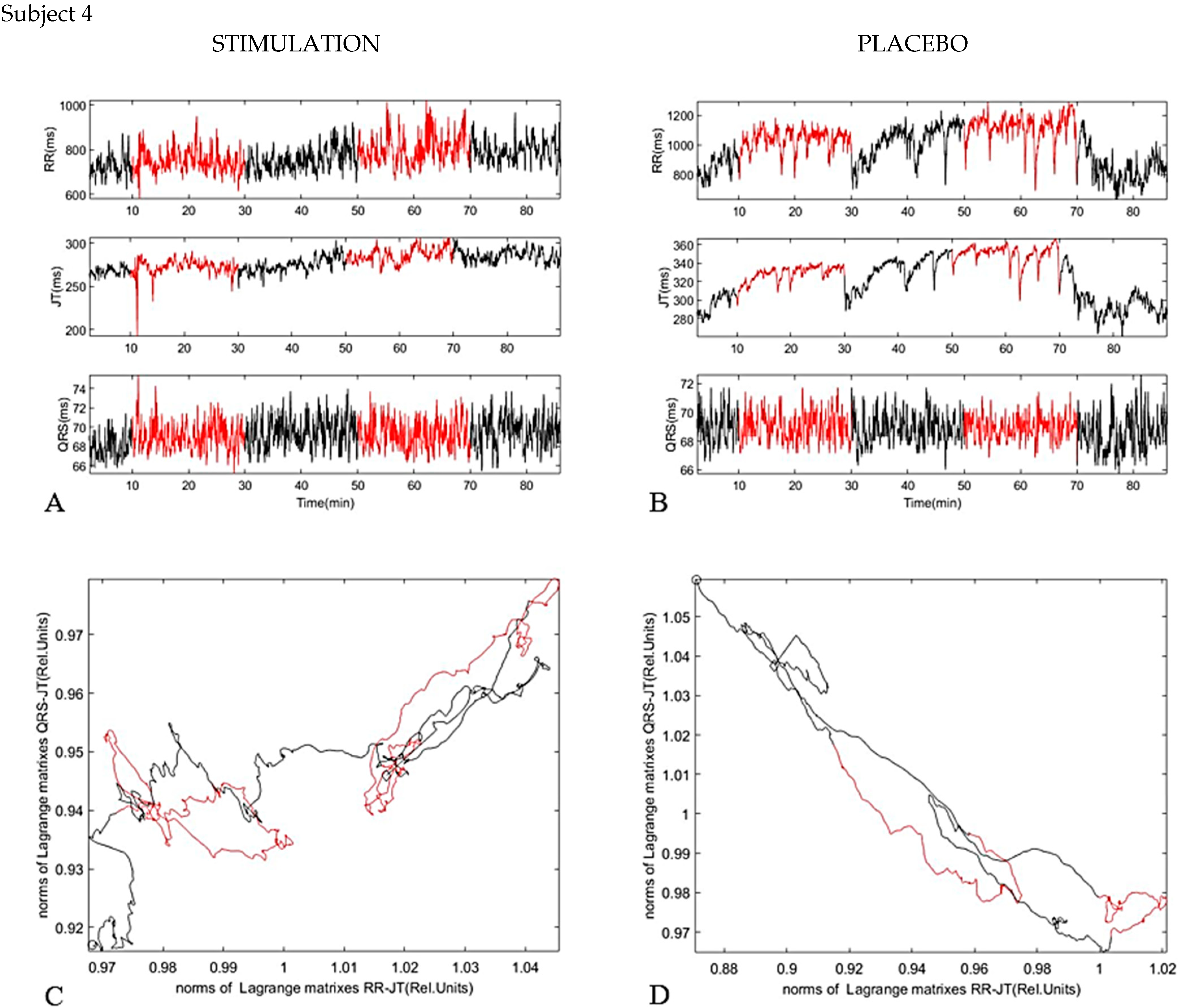
4. Results
5. Discussion
Strengths and Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, T.F.; Li, A.; Sun, X.; Arias-Carrion, O.; Machado, S. Vagus nerve stimulation in treating depression: A tale of two stories. Curr. Mol. Med. 2016, 16, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Browning, K.N.; Travagli, R.A. Central nervous system control of gastrointestinal motility and secretion and modulation of gastrointestinal functions. Compr. Physiol. 2014, 4, 1339–1368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, H.; Silberstein, S.D. Vagus nerve and vagus nerve stimulation, a comprehensive review: Part I. Headache 2016, 56, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Mercante, B.; Ginatempo, F.; Manca, A.; Melis, F.; Enrico, P.; Deriu, F. Anatomo-physiologic basis for auricular stimulation. Med. Acupunct. 2018, 30, 141–150. [Google Scholar] [CrossRef]
- Peuker, E.T.; Filler, T.J. The nerve supply of the human auricle. Clin. Anat. 2002, 15, 35–37. [Google Scholar] [CrossRef]
- Kaniusas, E.; Kampusch, S.; Tittgemeyer, M.; Panetsos, F.; Gines, R.F.; Papa, M.; Kiss, A.; Podesser, B.; Cassara, A.M.; Tanghe, E.; et al. Current directions in the auricular vagus nerve stimulation II–an engineering perspective. Front. Neurosci. 2019, 13, 772. [Google Scholar] [CrossRef]
- He, W.; Zhu, B.; Zhu, X.-L.; Li, L.; Bai, W.-Z.; Ben, H. The auriculo-vagal afferent pathway and its role in seizure suppression in rats. BMC Neurosci. 2013, 14, 85. [Google Scholar] [CrossRef] [Green Version]
- Breit, S.; Kupferberg, A.; Rogler, G.; Hasler, G. Vagus nerve as modulator of the brain–gut axis in psychiatric and inflammatory disorders. Front. Psychiatry 2018, 9, 44. [Google Scholar] [CrossRef] [Green Version]
- Berthoud, H.R.; Neuhuber, W.L. Functional and chemical anatomy of the afferent vagal system. Auton. Neurosci. 2001, 85, 1–17. [Google Scholar] [CrossRef]
- Széles, J.C.; Kampusch, S.; Le, V.H.; Enajat, D.P.; Kaniusas, E.; Neumayer, C. Clinical Effectiveness of Percutaneous Auricular Vagus Nerve Stimulation in Chronic Back Pain Patients-A Single-Centre Retrospective Analysis. Ann. Pain Med. 2021, 3, 1009. [Google Scholar]
- Kampusch, S.; Thürk, F.; Kaniusas, E.; Széles, J.C. Autonomous nervous system modulation by percutaneous auricular vagus nerve stimulation: Multiparametric assessment and implications for clinical use in diabetic foot ulcerations. In Proceedings of the 2015 IEEE Sensors Applications Symposium (SAS), Zadar, Croatia, 13–15 April 2015; pp. 1–6. [Google Scholar]
- Széles, J.C.; Kampusch, S.; Thürk, F.; Clodi, C.; Thomas, N.; Fichtenbauer, S.; Schwanzer, C.; Schwarzenberger, S.; Neumayer, C.; Kaniusas, E. Bursted auricular vagus nerve stimulation alters heart rate variability in healthy subjects. Physiol. Meas. 2021, 42, 105002. [Google Scholar] [CrossRef]
- Ziaukas, P.; Alabdulgader, A.; Vainoras, A.; Navickas, Z.; Ragulskis, M. New approach for visualization of relationships between RR and JT intervals. PLoS ONE 2017, 12, e0174279. [Google Scholar] [CrossRef]
- Saunoriene, L.; Siauciunaite, V.; Vainoras, A.; Bertasiute, V.; Navickas, Z.; Ragulskis, M. The characterization of the transit through the anaerobic threshold based on relationships between RR and QRS cardiac intervals. PLoS ONE 2019, 14, e0216938. [Google Scholar] [CrossRef]
- Šiaučiūnaitė, V.; Vainoras, A.; Navickas, Z.; Ragulskis, M. Detection of Ischemic Episodes Based on Two Consecutive Declines in the JT/ST Algebraic Relationship. Appl. Sci. 2021, 11, 4805. [Google Scholar] [CrossRef]
- Seely, A.J.; Christou, N.V. Multiple organ dysfunction syndrome: Exploring the paradigm of complex nonlinear systems. Crit. Care Med. 2000, 28, 2193–2200. [Google Scholar] [CrossRef] [PubMed]
- Que, C.L.; Kenyon, C.M.; Olivenstein, R.; Macklem, P.T.; Maksym, G.N. Homeokinesis and short-term variability of human airway caliber. J. Appl. Physiol. 2001, 91, 1131–1141. [Google Scholar] [CrossRef] [PubMed]
- Siauciunaite, V.; Kaniusas, E.; Kampusch, S.; Szeles, J.C.; Vainoras, A. Auricular vagus nerve stimulation affects fractality of the human body as resolved by advanced ECG. In Proceedings of the 2018 EMF-Med 1st World Conference on Biomedical Applications of Electromagnetic Fields (EMF-Med), Split, Croatia, 10–13 September 2018; pp. 1–2. [Google Scholar]
- Malik, M.; Färbom, P.; Batchvarov, V.; Hnatkova, K.; Camm, A.J. Relation between QT and RR intervals is highly individual among healthy subjects: Implications for heart rate correction of the QT interval. Heart 2002, 87, 220–228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaffer, F.; McCraty, R.; Zerr, C.L. A healthy heart is not a metronome: An integrative review of the heart’s anatomy and heart rate variability. Front. Psychol. 2014, 5, 1040. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McCraty, R.; Atkinson, M.; Tomasino, D.; Bradley, R.T. The coherent heart: Heart-brain interactions, psychophysiological coherence, and the emergence of system-wide order. Integral Rev. Transdiscipl. Transcult. J. New Thought Res. Prax. 2009, 5, 10–115. [Google Scholar]
- Rostagno, C.; Felici, M.; Caciolli, S.; Olivo, G.; Comeglio, M.; Galanti, G.; Serneri, G.G.N. Decreased baroreflex sensitivity assessed from phase IV of Valsalva maneuver in mild congestive heart failure. Angiology 1999, 50, 655–664. [Google Scholar] [CrossRef]
- Kaye, D.M.; Jennings, G.L.; Dart, A.M.; Esler, M.D. Differential effect of acute baroreceptor unloading on cardiac and systemic sympathetic tone in congestive heart failure. J. Am. Coll. Cardiol. 1998, 31, 583–587. [Google Scholar] [CrossRef] [Green Version]
- Segerstrom, S.C.; Nes, L.S. Heart rate variability reflects self-regulatory strength, effort, and fatigue. Psychol. Sci. 2007, 18, 275–281. [Google Scholar] [CrossRef]
- Vainoras, A. Kardiovaskulinė sistema ir sportinė veikla. In Kardiovaskulinė Sistema ir Sportinė Veikla; LTOK: Vilnius, Lithuania, 1996; pp. 3–8. [Google Scholar]
- Gargasas, L.; Vainoras, A.; Schwela, H.; Jaruševičius, G.; Ruseckas, R.; Miškinis, V. JT interval changes during bicycle ergometry. In Proceedings of the Kardiologia Polska: II Miedzynarodowy Kongres Polskiego Towarzystwa Kardiologieznego, Kotowice, Poland, 4–6 September 1998; p. 153. [Google Scholar]
- Muntianaitė-Dulkinienė, I. The Evaluation of the Complexity of Cardiovascular System Parameters When Performing Physical Tasks. Ph.D. Thesis, Kauno Medicinos Universiteto Leidykla, Kaunas, Lithuania, 2010. [Google Scholar]
- Batzel, J.J.; Kappel, F.; Schneditz, D.; Tran, H.T. Cardiovascular and Respiratory Systems Modeling, Analysis, and Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 105–119. [Google Scholar]
- Misigoj-Durakovic, M.; Durakovic, Z.; Prskalo, I. Heart rate-corrected QT and JT intervals in electrocardiograms in physically fit students and student athletes. Ann. Noninvasive Electrocardiol. 2016, 21, 595–603. [Google Scholar] [CrossRef] [PubMed]
- Prasad, K.; Gupta, M.M. Phase-invariant signature algorithm. A noninvasive technique for early detection and quantification of ouabain-induced cardiac disorders. Angiology 1979, 30, 721. [Google Scholar] [CrossRef]
- Sornmo, L.; Wohlfart, B.; Berg, J.; Pahlm, O. Beat-to-Beat QRS Variability in the 12-Lead ECG and the Detection of Coronary Artery Disease. J. Electrocardiol. 1998, 31, 336–344. [Google Scholar] [CrossRef]
- Johnson, R.L.; Wilson, C.G. A review of vagus nerve stimulation as a therapeutic intervention. J. Inflamm. Res. 2018, 11, 203–213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erem, B.; Orellana, R.M.; Hyde, D.E.; Peters, J.M.; Duffy, F.H.; Stovicek, P.; Warfield, S.K.; MacLeod, R.S.; Tadmor, G.; Brooks, D.H. Extensions to a manifold learning framework for time-series analysis on dynamic manifolds in bioelectric signals. Phys. Rev. E 2016, 93, 42218. [Google Scholar] [CrossRef] [Green Version]



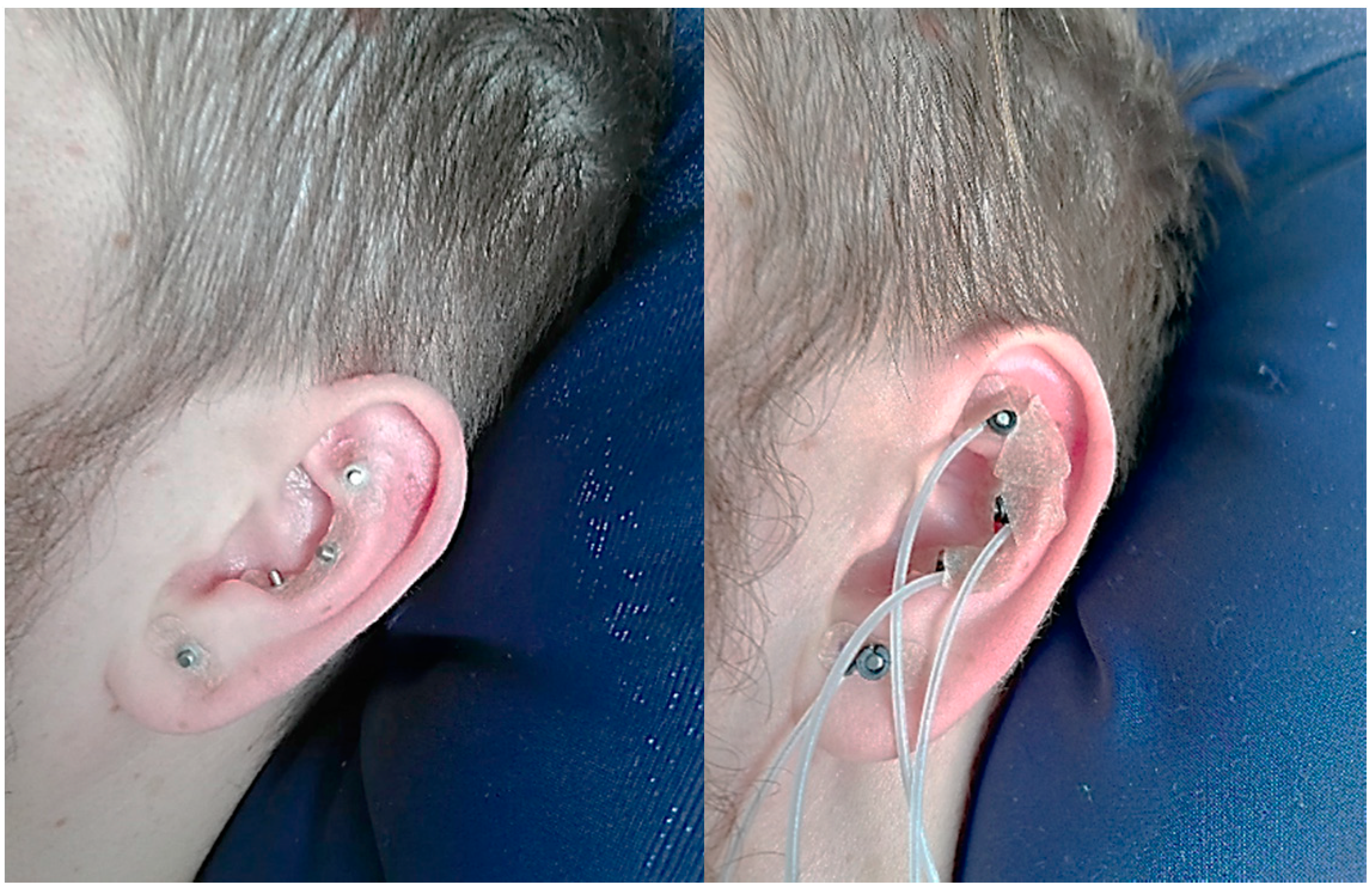

| Gender | Age, y | Height, m | Weight, kg | BMI, kg/m2 |
|---|---|---|---|---|
| M | 31 | 1.81 | 83 | 25.34 |
| F | 27 | 1.72 | 65 | 21.97 |
| M | 26 | 1.77 | 65 | 20.75 |
| F | 27 | 1.69 | 55 | 19.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šiaučiūnaitė, V.; Ragulskis, M.; Vainoras, A.; Dabiri, B.; Kaniusas, E. Visualization of Complex Processes in Cardiovascular System during Electrical Auricular Vagus Nerve Stimulation. Diagnostics 2021, 11, 2190. https://doi.org/10.3390/diagnostics11122190
Šiaučiūnaitė V, Ragulskis M, Vainoras A, Dabiri B, Kaniusas E. Visualization of Complex Processes in Cardiovascular System during Electrical Auricular Vagus Nerve Stimulation. Diagnostics. 2021; 11(12):2190. https://doi.org/10.3390/diagnostics11122190
Chicago/Turabian StyleŠiaučiūnaitė, Vaiva, Minvydas Ragulskis, Alfonsas Vainoras, Babak Dabiri, and Eugenijus Kaniusas. 2021. "Visualization of Complex Processes in Cardiovascular System during Electrical Auricular Vagus Nerve Stimulation" Diagnostics 11, no. 12: 2190. https://doi.org/10.3390/diagnostics11122190






