Low-Rate Characterization of a Mechanical Inerter
Abstract
:1. Introduction
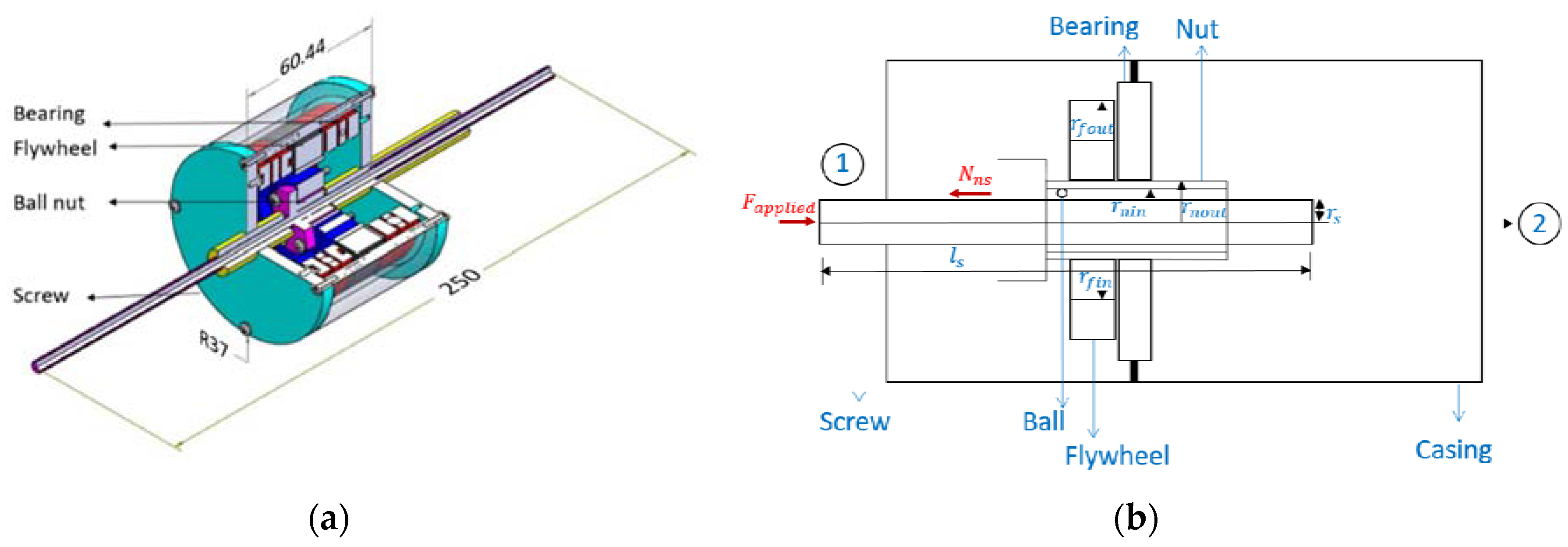
2. Modeling
2.1. Analytical Expressions for Specific Inertance
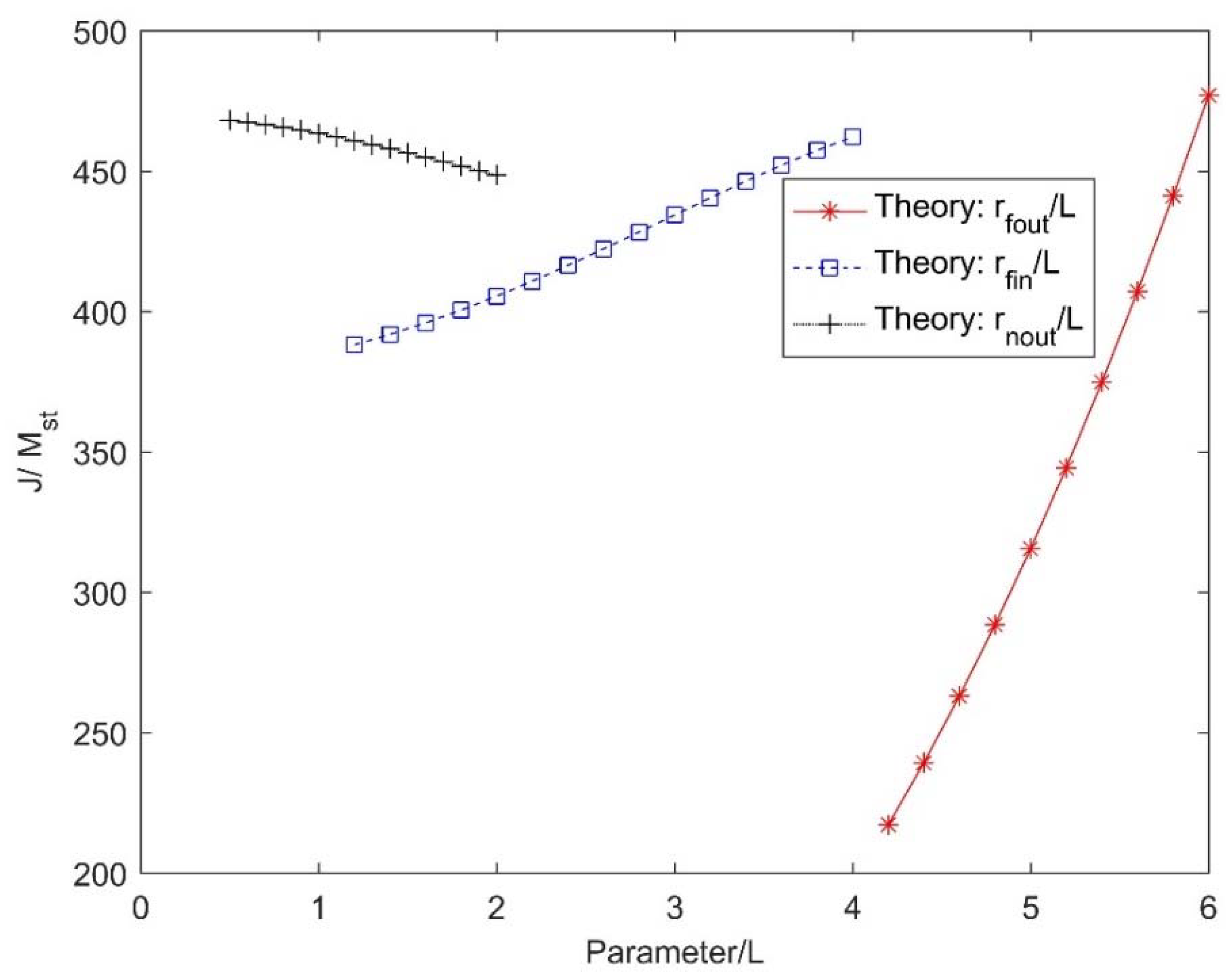
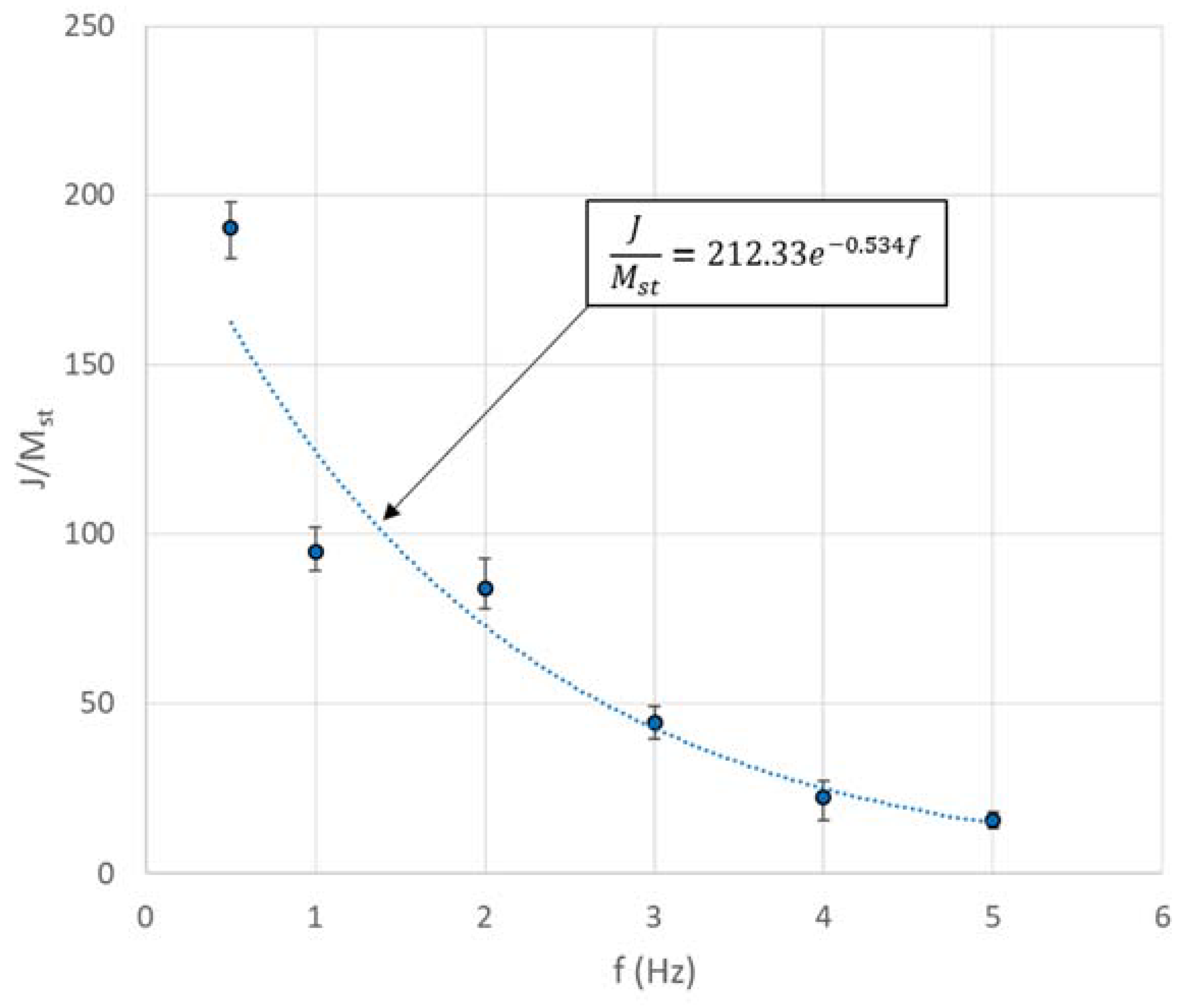
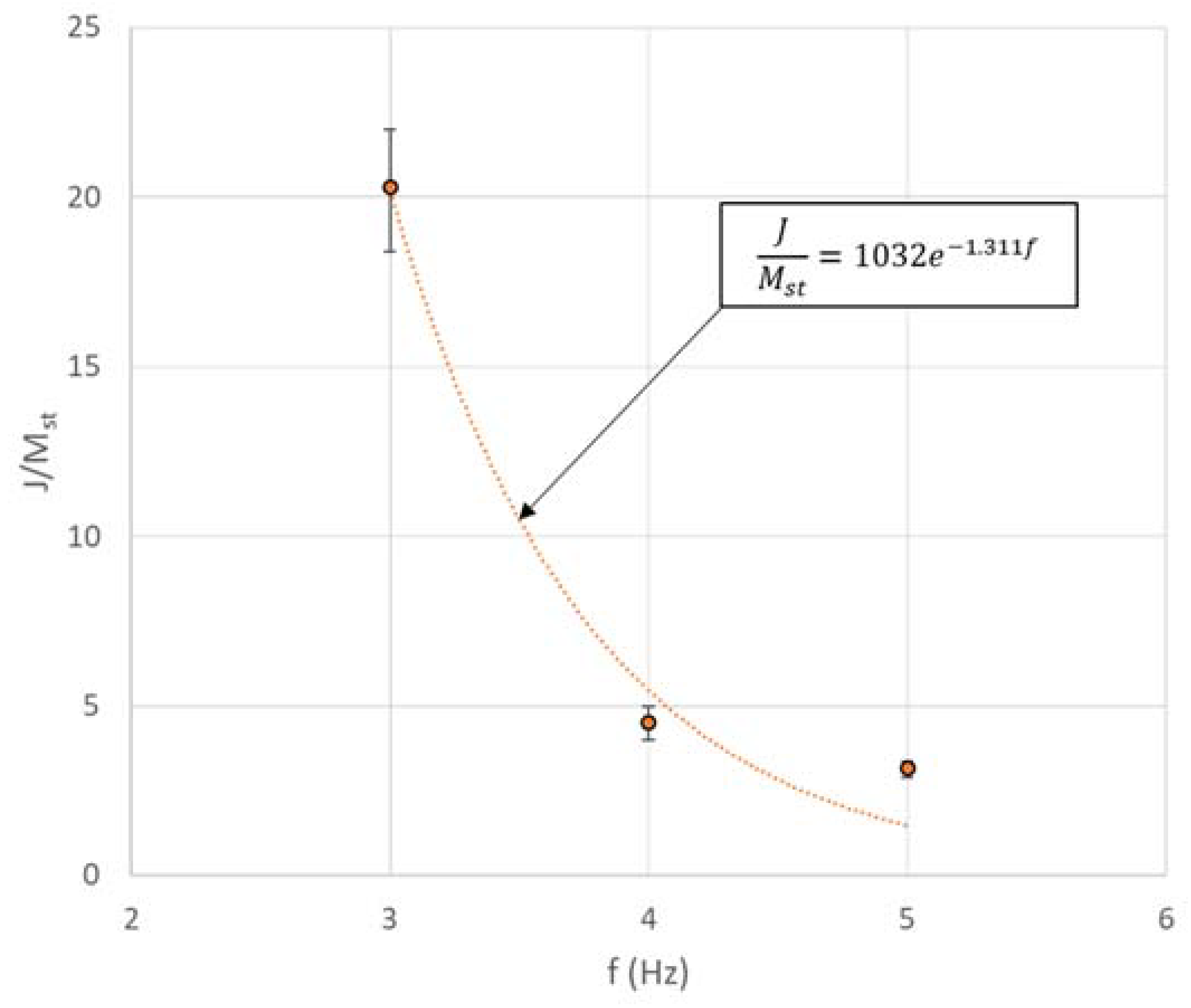
2.2. Parametric Study
3. Experimental Methods
3.1. Test Article Fabrication
3.2. Experimental Setup and Procedures
4. Results and Discussions
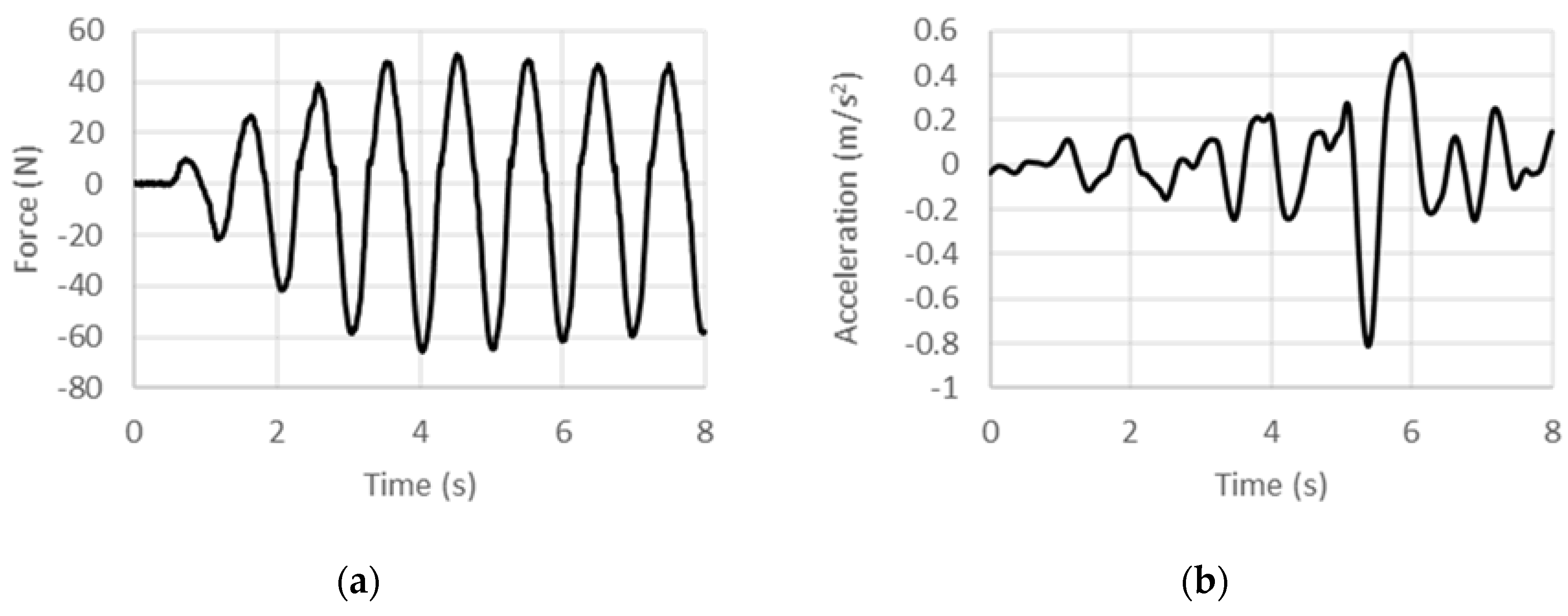
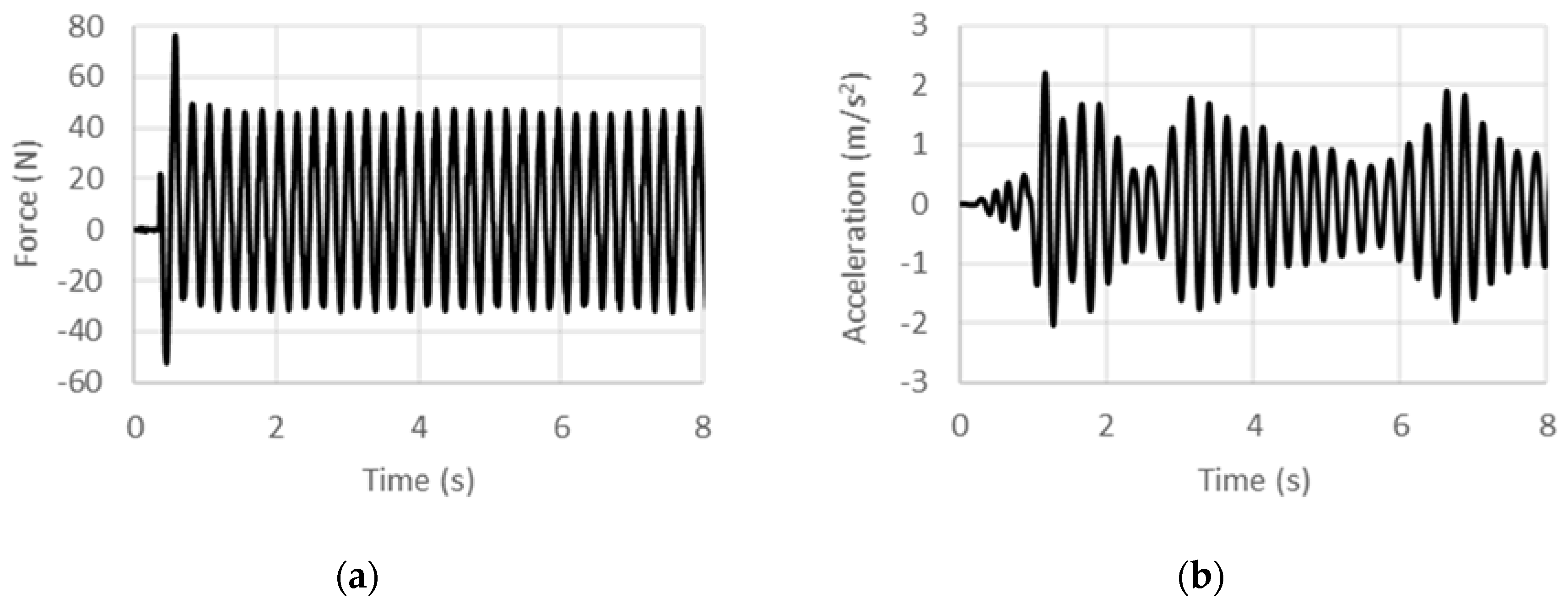
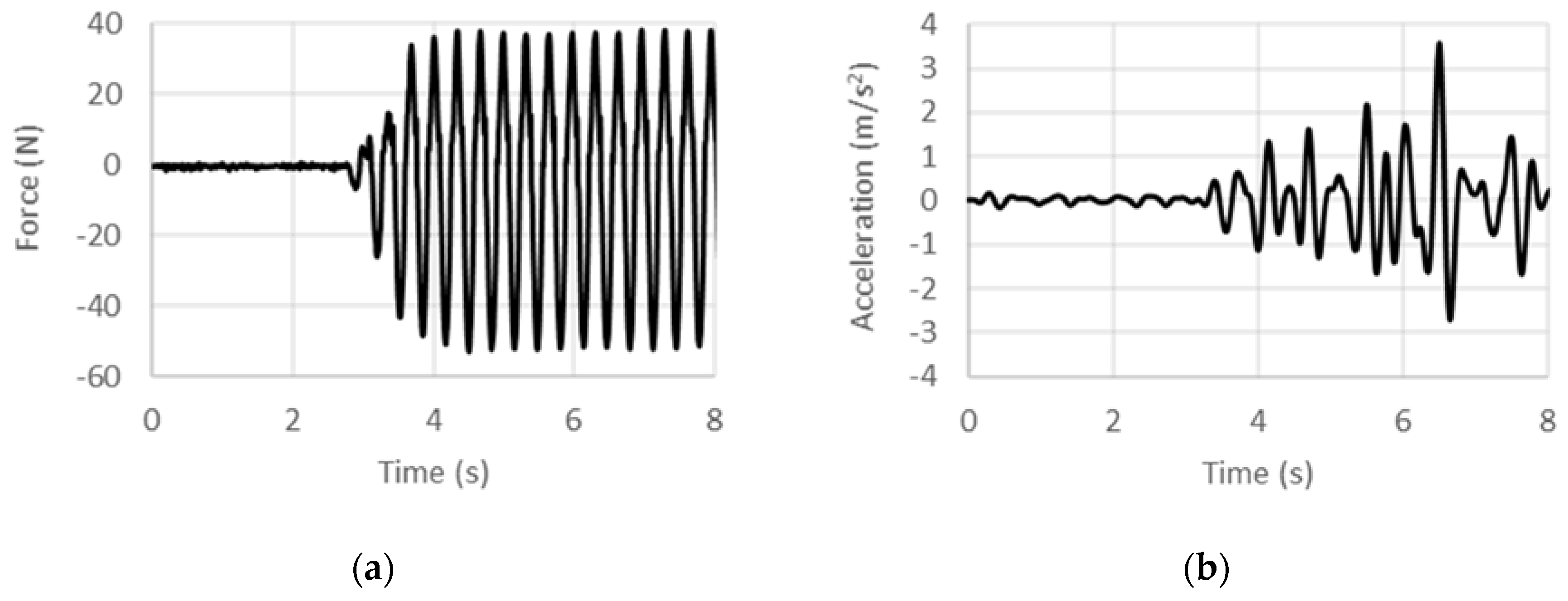
4.1. Displacement-Controlled Sinusoidal Excitation
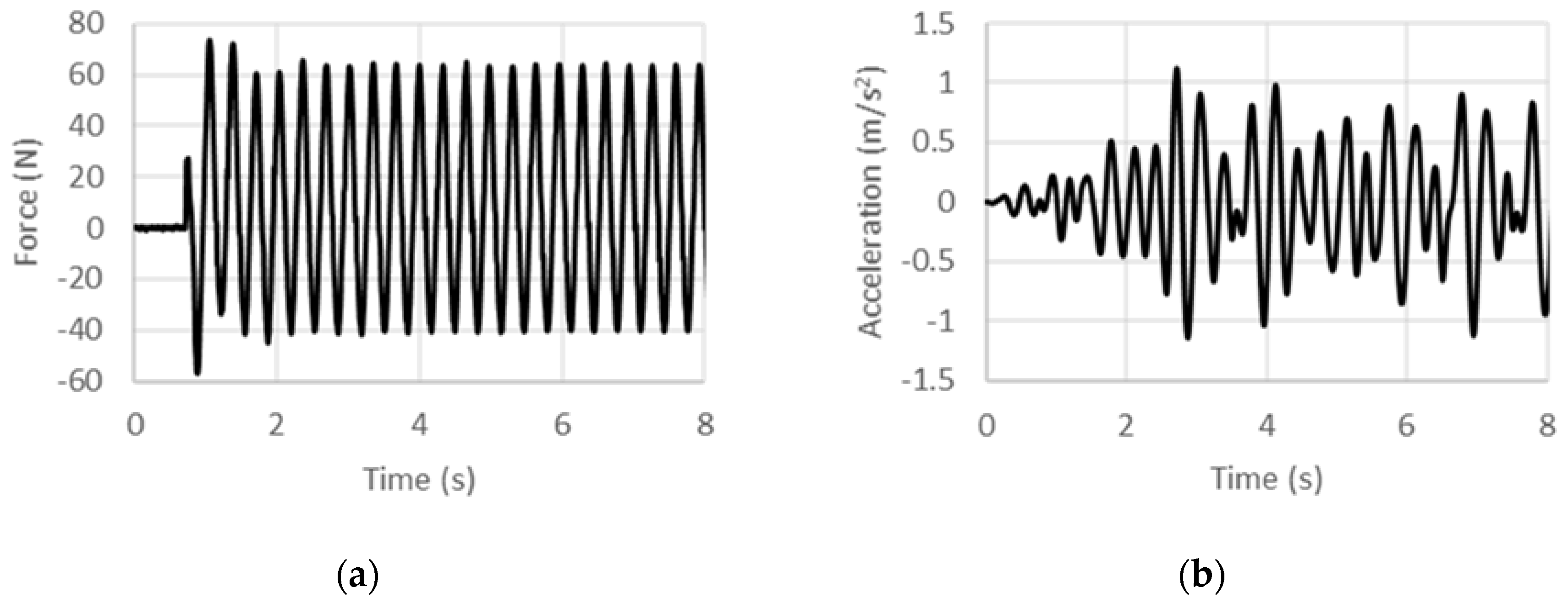
4.2. Acceleration-Controlled Sinusoidal Excitation
4.3. Estimation of Internal Stiffness and Damping
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Firestone, F.A. A new analogy between mechanical and electrical systems. J. Acoust. Soc. Am. 1933, 4, 249–267. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Automat. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Smith, M.C.; Wang, F.C. Performance benefits in passive vehicle suspensions employing inerters. Veh. Syst. Dyn. 2004, 42, 235–257. [Google Scholar] [CrossRef]
- Wang, F.C.; Yu, C.H.; Chang, M.L.; Hsu, M. The performance improvements of train suspension systems with inerters. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 1472–1477. [Google Scholar]
- Wang, F.C.; Su, W.J. Impact of inerter nonlinearities on vehicle suspension control. Veh. Syst. Dyn. 2008, 46, 575–595. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Chen, L.; Yang, X.; Shi, D.; Yang, J. Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension. J. Sound Vib. 2016, 361, 148–158. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Smith, M.C. Laboratory experimental testing of inerters. In Proceedings of the 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference, Seville, Spain, 12–15 December 2005; pp. 3351–3356. [Google Scholar]
- Wang, F.C.; Hong, M.F.; Lin, T.C. Designing and testing a hydraulic inerter. J. Mech. Eng. Sci. 2010. [Google Scholar] [CrossRef]
- Swift, S.J.; Smith, M.C.; Glover, A.R.; Papageorgiou, C.; Gartner, B.; Houghton, N.E. Design and modelling of a fluid inerter. Int. J. Control 2013, 86, 2035–2051. [Google Scholar] [CrossRef]
- Evangelou, S.S.; Limebeer, D.J.N.; Sharp, R.S.; Smith, M.C. Steering compensation for high-performance motorcycles. In Proceedings of the 43rd IEEE Conference on Decision and Control, Paradise Island, Bahamas, 14–17 December 2004; pp. 749–754. [Google Scholar]
- Chen, M.Z.Q.; Papageorgiou, C.; Scheibe, F.; Wang, F.C.; Smith, M.C. The missing mechanical circuit element. IEEE Trans. Circuits Syst. 2009, 9, 10–26. [Google Scholar] [CrossRef]
- Hu, Y.; Li, C.; Chen, M.Z.Q. Optimal control for semi-active suspension with inerter. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012. [Google Scholar]
- Chen, M.Z.Q.; Hu, Y.; Li, C.; Chen, G. Performance Benefits of Using Inerter in Semi Active Suspensions. IEEE. Trans. Control Syst. Technol. 2015. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Hu, Y.; Li, C.; Chen, G. Semi-active suspension with semi-active inerter and semi-active damper. In Proceedings of the 19th World Congress the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Zhang, X.J.; Ahmadian, M.; Guo, K.H. On the benefits of semi-active suspensions with inerters. Shock Vib. 2012, 19, 257–272. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Hu, Y.; Du, B. Suspension Performance with One Damper and One Inerter. In Proceedings of the 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012. [Google Scholar]
- Kuznetsov, A.; Mammadov, M.; Sultan, I.; Hajilarov, E. Optimization of improved suspension system with inerter device of the quarter-car model in vibration analysis. Arch. Appl. Mech. 2011, 81, 1427–1437. [Google Scholar] [CrossRef]
- Tran, T.T.; Hasegawa, H. Advanced Passive Suspension with Inerter Devices and optimization design for vehicle oscillation. Int. J. Mech. Eng. Robot. Res. 2015. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, M.Z.Q.; Huang, L. Frequency Response of a Suspension System with Inerter and Play. In Proceedings of the 21st International Congress on Sound and Vibration, Beijing, China, 13–17 July 2014. [Google Scholar]
- Hu, Y.; Wang, K.; Chen, M.Z.Q. Performance Optimization for Passive Suspensions with One Damper One Inerter and Three Springs. In Proceedings of the IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015. [Google Scholar]
- Shen, Y.; Chen, L.; Liu, Y.; Zhang, X. Analysis of vibration transfer characteristics of vehicle suspension system employing inerter. J. Theor. Appl. Mech. 2017, 55, 1245–1256. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, M.Z.Q.; Tian, Y. Nonlinearities in Landing Gear Model Incorporating Inerter. In Proceedings of the IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015. [Google Scholar]
- Xin, D.; Yuance, L.; Chen, M.Z.Q. Application of Inerter to Aircraft Landing Gear Suspension. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Hu, Y.; Chen, M.Z.Q. Performance evaluation for inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 2015, 99, 297–307. [Google Scholar] [CrossRef] [Green Version]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabil. Eng. Mech. 2014, 38, 156–164. [Google Scholar] [CrossRef]
- Brzeski, P.; Pavlovskaia, E.; Kapitaniak, T.; Perlikowski, P. The application of inerter in tuned mass absorber. Int. J. Nonlinear Mech. 2015, 70, 20–29. [Google Scholar] [CrossRef]
- Wang, F.-C.; Chen, C.-W.; Liao, M.-K.; Hong, M.-F. Performance analyses of building suspension control with inerters. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3786–3791. [Google Scholar]
- Wang, F.-C.; Hong, M.-F.; Chen, C.-W. Building suspensions with inerters. J. Mech. Eng. Sci. 2010, 224, 1605–1616. [Google Scholar] [CrossRef]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 2014, 43, 1129–1147. [Google Scholar] [CrossRef] [Green Version]
- Siami, A.; Cigada, A.; Karimi, H.R.; Zappa, E. Vibration Protection of a Famous Statue against Ambient and Earthquake Excitation Using a Tuned Inerter–Damper. Machines 2017, 5, 33. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.L.; Valiente-Blanco, I.; Cristache, C. Z-Damper: A New Paradigm for Attenuation of Vibrations. Machines 2016, 4, 12. [Google Scholar] [CrossRef]
- Li, P.; Lam, J.; Cheung, K.C. Investigation on Semi-Active Control of Vehicle Suspension using Adaptive Inerter. In Proceedings of the 21st International Congress on Sound and Vibration, Beijing, China, 13–17 July 2014. [Google Scholar]
- Brzeski, P.; Lazarek, M.; Perlikowski, P. Experimental study of the novel tuned mass damper with inerter which enables changes of inertance. J. Sound Vib. 2017, 404, 47–57. [Google Scholar] [CrossRef]
- Smith, N.D.J.; Wagg, D.J. A fluid inerter with variable inertance properties. In Proceedings of the 6th European Conference on Structural Control, Sheffield, England, 11–13 July 2016. [Google Scholar]
- Suciu, B.; Tsuji, Y. Theoretical Investigation on the Dynamic Characteristics of One Degree of Freedom Vibration System Equipped with Inerter of Variable Inertance. Int. J. Mech. Mechatron. Eng. 2017. [Google Scholar] [CrossRef]
- Brzeski, P.; Perlikowski, P. Effects of play and inerter nonlinearities on the performance of tuned mass damper. Nonlinear Dyn. 2017, 88, 1–15. [Google Scholar] [CrossRef]
- Sun, X.Q.; Chen, L.; Wang, S.H.; Zhang, X.L.; Yang, X.F. Performance Investigation of Vehicle Suspension System with Nonlinear Ball-Screw Inerter. Int. J. Automot. Technol. 2008, 17, 399–408. [Google Scholar] [CrossRef]
- Gonzalez-Buelga, A.; Lazar, I.F.; Jiang, J.Z.; Neild, S.A.; Inman, D.J. Assessing the Effect of Nonlinearities on the Performance of a Tuned Inerter Damper. Struct. Control Health Monit. 2017, 24. [Google Scholar] [CrossRef]
- Zhang, X.-L.; Gao, Q.; Nie, J. The Mem-Inerter: A New Mechanical Element with Memory. Adv. Mech. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef]








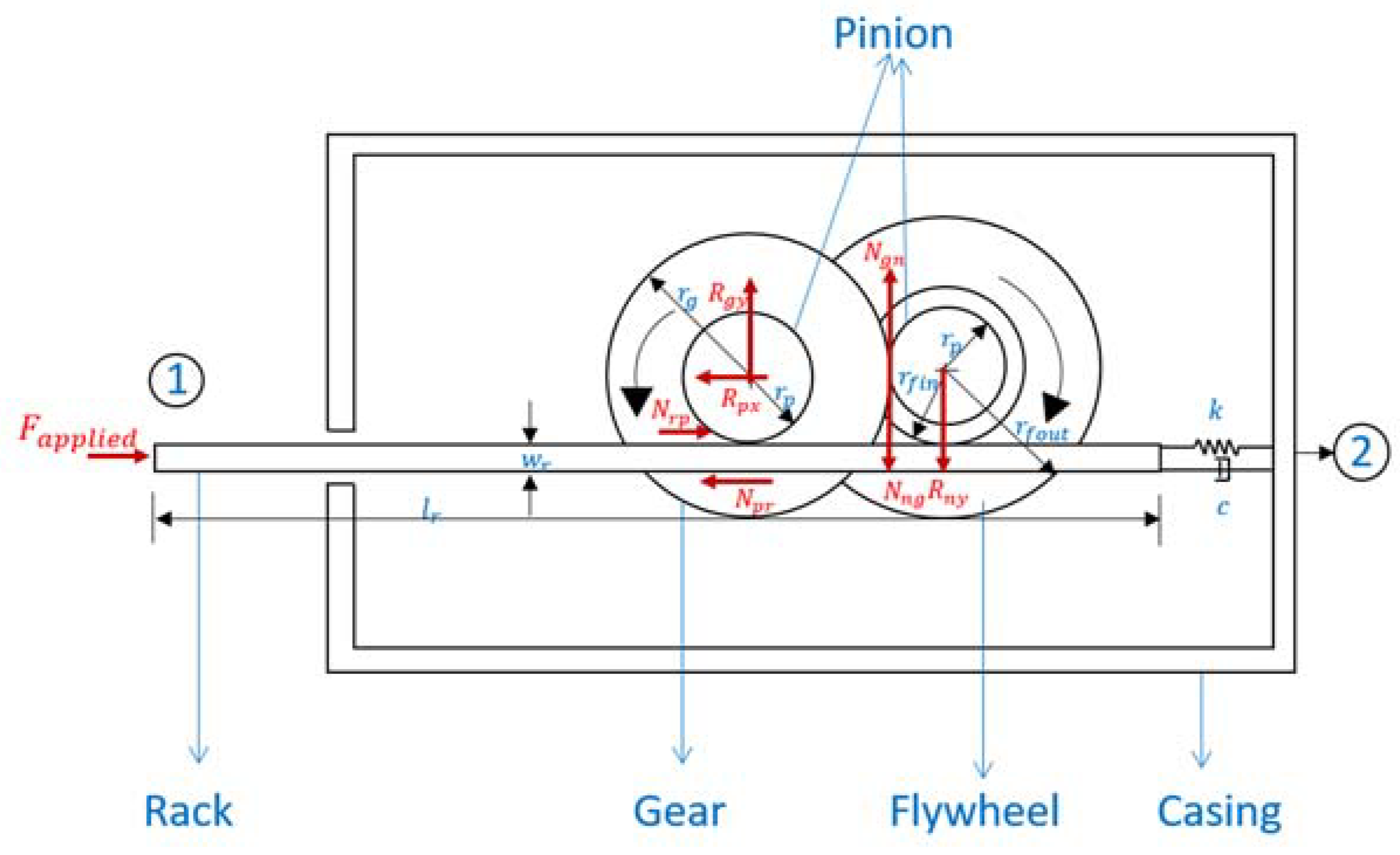
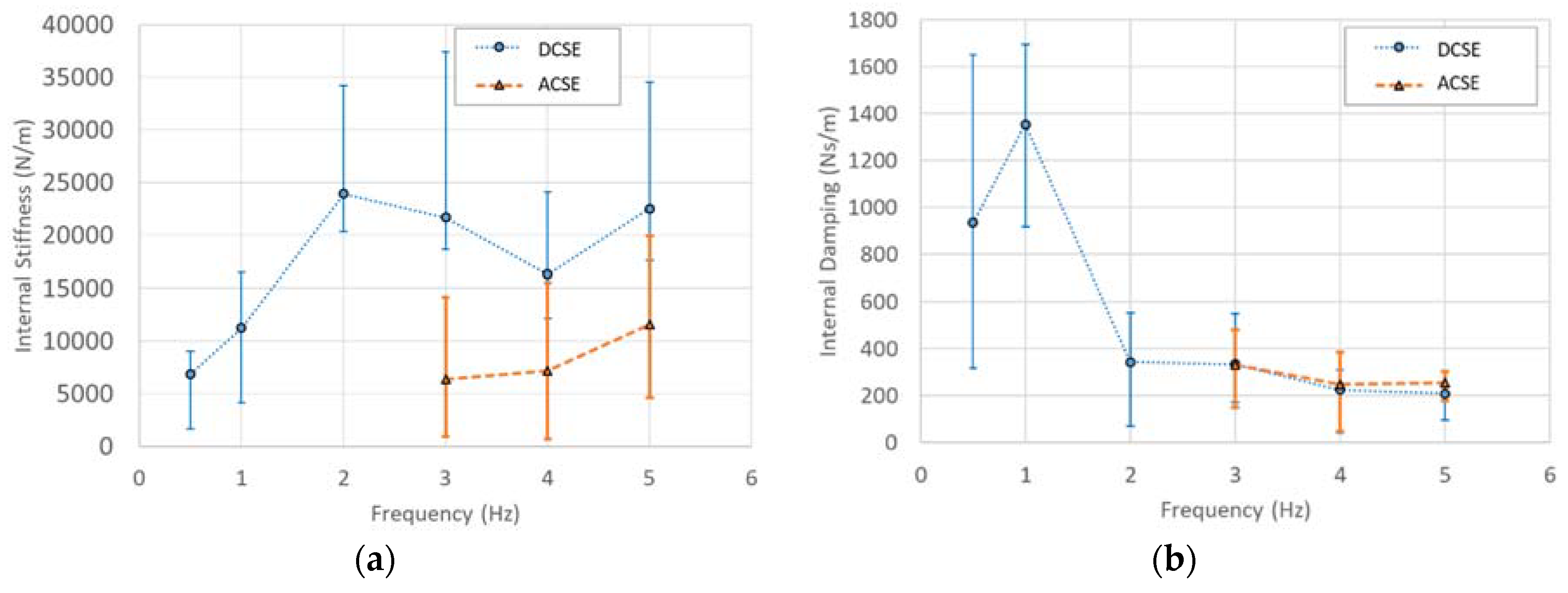
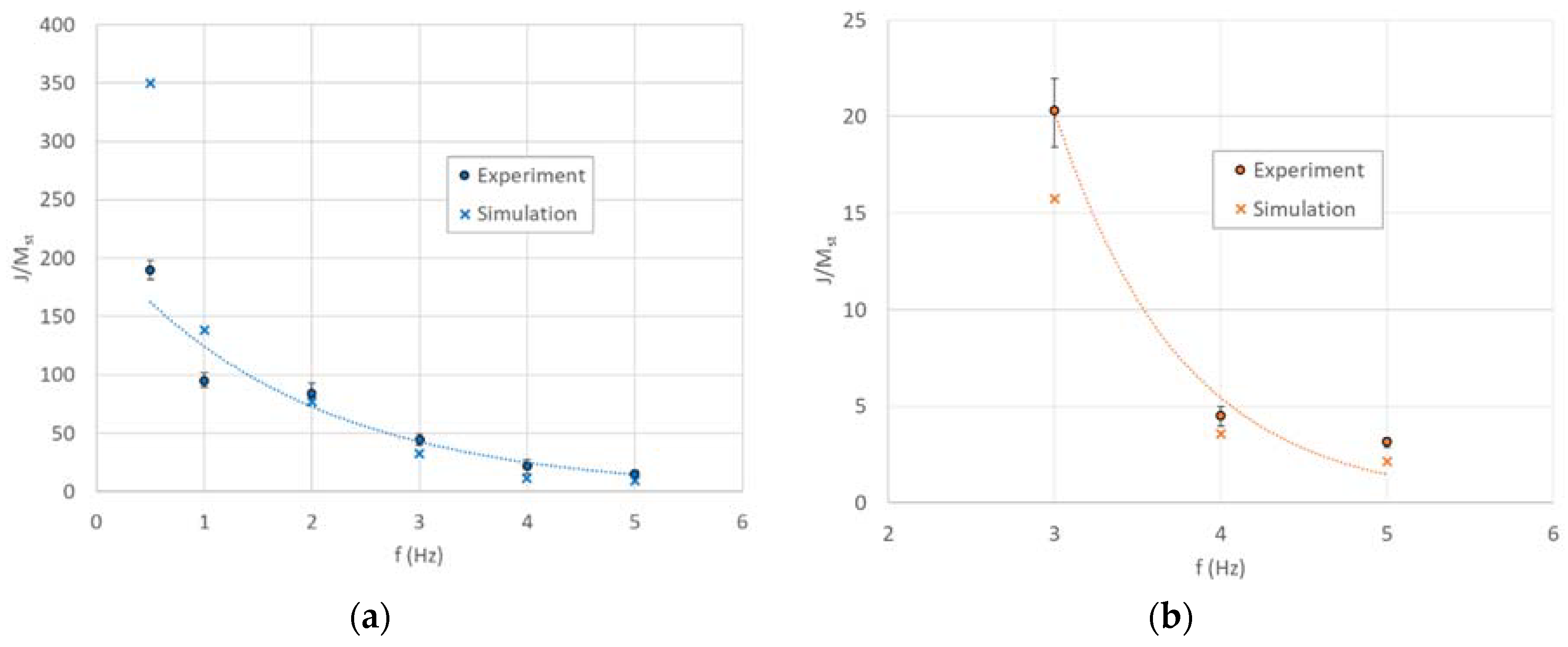

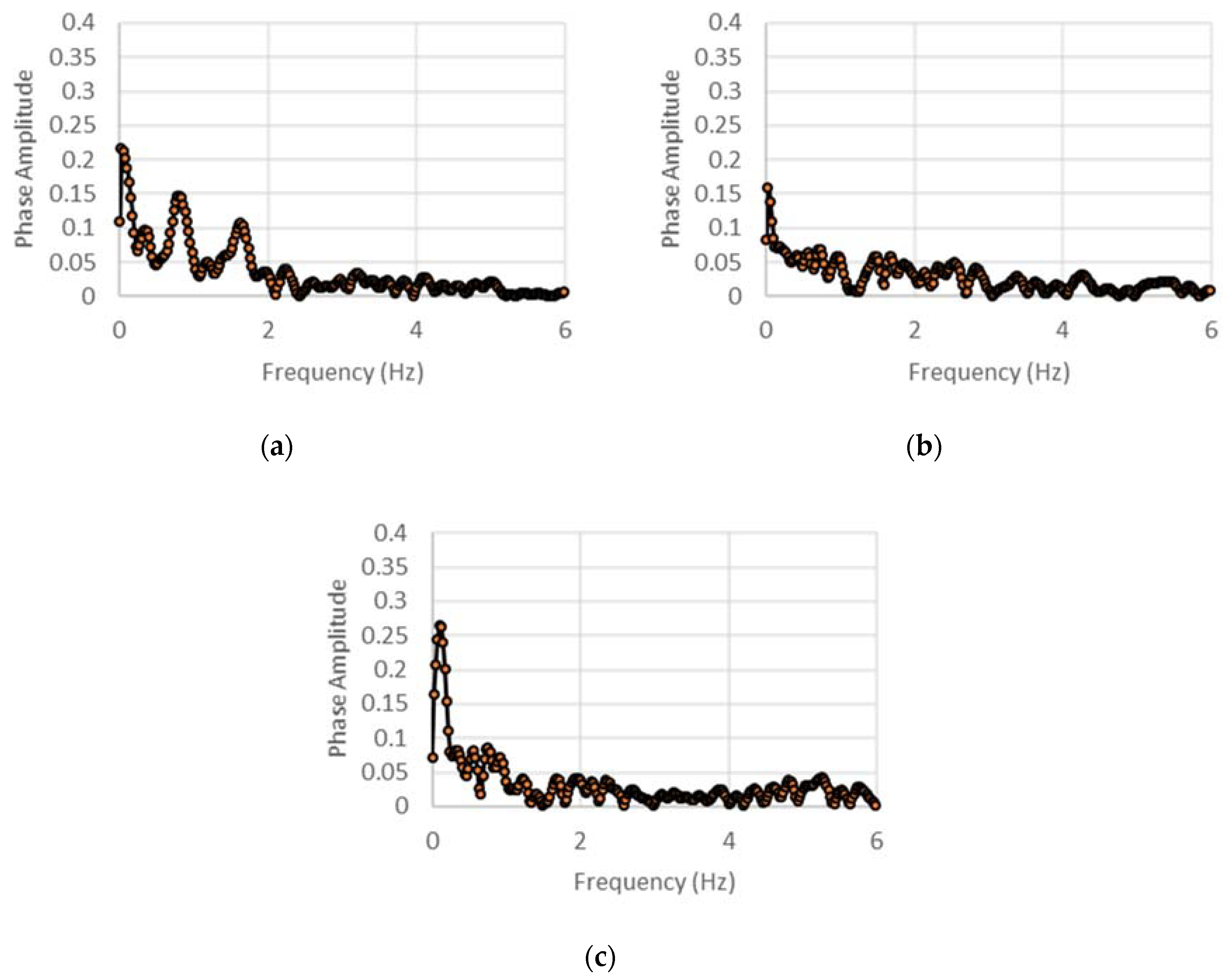
| Component | Parameter | Value |
|---|---|---|
| Nut | Density | 7890 kg/m3 |
| Thickness | 17 mm | |
| Outer radius | 5.5 mm | |
| Inner radius | 2 mm | |
| Flywheel | Density | 7890 kg/m3 |
| Thickness | 13 mm | |
| Outer radius | 30 mm | |
| Inner radius | 20 mm | |
| Ball-Screw | Density | 7890 kg/m3 |
| Length | 250 mm | |
| Radius | 2 mm | |
| Lead | 5 mm | |
| Casing | Mass | 0.2 kg |
| Bearing | Mass | 0.174 kg |
| Component | Parameter | Value |
|---|---|---|
| Gear | Density | 7890 kg/m3 |
| Thickness | 13 mm | |
| Outer radius | 47.6 mm | |
| Inner radius | 6.4 mm | |
| Pitch | 16 mm | |
| Flywheel | Density | 7890 kg/m3 |
| Thickness | 25.4 mm | |
| Outer radius | 50.8 mm | |
| Inner radius | 25.4 mm | |
| Pinion | Density | 7890 kg/m3 |
| Thickness | 13 mm | |
| Outer radius | 9.5 mm | |
| Inner radius | 6.4 mm | |
| Pitch | 16 mm | |
| Rack | Density | 7890 kg/m3 |
| Length | 500 mm | |
| Width | 12.7 mm | |
| Pitch | 16 mm | |
| Casing | Mass | 0.3 kg |
| S. No | Component | Material | Density (kg/m3) | Key Parameter | Source |
|---|---|---|---|---|---|
| 1 | Rack | Steel | 7890 | lr (length) | COTS |
| 2 | Pinion(s) | Steel | 7890 | rp (radius) | COTS |
| 3 | Gear | Steel | 7890 | rg (radius) | COTS |
| 4 | Flywheel | Aluminum | 2800 | rf (radius) | COTS |
| 5 | Casing | PLA/Acrylic | 1250 | mc (mass) | 3D printed |
| 6 | Hub | PLA | 1250 | - | 3D printed |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhamshetty, K.; Manimala, J.M. Low-Rate Characterization of a Mechanical Inerter. Machines 2018, 6, 32. https://doi.org/10.3390/machines6030032
Madhamshetty K, Manimala JM. Low-Rate Characterization of a Mechanical Inerter. Machines. 2018; 6(3):32. https://doi.org/10.3390/machines6030032
Chicago/Turabian StyleMadhamshetty, Karthik, and James M. Manimala. 2018. "Low-Rate Characterization of a Mechanical Inerter" Machines 6, no. 3: 32. https://doi.org/10.3390/machines6030032





