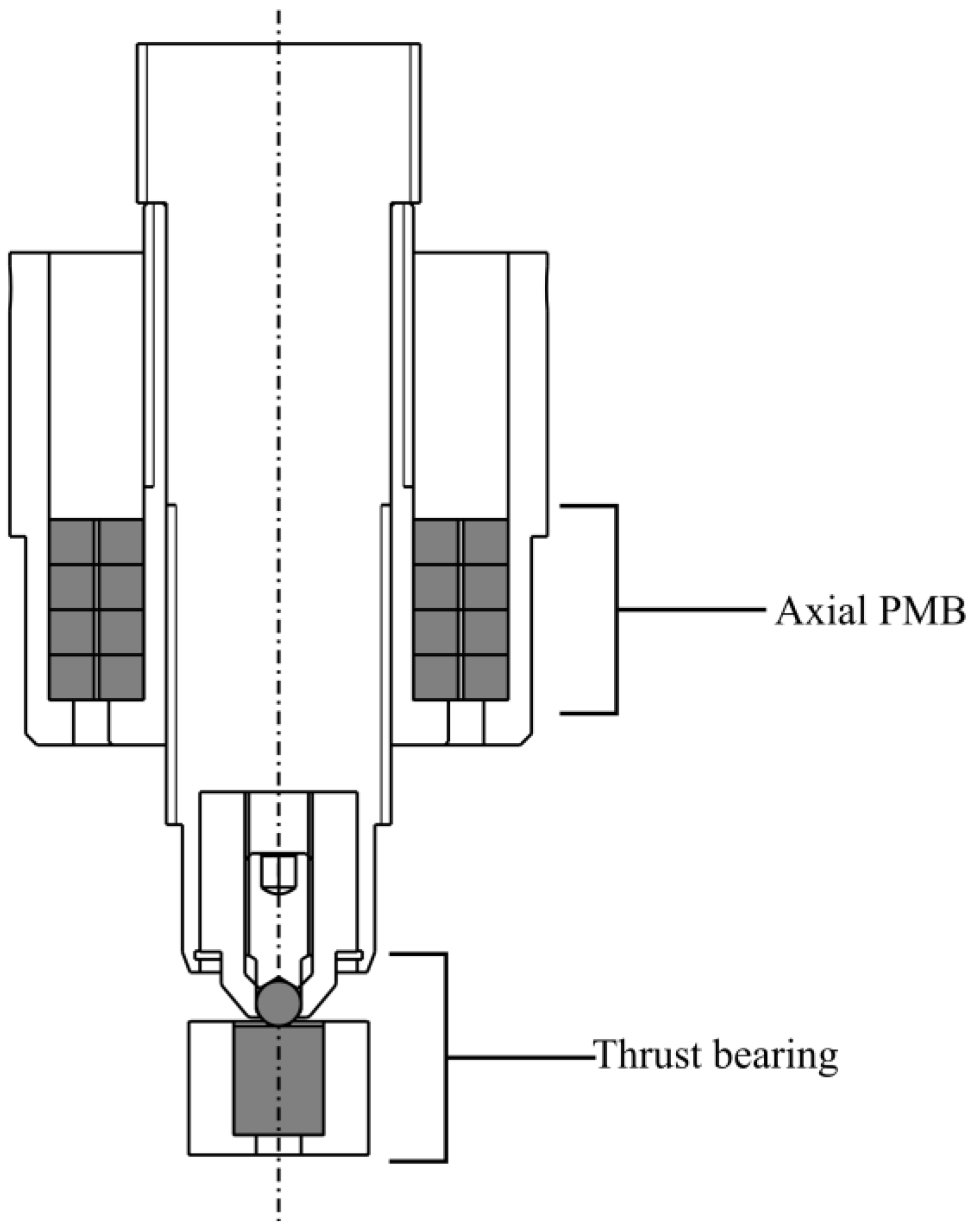
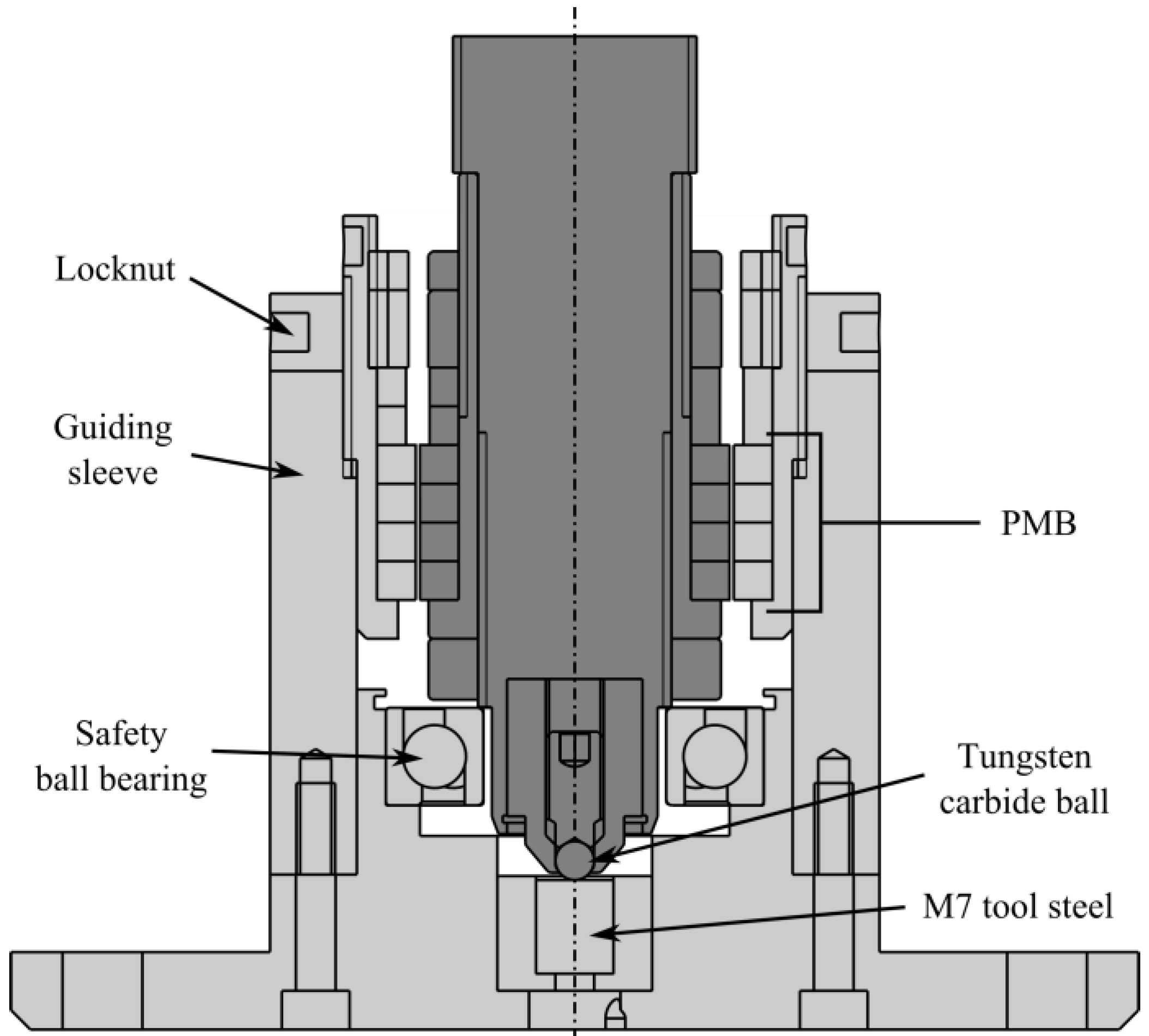
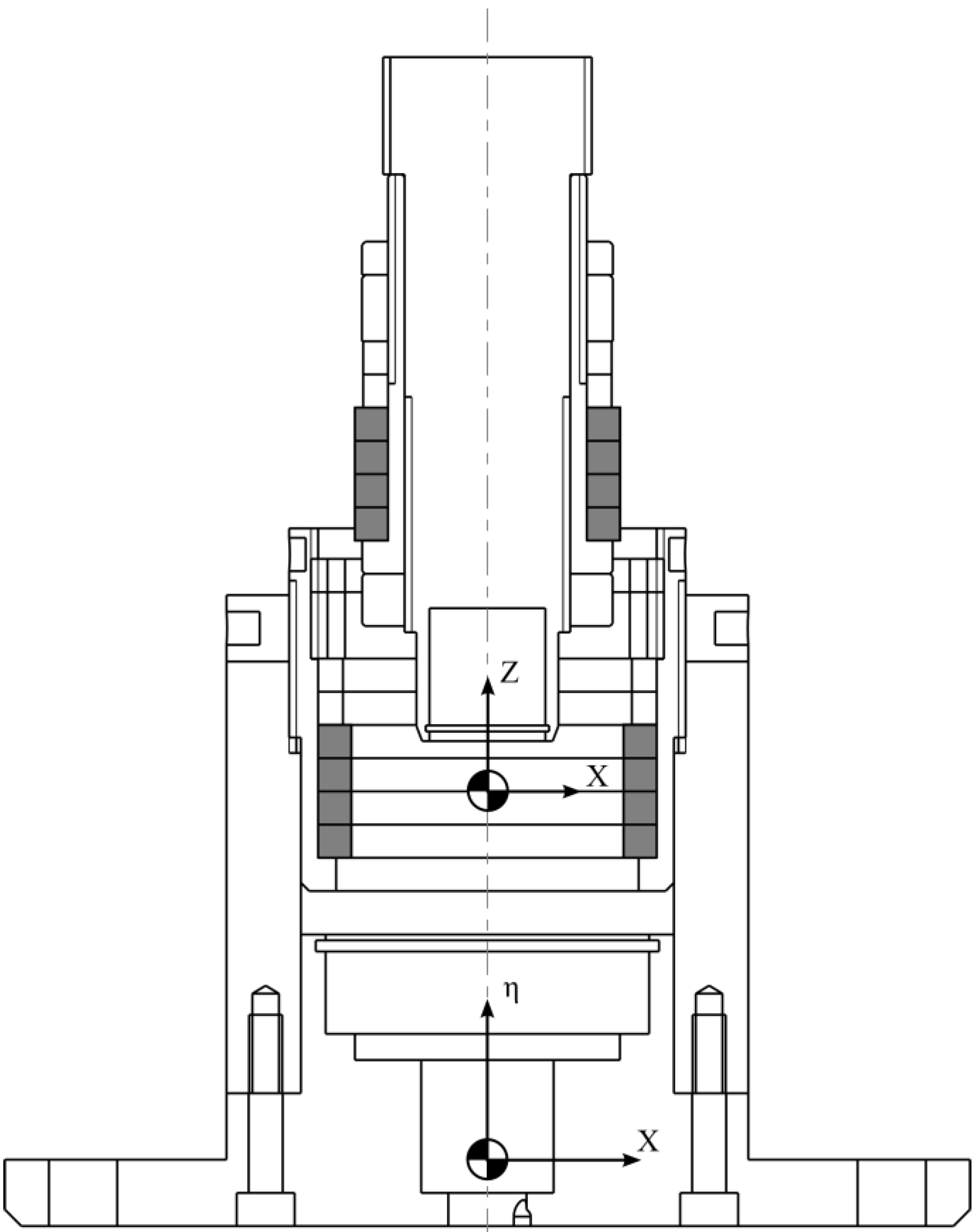
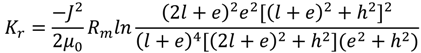3.1. Stiffness
Experimental results were obtained using the apparatus detailed in
Section 2.
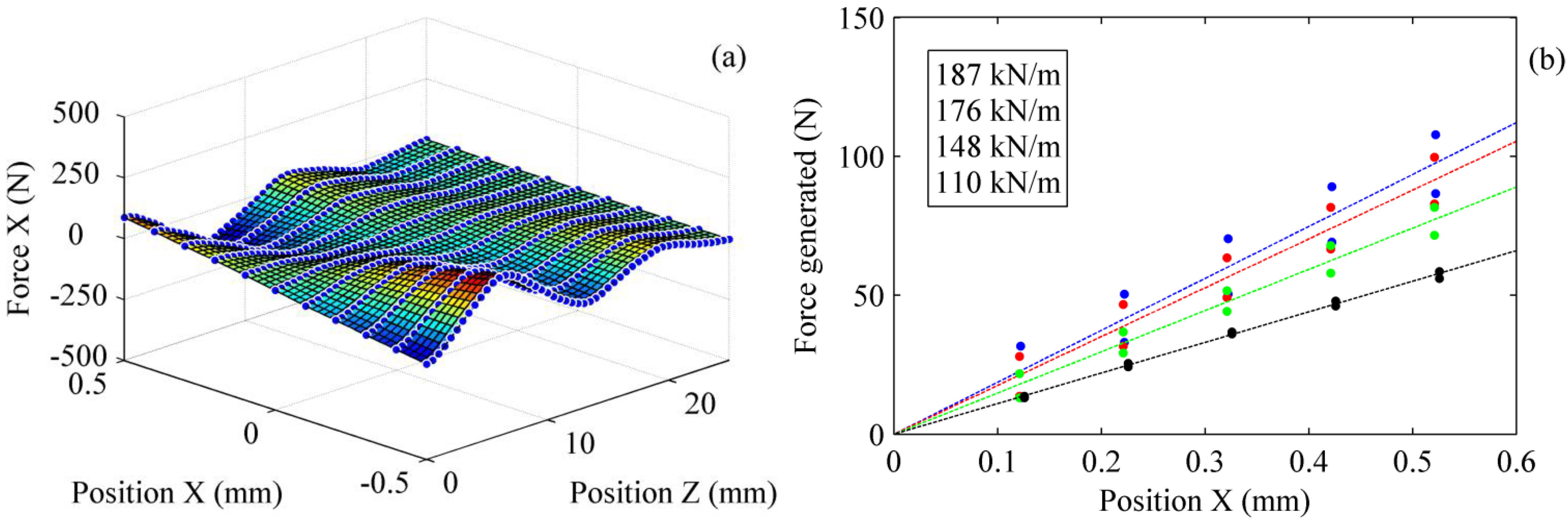
Figure 9a presents the two-dimensional mapping for the force measured in the x-direction with the dynamometer. These force values were obtained by moving the rotor vertically in the axial direction (z-axis), and repeating this process for different positions along the x-axis (radial direction). This measurement process is referred to as the vertical sweep.
Figure 9.
(a) Radial forces obtained by vertical sweep at different radial stations. (b) Experimental data and curve fit at four different rotor positions along the z-axis (blue z = 0.0 mm, red z = 0.5 mm, yellow z = 1.0 mm, and black z = 1.5 mm, respectively).
Figure 9.
(a) Radial forces obtained by vertical sweep at different radial stations. (b) Experimental data and curve fit at four different rotor positions along the z-axis (blue z = 0.0 mm, red z = 0.5 mm, yellow z = 1.0 mm, and black z = 1.5 mm, respectively).
In
Figure 9a, the repulsive forces are positive for positive X positions and negative for negative X positions. It can be observed that the repulsive force varies quickly for slight vertical displacements. The slope of each curve in
Figure 9b represents the radial stiffness, and it can be noticed that it varies notably for small vertical displacements (0 to 1.5 mm). In order to reduce the effects of rotor misalignment and geometric defects of the magnets, the repulsion force (in absolute value) on both sides of the rotation axis was used to evaluate the stiffness. The constant slope of the curves corresponds to the expected constant stiffness characterizing PMBs. The maximum stiffness of the bearing is 187 kN/m. The error between the experimental and the theoretical value (217 kN/m) is 14.1%. The difference may be caused by the assumptions made in the theoretical calculations, such as the perfect magnetization and geometry of the magnets. This shows that it is essential to characterize a PMB before using it in a mechanical system.
The characterization technique, with its combination of radial, vertical and rotational position variations, allows an interesting mapping of the forces and stiffness generated by the PMB. Inspecting the experimental mapping of
Figure 9 readily provides the possibility of taking advantage of the vertical lift force generated when the matching magnet pairs of the rotor and the stator are offset, thus enabling to decrease the friction value of the thrust bearing. Of course the choice of such an offset position implies a reduction of the radial stiffness and a compromise has to be made between this lift increase and the radial stiffness reduction.
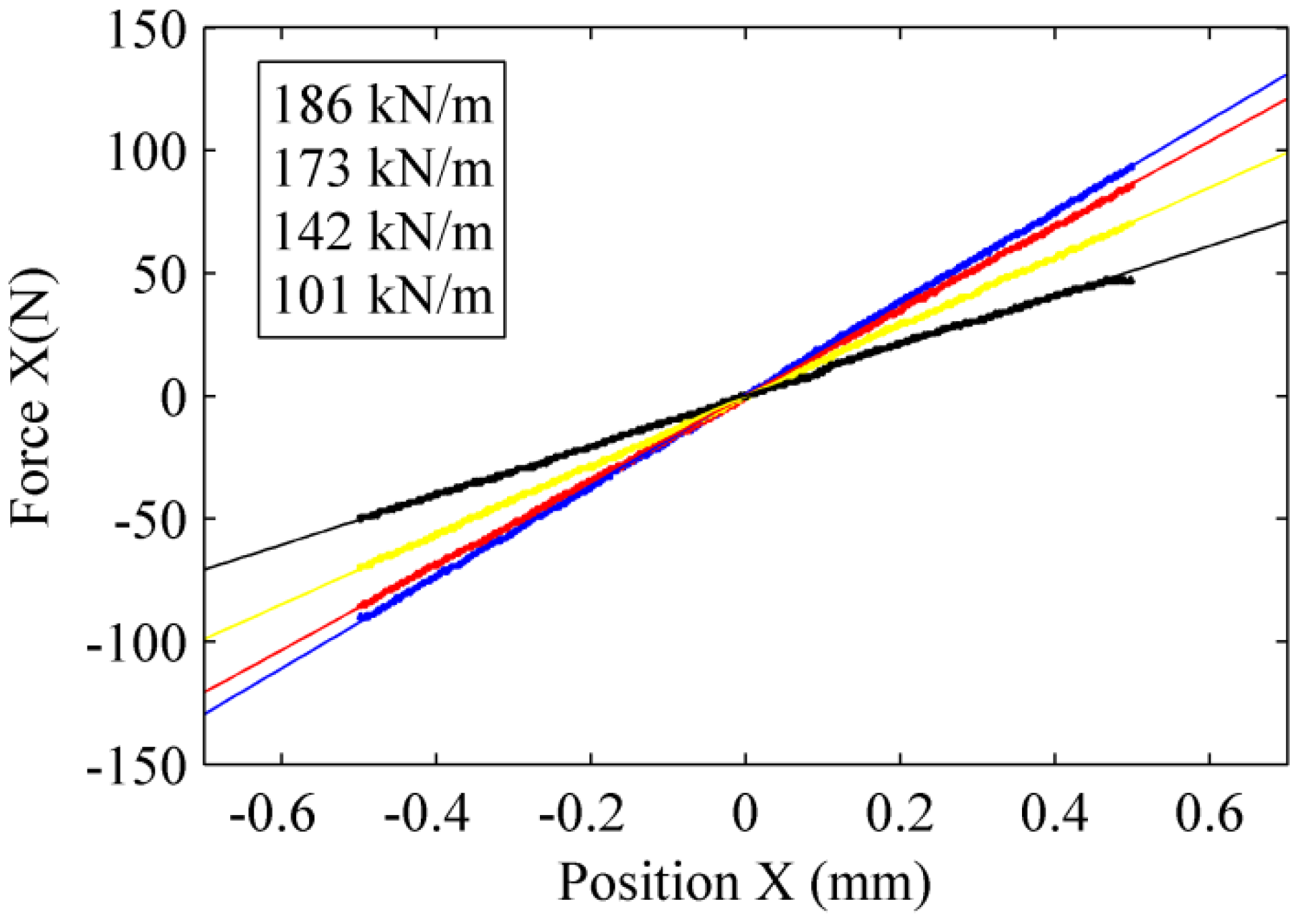
A lateral sweep was also performed to compare the results with those of the vertical sweep.
Figure 10 shows the force in the x-direction obtained for the same four axial positions that were computed and presented in
Figure 8b: 0 mm, 0.5 mm, 1.0 mm and 1.5 mm.
Figure 10.
Force measured by a lateral sweep for different heights of rotor (blue 0.0mm, red 0.5mm, yellow 1.0mm, and black 1.5mm).
Figure 10.
Force measured by a lateral sweep for different heights of rotor (blue 0.0mm, red 0.5mm, yellow 1.0mm, and black 1.5mm).
The stiffness is very similar to the values obtained with the vertical sweep. The slight differences may be attributed to an axial offset of the rotor between the two experiments, which is about 0.04 mm.
The vertical sweep was also used with other configurations of the PMB.
Table 2 shows the experimental radial stiffness of a PMB containing different number of magnets.
Table 2.
Stiffness of a radial PMB made from different combination of magnets. Results are presented for different axial positions of the rotor.
Table 2.
Stiffness of a radial PMB made from different combination of magnets. Results are presented for different axial positions of the rotor.
| Stiffness (kN/m) |
|---|
| Z = 0.0 mm | Z = 0.5 mm | Z = 1.0 mm | Z = 1.5 mm |
|---|
| 3 rotor–4 stator | 134.0 | 130.9 | 112.2 | 86.6 |
| 4 rotor–3 stator | 142.1 | 128.1 | 107.2 | 79.5 |
| 4 rotor–4 stator | 187.0 | 175.7 | 148.3 | 110.0 |
| 5 rotor–5 stator | 218.7 | 204.1 | 171.4 | 121.5 |
As expected, the radial stiffness of the bearing increases with the number of magnet pairs. Once again, there is a difference between the theoretical and experimental values for the bearing using the 5-magnet configuration (21%).
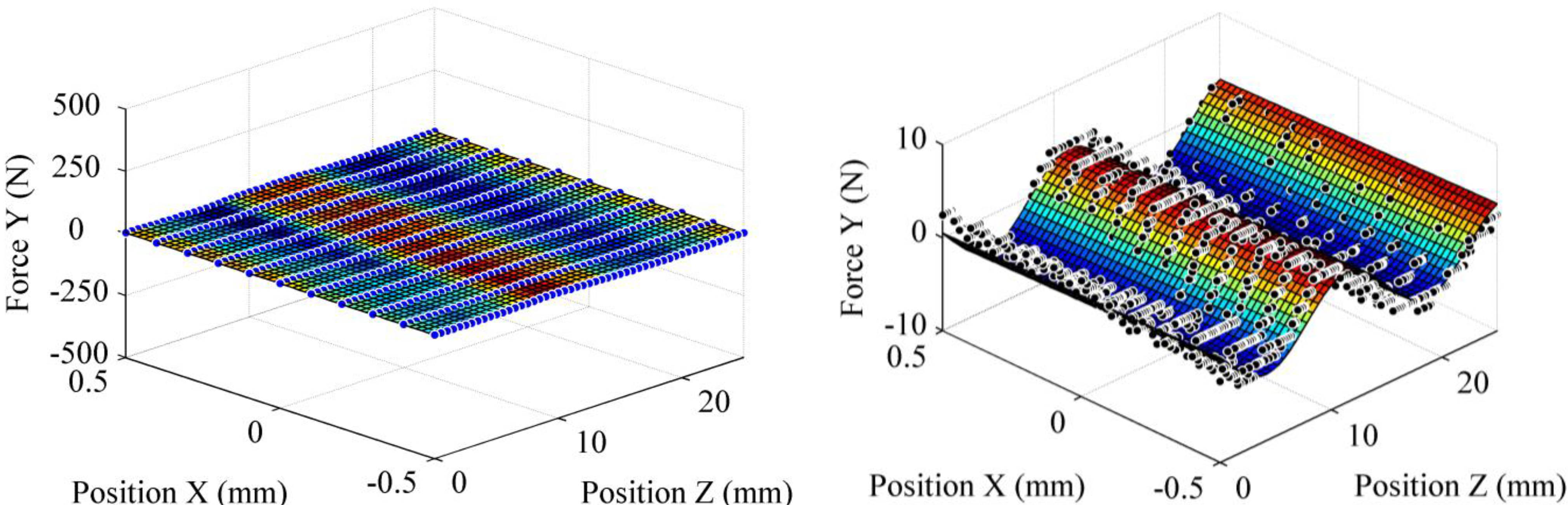
Figure 11 shows the radial force in the y-direction obtained with the vertical sweep technique, and corresponding to the same conditions as those of the force in the x-direction (
Figure 8). The surface is relatively flat and the forces measured are close to 0 N. This suggests that the magnets of the rotor are well centered.
Figure 11.
Lateral forces in the y-direction measure by vertical sweeping (large scale and close-up).
Figure 11.
Lateral forces in the y-direction measure by vertical sweeping (large scale and close-up).
Finally,
Figure 12 shows the surface obtained for the axial force (z-direction) with the vertical sweep technique. This graph illustrates the singular behaviour of a radial PMB. Indeed, the fact that a greater distance from the perfect alignment means a greater axial force is quite counterintuitive. This means that if the rotor is not well constrained, it will move up or down until it reaches a zone where the radial force attracts it.
Figure 12.
Axial force in the z-direction measured by vertical sweep.
Figure 12.
Axial force in the z-direction measured by vertical sweep.
It is useful to group the three forces in one plot to get a better idea of the behaviour of the bearing.
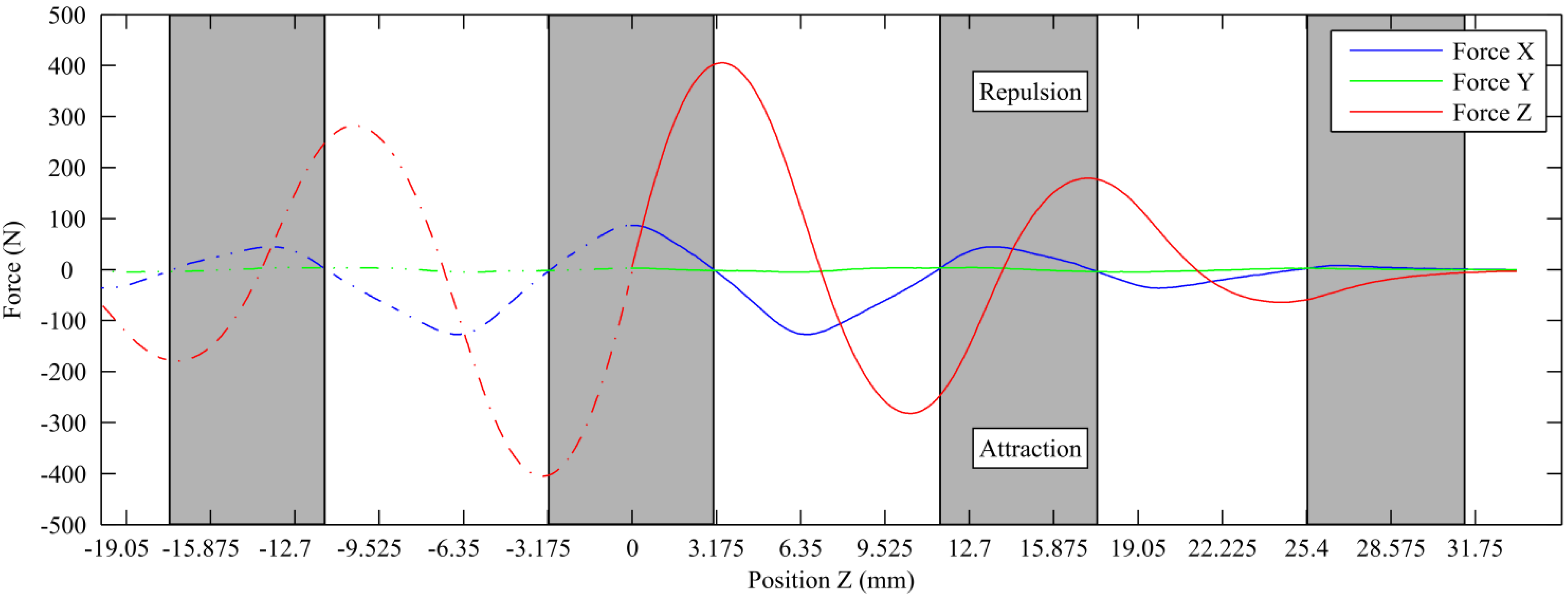
Figure 13 shows the variation of the forces for a displacement along the z-axis and for a slightly offset lateral position of X = 0.5 mm.
This graph allows the identification of the operating ranges of the bearing. Theses ranges (shaded areas) occur when the lateral force in the X direction is positive (repulsive). The slight force measured in the y-direction can be attributed to imperfections in the geometry and magnetization of the magnets rather than actual attractive or repulsive force. Knowledge of the operating range makes it possible to use the axial force Z to optimize the system without entering regions where the centering effect of the PMB does not operate. This force can be advantageously used to reduce the normal force applied on the plain bearing, thus reducing mechanical losses.
Figure 13.
Forces measured by a vertical sweeping for a lateral position of X = 0.5 mm. Dashed lines are extrapolation of measured data.
Figure 13.
Forces measured by a vertical sweeping for a lateral position of X = 0.5 mm. Dashed lines are extrapolation of measured data.
3.2. Damping
Damping measurements were performed according to the methodology outlined in
Section 2. The free vibration responses recorded during these trials were used to calculate the natural frequency of the system and the damping ratio of the bearing.
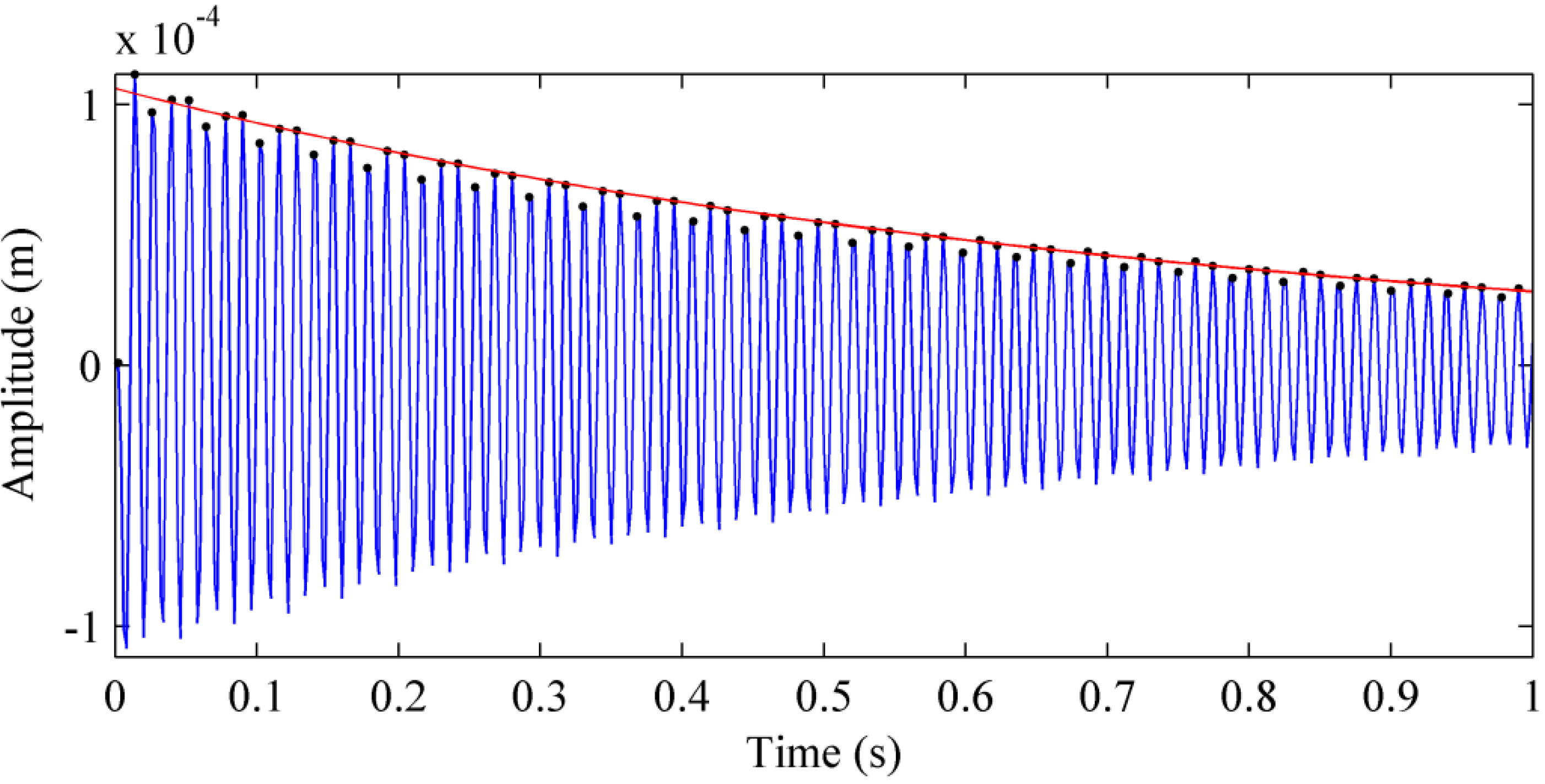
Figure 14 shows a typical graph obtained from a single test, where a damped second order response is observed. From this waveform, it is possible to calculate the natural frequency and the damping ratio of the magnetic bearing. It should be noted that the natural frequency depends on the mass supported by the bearing.
Figure 14.
Response of the system to an impact. The blue curve is the response, the black dots are the peak values and the red curve is a curve fit.
Figure 14.
Response of the system to an impact. The blue curve is the response, the black dots are the peak values and the red curve is a curve fit.
Numerous trials were performed to obtain admissible impacts and a mean value of the damping ratio. The equation of the curve that links the peaks is of the following form:
Using Matlab’s least mean square curve fitting tool, it was possible to evaluate the parameters of Equation (3), i.e., the parameters and
c and
ζωn the product of . The damped frequency of the system was evaluated using the oscillation period. The theoretical value of the damped frequency was calculated using Equation (4).
Table 3 presents the damping ratios and the undamped natural frequencies of the PMB with and without a rotor disk, and for 3 axial positions ranging from 0 to 1 mm. The disk, shown in
Figure 15, weighed 23 kg and was placed at a distance of 190.0 mm from the bearing and 190.0 mm from the universal joint, as shown in
Figure 15.
Table 3.
Damping ratios and undamped natural frequencies for different rotor positions without and with the disk.
Table 3.
Damping ratios and undamped natural frequencies for different rotor positions without and with the disk.
4 on Rotor
4 on Stator | Z = 0.0 mm | Z = 0.5 mm | Z = 1.0 mm |
|---|
| ζ | ωn (rad/s) | ζ | ωn (rad/s) | ζ | ωn (rad/s) |
|---|
| Without disk | 0.00289 | 496 | 0.00350 | 461 | 0.00594 | 395 |
| With disk | 0.00230 | 143 | 0.00402 | 137 | 0.00337 | 120 |
Figure 15.
Experimental apparatus including the steel disk used to measure the damping.
Figure 15.
Experimental apparatus including the steel disk used to measure the damping.
The measured damping ratios are relatively low compared to values documented in literature [
8], which is good for the global energy efficiency of the system. Even though damping is good of the stability of the FESS [
15], the eddy currents generated at high speed would significantly increase magnetic losses thus reducing the global efficiency. The damping is mainly induced by eddy currents generated by the variation of the magnetic flux within the magnets, but also by eddy currents in the surrounding aluminum parts. A small part of the global damping may also come from the compressibility of the air gap between the magnets. In both cases, the damping ratio increases with the axial displacement of the rotor. Although interesting, this phenomenon is complex and is not further investigated in this paper but should be explored in future works.
The undamped natural frequency also decreases with an axial displacement of the rotor. This is due to the lower stiffness of the bearing when the rotor is moved axially. The undamped natural frequency of the setup including the disk is much lower due to the higher mass of the system.
The damping was also studied for different bearing configurations.
Table 4 compiles the damping ratios and undamped natural frequencies for other configurations of the radial PMB.
Table 4.
Damping ratios, natural frequencies and amplitude of for different rotor positions and configurations.
Table 4.
Damping ratios, natural frequencies and amplitude of for different rotor positions and configurations.
| Z = 0.0 mm | Z = 0.5 mm | Z = 1.0 mm |
|---|
| Without Disk | ζ | ωn | Amplitude (m) | ζ | ωn | Amplitude (m) | ζ | ωn | Amplitude (m) |
|---|
| 4 rotor–4 stator | 0.0029 | 495 | 3 × 10−5 | 0.0035 | 461 | 3 × 10−5 | 0.0059 | 395 | 3.5 × 10−5 |
| 5 rotor–5 stator | 0.0028 | 559 | 3 × 10−5 | 0.0033 | 518 | 3 × 10−5 | 0.0049 | 439 | 3 × 10−5 |
The results indicate that the number of magnets used in the bearing has a limited influence the damping ratio, while it obviously increases the stiffness. According to the explanation given earlier, a greater number of magnets should not influence the damping. The conclusion that a greater number of magnets do not increase eddy currents is very counterintuitive. In order to make sure that the damping did not come from the universal joint, a study of that component was performed.
Table 4 shows that the amplitude of the oscillation for all conditions is very similar. Simple geometric considerations indicate that for all these oscillations, the physics of the torsion deformation of the rubber part of the universal joint shall be similar. The parameter that is different for these different tests is the frequency, but the damping is generally independent of the frequency. So it is reasonable to state that the damping produced by the rubber seal of the universal joint shall not vary significantly for all these experiments. The conclusion is that the very significant increase in the damping has to be caused by the PMB. However, it is possible that a certain part of the damping may be produced by the universal joint, but it is thought that this component is small and constant.
In addition, the significant differences between the damping ratios observed for very small variations of the axial position of the rotor of the PMB further indicates that the damping measured is mainly due to the eddy currents induced by the PMB, and not solely or mainly by the universal joint. As it can be observed from
Table 4, the damping ratio doubled for an axial displacement of 1 mm suggesting that the eddy currents have a major influence on the damping.
The experimental methodology proposed in this paper is an effective way to evaluate the damping of a magnetic bearing. As a result, it is possible to use the experimental parameters for the simulation and design of a safe and reliable mechanical system supported by PMBs.