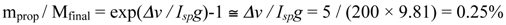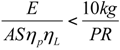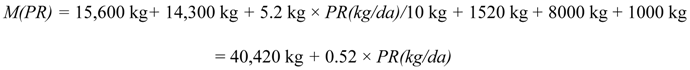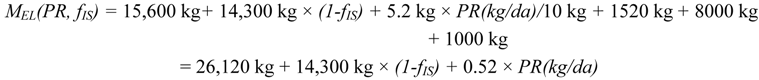1. Introduction
Recent news announcements of corporations formed for the purpose of mining off-Earth resources have received international attention. Both asteroids and the Moon have been cited as locations with valuable, accessible commodities, such as water ice, and raw materials for construction. Compared to asteroids, the Moon has a significant gravity well, thus requiring more energy to reach an off-lunar destination such as a fuel depot. The lack of a lunar atmosphere means that there is no drag heating during ascent.
The idea of using a fixed launcher rather than rocketry to move masses in the solar system has been discussed at least since the work of O’Neill [
1]. There are more recent discussions in the literature of electromagnetic launchers for Earth applications [
2,
3,
4] as well as lunar-based [
5,
6]. Such launchers are attractive alternatives to rocket-based ascent systems. Available references do not provide calculations of launcher masses. The mass of the launch system is the key to assessing both its manufacturing cost and its delivery cost to the Moon from Earth. This paper will infer properties from two extensively tested terrestrial electromagnetic launch systems to develop mass models of a conceptual electromagnetic lunar resource launcher (LRL). The specific application is the delivery of water or ice to the Earth-Moon Lagrange L1 point, hereinafter referred to as L1.
2. System Concept
The LRL model in this paper is based on the following system concept, which is illustrated schematically in
Figure 1:
The LRL location is near one or the other lunar pole, where ice is being mined.
The LRL uses an electromagnetic launch approach chosen from either of two terrestrial electromagnetic systems to be described.
Electric power is provided by photovoltaic panels.
The ice or water is placed into canisters, which may be manufactured on Earth, or manufactured locally from in situ resources.
The canisters are launched to a depot or processing station at L1. The required launch velocity is approximately 2.34 km/s.
Figure 1.
Schematic block diagram of lunar resource launcher with segmented design.
Figure 1.
Schematic block diagram of lunar resource launcher with segmented design.
Other key factors affecting overall system performance:
The ultimate use of the product is for refueling spacecraft in geosynchronous orbit (GSO). Hence L1 was selected over L2 or low lunar orbit. A vehicle must take the product from the L1 processing plant to GSO.
The canister velocity is assumed to be low at apolune, which is to be in the vicinity of L1.
The launch system will inevitably deliver some variations in launch velocity, although its design should aim to minimize these. Therefore some method must be included to correct their velocity and position L1 for acceptance at the processing station.
It should be noted that there are alternatives to electromagnetic launch, for example, a gas gun [
7]. The author does not have experience with such systems, and the remainder this paper will focus exclusively on electromagnetic launch.
The cost of the LRL will have two principal contributions: the manufacturing cost and the cost of delivery to the Moon. Both can be assumed to be functions of the system mass. The total mass
M(PR), a function of the maximum production (launch) rate the system can support, may be decomposed into
where
Ma = mass of accelerating components (magnets, shuttle if required, restraints)
Ms = mass of support structure (some of which may be produced in situ)
Me = mass of energy production components (primarily photovoltaic panels)
Mc = mass of energy storage components (primarily supercapacitors)
Mm = mass of construction machinery (hoisting, structure fabrication, anchoring)
Mp = mass of launch packages (a consumable, delivered periodically from Earth)
In
Figure 1, these component masses are indicated by uncolored blocks. The masses of the colored blocks (mainly control circuitry) have not been estimated but are not likely to contribute significantly to overall system mass.
The goal of this paper is to develop reasonable estimates for each of these components, eliminating variables except for the production rate of the resource. A driving requirement is that the launch packages (of mass mL) and cycle time tc between launches must keep up with that production rate, i.e. mL / tc > PR.
2.1. Existing Systems Used as Basis for the Accelerator Mass Model
This paper will use two exemplar launch systems that have established the required accelerator mass per unit length to deliver forces in the range of 106 N. The two exemplar systems are:
The Electromagnetic Aircraft Launch System (EMALS) [
8]. This system is being developed by the US company, General Atomics, for installation on the next generation aircraft carriers of the United States Navy. The goal is to replace the steam catapults used on current aircraft carriers with a lighter, more reliable system that requires less maintenance. EMALS is an open system, which is achieved by the use of a shuttle, riding on a track, which is accelerated by magnets along the track, and to which any of a number of different aircraft types can be attached.
The Electromagnetic Mortar (EMM) [
9,
10]. Two variants of this system were developed, sponsored by the US Defense Advanced Research Projects Agency and managed in part by the author. Test firings of both designs occurred. The goal was to determine the feasibility of an electromagnetic launcher for 120 mm mortar rounds that would provide higher launch velocities, improved accuracy and rapid fire capability. EMM is a closed system; the mortar rounds must be of fixed diameter, fitting inside a barrel which creates the propelling magnetic field. The mortar rounds themselves must contain conducting components which form part of the magnetic circuit.
The EMALS system is capable of imparting a maximum energy E of 122 MJ to an aircraft. This is accomplished using switched magnets emplaced along a 91 m track, which pull a shuttle to which the aircraft is attached. Available literature indicates that the total mass of the EMALS system is less than 225,000 kg, but does not break that down into masses for the magnets, track, shuttle, energy storage and control.
EMALS derived quantities:
Force: F = E / s = 1.22E8 / 9.1E1 = 1.34E6 N
Acceleration: assuming a 45,000 kg aircraft, a = F / m = 1.34E6 / 4.5E4 = 2.97E1 m/s2 = 3.03 g
Mass launched to L1 = 2E / v2 = 2 × 1.22E8 / (2.34E3)2 = 44.6 kg
Track mass per unit length: with total track mass of 200T, λ = M / L = 200 / 91 = 2200 kg/m
Both a coilgun and a railgun version of the EMM were developed. Both versions were required to accelerate a 120 mm mortar projectile, mass 18 kg, to 430 m/s. The railgun barrel was 2.4 m in length and weighed 950 kg. [The coilgun version was probably somewhat heavier, because it required more copper. A solid copper cylinder 2.4 m long and 30 cm in diameter would have a mass of 1,516 kg.]
EMM derived quantities:
Projectile kinetic energy: E = ½ mv2 = 0.5 × 1.8E1 × (4.3E2)2 = 1.66 MJ
Force: F = E / s = 1.66E6 / 2.4 = 6.93E5 N
Acceleration: a = v2 / 2s = (4.3E2)2 / (2 × 2.4) = 3.85E4 m/s2 = 3930 g
Mass to L1 = 2E / v2 = 2 × 1.66E6 / (2.34E3)2 = 0.61 kg
Mass per unit length: λ = M / L = 950 / 2.4 = 396 kg/m
EMALS and EMM have very different properties. EMALS is for accelerating very large masses to relatively low velocities with relatively low acceleration. EMM is for accelerating smaller masses to somewhat higher velocities; to keep the barrel length short, the acceleration must be much higher. Interestingly the force applied by each system is about the same, around one million Newtons. In one case, m is large and a is small; the other case is the opposite.
The EMALS mass per unit length is almost ten times that of EMM. This is probably due to the necessity to restrain large side loads. If the aircraft carrier rolls during launch, or if the aircraft path deviates for any other reason, the large lateral loads must be absorbed by the launcher and transferred to the ship structure, while keeping the aircraft on a straight path. This necessitates a lot of steel in the EMALS launcher construction. The lateral loads in the LRL are anticipated to be much smaller. The EMM lateral loads are primarily caused by the very strong repulsive forces within the rails or electromagnets. The EMM designs included composite bands and members to contain these repulsive forces.
3. Launch Requirements and Accelerator Mass
LRL must provide an exit velocity of 2.34 km/s, nearly the lunar escape velocity. This is independent of both the mass to be launched, and the acceleration. Requirements influencing the launched mass are:
Lower masses mean less total energy is required per shot.
Higher launch masses mean higher stresses on the LRL structure, and hence more support mass per unit length.
For a given resource recovery rate, the LRL must be able to shoot often enough to keep up with the mining. The longer the cycle time of the launcher, the larger the minimum payload mass must be.
At L1, something must be able to grapple a canister, deliver it to the processing station, and recycle to catch the next canister before it arrives. Again, the longer this cycle, the larger the minimum payload mass must be.
Requirements influencing the acceleration are:
Table 1.
LRL track lengths for various levels of acceleration.
Table 1.
LRL track lengths for various levels of acceleration.
| Acceleration. m/s2 | Track length = v2/2a |
|---|
| 196 = 20 g | 13.9 km |
| 1960 = 200 g | 1.39 km |
| 9800 = 1000 g | 278 m |
| 19,600 = 2000 g | 139 m |
Lower forces mean lower mass per unit length, but longer length, for the same payload mass.
If a shuttle is used as does EMALS, a longer track length will result in a longer cycle time, influencing the minimum payload mass (see above). If no shuttle is required, as for EMM, this is not a consideration. Use of a shuttle also increases the total energy required per launch, as some of the energy is imparted to the shuttle and some to the launch package.
3.1. Resource Canisters and Launch Stresses
The harvested resource, water or ice, must be contained for the launch. Higher acceleration means higher stresses within the canister containing the resource. Therefore the canister mass will increase, and become a larger fraction of the total mass launched.
Figure 2.
Schematic of a launch canister with relevant variables.
Figure 2.
Schematic of a launch canister with relevant variables.
Figure 2 defines the canister parameters. Assume a fluid mass
M of 9 kg (radius 10 cm, length 29 cm), and a canister shell of 6061 aluminum (density 2700 kg/m
3). We assign a conservative tensile stress limit
σ of 20,000 psi, or 1.38E8 N/m
2. The total aftward force on the shell due to the acceleration
F =
Ma is experienced as a tensile force in the shell of
F = 2π
rtσ. Therefore, to avoid canister failure,
t >
Ma/2π
rσ. Shell thicknesses and masses are shown in
Table 2 as a function of acceleration level.
Table 2.
Launch canister thicknesses and masses for various levels of acceleration.
Table 2.
Launch canister thicknesses and masses for various levels of acceleration.
| Acceleration, g | Min shell thickness, cm | Cylinder mass, kg |
|---|
| 20 | 0.002 | .0027 |
| 200 | 0.02 | .027 |
| 1000 | 0.1 | .13 |
| 2000 | 0.2 | .27 |
Thus even at 2000 g acceleration, the canister shell, if made of high quality aluminum alloy, adds little to the launch package mass. One might consider making canisters of in situ materials such as sintered regolith; however, these would probably have lower tensile strength, as well as requiring complex manufacturing equipment to be delivered to and operated on the Moon.
The canister will also contain a conducting component that enables the application of electromagnetic force. In the EMM coil-based design, the component was an aluminum ring added to the mortar shell. The eddy current induced in the ring by pulsing the coils generates an opposing magnetic field which results in the launch force. In the EMM rail-gun design, the mortar shell was augmented by a conducting bar that completed the circuit between the launch rails. In the EMM program, these components were fractions of 1 kg and would be no more massive for the LRL. The quality requirements on the conducting components will force their manufacture on Earth.
3.2. Launch Velocity Variations and the Need for Canister Propulsion
The launch trajectory is highly elliptical. Launch occurs at the lunar surface, the lunar radius being about 1738 km. L1 is located about 62,700 km from the center of the Moon.
With such highly elliptical trajectories, small errors in launch velocity can result in large errors in the position at apolune. Consider a cross-track velocity variation of 1 m/s, caused for example by vibration of the launching structure. In the several hours’ rise to apolune, this would result in apolune position variations of several kilometers. Along-track velocity errors would result in similar position variations, because apolune height for highly elliptical orbits is very sensitive to launch velocity.
Such errors could be corrected by a placing a retrieval vehicle at L1, which would match position and velocity with each canister, grapple them, and slow down for docking with the processing station at L1. Two considerations argue against this approach. The retrieval vehicle is likely to be much more massive than the canisters; therefore it will expend a considerably greater amount of propellant for its maneuvers. Also, with large position errors, it will have long transit times, and therefore greatly increase the cycle time for the system.
Therefore it will be assumed that each launch canister has a small propulsion system, including a radio receiver to enable control by signals sent from the L1 processing station. Correction of 5 m/sec total velocity error (much larger than, e.g. the design velocity variation of EMM which was 1.5 m/s) with a specific impulse of 200 s would add a propellant mass fraction of
This would be 0.025 kg for a 10 kg package. Using solid state digital thruster technology, digital radio and patch antennas, the overall control system should add less than 1 kg to package weight. Such a controllable thrust package should ensure accurate delivery to a depot at L1 and minimize the impact of launch velocity errors.
3.3. Selection of Accelerator Properties
It is likely that the feasible length of the launcher will be constrained, not merely by performance considerations, but by irregularities in the lunar topography. Therefore a relatively short design, 278 m, will be used. This fixes the required acceleration, v2/2s, at 9800 m/sec2 or 1000 g.
The package canister will be 5% of the total launch weight. However, the package mass will be increased by 1 kg for the propulsion package. This should represent a small fraction of the total launch weight for efficiency. Therefore a 10 kg launch mass is specified, which fixes the launch force at 98,000N, well within the capability of EMM as tested.
A closed-bore, fixed payload EMM-like design will be assumed. This is to limit the energy required per cycle, and the total force. With a shuttle, the energy is provided both to the launch package and the shuttle. With EMM, all energy goes into the launch package. This also avoids the need for a shuttle energy dissipation mechanism, and removes the impact on cycle time of shuttle retrieval. The disadvantage is the loss of adaptability; an open design, EMALS-like launcher would be able to launch packages of widely varying geometry, whereas the closed-bore design is restricted to canisters fitting the launcher bore.
Scaling the EMM down linearly to the lower launch force of 98,000N, the mass per unit length would be 56 kg/m. The resulting total mass for the 278 m accelerator is 15,600 kg.
4. Additional Mass Contributions to LRL Total Mass
4.1. Mass of Support Structure
The function of the LRL structure is to transfer launch loads to the lunar surface. The difference in mass per unit length of EMALS and EMM shows that structural mass can be a significant contributor to the total launch system mass. The breech and yoke assembly of EMM barrel weight were probably several hundred kg. These transferred the EMM launch force to the baseplate.
Figure 3 shows a subsection of the accelerator. It is anchored into regolith. A 20 kg anchor will be assumed to resist repeated applications of 10,000N. It is assumed that the launcher is basically constructed in subsections. The number of anchors per subsection of the launcher is then determined by the launch force, 98,000N, so 10 anchors per section are required, a mass of 200 kg. The longer the subsection, the smaller a fraction of the total mass this is; on the other hand, a longer subsection will require more support structure.
Figure 3.
Schematic of accelerator subsection with support structure and anchors.
Figure 3.
Schematic of accelerator subsection with support structure and anchors.
It is assumed that a support structure effective density of 5 kg/m3 will withstand 10,000N. This is much lighter than terrestrial structures, but a lunar structure does not need to withstand wind, ice or seismic forces. The structure to withstand 98,000N would therefore have a density of 50 kg/m3.The support structure volume is assumed to be 0.01 times the cube of the subsection length. Then the support structure mass per subsection is 50 × 0.01 × Ls3, and the total structure mass (including anchors) is (278 / Ls) × (200 + 0.5 × Ls3). Minimizing this function with respect to Ls gives a subsection length of 5.85m. 48 subsections are needed, and the total support structure mass with anchors is 14,300 kg.
Some of the structural mass could be obtained
in situ, for example by sintering regolith and using it to create the structural members. The use of
in situ materials would reduce the total mass launched from Earth. However, if the
in situ materials were of low tensile strength, an upper limit on the applied force would have to be imposed. In
Figure 3, the gray members and anchors could potentially be manufactured
in situ.
The ability to use in situ resources could greatly influence the total LRL cost. The assumption will be that only structural components, which do not require complex manufacturing processes, could be produced in situ. Therefore the structural mass which must be launched from Earth is Ms × (1 – fIS), where fIS is the defined as the fraction of structural mass produced in situ.
4.2. Masses for Energy Production and Storage
Photovoltaic panels for space applications of very high performance are being produced. The panels being installed on the JUNO spacecraft have efficiency of over 40%. Panels with energy density of 200 watts per kilogram are available. There are some cost implications for using the highest performance panels available, but these will be insignificant compared to overall LRL cost.
Assume a photovoltaic power source for the system, with area A and efficiency ηp. The solar constant S is 1.36E3 W/m2. Define the energy efficiency of the launch system as ηL. The energy recharge time te is the energy required, E / ηL , divided by the power delivered by the photovoltaic panels, ASηp .
The required cycle time tc is determined by the resource production rate PR in kg/day. With launch packages of 10 kg, we must have 10 kg / tc > PR or 1/tc > PR /10 kg, which is the number of launches per day.
At 42% efficiency, the required solar panel area is 1.8 square meters times the number of launches per day. At 2.87 kg per square meter, this contributes a mass to the system of only 5.2 kg times the number of launches per day.
High density energy storage is available today using lithium-ion batteries. Storage densities of 100 watt-hours per kilogram, or 0.36 MJ/kg, are standard. However, lithium ion batteries have limited discharge rates. A rapid-discharge energy storage solution, such as supercapacitors, must be included in the LRL design. Today’s supercapacitor energy storage densities are no more than 5 W·hr/kg (0.018 MJ/kg).
A 10 kg launch mass (which delivers 8.6 kg of resource) requires a kinetic energy at launcher exit of ½ × 10 × (2340)2 = 27.4 MJ. Assuming 30% launcher efficiency, the required mass of supercapacitors for rapid discharge energy storage is 1520 kg.
4.3. Machinery for LRL Construction
Two essential functions will require heavy machinery: hoisting and anchoring, i.e. a crane and an auger. (Actually augers do not work in compacted regolith, so a more appropriate anchoring mechanism would have to be developed.) If structural members are to be fabricated in situ, that will require an additional machine. It is assumed that the masses of these machines are independent of the launcher parameters.
Terrestrial cranes tend to weigh about two thirds of their lifting capacity. For example, the Liebherr LTM 1030-2.1 crane weighs 24T and can lift 35T. Roughly the same proportion should pertain on the Moon. A mass of 4T is assigned for the LRL assembly crane. This should permit lifting the 6m accelerator sections, with masses of 330 kg, without difficulty.
Compacted regolith must be removed by a process such as those being investigated by L. Bernhold. The equipment consists of pipes, blowers, separators and chambers. These must be mounted on a vehicle. A mass of 3T is assigned for the anchoring machinery.
Structural members might be fabricated by processes such as electric resistance heating, selective laser sintering, and 3D printing. A mass of 1T is assigned for structural member fabrication equipment.
5. Total System Mass and Factors Influencing LRL Cost
5.1. Mass Model
With the above assumptions, the system mass, equation (1), becomes
for the first 1,000 launches.
The mass delivered to the Moon is
where
fIS is the fraction of structural material produced on the lunar surface.
Clearly, the mass of the LRL is not very sensitive to the production rate. At 240 kg per day production rate (1 launch per hour), the energy harvesting mass of solar panels is only 130 kg.
5.2. System Delivery to the Moon
A scenario for delivery of the LRL components to the lunar surface will now be constructed, assuming the use of SpaceX Corporation’s Falcon Heavy vehicle now in development [
10]. That launch vehicle is being designed to deliver 53,000 kg to low Earth orbit (LEO). The company website states that they will charge US$128M per launch.
The Apollo stack of the Saturn V rocket [
12] included the means to return from lunar orbit to Earth (the Command and Service Modules). To deliver the LRL to the Moon, no return flight is needed; therefore the mass delivered to the lunar surface per launch can be greater.
Table 3 compares the Apollo Saturn V stack and the appropriately scaled figures for the Falcon Heavy.
With a Falcon Heavy-based transportation system, the mass of equation (4), delivered in 5050 kg payloads, requires nine launches with all material delivered from Earth (fIS = 0). Full in situ production of structural components (fIS = 1) would reduce this to six launches.
This delivery scenario would require two development projects: (1) upper stages for the Falcon Heavy, with performance equivalent to the S-II and S-IVB upper stages of the Saturn V; and (2) a LEM-like lander to deliver the LRL to the lunar surface. An underlying assumption of this paper is that assembly is performed by human construction workers on the Moon. These workers would require two-way transportation, habitats, consumables replenishment, etc. In developing the transportation system for the overall lunar resources enterprise, one capability should be delivery of the LRL.
Table 3.
Mass delivered to Moon by Falcon Heavy derived from Saturn V Apollo stack.
Table 3.
Mass delivered to Moon by Falcon Heavy derived from Saturn V Apollo stack.
| Parameter | Apollo Saturn V | Falcon Heavy + 1-way lunar |
|---|
| Mass to LEO | 127,000 kg | 53,000 kg |
| Mass to trans-lunar injection | 45,400 kg | 19,900 kg |
| Lunar Excursion Module mass | 14,454 kg | |
| Ascent stage fraction of LEM | 30.9% | 30.9% |
| P/L for 1-way lunar descent | | 6310 kg |
| LRL mass delivered (80%) | | 5050 kg |