Refinement Algorithms for Adaptive Isogeometric Methods with Hierarchical Splines
Abstract
:1. Introduction
2. The Hierarchical B-Spline Model
2.1. Basis Construction
2.2. Data Structures for the Implementation
- get_basis_functions: given an element , compute the indices of the basis functions in that do not vanish in Q;
- get_cells: given a function , compute the elements Q in the support of ;
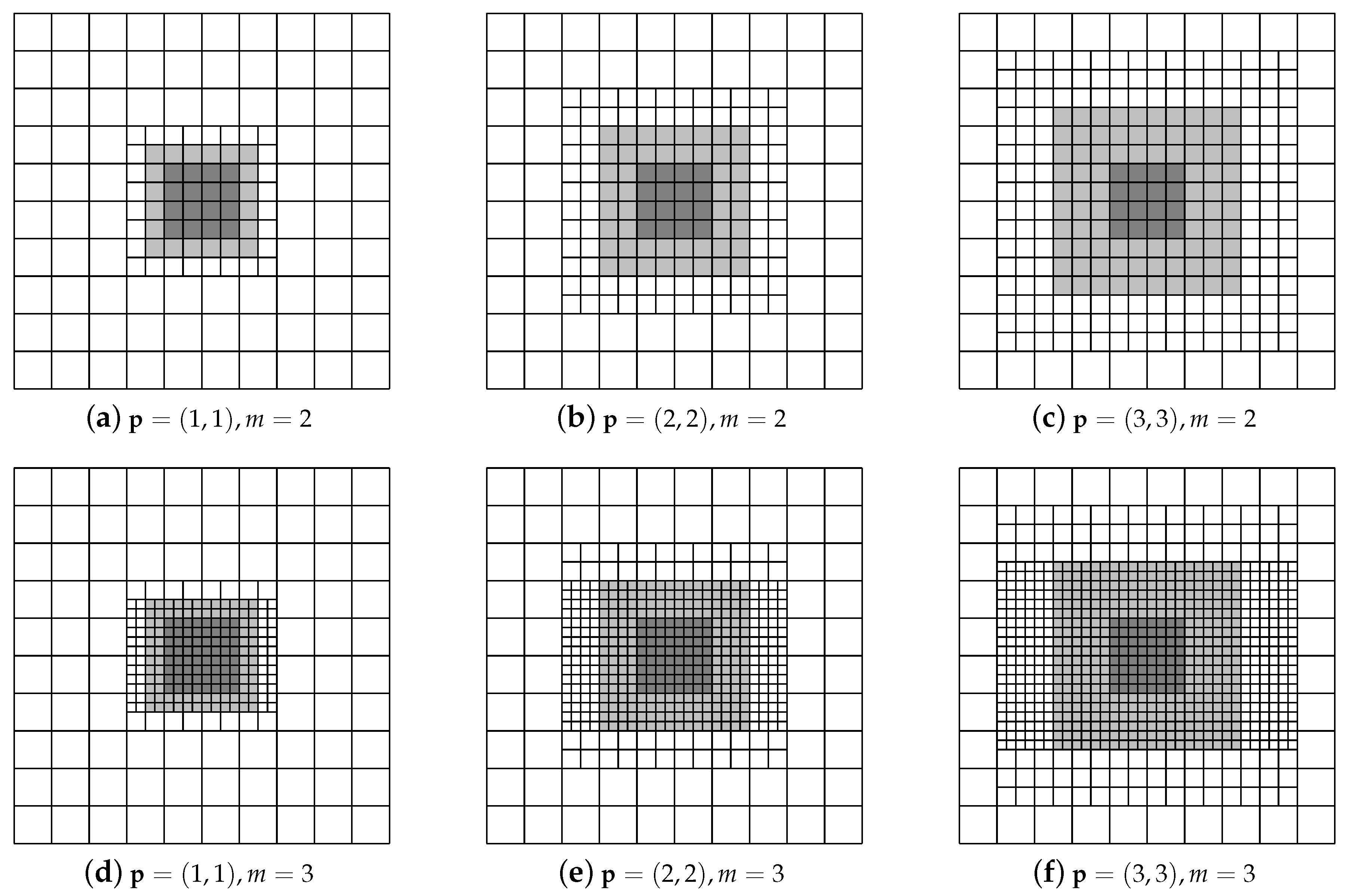
- get_support_extension: for a given element , compute its support extension , defined as
- the number of levels, N;
- for each level ℓ, a structure for the rectilinear grid ;
- for each level ℓ, the list of active elements , denoted by in the algorithms of Section 3;
- the kind of refinement (dyadic, triadic...) between levels.
- get_parent_of_cell: given a cell (or a list of cells), compute the index of its parent, that is, the unique cell such that ;
- get_ancestor_of_cell: given a cell (or a list of cells) of level ℓ, and given , return the unique index of the ancestor of Q of level k, that is, the unique cell such that .
| Algorithm 1: get_ancestor_of_cell. Description: get ancestor of level k for an element Q (or a list of elements) of level . |
Input:
|
- the number of levels, N;
- for each level ℓ, a space structure for the tensor-product space ;
- for each level ℓ, the set of active basis functions in ;
- the coefficients of the two-scale relation (2) between levels ℓ and .
3. Admissible Refinement Algorithms
| Algorithm 2: get_multilevel_support_extension. Description: Multilevel support extension of an element (or list of elements) Q of level ℓ, with respect to level , for a hierarchical space. |
Input:
|
| Algorithm 3: get_H-neighborhood. Description: -neighborhood of an element Q, of level ℓ, with respect to the admissibility class m. |
Input:
|
| Algorithm 4: get_T-neighborhood. Description: -neighborhood of an element Q, of level ℓ, with respect to the admissibility class m. |
Input:
|
- 1.
- if is strictly -admissible of class m, then it is -admissible of the class m.
- 2.
- if is strictly -admissible of class m, then it is -admissible of the class m.
- 3.
- if is (strictly) -admissible of class m, then it is (strictly) -admissible of the class m.
- 4.
- if is -admissible of class m and satisfies assumption (5), then it is strictly -admissible of the class m.
| Algorithm 5: admissible_refinement. Description: given a hierarchical mesh and a set of marked elements, generate a refined admissible mesh of class m. |
Input:
|
| Algorithm 6: mark_recursive. Description: recursive algorithm to mark the elements in the neighborhood of marked ones. |
Input:
|
- If , then . Obviously, since for every k, it holds (both for - and -admissible), and we obtain the desired result.
- If , by Lemma 1, it is obtained by a single refinement of an element , thus . The definition of multilevel support extension immediately gives, for any ,Moreover, since is strictly admissible we know that , which combined with the previous equation and the definition of yieldsAccording to this, let us introduce for strictly -admissible meshes, and for strictly -admissible meshes. Since was a marked element (either , or it was marked during the recursive marking), it has been used as an input for mark_recursive (Algorithm 6), and as a consequence all the active elements in have been marked. Hence, , and by definition of the result is proved.
4. Adaptive Isogeometric Methods
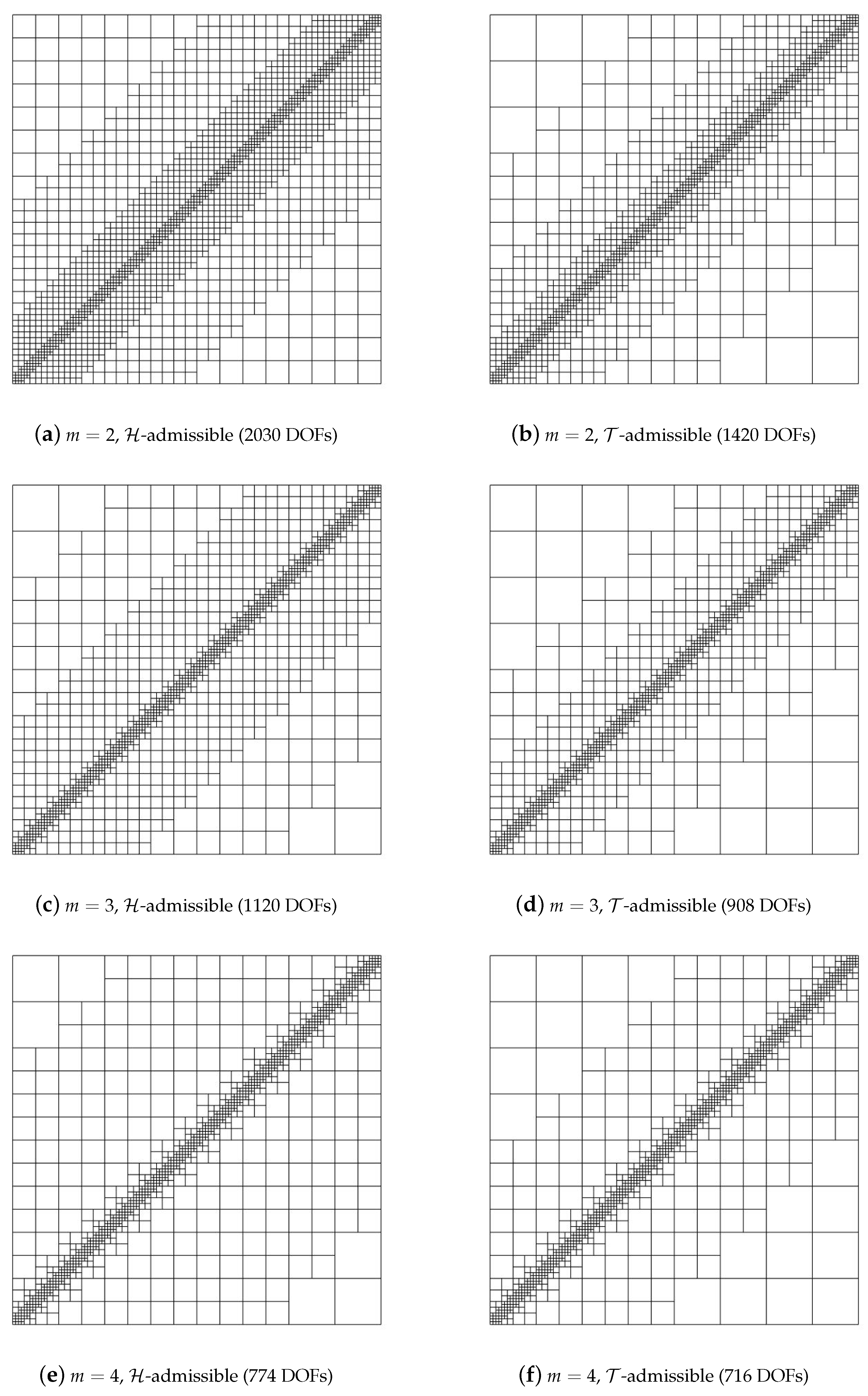
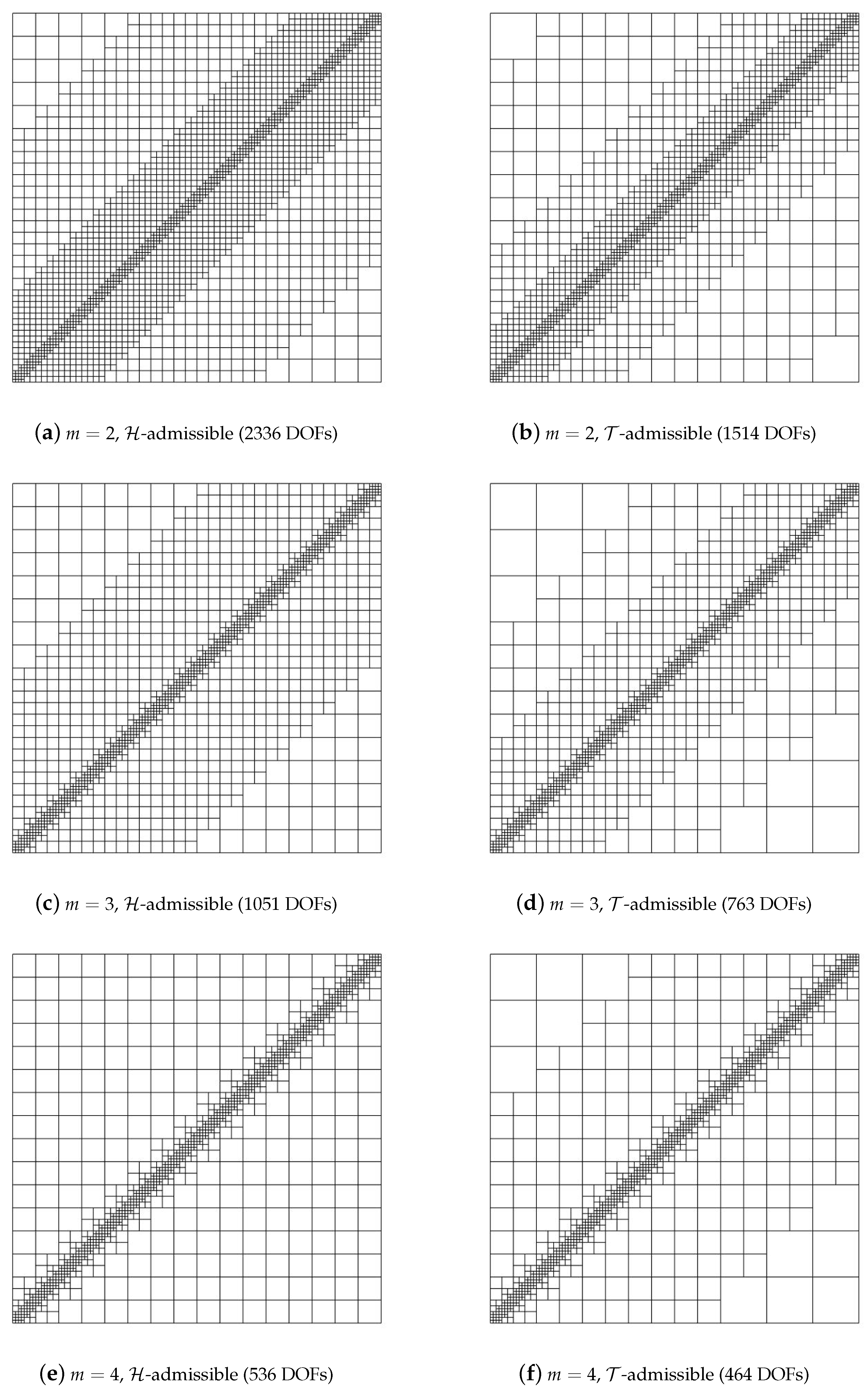
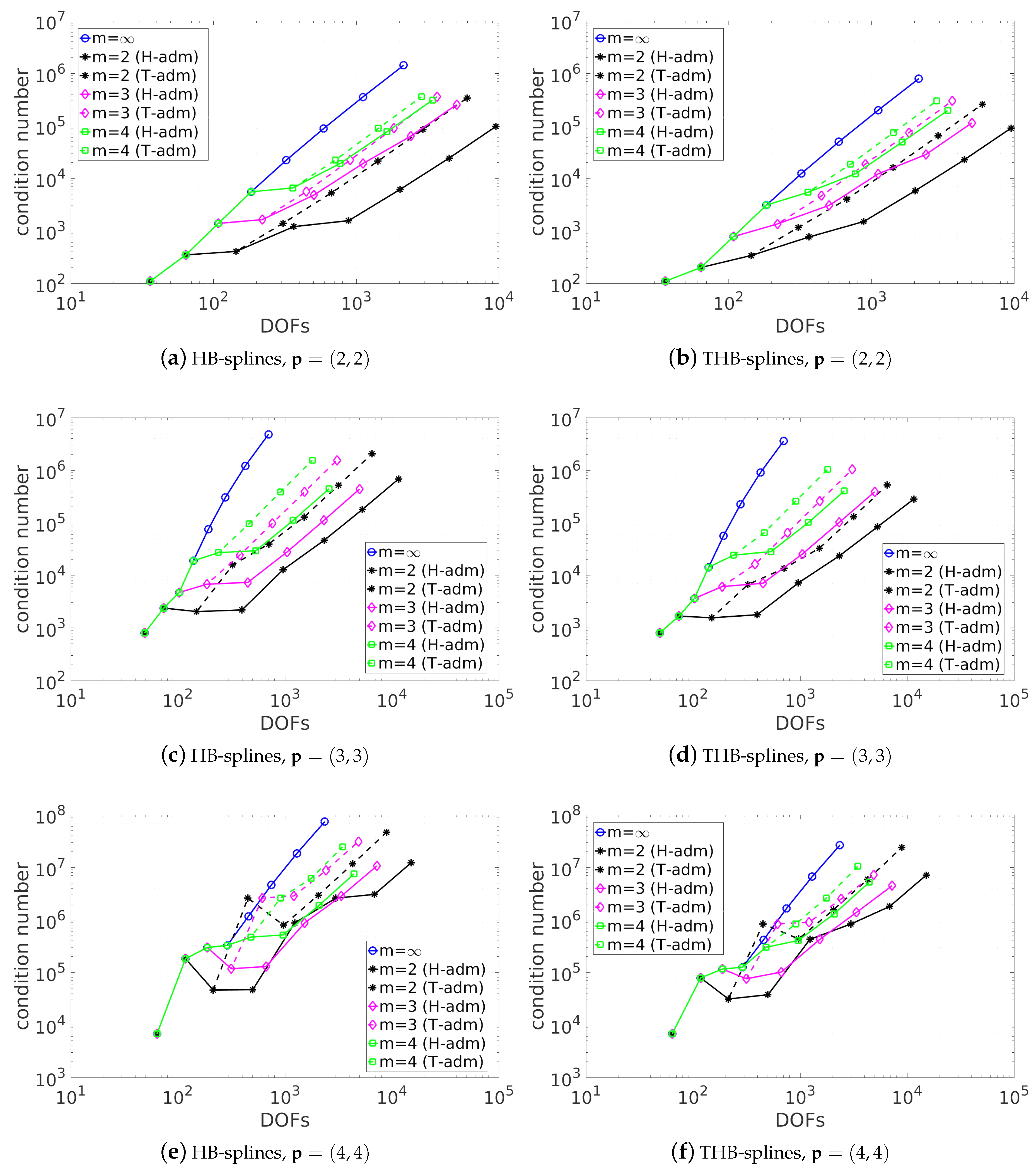
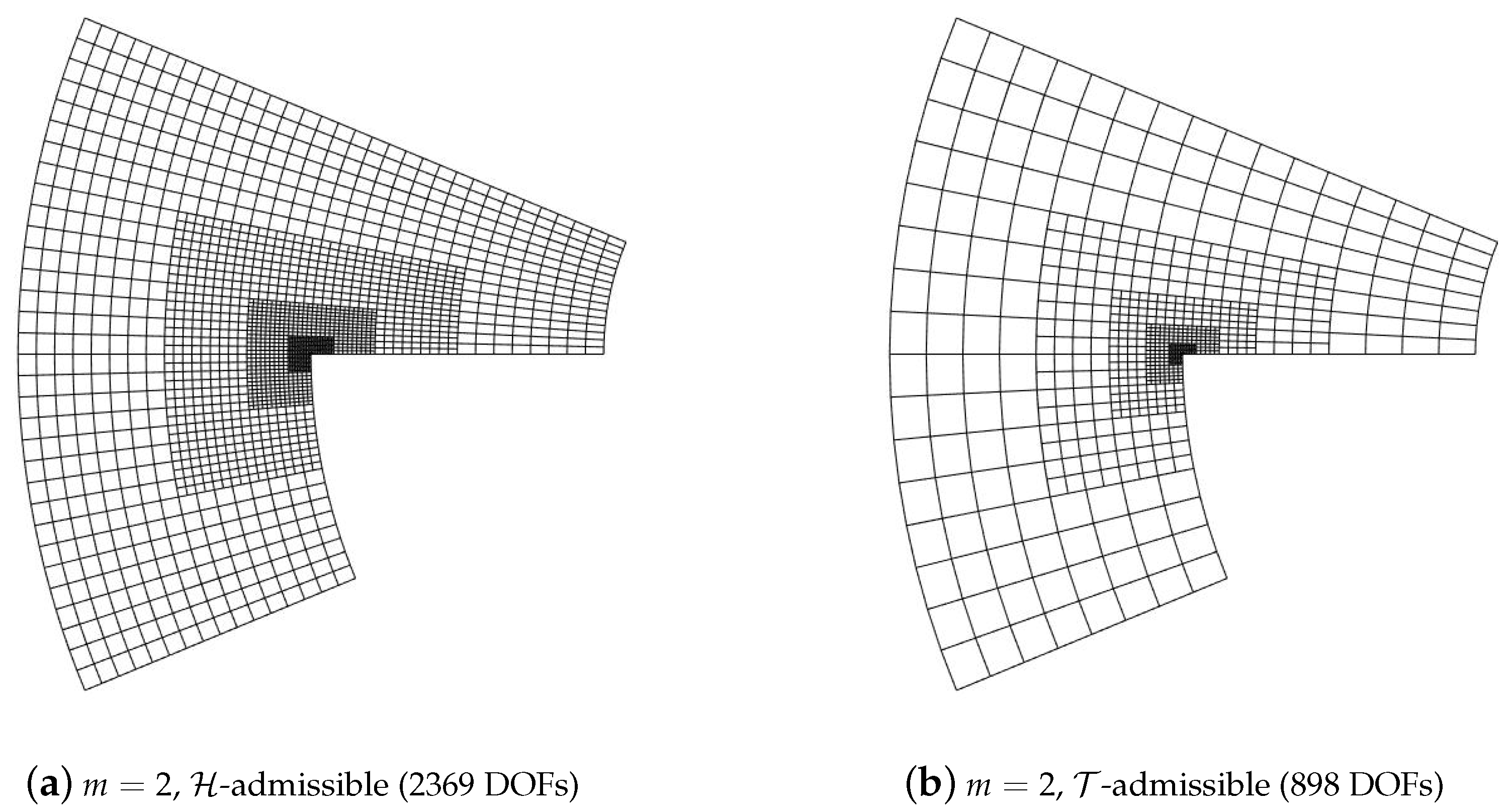
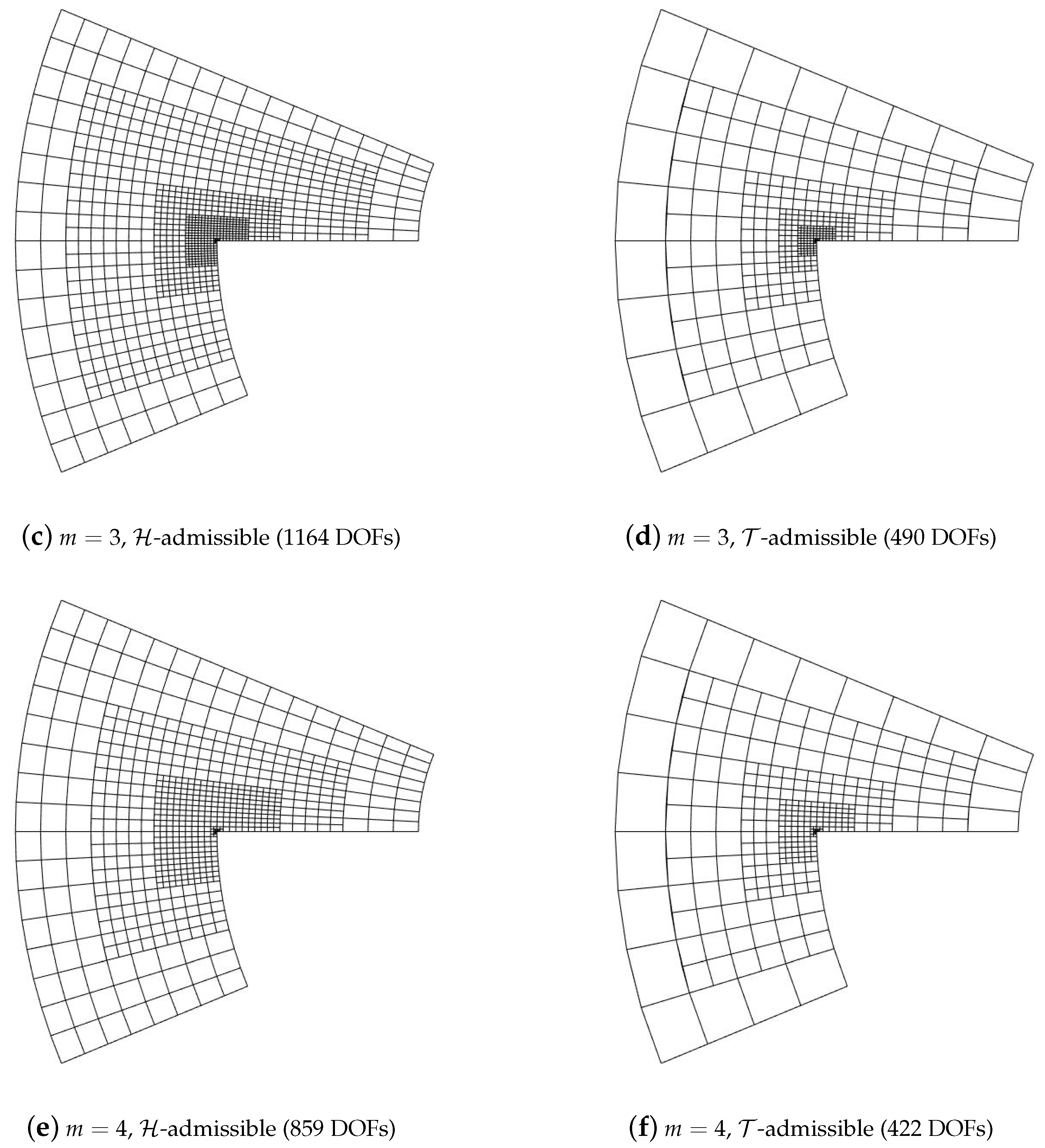
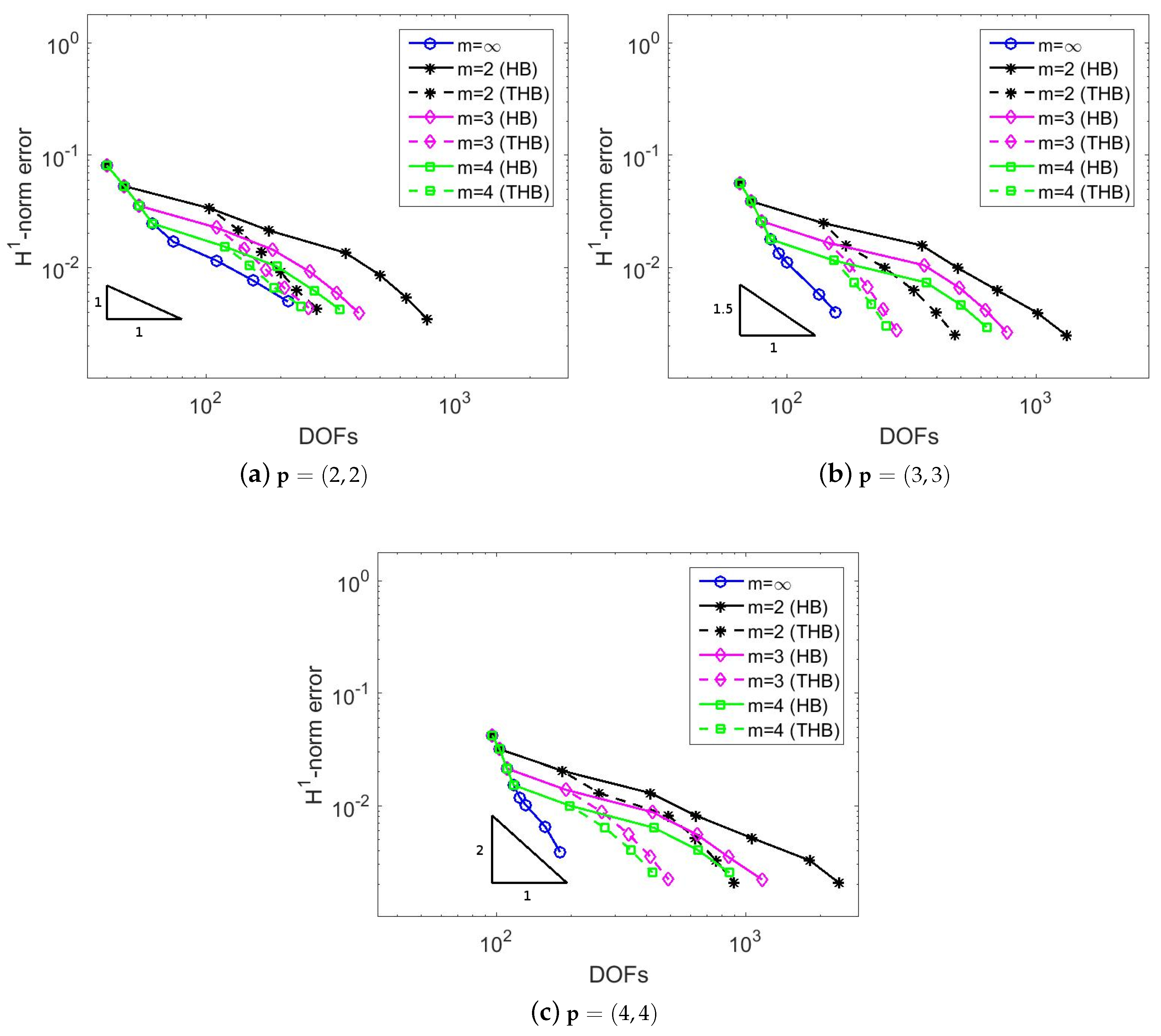
5. Numerical Results
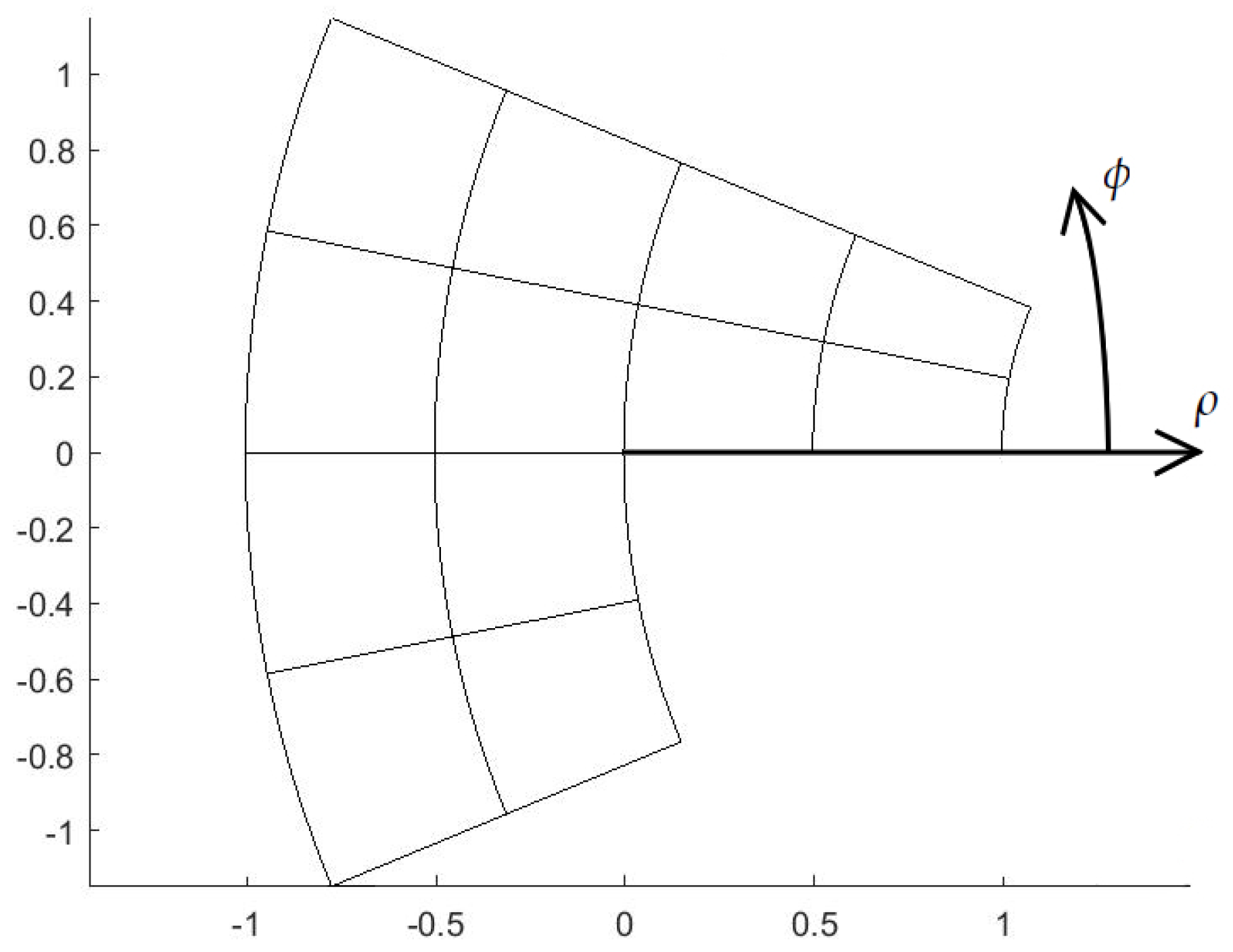
5.1. Diagonal Refinement of the Unit Square
5.2. Adaptive Method
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cottrell, J.A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Kraft, R. Adaptive and Linearly Independent Multilevel B-Splines. In Surface Fitting and Multiresolution Methods; Le Méhauté, A., Rabut, C., Schumaker, L.L., Eds.; Vanderbilt University Press: Nashville, TN, USA, 1997; pp. 209–218. [Google Scholar]
- Vuong, A.V.; Giannelli, C.; Jüttler, B.; Simeon, B. A hierarchical approach to adaptive local refinement in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2011, 200, 3554–3567. [Google Scholar] [CrossRef] [Green Version]
- Buffa, A.; Giannelli, C. Adaptive isogeometric methods with hierarchical splines: Error estimator and convergence. Math. Models Methods Appl. Sci. 2016, 26, 1–25. [Google Scholar] [CrossRef]
- Buffa, A.; Giannelli, C. Adaptive isogeometric methods with hierarchical splines: Optimality and convergence rates. Math. Models Methods Appl. Sci. 2017, 27, 2781–2802. [Google Scholar] [CrossRef]
- Gantner, G.; Haberlik, D.; Praetorius, D. Adaptive IGAFEM with optimal convergence rates: Hierarchical B-splines. Math. Models Methods Appl. Sci. 2017, 27, 2631–2674. [Google Scholar] [CrossRef] [Green Version]
- Giannelli, C.; Jüttler, B.; Speleers, H. THB-Splines: The truncated basis for hierarchical splines. Comput. Aided Geom. Des. 2012, 29, 485–498. [Google Scholar] [CrossRef]
- Bornemann, P.; Cirak, F. A subdivision-based implementation of the hierarchical B-spline finite element method. Comput. Methods Appl. Mech. Eng. 2013, 253, 584–598. [Google Scholar] [CrossRef]
- Scott, M.A.; Thomas, D.C.; Evans, E.J. Isogeometric spline forests. Comput. Methods Appl. Mech. Eng. 2014, 269, 222–264. [Google Scholar] [CrossRef]
- Garau, E.; Vázquez, R. Algorithms for the implementation of adaptive isogeometric methods using hierarchical B-splines. Appl. Numer. Math. 2018, 123, 58–87. [Google Scholar] [CrossRef]
- Kiss, G.; Giannelli, C.; Jüttler, B. Algorithms and data structures for truncated hierarchical B-splines. In Mathematical Methods for Curves and Surfaces; Floater, M., Lyche, T., Mazure, M.-L., Moerken, K., Schumaker, L.L., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8177, pp. 304–323. [Google Scholar]
- Giannelli, C.; Jüttler, B.; Kleiss, S.K.; Mantzaflaris, A.; Simeon, B.; Špeh, J. THB-splines: An effective mathematical technology for adaptive refinement in geometric design and isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2016, 299, 337–365. [Google Scholar] [CrossRef]
- Hennig, P.; Müller, S.; Kästner, M. Bézier extraction and adaptive refinement of truncated hierarchical NURBS. Comput. Methods Appl. Mech. Eng. 2016, 305, 316–339. [Google Scholar] [CrossRef]
- D’Angella, D.; Kollmannsberger, S.; Rank, E.; Reali, A. Multi-level Bézier extraction for hierarchical local refinement of Isogeometric Analysis. Comput. Methods Appl. Mech. Eng. 2018, 328, 147–174. [Google Scholar] [CrossRef]
- Vázquez, R. A new design for the implementation of isogeometric analysis in Octave and Matlab: GeoPDEs 3.0. Comput. Math. Appl. 2016, 72, 523–554. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines, revised ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Schumaker, L.L. Spline Functions: Basic Theory, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Morgenstern, P. Mesh Refinement Strategies for the Adaptive Isogeometric Method. Ph.D. Thesis, Institut für Numerische Simulation, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, Germany, 2017. [Google Scholar]
- Buffa, A.; Giannelli, C.; Morgenstern, P.; Peterseim, D. Complexity of hierarchical refinement for a class of admissible mesh configurations. Comput. Aided Geom. Des. 2016, 47, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Binev, P.; Dahmen, W.; DeVore, R. Adaptive finite element methods with convergence rates. Numer. Math. 2004, 97, 219–268. [Google Scholar] [CrossRef]
- Stevenson, R. Optimality of a standard adaptive finite element method. Found. Comput. Math. 2007, 7, 245–269. [Google Scholar] [CrossRef]
- Buffa, A.; Garau, E.M. A posteriori error estimators for hierarchical B-spline discretizations. Math. Models Methods Appl. Sci. 2016. [Google Scholar] [CrossRef]
- Kumar, M.; Kvamsdal, T.; Johannessen, K.A. Superconvergent patch recovery and a posteriori error estimation technique in adaptive isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2017, 316, 1086–1156. [Google Scholar] [CrossRef]
- Anitescu, C.; Hossain, M.N.; Rabczuk, T. Recovery-based error estimation and adaptivity using high-order splines over hierarchical T-meshes. Comput. Methods Appl. Mech. Eng. 2018, 328, 638–662. [Google Scholar] [CrossRef]
- Dörfler, W. A convergent algorithm for Poisson’s equation. SIAM J. Numer. Anal. 1996, 33, 1106–1124. [Google Scholar] [CrossRef]
- Buchegger, F.; Jüttler, B.; Mantzaflaris, A. Adaptively refined multi-patch B-splines with enhanced smoothness. Appl. Math. Comput. 2016, 272, 159–172. [Google Scholar] [CrossRef]
- Hennig, P.; Kästner, M.; Morgenstern, P.; Peterseim, D. Adaptive mesh refinement strategies in isogeometric analysis—A computational comparison. Comput. Methods Appl. Mech. Eng. 2017, 316, 424–448. [Google Scholar] [CrossRef]
- Lorenzo, G.; Scott, M.A.; Tew, K.; Hughes, T.J.R.; Gomez, H. Hierarchically refined and coarsened splines for moving interface problems, with particular application to phase-field models of prostate tumor growth. Comput. Methods Appl. Mech. Eng. 2017, 319, 515–548. [Google Scholar] [CrossRef]
- Hennig, P.; Ambati, M.; De Lorenzis, L.; Kästner, M. Projection and transfer operators in adaptive isogeometric analysis with hierarchical B-splines. Comput. Methods Appl. Mech. Eng. 2018, 334, 313–336. [Google Scholar] [CrossRef]



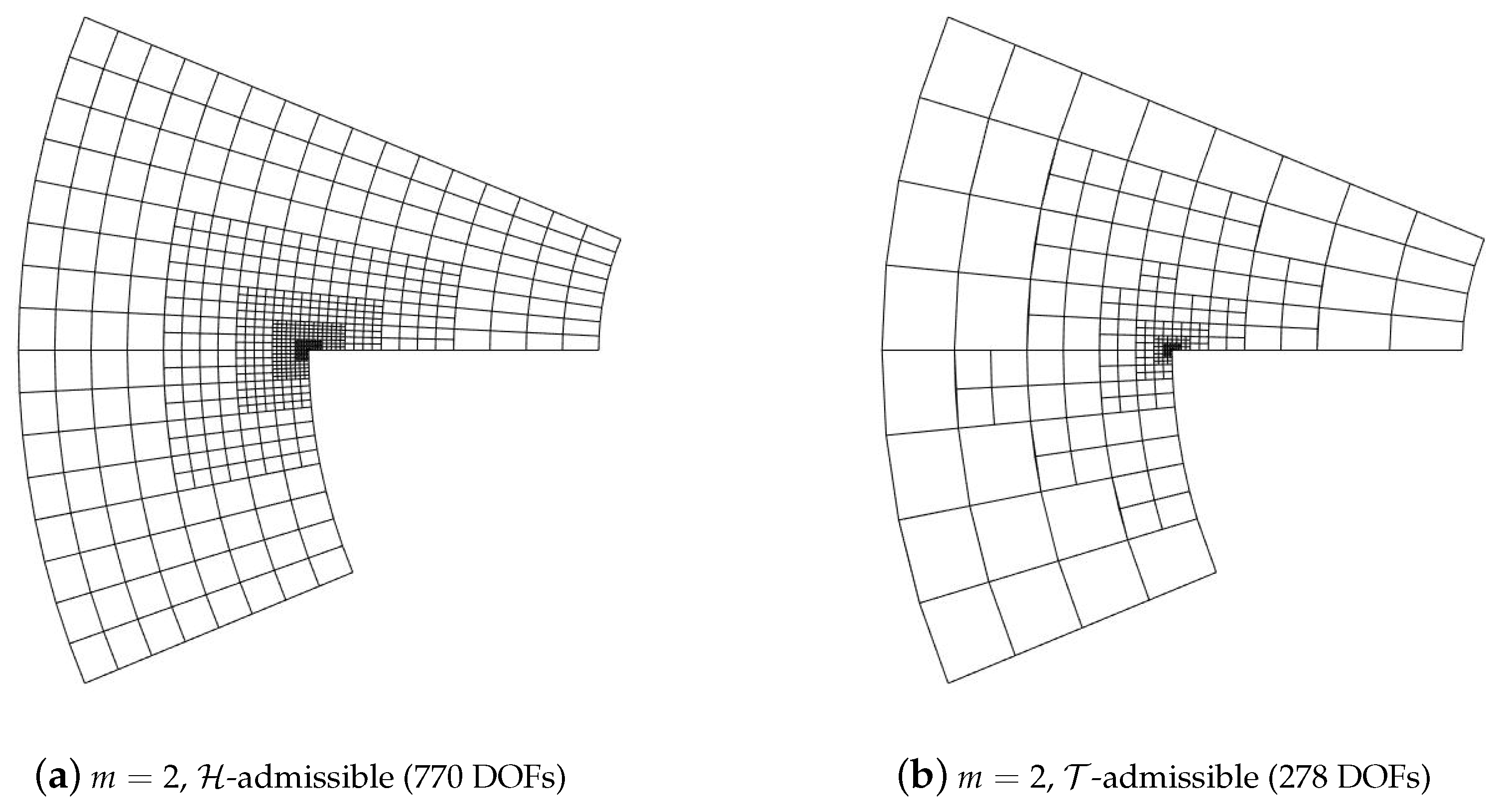
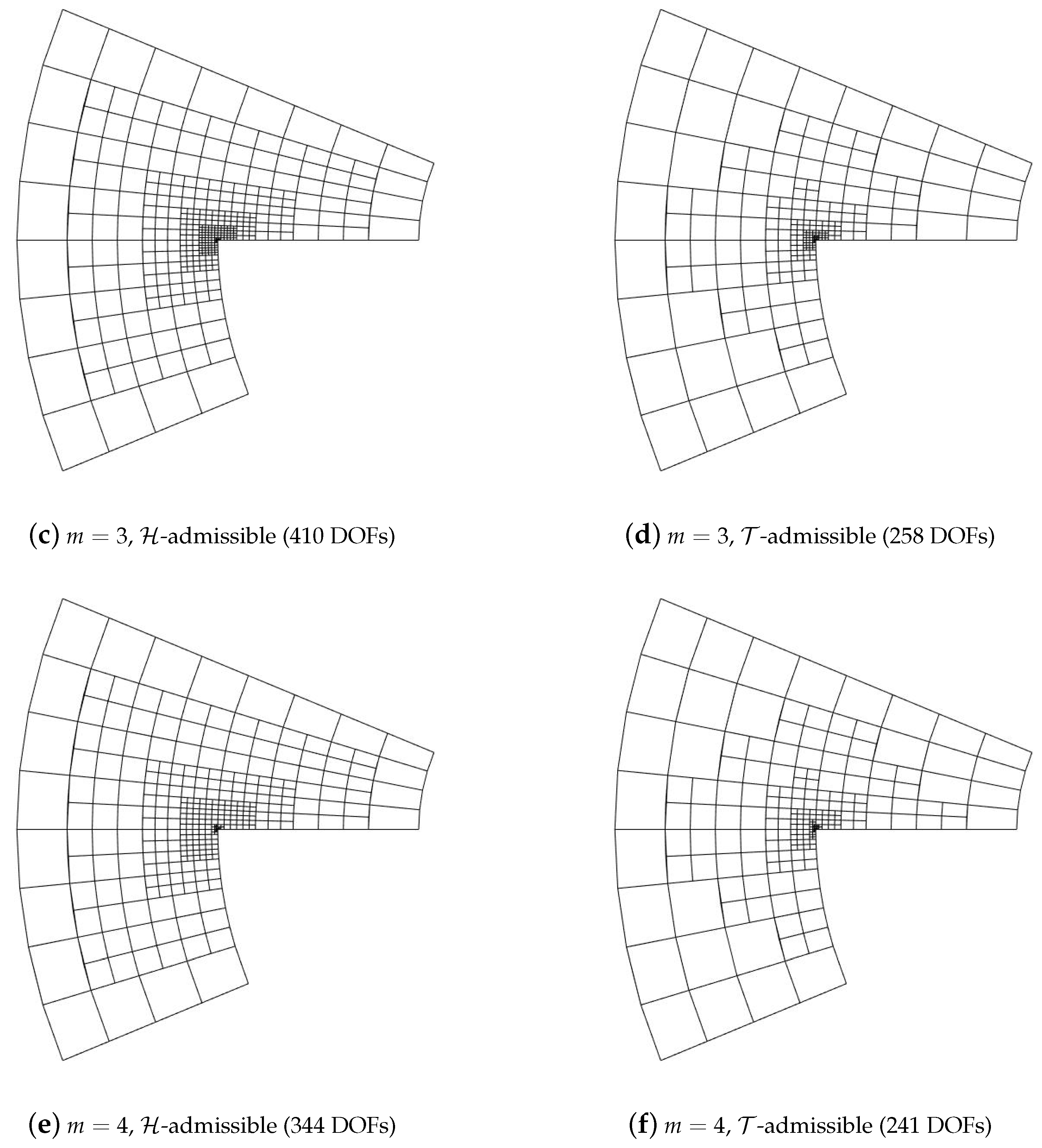
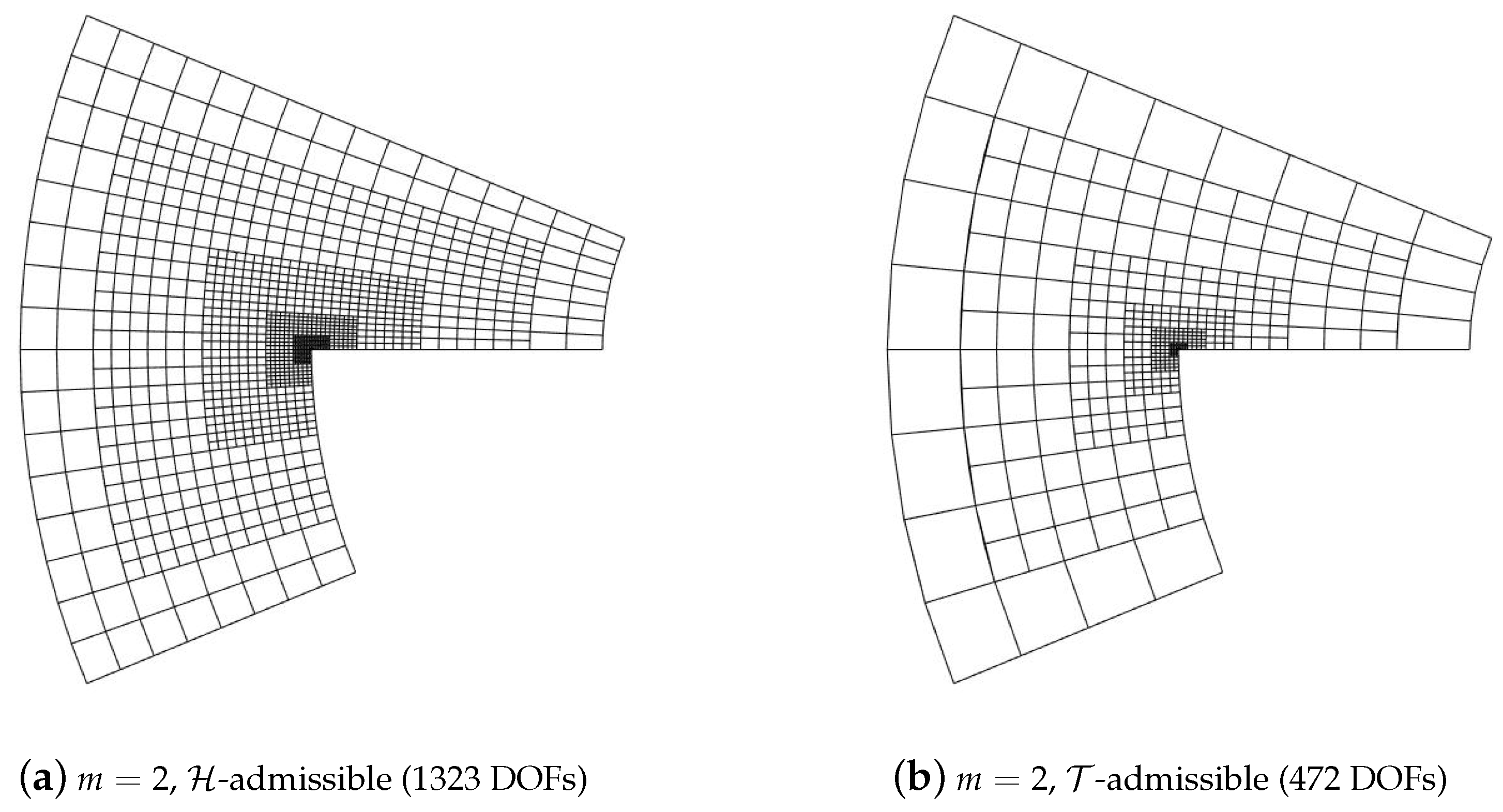

| DOFs | HB | (%) | THB | (%) | |||
|---|---|---|---|---|---|---|---|
| 8228 | 808,628 | (1.19) | 542,548 | (0.80) | |||
| -admissible | 40,058 | 1,248,786 | (0.08) | 1,099,583 | (0.07) | ||
| -admissible | 21,028 | 749,616 | (0.17) | 627,864 | (0.14) | ||
| -admissible | 14,106 | 589,834 | (0.30) | 476,115 | (0.24) | ||
| -admissible | 24,200 | 990,728 | (0.17) | 706,113 | (0.12) | ||
| -admissible | 14,664 | 898,652 | (0.42) | 478,963 | (0.22) | ||
| -admissible | 11,360 | 714,736 | (0.55) | 412,453 | (0.32) |
| DOFs | HB | (%) | THB | (%) | |||
|---|---|---|---|---|---|---|---|
| 2186 | 156,764 | (3.28) | 122,728 | (2.57) | |||
| -admissible | 49,940 | 2,941,926 | (0.12) | 2,620,770 | (0.11) | ||
| -admissible | 21,227 | 1,318,125 | (0.29) | 1,118,981 | (0.25) | ||
| -admissible | 11,064 | 674,020 | (0.55) | 571,544 | (0.47) | ||
| -admissible | 26,554 | 2,087,894 | (0.30) | 1,486,588 | (0.21) | ||
| -admissible | 12,107 | 1,466,741 | (1.00) | 709,261 | (0.48) | ||
| -admissible | 7020 | 746,362 | (1.51) | 392,128 | (0.80) |
| DOFs | HB | (%) | THB | (%) | |||
|---|---|---|---|---|---|---|---|
| 8446 | 1,819,856 | (2.55) | 1,410,796 | (1.98) | |||
| -admissible | 66,390 | 6,548,354 | (0.15) | 5,885,286 | (0.13) | ||
| -admissible | 31,112 | 3,299,540 | (0.34) | 2,861,116 | (0.30) | ||
| -admissible | 18,778 | 2,075,442 | (0.59) | 1,805,250 | (0.51) | ||
| -admissible | 36,516 | 4,819,354 | (0.36) | 3,499,152 | (0.26) | ||
| -admissible | 19,412 | 3,613,896 | (0.96) | 2,002,780 | (0.53) | ||
| -admissible | 13,456 | 2,773,686 | (1.53) | 1,437,096 | (0.79) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bracco, C.; Giannelli, C.; Vázquez, R. Refinement Algorithms for Adaptive Isogeometric Methods with Hierarchical Splines. Axioms 2018, 7, 43. https://doi.org/10.3390/axioms7030043
Bracco C, Giannelli C, Vázquez R. Refinement Algorithms for Adaptive Isogeometric Methods with Hierarchical Splines. Axioms. 2018; 7(3):43. https://doi.org/10.3390/axioms7030043
Chicago/Turabian StyleBracco, Cesare, Carlotta Giannelli, and Rafael Vázquez. 2018. "Refinement Algorithms for Adaptive Isogeometric Methods with Hierarchical Splines" Axioms 7, no. 3: 43. https://doi.org/10.3390/axioms7030043





